Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia
Abstract
1. Introduction
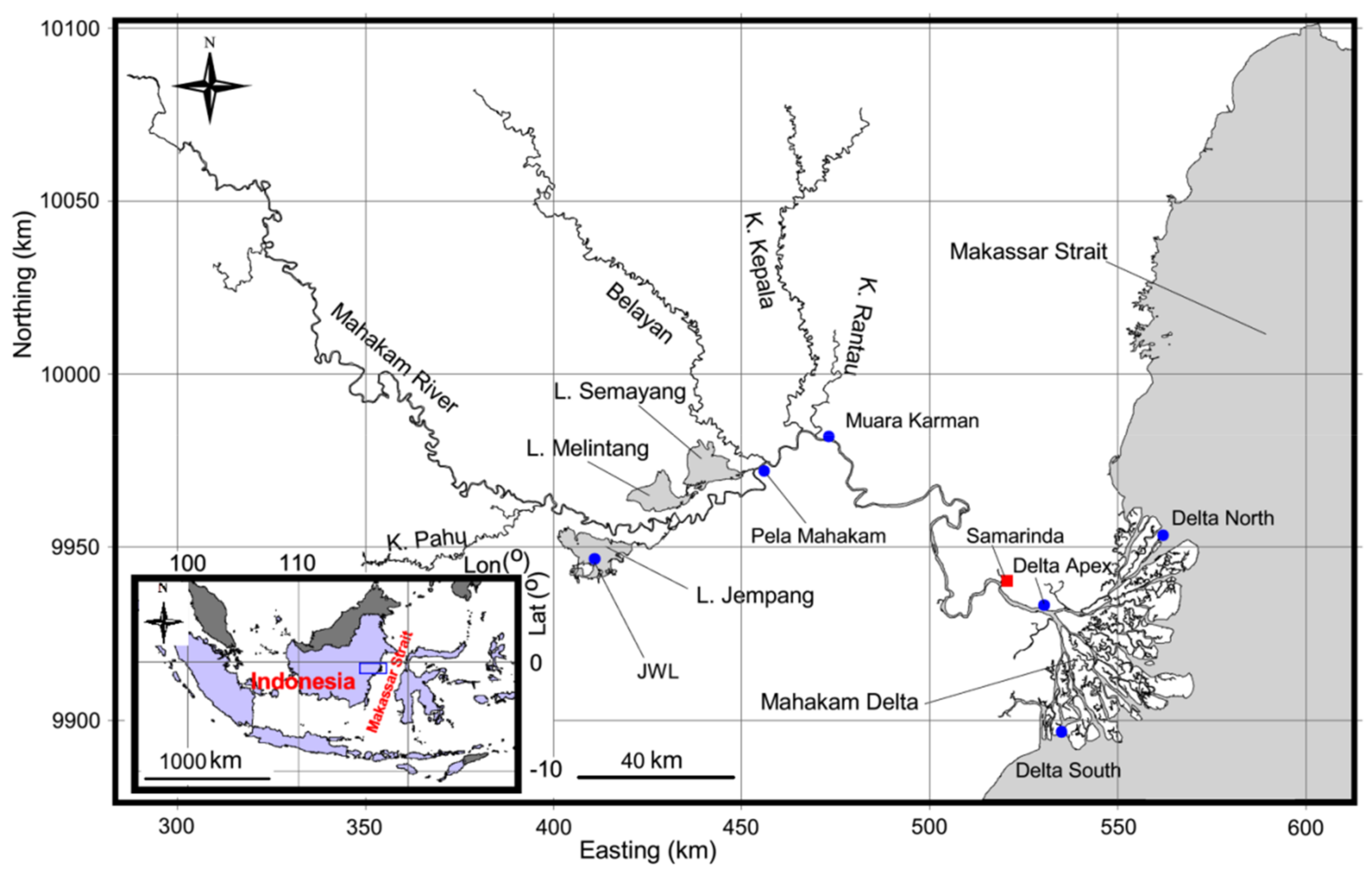
2. Study Area
3. Method
3.1. Hydrodynamics Model
3.2. Water Renewal Timescales
3.2.1. Age of Water
3.2.2. Residence Time
3.2.3. Exposure Time
3.2.4. Finite Element Implementation
4. Results and Discussion
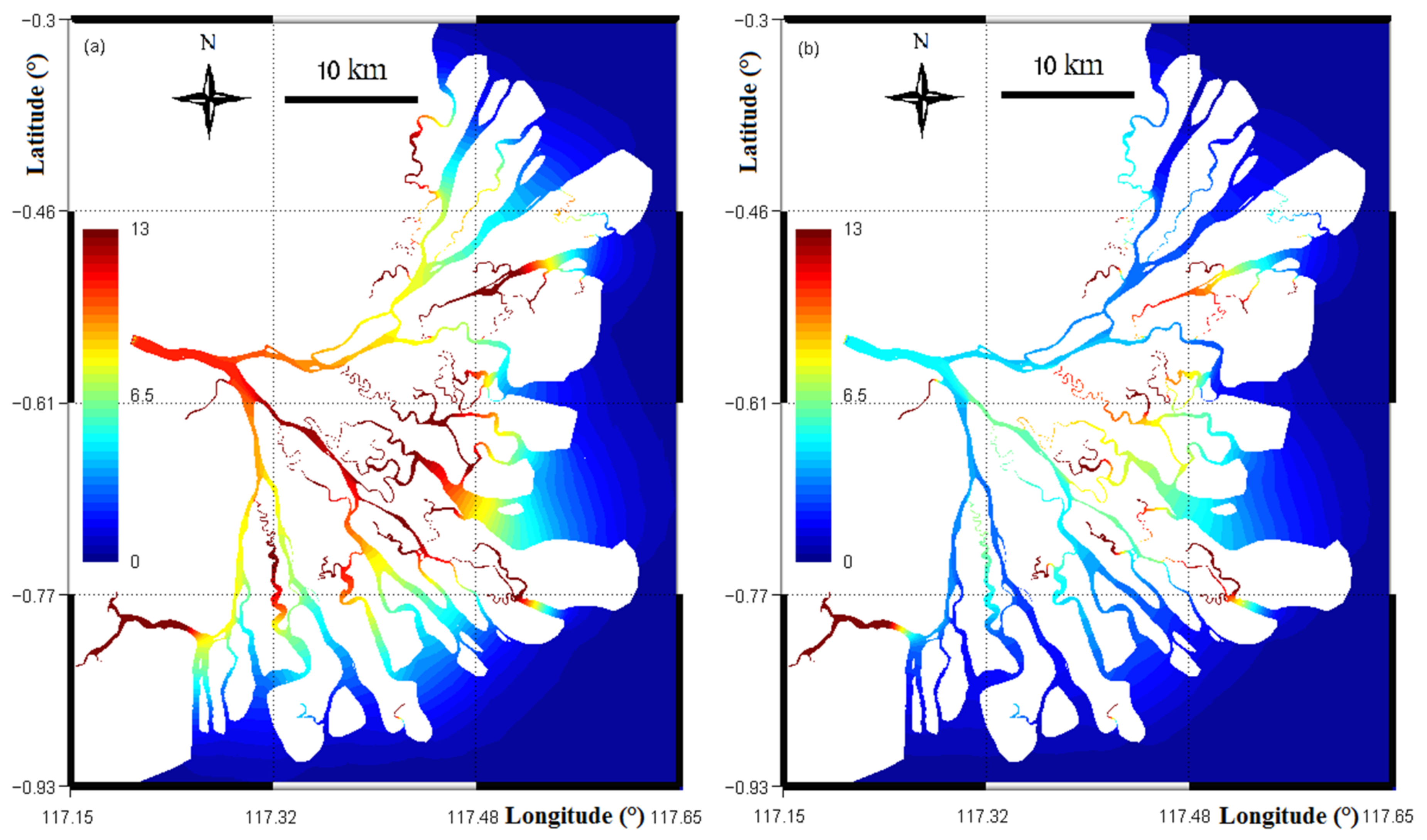
4.1. Age of Water
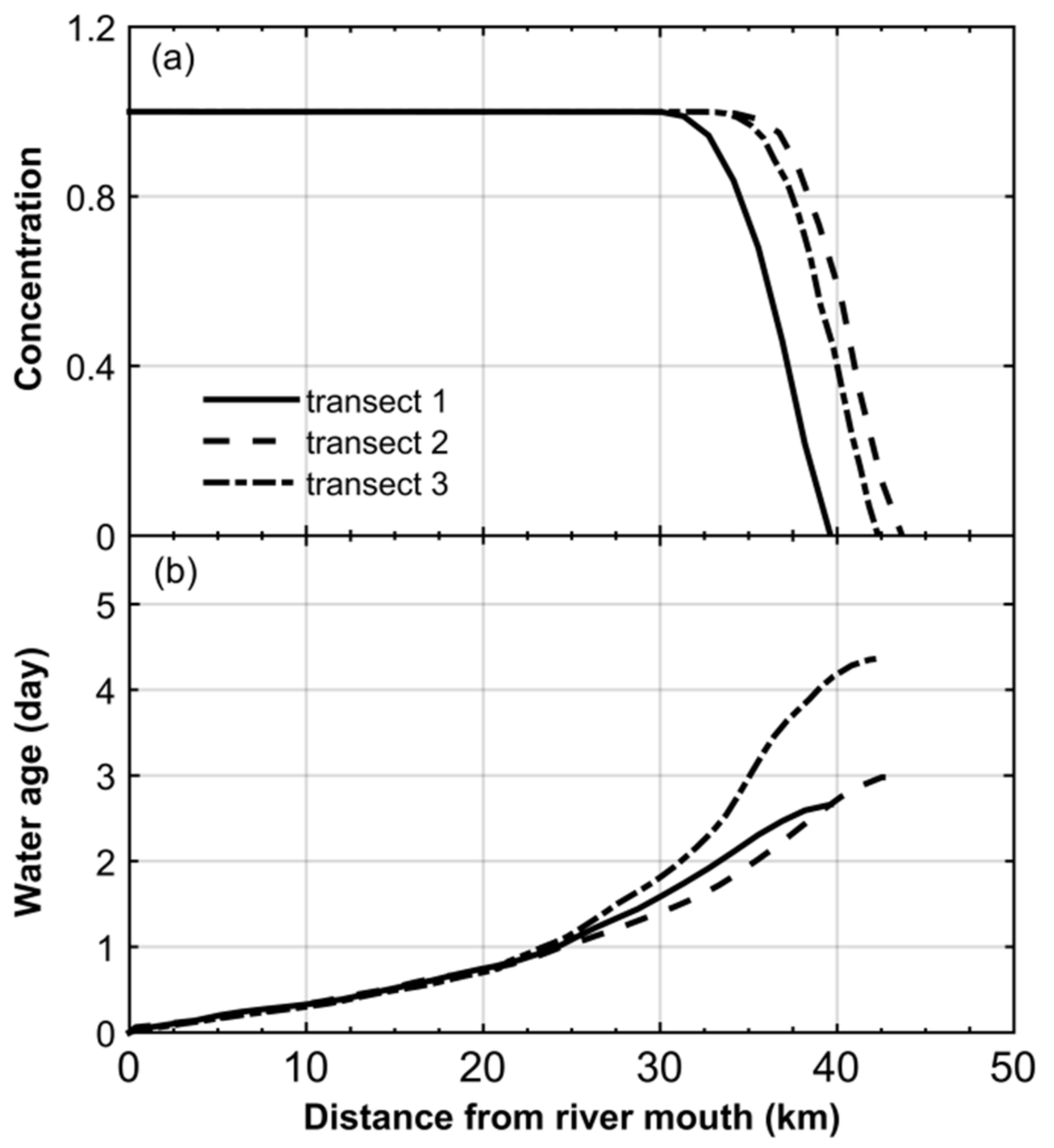
4.1.1. River Water
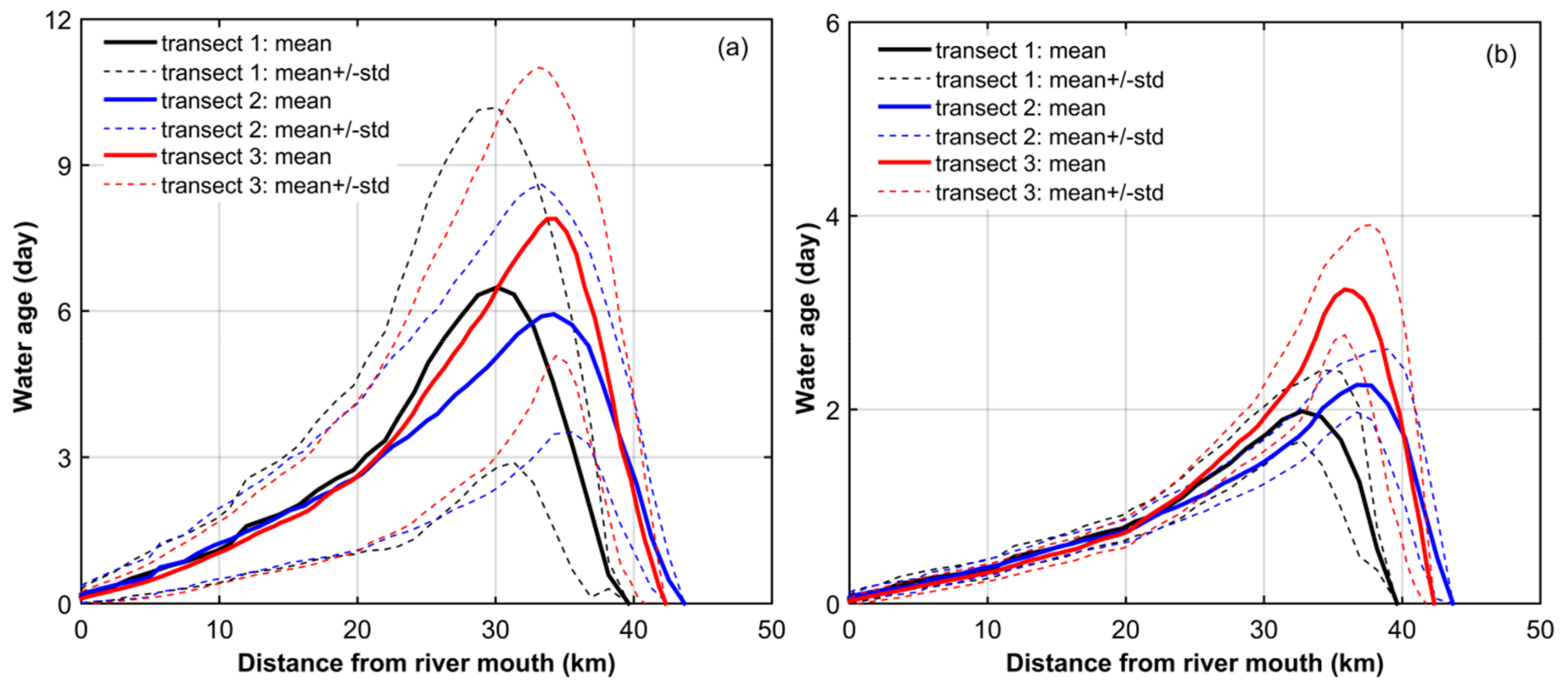
4.1.2. Total Renewing Water
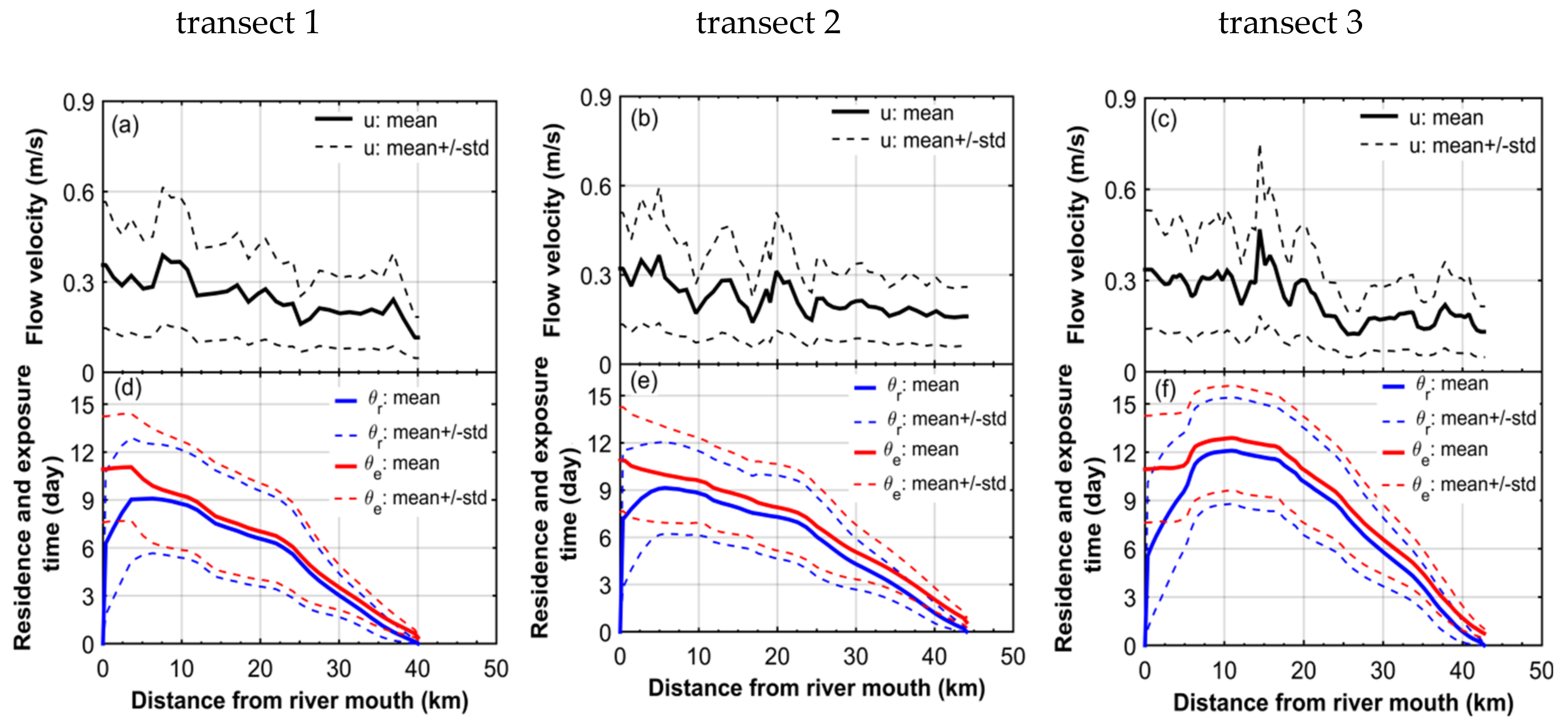
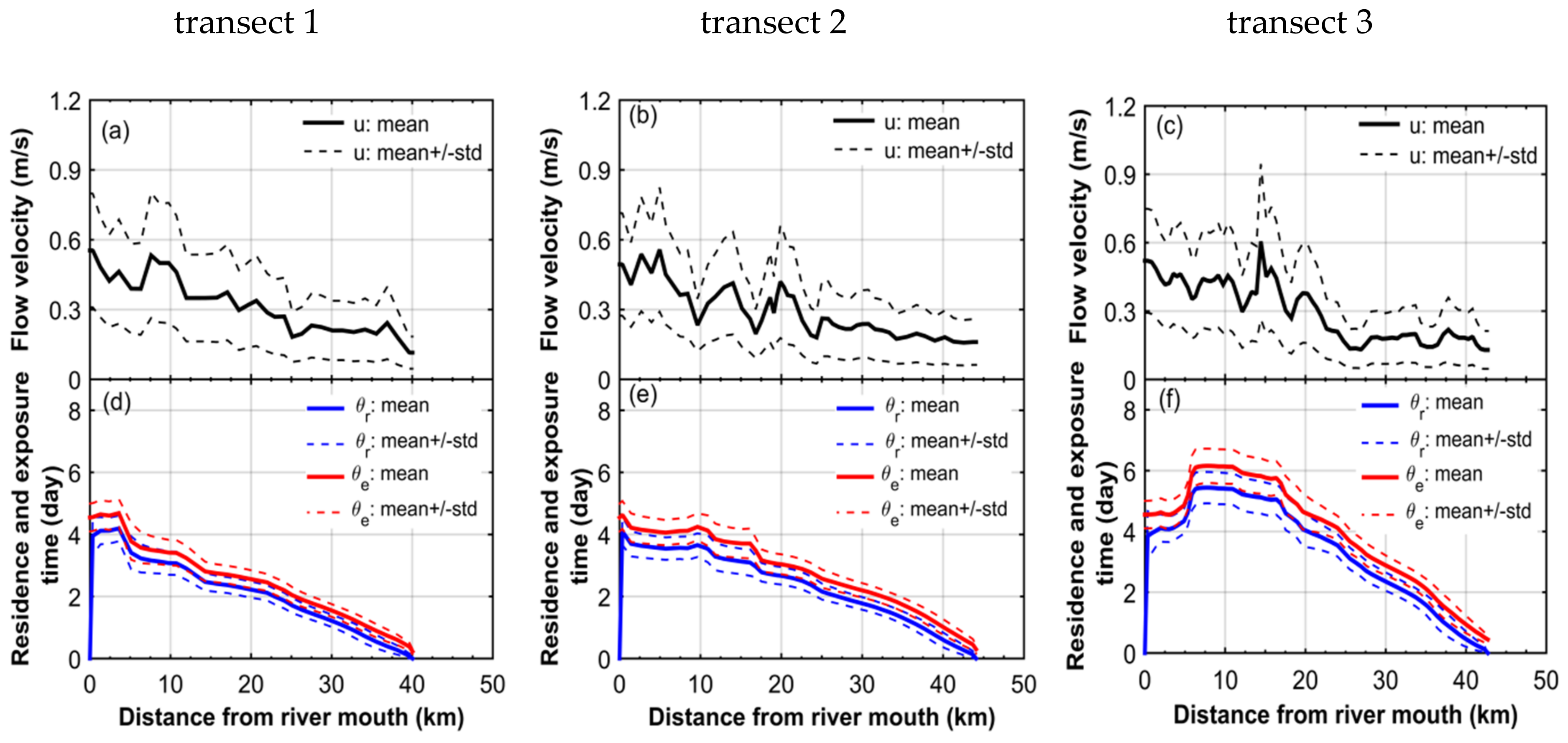
4.2. Residence Time
4.3. Exposure Time
4.4. Return Coefficient
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jay, D.A.; Greyer, W.R.; Montgomery, D.R. An ecological perpective on estuarine classification. In A Synthetic Approach to Research and Practice; Island Press: Washington, DC, USA, 2000; pp. 149–175. [Google Scholar]
- Halpern, B.S.; Walbridge, S.; Selkoe, K.A.; Kappel, C.V.; Micheli, F.; D’Agrosa, C.; Bruno, J.F.; Casey, K.S.; Ebert, C.; Fox, H.E.; et al. A Global Map of Human Impact on Marine Ecosystems. Science 2008, 319, 948–952. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Yu, X. Application of transport timescales to coastal environmental assessment: A case study. J. Environ. Manag. 2013, 130, 176–184. [Google Scholar] [CrossRef] [PubMed]
- Monsen, N.; Cloern, J.; Lucas, L.; Monismith, S. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- De Brye, B.; De Brauwere, A.; Gourgue, O.; Delhez, E.J.M.; Deleersnijder, E. Water renewal timescales in the Scheldt Estuary. J. Mar. Syst. 2012, 94, 74–86. [Google Scholar] [CrossRef]
- Viero, D.P.; Defina, A. Water age, exposure time, and local flushing time in semienclosed, tidal basins with negligible freshwater inflow. J. Mar. Syst. 2016, 156, 16–29. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- Zimmerman, J.T.F. Mixing and flushing of tidal embayments in the western Dutch wadden sea part I: Distribution of salinity and calculation of mixing time scales. Neth. J. Sea Res. 1976, 10, 149–191. [Google Scholar] [CrossRef]
- Huang, W.; Liu, X.; Chen, X.; Flannery, M.S. Estimating river flow effects on water ages by hydrodynamic modeling in Little Manatee River estuary, Florida, USA. Environ. Fluid Mech. 2010, 10, 197–211. [Google Scholar] [CrossRef]
- Gross, E.; Andrews, S.; Bergamaschi, B.; Downing, B.; Holleman, R.; Burdick, S.; Durand, J. The use of stable isotope-based water age to evaluate a hydrodynamic model. Water 2019, 11, 2207. [Google Scholar] [CrossRef]
- Takeoka, H. Fundamental concepts of exchange and transport time scales in a coastal sea. Cont. Shelf Res. 1984, 3, 311–326. [Google Scholar] [CrossRef]
- Liu, W.-C.; Chen, W.-B.; Kuo, J.-T.; Wu, C. Numerical determination of residence time and age in a partially mixed estuary using three-dimensional hydrodynamic model. Cont. Shelf Res. 2008, 28, 1068–1088. [Google Scholar] [CrossRef]
- Ren, Y.; Lin, B.; Sun, J.; Pan, S. Predicting water age distribution in the Pearl River Estuary using a three-dimensional model. J. Mar. Syst. 2014, 139, 276–287. [Google Scholar] [CrossRef]
- Kärnä, T.; Baptista, A.M. Water age in the Columbia River estuary. Estuar. Coast. Shelf Sci. 2016, 183, 249–259. [Google Scholar] [CrossRef]
- Yang, J.; Kong, J.; Tao, J. Modeling the water-flushing properties of the Yangtze estuary and adjacent waters. J. Ocean Univ. China 2019, 18, 93–107. [Google Scholar] [CrossRef]
- Shang, J.; Sun, J.; Tao, L.; Li, Y.; Nie, Z.; Liu, H.; Chen, R.; Yuan, D. Combined effect of tides and wind on water exchange in a semi-enclosed shallow sea. Water 2019, 11, 1762. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Campin, J.-M.; Delhez, E.J.M. The concept of age in marine modelling I. Theory and preliminary model results. J. Mar. Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef]
- De Serio, F.; Armenio, E.; Ben Meftah, M.; Capasso, G.; Corbelli, V.; De Padova, D.; De Pascalis, F.; Di Bernardino, A.; Leuzzi, G.; Monti, P.; et al. Detecting sensitive areas in confined shallow basins. Environ. Model. Softw. 2020, 126, 104659. [Google Scholar] [CrossRef]
- Braunschweig, F.; Martins, F.; Chambel, P.; Neves, R. A methodology to estimate renewal time scales in estuaries: The Tagus Estuary case. Ocean Dyn. 2003, 53, 137–145. [Google Scholar] [CrossRef]
- Shen, J.; Haas, L. Calculating age and residence time in the tidal York River using three-dimensional model experiments. Estuar. Coast. Shelf Sci. 2004, 61, 449–461. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Heemink, A.W.; Deleersnijder, E. Residence time in a semi-enclosed domain from the solution of an adjoint problem. Estuar. Coast. Shelf Sci. 2004, 61, 691–702. [Google Scholar] [CrossRef]
- Cloern, J.E.; Cole, B.E.; Wong, R.L.J.; Alpine, A.E. Temporal dynamics of estuarine phytoplankton: A case study of San Francisco Bay. Hydrobiologia 1985, 129, 153–176. [Google Scholar] [CrossRef]
- Delesalle, B.; Sournia, A. Residence time of water and phytoplankton biomass in coral reef lagoons. Cont. Shelf Res. 1992, 12, 939–949. [Google Scholar] [CrossRef]
- Lucas, L.; Thompson, J.; Brown, L. Why are diverse relationships observed between phytoplankton biomass and transport time? Limnol. Oceanogr. 2009, 54, 381–390. [Google Scholar] [CrossRef]
- Arega, F.; Armstrong, S.; Badr, A.W. Modeling of residence time in the East Scott Creek Estuary, South Carolina, USA. J. Hydro-Environ. Res. 2008, 2, 99–108. [Google Scholar] [CrossRef]
- De Brauwere, A.; De Brye, B.; Blaise, S.; Deleersnijder, E. Residence time, exposure time and connectivity in the Scheldt Estuary. J. Mar. Syst. 2011, 84, 85–95. [Google Scholar] [CrossRef]
- Andutta, F.P.; Ridd, P.V.; Deleersnijder, E.; Prandle, D. Contaminant exchange rates in estuaries—New formulae accounting for advection and dispersion. Prog. Oceanogr. 2014, 120, 139–153. [Google Scholar] [CrossRef]
- Huguet, J.R.; Brenon, I.; Coulombier, T. Characterisation of the water renewal in a macro-tidal Marina using several transport timescales. Water 2019, 11, 2050. [Google Scholar] [CrossRef]
- Cheng, Y.; Mu, Z.; Wang, H.; Zhao, F.; Li, Y.; Lin, L. Water residence time in a typical tributary bay of Three Corges reservoir. Water 2019, 11, 1585. [Google Scholar] [CrossRef]
- Lovecchio, S.; Marchioli, C.; Soldati, A. Time persistency of floating particle clusters in free-surface turbulence. Phys. Rev. E 2013, 88, 033003. [Google Scholar] [CrossRef]
- Gutiérrez, P.; Aumaitre, S. Clustering of floaters on the free surface of a turbulent flow: An experimental study. Eur. J. Mech. B/Fluids 2016, 60, 24–32. [Google Scholar] [CrossRef]
- Allen, G.P.; Chambers, J.L.C. Sedimentation in the Modern and Miocene Mahakam Delta; Indonesian Petroleum Association: Jakarta, Indonesia, 1998; p. 236. Available online: https://books.google.be/books?id=2j9OAQAAIAAJ (accessed on 1 January 1998).
- Chaîneau, C.-H.; Mine, J.; Suripno. The integration of biodiversity conservation with oiland gas exploration in sensitive tropical environments. Biodivers. Conserv. 2010, 19, 587–600. [Google Scholar] [CrossRef]
- Budiyanto, F. Study of metal contaminant level in the Mahakam Delta: Sediment and dissolved metal perpectives. J. Coast. Dev. 2013, 16, 147–157. [Google Scholar]
- De Brye, B. Multiscale Finite-Element Modelling of River-Sea Continua. Ph.D. Thesis, Université Catholique de Louvain, Louvain-la-Neuve, Belgium, 2011. [Google Scholar]
- Pham Van, C.; De Brye, B.; Spinewine, B.; Deleersnijder, E.; Hoitink, A.J.F.; Sassi, M.G.; Hidayat, H.; Soares-Frazão, S. Simulations of flow in the tropical river-lake-delta system of the Mahakam land-sea continuum, Indonesia. Environ. Fluid Mech. 2016, 16, 603–633. [Google Scholar] [CrossRef]
- Comblen, R.; Lambrechts, J.; Remacle, J.-F.; Legat, V. Practical evaluation of five partly discontinuous finite element pairs for the non-conservative shallow water equations. Int. J. Numer. Methods Fluids 2010, 63, 701–724. [Google Scholar] [CrossRef]
- De Brye, B.; De Brauwere, A.; Gourgue, O.; Kärnä, T.; Lambrechts, J.; Comblen, R.; Deleersnijder, E. A finite-element, multi-scale model of the Scheldt tributaries, river, estuary and ROFI. Coast. Eng. 2010, 57, 850–863. [Google Scholar] [CrossRef]
- Kärnä, T.; De Brye, B.; Gourgue, O.; Lambrechts, J.; Comblen, R.; Legat, V.; Deleersnijder, E. A fully implicit wetting-drying method for DG-FEM shallow water models, with an application to the Scheldt Estuary. Comput. Methods Appl. Mech. Eng. 2011, 200, 509–524. [Google Scholar] [CrossRef]
- Gourgue, O.; Deleersnijder, E.; White, L. Toward a generic method for studying water renewal, with application to the epilimnion of Lake Tanganyika. Estuar. Coast. Shelf Sci. 2007, 74, 628–640. [Google Scholar] [CrossRef]
- Okubo, A. Oceanic diffusion diagrams. Deep Sea Res. 1971, 18, 789–802. [Google Scholar] [CrossRef]
- Pham Van, C.; Gourgue, O.; Sassi, M.; Deleersnijder, E.; Hoitink, A.J.F.; Soares-Frazao, S. Modelling fine-grained sediment transport in the Mahakam land-sea continuum, Indonesia. J. Hydro-Environ. Res. 2016, 13, 103–120. [Google Scholar] [CrossRef]
- Blaise, S.; De Brye, B.; De Brauwere, A.; Deleersijder, E.; Delhez, E.J.M.; Comblen, R. Capturing the residence time boundary layer—Application to the Scheldt Estuary. Ocean Dyn. 2010, 60, 535–554. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Deleersnijder, E. The boundary layer of the residence time field. Ocean Dyn. 2006, 56, 139–150. [Google Scholar] [CrossRef]
- De Brye, B.; Schellen, S.; Sassi, M.; Vermeulen, B.; Karna, T.; Deleersijder, E.; Hoitink, T. Preliminary results of a finite-element, multi-scale model of the Mahakam Delta (Indonesia). Ocean Dyn. 2011, 61, 1107–1120. [Google Scholar] [CrossRef]
- Andutta, F.P.; Helfer, F.; De Miranda, L.B.; Deleersnijder, E.; Thomas, C.; Lemckert, C. An assessment of transport timescales and return coefficient in adjacent tropical estuaries. Cont. Shelf Res. 2016, 124, 49–62. [Google Scholar] [CrossRef][Green Version]
- Budhiman, S.; Salama, S.M.; Vekerdy, Z.; Verhoef, W. Deriving optical properties of Mahakam Delta coastal waters, Indonesia using in situ measurements and ocean color model inversion. ISPRS J. Photogramm. Remote Sens. 2012, 68, 157–169. [Google Scholar] [CrossRef]
- Suroso, B.; Hutabarat, J.; Afiati, N. The Potential of Tiger Prawn Fry from Delta Mahakam, East Kalimantan Indonesia. Int. J. Sci. Eng. 2013, 6, 43–46. [Google Scholar] [CrossRef]
- Furnas, M.J.; Mitchell, A.W.; Gilmartin, M.; Revelante, N. Phytoplantonk biomass and primary production in semi-enclosed reef lagoons of the central Great Barrier Reef, Australia. Coral Reefs 1990, 9, 1–10. [Google Scholar] [CrossRef]






| Original Water | Renewing Water | |||||
|---|---|---|---|---|---|---|
| River Water | Total Renewing Water | |||||
| t = 0 | Co = 1 | αo = 0 | Cu = 0 | αu = 0 | Cr = 0 | αr = 0 |
| x ∈ Γu | Co = 0 | αo = 0 | Cu = 1 | αu = 0 | Cr = 1 | αr = 0 |
| x ∈ Γd | Co = 0 | αo = 0 | Cu = 0 | αu = 0 | Cr = 1 | αr = 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham Van, C.; De Brye, B.; De Brauwere, A.; Hoitink, A.J.F.; Soares-Frazao, S.; Deleersnijder, E. Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia. Water 2020, 12, 1017. https://doi.org/10.3390/w12041017
Pham Van C, De Brye B, De Brauwere A, Hoitink AJF, Soares-Frazao S, Deleersnijder E. Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia. Water. 2020; 12(4):1017. https://doi.org/10.3390/w12041017
Chicago/Turabian StylePham Van, Chien, Benjamin De Brye, Anouk De Brauwere, A.J.F. (Ton) Hoitink, Sandra Soares-Frazao, and Eric Deleersnijder. 2020. "Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia" Water 12, no. 4: 1017. https://doi.org/10.3390/w12041017
APA StylePham Van, C., De Brye, B., De Brauwere, A., Hoitink, A. J. F., Soares-Frazao, S., & Deleersnijder, E. (2020). Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia. Water, 12(4), 1017. https://doi.org/10.3390/w12041017







