Analyzing the Effectiveness of a Multi-Purpose Dam Using a System Dynamics Model
Abstract
1. Introduction
1.1. System Dynamics Approach for Water Management under Changing Environment
1.2. Literature Review of Systems Approaches for Water Resources Management
1.3. Research Background and Purpose
2. Materials and Methods
2.1. Study Area
2.2. System Dynamics Model Construction
2.2.1. System Dynamics
2.2.2. Causal Loop
2.2.3. Sub-Modules of the Socio-System
2.2.4. Sub-Modules of the Hydro-System
2.3. Scenario Development
2.3.1. Baseline (Scenario 1)
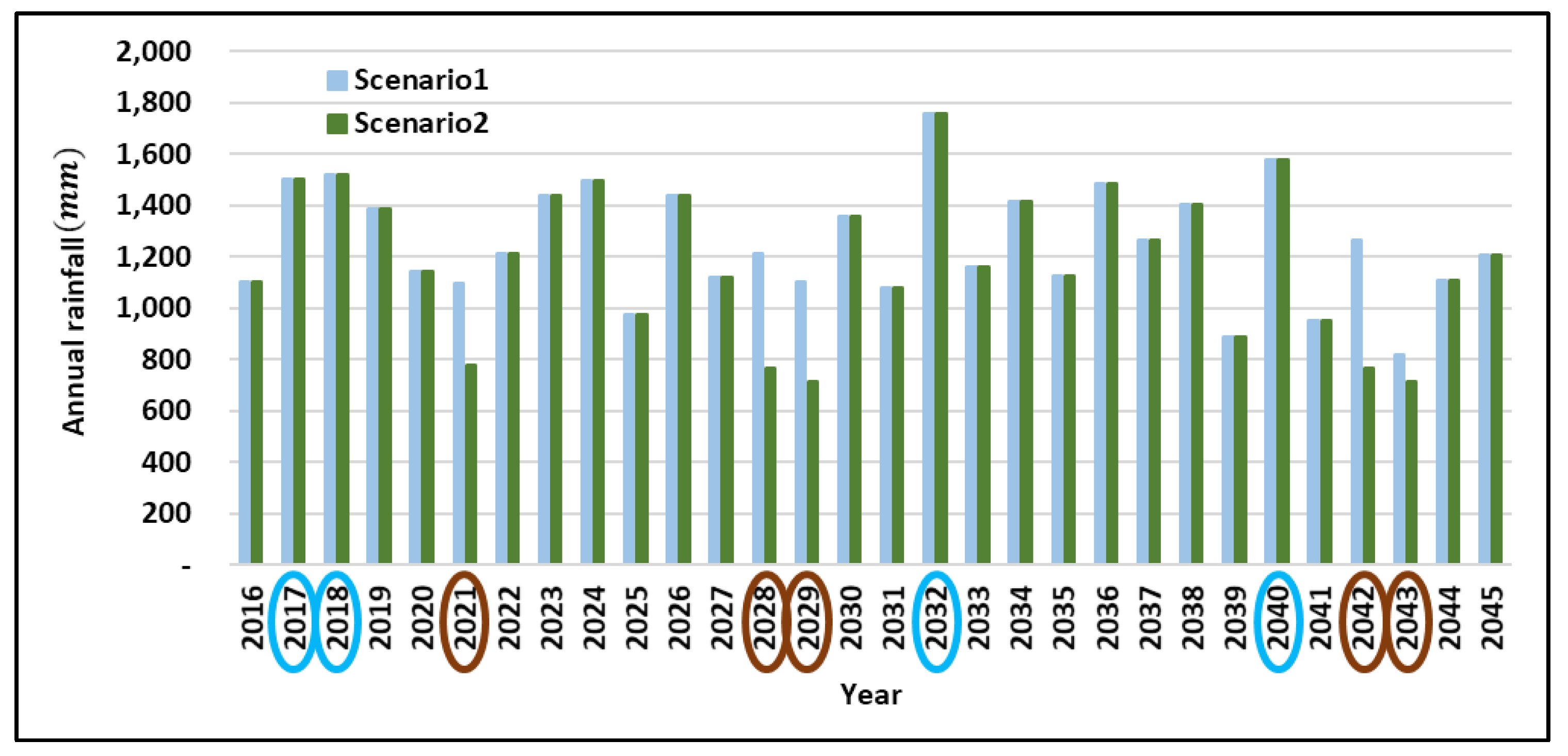
2.3.2. Extreme Climate (Scenario 2)
2.3.3. Rapid Urbanization (Scenario 3)
3. Results and Discussion
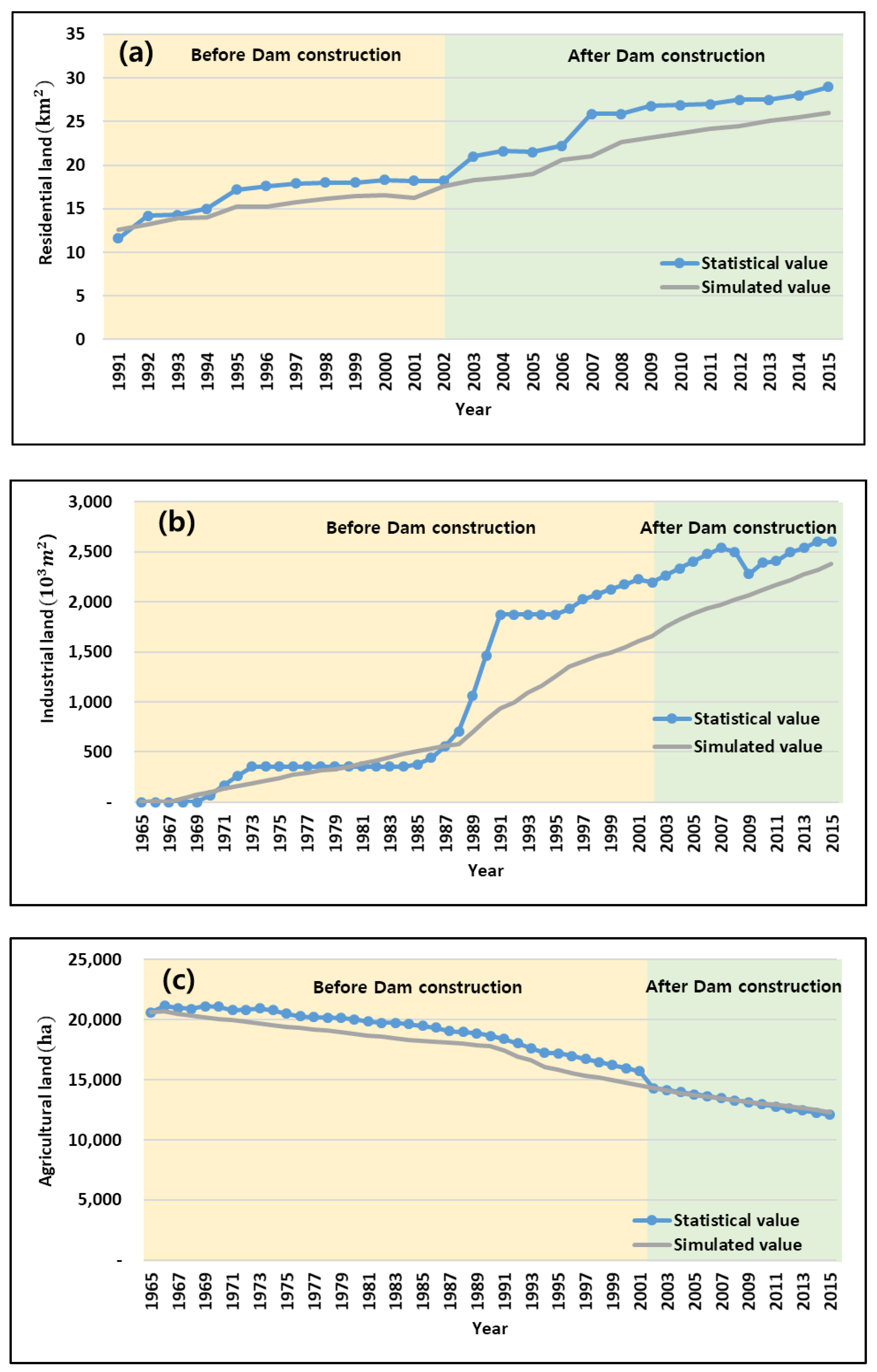
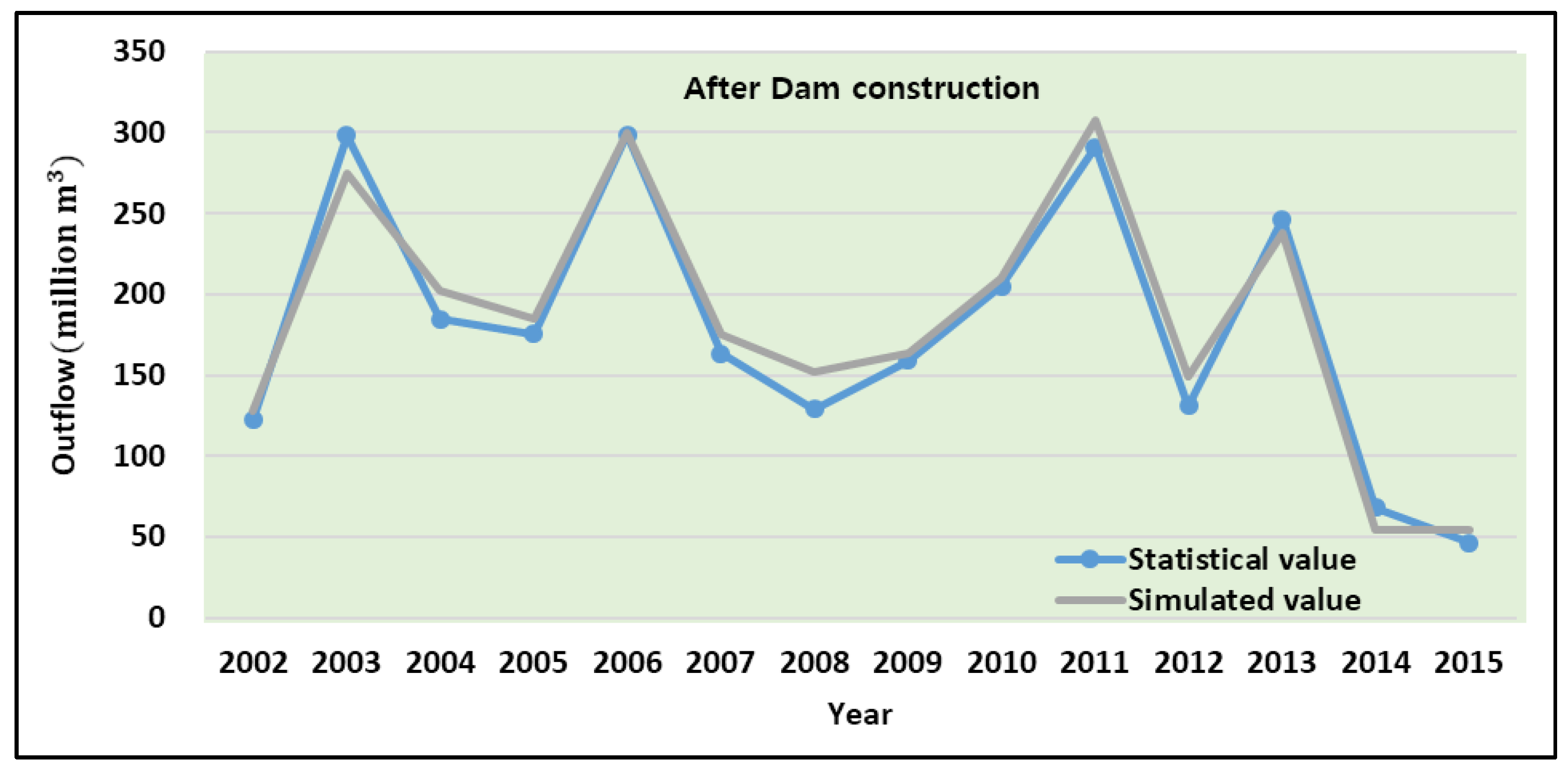
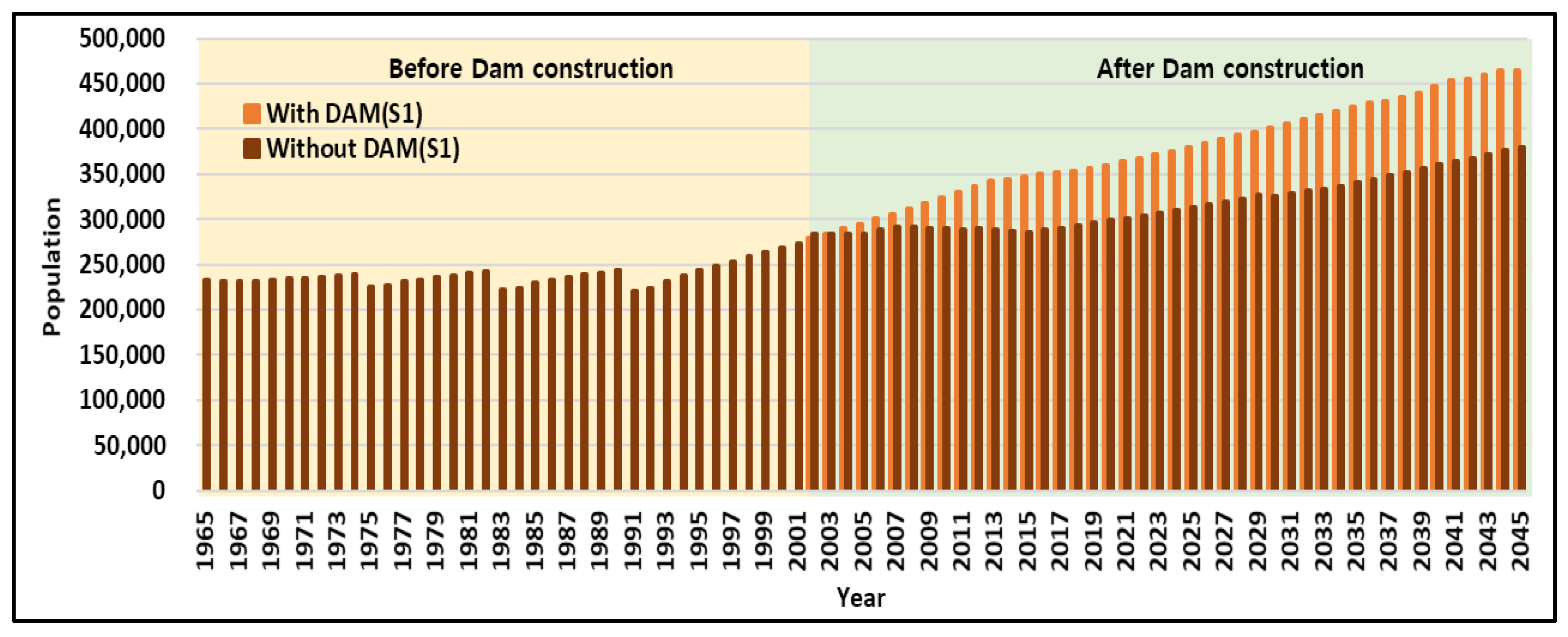
3.1. Model Calibration
3.1.1. Population
3.1.2. Land Use
3.1.3. Flooded Area
3.1.4. Dam Outflow
3.2. Scenario Analysis
3.2.1. Baseline (Scenario 1)
Population
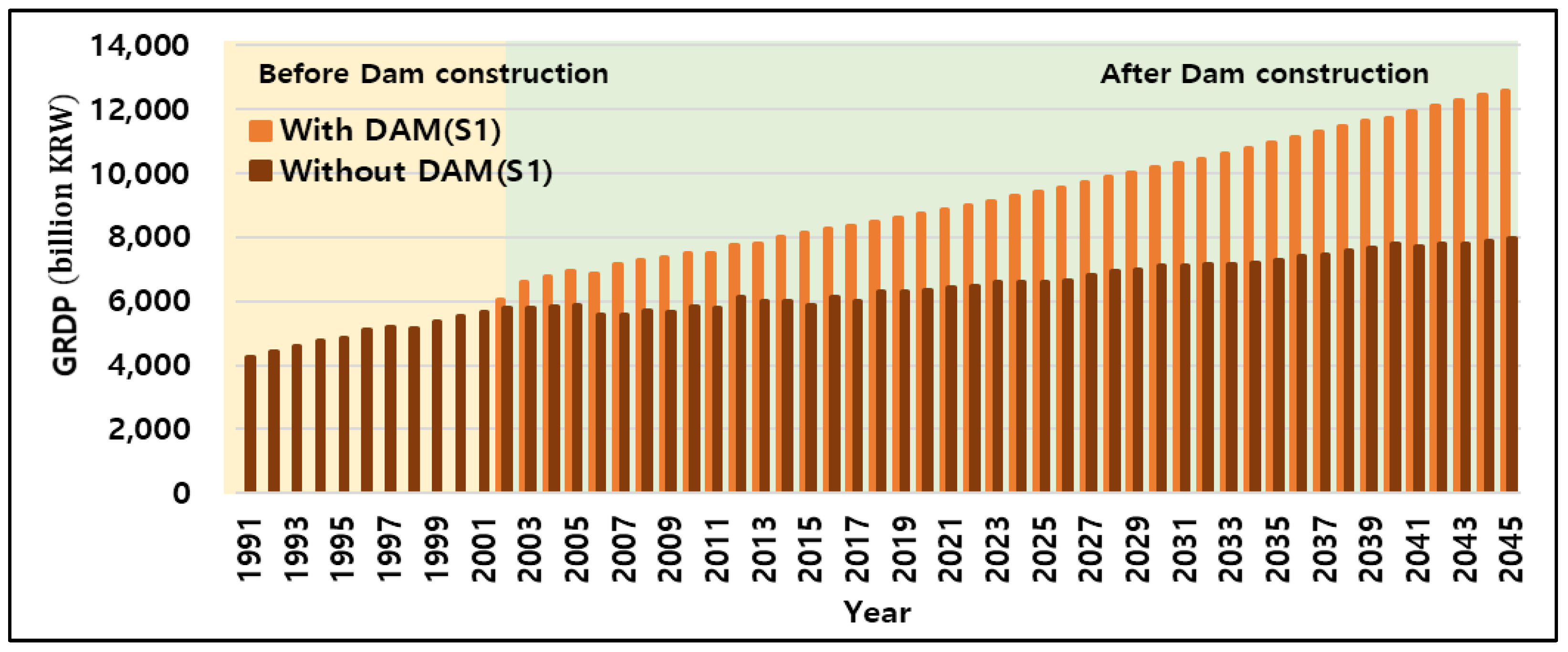
Gross Regional Domestic Product (GRDP)
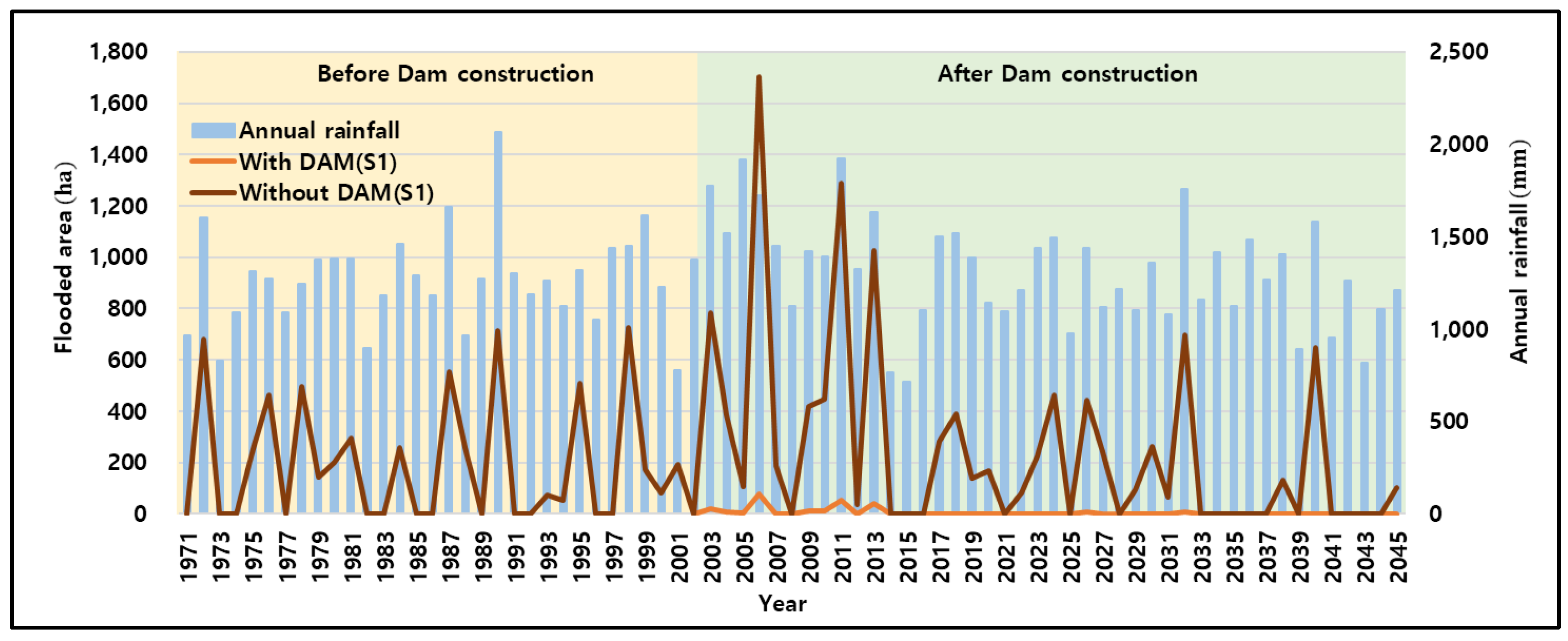
Flooded Area
Water Supply Rate
3.2.2. Extreme Climate (Scenario 2)
3.2.3. Rapid Urbanization (Scenario 3)
4. Conclusions
- 1.
- For Scenario 1, two case simulations were performed, one assuming dam construction (With DAM) and the other assuming no dam construction (Without DAM), and the results were compared to analyze the effects of the Hoengseong dam on the downstream area. When changes for the next 30 years were simulated, the population and GRDP were predicted to increase by approximately 80,000 and four trillion KRW, respectively, as of 2045 due to the 2002 completion of the Hoengseong dam. Furthermore, the flooded area will decrease by approximately 4480 ha, and the water supply rate will increase by approximately 1.4 times.
- 2.
- Scenario 2 simulated flood and drought years to analyze the effects of future climate changes in the target area. When Scenarios 1 and 2 were compared and analyzed from 2016 to 2045, it was concluded that future extreme climate events in the target area would not cause significant changes to social and hydrological elements. It appeared that no massive damage caused by flooding or drought would occur in the area, and the population and GRDP were expected to increase consistently.
- 3.
- Scenario 3 assumed increases in births, water consumption per capita, and production per unit of industrial land in the target area. The total water use, including domestic and industrial water, was expected to increase due to urbanization and economic revitalization. The 30-year average water supply rate dropped significantly; thus, water security plans would be required in conjunction with efficient dam operations.
Author Contributions
Funding
Conflicts of Interest
References
- Sterman, J.D. Business Dynamics, Systems Thinking and Modeling for a Complex World; McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H.; Zhang, X.W. Sustainability analysis for Yellow River water resources using the system dynamics approach. Water Resour. Manag. 2002, 16, 239–261. [Google Scholar] [CrossRef]
- Zomorodian, M.; Lai, S.H.; Homayounfar, M.; Ibrahim, S.; Fatemi, S.E.; El-Shafie, A. The state-of-the-art system dynamics application in integrated water resources modeling. J. Environ. Manag. 2018, 227, 294–304. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Yang, H.; Song, J.; Abbaspour, K.C.; Xu, Z. System dynamics simulation model for assessing socio-economic impacts of different levels of environmental flow allocation in the Weihe River Basin, China. Eur. J. Oper. Res. 2012, 221, 248–262. [Google Scholar] [CrossRef]
- Park, S.W.; Lee, T.G.; Kim, B.J.; Kim, T.Y. Development of a System Dynamics Model for the Efficient Operation and Maintenance of Sewerage Systems. J. Korea Water Resour. Assoc. 2012, 45, 101–111. [Google Scholar] [CrossRef]
- Ahmad, S.; Simonovic, S.P. System dynamics modeling of reservoir operations for flood management. J. Comput. Civil Eng. 2000, 14, 190–198. [Google Scholar] [CrossRef]
- Simonovic, S.P. Managing Water Resources: Methods and Tools for a Systems Approach; UNESCO: Paris, France; Earthscan James & James: London, UK, 2009. [Google Scholar]
- Kim, Y.J.; Jeong, E.S. Socio-hydrology or Hydro-sociology: Study on the co-evolution between human and the water cycle. Water Future 2015, 48, 34–43. [Google Scholar]
- Li, L.; Simonovic, S.P. System dynamics model for predicting floods from snowmelt in North American prairie watersheds. Hydrol. Process. 2002, 16, 2645–2666. [Google Scholar] [CrossRef]
- Simonovic, S.P. World water dynamics: Global modeling of water resources. J. Environ. Manag. 2002, 66, 249–267. [Google Scholar] [CrossRef]
- Stave, K.A. A system dynamics model to facilitate public understanding of water management options in Las Vegas, Nevada. J. Environ. Manag. 2003, 67, 303–313. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Rajasekaram, V. Integrated analyses of Canada’s water resources: A system dynamics approach. Can. Water Resour. J./Revue Can. des Ressour. Hydr. 2004, 29, 223–250. [Google Scholar] [CrossRef]
- Neto, A.D.C.L.; Legey, L.F.; González-Araya, M.C.; Jablonski, S. A system dynamics model for the environmental management of the Sepetiba Bay watershed, Brazil. Environ. Manag. 2006, 38, 879–888. [Google Scholar] [CrossRef] [PubMed]
- Madani, K.; Mariño, M.A. System dynamics analysis for managing Iran’s Zayandeh-Rud river basin. Water Resour. Manag. 2009, 23, 2163–2187. [Google Scholar] [CrossRef]
- Khan, S.; Yufeng, L.; Ahmad, A. Analysing complex behaviour of hydrological systems through a system dynamics approach. Environ. Model. Softw. 2009, 24, 1363–1372. [Google Scholar] [CrossRef]
- Davies, E.G.; Simonovic, S.P. Global water resources modeling with an integrated model of the social–economic–environmental system. Adv. Water Resour. 2011, 34, 684–700. [Google Scholar] [CrossRef]
- Gaupp, F.; Hall, J.; Dadson, S. The role of storage capacity in coping with intra-and inter-annual water variability in large river basins. Environ. Res. Lett. 2015, 10, 125001. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Wanders, N.; AghaKouchak, A.; Kuil, L.; Rangecroft, S.; Veldkamp, T.I.; Van Loon, A.F. Water shortages worsened by reservoir effects. Nat. Sustain. 2018, 1, 617–622. [Google Scholar] [CrossRef]
- Wang, K.; Davies, E.G.; Liu, J. Integrated water resources management and modeling: A case study of Bow river basin, Canada. J. Clean. Prod. 2019, 240, 118242. [Google Scholar] [CrossRef]
- Park, S.W.; Kim, K.L.; Kim, B.J.; Lim, K.Y. Development of a System Dynamics Model to Support the Decision Making Processes in the Operation and Management of Water Supply Systems. J. Korea Water Resour. Assoc. 2010, 43, 609–623. [Google Scholar] [CrossRef][Green Version]
- Ministry of Environment. 2016 Water Supply Statistics; Ministry of Environment: Sejong-si, Korea, 2018. [Google Scholar]
- Korean Statistical Information Service (KOSIS). Available online: http://kosis.kr/ (accessed on 8 April 2020).
- Water Management Information System (WAMIS). Available online: http://wamis.go.kr/ (accessed on 8 April 2020).
- Forrester, J. Industrial Dynamics; The MIT Press: Cambridge, MA, USA; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Hjorth, P.; Bagheri, A. Navigating towards sustainable development: A system dynamics approach. Futures 2006, 38, 74–92. [Google Scholar] [CrossRef]
- Jung, S.H.; Joo, Y.J. A Study on the Analysis of Policy Effects for System Dynamics Methodology: Focusing on the sex trade special law. Korean Assoc. Public Adm. 2005, 39, 219–236. [Google Scholar]
- Jeong, H.S. Modeling Socio-Hydrological Systems for Wastewater Reused Watersheds. Ph.D. Thesis, The Graduate School Seoul National University, Seoul, Korea, 2014. [Google Scholar]
- Ventana Systems. Vensim User’s Guide Version 6; VENTANA Systems Inc.: Harvard, MA, USA, 2013. [Google Scholar]
- Kim, K.C.; Jung, K.Y.; Kim, S.W. SYSTEM DYNAMICS Using Vensim; Seoul Economic Management Publisher: Seoul, Korea, 2014. [Google Scholar]
- IPCC. Summary for Policy makers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Dubash, N.K. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (p. 151); IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Riahi, K.; Rao, S.; Krey, V.; Cho, C.; Chirkov, V.; Fischer, G.; Rafaj, P. RCP 8.5—A scenario of comparatively high greenhouse gas emissions. Clim. Chang. 2011, 109, 33. [Google Scholar] [CrossRef]
- Korea Meteorological Administration (KMA). Available online: https://www.weather.go.kr/ (accessed on 8 April 2020).









| Height | 48.5 |
| Length | 205.0 |
| Basin area | 209.0 |
| Designed flood level | 180.0 |
| Restricted water level | 178.2 |
| Low water level | 160.0 |
| Total storage capacity | 86.9 |
| Effective storage capacity | 73.4 |
| Element | Value in 2015 | Available Data Period |
|---|---|---|
| Population | 370,000 | 1965–2015 |
| Residential land | 29.0 | 1991–2015 |
| Industrial land | 2.6 | 1965–2015 |
| Agricultural land | 121.0 | 1965–2015 |
| GRDP (billion KRW) | 8,600 | 1991–2015 |
| Annual rainfall | 717 | 1965–2015 |
| Annual water use | 59 | 1965–2015 |
| Element | Parameter | Description | Unit |
|---|---|---|---|
| Population | population density in the industrial area | person/km2 | |
| population density in the residential area | person/km2 | ||
| population growth per GRDP increment | person/KRW | ||
| Residential area | residential land change per population change | km2/person | |
| residential land change per GRDP increment | km2/KRW | ||
| residential land change due to the agricultural land change | km2/km2 | ||
| residential land change due to the industrial land change | km2/km2 | ||
| Industrial area | industrial land change per population change | km2/person | |
| industrial land change per GRDP increment | km2/KRW | ||
| industrial land change due to the residential land change | km2/km2 | ||
| industrial land change due to the agricultural land change | km2/km2 | ||
| Agricultural area | agricultural land change per GRDP increment | km2/KRW | |
| agricultural land change due to the industrial land change | km2/km2 | ||
| agricultural land change due to the residential land change | km2/km2 | ||
| Flooded area | regression parameter for total runoff | - | |
| regression parameter for maximum runoff | - | ||
| GRDP | production per capita | KRW/person | |
| production per industrial land area | KRW/km2 | ||
| production per agricultural land area | KRW/km2 | ||
| Dam operation | Runoff coefficient | - | |
| Evaporation | m3/month |
| Element | RMSE | Unit |
|---|---|---|
| Population | 2095 | person |
| Residential land | 2.24 | km2 |
| Industrial land | 0.18 | km2 |
| Agricultural land | 1.30 | km2 |
| Flooded area | 0.18 | km2 |
| Dam outflow | 4.4 | million m3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kang, D. Analyzing the Effectiveness of a Multi-Purpose Dam Using a System Dynamics Model. Water 2020, 12, 1062. https://doi.org/10.3390/w12041062
Lee S, Kang D. Analyzing the Effectiveness of a Multi-Purpose Dam Using a System Dynamics Model. Water. 2020; 12(4):1062. https://doi.org/10.3390/w12041062
Chicago/Turabian StyleLee, Sleemin, and Doosun Kang. 2020. "Analyzing the Effectiveness of a Multi-Purpose Dam Using a System Dynamics Model" Water 12, no. 4: 1062. https://doi.org/10.3390/w12041062
APA StyleLee, S., & Kang, D. (2020). Analyzing the Effectiveness of a Multi-Purpose Dam Using a System Dynamics Model. Water, 12(4), 1062. https://doi.org/10.3390/w12041062





