Simulating the Hydraulic Heave Phenomenon with Multiphase Fluid Flows Using CFD-DEM
Abstract
:1. Introduction
2. Methodology
3. Observations of the Hydraulic Heave Phenomenon
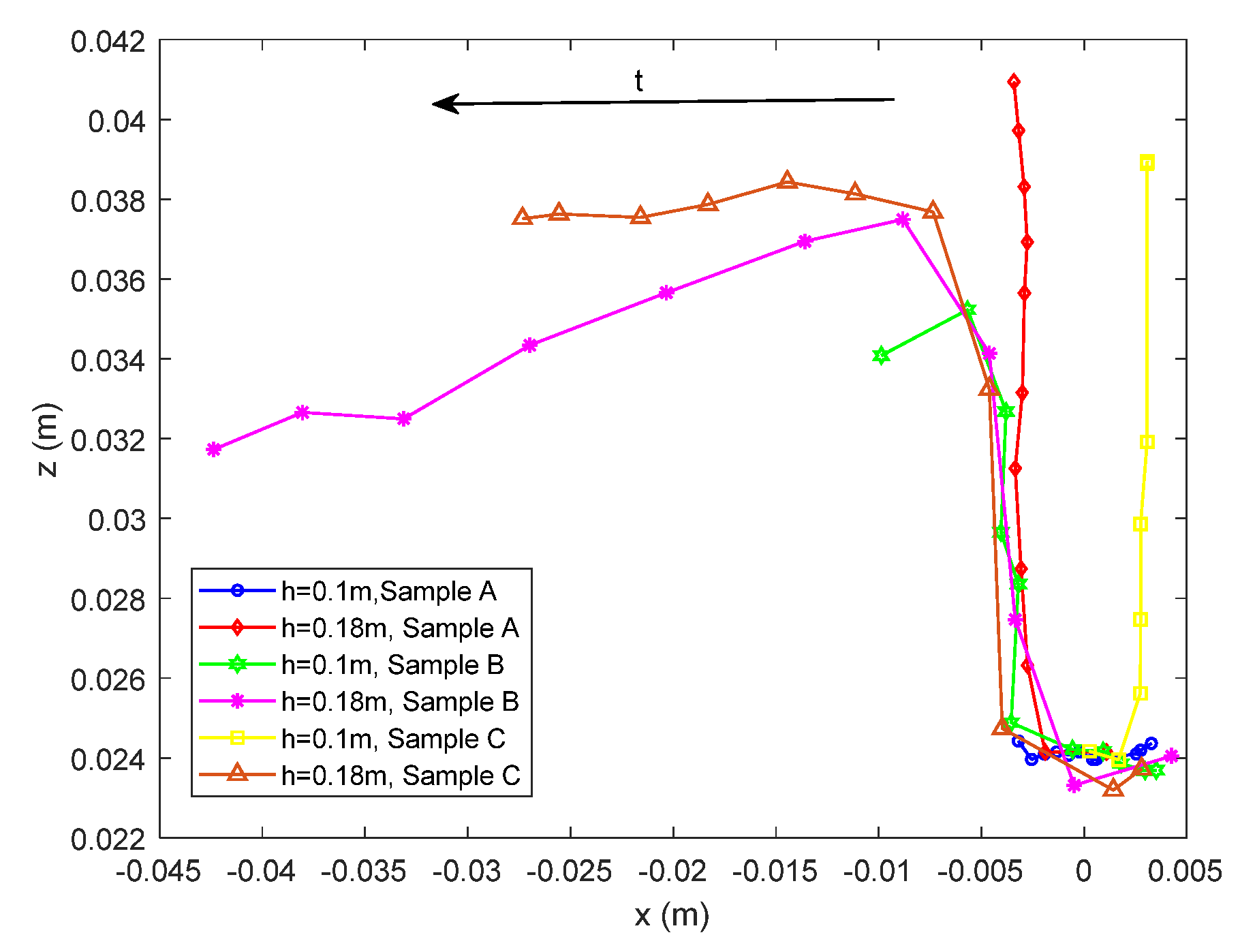
3.1. Impact of Stratified Soils
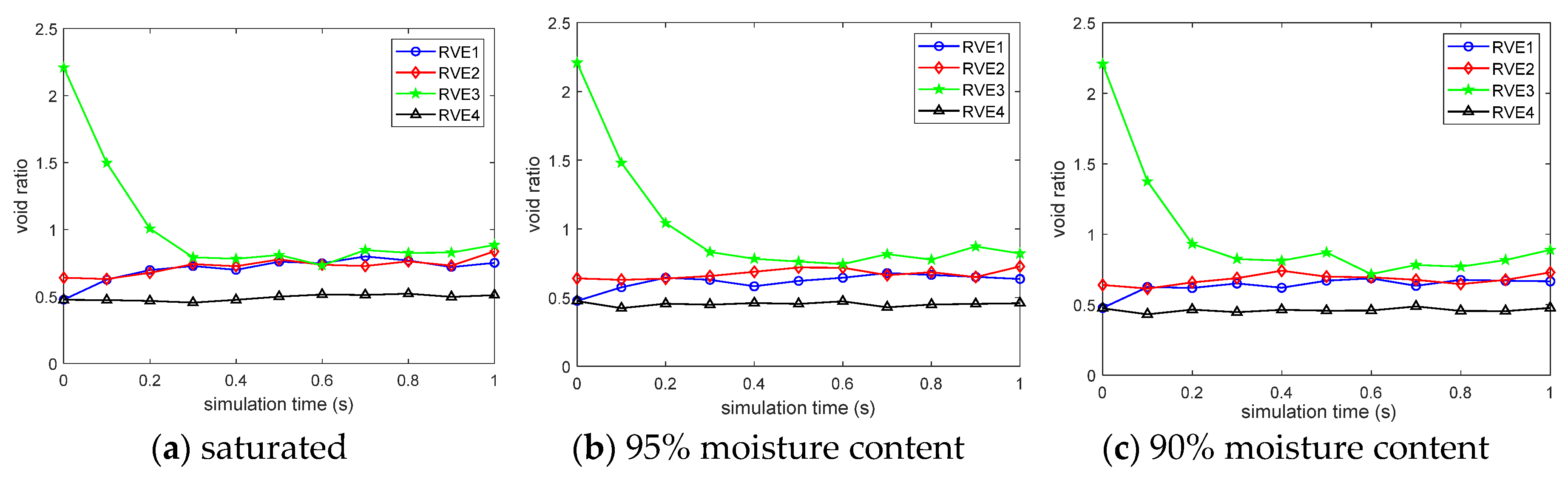
3.2. Impact of Unsaturated Condition
4. Discussions on the Development of Heave Failure
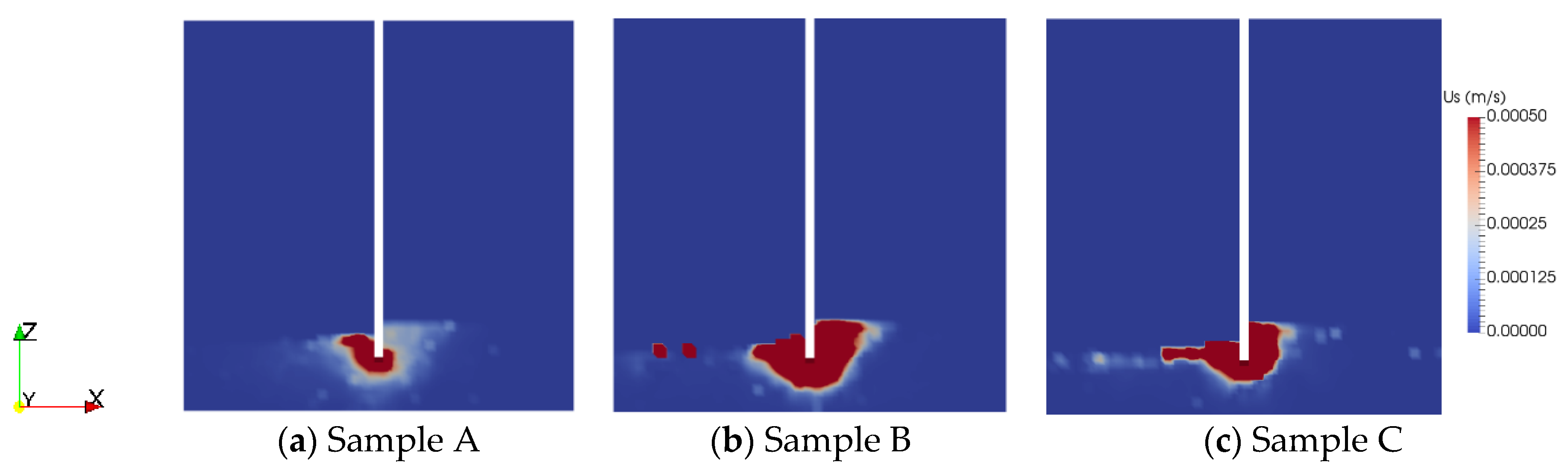
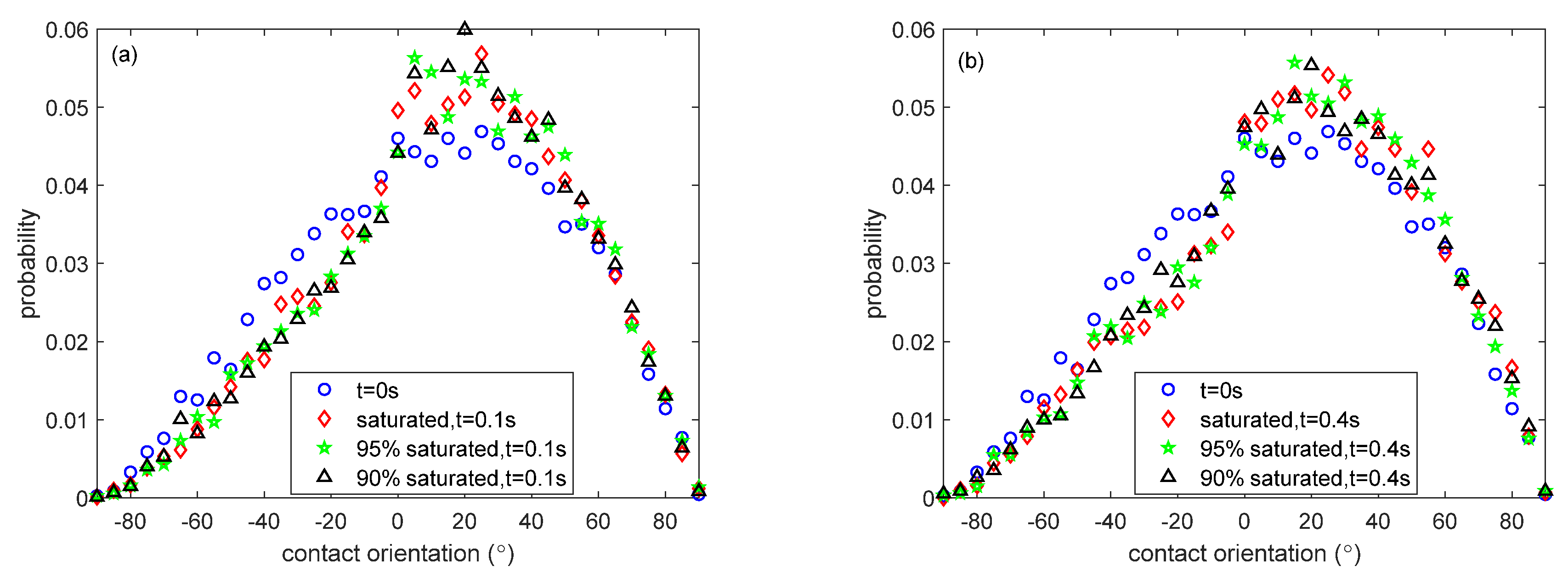
4.1. Spatial Distribution of Internal Structure
4.2. Spatial Distribution of Drag Force
5. Conclusions
Funding
Conflicts of Interest
References
- McNamee, J. Seepage into a Sheeted Excavation. Géotechnique 1949, 1, 229–241. [Google Scholar] [CrossRef]
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: Hoboken, NJ, USA, 1943. [Google Scholar]
- Fleshman, M.S.; Rice, J.D. Laboratory modeling of the mechanisms of piping erosion initiation. J. Geotech. Geoenviron. Eng. 2014, 140, 04014017. [Google Scholar] [CrossRef]
- Xie, Q.; Liu, J.; Han, B.; Li, H.; Li, Y.; Li, X. Critical hydraulic gradient of internal erosion at the soil-structure interface. Processes 2018, 6, 92. [Google Scholar] [CrossRef] [Green Version]
- Chang, D.; Zhang, L. Critical hydraulic gradients of internal erosion under complex stress states. J. Geotech. Geoenviron. Eng. 2013, 139, 1454–1467. [Google Scholar] [CrossRef]
- Miura, K.; Supachawarote, C.; Ikeda, K. Estimation of 3D seepage force inside cofferdam regarding boiling type of failure. In Proceedings of the Geotech-Year 2000 Developments in Geotechnical Engineering, Bangkok, Thailand, 27–30 November 2000; pp. 371–380. [Google Scholar]
- Tanaka, T. Boiling occurred within a braced cofferdam due to two dimensionally concentrated seepage flow. In Proceedings of the 3rd International Symposium, Geotechnical Aspects of Underground Construction in Soft Ground, Toulouse, France, 23–25 October 2002; pp. 33–38. [Google Scholar]
- Tanaka, T.; Tomoya, K.; Shigeru, N.; Daisuke, H. Characteristics of seepage failure of soil under various flow conditions. In Proceedings of the Nineteenth International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009; pp. 21–26. [Google Scholar]
- Tanaka, T.; Verruijt, A. Seepage failure of sand behind sheet piles—The mechanism and practical approach to analyze. Soils Found. 1999, 39, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Moffat, R.; Fannin, R.J.; Garner, S.J. Spatial and temporal progression of internal erosion in cohesionless soil. Can. Geotech. J. 2011, 48, 399–412. [Google Scholar] [CrossRef]
- Luo, Y.; Nie, M.; Xiao, M. Flume-scale experiments on suffusion at bottom of cutoff wall in sandy gravel alluvium. Can. Geotech. J. 2017, 54, 1716–1727. [Google Scholar] [CrossRef] [Green Version]
- Wan, C.F.; Fell, R. Investigation of rate of erosion of soils in embankment dams. J. Geotech. Geoenviron. Eng. 2004, 130, 373–380. [Google Scholar] [CrossRef]
- Kawano, K.; O’Sullivan, C.; Shire, T. Using DEM to assess the influence of stress and fabric inhomogeneity and anisotropy on susceptibility to suffusion. In Proceedings of the 8th International Conference on Scour and Erosion, Oxford, UK, 12–15 September 2016; pp. 85–94. [Google Scholar]
- Shire, T.; O’Sullivan, C.; Hanley, K.J.; Fannin, R.J. Fabric and effective stress distribution in internally unstable soils. J. Geotech. Geoenviron. Eng. 2014, 140, 04014072. [Google Scholar] [CrossRef] [Green Version]
- Maeda, K.; Sakai, H. Seepage failure and erosion of ground with air bubble dynamics. Soil Behav. Geo-Micromech. 2010. [Google Scholar] [CrossRef]
- Swain, S.; Mohanty, S. A 3-dimensional Eulerian—Eulerian CFD simulation of a hydrocyclone. Appl. Math. Model. 2013, 37, 2921–2932. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.V.; Fenton, G.A. Seepage beneath water retaining structures founded on spatially random soil. Géotechnique 1993, 43, 577–587. [Google Scholar] [CrossRef] [Green Version]
- Koltuk, S.; Song, J.; Iyisan, R.; Azzam, R. Seepage failure by heave in sheeted excavation pits constructed in stratified cohesionless soils. Front. Struct. Civ. Eng. 2019, 13, 1415–1431. [Google Scholar] [CrossRef]
- Benmebarek, N.; Benmebarek, S.; Kastner, R. Numerical studies of seepage failure of sand within a cofferdam. Comput. Geotech. 2005, 32, 264–273. [Google Scholar] [CrossRef]
- Zou, Y.-H.; Chen, Q.; Chen, X.-Q.; Cui, P. Discrete numerical modeling of particle transport in granular filters. Comput. Geotech. 2013, 47, 48–56. [Google Scholar] [CrossRef]
- Huang, Q.-F.; Zhan, M.-L.; Sheng, J.-C.; Luo, Y.-L.; Su, B.-Y. Investigation of fluid flow-induced particle migration in granular filters using a DEM-CFD method. J. Hydrodyn. 2014, 26, 406–415. [Google Scholar] [CrossRef]
- Kawano, K.; Shire, T.; O’Sullivan, C. Coupled DEM-CFD analysis of the initiation of internal instability in a gap-graded granular embankment filter. EPJ Web Conf. 2017, 140, 10005. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Yang, Y.; Yu, X.B. Influence of particle shape on the erodibility of non-cohesive soil: Insights from coupled CFD–DEM simulations. Particuology 2018, 39, 12–24. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, C.; Zhang, L. Simulating progression of internal erosion in gap-graded sandy gravels using coupled CFD-DEM. Int. J. Géoméch. 2020, 20, 04019135. [Google Scholar] [CrossRef]
- Tao, H.; Tao, J. Quantitative analysis of piping erosion micro-mechanisms with coupled CFD and DEM method. Acta Geotech. 2017, 12, 573–592. [Google Scholar] [CrossRef]
- Bannari, R.; Kerdouss, F.; Selma, B.; Bannari, A.; Proulx, P. Three-dimensional mathematical modeling of dispersed two-phase flow using class method of population balance in bubble columns. Comput. Chem. Eng. 2008, 32, 3224–3237. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, University of London, London, UK, 2002. [Google Scholar]
- Kodaka, T.; Asaoka, A. Formation of air bubbles in sandy soil during seepage process. J. JSCE 1994, 487, 129–138. (In Japanese) [Google Scholar]
- Sakai, H.; Maeda, K. Seepage Failure and Erosion Mechanism of Granular Material with Evolution of Air Bubbles Using SPH. In Proceedings of the 6th International Conference on Micromechanics of Granular Media, Golden, CO, USA, 13–17 July 2009. [Google Scholar]
- LIGGGHTS. LIGGGHTS (R)-Public Documentation, Version 3.X. Available online: http://www.cfdem.com (accessed on 18 February 2015).
- OpenFOAM. OpenFOAM—The Open Source CFD Toolbox. The OpenFOAM Foundation, 2015. Available online: http://www.openfoam.org (accessed on 22 May 2015).
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, J.-P. CFD–DEM simulations of seepage-induced erosion. Water 2020, 12, 678. [Google Scholar] [CrossRef] [Green Version]
- Gupta, P.; Alam, J.; Muzzammil, M. Influence of thickness and position of the individual layer on the permeability of the stratified soil. Perspect. Sci. 2016, 8, 757–759. [Google Scholar] [CrossRef] [Green Version]
- El Shamy, U.; Zeghal, M. Coupled continuum-discrete model for saturated granular soils. J. Eng. Mech. 2005, 131, 413–426. [Google Scholar] [CrossRef]
- Tanaka, T.; Kageyama, T.; Nagai, S. Seepage failure test of sand within cofferdam-test apparatus and seepage flow pattern. In Proceedings of the 40th Geotechnical Engineering Symposium on New Problems and New Technology, New Delhi, India, 7–11 April 1995; pp. 323–330. [Google Scholar]
- Brewer, R. Fabric and mineral analysis of soils. Soil Sci. 1965, 100, 73. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
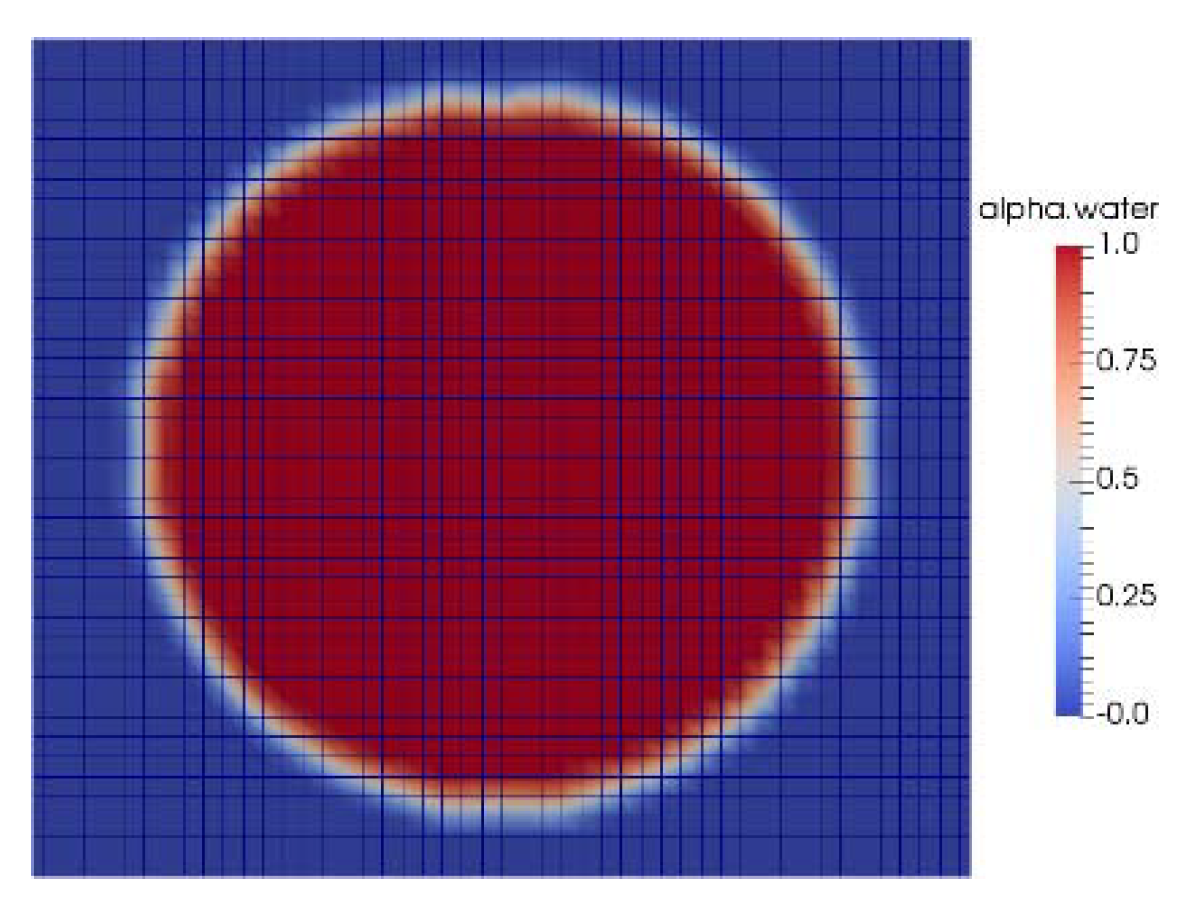
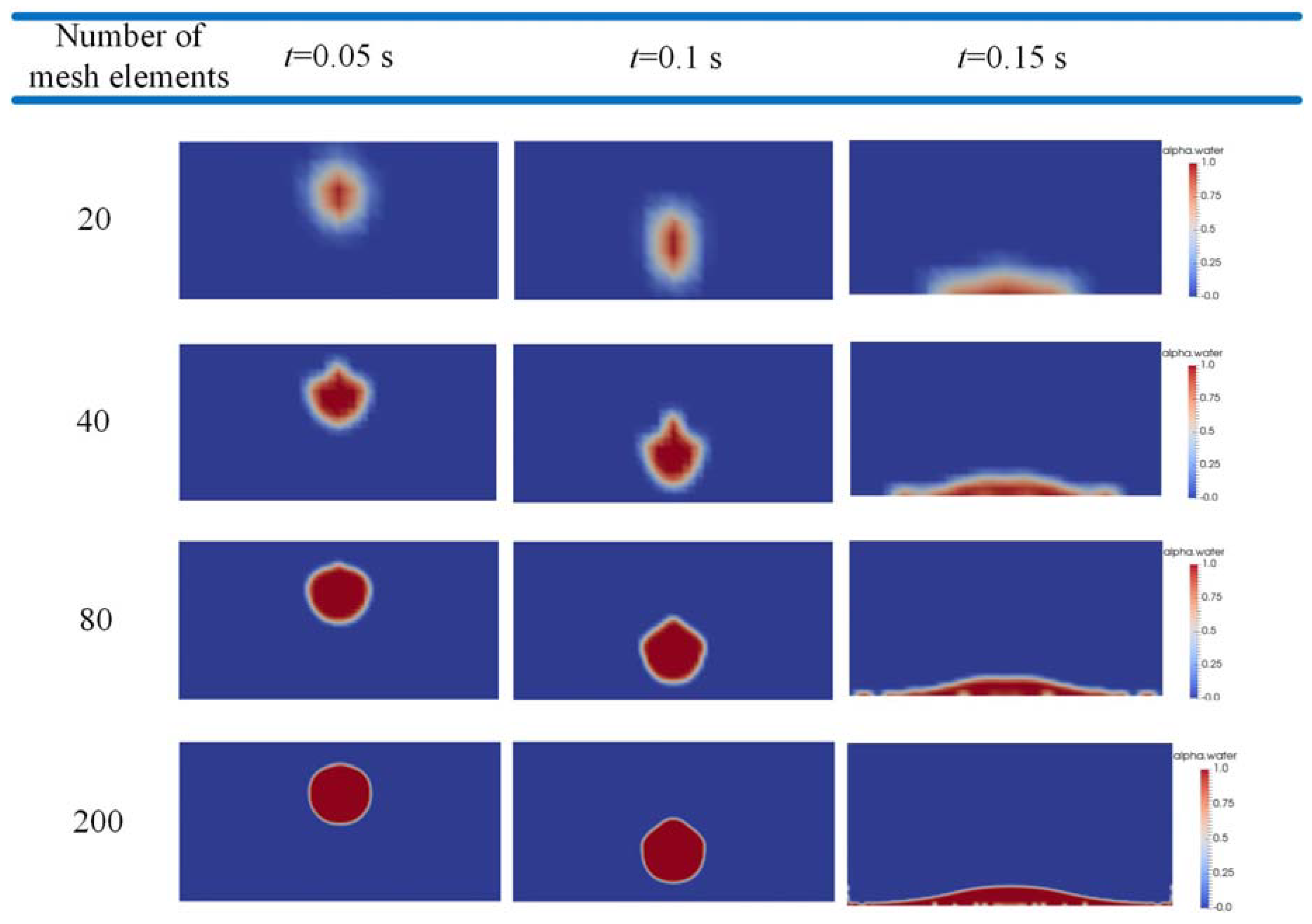

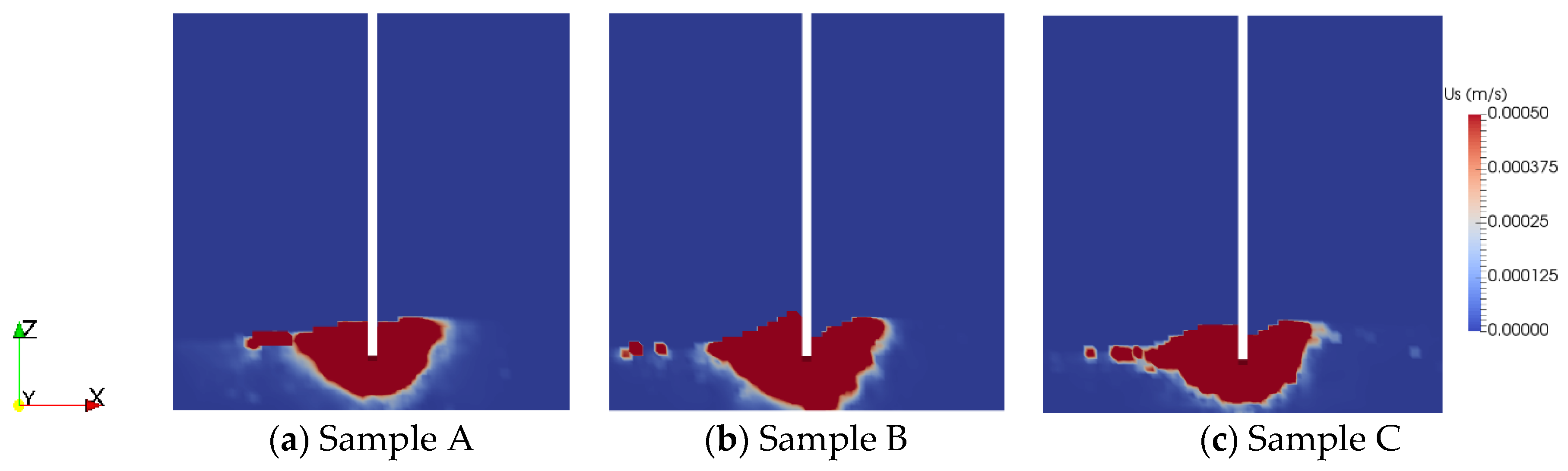
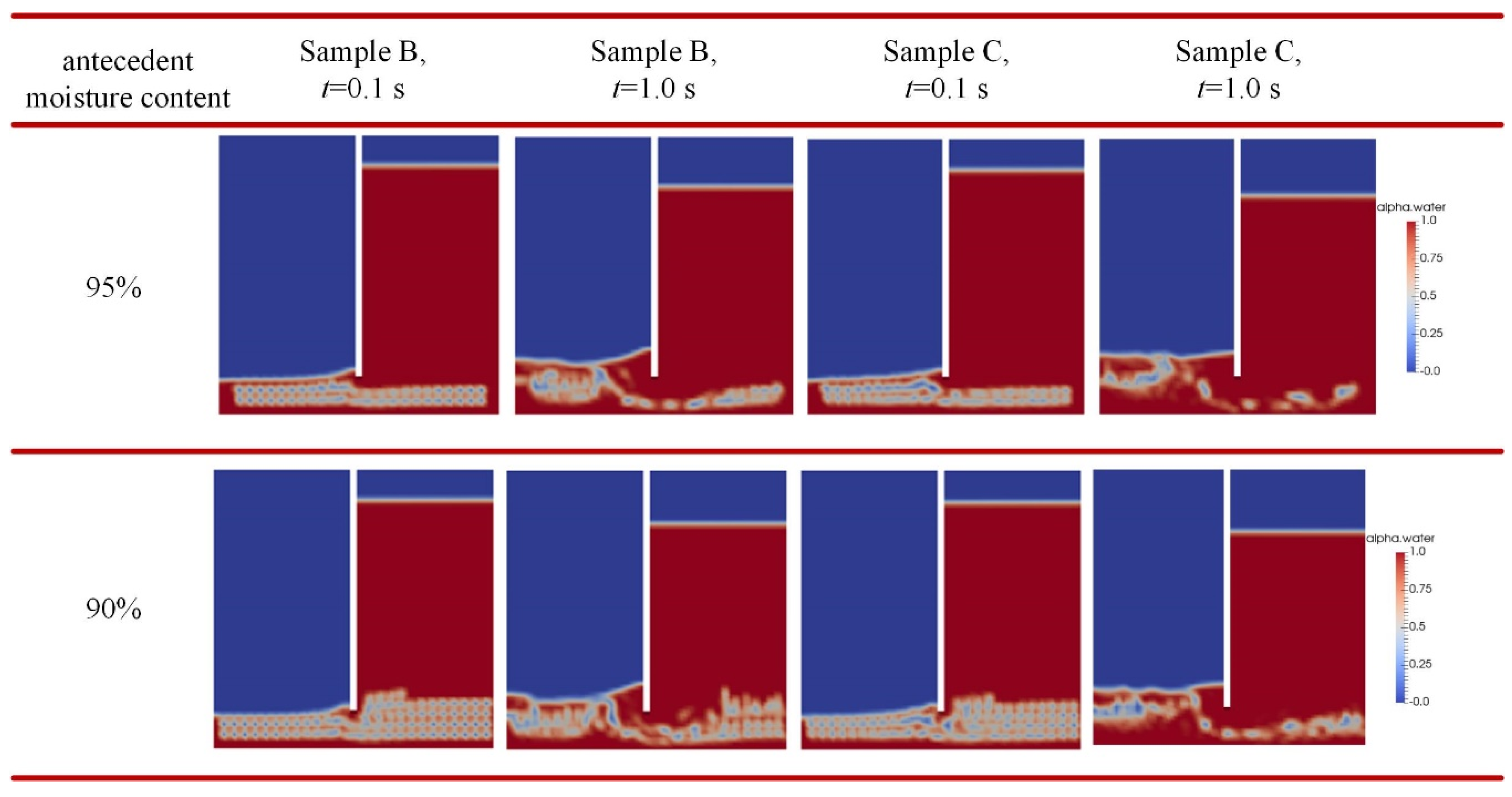
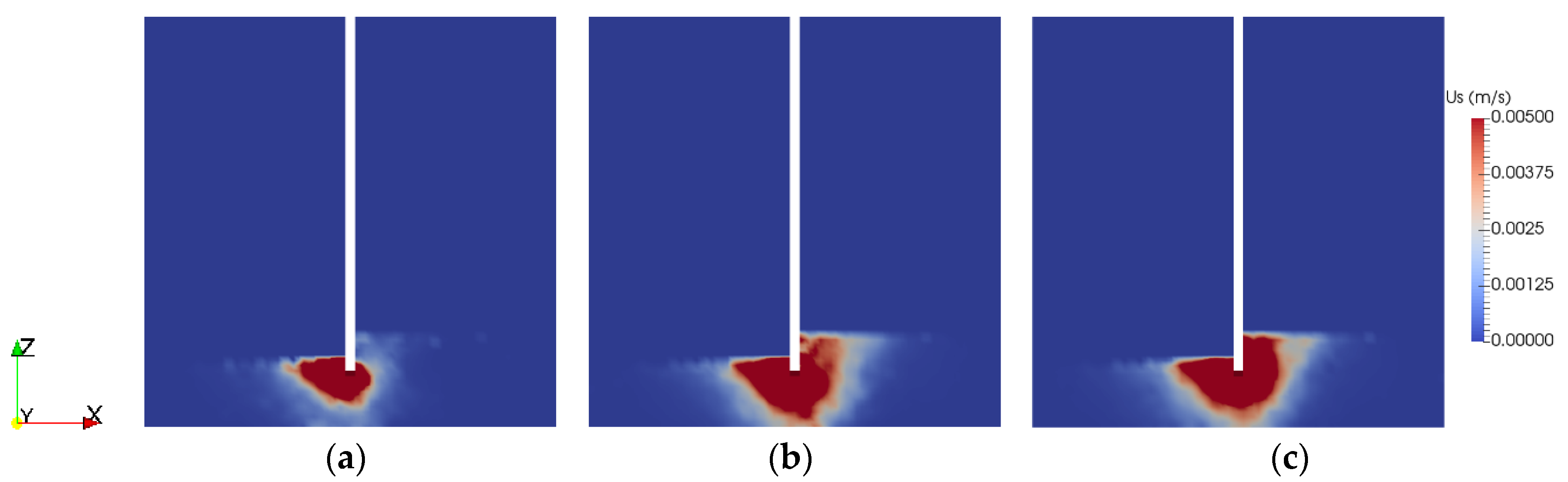
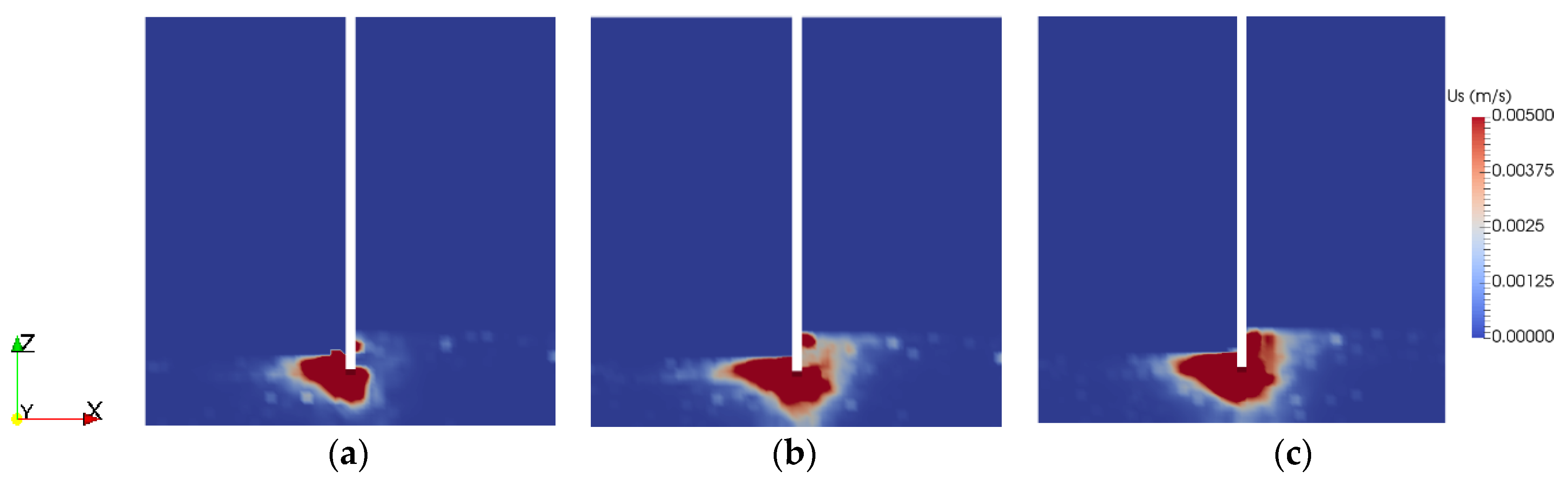
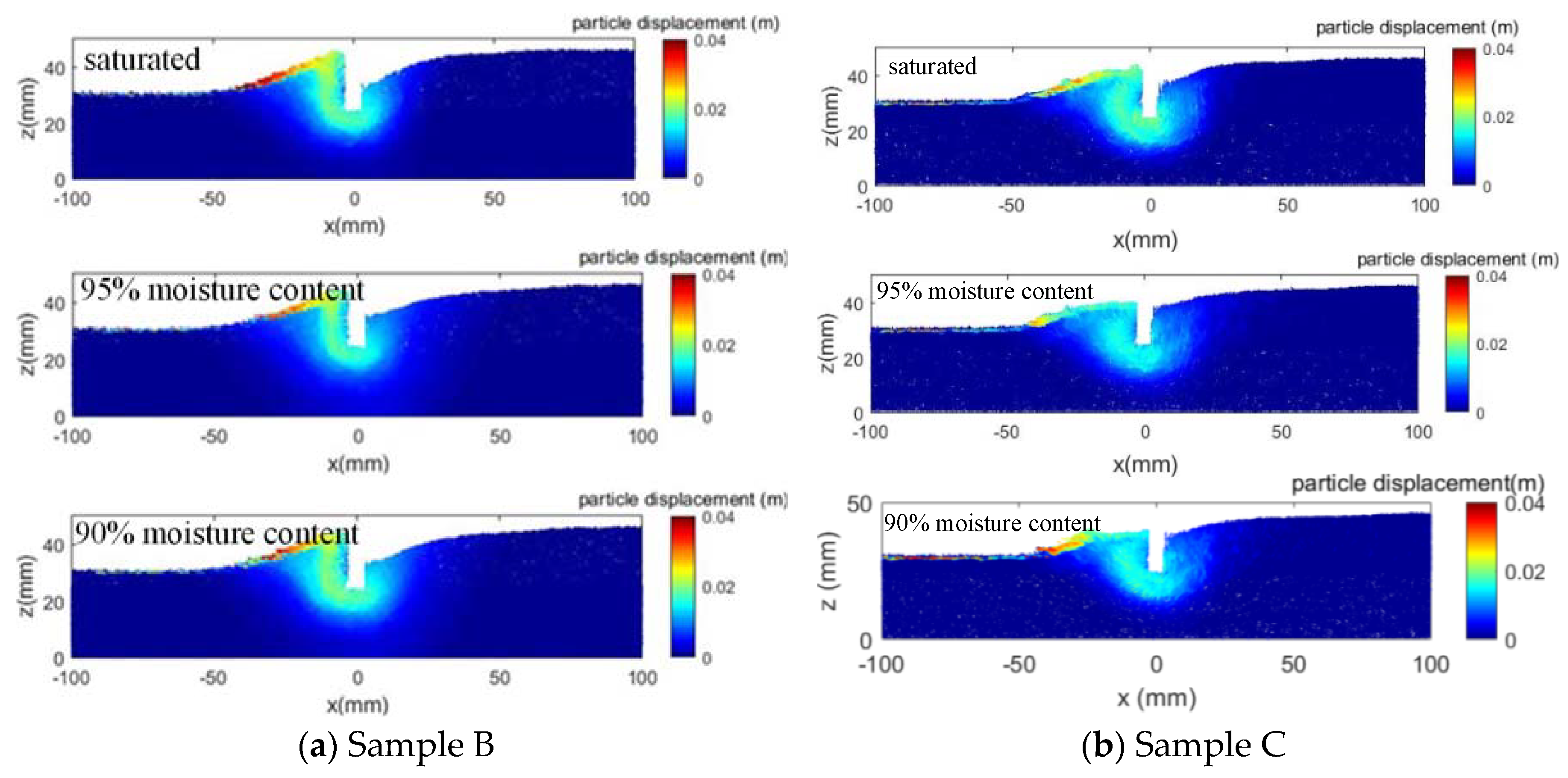
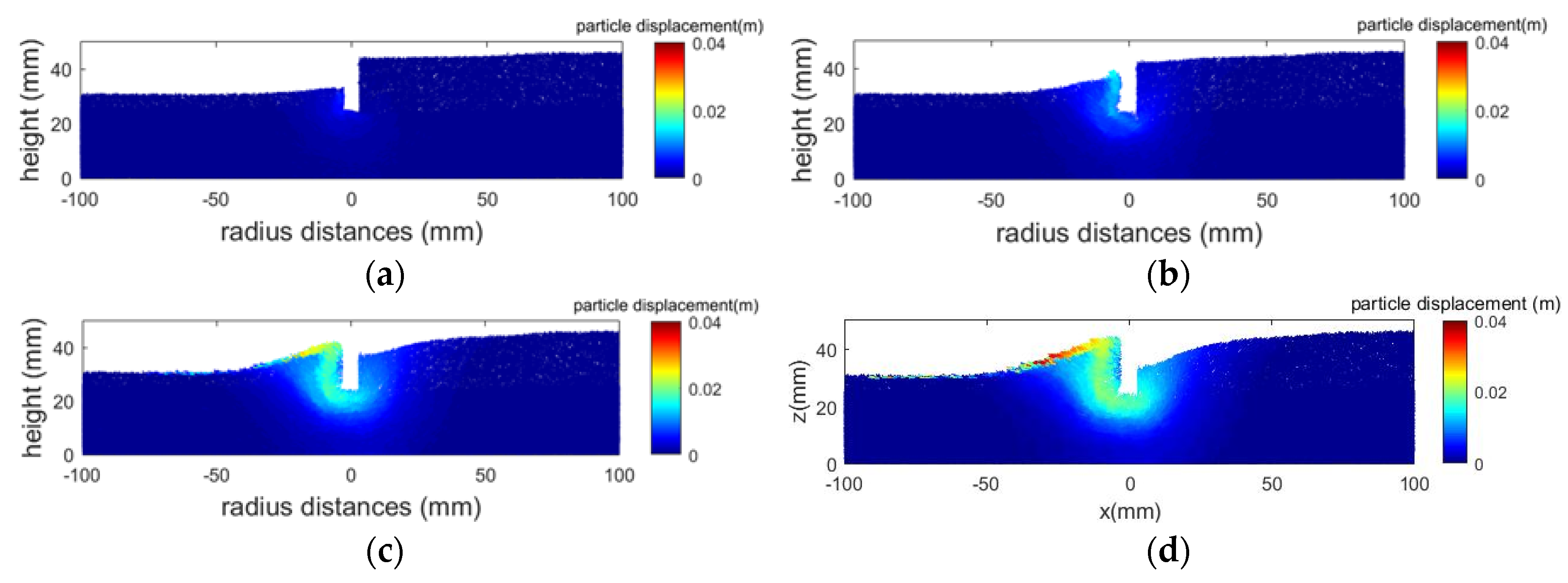
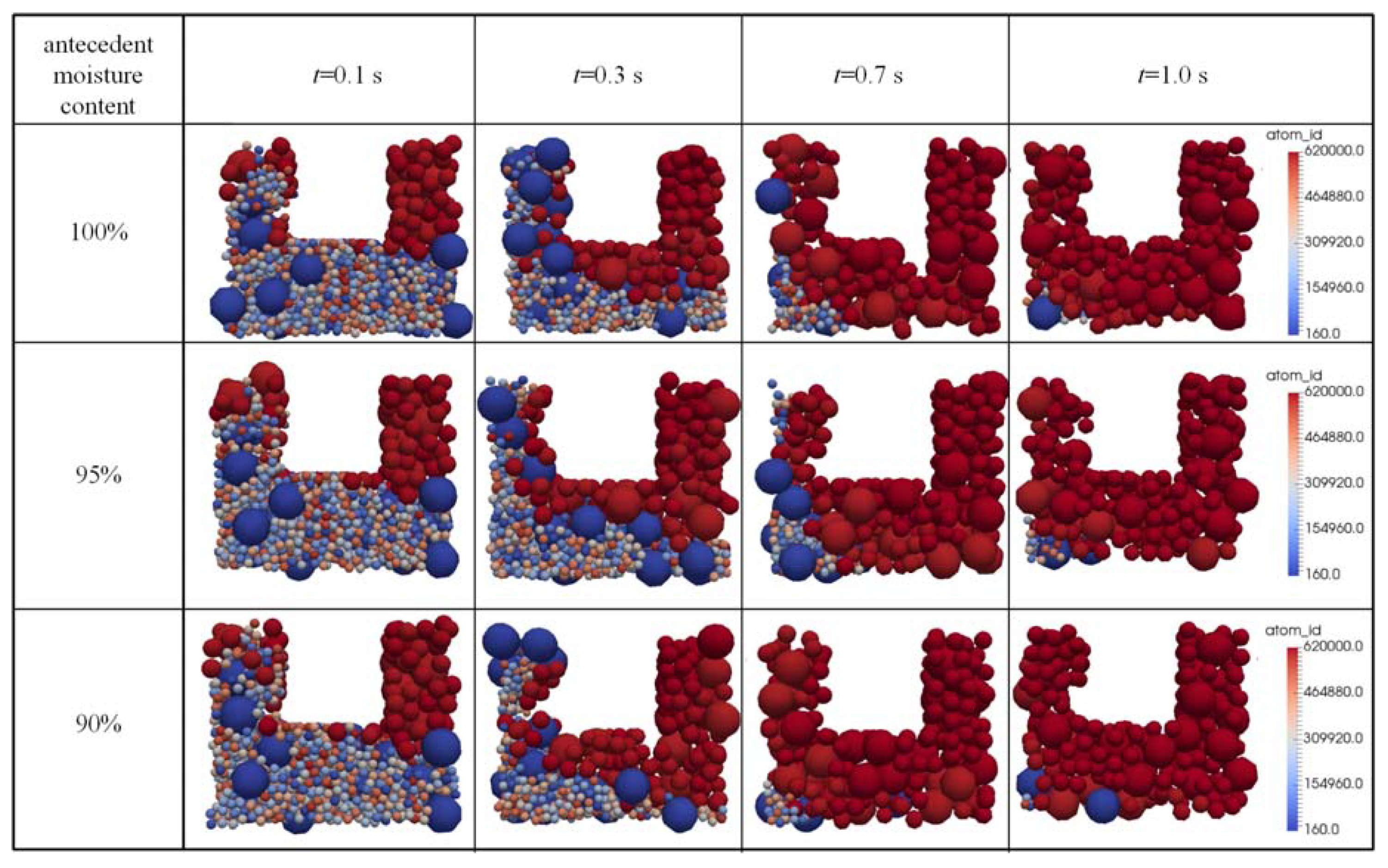
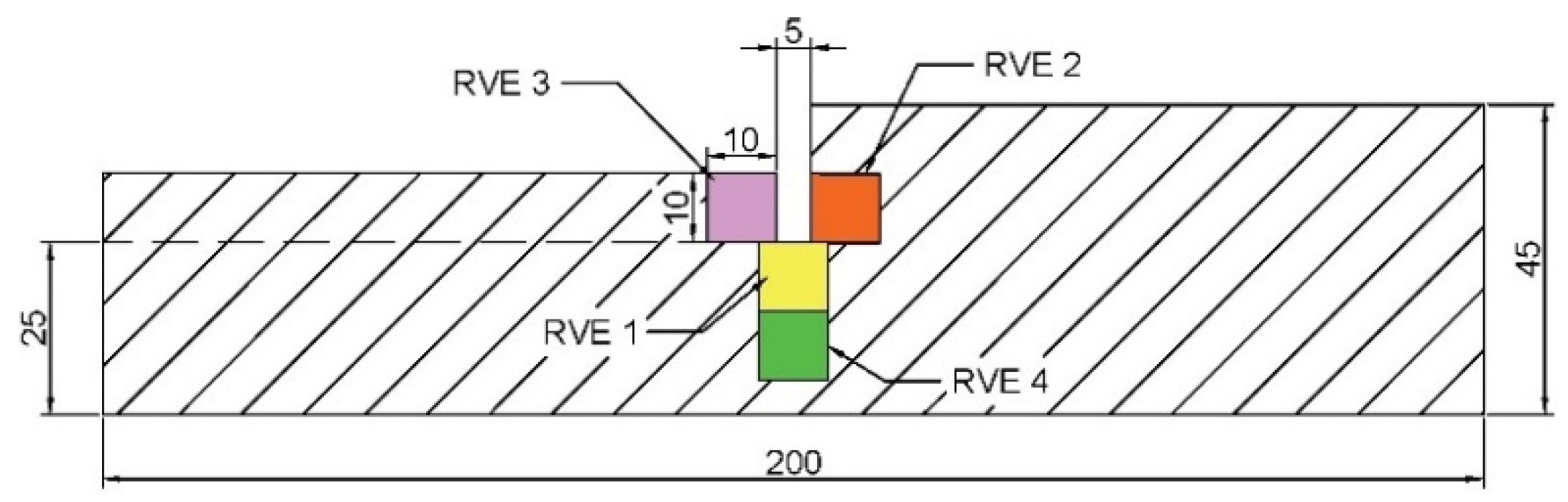






| Number of Mesh Elements | 20 | 40 | 80 | 200 |
| Simulation Time (s) | 29 | 60 | 490 | 21,524 |
| Sample Information | Sample A | Sample B | Sample C |
|---|---|---|---|
| Number of Particles | 816,692 | 550,806 | 237,597 |
| Parameters | Magnitudes |
|---|---|
| Young’s Modulus | 5 MPa |
| Friction Coefficient | 0.5 |
| Poisson’s Ratio | 0.45 |
| Restitution Coefficient | 0.1 |
| Kinematic Viscosity of Water | 1 × 10−6 m2/s |
| Density of Water | 1000 kg/m3 |
| Kinematic Viscosity of Air | 1.506 × 10−5 m2/s |
| Density of Air | 1.2041 kg/m3 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Q. Simulating the Hydraulic Heave Phenomenon with Multiphase Fluid Flows Using CFD-DEM. Water 2020, 12, 1077. https://doi.org/10.3390/w12041077
Xiao Q. Simulating the Hydraulic Heave Phenomenon with Multiphase Fluid Flows Using CFD-DEM. Water. 2020; 12(4):1077. https://doi.org/10.3390/w12041077
Chicago/Turabian StyleXiao, Qiong. 2020. "Simulating the Hydraulic Heave Phenomenon with Multiphase Fluid Flows Using CFD-DEM" Water 12, no. 4: 1077. https://doi.org/10.3390/w12041077
APA StyleXiao, Q. (2020). Simulating the Hydraulic Heave Phenomenon with Multiphase Fluid Flows Using CFD-DEM. Water, 12(4), 1077. https://doi.org/10.3390/w12041077




