Investigation on the Role of Water for the Stability of Shallow Landslides—Insights from Experimental Tests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
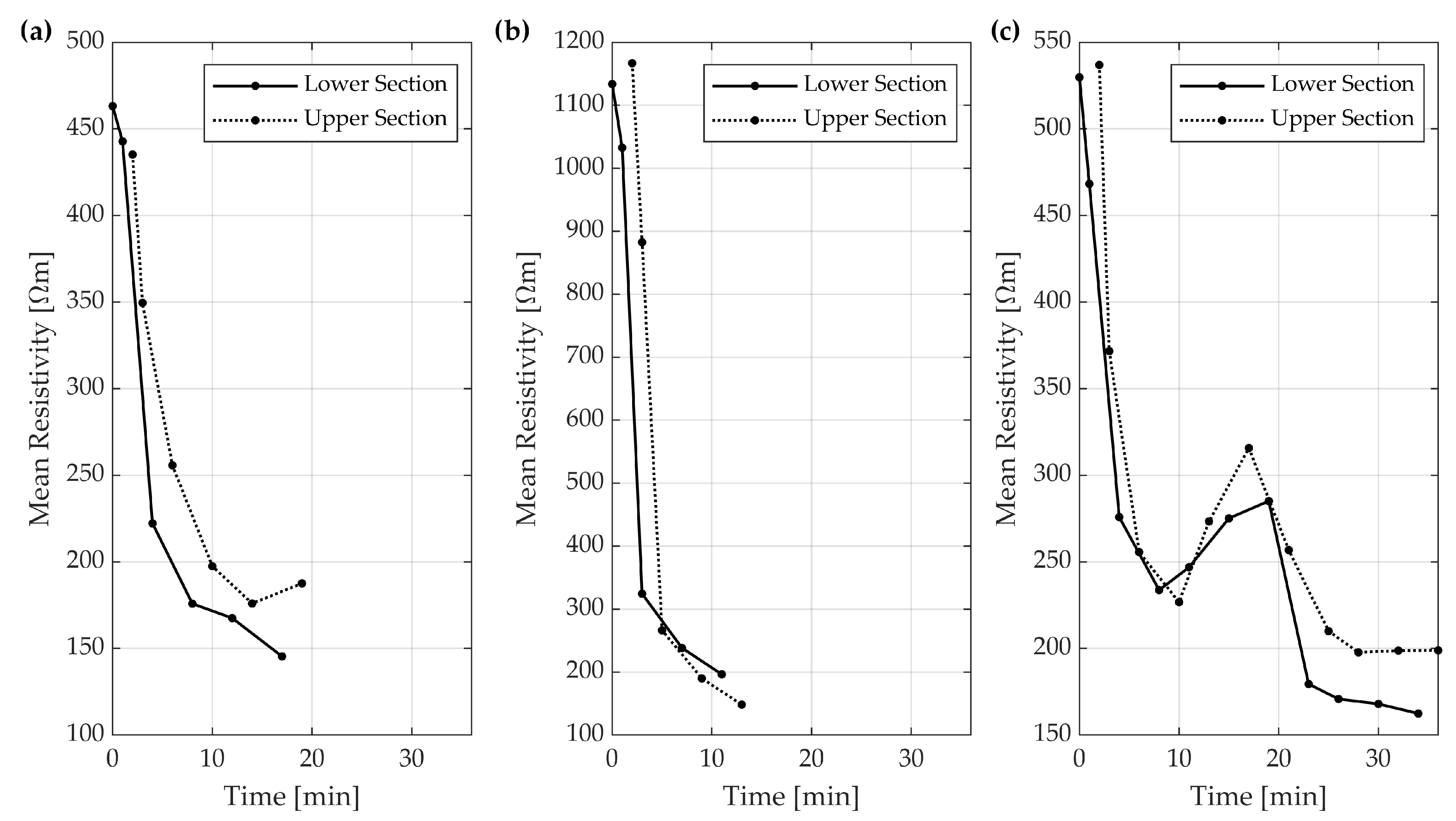
2.2. Geoelectrical Surveys
2.3. Data Analysis
2.3.1. Dimensional Analysis
2.3.2. Principal Component Analysis
3. Results and Discussion
3.1. Geoelectrical Measurements
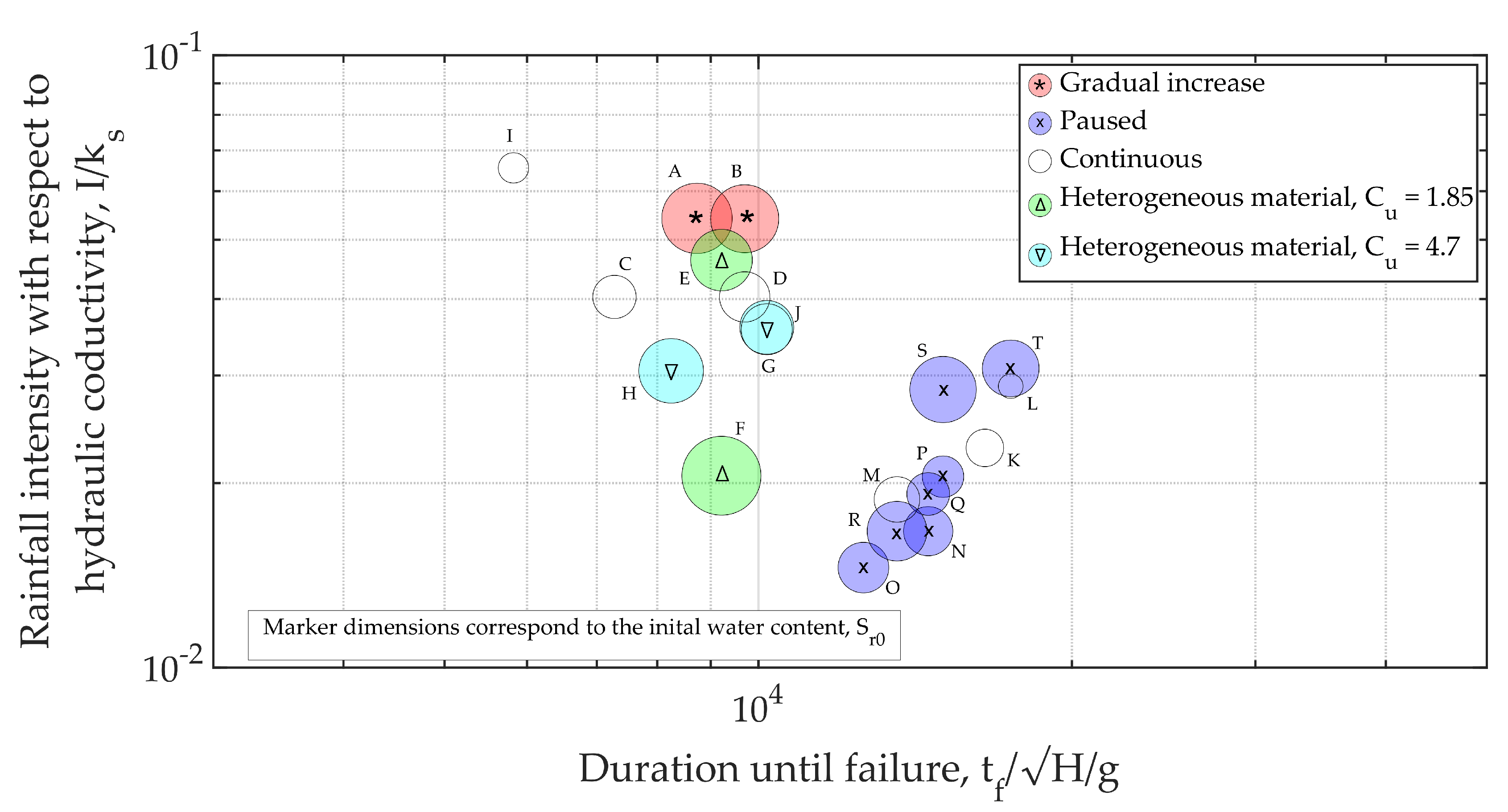
3.2. Principal Component Analysis
- Experiments which featured a pause tend to cluster together towards the left-hand side of the plot, indicating their higher duration until collapse. Experiments S and T make an exception, as the rainfall intensity during those tests was slightly higher and thus, they deviate from the cluster. Amidst those, the experiment with the lowest rainfall intensity can be found (M), as well as Experiment K, which featured a concentrated rainfall in the upper part of the landslide.
- Experiments with a gradual increase of rainfall simulation cluster together (A, B).
- Experiments with heterogeneous material demonstrate a different behaviour according to the initial state of the soil (E, F, G, H).
- Experiments representing extreme conditions can be outlined as well: Experiment I, characterized by an extremely high precipitation rate, is situated in the lower left corner of the plot, indicating that despite the lower initial soil moisture content, a prompt failure occurred. The experiment with the lowest inclination and initial degree of saturation can be found in the lower left corner of the plot as well (L).
3.3. Parametric Trends
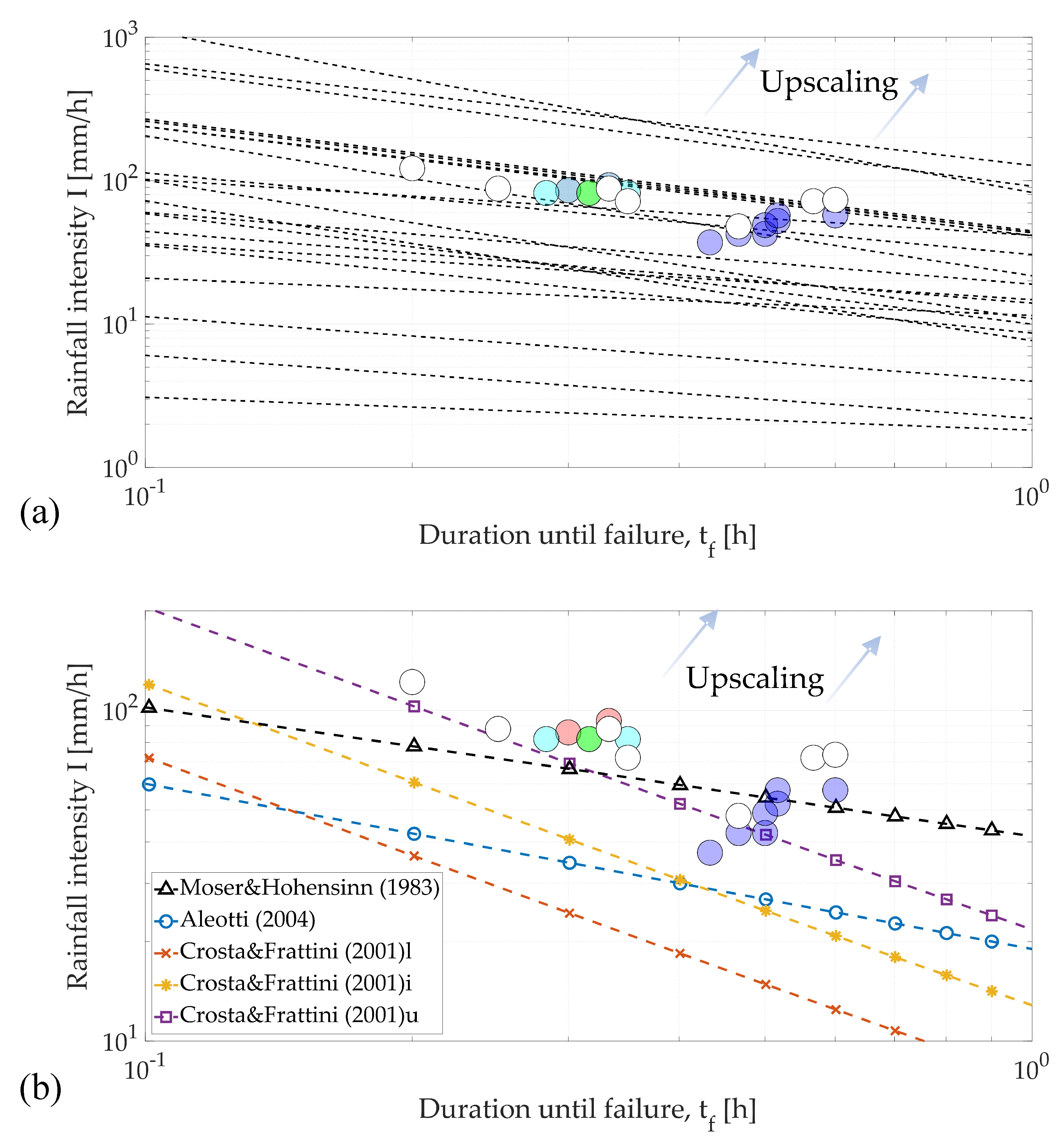
3.4. Rainfall Thresholds
3.5. Scale Effects
- The resulting scale relationships between parameters demonstrate the intrinsic interconnection or “chain” that relates variables. Thus, decreasing the dimensions of the landslide would inevitably have an effect on all other variables.
- This relation could be directly proportional to the scale factor or follow a different degree of proportionality. Hence, downscaling a real event should be carried out with care, as time scales differ from spatial scales for a land mass failure problem, leading to:
- Simulations carried out with soil samples collected from a real case study, and reproducing its triggering rainfall event, could lead to a misinterpretation, if the proper scales are not taken into account.
3.6. Summary
4. Conclusions
- the coupled interaction between rainfall intensity, hydraulic conductivity and soil moisture gradient is governing the stability of soil, and while rainfall intensity and duration are essential instability predictors, they must be integrated with antecedent moisture and site-specific soil property information;
- The above consideration partially explains the great variability of rainfall thresholds for shallow landslide stability found throughout the literature;
- The dynamics of the hydrologic event plays an important role for the advancement of the wetting front and further development of instability, evidenced by the differences outlined during ERT measurement;
- succession of rainfall events predisposes the terrain to failure—a scenario which can be easily translated into large-scale phenomena. The observation of a single hydrological event is therefore insufficient in terms of stability definition;
- the comparison of the dataset with a list of rainfall intensity-duration thresholds suggests that downscaled simulations could potentially be employed for the validation of rainfall thresholds.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2013, 11, 167–194. [Google Scholar] [CrossRef]
- Lee, D.-H.; Lai, M.-H.; Wu, J.-H.; Chi, Y.-Y.; Ko, W.-T.; Lee, B.-L. Slope management criteria for Alishan Highway based on database of heavy rainfall-induced slope failures. Eng. Geol. 2013, 162, 97–107. [Google Scholar] [CrossRef]
- Gabet, E.J.; Mudd, S. The mobilization of debris flows from shallow landslides. Geomorphology 2006, 74, 207–218. [Google Scholar] [CrossRef]
- Radice, A.; Longoni, L.; Papini, M.; Brambilla, D.; Ivanov, V. Generation of a Design Flood-Event Scenario for a Mountain River with Intense Sediment Transport. Water 2016, 8, 597. [Google Scholar] [CrossRef] [Green Version]
- Papini, M.; Ivanov, V.; Brambilla, D.; Arosio, D.; Longoni, L. Monitoring bedload sediment transport in a pre-Alpine river: An experimental method. Rend. Online 2017, 43, 57–63. [Google Scholar] [CrossRef]
- Baum, R.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. Space Phys. 2010, 115, 115. [Google Scholar] [CrossRef]
- Fan, L.; Lehmann, P.; Or, D. Effects of hydromechanical loading history and antecedent soil mechanical damage on shallow landslide triggering. J. Geophys. Res. Earth Surf. 2015, 120, 1990–2015. [Google Scholar] [CrossRef]
- Borja, R.I.; Liu, X.; White, J.A. Multiphysics hillslope processes triggering landslides. Acta Geotech. 2012, 7, 261–269. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2007, 5, 3–17. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M.; Manfreda, S. The role of antecedent soil moisture conditions on rainfall-triggered shallow landslides. Nat. Hazards Earth Syst. Sci. Discuss. 2018, 1–11. Available online: https://www.nat-hazards-earth-syst-sci-discuss.net/nhess-2018-371/nhess-2018-371.pdf (accessed on 22 April 2020). [CrossRef] [Green Version]
- Tiranti, D.; Nicolò, G.; Gaeta, A.R. Shallow landslides predisposing and triggering factors in developing a regional early warning system. Landslides 2018, 16, 235–251. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Han, D.; Dai, H.; Mao, J.; Zhuo, L. Antecedent wetness and rainfall information in landslide threshold definition. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–26. Available online: https://www.hydrol-earth-syst-sci-discuss.net/hess-2019-150/hess-2019-150.pdf (accessed on 22 April 2020). [CrossRef]
- Thomas, M.A.; Mirus, B.; Collins, B.D. Identifying Physics-Based Thresholds for Rainfall-Induced Landsliding. Geophys. Res. Lett. 2018, 45, 9651–9661. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Montrasio, L.; Schilirò, L.; Terrone, A. Physical and numerical modelling of shallow landslides. Landslides 2015, 13, 873–883. [Google Scholar] [CrossRef]
- Schenato, L.; Palmieri, L.; Camporese, M.; Bersan, S.; Cola, S.; Pasuto, A.; Galtarossa, A.; Salandin, P.; Simonini, P. Distributed optical fibre sensing for early detection of shallow landslides triggering. Sci. Rep. 2017, 7, 14686. [Google Scholar] [CrossRef]
- Schilirò, L.; Djueyep, G.P.; Esposito, C.; Mugnozza, G.S. The Role of Initial Soil Conditions in Shallow Landslide Triggering: Insights from Physically Based Approaches. Geofluids 2019, 2019, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Moriwaki, H.; Inokuchi, T.; Hattanji, T.; Sassa, K.; Ochiai, H.; Wang, G. Failure processes in a full-scale landslide experiment using a rainfall simulator. Landslides 2004, 1, 277–288. [Google Scholar] [CrossRef]
- Michlmayr, G.; Chalari, A.; Clarke, A.; Or, D. Fiber-optic high-resolution acoustic emission (AE) monitoring of slope failure. Landslides 2016, 14, 1139–1146. [Google Scholar] [CrossRef]
- Papini, M.; Ivanov, V.I.; Brambilla, D.; Ferrario, M.; Brunero, M.; Cazzulani, G.; Longoni, L. First steps for the development of an optical fibre strain sesnor for shallow landslide stability monitoring through laboratory experiments. In Applied Geology: Approaches to Future Resource Management; De Maio, M., Tiwari, A.K., Eds.; Springer: Berlin, Germany, 2020; in press. [Google Scholar]
- Iverson, R.M. Scaling and design of landslide and debris-flow experiments. Geomorphology 2015, 244, 9–20. [Google Scholar] [CrossRef]
- Arosio, D.; Hojat, A.; Ivanov, V.; Loke, M.; Longoni, L.; Papini, M.; Tresoldi, G.; Zanzi, L. A Laboratory Experience to Assess the 3D Effects on 2D ERT Monitoring of River Levees. In Proceedings of the 24th European Meeting of Environmental and Engineering Geophysics, Porto, Portugal, 9–12 September 2018. [Google Scholar] [CrossRef]
- Tenax Geosynthetics. Tenax HF-HF PLUS Technical Data Sheet. Available online: https://www.tenax.net/wp-content/uploads/2017/11/Scheda_Tecnica_TENAX_HF-HF-Plus_i.pdf (accessed on 22 April 2020).
- Scaioni, M.; Crippa, J.; Yordanov, V.; Longoni, L.; Ivanov, V.; Papini, M. Some tools to support teaching photogrammetry for slope stability assessment and monitoring. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, 453–460. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.-P.; François, B.; Lambert, P. Equations for hydraulic conductivity estimation from particle size distribution: A dimensional analysis. Water Resour. Res. 2017, 53, 8127–8134. [Google Scholar] [CrossRef]
- Wu, J.-H.; Lin, H.-M.; Lee, D.-H.; Fang, S.-C. Integrity assessment of rock mass behind the shotcreted slope using thermography. Eng. Geol. 2005, 80, 164–173. [Google Scholar] [CrossRef]
- Chambers, J.; Gunn, D.; Wilkinson, P.; Meldrum, P.; Haslam, E.; Holyoake, S.; Kirkham, M.; Kuras, O.; Merritt, A.; Wragg, J. 4D electrical resistivity tomography monitoring of soil moisture dynamics in an operational railway embankment. Near Surf. Geophys. 2012, 12, 61–72. [Google Scholar] [CrossRef] [Green Version]
- Lai, S.-L.; Lee, D.-H.; Wu, J.-H.; Dong, Y.-M. Detecting the cracks and seepage line associated with an earthquake in an earth dam using the nondestructive testing technologies. J. Chin. Inst. Eng. 2013, 37, 428–437. [Google Scholar] [CrossRef]
- Zhang, Z.; Arosio, D.; Hojat, A.; Taruselli, M.; Zanzi, L. Construction of a 3D velocity model for microseismic event location on a monitored rock slope. In Proceedings of the EAGE-GSM 2nd Asia Pacific Meeting on Near Surface Geoscience and Engineering, Kuala Lumpur, Malaysia, 24–25 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Nasab, S.K.; Hojat, A.; Kamkar-Rouhani, A.; Javar, H.A.; Maknooni, S. Successful Use of Geoelectrical Surveys in Area 3 of the Gol-e-Gohar Iron Ore Mine, Iran. Mine Water Environ. 2011, 30, 208–215. [Google Scholar] [CrossRef]
- Supper, R.; Ottowitz, D.; Jochum, B.; Kim, J.-H.; Römer, A.; Baroň, I.; Pfeiler, S.; Lovisolo, M.; Gruber, S.; Vecchiotti, F. Geoelectrical monitoring: An innovative method to supplement landslide surveillance and early warning. Near Surf. Geophys. 2013, 12, 133–150. [Google Scholar] [CrossRef] [Green Version]
- Arosio, D.; Munda, S.; Tresoldi, G.; Papini, M.; Longoni, L.; Zanzi, L. A customized resistivity system for monitoring saturation and seepage in earthen levees: Installation and validation. Open Geosci. 2017, 9, 457–467. [Google Scholar] [CrossRef]
- Tresoldi, G.; Arosio, D.; Hojat, A.; Longoni, L.; Papini, M.; Zanzi, L. Long-term hydrogeophysical monitoring of the internal conditions of river levees. Eng. Geol. 2019, 259, 105139. [Google Scholar] [CrossRef]
- Hojat, A.; Arosio, D.; Ivanov, V.I.; Longoni, L.; Papini, M.; Scaioni, M.; Tresoldi, G.; Zanzi, L. Geoelectrical characterization and monitoring of slopes on a rainfall-triggered landslide simulator. J. Appl. Geophys. 2019, 170, 103844. [Google Scholar] [CrossRef]
- Bridgman, P.W. Dimensional Analysis; Yale University Press: New Haven, CT, USA, 1922. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002; p. 29. [Google Scholar]
- Pempkowiak, J.; Beldowski, J.; Pazdro, K.; Staniszewski, A.; Zaborska, A.; Leipe, T.; Emeis, K. Factors influencing fluffy layer suspended matter (FLSM) properties in the Odra River—Pomeranian Bay—Arkona Deep System (Baltic Sea) as derived by principal components analysis (PCA), and cluster analysis (CA). Hydrol. Earth Syst. Sci. 2005, 9, 67–80. [Google Scholar] [CrossRef]
- Lora, M.; Camporese, M.; Troch, P.A.; Salandin, P. Rainfall-triggered shallow landslides: Infiltration dynamics in a physical hillslope model. Hydrol. Process. 2016, 30, 3239–3251. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Theor. Appl. Clim. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Moser, M.; Hohensinn, F. Geotechnical aspects of soil slips in Alpine regions. Eng. Geol. 1983, 19, 185–211. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Rainfall thresholds for triggering soil slips and debris flow. In Proceedings of the 2nd EGS Plinius Conference on Mediterranean Storms, Siena, Italy, 16–18 October 2001; Volume 1, pp. 463–487. [Google Scholar]
- Abbate, A.; Longoni, L.; Ivanov, V.; Papini, M. Wildfire Impacts on Slope Stability Triggering in Mountain Areas. Geosciences 2019, 9, 417. [Google Scholar] [CrossRef] [Green Version]





| Value | Rainfall Intensity I [mm/h] | Volume of Water Vw [l] | Porosity n [-] | VWC θ [-] | Degree of Saturation Sr0 [-] | Slope α [deg] | Hydraulic Conductivity ks [m/s] | First Failure tf [min] |
|---|---|---|---|---|---|---|---|---|
| Min | 48 | 12 | 0.44 | 0.044 | 0.08 | 30 | 4.4 × 10−4 | 12 |
| Mean | 79 | 40 | 0.5 | 0.1 | 0.34 | 37.5 | 6.6 × 10−4 | 24 |
| Max | 122 | 69 | 0.54 | 0.18 | 0.2 | 40 | 1.1 × 10−3 | 36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, V.; Arosio, D.; Tresoldi, G.; Hojat, A.; Zanzi, L.; Papini, M.; Longoni, L. Investigation on the Role of Water for the Stability of Shallow Landslides—Insights from Experimental Tests. Water 2020, 12, 1203. https://doi.org/10.3390/w12041203
Ivanov V, Arosio D, Tresoldi G, Hojat A, Zanzi L, Papini M, Longoni L. Investigation on the Role of Water for the Stability of Shallow Landslides—Insights from Experimental Tests. Water. 2020; 12(4):1203. https://doi.org/10.3390/w12041203
Chicago/Turabian StyleIvanov, Vladislav, Diego Arosio, Greta Tresoldi, Azadeh Hojat, Luigi Zanzi, Monica Papini, and Laura Longoni. 2020. "Investigation on the Role of Water for the Stability of Shallow Landslides—Insights from Experimental Tests" Water 12, no. 4: 1203. https://doi.org/10.3390/w12041203
APA StyleIvanov, V., Arosio, D., Tresoldi, G., Hojat, A., Zanzi, L., Papini, M., & Longoni, L. (2020). Investigation on the Role of Water for the Stability of Shallow Landslides—Insights from Experimental Tests. Water, 12(4), 1203. https://doi.org/10.3390/w12041203








