Environmental Control on Transpiration: A Case Study of a Desert Ecosystem in Northwest China
Abstract
:1. Introduction
2. Material and Methods
2.1. Site Description
2.2. Vegetation Measurement
2.3. Environmental Measurements
2.4. Sap Flow Measurements and Estimation of Stand Transpiration
2.5. Characterizing Hysteresis and Modeling Stand Transpiration
3. Results and Discussion
3.1. Stand Characteristics and Environmental Conditions
3.2. Diurnal Courses of Environmental Variables and Transpiration
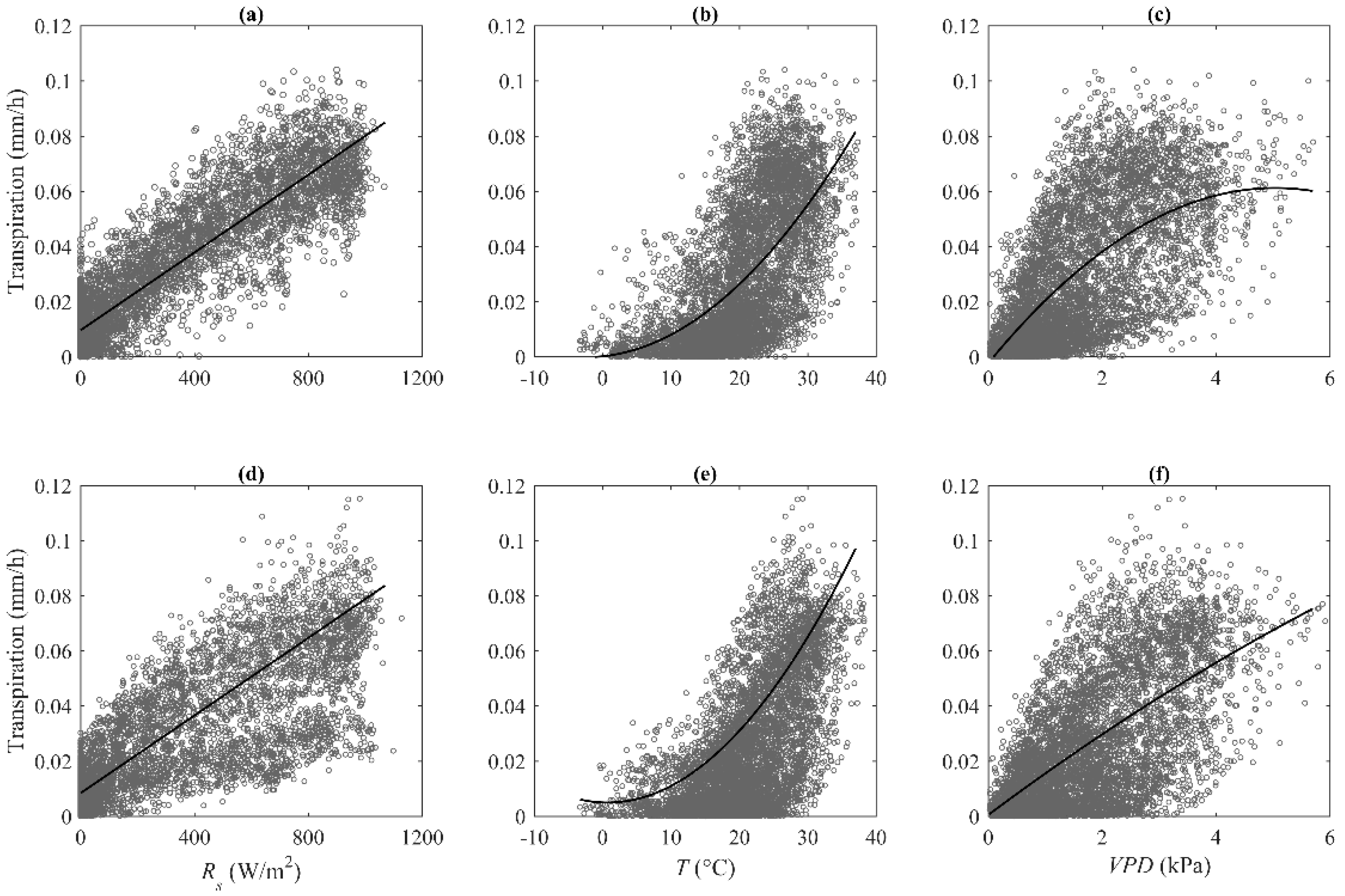
3.3. Control of Environment Variables on Stand Transpiration
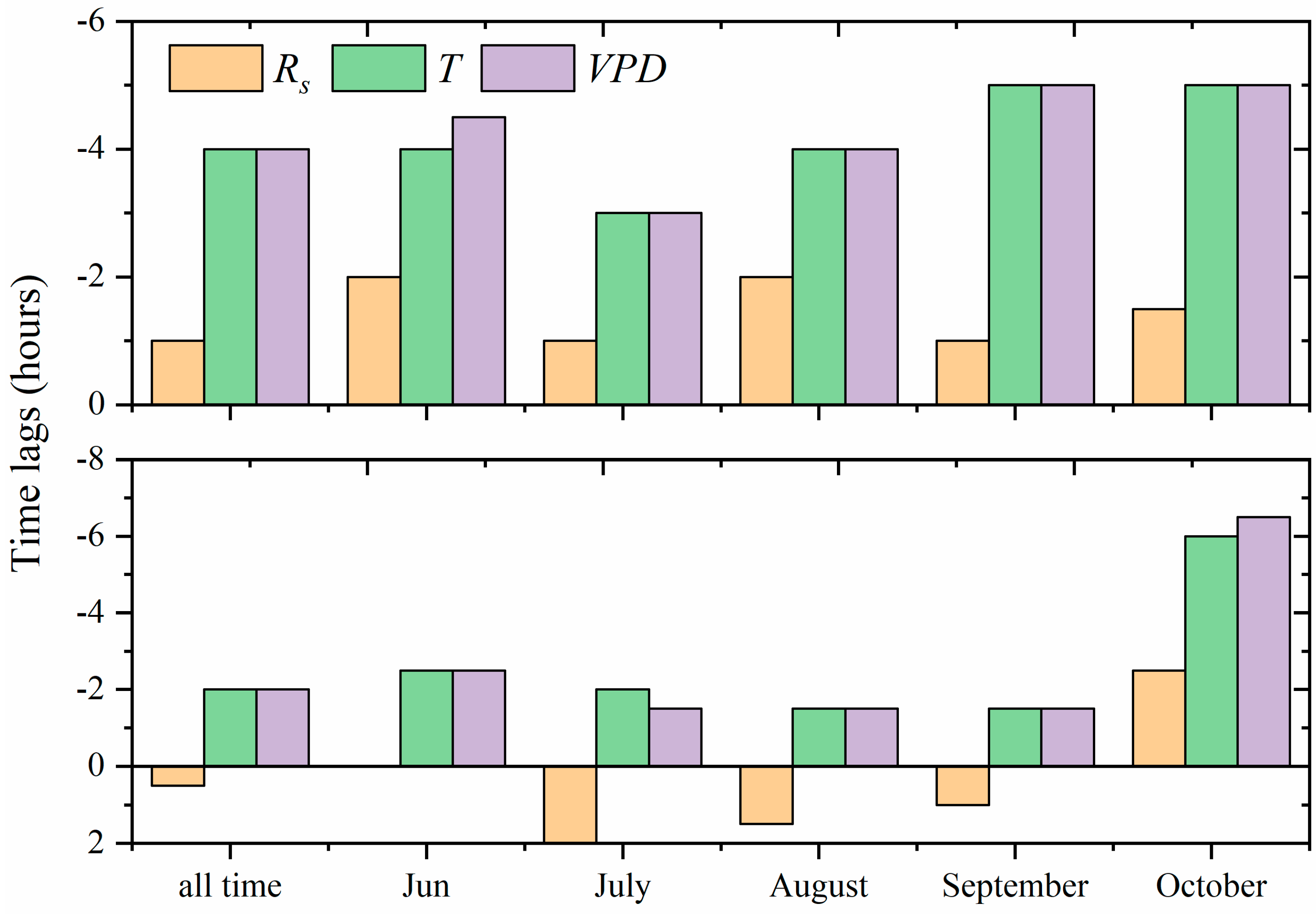
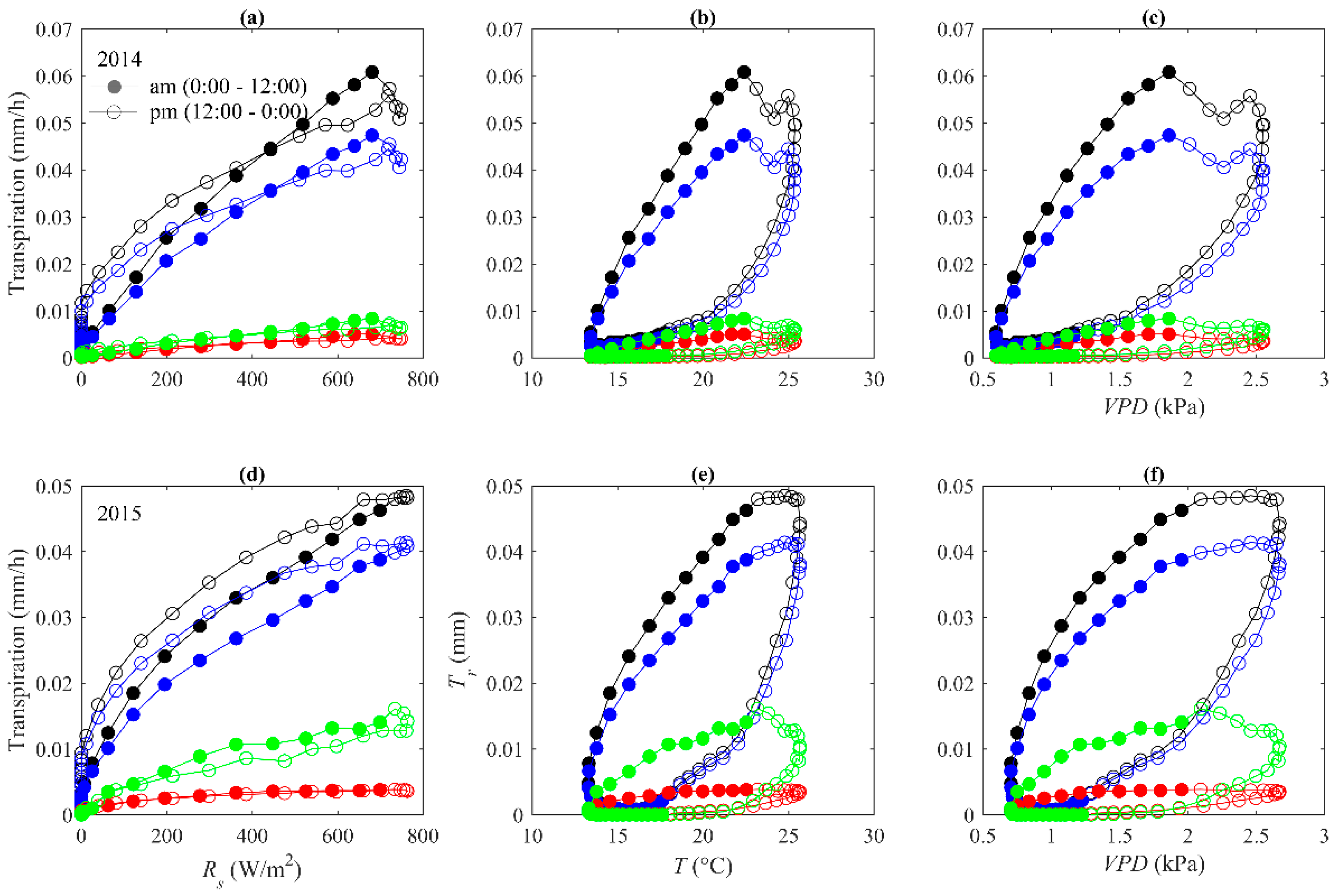
3.4. Hysteresis between Stand Transpiration and Environmental Variables
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Time | Rs, T & VPD | Rs & T | Rs & VPD | T & VPD | |
|---|---|---|---|---|---|
| 2014 | all-time | Et = 0.001 + 0.0001Rs + 0.0003T + 0.004VPD | Et = −0.003 + 0.0001Rs + 0.0007T | Et = −0.003 + 0.0001Rs + 0.004VPD | Et = −0.004 + 0.0008T + 0.011VPD |
| Jun | Et = −0.002 + 0.0001Rs + 0.0004T + 0.005VPD | Et = −0.014 + 0.0001Rs + 0.0014T | Et = −0.014 + 0.0001Rs + 0.005VPD | Et = −0.022 + 0.002T + 0.006VPD | |
| July | Et = 0.007 + 0.0001Rs − 0.0002T + 0.005VPD | Et = −0.009 + 0.0001Rs + 0.001T | Et = −0.009 + 0.0001Rs + 0.005VPD | Et = −0.033 + 0.0025T + 0.004VPD | |
| August | Et = −0.003 + 0.0001Rs + 0.0006T + 0.001VPD | Et = −0.007 + 0.0001Rs + 0.001T | Et = −0.007 + 0.0001Rs +0.001 VPD | Et = −0.041 + 0.0033 T − 0.002 VPD | |
| September | Et = −0.004 + 0.0001Rs +0.0008T + 0.001VPD | Et = −0.005 + 0.0001Rs + 0.0009T | Et = −0.005 + 0.001Rs + 0.001 VPD | Et = −0.022 + 0.0001T + 0.003VPD | |
| October | Et = 0.002 + 0.0001Rs +0.0005T + 0.003VPD | Et = 0.002 + 0.0001Rs + 0.0002T | Et = 0.002 + 0.0001Rs + 0.001 VPD | Et = 0.001 + 0.001T + 0.005VPD | |
| 2015 | all-time | Et = −0.009 + 0.0001Rs +0.0007T + 0.003VPD | Et = −0.012 + 0.0001Rs + 0.001T | Et = −0.012 + 0.0001Rs + 0.003VPD | Et = −0.009 + 0.001T + 0.009VPD |
| Jun | Et = −0.002 + 0.0001Rs +0.0004T + 0.005VPD | Et = −0.014 + 0.0001Rs + 0.0014T | Et = −0.014 + 0.0001Rs + 0.005VPD | Et = −0.022 + 0.0021T + 0.006VPD | |
| July | Et = 0.007 + 0.0001Rs − 0.0002T + 0.005VPD | Et = −0.009 + 0.0001Rs + 0.0009T | Et = −0.009 + 0.0001Rs + 0.005VPD | Et = −0.033 + 0.0024T + 0.004VPD | |
| August | Et = −0.003 + 0.0001Rs +0.0006T + 0.001VPD | Et = −0.007 + 0.0001Rs + 0.0009T | Et = −0.007 + 0.0001Rs + 0.001VPD | Et = −0.041 + 0.0033T − 0.002VPD | |
| September | Et = −0.004 + 0.0001Rs +0.0008T + 0.001VPD | Et = −0.005 + 0.0001Rs + 0.0009T | Et = −0.004 + 0.0001Rs + 0.001VPD | Et = −0.022 + 0.0025T − 0.003VPD | |
| October | Et = 0.002 + 0.0001Rs +0.0002T + 0.003VPD | Et =0.002 + 0.0001Rs + 0.0005T | Et = 0.002 + 0.0001Rs + 0.003VPD | Et = 0.001 + 0.001T − 0.005VPD | |
References
- Beuhler, M. Potential impacts of global warming on water resources in southern California. Water Sci. Technol. 2003, 47, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Wang, H.; Tetzlaff, D.; Soulsby, C. Hysteretic response of sap flow in Scots pine (Pinus sylvestris) to meteorological forcing in a humid low-energy headwater catchment. Ecohydrology 2019, 12, e2125. [Google Scholar] [CrossRef]
- Smith, D.; Allen, S. Measurement of sap flow in plant stems. J. Exp. Bot. 1996, 47, 1833–1844. [Google Scholar] [CrossRef] [Green Version]
- Bovard, B.D.; Curtis, P.S.; Vogel, C.S.; Su, H.; Schmid, H.P. Environmental controls on sap flow in a northern hardwood forest. Tree Physiol. 2005, 25, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Dalsgaard, L.; Mikkelsen, T.N.; Bastrup-Birk, A. Sap flow for beech (Fagus sylvatica L.) in a natural and a managed forest—effect of spatial heterogeneity. J. Plant Ecol. 2011, 4, 23–35. [Google Scholar] [CrossRef]
- Otieno, D.; Li, Y.; Liu, X.; Zhou, G.; Cheng, J.; Ou, Y.; Liu, S.; Chen, X.; Zhang, Q.; Tang, X. Spatial heterogeneity in stand characteristics alters water use patterns of mountain forests. Agric. For. Meteorol. 2017, 236, 78–86. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, B.; Chang, X.; Yang, Q.; Yang, Y.; Liu, Z.; Cleverly, J.; Eamus, D. Evapotranspiration partitioning, stomatal conductance, and components of the water balance: A special case of a desert ecosystem in China. J. Hydrol. 2016, 538, 374–386. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, Y.; Yin, L.; Wenninger, J.; Zhang, J.; Hou, G.; Zhang, E.; Uhlenbrook, S. Climatic controls on sap flow dynamics and used water sources of Salix psammophilain a semi-arid environment in northwest China. Environ. Earth Sci. 2015, 73, 289–301. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, Q. Seasonal and annual variation in transpiration of a dominant desert species, Haloxylon ammodendron, in Central Asia up-scaled from sap flow measurement. Ecohydrology 2014, 8, 948–960. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Y.; Li, W.; Huang, X.; Zhu, C.; Ma, X. Sap flow characteristics of four typical species in desert shelter forest and their responses to environmental factors. Environ. Earth Sci. 2012, 67, 151–160. [Google Scholar] [CrossRef]
- Shen, Q.; Gao, G.; Fu, B.; Lv, Y. Sap flow and water use sources of shelter-belt trees in an arid inland river basin of Northwest China. Ecohydrology 2015, 8, 1446–1458. [Google Scholar] [CrossRef]
- Bai, Y.; Zhu, G.; Su, Y.; Zhang, K.; Han, T.; Ma, J.; Wang, W.; Ma, T.; Feng, L. Hysteresis loops between canopy conductance of grapevines and meteorological variables in an oasis ecosystem. Agric. For. Meteorol. 2015, 214, 319–327. [Google Scholar] [CrossRef]
- Zhang, Q.; Stefano, M.; Gabriel, K.; Amilcare, P.; Dawen, Y. The hysteretic evapotranspiration—Vapor pressure deficit relation. J. Geophys. Res. Biogeo. 2014, 119, 125–140. [Google Scholar] [CrossRef]
- Hong, L.; Guo, J.; Liu, Z.; Wang, Y.; Ma, J.; Wang, X.; Zhang, Z. Time-Lag effect between sap flow and environmental factors of Larix principis-rupprechtii Mayr. Forests 2019, 10, 971. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Li, X.; Liu, S.; Wang, P. Modelling diurnal and seasonal hysteresis phenomena of canopy conductance in an oasis forest ecosystem. Agric. For. Meteorol. 2017, 246, 98–110. [Google Scholar] [CrossRef]
- Lin, C.; Gentine, P.; Frankenberg, C.; Zhou, S.; Kennedy, D.; Li, X. Evaluation and mechanism exploration of the diurnal hysteresis of ecosystem fluxes. Agric. For. Meteorol. 2019, 278, 107642. [Google Scholar] [CrossRef]
- Xu, S.; Ji, X.; Jin, B.; Zhang, J. Root distribution of three dominant desert shrubs and their water uptake dynamics. J. Plant Ecol. 2017, 10, 780–790. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.; Kang, E.; Chen, R.; Zhao, W.; Zhang, Z.; Jin, B. The impact of the development of water resources on environment in arid inland river basins of Hexi region, Northwestern China. Environ. Geol. 2006, 50, 793–801. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, X.-J.; Li, Y.; Xu, G. Varying responses of two Haloxylon species to extreme drought and groundwater depth. Environ. Exp. Bot. 2019, 158, 63–72. [Google Scholar] [CrossRef]
- Lü, X.; Gao, H.; Zhang, L.; Wang, Y.; Shao, K. Dynamic responses of Haloxylon ammodendron to various degrees of simulated drought stress. Plant Physiol. Biochem. 2019, 139, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Yu, D.; Li, Y. Patterns of biomass allocation in Haloxylon persicum woodlands and their understory herbaceous layer along a groundwater depth gradient. For. Ecol. Manag. 2017, 395, 37–47. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Zhang, K.; Ji, X.; Yang, C.; Sudicky, E.A. Simulating canopy conductance of the Haloxylon ammodendron shrubland in an arid inland river basin of northwest China. Agric. For. Meteorol. 2018, 249, 22–34. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Baker, J.M.; Van Bavel, C.H.M. Measurement of mass flow of water in the stems of herbaceous plants. Plant Cell Environ. 1987, 10, 777–782. [Google Scholar]
- Dynamax. Dynagage Sap Flow Sensor User Manual. 2009. Available online: http://dynamax.com/images/uploads/papers/Dynagage_Manual.pdf (accessed on 6 April 2013).
- Köstner, B.; Granier, A.; Cermák, J. Sapflow measurements in forest stands: Methods and uncertainties. Ann. For. Sci. 1998, 55, 13–27. [Google Scholar] [CrossRef]
- Hatton, T.J.; Wu, H.I. Scaling theory to extrapolate individual tree water use to stand water use. Hydrol. Process. 1995, 9, 527–540. [Google Scholar] [CrossRef]
- Hatton, T.J.; Moore, S.J.; Reece, P.H. Estimating stand transpiration in a Eucalyptus populnea woodland with the heat pulse method: Measurement errors and sampling strategies. Tree Physiol. 1995, 15, 219–227. [Google Scholar] [CrossRef]
- Allen, S.; Grime, V. Measurements of transpiration from savannah shrubs using sap flow gauges. Agric. For. Meteorol. 1995, 75, 23–41. [Google Scholar] [CrossRef]
- Ford, C.R.; McGuire, M.A.; Mitchell, R.J.; Teskey, R.O. Assessing variation in the radial profile of sap flux density in Pinus species and its effect on daily water use. Tree Physiol. 2004, 24, 241–249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gartner, K.; Nadezhdina, N.; Englisch, M.; Čermak, J.; Leitgeb, E. Sap flow of birch and Norway spruce during the European heat and drought in summer 2003. For. Ecol. Manag. 2009, 258, 590–599. [Google Scholar] [CrossRef] [Green Version]
- Yu, O.; Goudriaan, J.; Wang, T. Modelling diurnal courses of photosynthesis and transpiration of leaves on the basis of stomatal and non-stomatal responses, including photoinhibition. Photosynthetica 2001, 39, 43–51. [Google Scholar] [CrossRef]
- Rodrigues, T.R.; Vourlitis, G.L.; Lobo, F.d.A.; Santanna, F.B.; de Arruda, P.H.; Nogueira, J.d.S. Modeling canopy conductance under contrasting seasonal conditions for a tropical savanna ecosystem of south central Mato Grosso, Brazil. Agric. For. Meteorol. 2016, 218, 218–229. [Google Scholar] [CrossRef] [Green Version]
- Wullschleger, S.D.; Wilson, K.B.; Hanson, P.J. Environmental control of whole-plant transpiration, canopy conductance and estimates of the decoupling coefficient for large red maple trees. Agric. For. Meteorol. 2000, 104, 157–168. [Google Scholar] [CrossRef]
- Clausnitzer, F.; Köstner, B.; Schwärzel, K.; Bernhofer, C. Relationships between canopy transpiration, atmospheric conditions and soil water availability—Analyses of long-term sap-flow measurements in an old Norway spruce forest at the Ore Mountains/Germany. Agric. For. Meteorol. 2011, 151, 1023–1034. [Google Scholar] [CrossRef]
- Meinzer, F.; Goldstein, G.; Holbrook, N.; Jackson, P.; Cavelier, J. Stomatal and environmental control of transpiration in a lowland tropical forest tree. Plant Cell Environ. 1993, 16, 429–436. [Google Scholar] [CrossRef]
- Motzer, T.; Munz, N.; Küppers, M.; Schmitt, D.; Anhuf, D. Stomatal conductance, transpiration and sap flow of tropical montane rain forest trees in the southern Ecuadorian Andes. Tree Physiol. 2005, 25, 1283–1293. [Google Scholar] [CrossRef] [Green Version]
- Tie, Q.; Hu, H.; Tian, F.; Guan, H.; Lin, H. Environmental and physiological controls on sap flow in a subhumid mountainous catchment in North China. Agric. For. Meteorol. 2017, 240, 46–57. [Google Scholar] [CrossRef]
- Du, S.; Wang, Y.; Kume, T.; Zhang, J.; Otsuki, K.; Yamanaka, N.; Liu, G. Sapflow characteristics and climatic responses in three forest species in the semiarid Loess Plateau region of China. Agric. For. Meteorol. 2011, 151, 1–10. [Google Scholar] [CrossRef]
- Yin, L.; Zhou, Y.; Huang, J.; Wenninger, J.; Uhlenbrook, S. Dynamics of willow tree (Salix matsudana) water use and its response to environmental factors in the semi-arid Hailiutu River catchment, Northwest China. Environ. Earth Sci. 2014, 71, 4997–5006. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Q.; Zhu, X.; Li, Y.; Yu, G. Hysteresis responses of evapotranspiration to meteorological factors at a diel timescale: Patterns and causes. PLoS ONE 2014, 9, e98857. [Google Scholar] [CrossRef] [PubMed]
- O’Grady, A.P.; Worledge, D.; Battaglia, M. Constraints on transpiration of Eucalyptus globulus in southern Tasmania, Australia. Agric. For. Meteorol. 2008, 148, 453–465. [Google Scholar] [CrossRef]
- Matheny, A.M.; Bohrer, G.; Vogel, C.S.; Morin, T.H.; He, L.; Frasson, R.P.d.M.; Mirfenderesgi, G.; Schäfer, K.V.; Gough, C.M.; Ivanov, V.Y. Species-specific transpiration responses to intermediate disturbance in a northern hardwood forest. J. Geophys. Res. Biogeo. 2014, 119, 2292–2311. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Zhang, Z.; Li, Z.; Tang, J.; Caldwell, P.; Zhang, W. Biophysical control of whole tree transpiration under an urban environment in Northern China. J. Hydrol. 2011, 402, 388–400. [Google Scholar] [CrossRef]
- Meinzer, F.C.; James, S.A.; Goldstein, G. Dynamics of transpiration, sap flow and use of stored water in tropical forest canopy trees. Tree Physiol. 2004, 24, 901–909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldstein, G.; Andrade, J.; Meinzer, F.; Holbrook, N.; Cavelier, J.; Jackson, P.; Celis, A. Stem water storage and diurnal patterns of water use in tropical forest canopy trees. Plant Cell Environ. 1998, 21, 397–406. [Google Scholar] [CrossRef]
- Dawson, T.E.; Burgess, S.S.; Tu, K.P.; Oliveira, R.S.; Santiago, L.S.; Fisher, J.B.; Simonin, K.A.; Ambrose, A.R. Nighttime transpiration in woody plants from contrasting ecosystems. Tree Physiol. 2007, 27, 561–575. [Google Scholar] [CrossRef] [Green Version]
- Rosado, B.H.; Oliveira, R.S.; Joly, C.A.; Aidar, M.P.; Burgess, S.S. Diversity in nighttime transpiration behavior of woody species of the Atlantic Rain Forest, Brazil. Agric. For. Meteorol. 2012, 158, 13–20. [Google Scholar] [CrossRef]
- Snyder, K.; Richards, J.; Donovan, L. Night-time conductance in C3 and C4 species: Do plants lose water at night? J. Exp. Bot. 2003, 54, 861–865. [Google Scholar] [CrossRef]
- Daley, M.J.; Phillips, N.G. Interspecific variation in nighttime transpiration and stomatal conductance in a mixed New England deciduous forest. Tree Physiol. 2006, 26, 411–419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, N.; Ryan, M.; Bond, B.; McDowell, N.; Hinckley, T.; Čermák, J. Reliance on stored water increases with tree size in three species in the Pacific Northwest. Tree Physiol. 2003, 23, 237–245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, N.G.; Lewis, J.D.; Logan, B.A.; Tissue, D.T. Inter-and intra-specific variation in nocturnal water transport in Eucalyptus. Tree Physiol. 2010, 30, 586–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Environmental Variables | T | RH | VPD | u | P | Ts | θ10cm |
|---|---|---|---|---|---|---|---|
| Rs | 0.52 | −0.44 | 0.55 | 0.34 | / | / | / |
| T | −0.59 | 0.88 | 0.40 | / | 0.85 | / | |
| RH | −0.81 | −0.33 | 0.21 | −0.41 | / | ||
| VPD | 0.41 | / | 0.71 | / | |||
| u | x | 0.28 | / | ||||
| P | / | / | |||||
| Ts | / |
| Axis Number | Eigenvalues | Variance Explained (%) | Cumulative Variance Explained (%) |
|---|---|---|---|
| 1 | 3.707 | 46 | 46 |
| 2 | 1.130 | 14 | 60 |
| 3 | 1.022 | 13 | 73 |
| Environmental Variables | Component Number | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Rs | 0.670 | −0.153 | −0.084 |
| T | 0.874 | 0.387 | 0.025 |
| RH | −0.789 | 0.035 | 0.288 |
| VPD | 0.929 | 0.217 | −0.110 |
| u | 0.616 | −0.201 | 0.167 |
| P | −0.066 | −0.019 | 0.956 |
| Ts | 0.677 | 0.517 | 0.127 |
| θ10cm | −0.057 | 0.850 | −0.043 |
| Year | Variable | All-time | Jun | July | August | September | October |
|---|---|---|---|---|---|---|---|
| 2014 | Rs, T, VPD | 0.84 | 0.87 | 0.83 | 0.84 | 0.88 | 0.80 |
| Rs, T | 0.84 | 0.87 | 0.83 | 0.84 | 0.88 | 0.79 | |
| Rs, VPD | 0.84 | 0.87 | 0.83 | 0.84 | 0.88 | 0.79 | |
| T, VPD | 0.43 | 0.49 | 0.41 | 0.43 | 0.43 | 0.79 | |
| 2015 | Rs, T, VPD | 0.77 | 0.87 | 0.84 | 0.84 | 0.88 | 0.80 |
| Rs, T | 0.76 | 0.87 | 0.83 | 0.84 | 0.88 | 0.79 | |
| Rs, VPD | 0.76 | 0.87 | 0.83 | 0.84 | 0.88 | 0.79 | |
| T, VPD | 0.43 | 0.49 | 0.41 | 0.43 | 0.43 | 0.40 |
| Period | Equation | R2 |
|---|---|---|
| 2014 | SF = 0.0002 + 0.0137VPD + 0.0040u | 0.44 |
| 2015 | SF = − 0.0012 + 0.013VPD + 0.0026u | 0.41 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Yu, Z. Environmental Control on Transpiration: A Case Study of a Desert Ecosystem in Northwest China. Water 2020, 12, 1211. https://doi.org/10.3390/w12041211
Xu S, Yu Z. Environmental Control on Transpiration: A Case Study of a Desert Ecosystem in Northwest China. Water. 2020; 12(4):1211. https://doi.org/10.3390/w12041211
Chicago/Turabian StyleXu, Shiqin, and Zhongbo Yu. 2020. "Environmental Control on Transpiration: A Case Study of a Desert Ecosystem in Northwest China" Water 12, no. 4: 1211. https://doi.org/10.3390/w12041211
APA StyleXu, S., & Yu, Z. (2020). Environmental Control on Transpiration: A Case Study of a Desert Ecosystem in Northwest China. Water, 12(4), 1211. https://doi.org/10.3390/w12041211




