Improved Land Evapotranspiration Simulation of the Community Land Model Using a Surrogate-Based Automatic Parameter Optimization Method
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.2. Systematic Parameter Optimization Framework
2.2.1. Good Lattice Points (GLP) Uniform Sampling Method
2.2.2. Multivariate Adaptive Regression Splines (MARS) Sensitivity Analysis Method
2.2.3. Adaptive Surrogate Modeling-Based Optimization (ASMO) Parameter Optimization Method
- The perturbed parameter samples were obtained by sampling the sensitivity parameter adjustable ranges using the GLP sampling method. Then, these samples were put into the physical model (e.g., CLM4) instead of the default parameters, to obtain either the required model outputs (e.g., ET) or the output errors compared with observations. The perturbed parameters and their simulated outputs constituted the initial sample set.
- Based on the initial sample set, a statistical surrogate model was built between parameters and model outputs using the MARS regression method. Then, the traditional parameter optimization (e.g., the shuffled complex evolution (SCE-UA) global optimization method [23]) was used to search the optimal parameter values of the surrogate model.
- The optimal parameter values of the surrogate model were put into the physical model to obtain a new model output. As a new sample point, the optimal parameters of the surrogate model and their physical model output were added into the initial sample set.
- Steps 2 and 3 were repeatedly conducted until the convergence criterion was met. In this study, the convergence criterion was that the local optimal values remain unchanged after a number of searches equal to five or ten times the number of parameters.
2.3. Model Setup
3. Results
3.1. Sensitivity Analysis Results
3.2. Sensitivity Parameter Optimization Results
3.3. Comparison Analyses of Optimization Results
3.4. Validation Analyses of Community Land Model Version 4.0 Optimal Parameters
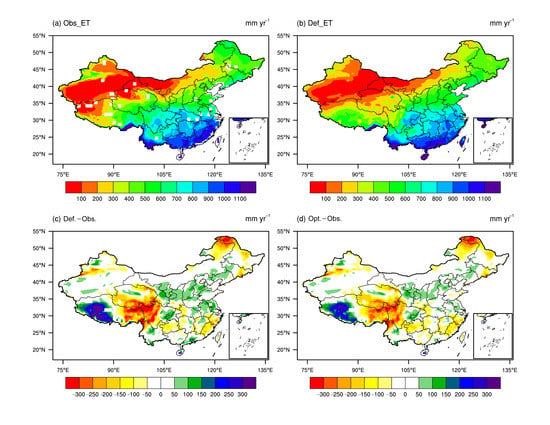
3.5. Comparisons between Default and Optimal Parameters
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. B. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and Environment. In The State and Movement of Water in Living Organism; Fogg, B.D., Ed.; Symposium of the Society of Experimental Biology XIX: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Priestley, C.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, 1131–1151. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E.; Su, H. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. J. Geophys. Res. Atmos. 2007, 112, D07103. [Google Scholar] [CrossRef]
- Christensen, N.S.; Wood, A.W.; Voisin, N.; Lettenmaier, D.P. The effects of climate change on the hydrology and water resources of the Colorado River basin. Climatic Change 2004, 62, 337–363. [Google Scholar] [CrossRef]
- Budyko, M.I. The Heat Balance of the Earth’s Surface; U.S. Dept. of Commerce: Washington, DC, USA, 1958.
- Sellers, P.J.; Randall, D.A.; Collatz, G.J.; Berry, J.A.; Field, C.B.; Dazlich, D.A.; Zhang, C.; Collelo, G.D.; Bounoua, L. A revised land surface parameterization (SiB2) for atmospheric GCMs. Part I: Model formulation. J. Climate 1996, 9, 676–705. [Google Scholar] [CrossRef]
- Niyogi, D.; Alapaty, K.; Raman, S.; Chen, F. Development and evaluation of a coupled photosynthesis-based gas exchange evapotranspiration model (GEM) for mesoscale weather forecasting applications. J. Appl. Meteorol. Clim. 2009, 48, 349–368. [Google Scholar] [CrossRef] [Green Version]
- Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Flanner, M.G.; Kluzek, E.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Thornton, P.E.; Dai, A.; et al. Technical Description of Version 4.0 of the Community Land Model (CLM); Rep. NCAR/TN-478 + STR; NCAR: Boulder, CO, USA, 2010; p. 257. [Google Scholar]
- Dirmeyer, P.A.; Dolman, A.J.; Sato, N. The pilot phase of the global soil wetness project. B. Am. Meteorol. Soc. 1999, 80, 851–878. [Google Scholar] [CrossRef] [Green Version]
- Amthor, J.S.; Chen, J.M.; Clein, J.S.; Frolking, S.E.; Goulden, M.L.; Grant, R.F.; Kimball, J.S.; King, A.W.; McGuire, A.D.; Nikolov, N.T.; et al. Boreal forest CO2 exchange and evapotranspiration predicted by nine ecosystem process models: Intermodel comparisons and relationships to field measurements. J. Geophys. Res. Atmos. 2001, 106, 33623–33648. [Google Scholar] [CrossRef] [Green Version]
- Charney, J.G. Dynamical forecasting by numerical process. In Compendium of Meteorology; Malone, T.F., Ed.; American Meteorological Society: Boston, MA, USA, 1951; pp. 470–482. [Google Scholar]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Liu, S.; Liang, S.; Qin, J. Improving predictions of water and heat fluxes by assimilating MODIS land surface temperature products into the common land model. J. Hydrometeorol. 2011, 12, 227–244. [Google Scholar] [CrossRef]
- Stensrud, D.J. Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Zeng, Y.; Xie, Z.; Yu, Y.; Liu, S.; Wang, L.; Zou, J.; Qin, P.; Jia, B. Effects of anthropogenic water regulation and groundwater lateral flow on land processes. J. Adv. Model. Earth Syst. 2016, 8, 1106–1131. [Google Scholar] [CrossRef]
- Liu, J.; Jia, B.; Xie, Z.; Shi, C. Ensemble simulation of land evapotranspiration in China based on a multi-forcing and multi-model approach. Adv. Atmos. Sci. 2016, 33, 673–684. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Högström, U.; Bergström, H. Organized turbulence structures in the near-neutral atmospheric surface layer. J. Atmos. Sci. 1996, 53, 2452–2464. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Lettenmaier, D.; Lohmann, D.; Wood, E.F.; Liang, X. PILPS-2c Workshop Report; Princeton University: Princeton, NJ, USA, 1996. [Google Scholar]
- Gupta, H.V.; Bastidas, L.A.; Sorooshian, S.; Shuttleworth, W.; Yang, Z. Parameter estimation of a land surface scheme using multicriteria methods. J. Geophys. Res. Atmos. 1999, 104, 19491–19503. [Google Scholar] [CrossRef] [Green Version]
- Jackson, C.; Xia, Y.; Sen, M.K.; Stoffa, P.L. Optimal parameter and uncertainty estimation of a land surface model: A case study using data from Cabauw, Netherlands. J. Geophys. Res. Atmos. 2003, 108, 4583. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gupta, H.V.; Sorooshian, S.; Bastidas, L.A.; Shuttleworth, W.J. Constraining land surface and atmospheric parameters of a locally coupled model using observational data. J. Hydrometeorol. 2005, 6, 156–172. [Google Scholar] [CrossRef]
- Hou, Z.; Huang, M.; Leung, L.R.; Lin, G.; Ricciuto, D.M. Sensitivity of surface flux simulations to hydrologic parameters based on an uncertainty quantification framework applied to the Community Land Model. J. Geophys. Res. Atmos. 2012, 117, 156–169. [Google Scholar] [CrossRef]
- Li, J.; Duan, Q.; Gong, W.; Ye, A.; Dai, Y.; Miao, C.; Di, Z.; Tong, C.; Sun, Y. Assessing parameter importance of the Common Land Model based on qualitative and quantitative sensitivity analysis. Hydrol. Earth Syst. Sc. 2013, 17, 3279–3293. [Google Scholar] [CrossRef] [Green Version]
- Gan, Y.; Liang, X.; Duan, Q.; Choi, H.I.; Dai, Y.; Wu, H. Stepwise sensitivity analysis from qualitative to quantitative: Application to the terrestrial hydrological modeling of a Conjunctive Surface-Subsurface Process (CSSP) land surface model. J. Adv. Model. Earth Syst. 2015, 7, 648–669. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Duan, Q.; Gong, W.; Ye, A.; Di, Z.; Miao, C. An evaluation of adaptive surrogate modeling based optimization with two benchmark problems. Environ Modell. Softw. 2014, 60, 167–179. [Google Scholar] [CrossRef] [Green Version]
- Gong, W.; Duan, Q.; Li, J.; Wang, C.; Di, Z.; Dai, Y.; Ye, A.; Miao, C. Multi-objective parameter optimization of Common Land Model using adaptive surrogate modeling. Hydrol. Earth Syst. Sc. 2015, 19, 2409–2425. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; de Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Viovy, N. CRUNCEP Version 7-Atmospheric Forcing Data for the Community Land Model; Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Statist. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Fang, K.; Lin, D.K.J.; Winker, P.; Zhang, Y. Uniform design: Theory and application. Technometrics 2000, 42, 237–248. [Google Scholar] [CrossRef]
- Di, Z.; Duan, Q.; Gong, W.; Ye, A.; Miao, C. Parametric sensitivity analysis of precipitation and temperature based on multi-uncertainty quantification methods in the weather research and forecasting model. Sci. China Earth Sci. 2017, 60, 876–898. [Google Scholar] [CrossRef]
- Di, Z.; Duan, Q.; Wang, C.; Ye, A.; Miao, C.; Gong, W. Assessing the applicability of WRF optimal parameters under the different precipitation simulations in the Greater Beijing Area. Clim. Dyn. 2018, 50, 1927–1948. [Google Scholar] [CrossRef]
- Di, Z.; Duan, Q.; Shen, C.; Xie, Z. Improving WRF typhoon precipitation and intensity simulation using a surrogate-based automatic parameter optimization method. Atmosphere 2020, 11, 89. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Huang, G.; Gan, W.; Chen, M. Multi-scale temporal characteristics of the dryness/wetness over Northern China during the last century. Chin. J. Atmos. Sci. 2005, 29, 671–681. (In Chinese) [Google Scholar]
- Peters-Lidard, C.D.; Zion, M.S.; Wood, E.F. A soil-vegetation-atmosphere transfer scheme for modeling spatially variable water and energy balance processes. J. Geophys. Res. Atmos. 1997, 102, 4303–4324. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State–NCAR MM5 modeling system part I: Model implementation and sensitivity. Mon. Wea. Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Hou, Z.; Leung, L.R.; Ke, Y.; Liu, Y.; Fang, Z.; Sun, Y. Uncertainty analysis of runoff simulations and parameter identifiability in the Community Land Model: Evidence from MOPEX basins. J. Hydrometeorol. 2013, 14, 1754–1772. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land–atmosphere interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Gan, Y.; Duan, Q.; Gong, W.; Tong, C.; Sun, Y.; Chu, W.; Ye, A.; Miao, C.; Di, Z. A comprehensive evaluation of various sensitivity analysis methods: A case study with a hydrological model. Environ. Modell. Softw. 2014, 51. [Google Scholar] [CrossRef] [Green Version]











| Index | Parameter | Default | Range | Description |
|---|---|---|---|---|
| P2 | fdrai | 2.5 | (0.1, 5) | Decay factor of subsurface flow (m−1) |
| P4 | Sy | 0.2 | (0.02, 0.27) | Fraction of water volume drained by gravity in an unconfined aquifer |
| P6 | poro_b | 0.489 | (0.4401, 0.5379) | The intercept of mineral soil porosity pedotransfer function |
| P10 | suc_b | 1.88 | (1.692, 2.068) | The intercept of pedotransfer function of saturated mineral soil matric potential |
| P16 | z0mr | 1 | (0.7, 1.3) | Ratio of momentum roughness length to canopy top height |
| P32 | rholnir | 1 | (0.7, 1.3) | Leaf reflectance: near-infrared radiation |
| P36 | taulnir | 1 | (0.7, 1.3) | Leaf transmittance: near-infrared radiation |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Di, Z.; Duan, Q.; Xie, Z.; Gong, W. Improved Land Evapotranspiration Simulation of the Community Land Model Using a Surrogate-Based Automatic Parameter Optimization Method. Water 2020, 12, 943. https://doi.org/10.3390/w12040943
Zhang C, Di Z, Duan Q, Xie Z, Gong W. Improved Land Evapotranspiration Simulation of the Community Land Model Using a Surrogate-Based Automatic Parameter Optimization Method. Water. 2020; 12(4):943. https://doi.org/10.3390/w12040943
Chicago/Turabian StyleZhang, Chong, Zhenhua Di, Qingyun Duan, Zhenghui Xie, and Wei Gong. 2020. "Improved Land Evapotranspiration Simulation of the Community Land Model Using a Surrogate-Based Automatic Parameter Optimization Method" Water 12, no. 4: 943. https://doi.org/10.3390/w12040943
APA StyleZhang, C., Di, Z., Duan, Q., Xie, Z., & Gong, W. (2020). Improved Land Evapotranspiration Simulation of the Community Land Model Using a Surrogate-Based Automatic Parameter Optimization Method. Water, 12(4), 943. https://doi.org/10.3390/w12040943