Using Wastewater in Irrigation: The Effects on Infiltration Process in a Clayey Soil

Abstract

Soil water infiltration is a critical process in the soil water cycle and agricultural practices, especially when wastewater is used for irrigation. Although research has been conducted to evaluate the changes in the physical and chemical characteristics of soils irrigated by treated wastewater, a quantitative analysis of the effects produced on the infiltration process is still lacking. The objective of this study is to address this issue. Field experiments previously conducted on three adjacent field plots characterized by the same clayey soil but subjected to three different irrigation treatments have been used. The three irrigation conditions were: non-irrigated (natural conditions) plot, irrigated plot with treated wastewater for two years, and irrigated plot with treated wastewater for five years. Infiltration measurements performed by the Hood infiltrometer have been used to estimate soil hydraulic properties useful to calibrate a simplified infiltration model widely used under ponding conditions, that were existing during the irrigation stage. Our simulations highlight the relevant effect of wastewater usage as an irrigation source in reducing cumulative infiltration and increasing overland flow as a result of modified hydraulic properties of soils characterized by a lower capacity of water drainage. These outcomes can provide important insights for the optimization of irrigation techniques in arid areas where the use of wastewater is often required due to the chronic shortage of freshwater.

1. Introduction

A quantitative study of water movement in the vadose zone allows us to identify strategies for water conservation, flood/runoff and erosion control, and the assessment of aquifer potential contamination due to migration of water-soluble chemicals [1]. Infiltration of irrigation water is one of the most critical processes for successful agricultural activities [2]. It is a key dynamic process to be considered for the design of irrigation systems and optimization, irrigation scheduling, and irrigation management [3]. This process assumes much more importance in arid and semi-arid regions where, because of short periods and low amounts of rainfall, water is a scarce resource considered as a limiting factor for agricultural production. In these areas, the chronic water shortage has compelled the decision-makers to look for non-conventional water sources for irrigation. One of these is the treated wastewater (TWW) [4], which also gives the advantage of low cost if compared with other solutions such as seawater. In this context, a continuous monitoring of the TWW and soil parameters is required to guarantee a sufficient level of water and soil quality for efficient plant development. In comparison to freshwater, usually, TWW has a higher content of organic matter and nutrients that, particularly in arid soils, are required for plant growth. However, it contains some elements that can adversely affect soil and plant [5]. Major effects produced by TWW are the physical clogging by suspended solids and the bioclogging facilitated by dissolved organic matter [6,7]. The clogging process typically results in the reduction of soil porosity and potential hydraulic conductivity. Bedbabis et al. [6] reported a decrease in soil infiltration after 4 years of using treated wastewater in irrigation. Similar results were obtained by Alizadeh et al. [8] in Iran as a result of using treated wastewater for irrigation of a cornfield for 2 years where the infiltration rate decreased by 15.6%. Moreover, Tunc and Sahin [7] reported a decrease in soil infiltration after having used treated wastewater in irrigating different crops grown in loamy soil, as a result of decreasing macropores by the suspended materials in the TWW.

On these bases, it is clear that a recommended use of TWW as the irrigation water source requires complete knowledge of its long-term effects on both hydraulic characteristics and the quality level of agricultural soils. Recently, Gharaibeh et al. [9] investigated the long-term impacts of irrigation with TWW on the physicochemical properties of soil through multi-year field trials. Infiltration measurements on three plots subjected to different irrigation durations were involved. They found that irrigation with TWW for a few years affected soil physicochemical properties producing an increase of electrical conductivity and sodium adsorption ratio. On the other hand, a decrease in pH, infiltration and unsaturated hydraulic conductivity due to pore-clogging by surface deposition of suspended materials was also observed. Furthermore, a slight decrease in bulk density and observable increases in aggregation percentage due to a significant increase in the organic matter were also highlighted. However, in this study, the effects of physical and chemical modifications of soil on the soil capability of absorbing water and generating surface runoff were not quantitatively extrapolated.

The objective of this work is to integrate the analysis by Gharaibeh et al. [9] through a quantitative estimate of the expected effects on the infiltration and runoff production processes due to multi-year TWW irrigation. This issue represents an open challenge in the light of optimizing irrigation techniques in arid and semi-arid geographic zones. Field experiments previously conducted on three adjacent field plots characterized by the same clayey soil but subjected to three different irrigation treatments have been used to address this issue. The three irrigation conditions were: non-irrigated (natural conditions) plot, irrigated plot with TWW for two years, and irrigated plot with TWW for five years. Data of infiltration measurements, earlier performed by the Hood infiltrometer, have been used here to estimate the soil hydraulic properties. These quantities have enabled us to calibrate a well-known infiltration model under the ponded conditions representative of the irrigation stage. The adopted approach has provided insights that can be useful in irrigation system designing as well as in optimizing the use of TWW.

2. Materials: Field Experiments

2.1. Experimental Site

The field experiments used here and previously described by Gharaibeh et al. [9] were conducted at Jordan University of Science & Technology (JUST) (32°27′57.4” N latitude, 35°57′54.4” E longitude), 70 km north of Amman, Jordan. The experiments were performed on three adjacent field plots (each of 0.8 ha) characterized by the same soil texture. The soil is classified as fine and mixed with clayey soil texture (clay 48%, silt 37%, and sand 15%) and thermic Typic Calcixerert characterized by 15% CaCO₃ content. The three plots were subjected to three different TWW irrigation patterns. The first plot was not-irrigated (rain-fed) and is used here as the no-TWW benchmark. The second plot was irrigated with TWW for two years, while the third plot was irrigated with TWW for five years. The TWW used in the experiments was supplied from a wastewater treatment plant located in the JUST campus, which uses rotating biological contactors. More details about water characteristics and irrigation strategies can be found in Gharaibeh et al. [9]. In the following sections, these treatments are referred to as 0 YR, 2 YR, and 5 YR, respectively. The main chemical soil characteristics of the three plots are presented in

Table 1. Selected chemical properties for the soil of the three plots: pH, electrical conductivity (EC), organic matter (OM), and cation-exchange capacity (CEC).

Treatment/Plot	pH	EC (dS m−1)	OM (%)	CEC (cmole(+) kg−1)
0YR	6.9	0.7	2.77	32.49
2YR	7.7	1.68	4.37	31.16
5YR	7.4	2.09	7.19	33.44

.

2.2. Measurements of Hydraulic Properties

The Hood infiltrometer (IL-2700, Umwelt-Gerate-Technik GmbH, Muncheberg, Germany) was used for in-situ infiltration measurements following Schwarzel and Punzel [10]. This device was chosen because it maintains the soil surface and pore system undisturbed. Furthermore, it allows us to perform infiltration measurements at different water tensions. The measurements were realized in 2013 on an undisturbed soil surface. Each experiment was performed at least three days after the last rain or irrigation event. Five measurements (replicates) per each site (treatment) were conducted on randomly distributed locations. Infiltration tests were carried out by applying on the soil surface tensions ranging from 0 mm to the value of the soil bubbling point with steps of 20 mm. For each tension value, the infiltration rate was allowed to reach steady conditions for approximately 8 min before the tension level was changed to the next level.

Following Gharaibeh et al. [9], steady-state infiltration can be described using Wooding model [11]:

$${\mathrm{q}}_{\mathrm{s}}\left(\mathsf{\Psi }\right)=\mathrm{K}\left(\mathsf{\Psi }\right)(1+\frac{4}{\mathsf{\pi }\mathrm{r}\mathsf{\alpha }})$$

(1)

where q_s($\mathsf{\Psi }$) is the steady infiltration rate at the fixed tension $\mathsf{\Psi }$, K($\mathsf{\Psi }$) is the unsaturated hydraulic conductivity, r is the infiltrometer radius and α is the sorptive number. Substituting the exponential model of Gardner [12]:

$$\mathrm{K}\left(\mathsf{\Psi }\right)={\mathrm{K}}_{\mathrm{s}}{\mathrm{e}}^{\mathsf{\alpha }\mathsf{\Psi }}$$

(2)

and applying the natural logarithm to both sides, Equation (1) becomes:

$$\ln [{\mathrm{q}}_{\mathrm{s}}(\mathsf{\Psi })]=\mathsf{\alpha }\mathsf{\Psi }+\ln [{\mathrm{K}}_{\mathrm{s}}(1+\frac{4}{\mathsf{\pi }\mathrm{r}\mathsf{\alpha }})]$$

(3)

where K_s is the saturated hydraulic conductivity. Equation (3) highlights a linear relationship between ln[q_s($\mathsf{\Psi }$)] and $\mathsf{\Psi }$ with α representing the slope. Linear regression can be therefore used on experimental pairs of ln[q_s($\mathsf{\Psi }$)] and $\mathsf{\Psi }$ for estimating α. The estimate of K_s can be then obtained by Equation (1) for $\mathsf{\Psi }$= 0:

$${\mathrm{K}}_{\mathrm{s}}=\frac{{\mathrm{q}}_{\mathrm{s}}\left(0\right)}{1+\left(4/\mathsf{\pi }\mathrm{r}\mathsf{\alpha }\right)}$$

(4)

Figure 1 shows an example of results based on the experiments performed on the three plots and described by Gharaibeh et al. [9]. Specifically, Figure 1a shows the instantaneous infiltration curves obtained during the first replicate of the infiltration experiment in each of the three plots subjected to different irrigation treatments (0YR, 2YR, and 5YR). Figure 1b represents cumulative infiltration curves averaged over the five replicates performed in each plot. As can be seen, the cumulative infiltration at the end of the 90 min experiments for the 0YR, 2YR, and 5YR treatments were 140 mm, 68 mm, and 59 mm, respectively, showing a significant reduction of soil infiltration capacity when TWW is applied. This reduction is likely due to the high load of the suspended solids present in the treated wastewater [9,13].

Through the procedure described in Section 2.2, Gharaibeh et al. [9] obtained the saturated hydraulic conductivity and sorptive number averaged over five replicates of infiltration measurements realized on each plot/treatment (

Table 2. Saturated hydraulic conductivity, K_s, and sorptive number, α, estimated through the procedure described in Section 2.2 and averaged on five replicates of the infiltration tests performed on each plot [9].

Treatment/Plot	Ks (cm/h)	α (1/cm)
0YR	2.94	0.056
2YR	2.75	0.161
5YR	2.69	0.212

). Based on these results K_s is not significantly different among the three considered treatments even though a slightly decreasing trend can be detected with increasing the number of TWW irrigation years. This result suggests that the usage of TWW in irrigation does not alter morphology and connectivity of the largest pores which mainly influences the saturated hydraulic conductivity. However, the estimate of the sorptive number shows a relevant difference in the three plots with values significantly increased for TWW irrigated sites where, as a consequence, the unsaturated hydraulic conductivity expressed through the Gardner [12] model had lower values (see Figure 2). Considering that the sorptive number parameter indicates the relative magnitudes of gravity and capillarity forces during unsaturated flow [14], this outcome suggests a significant reduction of fine pores, that drain water at suction levels < 0 cm, with respect to the total porosity. This evidence was justified by Gharaibeh et al. [9] also with the presence in TWW of both high loads of organic material and suspended solids that tend to settle in the finer soil pore spaces where the flow velocity is lower. Furthermore, the application for long periods of wastewater determined a reduction and disconnection of soil micro- and mesopores leading to a significant drop in hydraulic conductivity of unsaturated soils.

3. Methodology

In this study, a simplified infiltration model widely used under ponding conditions was selected [15] This model is based on an infinite-series solution of the Richards flow equation [16] under the hypothesis of ponding conditions, which results in a two-term infiltration equation expressed as:

$$\mathrm{I}={\mathrm{St}}^{1/2}+\mathrm{At}$$

(5)

where I is the cumulative infiltration, t is the time, S is the soil sorptivity, and A is a constant that is related to the saturated hydraulic conductivity (typically assumed as 0.4 Ks).

The sorptivity parameter can be defined as

$$\mathrm{S}\left({\mathsf{\Psi }}_0\right)=\lceil \mathsf{\gamma }\left(\mathsf{\theta }\left({\mathsf{\Psi }}_0\right)-\mathsf{\theta }\left({\mathsf{\Psi }}_{\mathrm{i}}\right)\right){{\displaystyle \int }}_{{\mathsf{\Psi }}_{\mathrm{i}}}^{{\mathsf{\Psi }}_0}\mathrm{K}\left(\mathsf{\Psi }\right){\mathrm{d}\mathsf{\Psi }\rceil }^{\frac{1}{2}} {\mathsf{\Psi }}_{\mathrm{i}}<{\mathsf{\Psi }}_0<0,\mathsf{\theta }\left({\mathsf{\Psi }}_{\mathrm{i}}\right)={\mathsf{\theta }}_{\mathrm{i}}<\mathsf{\theta }\left({\mathsf{\Psi }}_0\right)<{\mathsf{\theta }}_{\mathrm{s}}$$

(6)

where $\mathsf{\theta }$ is the soil volumetric water content, the subscripts i and s refer to initial and saturated conditions, respectively, and γ =1.818 is a dimensionless empirical constant [17] related to the shape of the wetting front. Following Reynolds and Clarke Topp [18] and using Equation (2), the following equation holds:

$$\mathrm{S}\left({\mathsf{\Psi }}_0\right)=\lceil \mathsf{\gamma }\left(\mathsf{\theta }\left({\mathsf{\Psi }}_0\right)-\mathsf{\theta }\left({\mathsf{\Psi }}_{\mathrm{i}}\right)\right){\frac{\mathrm{K}\left({\mathsf{\Psi }}_0\right)}{\mathsf{\alpha }\left({\mathsf{\Psi }}_0\right)}\rceil }^{\frac{1}{2}}$$

(7)

This equation highlights that sorptivity reduces with increasing antecedent water content, decreasing hydraulic conductivity and increasing sorptive number. For ${\mathsf{\Psi }}_0=0$ Equation (7) becomes:

$$\mathrm{S}=\lceil \mathsf{\gamma }\left({\mathsf{\theta }}_{\mathrm{s}}-{\mathsf{\theta }}_{\mathrm{i}}\right){\frac{{\mathrm{K}}_{\mathrm{s}}}{\mathsf{\alpha }}\rceil }^{\frac{1}{2}}$$

(8)

Based on Equation (8) values of sorptivity have been estimated for the three plots/treatments of this study (

Table 3. Philip’s model parameters estimated for the three experimental plots of this study. The difference between saturated soil water content, ${\mathsf{\theta }}_{\mathrm{s}}$, and initial soil water content, ${\mathsf{\theta }}_{\mathrm{i}}$, is also given.

Treatment/Plot	${\mathsf{\theta }}_{\mathbf{s}}-{\mathsf{\theta }}_{\mathbf{i}}$	S	A
		(cm/h0.5)	(cm/h)
0 YR	0.49	6.84	1.18
2 YR	0.42	3.61	1.10
5 YR	0.41	3.08	1.08

).

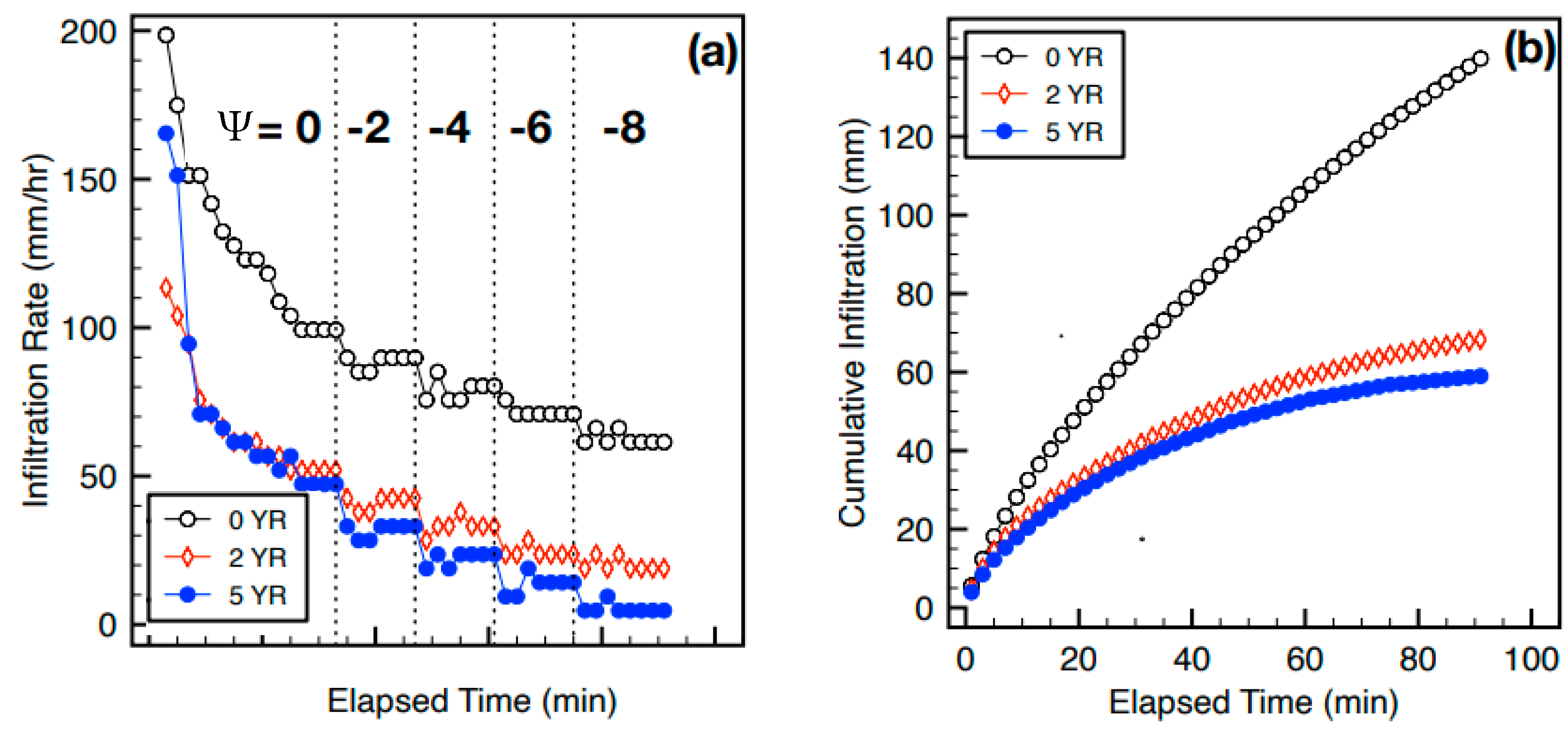
4. Results and Discussion

Based on the Philip model parameters estimated for the three experimental plots/treatments and shown in Table 3, it can be deduced that the sorptivity markedly decreases with increasing the period of irrigation using TWW. On the other hand, the A parameter is rather similar for all treatments. These results suggest that A, which is related to the saturated hydraulic conductivity and connectivity of the largest pores, is not affected by the TWW movement. In contrast, the decrease of S could be due to the clogging of the small pores being this parameter mainly influenced by the sorptive number for invariant values of K_s (Equation (8)). In this context small differences of antecedent soil conditions in terms of ${\mathsf{\theta }}_{\mathrm{s}}-{\mathsf{\theta }}_{\mathrm{i}}$—slightly decreasing from 0YR to 5YR treatments—were observed among the three plots (see Table 3).

Adopting the parameters of Table 3, the Philip model has been applied in the case of an irrigation process of duration 1.5 h and rate sufficiently high to determine quickly the saturation of soil surface in the three plots with different earlier irrigation treatments. The results obtained are shown in Figure 3 in terms of cumulative infiltration. The simulated cumulative infiltrations (Figure 3) at the irrigation end for the 0YR, 2YR, and 5YR plots were 101, 61, and 54 mm, respectively. Statistical analysis, involving one-way ANOVA test at the probability level p < 0.001 and Tukey’s Honestly Significant Difference test at level p < 0.05, has shown that there are no significant differences between the two plots irrigated with TWW (2YR and 5YR treatments), while the cumulative infiltration in these two plots is significantly lower than that of the control plot (0YR). This significant decrease in cumulative infiltration in the 2YR and 5YR TWW irrigated soils could be explained by the high load of suspended solids present in the TWW. When soil is irrigated by TWW, these suspended materials settle in the smaller pores. With time, the micropores as well as the mesopores become smaller and disconnected producing a significant reduction in infiltration rate and cumulative infiltration. In agreement with this conclusion, Viviani and Iovino [19] showed a reduction in soil porosity which led to a decrease in soil infiltration rate as a result of pore-clogging due to the use of TWW. Similarly, Bardhan et al. [13] concluded that suspended solids loaded in the TWW reduced soil infiltrability due to pore-clogging.

The aforementioned results can have relevant implications in arid and semi-arid regions where water is limited for the majority of irrigation farms. In this context, water use efficiency is an important issue to be considered because with its increase more crops can be irrigated. Based on our outcomes, for a fixed irrigation pattern able to produce approximately immediate soil surface ponding, the use of TWW reduces gradually in time the amount of water entering the soil and increases runoff. To better specify this element, Figure 4 shows the reduction in time of water amount that the soil can absorb in 2YR and 5YR plots with respect to the control plot (0YR) for irrigation duration up to 3 h. From this figure it can be observed that for an irrigation period of 1.5 h the water amount absorbed by the soil in 2YR and 5YR plots is reduced by 41 mm and 47 mm, respectively; for an irrigation stage of 3 h, the infiltrated water depth decreases by 58 and 68 mm, respectively. The water amount that the soil is not able to absorb becomes surface runoff. This implies that for an irrigation scheduled time a reduced water amount is requested in these two plots to avoid an increased runoff. The reduction of absorbable water is here interpreted as gained water and expressed in percentage, with respect to the water infiltrated in the control plot, is defined as irrigation efficiency. The trend of this quantity in the function of irrigation duration is represented in Figure 5, which highlights a decreasing advantage with increasing irrigation periods. For durations ranging from 30 min to 180 min, the irrigation efficiency tends to decrease from 50% to 44% and from 48% to 38% for 5YR and 2YR plots, respectively. In any case, the above values show how after just 2 years the efficiency is significantly increased and after a further 3 years, it becomes almost 50%.

5. Conclusions

Insights about the effects on the infiltration process produced by continuous use of TWW for irrigation have been provided. Infiltration measurements earlier realized by the Hood infiltrometer in three adjacent field plots characterized by the same soil type and different durations of TWW irrigation (0, 2, and 5 years, named 0YR, 2YR, and 5YR) have been exploited to estimate the associated Philip model parameters, saturated hydraulic conductivity K_s, and sorptivity S. From infiltration simulations performed by the model under the hypothesis of ponded conditions, applicable during irrigation, a quantitative estimate of TWW usage effects has been carried out.

Specifically:

• The continuous usage of TWW for irrigation determines a lower capacity of water drainage in unsaturated conditions mainly due to the clogging process of the smaller pores by the accumulation of suspended sediments. This leads to a significant decrease of the S parameter in 2YR and 5YR plots, while the saturated hydraulic conductivity linked with the connectivity of larger pores is only weakly affected.
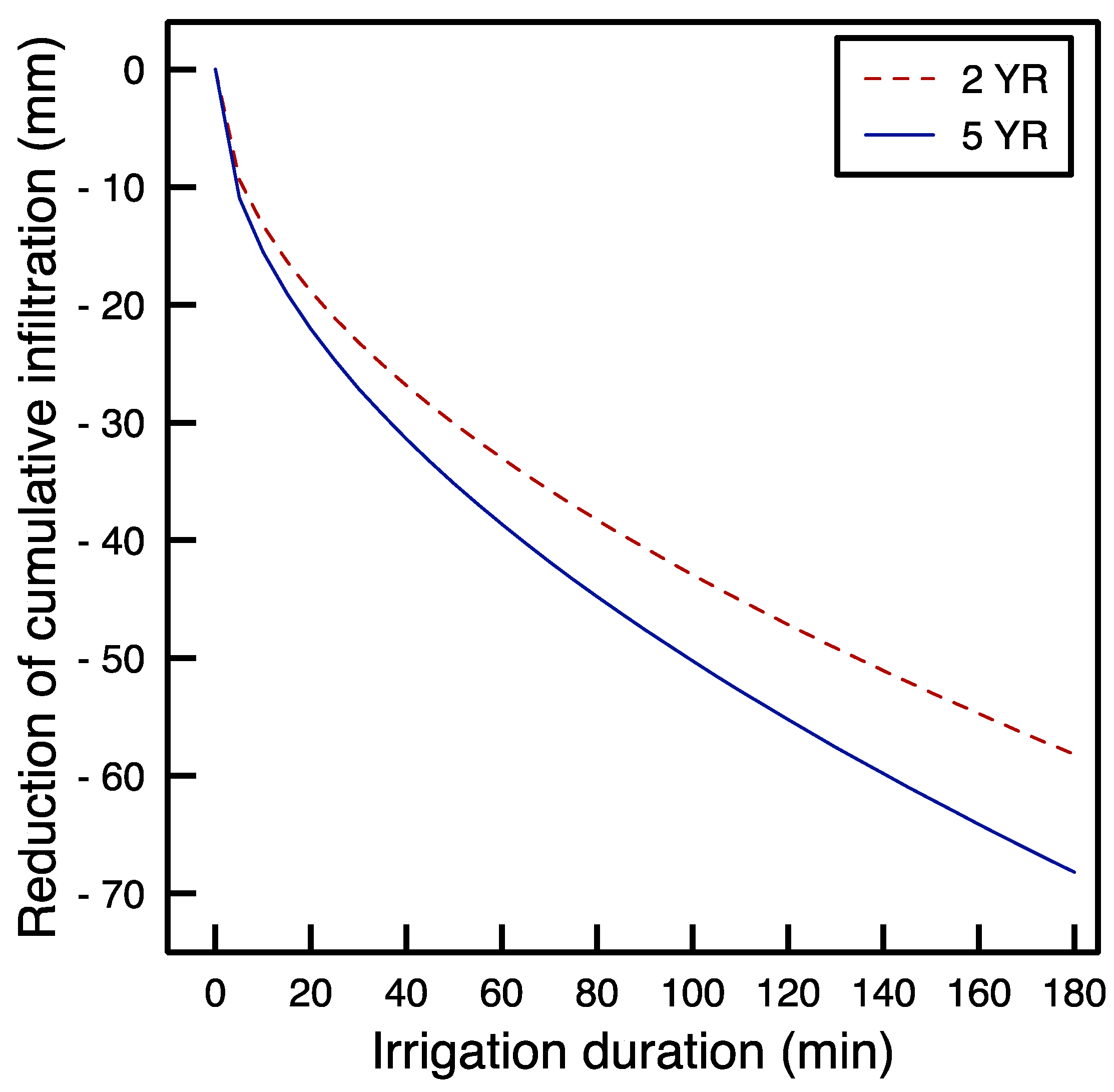
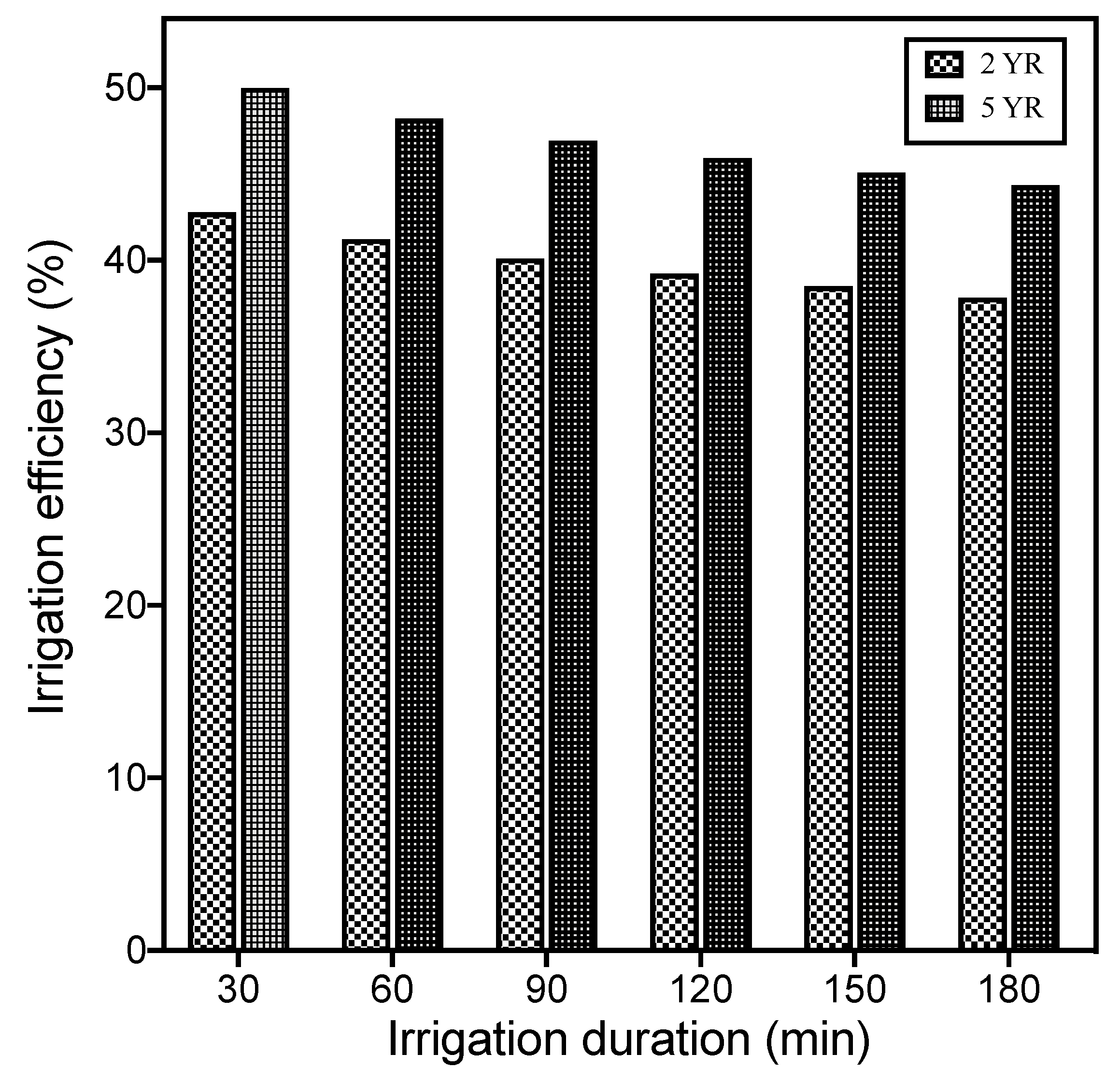
• The simulations by the Philip model with the decreased values of sorptivity have highlighted reductions of cumulative infiltration in a plot with TWW treatment. For an irrigation pattern with a duration of 1.5 h, the reduction of absorbable water amount with respect to 0YR plot has been found equal to 40% and 47% in 2YR and 5YR plots, respectively, with irrigation duration equal to 3 h the percentages reduce to 38% and 44%, respectively. Equivalent increases of runoff have to be expected if the irrigation water amount remains the same. Hence, the percentage reductions of cumulative infiltration have been here interpreted as water amounts that can be saved for that planned irrigation pattern and have been considered a measure of the gained irrigation efficiency.
• The above-defined advantages of TWW usage (in terms of irrigation efficiency) slightly decrease with increasing irrigation duration (30 min up to 180 min) ranging from 50% to 44% and from 48% to 38% for the 5YR and 2YR plots, respectively. Anyway, the irrigation efficiency is significant and can be relevant in arid and semi-arid areas.

The results of this research would indicate that the use of treated wastewater leads to the reduction of the required water used to irrigate soil limiting runoff. This is an important outcome of this work that indicates the use of treated wastewater in irrigation practice as one of the possible strategies to be adopted in arid zones to increase irrigation efficiency. However, further investigations are required to establish the link between irrigation efficiency defined here and crop production. Furthermore, complete knowledge of TWW long-term effects on quality characteristics of water and agricultural soils is still lacking.