Monitoring and Modelling Interactions between the Montagna dei Fiori Aquifer and the Castellano Stream (Central Apennines, Italy)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hydrogeological and Geomechanical Setting of the Study Area
2.2. Monitoring Strategy
2.3. Numerical Model Set-Up
3. Results
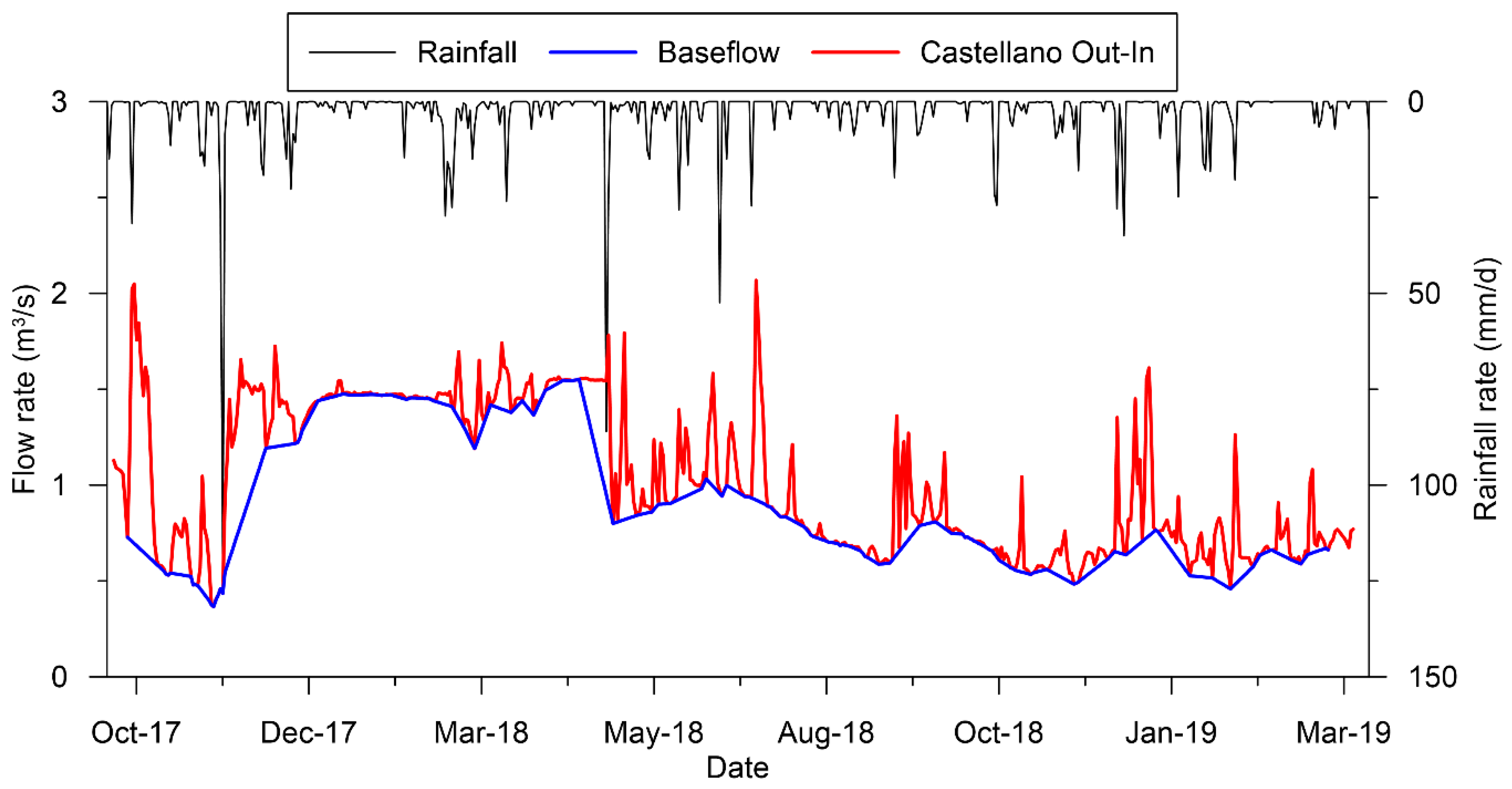
3.1. Monitoring Results
3.2. Steady State Model Results
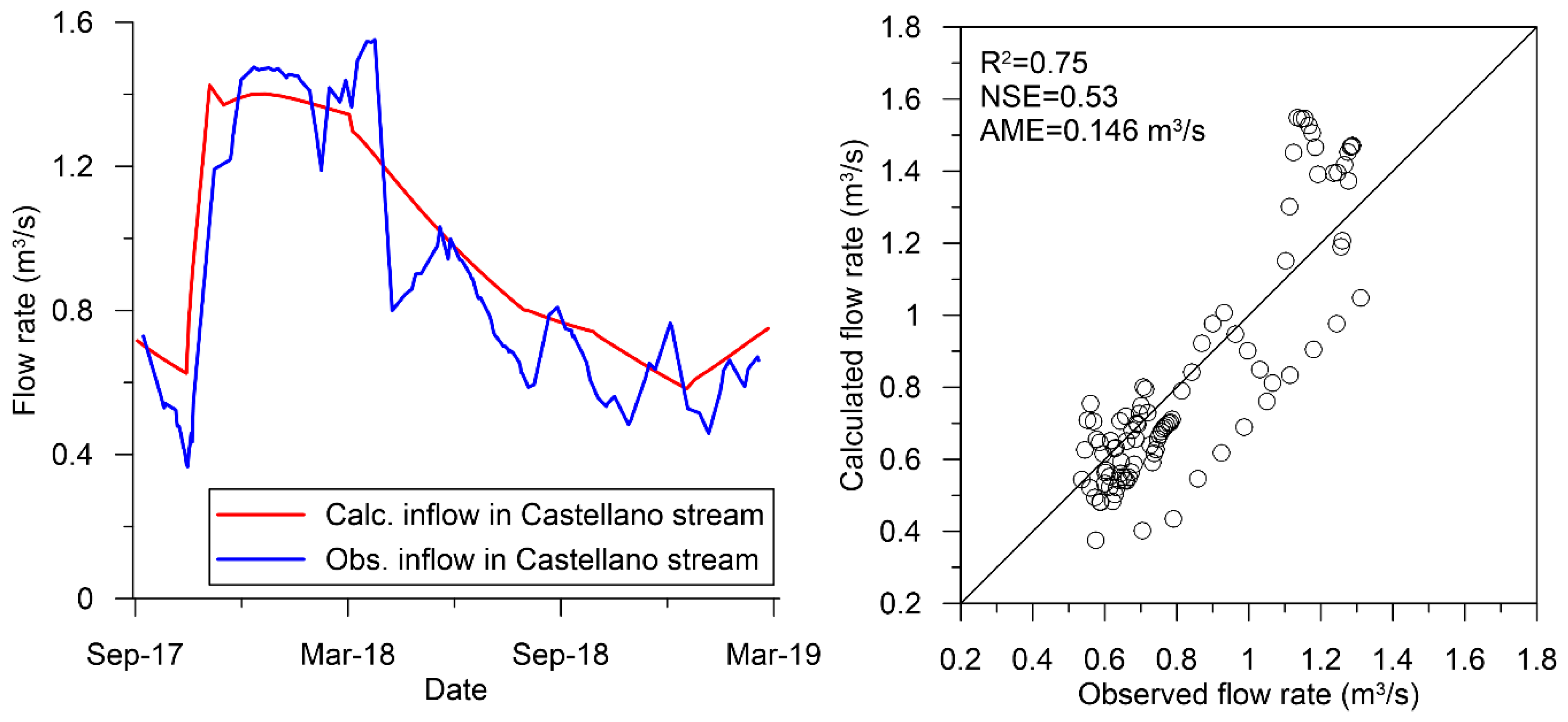
3.3. Transient State Model Results
3.4. Sensitivity Analysis Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaandorp, V.P.; Molina-Navarro, E.; Andersen, H.E.; Bloomfield, J.P.; Kuijper, M.J.; de Louw, P.G. A conceptual model for the analysis of multi-stressors in linked groundwater–surface water systems. Sci. Total. Environ. 2018, 627, 880–895. [Google Scholar] [CrossRef] [PubMed]
- Essaid, H.I.; Zamora, C.M.; McCarthy, K.A.; Vogel, J.R.; Wilson, J.T. Using heat to characterize streambed water flux variability in four stream reaches. J. Environ. Qual. 2008, 37, 1010–1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, C.; Bayer-Raich, M.; Schirmer, M. Characterization of spatial heterogeneity of groundwater-stream water interactions using multiple depth streambed temperature measurements at the reach scale. Hydrol. Earth Sys. Sci. 2006, 10, 849–859. [Google Scholar] [CrossRef] [Green Version]
- Conant, B., Jr. Delineating and quantifying ground water discharge zones using streambed temperatures. Ground Water 2004, 42, 243–257. [Google Scholar] [CrossRef]
- Anibas, C.; Schneidewind, U.; Vandersteen, G.; Joris, I.; Seuntjens, P.; Batelaan, O. From streambed temperature measurements to spatial-temporal flux quantification: Using the LPML method to study groundwater-surface water interaction. Hydrol. Process. 2016, 30, 203–216. [Google Scholar] [CrossRef]
- Kazakis, N.; Oikonomidis, D.; Voudouris, K.S. Groundwater vulnerability and pollution risk assessment with disparate models in karstic, porous, and fissured rock aquifers using remote sensing techniques and GIS in Anthemountas basin, Greece. Environ. Earth Sci. 2015, 74, 6199–6209. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Schornberg, C.; Schmidt, C.; Kalbus, E.; Fleckenstein, J.H. Simulating the effects of geologic heterogeneity and transient boundary conditions on streambed temperatures—Implications for temperature-based water flux calculations. Adv. Water Resour. 2010, 33, 1309–1319. [Google Scholar] [CrossRef]
- Briggs, M.A.; Buckley, S.F.; Bagtzoglou, A.C.; Werkema, D.D.; Lane, J.W., Jr. Actively heated high-resolution fiber-optic-distributed temperature sensing to quantify streambed flow dynamics in zones of strong groundwater upwelling. Water Resour. Res. 2016, 52, 5179–5194. [Google Scholar] [CrossRef] [Green Version]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Zhang, Y.-K.; Bai, E.-W.; Libra, R.; Rowden, R.; Liu, H. Simulation of spring discharge from a limestone aquifer in Iowa. Hydrogeol. J. 1996, 4, 41–54. [Google Scholar] [CrossRef]
- Granata, F.; Saroli, M.; de Marinis, G.; Gargano, R. Machine learning models for spring discharge forecasting. Geofluids 2018, 8328167. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Mace, R.E.; Barrett, M.E.; Smith, B. Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J. Hydrol. 2003, 276, 137–158. [Google Scholar] [CrossRef]
- Martínez-Santos, P.; Andreu, J.M. Lumped and distributed approaches to model natural recharge in semiarid karst aquifers. J. Hydrol. 2010, 388, 389–398. [Google Scholar] [CrossRef]
- Panagopoulos, G. Application of MODFLOW for simulating groundwater flow in the Trifilia karst aquifer, Greece. Environ. Earth Sci. 2012, 67, 1877. [Google Scholar] [CrossRef]
- Sanford, W. Recharge and groundwater models: An overview. Hydrogeol. J. 2002, 10, 110–120. [Google Scholar] [CrossRef]
- Fleury, P.; Plagnes, V.; Bakalowicz, M. Modelling of the functioning of karst aquifers with a reservoir model: Application to Fontaine de Vaucluse (South of France). J. Hydrol. 2007, 345, 38–49. [Google Scholar] [CrossRef]
- Sun, W.; Wu, Q.; Liu, H.; Jiao, J. Prediction and assessment of the disturbances of the coal mining in Kailuan to karst groundwater system. Phys. Chem. Earth. 2015, 89, 136–144. [Google Scholar] [CrossRef]
- Xue, S.; Liu, Y.; Liu, S.; Li, W.; Wu, Y.; Pei, Y. Numerical simulation for groundwater distribution after mining in Zhuanlongwan mining area based on visual MODFLOW. Environ. Earth Sci. 2018, 77, 400. [Google Scholar] [CrossRef]
- Fernández-Álvarez, J.P.; Álvarez-Álvarez, L.; Díaz-Noriega, R. Groundwater numerical simulation in an open pit mine in a limestone formation using MODFLOW. Mine Water Environ. 2016, 35, 145–155. [Google Scholar] [CrossRef]
- Ragab, R.; Bromley, J.; Dörflinger, G.; Katsikides, S. IHMS—Integrated Hydrological Modelling System. Part 2. Application of linked unsaturated, DiCaSM and saturated zone, MODFLOW models on Kouris and Akrotiri catchments in Cyprus. Hydrol. Process. 2010, 24, 2681–2692. [Google Scholar] [CrossRef]
- Shoemaker, W.B.; Cunningham, K.J.; Kuniansky, E.L.; Dixon, J. Effects of turbulence on hydraulic heads and parameter sensitivities in preferential groundwater flow layers. Water Resour. Res. 2008, 44, W03501. [Google Scholar] [CrossRef]
- Surinaidu, L.; Bacon, C.G.D.; Pavelic, P. Agricultural groundwater management in the Upper Bhima Basin, India: Current status and future scenarios. Hydrol. Earth Sys. Sci. 2013, 17, 507–517. [Google Scholar] [CrossRef] [Green Version]
- Guthke, A. Defensible Model Complexity: A Call for Data-Based and Goal-Oriented Model Choice. Ground Water 2017, 55, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey modular ground-water model: The ground-water flow process. U.S. Geological Survey Techniques and Methods 6-A16; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005; 253p.
- Chiang, W.H. Processing Modflow: An Integrated Modeling Environment for the Simulation of Groundwater Flow, Transport and Reactive Processes; Simcore Software: Irvine, CA, USA, 2012; 484p. [Google Scholar]
- Snow, D.T. Anistotropic permeability of fractured media. Water Resour. Res. 1969, 5–6, 1273–1289. [Google Scholar] [CrossRef]
- Mechal, A.; Birk, S.; Dietzel, M.; Leis, A.; Winkler, G.; Mogessie, A.; Kebede, S. Groundwater flow dynamics in the complex aquifer system of Gidabo River Basin (Ethiopian Rift): A multi-proxy approach. Hydrogeol. J. 2017, 25, 519–538. [Google Scholar] [CrossRef] [Green Version]
- Boni, C.F.; Mastrorillo, L.; Petitta, M. Scomposizione della portata dei corsi d’acqua dell’Appennino Marchigiano con il metodo delle portate mensili caratteristiche. Geol. Appl. Idrogeol. 1993, 28, 121–129. [Google Scholar]
- Mastrorillo, L.; Petitta, M. Effective infiltration variability in the Umbria-Marche carbonate aquifers of central Italy. J. Mediter. Earth Sci. 2010, 2, 9–18. [Google Scholar] [CrossRef]
- Morawietz, M.; (University of Oslo, Oslo, Norway). Personal communication, 1997.
- Gentilucci, M.; Barbieri, M.; Lee, H.S.; Zardi, D. Analysis of Rainfall Trends and Extreme Precipitation in the Middle Adriatic Side, Marche Region (Central Italy). Water 2019, 11, 1948. [Google Scholar] [CrossRef] [Green Version]
- Nanni, T.; Vivalda, P. The aquifers of the Umbria-Marche Adriatic region: Relationships between structural setting and groundwater chemistry. Boll. Soc. Geol. Ital. 2005, 124, 523–542. [Google Scholar]
- Hazen, A. Some physical properties of sands and gravels. Mass. State Board Health Ann. Rept. 1892, 539–556. [Google Scholar]
- Mussi, M.; Nanni, T.; Tazioli, A.; Vivalda, P.M. The Mt Conero limestone ridge: The contribution of stable isotopes to the identification of the recharge area of aquifers. Ital. J. Geosci. 2017, 136, 186–197. [Google Scholar] [CrossRef]
- Hill, M.C.; Banta, E.R.; Harbaugh, A.W.; Anderman, E.R. MODFLOW-2000, the US Geological Survey Modular Ground-Water Model; User Guide to the Observation, Sensitivity, and Parameter-Estimation Processes and Three Post-Processing Programs No. 2000-184; US Geological Survey: Reston, VA, USA, 2000.
- Krause, S.; Blume, T. Impact of seasonal variability and monitoring mode on the adequacy of fiber-optic distributed temperature sensing at aquifer-river interfaces. Water Resour. Res. 2013, 49, 2408–2423. [Google Scholar] [CrossRef]
- Loheide, S.P.; Gorelick, S.M. Quantifying stream—Aquifer interactions through the analysis of remotely sensed thermographic profiles and in situ temperature histories. Environ. Sci. Technol. 2006, 40, 3336–3341. [Google Scholar] [CrossRef] [PubMed]
- Partington, D.; Brunner, P.; Simmons, C.T.; Werner, A.D.; Therrien, R.; Maier, H.R.; Dandy, G.C. Evaluation of outputs from automated baseflow separation methods against simulated baseflow from a physically based, surface water-groundwater flow model. J. Hydrol. 2012, 458, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Sophocleous, M.; Perkins, S.P. Calibrated models as management tools for stream-aquifer systems: The case of central Kansas, USA. J. Hydrol. 1993, 152, 31–56. [Google Scholar] [CrossRef]

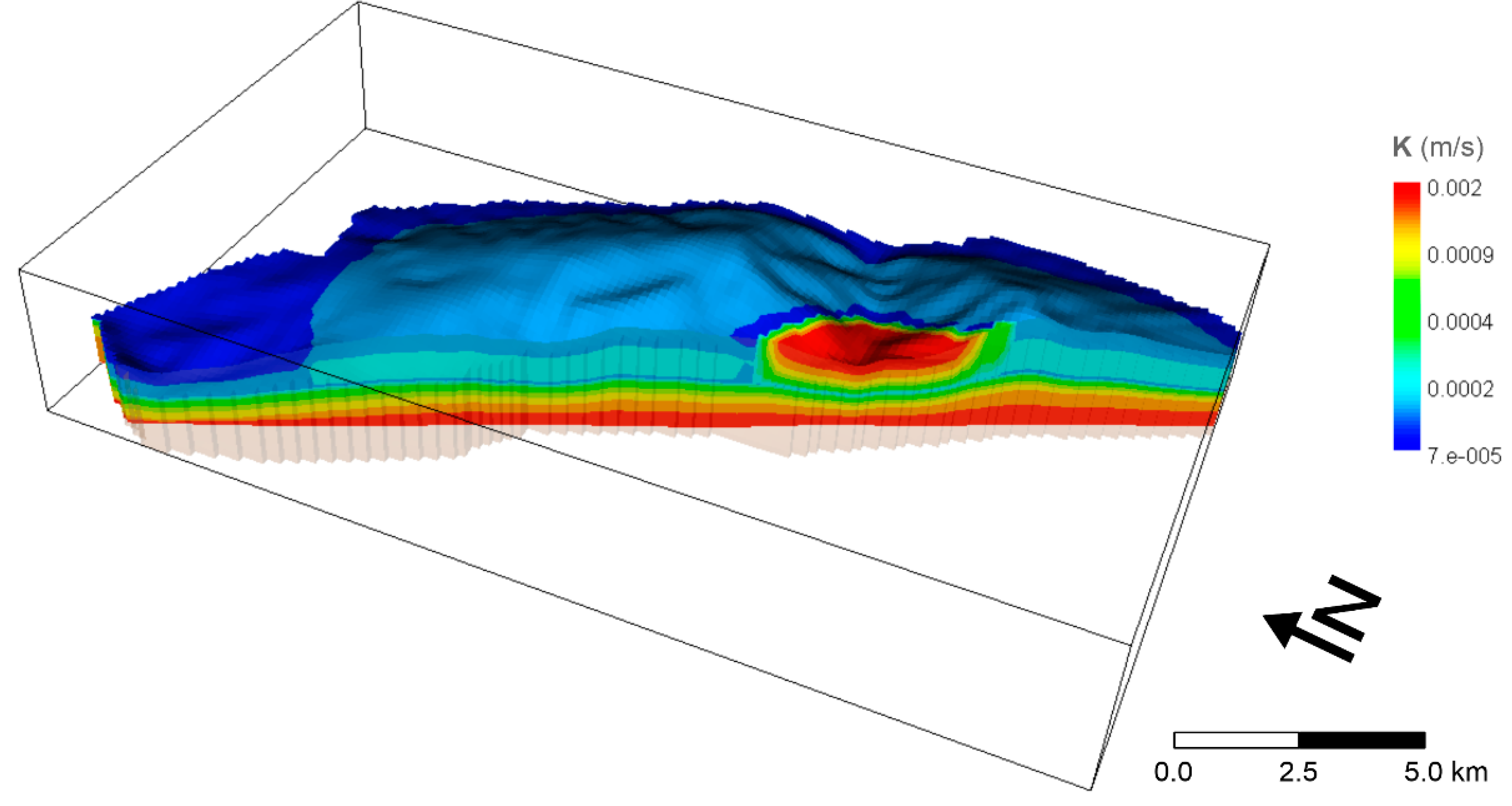



| Geomechanical Tation | Hydrogeological Unit | Elevation (m ASL) | Kmax (m/s) | Orientation and Dipping Plane | Keq (m/s) |
|---|---|---|---|---|---|
| G1 | Calcare Massiccio | 951 | 2.0 × 10−3 | N352°/5° | 1.8 × 10−3 |
| G2 | Calcare Massiccio | 935 | 6.5 × 10−2 | N173°/16° | 3.5 × 10−2 |
| G3 | Calcare Massiccio | 907 | 4.5 × 10−4 | N116°/15° | 2.4 × 10−4 |
| G4 | Jurassic Aquiclude | 868 | 9.8 × 10−5 | N159°/4° | 6.8 × 10−5 |
| G5 | Maiolica Complex | 843 | 3.0 × 10−4 | N2°/2° | 1.8 × 10−4 |
| G6 | Scaglia Complex | 1431 | 3.0 × 10−4 | N181°/45° | 1.5 × 10−4 |
| Flow Term | In (m3/s) | Out (m3/s) | In-Out (m3/s) |
|---|---|---|---|
| Constant Head | 0.0 | 0.108 | −0.108 |
| Recharge | 0.575 | 0.0 | 0.575 |
| River | 0.067 | 0.533 | −0.466 |
| Sum | 0.642 | 0.642 | 0.0 |
| Discrepancy (%) | 0.0 |
| Parameter | Optimized Values | Composite Scaled Sensitivity |
|---|---|---|
| Recharge in stress period 2 | 518 mm/y | 0.392 |
| Recharge in stress period 3 | 259 mm/y | 0.204 |
| Recharge in stress period 7 | 52 mm/y | 0.039 |
| Recharge in stress period 10 | 181 mm/y | 0.030 |
| K layer 1 | 1.1 × 10−4 m/s | 0.049 |
| K layer 2 | 2.2 × 10−4 m/s | 0.057 |
| Castellano river conductance | 1.9 × 10−2 m2/s | 0.133 |
| HFB K | 1.0 × 10−9 m/s | 1.0 × 10-4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tazioli, A.; Colombani, N.; Palpacelli, S.; Mastrocicco, M.; Nanni, T. Monitoring and Modelling Interactions between the Montagna dei Fiori Aquifer and the Castellano Stream (Central Apennines, Italy). Water 2020, 12, 973. https://doi.org/10.3390/w12040973
Tazioli A, Colombani N, Palpacelli S, Mastrocicco M, Nanni T. Monitoring and Modelling Interactions between the Montagna dei Fiori Aquifer and the Castellano Stream (Central Apennines, Italy). Water. 2020; 12(4):973. https://doi.org/10.3390/w12040973
Chicago/Turabian StyleTazioli, Alberto, Nicolò Colombani, Stefano Palpacelli, Micòl Mastrocicco, and Torquato Nanni. 2020. "Monitoring and Modelling Interactions between the Montagna dei Fiori Aquifer and the Castellano Stream (Central Apennines, Italy)" Water 12, no. 4: 973. https://doi.org/10.3390/w12040973
APA StyleTazioli, A., Colombani, N., Palpacelli, S., Mastrocicco, M., & Nanni, T. (2020). Monitoring and Modelling Interactions between the Montagna dei Fiori Aquifer and the Castellano Stream (Central Apennines, Italy). Water, 12(4), 973. https://doi.org/10.3390/w12040973








