Study on the Transport of Terrestrial Dissolved Substances in the Pearl River Estuary Using Passive Tracers
Abstract
:1. Introduction
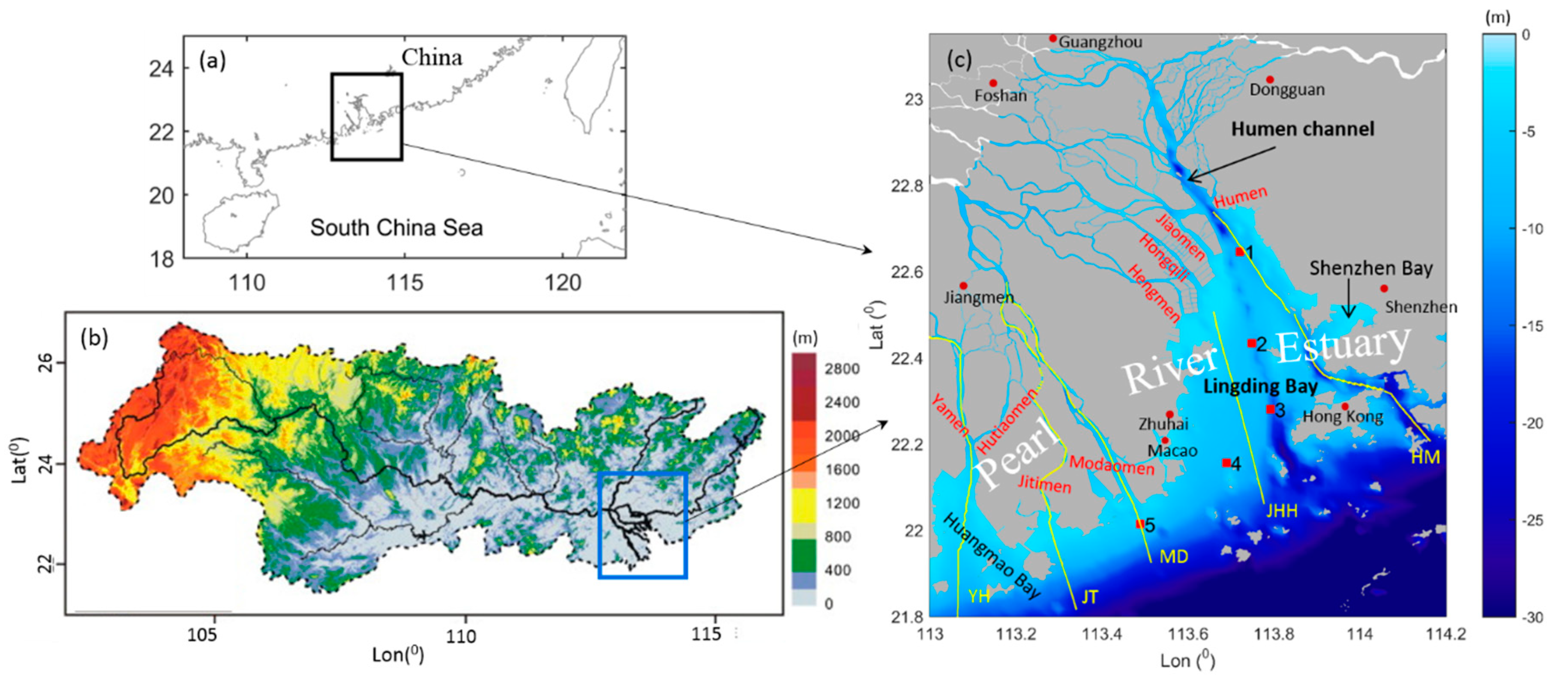
2. Materials and Methods
2.1. Numerical Model Description
2.2. Strategy for Modeling the Transport of Terrestrial Dissolved Substances
3. Results
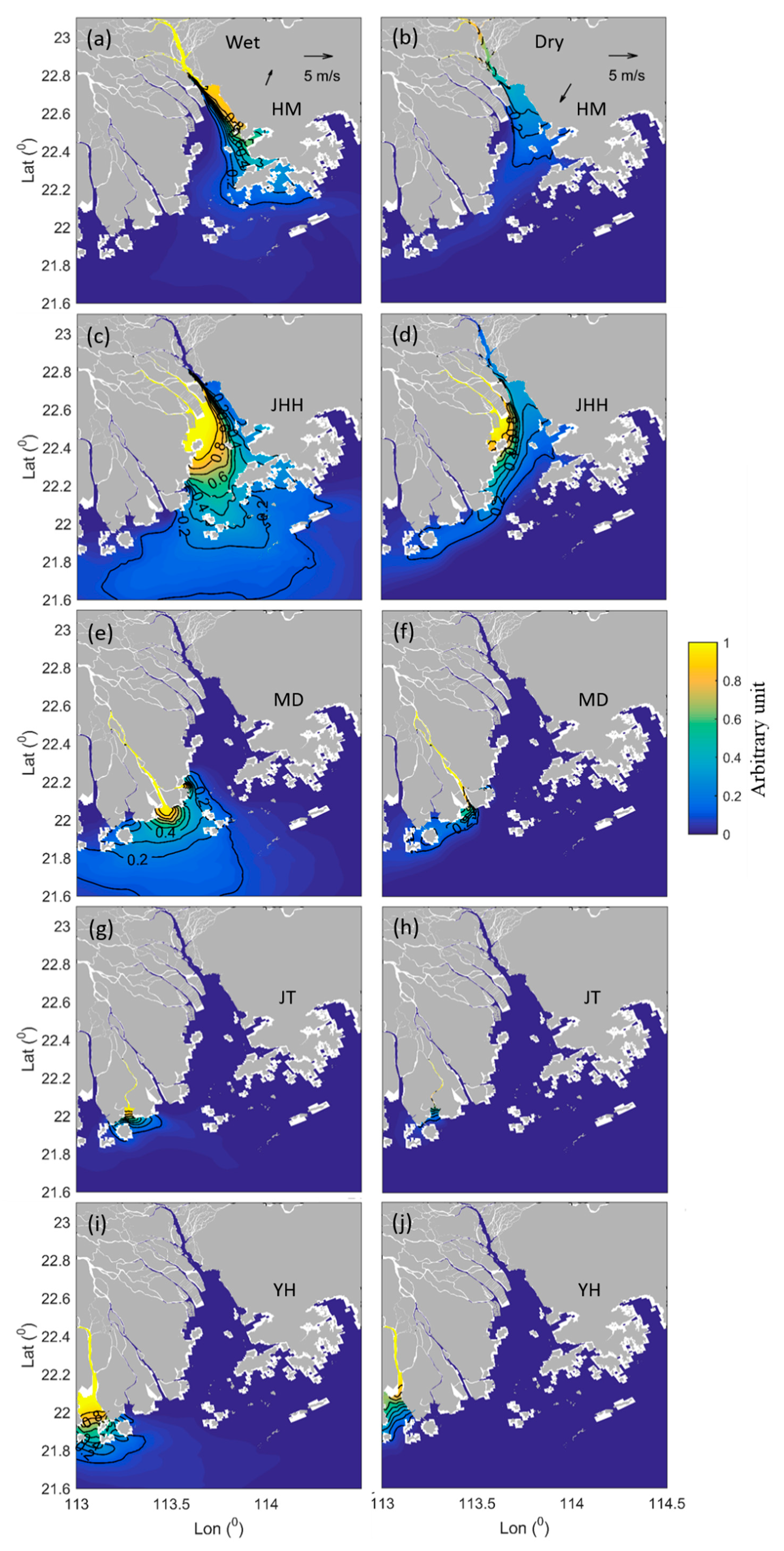
3.1. Distribution of Terrestrial Dissolved Substances Coming from Different Outlets
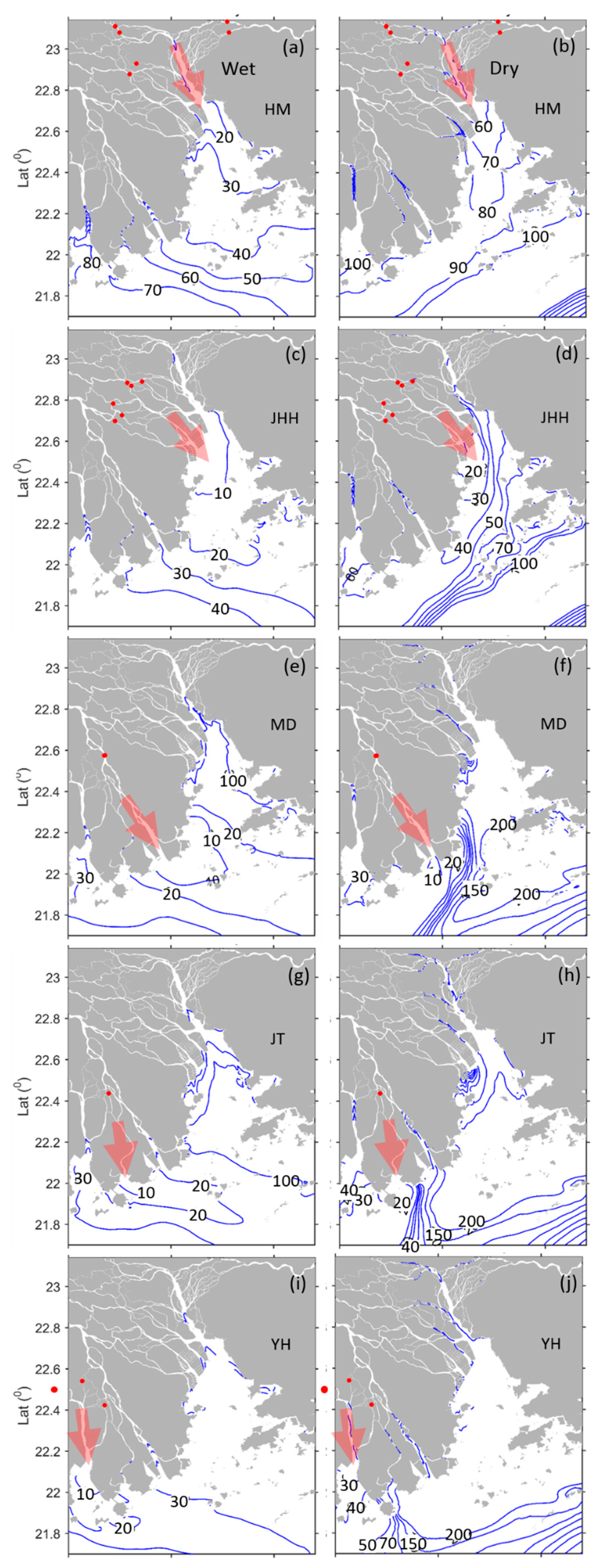
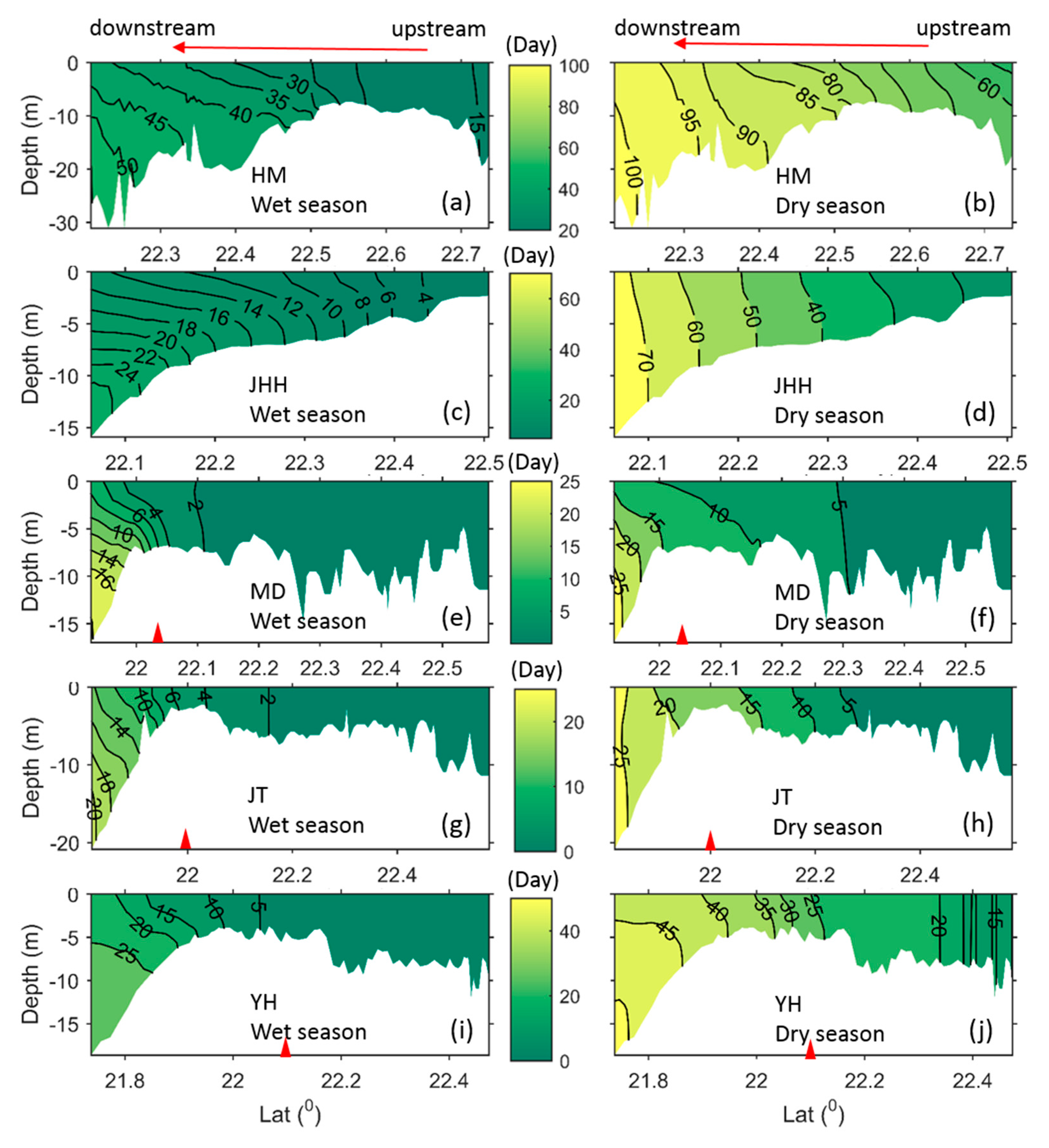
3.2. Transport Time of Terrestrial Dissolved Substances from Each Outlet
4. Discussion
4.1. Variations in Impacted Area
4.2. Effect of Hydrodynamic Condition
4.3. Correlation Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kemp, W.; Boynton, W.; Adolf, J.; Boesch, D.; Boicourt, W.; Brush, G.; Cornwell, J.; Fisher, T.; Glibert, P.M.; Hagy, J.; et al. Eutrophication of Chesapeake Bay: Historical trends and ecological interactions. Mar. Ecol. Prog. Ser. 2005, 303, 1–29. [Google Scholar] [CrossRef]
- Murphy, R.R.; Kemp, W.M.; Ball, W.P. Long-Term Trends in Chesapeake Bay Seasonal Hypoxia, Stratification, and Nutrient Loading. Chesap. Sci. 2011, 34, 1293–1309. [Google Scholar] [CrossRef]
- Nixon, S.W. Coastal marine eutrophication: A definition, social causes, and future concerns. Ophelia 1995, 41, 199–219. [Google Scholar] [CrossRef]
- Paerl, H.W.; Valdes, L.M.; Peierls, B.L.; Adolf, J.E.; Harding, L.W. Anthropogenic and climatic influences on the eutrophication of large estuarine ecosystems. Limnol. Oceanogr. 2006, 51, 448–462. [Google Scholar] [CrossRef] [Green Version]
- WWAP (World Water Assessment Programme). United Nations World Water Development Report 2015: Water for a Sustainable World; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2015. [Google Scholar]
- Liu, B.; Peng, S.; Liao, Y.; Long, W. The causes and impacts of water resources crises in the Pearl River Delta. J. Clean. Prod. 2018, 177, 413–425. [Google Scholar] [CrossRef]
- Rahman, M.; Penny, G.; Mondal, M.; Zaman, M.; Kryston, A.; Salehin, M.; Nahar, Q.; Islam, M.; Bolster, D.; Tank, J.; et al. Salinization in large river deltas: Drivers, impacts and socio-hydrological feedbacks. Water Secur. 2019, 6, 100024. [Google Scholar] [CrossRef]
- Du, J.; Shen, J. Transport of Riverine Material From Multiple Rivers in the Chesapeake Bay: Important Control of Estuarine Circulation on the Material Distribution. J. Geophys. Res. Biogeosci. 2017, 122, 2998–3013. [Google Scholar] [CrossRef]
- Hirst, A.C. Determination of water component age in ocean models: Application to the fate of North Atlantic Deep Water. Ocean Model. 1999, 1, 81–94. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Deleersnijder, E. The concept of age in marine modeling II. Concentration distribution function in the English Channel and the North Sea. J. Mar. Syst. 2002, 31, 279–297. [Google Scholar] [CrossRef] [Green Version]
- Döös, K.; Engqvist, A. Assessment of water exchange between a discharge region and the open sea—A comparison of different methodological concepts. Estuar. Coast. Shelf Sci. 2007, 74, 709–721. [Google Scholar] [CrossRef]
- Hong, B.; Panday, N.; Shen, J.; Wang, H.V.; Gong, W.; Soehl, A. Modeling water exchange between Baltimore Harbor and Chesapeake Bay using artificial tracers: Seasonal variations. Mar. Environ. Res. 2010, 70, 102–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, J.; Haas, L. Calculating age and residence time in the tidal York River using three-dimensional model experiments. Estuar. Coast. Shelf Sci. 2004, 61, 449–461. [Google Scholar] [CrossRef]
- Gustafsson, K.E.; Bendtsen, J. Elucidating the dynamics and mixing agents of a shallow fjord through age tracer modelling. Estuar. Coast. Shelf Sci. 2007, 74, 641–654. [Google Scholar] [CrossRef]
- Hong, B.; Shen, J. Responses of estuarine salinity and transport processes to potential future sea-level rise in the Chesapeake Bay. Estuar. Coast. Shelf Sci. 2012, 104, 33–45. [Google Scholar] [CrossRef]
- Hong, B.; Shen, J. Linking dynamics of transport timescale and variations of hypoxia in the Chesapeake Bay. J. Geophys. Res. Oceans 2013, 118, 6017–6029. [Google Scholar] [CrossRef] [Green Version]
- Kärnä, T.; Baptista, A.M. Water age in the Columbia River estuary. Estuar. Coast. Shelf Sci. 2016, 183, 249–259. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Park, K.; Yu, X.; Zhang, Y.J.; Ye, F. Massive pollutants released to Galveston Bay during Hurricane Harvey: Understanding their retention and pathway using Lagrangian numerical simulations. Sci. Total. Environ. 2020, 704, 135364. [Google Scholar] [CrossRef]
- He, B.; Dai, M.; Zhai, W.-D.; Guo, X.; Wang, L. Hypoxia in the upper reaches of the Pearl River Estuary and its maintenance mechanisms: A synthesis based on multiple year observations during 2000–2008. Mar. Chem. 2014, 167, 13–24. [Google Scholar] [CrossRef]
- Dai, M.; Guo, X.; Zhai, W.-D.; Yuan, L.; Wang, B.; Wang, L.; Cai, P.; Tang, T.; Cai, W. Oxygen depletion in the upper reach of the Pearl River estuary during a winter drought. Mar. Chem. 2006, 102, 159–169. [Google Scholar] [CrossRef]
- Yan, M.; Nie, H.; Xu, K.; He, Y.; Hu, Y.; Huang, Y.; Wang, J. Microplastic abundance, distribution and composition in the Pearl River along Guangzhou city and Pearl River estuary, China. Chemosphere 2019, 217, 879–886. [Google Scholar] [CrossRef]
- Dai, M.; Gan, J.; Han, A.; Kung, H.S.; Yin, Z. Physical dynamics and biogeochemistry of the Pearl River plume. In Biogeochemical Dynamics at Major River-Coastal Interfaces; Bianchi, T.S., Allison, M.A., Cai, W., Eds.; Cambridge University Press (CUP): Cambridge, UK, 2013; pp. 321–352. [Google Scholar]
- Hu, J.; Li, S.; Geng, B. Modeling the mass flux budgets of water and suspended sediments for the river network and estuary in the Pearl River Delta, China. J. Mar. Syst. 2011, 88, 252–266. [Google Scholar] [CrossRef]
- Qiu, D.; Huang, L.; Zhang, J.; Lin, S. Phytoplankton dynamics in and near the highly eutrophic Pearl River Estuary, South China Sea. Cont. Shelf Res. 2010, 30, 177–186. [Google Scholar] [CrossRef]
- Wilson, R.E.; Swanson, R.L.; Crowley, H.A. Perspectives on long-term variations in hypoxic conditions in western Long Island Sound. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Scully, M.E. Wind Modulation of Dissolved Oxygen in Chesapeake Bay. Chesap. Sci. 2010, 33, 1164–1175. [Google Scholar] [CrossRef]
- Hamrick, J.M.; Wu, T.S. Computational design and optimization of the EFDC/HEM3D surface water hydrodynamic and eutrophication models. In Next Generation Environmental Models and Computational Methods; Delich, G., Wheeler, M., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997; pp. 143–161. [Google Scholar]
- Gong, W.; Shen, J.; Hong, B. The influence of wind on the water age in the tidal Rappahannock River. Mar. Environ. Res. 2009, 68, 203–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, B.; Shen, J.; Xu, H. Upriver transport of dissolved substances in an estuary and sub-estuary system of the lower James River, Chesapeake Bay. Front. Earth Sci. 2018, 12, 583–599. [Google Scholar] [CrossRef]
- Hong, B.; Liu, Z.; Shen, J.; Wu, H.; Gong, W.; Xu, H.; Wang, D. Potential physical impacts of sea-level rise on the Pearl River Estuary, China. J. Mar. Syst. 2020, 201, 103245. [Google Scholar] [CrossRef]
- PRWRC (Pearl River Water Resource Conservancy). The Pearl River Records 1 (Zhujiang Zhi); Guangdong Science & Technology Press: Guangzhou, China, 1991. (In Chinese) [Google Scholar]
- Cheng, Z.L. Decadal variation of hydrological status in stream network area and the eight outlets of Pearl River Delta. Acta Sci. Nat. Univ. Sunyatseni 2001, 40 (Suppl. 2), 29–31. [Google Scholar]
- Zhao, H. The Evolution of the Pearl River Estuary; China Ocean Press: Beijing, China, 1990; p. 357. [Google Scholar]
- Deleersnijder, E.; Campin, J.; Delhez, E. The concept of age in marine modeling I. Theory and preliminary model results. J. Marine Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef] [Green Version]
- Delhez, E.J.; Campin, J.-M.; Hirst, A.C.; Deleersnijder, E. Toward a general theory of the age in ocean modelling. Ocean Model. 1999, 1, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Shen, J. Water residence time in Chesapeake Bay for 1980–2012. J. Mar. Syst. 2016, 164, 101–111. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Liu, X.; Chen, X.; Flannery, M.S. Estimating river flow effects on water ages by hydrodynamic modeling in Little Manatee River estuary, Florida, USA. Environ. Fluid Mech. 2009, 10, 197–211. [Google Scholar] [CrossRef]
- Alber, M.; Sheldon, J. Use of a Date-specific Method to Examine Variability in the Flushing Times of Georgia Estuaries. Estuar. Coast. Shelf Sci. 1999, 49, 469–482. [Google Scholar] [CrossRef]
- Hagy, J.D.; Boynton, W.; Sanford, L.P. Estimation of Net Physical Transport and Hydraulic Residence Times for a Coastal Plain Estuary Using Box Models. Estuaries 2000, 23, 328. [Google Scholar] [CrossRef]
- Geyer, W.R.; Morris, J.T.; Pahl, F.G.; Jay, D.A. Interaction between physical processes and ecosystem structure: A comparative approach. In Estuarine Science: A Synthetic Approach to Research and Practice; Hobbie, J.E., Ed.; Island Press: Washington, DC, USA, 2000; pp. 177–210. [Google Scholar]
- Oliveira, A.; Baptista, A. Diagnostic modeling of residence times in estuaries. Water Resour. Res. 1997, 33, 1935–1946. [Google Scholar] [CrossRef]
- Rayson, M.; Gross, E.S.; Hetland, R.D.; Fringer, O.B. Time scales in Galveston Bay: An unsteady estuary. J. Geophys. Res. Oceans 2016, 121, 2268–2285. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, J. Mixing and flushing of tidal embayments in the western Dutch Wadden Sea part I: Distribution of salinity and calculation of mixing time scales. Neth. J. Sea Res. 1976, 10, 149–191. [Google Scholar] [CrossRef]
- De Brye, B.; De Brauwere, A.; Gourgue, O.; Delhez, E.J.; Deleersnijder, E. Water renewal timescales in the Scheldt Estuary. J. Mar. Syst. 2012, 94, 74–86. [Google Scholar] [CrossRef]
- Li, Y.; Feng, H.; Zhang, H.; Sun, J.; Yuan, D.; Guo, L.; Nie, J.; Du, J. Hydrodynamics and water circulation in the New York/New Jersey Harbor: A study from the perspective of water age. J. Mar. Syst. 2019, 199, 103219. [Google Scholar] [CrossRef]
- Harrison, P.J.; Yin, K.; Lee, J.; Gan, J.; Liu, H. Physical–biological coupling in the Pearl River Estuary. Cont. Shelf Res. 2008, 28, 1405–1415. [Google Scholar] [CrossRef]
- Cui, Y.; Wu, J.; Ren, J.; Xu, J. Physical dynamics structures and oxygen budget of summer hypoxia in the Pearl River Estuary. Limnol. Oceanogr. 2018, 64, 131–148. [Google Scholar] [CrossRef]







| Station | HM | JHH | MD | JT | YH |
|---|---|---|---|---|---|
| Stn. 1 | 365 | 365 | 0 | 0 | 0 |
| Stn. 2 | 71 | 365 | 0 | 0 | 0 |
| Stn. 3 | 21 | 197 | 0 | 0 | 0 |
| Stn. 4 | 2 | 170 | 10 | 0 | 0 |
| Stn. 5 | 0 | 154 | 293 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, B.; Wang, G.; Xu, H.; Wang, D. Study on the Transport of Terrestrial Dissolved Substances in the Pearl River Estuary Using Passive Tracers. Water 2020, 12, 1235. https://doi.org/10.3390/w12051235
Hong B, Wang G, Xu H, Wang D. Study on the Transport of Terrestrial Dissolved Substances in the Pearl River Estuary Using Passive Tracers. Water. 2020; 12(5):1235. https://doi.org/10.3390/w12051235
Chicago/Turabian StyleHong, Bo, Guangyu Wang, Hongzhou Xu, and Dongxiao Wang. 2020. "Study on the Transport of Terrestrial Dissolved Substances in the Pearl River Estuary Using Passive Tracers" Water 12, no. 5: 1235. https://doi.org/10.3390/w12051235
APA StyleHong, B., Wang, G., Xu, H., & Wang, D. (2020). Study on the Transport of Terrestrial Dissolved Substances in the Pearl River Estuary Using Passive Tracers. Water, 12(5), 1235. https://doi.org/10.3390/w12051235





