Evaluating Maize Drought and Wet Stress in a Converted Japanese Paddy Field Using a SWAP Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. SWAP Model Description
2.1.1. Soil Water Movement
2.1.2. Boundary Conditions
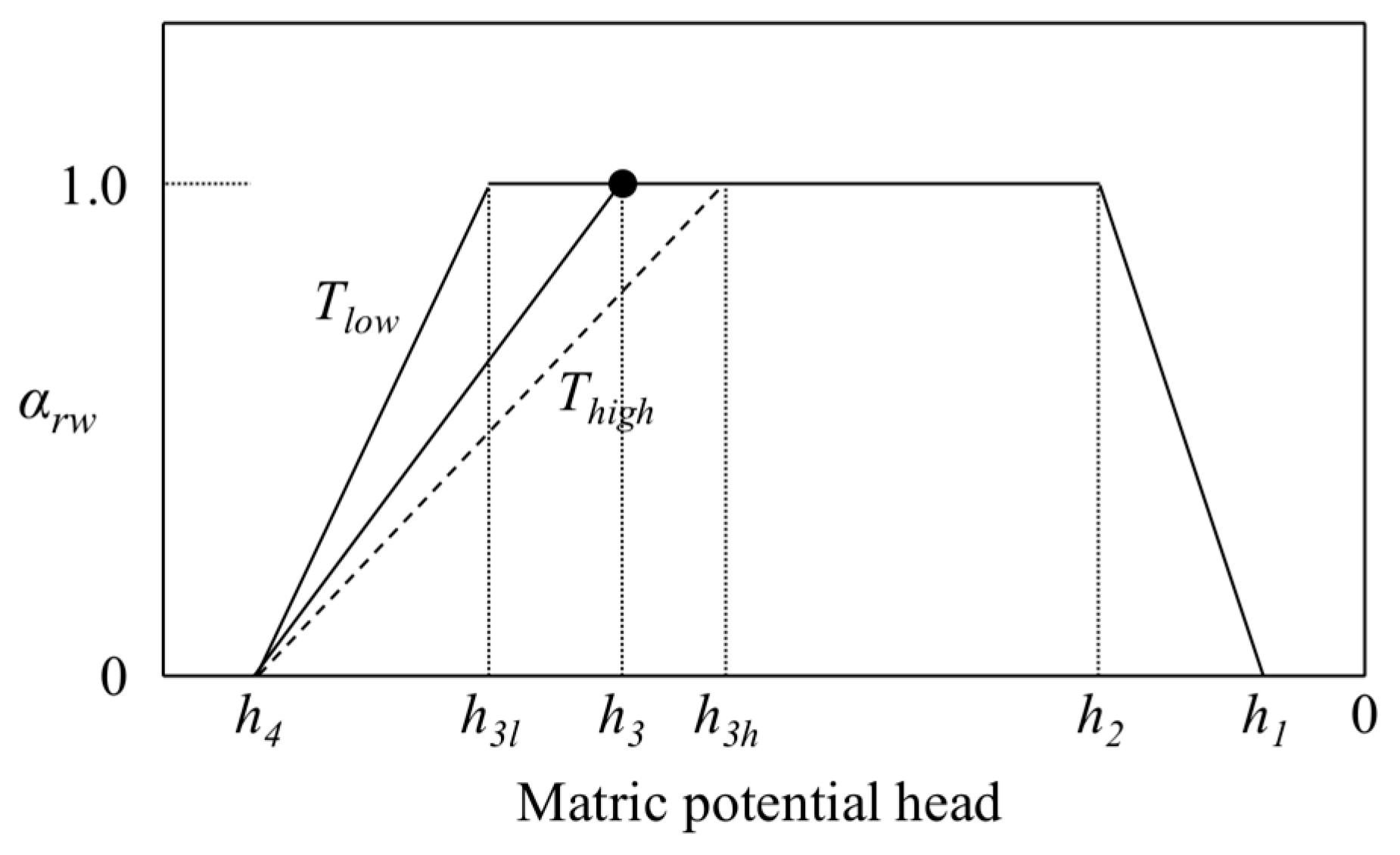
2.1.3. Crop Water Stress
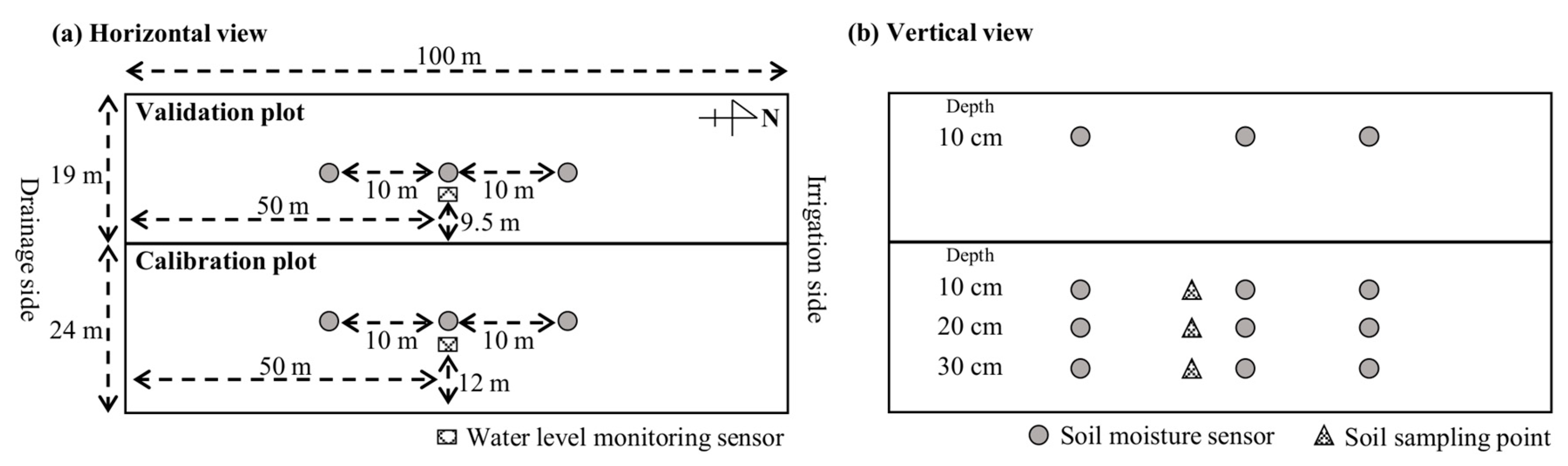
2.2. Field Experiment
2.2.1. Field Experiment for Model Calibration
2.2.2. Field Experiment for Model Validation
2.3. Model Calibration and Validation
2.3.1. Data for SWAP Model Simulation
2.3.2. Model Calibration
2.3.3. Model Validation
2.3.4. Evaluation of Calculation Error
2.3.5. Evaluation of Water Stress under Actual and Scenario Conditions
3. Results and Discussion
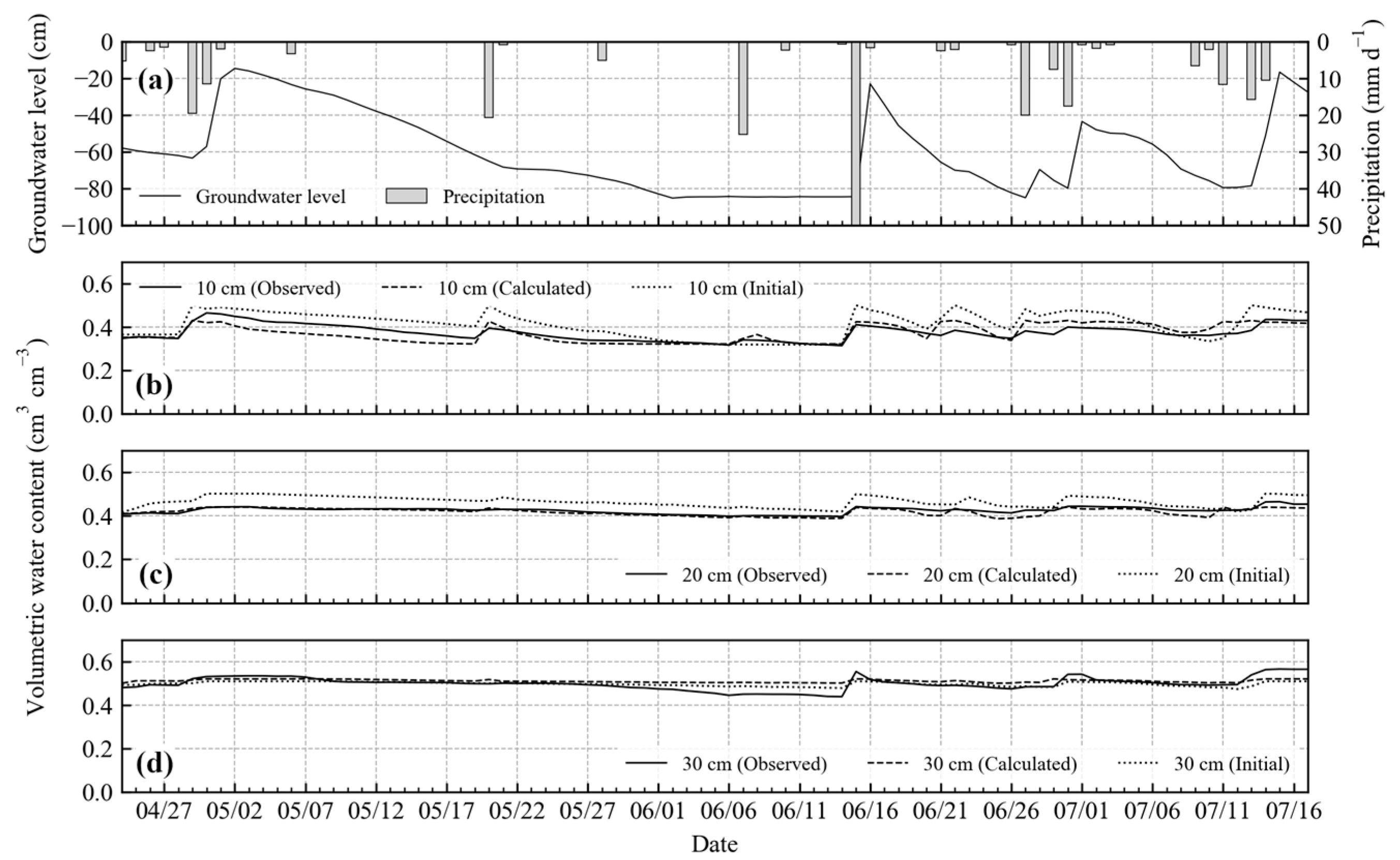
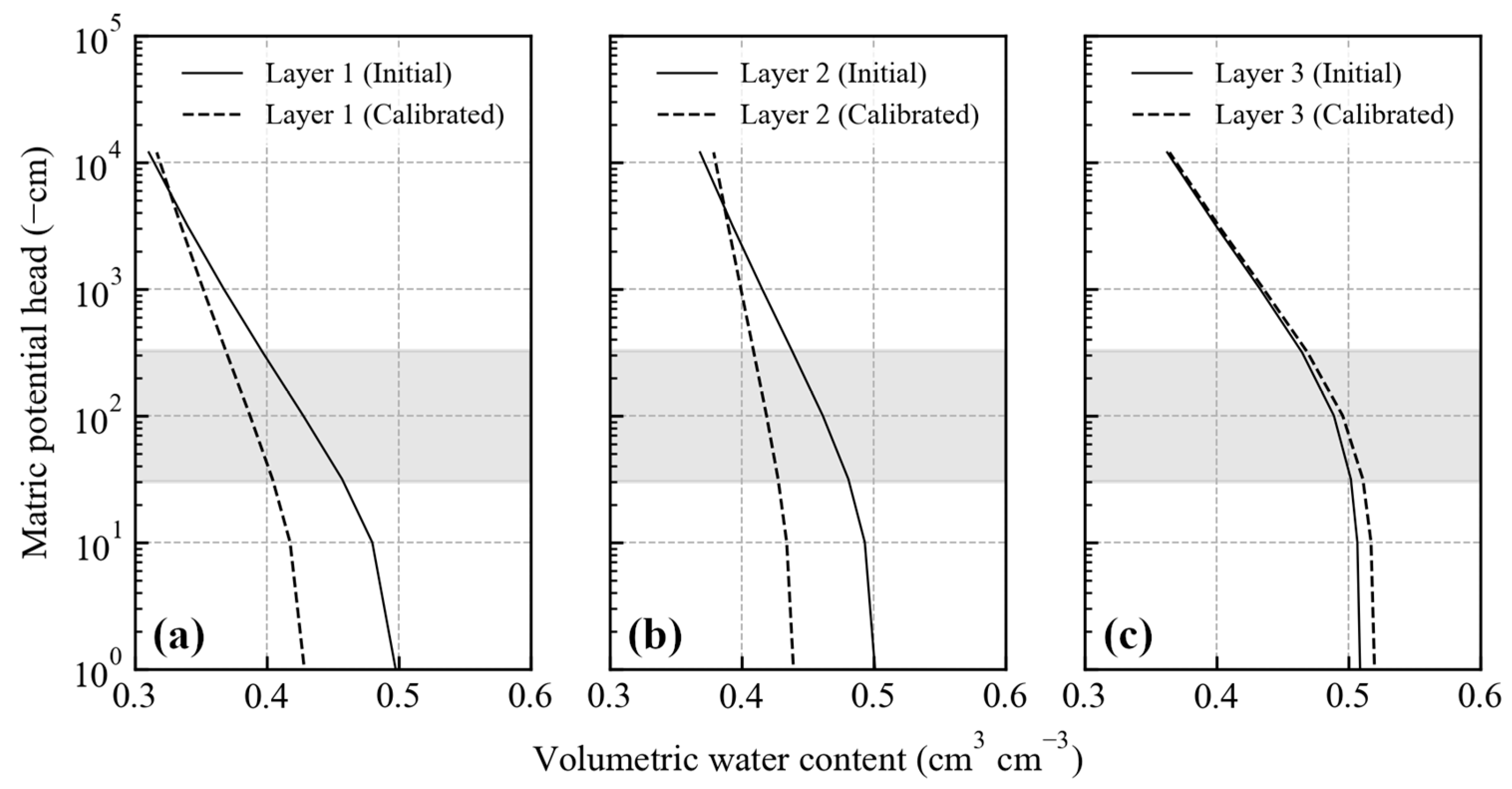
3.1. Model Calibration
3.2. Model Validation
3.3. Change in Matric Potential in the Calibration Plot
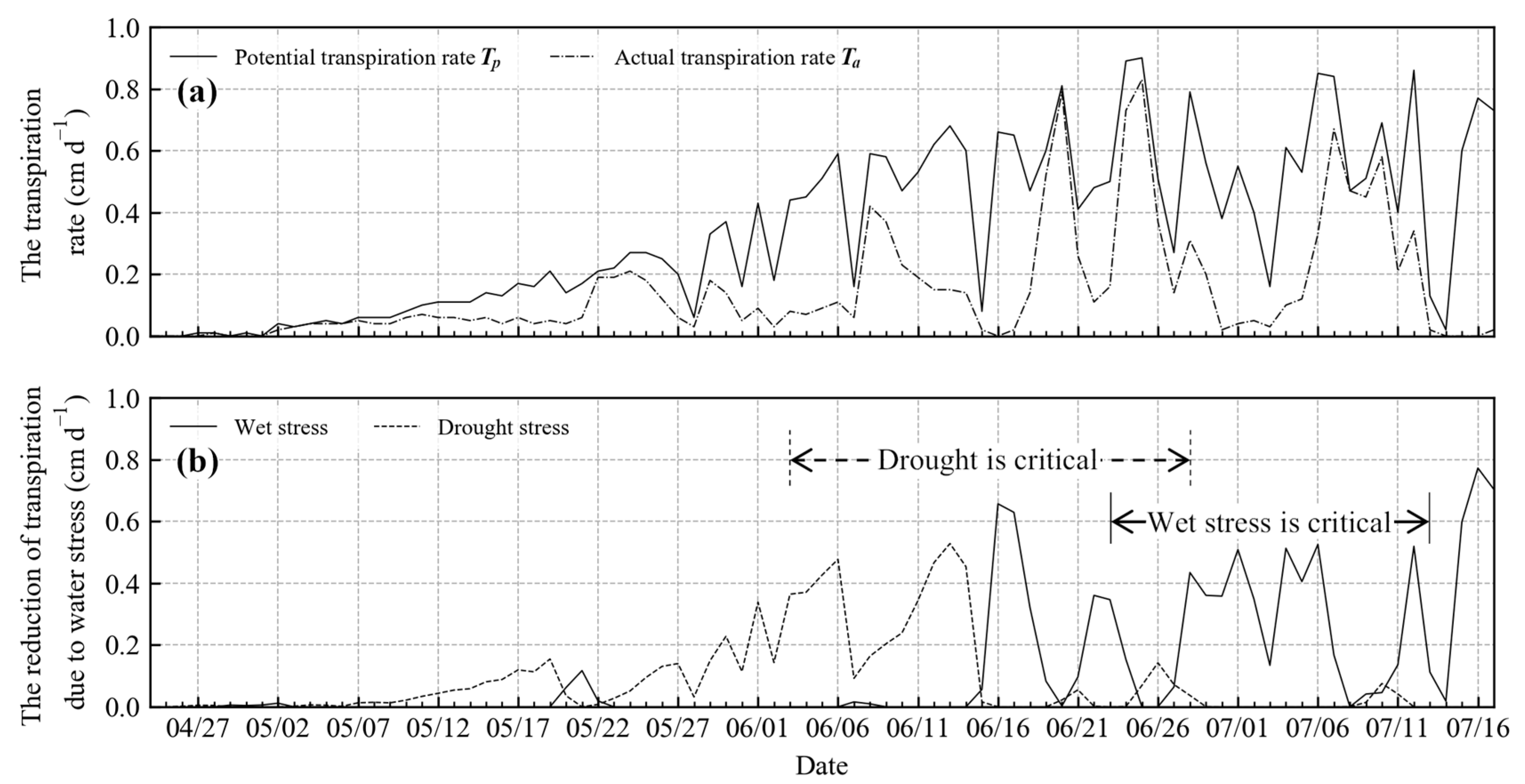
3.4. Water Stress under Actual Conditions
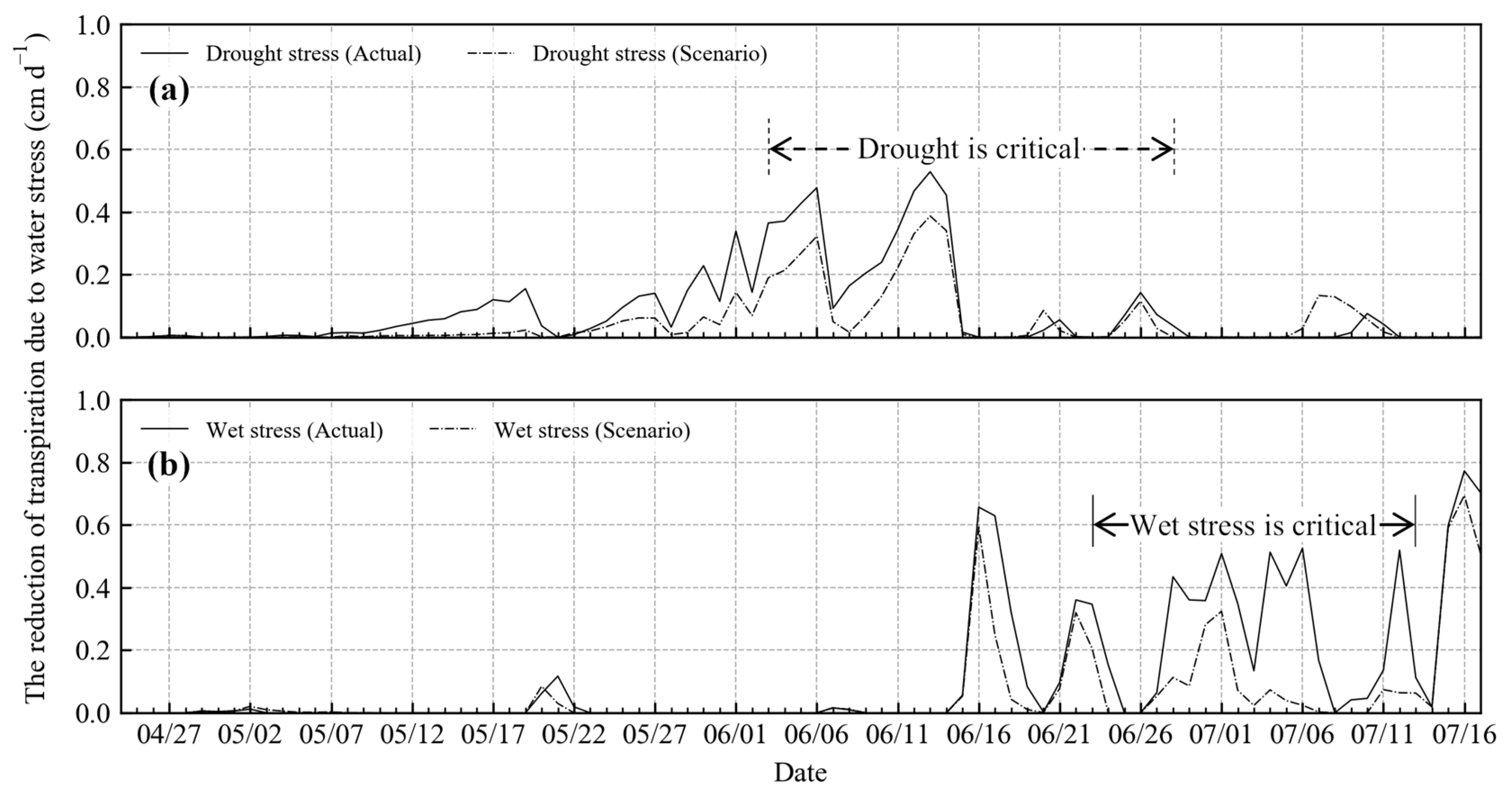
3.5. Illustrative Example: Reduction of Water Stress by Changing Tillage Depth
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hashimoto, I. Studies on irrigation management and water requirements of upland fields converted from paddy fields and those of protected cultivation fields. Bull. Ishikawa Agric. Coll. 1999, 29, 1–28. [Google Scholar]
- Taki, S.; Kujira, Y. Effects of different soil condition on growth of soybean cv. Enrei. Hokuriku Crop Sci. 2009, 44, 41–45, (In Japanese with English abstract). [Google Scholar]
- Çakir, R. Effect of water stress at different development stages on vegetative and reproductive growth of corn. Field Crop. Res. 2004, 89, 1–16. [Google Scholar] [CrossRef]
- Kanwar, R.S.; Baker, J.L.; Mukhtar, S. Excessive soil water effects at various stages of development on the growth and yield of corn. Trans. ASAE 1988, 31, 133–141. [Google Scholar] [CrossRef] [Green Version]
- van Dam, J.S.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; van Walsum, P.E.V.; Groenendijk, P.; van Diepen, C.A. Theory of SWAP Version 2.0; Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; DLO Winand Staring Centre: Wageningen, The Netherlands, 1997. [Google Scholar]
- Kroes, J.G.; van Dam, J.C.; Bartholomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Mulder, H.M.; Supit, I.; van Walsum, P.E.V. SWAP Version 4. Theory Description and User Manual; Wageningen Environmental Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Anan, M.; Hamada, K.; Yuge, K. Risk prediction of water stress by rainfall and continuous drought weather in reclaimed crop field. J. Rainwater Catchment Syst. 2015, 21, 37–42, (In Japanese with English abstract). [Google Scholar] [CrossRef] [Green Version]
- Yuge, K.; Hamada, K.; Anan, M.; Hamagami, K.; van Dam, J.S.; Kroes, J.G. Evaluation of water stress and optimization of irrigation regime at crop fields in polder. IDRE J. 2018, 306, I_55–I_62, (In Japanese with English abstract). [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Penman, H.L. Natural evaporation from open water, bare soil, and grass. Proc. R. Soc. A 1948, 193, 120–146. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.L. Evaporation and Environment. In The State and Movement of Water in Living Organisms; Fogg, G.E., Ed.; Cambridge University Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Kanda, T.; Takata, Y.; Kohyama, K.; Ohkura, T.; Maejima, Y.; Wakabayashi, S.; Obara, H. New soil maps of Japan based on the comprehensive soil classification system of Japan—First approximation and its application to the world reference base for soil resources 2006. Jpn. Agric. Res. Q. 2018, 52, 285–292. [Google Scholar] [CrossRef] [Green Version]
- Black, C.A.; Evans, D.D.; Ensminger, L.E.; White, J.L.; Clark, F.E. (Eds.) Methods of Soil Analysis. Part 1. Physical and Mineralogical Properties, Including Statistics of Measurement and Sampling; American Society of Agronomy Inc.: Madison, WI, USA, 1965. [Google Scholar]
- Tomohiro, N. Control of water erosion loss of soils using appropriate surface management in Tanzania and Cameroon. In Soils, Ecosystems Processes, and Agricultural Development: Tropical Asia and Sub-Saharan Africa; Funakawa, S., Ed.; Springer: Tokyo, Japan, 2017; p. 344. [Google Scholar]
- Jury, W.A.; Horton, R. Soil Physics, 6th ed.; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Ono, H.; Sasaki, K.; Ohara, G.; Nakazono, K. Development of grid square air temperature and precipitation data compiled from observed, forecasted, and climatic normal data. Clim. Biosph. 2016, 16, 71–79, (In Japanese with English abstract). [Google Scholar] [CrossRef] [Green Version]
- Maddonni, G.A.; Otegui, M.E. Leaf area, light interception, and crop development in maize. Field Crop. Res. 1996, 48, 81–87. [Google Scholar] [CrossRef]
- Wesseling, J.G.; Elbers, J.A.; Kabat, P.; van den Broek, B.J. SWATRE: Instructions for Input. Internal Note; Winand Staring Centre: Wageningen, The Netherlands, 1991. [Google Scholar]
- Jiang, J.; Feng, S.; Huo, Z.; Zhao, Z.; Jia, B. Application of the SWAP model to simulate water-salt transport under deficit irrigation with saline water. Math. Comput. Model. 2011, 54, 902–911. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, S.; Ma, J.; Huo, Z.; Zhang, C. Irrigation management for spring maize grown on saline soil based on SWAP model. Field Crop. Res. 2016, 196, 85–97. [Google Scholar] [CrossRef]
- Kumar, P.; Sarangi, A.; Singh, D.K.; Parihar, S.S.; Sahoo, R.N. Simulation of salt dynamics in the root zone and yield of wheat crop under irrigated saline regimes using SWAP model. Agric. Water Manag. 2015, 148, 72–83. [Google Scholar] [CrossRef]
- Crescimanno, G.; Garofalo, P. Management of irrigation with saline water in cracking clay soils. Soil Sci. Soc. Am. J. 2006, 70, 1774–1787. [Google Scholar] [CrossRef]
- Strudley, M.W.; Green, T.R.; Ascugh II, J.C. Tillage effects on soil hydraulic properties in space and time: State of the science. Soil Till. Res. 2008, 99, 4–48. [Google Scholar] [CrossRef]
- Or, D.; Leij, F.J.; Snyder, V.; Ghezzehei, T.A. Stochastic model for posttillage soil pore space evolution. Water Resour. Res. 2000, 36, 1641–1652. [Google Scholar] [CrossRef] [Green Version]
- Kita, D.; Tarumi, H.; Mori, H.; Kawaguchi, K. A new theory of the function of bentonite in suppressing the water percolation through soils. Jpn. J. Soc. Soil Sci. Plant Nutr. 1964, 35, 47–52. (In Japanese) [Google Scholar]



| Soil hydraulic data | ||
 | Estimated by nonlinear optimization using the Mualem–van Genuchten model | |
| Saturated hydraulic conductivity Ksat | Measured | |
| Soil water retention curve | Measured | |
| Meteorological data | ||
 | Obtained from the Agro-Meteorological Grid Square Data, NARO, which generates the Japanese meteorological data for every 1 km2 [18] | |
| Crop data | ||
| Crop height | Measured | |
| Rooting depth | Measured | |
| LAI | Determined based on Maddonni and Otegui [19] | |
| Critical pressure heads of water stress | Data from Wesseling et al. [20] | |
| Initial and bottom boundary conditions | ||
| Matric potential head | Converted from observed volumetric water content | |
| Groundwater level | Measured | |
| Data for calibration | ||
| Volumetric water content | Measured | |
| Depth (cm) | 0–3 | 3–23 | 23–35 | 35–100 |
| Nodal spacing (cm) | 0.2 | 1.0 | 2.0 | 5.0 |
| Maximum rooting depth (cm) | 50.0 | (17 July 2019; observed) |
| Crop height in the calibration plot (cm) | 27.2 | (9 May 2019; observed) |
| 58.0 | (23 May 2019; observed) | |
| 158.5 | (12 June 2019; observed) | |
| 230.1 | (25 June 2019; observed) | |
| 258.6 | (17 July 2019; interpolated) | |
| Crop height in the validation plot (cm) | 17.7 | (10 August 2018; observed) |
| 246.1 | (5 November 2018; observed) | |
| Critical pressure heads: h1, h2, h3h, h3l, h4 (−cm) | 15, 30, 325, 600, 8000 | |
| Layer No. | Depth (cm) | θres (cm3 cm−3) | θsat (cm3 cm−3) | α (cm−1) | n (-) | Ksat (cm s−1) | λ (-) | Dry Bulk Density (g cm−3) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0–12 | 0.010 | 0.500 | 0.090 | 1.07 | 1.06 × 10−3 | 0.50 | 1.15 |
| 2 | 12–23 | 0.010 | 0.502 | 0.047 | 1.05 | 5.89 × 10−4 | 0.50 | 1.31 |
| 3 | 23–100 | 0.010 | 0.509 | 0.008 | 1.08 | 1.44 × 10−4 | 0.50 | 1.31 |
| Layer No. | Depth (cm) | θres (cm3 cm−3) | θsat (cm3 cm−3) | α (cm−1) | n (-) | Ksat (cm s−1) | λ (-) |
|---|---|---|---|---|---|---|---|
| 1 | 0–12 | 0.050 | 0.430 | 0.100 | 1.05 | 5.21 × 10−3 | 0.50 |
| 2 | 12–23 | 0.010 | 0.440 | 0.090 | 1.02 | 2.91 × 10−4 | 0.50 |
| 3 | 23–100 | 0.010 | 0.520 | 0.010 | 1.08 | 5.86 × 10−4 | 0.50 |
| Depth | Condition | Drought-Dominant Period (3–15 June 2019; 12 days) | Wet Stress Critical Period (23 June–13 July 2019; 20 days) | ||
|---|---|---|---|---|---|
| Average Volumetric Water Content (cm3 cm−3) | Stress Occurrence Days | Average Volumetric Water Content (cm3 cm−3) | Stress Occurrence Days | ||
| 10 cm | Actual | 0.330 | 12 | 0.405 | 13 |
| Scenario | 0.331 | 12 | 0.375 | 4 | |
| 20 cm | Actual | 0.393 | 12 | 0.416 | 8 |
| Scenario | 0.380 | 0 | 0.390 | 1 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamada, K.; Inoue, H.; Mochizuki, H.; Asakura, M.; Shimizu, Y.; Takemura, T. Evaluating Maize Drought and Wet Stress in a Converted Japanese Paddy Field Using a SWAP Model. Water 2020, 12, 1363. https://doi.org/10.3390/w12051363
Hamada K, Inoue H, Mochizuki H, Asakura M, Shimizu Y, Takemura T. Evaluating Maize Drought and Wet Stress in a Converted Japanese Paddy Field Using a SWAP Model. Water. 2020; 12(5):1363. https://doi.org/10.3390/w12051363
Chicago/Turabian StyleHamada, Kosuke, Hisayoshi Inoue, Hidetoshi Mochizuki, Mayuko Asakura, Yuta Shimizu, and Takeshi Takemura. 2020. "Evaluating Maize Drought and Wet Stress in a Converted Japanese Paddy Field Using a SWAP Model" Water 12, no. 5: 1363. https://doi.org/10.3390/w12051363
APA StyleHamada, K., Inoue, H., Mochizuki, H., Asakura, M., Shimizu, Y., & Takemura, T. (2020). Evaluating Maize Drought and Wet Stress in a Converted Japanese Paddy Field Using a SWAP Model. Water, 12(5), 1363. https://doi.org/10.3390/w12051363





