Experimental and Numerical Investigations of Turbulent Open Channel Flow over a Rough Scour Hole Downstream of a Groundsill
Abstract
:1. Introduction
2. Background of the Experiments and Model Setups
2.1. Experimental Equipment and Setups
2.2. Setups of Numerical Simulations
3. Results and Discussion
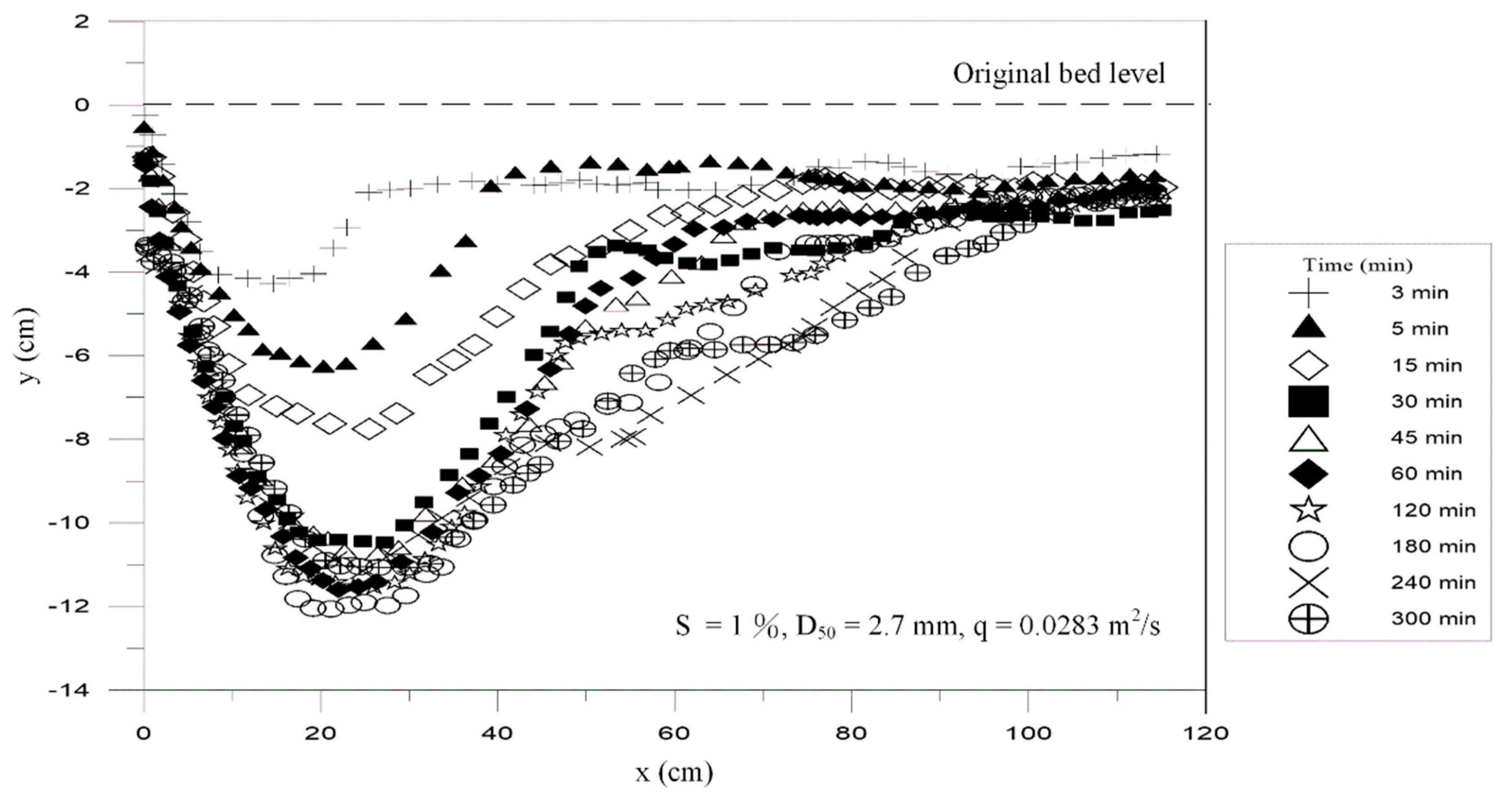
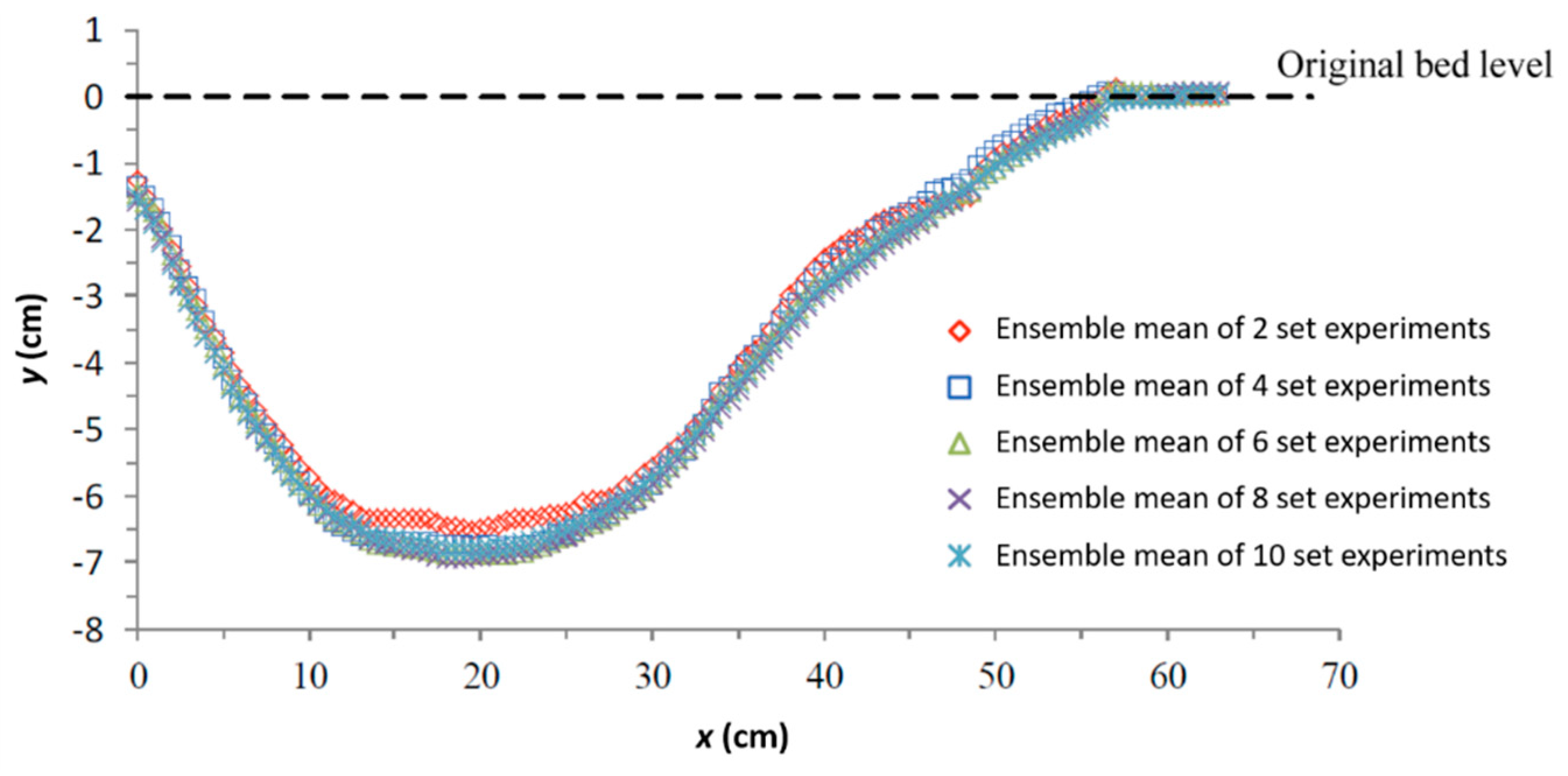
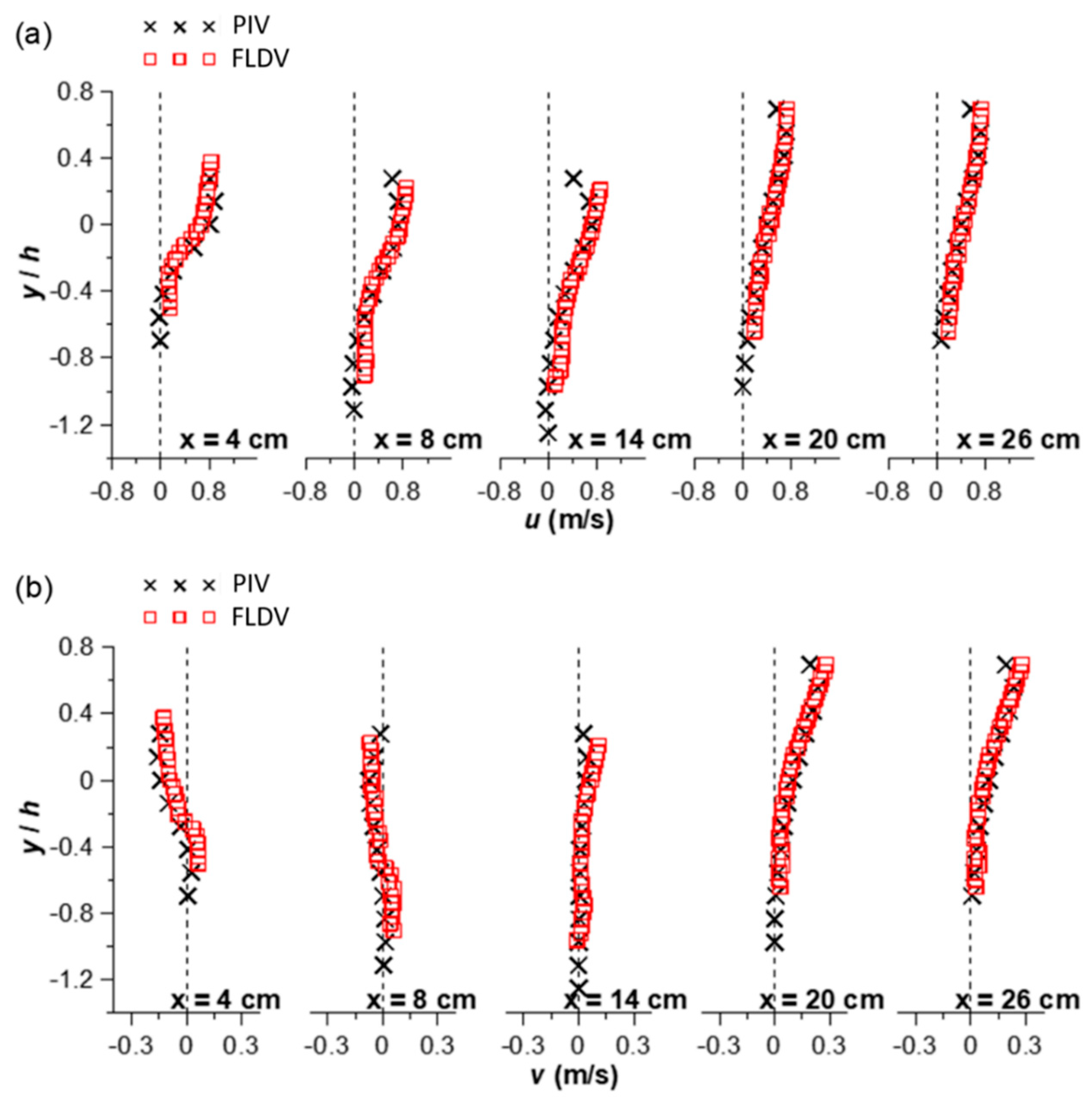
3.1. Scour Hole Model and Measurement System Verification
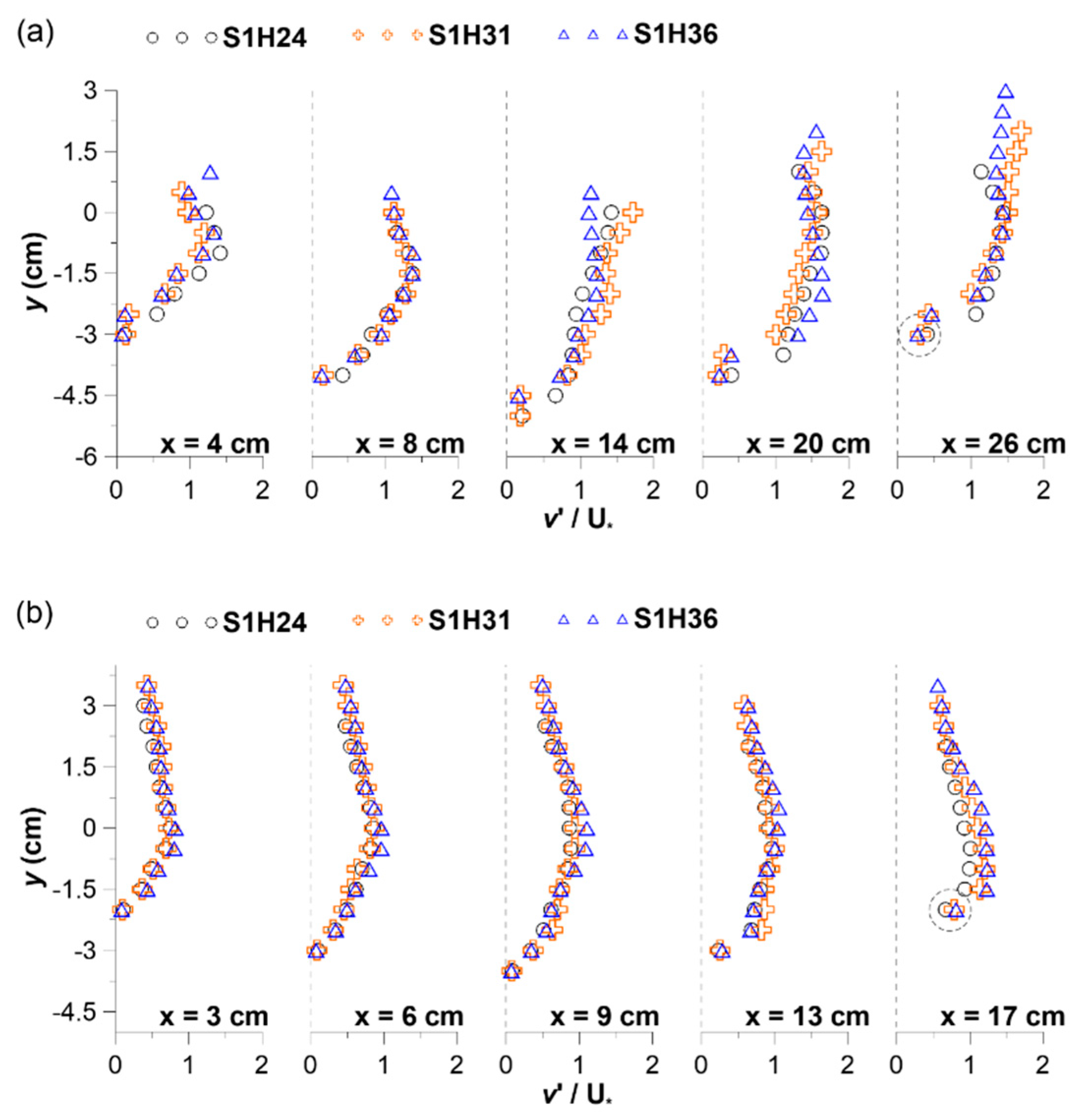
3.2. Discussion of Experimental Results
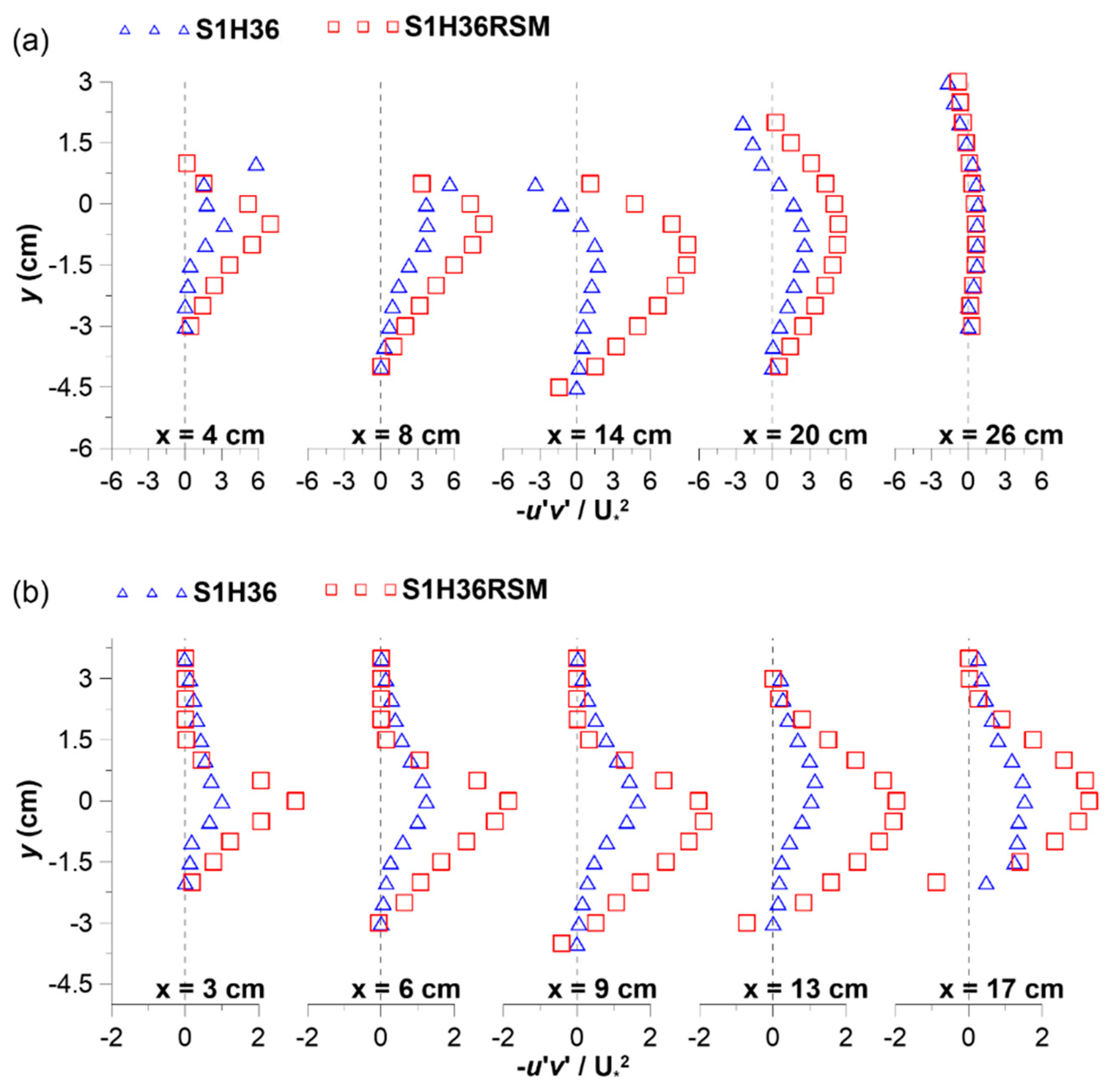
3.3. Comparison of Experimental and Simulation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill Book Company: New York, NY, USA, 1979; pp. 596–602. [Google Scholar]
- Khan, L.A. A Three-Dimensional Computational Fluid Dynamics (CFD)Model Analysis of Free Surface Hydrodynamics and Fish Passage Energetics in a Vertical-Slot Fishway. N. Am. J. Fish. Manag. 2006, 26, 181–193. [Google Scholar] [CrossRef]
- Yazdi, J.; Azamathulla, H.M.; Ghani, A.A. 3D simulation of flow around a single spur dike with free-surface flow. Int. J. River Basin Manag. 2010, 8, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Salaheldin, T.M.; Jasim, I.; Chaudhry, M.H. Numerical Modeling of Three-Dimensional Flow Field Around Circular Piers. J. Hydraul. Eng. 2004, 130, 91–100. [Google Scholar] [CrossRef]
- Breusers, H.N.C. Conformity and time scale in two-dimensional local scour. In Proc. Symposium on Model and Prototype Conformity: 1–8; Hydraulic Research Laboratory: Poona, India, 1966. [Google Scholar]
- Dietz, J.W. Scouring in fine or lightweight bed materials by subcritical flow. In Mitteilungen der Versuchsanstalt für Wasserbau und Kulturtechnik, Theodor-Rehbock-Flußbaulaboratorium; Universität Karlsruhe: Heft, Germany, 1969; pp. 1–120. (In German) [Google Scholar]
- Zanke, U. Zusammenhange Zwischen Stromung und Sedimenttransport; Mitt. Des Franzius Instituts der Univ. Hannover: Hannover, Germay; Springer: Berlin, Germany, 1978. (In German) [Google Scholar]
- Gaudio, R.; Marion, A.; Bovolin, V. Morphological effects of bed sills in degrading rivers. J. Hydraul. Res. 2000, 38, 89–96. [Google Scholar] [CrossRef]
- Gaudio, R.; Marion, A. Time evolution of scouring downstream of bed sills. J. Hydraul. Res. 2003, 41, 271–284. [Google Scholar] [CrossRef]
- Ben Meftah, M.; De Serio, F.; De Padova, D.; Mossa, M. Hydrodynamic Structure with Scour Hole Downstream of Bed Sills. Water 2020, 12, 186. [Google Scholar] [CrossRef] [Green Version]
- Guan, D.W.; Melville, B.W.; Friedrich, H. Local scour at submerged weirs in sand-bed channels. J. Hydraul. Res. 2016, 54, 172–184. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Guan, D. Effects of upstream weir slope on local scour at submerged weirs. J. Hydraul. Eng. 2018, 144, 04018002. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Guan, D.; Whittaker, C.N. Local Scour at Downstream Sloped Submerged Weirs. J. Hydraul. Eng. 2018, 144, 04018044. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. New approach to predicting local scour downstream of grade-control structure. J. Hydraul. Eng. 2020, 146, 04019058. [Google Scholar] [CrossRef]
- Lu, S.Y.; Lu, J.Y.; Shih, D.S. Temporal and Spatial Flow Variations over a Movable Scour Hole Downstream of a Grade-Control Structure with a PIV System. Water 2018, 10, 1002. [Google Scholar] [CrossRef] [Green Version]
- Shih, D.S.; Lai, T.Y.; Hsu, Z.M. Applying Biomineralization Technology to Study the Effects of Rainfall Induced Soil Erosion. Water 2019, 11, 2555. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Al-Sharif, S.F. Reynolds Stress Transport Modelling. Comput. Simul. Appl. 2011, 1. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.Y.; Hong, J.H.; Chang, K.P.; Lu, T.F. Evolution of scouring process downstream of grade-control structures under steady and unsteady flows. Hydrol. Process. 2013, 27, 2699–2709. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Whittaker, C.N.; Guan, D. Scour estimation downstream of submerged weirs. J. Hydraul. Eng. 2019, 145, 06019016. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Characteristics of horseshoe vortex in developing scour holes at piers. J. Hydraul. Eng. 2007, 133, 399–413. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Scour holes downstream of bed sills in low-gradient channels. J. Hydraul. Res. 2006, 44, 497–509. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.M.; Friedrich, H. Flow patterns and turbulence structures in a scour hole downstream of a submerged weir. J. Hydraul. Eng. 2014, 140, 68–76. [Google Scholar] [CrossRef]
- Hsiao, K.T. PIV Measurement of the Flow Field Downstream of a Grade Control Structure—Preliminary Investigation of Bursting Phenomenon. Master’s Thesis, National Chung-Hsing University, Taichung, Taiwan, 2017. (In Chinese). [Google Scholar]










| Case | S (%) | h (cm) | Q (m2/s) | U (m/s) | (m/s) | Fr | Re | B/h |
|---|---|---|---|---|---|---|---|---|
| S1H24 | 1/100 | 2.40 | 0.0030 | 0.50 | 0.0444 | 1.03 | 10,029 | 10.42 |
| S1H31 | 1/100 | 3.10 | 0.0058 | 0.75 | 0.0494 | 1.36 | 18,559 | 8.06 |
| S1H36 | 1/100 | 3.60 | 0.0085 | 0.94 | 0.0524 | 1.59 | 26,174 | 6.94 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-K.; Lu, J.-Y.; Lu, S.-Y.; Wang, Z.-X.; Shih, D.-S. Experimental and Numerical Investigations of Turbulent Open Channel Flow over a Rough Scour Hole Downstream of a Groundsill. Water 2020, 12, 1488. https://doi.org/10.3390/w12051488
Chang C-K, Lu J-Y, Lu S-Y, Wang Z-X, Shih D-S. Experimental and Numerical Investigations of Turbulent Open Channel Flow over a Rough Scour Hole Downstream of a Groundsill. Water. 2020; 12(5):1488. https://doi.org/10.3390/w12051488
Chicago/Turabian StyleChang, Cheng-Kai, Jau-Yau Lu, Shi-Yan Lu, Zhong-Xiang Wang, and Dong-Sin Shih. 2020. "Experimental and Numerical Investigations of Turbulent Open Channel Flow over a Rough Scour Hole Downstream of a Groundsill" Water 12, no. 5: 1488. https://doi.org/10.3390/w12051488
APA StyleChang, C.-K., Lu, J.-Y., Lu, S.-Y., Wang, Z.-X., & Shih, D.-S. (2020). Experimental and Numerical Investigations of Turbulent Open Channel Flow over a Rough Scour Hole Downstream of a Groundsill. Water, 12(5), 1488. https://doi.org/10.3390/w12051488






