Experimental Investigation of Erosion Characteristics of Fine-Grained Cohesive Sediments
Abstract
:1. Introduction
2. Material and Methods
2.1. Rotating Annular Flume
2.2. Methodology of Krone
2.3. Mathematical Model of Cohesive Sediment Transport Developed by Krishnappan
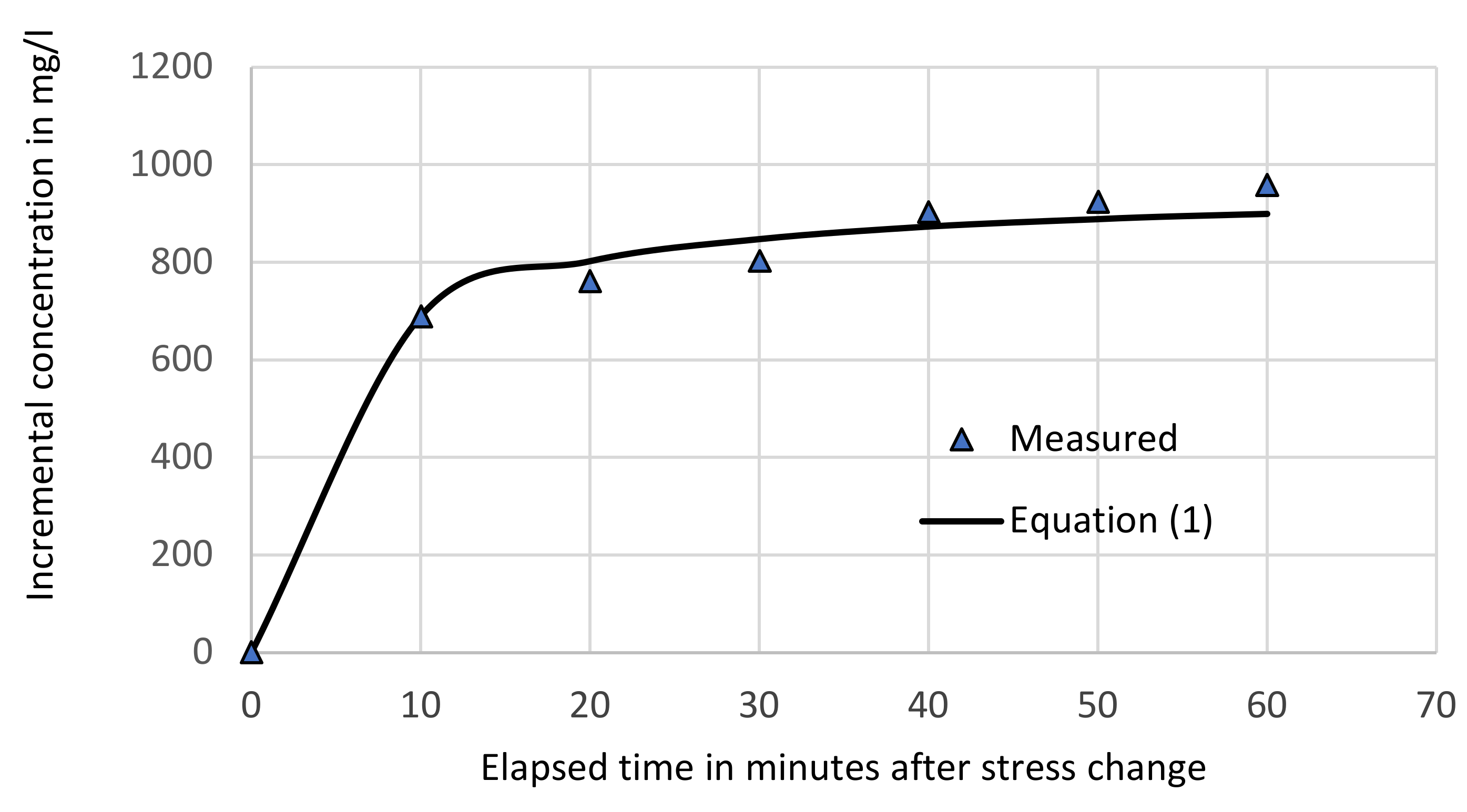
2.3.1. Settling Stage
2.3.2. Flocculation Stage
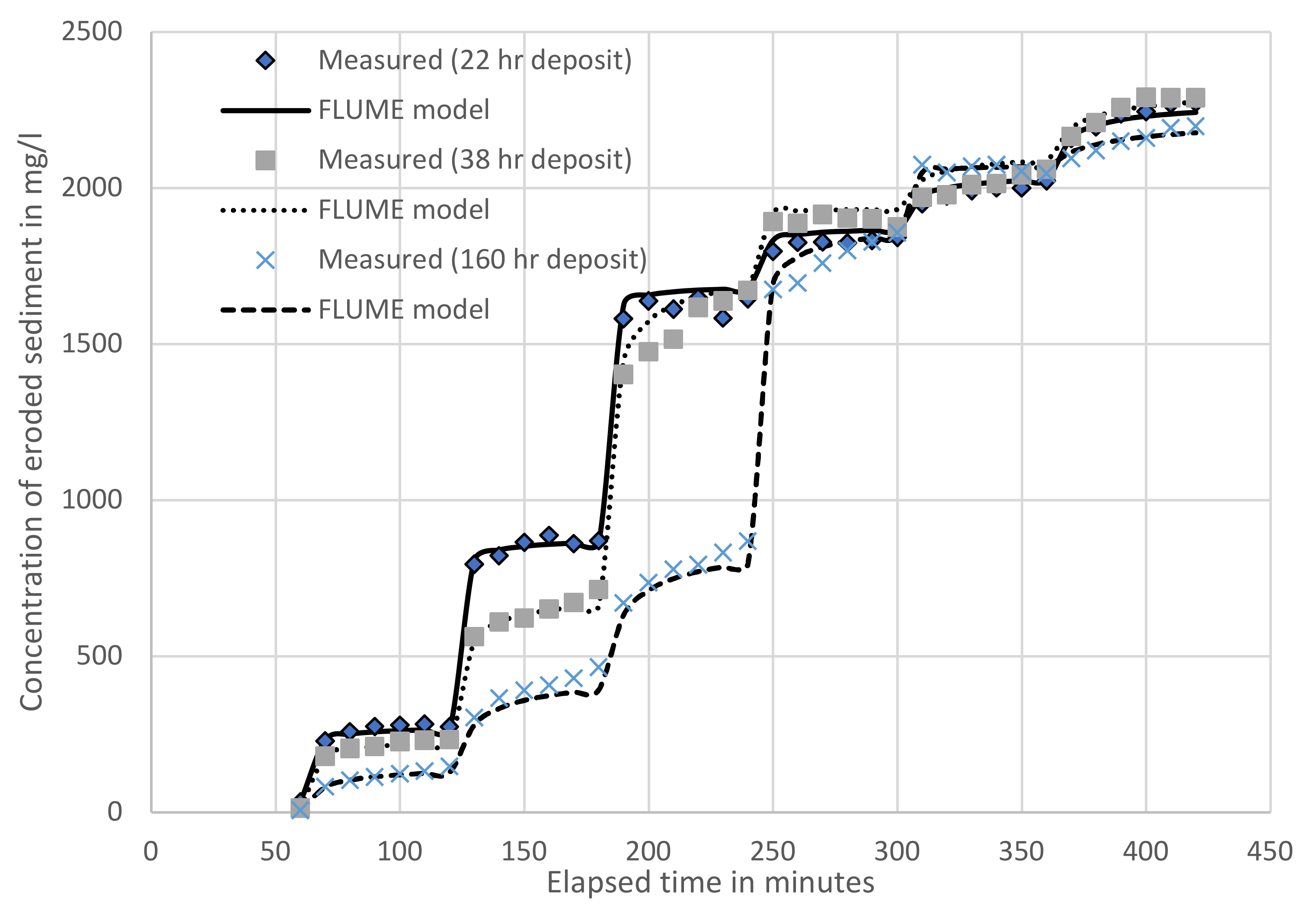
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horowitz, A.J.; Elrick, K.A. The relation of stream sediment surface area, grain size and composition to trace element chemistry. Appl. Geochem. 1987, 2, 437–451. [Google Scholar] [CrossRef]
- Luoma, S.N.; Rainbow, P.S. Metal Contamination in Aquatic Environments: Science and Lateral Management; Cambridge University Press: Cambridge, UK, 2008; 573p. [Google Scholar]
- Grabowski, R.C.; Droppo, I.C.; Wharton, G. Erodibility of cohesive sediment: The importance of sediment properties. Earth Sci. Rev. 2011, 105, 101–120. [Google Scholar] [CrossRef]
- Amos, C.L.; Li, M.Z.; Sutherland, T.F. The contribution of ballistic momentum flux to the erosion of cohesive beds by flowing water. J. Coast. Res. 1998, 14, 564–569. [Google Scholar]
- Lick, W.; McNeil, J. Effects of sediment bulk properties on erosion rates. Sci. Total Environ. 2001, 266, 41–48. [Google Scholar] [CrossRef]
- Friend, P.L.; Ciavola, P.; Cappucci, S.; Santos, R. Bio-dependent bed parameters as a proxy tool for sediment stability in mixed habitat intertidal areas. Cont. Shelf Res. 2003, 23, 1899–1917. [Google Scholar] [CrossRef]
- Lau, Y.L.; Droppo, I.G.; Krishnappan, B.G. Sequential erosion/deposition experiments demonstrating the effects of depositional history on sediment erosion. Water Res. 2001, 35, 2767–2773. [Google Scholar] [CrossRef]
- Roberts, J.; Jepsen, R.; Gotthard, D.; Lick, W. Effects of particle size and bulk density on erosion of quartz particles. J. Hydraul. Eng. ASCE 1998, 124, 1261–1267. [Google Scholar] [CrossRef]
- Zreik, D.A.; Krishnappan, B.G.; Germaine, J.T.; Masden, O.S.; Ladd, C.C. Erosional and mechanical strengths of deposited cohesive sediments. J. Hydraul. Eng. ASCE 1998, 124, 1076–1085. [Google Scholar] [CrossRef]
- Krone, R.B. Effects of bed structure on erosion of cohesive sediments. J. Hydraul. Eng. ASCE 1999, 125, 1297–1301. [Google Scholar] [CrossRef]
- Lambert, C.P.; Walling, D.E. Measurement of channel storage of suspended sediment in a gravel-bed river. Catena 1988, 15, 65–80. [Google Scholar] [CrossRef]
- Duerdoth, C.P.; Arnold, A.; Murphy, J.F.; Naden, P.S.; Scarlett, P.; Collins, A.L.; Sear, D.A.; Jones, J.I. Assessment of a rapid method for quantitative reach-scale estimates of deposited fine sediment in rivers. Geomorphology 2015, 230, 37–50. [Google Scholar] [CrossRef]
- Naden, P.S.; Murphy, J.S.; Old, G.H.; Newman, J.; Scarlett, P.; Harman, M.; Duerdoth, C.P.; Hawczak, A.; Pretty, J.L.; Arnold, A.; et al. Understanding the controls on deposited fine sediment in the streams of agricultural catchments. Sci. Total Environ. 2016, 347, 366–381. [Google Scholar] [CrossRef] [Green Version]
- Krishnappan, B.G. Recent Advances in basic and applied research in cohesive sediment transport in aquatic systems. Can. J. Civ. Eng. 2007, 34, 731–743. [Google Scholar] [CrossRef]
- Petersen, O.; Krishnappan, B.G. Measurement and analysis of flow characteristics in a circular flume. J. Hydraul. Res. IAHR 1994, 32, 483–494. [Google Scholar] [CrossRef]
- Rosten, H.I.; Spalding, D.B. The PHOENICS Reference Manual; TR/200; CHAM Ltd.: Wimbledon, London, UK, 1984. [Google Scholar]
- Krishnappan, B.G.; Engel, P. Distribution of bed shear stress in Rotating Circular Flume. J. Hydraul. Eng. 2004, 130, 324–331. [Google Scholar] [CrossRef]
- Krishnappan, B.G. Rotating Circular Flume. J. Hydraul. Eng. ASCE 1993, 119, 758–767. [Google Scholar] [CrossRef]
- Partheniades, E. A Study of Erosion and Deposition of Cohesive Soils in Salt Water. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1962. [Google Scholar]
- Mehta, A.J.; Partheniades, E. An investigation of the depositional properties of flocculated fine sediments. J. Hydraul. Res. IAHR 1975, 13, 361–381. [Google Scholar] [CrossRef]
- Parchure, T.M. Erosional Behaviour of Deposited Cohesive Sediments. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 1984. [Google Scholar]
- Lick, W. Entrainment, deposition and transport of fine grained sediments in Lakes. Hydrobiologia 1982, 91, 31–40. [Google Scholar] [CrossRef]
- Krishnappan, B.G. Erosion behaviour of fine sediment deposits. Can. J. Civ. Eng. 2004, 31, 759–766. [Google Scholar] [CrossRef]
- Krone, R.B. Flume Studies of the Transport of Sediments in Estuarial Shoaling Processes; Report; Hydr. Engr. Lab. and Sanitary Engr. Lab. University of California: Berkeley, CA, USA, 1962. [Google Scholar]
- Fuchs, N.A. The Mechanics of Aerosols; Pergamon: New York, NY, USA, 1964; 408p. [Google Scholar]
- Lau, Y.L.; Krishnappan, B.G. Measurement of Size Distribution of Settling Flocs; Report No. 97–223; National Water Research Institute; Environment Canada; CCIW: Burlington, ON, Canada, 1997. [Google Scholar]
- Valioulis, I.A.; List, E.J. Numerical simulation of a sedimentation basin. 1 Model development. Environ. Sci. Technol. 1984, 18, 242–247. [Google Scholar] [CrossRef]
- Tambo, N.; Watanabe, Y. Physical aspects of flocculation processes—I Fundamental Treatise. Water Res. 1979, 13, 429–439. [Google Scholar] [CrossRef]
- Stone, M.; Krishnappan, B.G.; Emelko, M. The effect of bed age and shear stress on the particle morphology of eroded cohesive sediment in an annular flume. Water Res. 2008, 42, 4179–4187. [Google Scholar] [CrossRef]
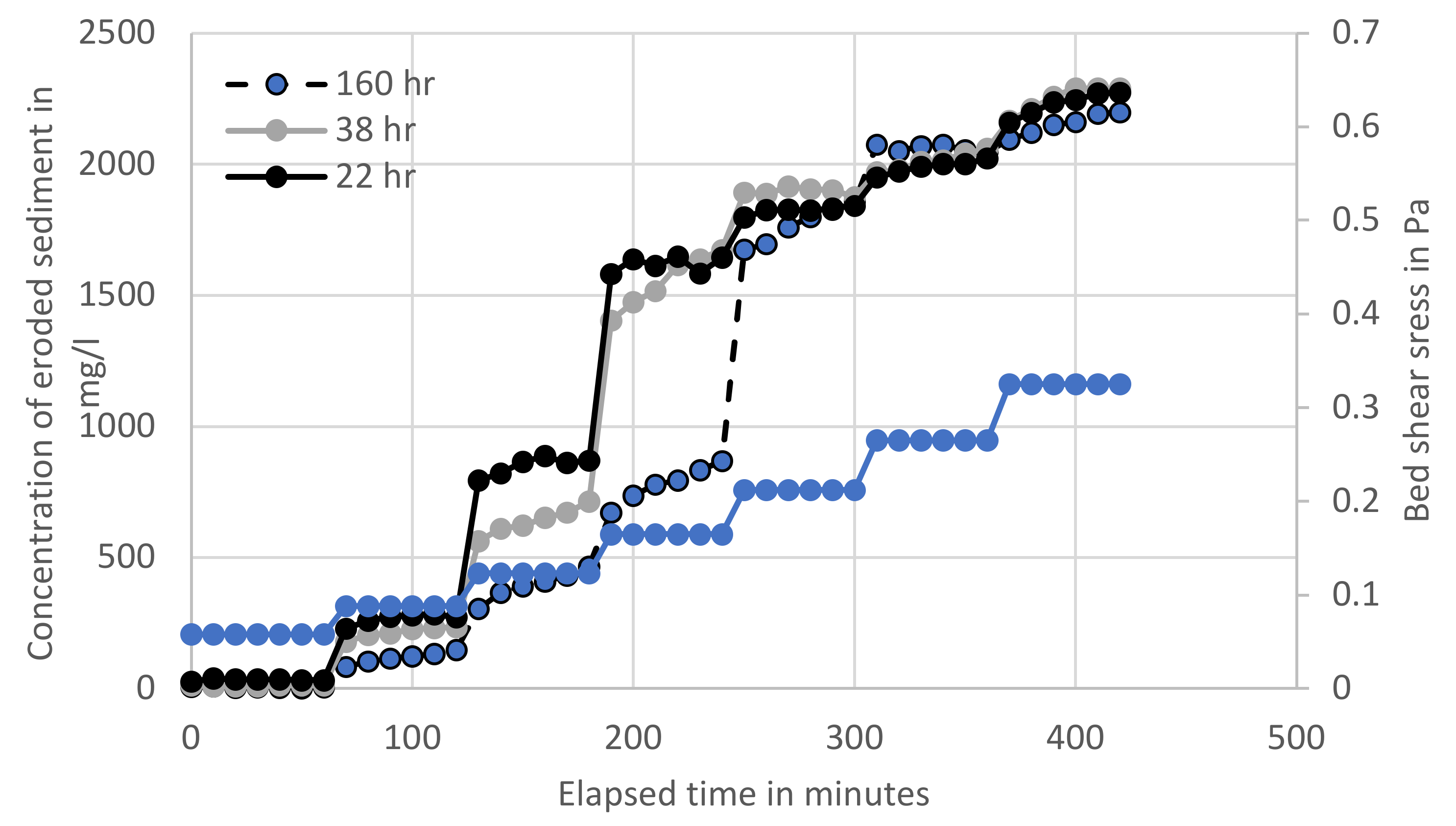
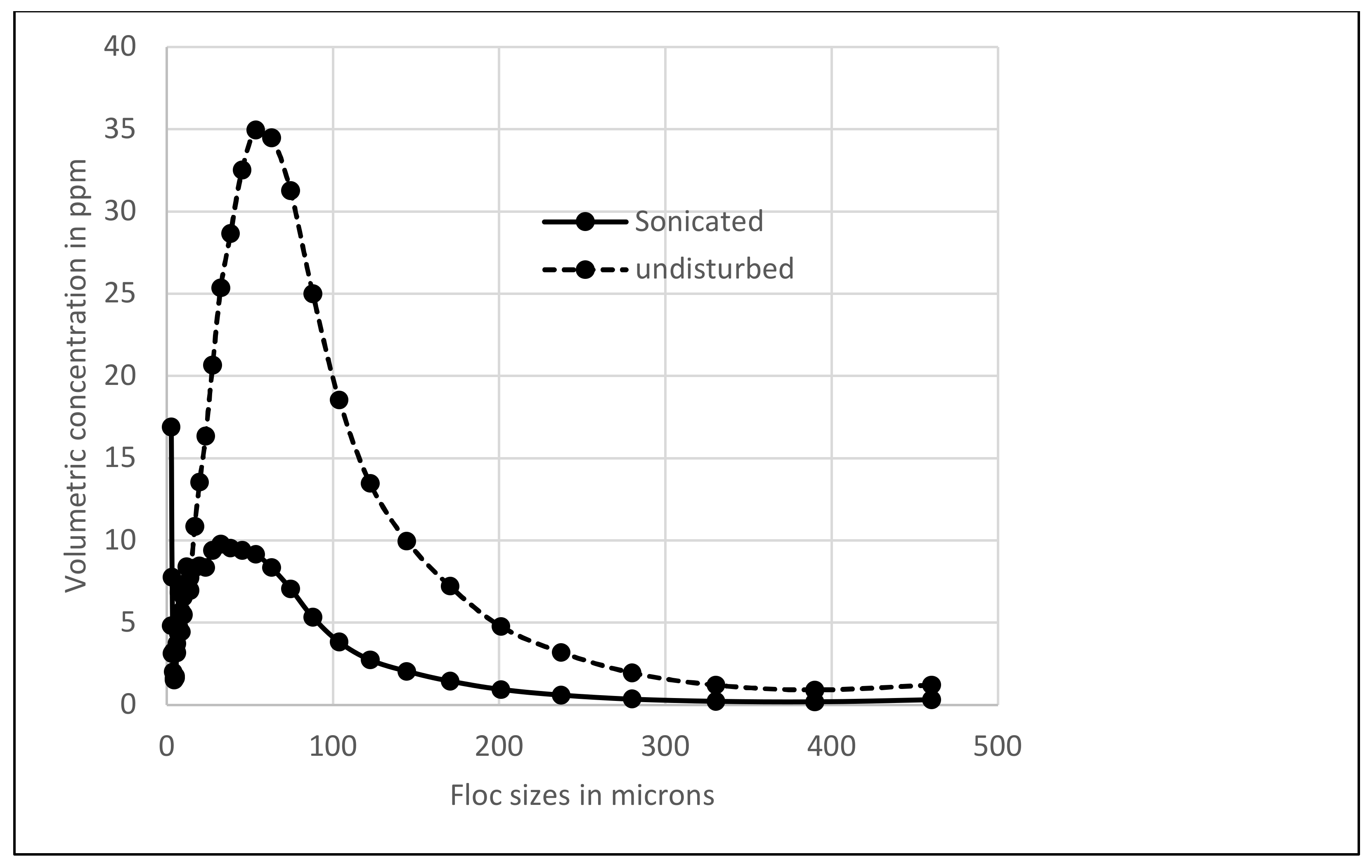
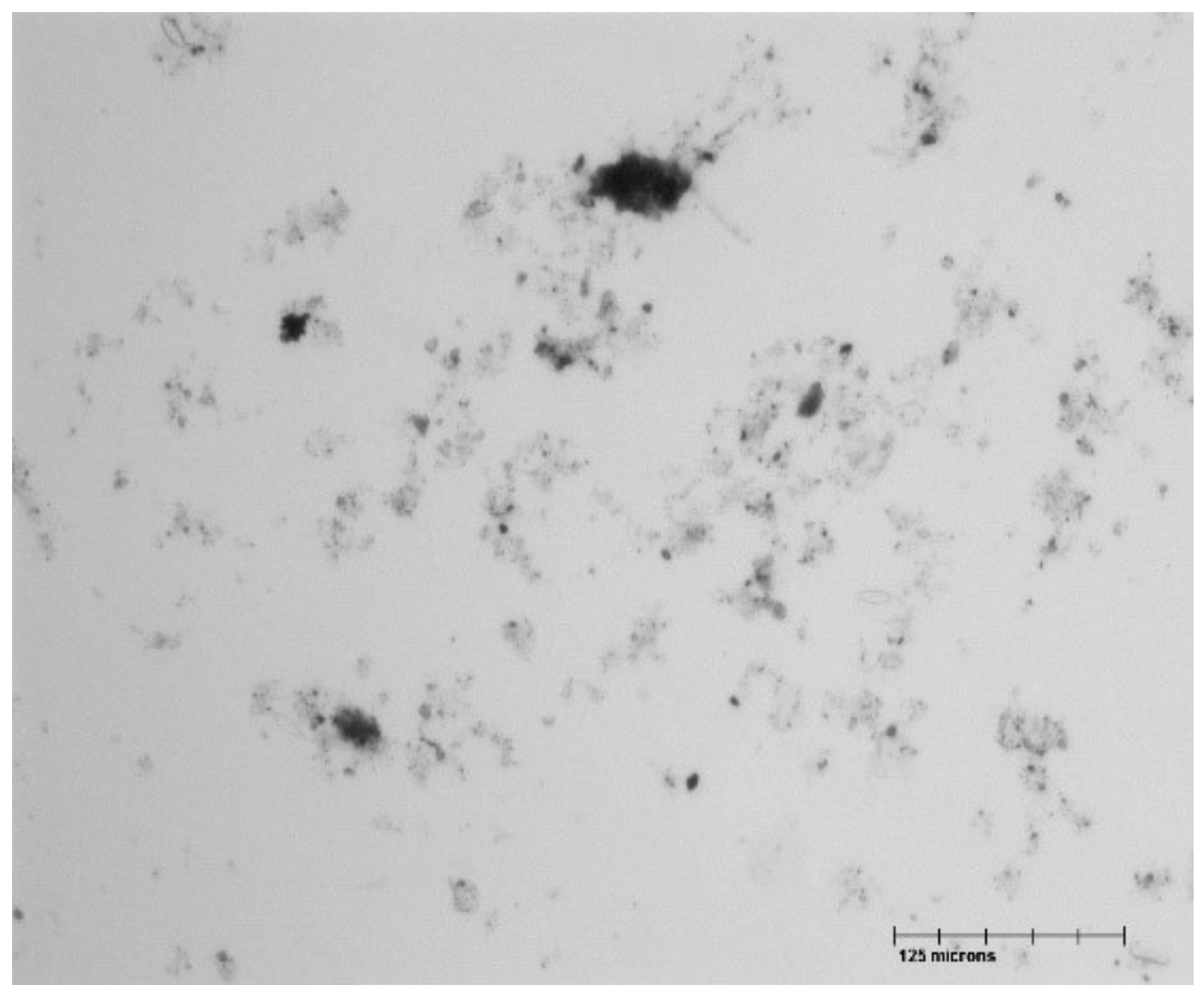
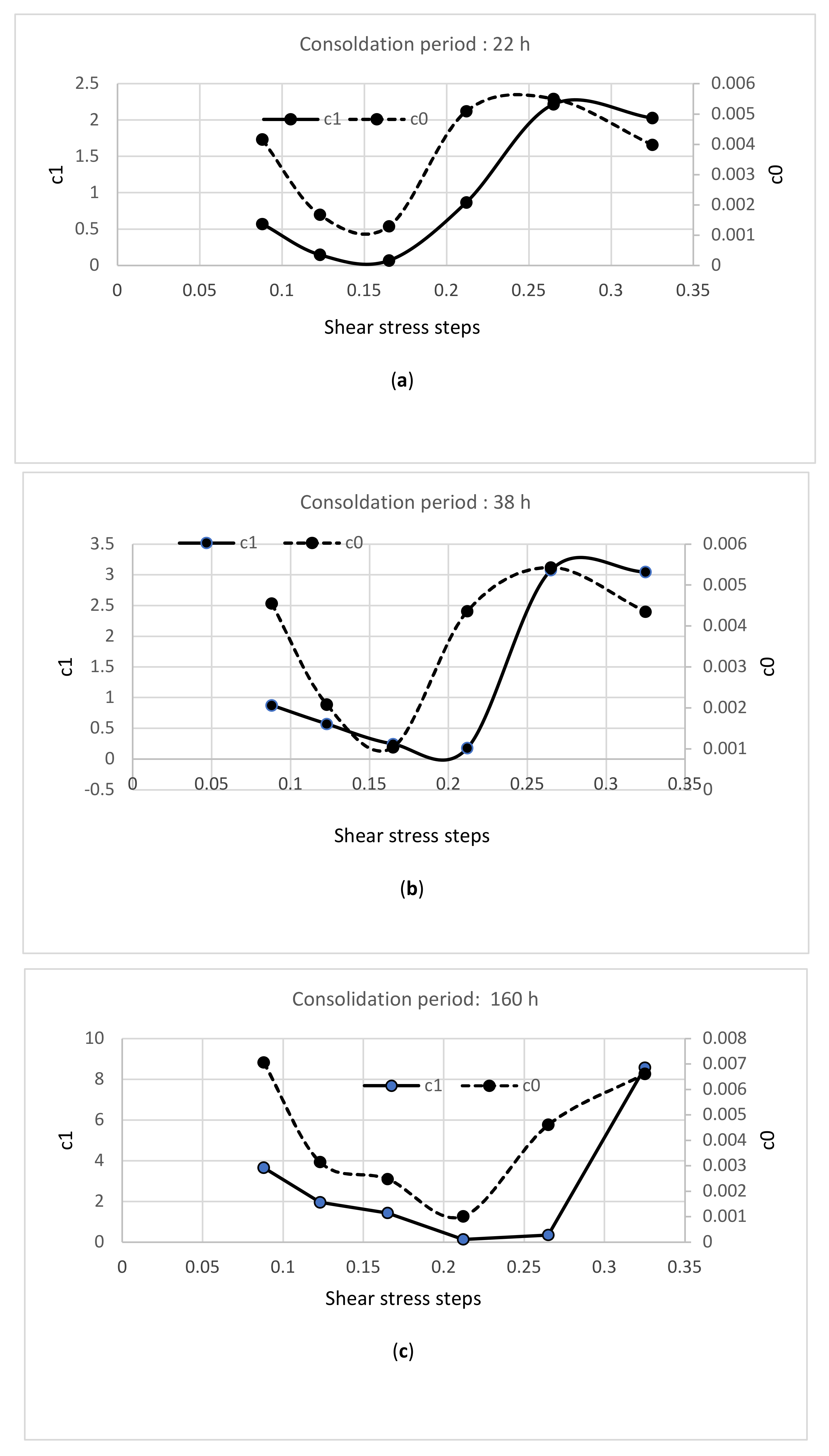
| Shear Stress Steps | Age of Deposit 22 h | Age of Deposit 38 h | Age of Deposit 160 h | |||
|---|---|---|---|---|---|---|
| 0.09 Pa | 4.2 × 10−3 | 0.57 | 4.6 × 10−3 | 0.88 | 7.1 × 10−3 | 3.65 |
| 0.12 Pa | 1.7 × 10−3 | 0.15 | 2.1 × 10−3 | 0.57 | 3.2 × 10−3 | 1.95 |
| 0.17 Pa | 1.3 × 10−3 | 0.07 | 1.0 × 10−3 | 0.24 | 2.5 × 10−3 | 1.43 |
| 0.21 Pa | 5.1 × 10−3 | 0.87 | 4.4 × 10−3 | 0.18 | 1.0 × 10−3 | 0.14 |
| 0.27 Pa | 5.5 × 10−3 | 2.22 | 5.4 × 10−3 | 3.08 | 4.6 × 10−3 | 0.35 |
| 0.33 Pa | 4.0 × 10−3 | 2.03 | 4.4 × 10−3 | 3.05 | 6.6 × 10−3 | 8.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gounder Krishnappan, B.; Stone, M.; Granger, S.J.; Upadhayay, H.R.; Tang, Q.; Zhang, Y.; Collins, A.L. Experimental Investigation of Erosion Characteristics of Fine-Grained Cohesive Sediments. Water 2020, 12, 1511. https://doi.org/10.3390/w12051511
Gounder Krishnappan B, Stone M, Granger SJ, Upadhayay HR, Tang Q, Zhang Y, Collins AL. Experimental Investigation of Erosion Characteristics of Fine-Grained Cohesive Sediments. Water. 2020; 12(5):1511. https://doi.org/10.3390/w12051511
Chicago/Turabian StyleGounder Krishnappan, Bommanna, Mike Stone, Steven J. Granger, Hari Ram Upadhayay, Qiang Tang, Yusheng Zhang, and Adrian L. Collins. 2020. "Experimental Investigation of Erosion Characteristics of Fine-Grained Cohesive Sediments" Water 12, no. 5: 1511. https://doi.org/10.3390/w12051511
APA StyleGounder Krishnappan, B., Stone, M., Granger, S. J., Upadhayay, H. R., Tang, Q., Zhang, Y., & Collins, A. L. (2020). Experimental Investigation of Erosion Characteristics of Fine-Grained Cohesive Sediments. Water, 12(5), 1511. https://doi.org/10.3390/w12051511








