Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds
Abstract
1. Introduction
2. Methods
2.1. Research Data and Study Area
2.1.1. Umgeni River Catchment
2.1.2. Umdloti River Catchment
2.1.3. Nungwane River Catchment
2.1.4. Umzinto/uMuziwezinto River Catchment
2.2. Water Quality Assessment
- (a)
- Variables: thirteen predefined explanatory water quality parameters (NH3, Ca, Cl, Chl-a, EC, F, CaCO3, Mg, Mn, NO3, pH, SO4 and Turb), which are listed based on expert opinion [27]. Rand Corporation’s Delphi Technique was applied to incorporate expert opinion from a panel of thirty water specialists from government parastatals, private sector and academia. Delphi Questionnaires were circulated to the participants and were asked to consider twenty-one water quality parameters for their possible inclusion in the UWQI. The panelists were instructed to designate each variable as: “Include” and “Exclude” and further assign a relative significance rating against each variable elected as “Include.” The rating scale ranged from one to five, whereby “scale 1” denoted the uppermost significance and “scale 5” represented a comparatively low significance. In addition to the prescribed twenty-one parameters, the experts were allowed to add at most five more variables if desired. A total of twenty-one questionnaires were returned out of the thirty questionnaires circulated. The Rand Corporation’s Delphi Technique is described in detail by Horton [36], Brown, et al. [37] and Linstone and Turoff [38,39], and the method is applied in several studies which include Kumar and Alappat [40], Nagels, et al. [41] and Almeida, et al. [42].
- (b)
- Weight coefficients: weight ratings (bi) ranging from one (minimum impact) to five (maximum impact) were assigned to each parameter upon aggregating significance ratings derived from the participatory based Delphi method together with significance ratings extracted from literature. Thereafter, weightage coefficients (wi) were obtained from the following Equation (1) [27,43]:where: bi is the assigned significance rating of the ith water parameter (one being the lowest rating and five the highest rating); wi is the weighted coefficient for the ith water parameter (decimal value); and n total number of the rated water quality parameters. The coefficients are represented as decimal numbers and the sum of all coefficients is one, thereby guaranteeing that the overall index value does not exceed hundred percent (w1 + w2 + w3 + …+ wn = 1 for Equations (1)). Otherwise, aggregation of sub-indices will be compromised, and deem the index model dysfunctional. The weight coefficients are presented in Table 3.wi = bi/(b1 + b2 + … + bn)
- (c)
- Sub-index rating curves and functions: Sub-indices (si) and sub-index rating curves; considering that water quality parameters are monitored in different scientific units; sub-indices are applied to convert the different units of measure into a single common non-dimensional scale [44]. This is a common practice and the conventional method involves sub-index rating curves which are later transformed into mathematical functions commonly known as sub-indices. For practical purposes, fixed key points of the rating curves were graphically established with reference to the permissible concentration limits. Straight-line graphs were used to converge the plotted points and produce a series of linear graphs, which were further converted into linear sub-index functions. Target Water Quality Ranges (TWQRs) as prescribed by DWAF [45,46,47] were consulted in the process. Due to the nature of the article, only the sub-index rating curve and mathematical function for NH3 are presented herein as Figure 2 and Equation (2).where: SIa is the sub-index for ammonia (NH3) and xa is the observed water quality reading of the respective water quality parameter.
- (d)
- Aggregation formula: weighted arithmetic sum model (UWQI), which is an improved version of the weighted sum method. Scenario-based analysis was used to modify and align the model with local conditions to develop the final universal water quality index (UWQI) model as shown with Equation (3) [27]:where: UWQI is the aggregated index value ranging from zero to hundred, with zero representing water of poor quality and hundred denoting water of the highest quality; si is the sub-index value of the ith water quality parameter obtained from the sub-index linear functions and the values range from zero to hundred, similar to WQI values; wi is the weight coefficient value for the ith parameter represented as a decimal number and the sum of all coefficients is one, (w1 + w2 + w3 + … + wn = 1); n is the total number of sub-indices and in this case n = 13. WQI scores are presented as numerical value ranging from 0 to 100, where zero denotes poor water quality and hundred signifies excellent water quality.
2.3. Surrogate Water Quality Index (WQI)
2.4. Water Classification
3. Results and Discussion
3.1. Rationale for Developing Surrogate Water Quality Index (Multiple Linear Regression Model)
3.2. Significant Parameters Applicable to the Surrogate Water Quality Index (WQI)
3.3. Multivariate Statistical Analysis
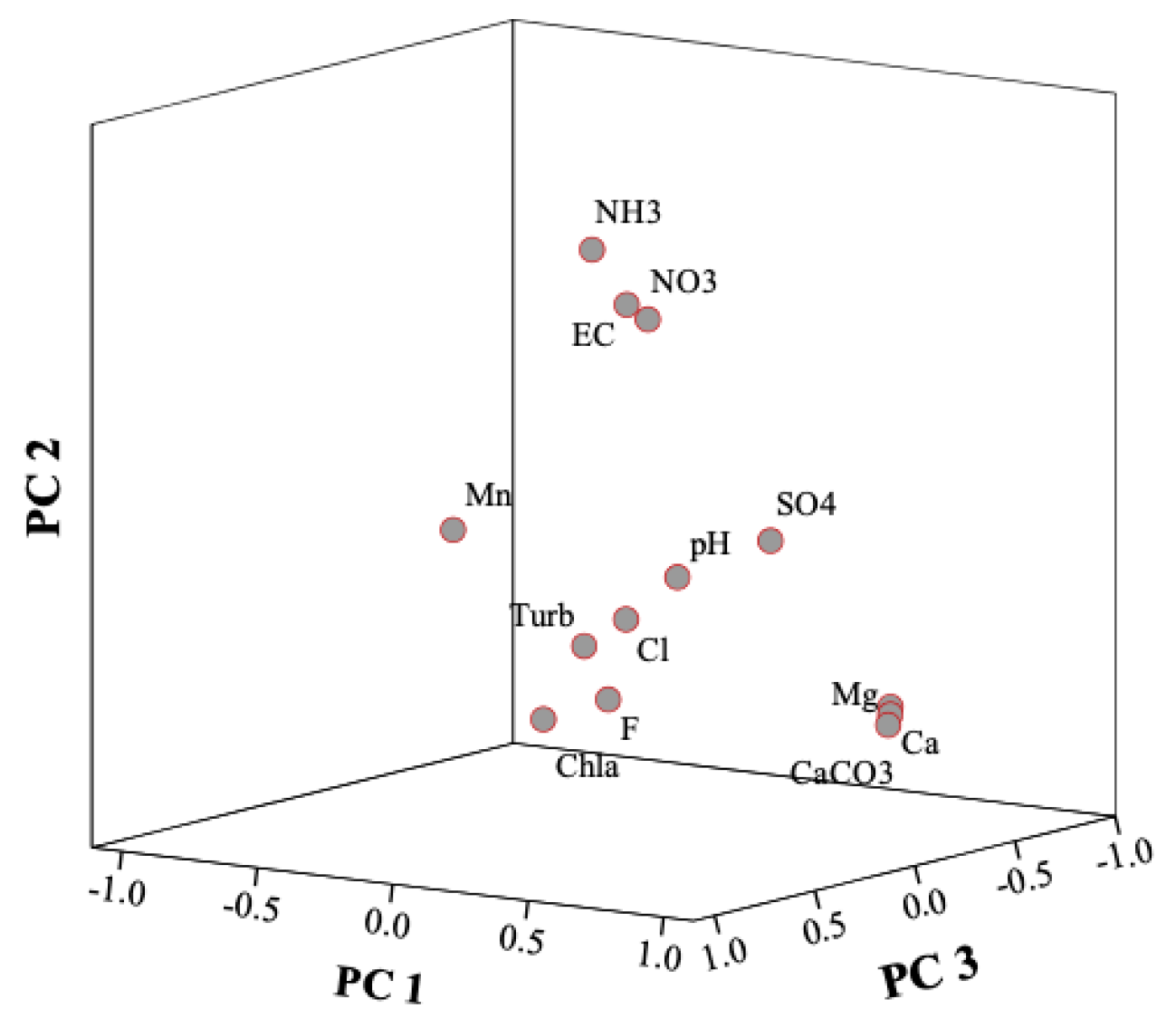
3.3.1. Principal Component Analysis (PCA)
- (a)
- Related eigenvalues that are greater than one (>1.0);
- (b)
- Initial eigenvalues percentage of variance of greater than ten percent (>10%); and
- (c)
- Cumulative percentage of variance of greater than sixty percent (>60%).
3.3.2. Hierarchical Cluster Analysis (HCA)
- (a)
- Turb, Chl-a, EC and SO4 —proxy WQI(a); and
- (b)
- Turb, Chl-a, EC and pH—proxy WQI(b).
3.3.3. Multiple Linear Regression (MLR)
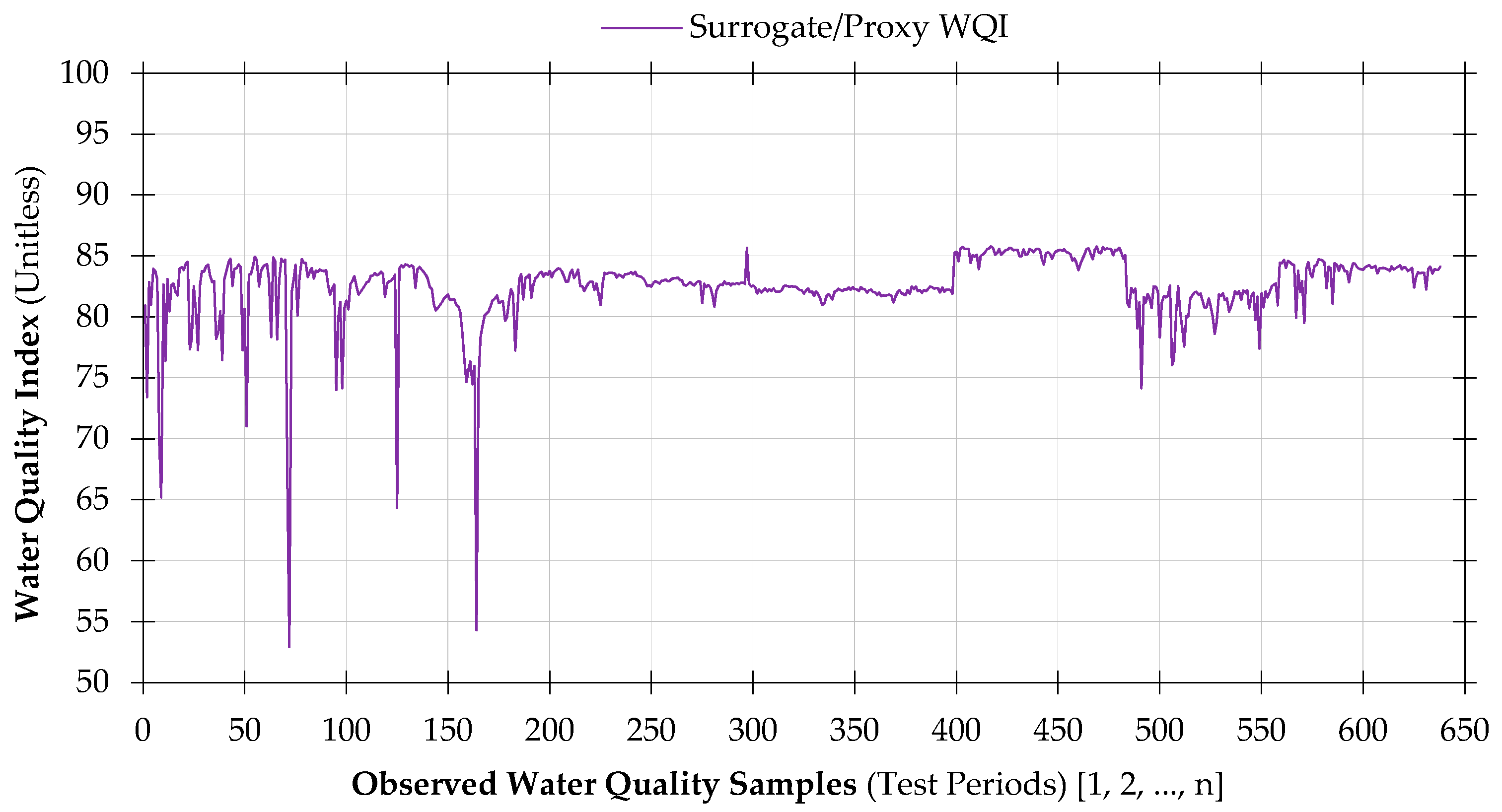
3.4. Scenario-Based Model Validation Analysis
3.5. Index Categorisation Schema
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pegram, G.; Görgens, A. A Guide to Non-Point Source Assessment: To Support Water Quality Management of Surface Water Resources in South Africa (WRC Project No. 696/2/01); Water Research Commission: Cape Town, South Africa, 2001; p. 127. [Google Scholar]
- Ochieng, G.M. Hydrological and Water Quality Modelling of the Upper Vaal Water Management Areas Using a Stochastic Mechanistic Approach. DTech Thesis, Tshwane University of Technology, Pretoria, South Africa, 2007. [Google Scholar]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Schultz Martin, T.; Small Mitchell, J.; Farrow, R.S.; Fischbeck Paul, S. State Water pollution control policy insights from a reduced-form model. J. Water Resour. Plan. Manag. 2004, 130, 150–159. [Google Scholar] [CrossRef]
- Shamir, U.; Salomons, E. Optimal real-time operation of urban water distribution systems using reduced models. J. Water Resour. Plan. Manag. 2008, 134, 181–185. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R.; Antenucci, J.P. A multiobjective response surface approach for improved water quality planning in lakes and reservoirs. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Preis, A.; Whittle Andrew, J.; Ostfeld, A.; Perelman, L. Efficient hydraulic state estimation technique using reduced models of urban water networks. J. Water Resour. Plan. Manag. 2011, 137, 343–351. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Coupled simulation-optimization model for coastal aquifer management using genetic programming-based ensemble surrogate models and multiple-realization optimization. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Tripathi, M.; Singal, S.K. Use of Principal Component Analysis for parameter selection for development of a novel Water Quality Index: A case study of river Ganga India. Ecol. Indic. 2019, 96, 430–436. [Google Scholar] [CrossRef]
- Jahin, H.S.; Abuzaid, A.S.; Abdellatif, A.D. Using multivariate analysis to develop irrigation water quality index for surface water in Kafr El-Sheikh Governorate, Egypt. Environ. Technol. Innov. 2020, 17, 100532–100543. [Google Scholar] [CrossRef]
- Namugize, J.N.; Jewitt, G.; Graham, M. Effects of land use and land cover changes on water quality in the uMngeni river catchment, South Africa. Phys. Chem. Earth Parts A/B/C 2018, 105, 247–264. [Google Scholar] [CrossRef]
- Schullehner, J.; Jensen, N.L.; Thygesen, M.; Hansen, B.; Sigsgaard, T. Drinking water nitrate estimation at household-level in Danish population-based long-term epidemiologic studies. J. Geochem. Explor. 2017, 183, 178–186. [Google Scholar] [CrossRef]
- Shoko, C. The effect of spatial resolution in remote sensing estimates of total evaporation in the uMgeni catchment. Master's Thesis, University of KwaZulu-Natal, Pietermaritzburg, South Africa, 2014. [Google Scholar]
- Hughes, C.; de Winnaar, G.; Schulze, R.; Mander, M.; Jewitt, G. Mapping of water-related ecosystem services in the uMngeni catchment using a daily time-step hydrological model for prioritisation of ecological infrastructure investment–Part 1: Context and modelling approach. Water SA 2018, 44, 577–589. [Google Scholar] [CrossRef]
- Umgeni Water. Umgeni Water Annual Report 2017/2018 Financial Year; Umgeni Water: Pietermaritzburg, South Africa, 2018; p. 208. [Google Scholar]
- Umgeni Water. Infrastructure Master Plan 2019/2020–2049/2050, Volume 2: Mgeni System; Umgeni Water: Pietermaritzburg, South Africa, 2019; p. 185. [Google Scholar]
- Umgeni Water. Infrastructure Master Plan 2019/2020–2049/2050, Volume 3: UMkhomazi System; Umgeni Water: Pietermaritzburg, South Africa, 2019; p. 35. [Google Scholar]
- Republic of South Africa. Proposed new nine (9) water management areas of South Africa. In Government Gazette No. 35517, Notice No. 547; Department of Water Affairs and Foresty: Pretoria, South Africa, 2012; Volume 565, p. 72. [Google Scholar]
- Chiluwe, Q.W. Assessing the Role of Property Rights in Managing Water Demand: The Case of uMgeni River Catchment; Monash South Africa: Johannesburg, South Africa, 2014. [Google Scholar]
- Warburton, M.L.; Schulze, R.E.; Jewitt, G.P.W. Hydrological impacts of land use change in three diverse South African catchments. J. Hydrol. 2012, 414, 118–135. [Google Scholar] [CrossRef]
- Rangeti, I. Determinants of key drivers for potable water treatment cost in uMngeni Basin. Master's Thesis, Durban University of Technology, Durban, South Africa, 2015. [Google Scholar]
- Olaniran, A.O.; Naicker, K.; Pillay, B. Assessment of physico-chemical qualities and heavy metal concentrations of Umgeni and Umdloti Rivers in Durban, South Africa. Environ. Monit. Assess. 2014, 186, 2629–2639. [Google Scholar] [CrossRef] [PubMed]
- Gakuba, E.; Moodley, B.; Ndungu, P.; Birungi, G. Occurrence and significance of polychlorinated biphenyls in water, sediment pore water and surface sediments of Umgeni River, KwaZulu-Natal, South Africa. Environ. Monit. Assess. 2015, 187, 568. [Google Scholar] [CrossRef]
- Namugize, J.N.; Jewitt, G.P.W. Sensitivity analysis for water quality monitoring frequency in the application of a water quality index for the uMngeni River and its tributaries, KwaZulu-Natal, South Africa. Water SA 2018, 44, 516–527. [Google Scholar] [CrossRef]
- Banda, T.D.; Kumarasamy, M. Development of a Universal Water Quality Index (UWQI) for South African river catchments. Water 2020, 12, 1534. [Google Scholar] [CrossRef]
- Umgeni Water. Infrastructure Master Plan 2019/2020–2049/2050, Volume 5: North Coast System; Umgeni Water: Pietermaritzburg, South Africa, 2019; p. 116. [Google Scholar]
- Govender, S. An Investigation of the Natural and Human Induced Impacts on the Umdloti Catchment. Master's Thesis, University of KwaZulu, Natal, Durban, 2009. [Google Scholar]
- Umgeni Water. Infrastructure Master Plan 2019/2020–2049/2050, Volume 4: South Coast System; Umgeni Water: Pietermaritzburg, South Africa, 2019; p. 116. [Google Scholar]
- Mwelase, L.T. Non-revenue water: Most suitable business model for water services authorities in South Africa: Ugu District Municipality. Master's Thesis, Durban University of Technology, Durban, South Africa, 2016. [Google Scholar]
- Luzati, S.; Jaupaj, O. Assessment of Water Quality Index of Durresi-Kavaja Basin, Albania. J. Int. Environ. Appl. Sci. 2016, 11, 277–284. [Google Scholar]
- Wanda, E.M.; Mamba, B.B.; Msagati, T.A. Determination of the water quality index ratings of water in the Mpumalanga and North West provinces, South Africa. Phys. Chem. Earth 2016, 92, 70–78. [Google Scholar] [CrossRef]
- Guettaf, M.; Maoui, A.; Ihdene, Z. Assessment of water quality: A case study of the Seybouse River (North East of Algeria). Appl. Water Sci. 2017, 7, 295–307. [Google Scholar] [CrossRef]
- Paun, I.; Cruceru, L.V.; Chiriac, L.F.; Niculescu, M.; Vasile, G.G.; Marin, N.M. Water Quality Indices-methods for evaluating the quality of drinking water. In Proceedings of the 19th INCD ECOIND International Symposium—SIMI 2016, “The Environment and the Industry”, Bucharest, Romania, 13–14 October 2016; pp. 395–402. [Google Scholar]
- Horton, R.K. An Index-Number System for Rating Water Quality. J. Water Pollut. Control. Fed. 1965, 37, 300–306. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A water quality index—Do we dare? Water Sew. Work. 1970, 117, 339–343. [Google Scholar]
- Linstone, H.A.; Turoff, M. The Delphi method: Techniques and applications; Addison-Wesley Reading: Reading, MA, USA, 1975; Volume 29. [Google Scholar]
- Linstone, H.A.; Turoff, M. The Delphi Method: Techniques and applications; Addison-Wesley Publishing Company, Advanced Book Program: Newark, NJ, USA, 2002; Volume 18. [Google Scholar]
- Kumar, D.; Alappat, B.J. NSF-Water Quality Index: Does It Represent the Experts’ Opinion? Pract. Period. Hazard., Toxic, Radioact. Waste Manag. 2009, 13, 75–79. [Google Scholar] [CrossRef]
- Nagels, J.; Davies-Colley, R.; Smith, D. A water quality index for contact recreation in New Zealand. Water Sci. Technol. 2001, 43, 285–292. [Google Scholar] [CrossRef] [PubMed]
- Almeida, C.; González, S.O.; Mallea, M.; González, P. A recreational water quality index using chemical, physical and microbiological parameters. Environ. Sci. Pollut. Res. 2012, 19, 3400–3411. [Google Scholar] [CrossRef] [PubMed]
- Banda, T.D. Developing an equitable raw water pricing model: The Vaal case study. Master's Thesis, Tshwane University of Technology, Pretoria, South Africa, 2015. [Google Scholar]
- Banda, T.D.; Kumarasamy, M.V. Development of Water Quality Indices (WQIs): A Review. Pol. J. Environ. Stud. 2020, 29, 2011–2021. [Google Scholar] [CrossRef]
- DWAF. South African Water Quality Guidelines: Volume 1: Domestic Water Use; Department of Water Affairs and Forestry: Pretoria, South Africa, 1996; p. 190.
- DWAF. South African Water Quality Guidelines: Volume 3: Industrial Use; Department of Water Affairs and Forestry: Pretoria, South Africa, 1996.
- DWAF. South African Water Quality Guidelines: Volume 7: Aquatic Ecosystems; Department of Water Affairs and Forestry: Pretoria, South Africa, 1996.
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Bouza-Deaño, R.; Ternero-Rodriguez, M.; Fernández-Espinosa, A. Trend study and assessment of surface water quality in the Ebro River (Spain). J. Hydrol. 2008, 361, 227–239. [Google Scholar] [CrossRef]
- Zhao, Y.; Xia, X.H.; Yang, Z.F.; Wang, F. Assessment of water quality in Baiyangdian Lake using multivariate statistical techniques. Procedia Environ. Sci. 2012, 13, 1213–1226. [Google Scholar] [CrossRef]
- Khalil, B.; Ou, C.; Proulx-McInnis, S.; St-Hilaire, A.; Zanacic, E. Statistical assessment of the surface water quality monitoring network in Saskatchewan. Water, Air, Soil Pollut. 2014, 225, 2128. [Google Scholar] [CrossRef]
- Karamizadeh, S.; Abdullah, S.M.; Manaf, A.A.; Zamani, M.; Hooman, A. An overview of principal component analysis. J. Signal Inf. Process. 2013, 4, 173. [Google Scholar] [CrossRef]
- SPSS Inc. IBM SPSS Statistics, 24; SPSS Inc.,: Chicago IL, USA, 2016. [Google Scholar]
- Jurečková, J. Adaptive linear regression. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2011; pp. 10–12. [Google Scholar]
- Vatanpour, N.; Malvandi, A.M.; Hedayati Talouki, H.; Gattinoni, P.; Scesi, L. Impact of rapid urbanization on the surface water’s quality: A long-term environmental and physicochemical investigation of Tajan river, Iran (2007–2017). Environ. Sci. Pollut. Res. 2020, 27, 8439–8450. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal component analysis. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2011; pp. 1094–1096. [Google Scholar]
- Awomeso, J.A.; Ahmad, S.M.; Taiwo, A.M. Multivariate assessment of groundwater quality in the basement rocks of Osun State, Southwest, Nigeria. Environ. Earth Sci. 2020, 79, 108–116. [Google Scholar] [CrossRef]
- Kim, B.S.M.; Angeli, J.L.F.; Ferreira, P.A.L.; de Mahiques, M.M.; Figueira, R.C.L. A multivariate approach and sediment quality index evaluation applied to Baixada Santista, Southeastern Brazil. Mar. Pollut. Bull. 2019, 143, 72–80. [Google Scholar] [CrossRef]
- Nnorom, I.C.; Ewuzie, U.; Eze, S.O. Multivariate statistical approach and water quality assessment of natural springs and other drinking water sources in Southeastern Nigeria. Heliyon 2019, 5, 1–36. [Google Scholar] [CrossRef]
- Paca, J.M.; Santos, F.M.; Pires, J.C.M.; Leitão, A.A.; Boaventura, R.A.R. Quality assessment of water intended for human consumption from Kwanza, Dande and Bengo rivers (Angola). Environ. Pollut. 2019, 254, 113037–113044. [Google Scholar] [CrossRef]
- Njuguna, S.M.; Onyango, J.A.; Githaiga, K.B.; Gituru, R.W.; Yan, X. Application of multivariate statistical analysis and water quality index in health risk assessment by domestic use of river water. Case study of Tana River in Kenya. Process. Saf. Environ. Prot. 2020, 133, 149–158. [Google Scholar] [CrossRef]
- Tripathi, M.; Singal, S.K. Allocation of weights using factor analysis for development of a novel water quality index. Ecotoxicol. Environ. Saf. 2019, 183, 109510–109516. [Google Scholar] [CrossRef]
- Gradilla-Hernández, M.S.; de Anda, J.; Garcia-Gonzalez, A.; Meza-Rodríguez, D.; Yebra Montes, C.; Perfecto-Avalos, Y. Multivariate water quality analysis of Lake Cajititlán, Mexico. Environ. Monit. Assess. 2020, 192, 5–26. [Google Scholar] [CrossRef] [PubMed]
- Horn, J.L. A rationale and test for the number of factors in factor analysis. Psychometrika 1965, 30, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Mitra, S.; Ghosh, S.; Satpathy, K.K.; Bhattacharya, B.D.; Sarkar, S.K.; Mishra, P.; Raja, P. Water quality assessment of the ecologically stressed Hooghly River Estuary, India: A multivariate approach. Mar. Pollut. Bull. 2018, 126, 592–599. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, A.; Hassani, H.; Hassani, S.; Jabbari, N.; Fard Mousavi, S.B.; Rezaei, S. Evaluation of groundwater quality and heavy metal pollution indices in Bazman basin, southeastern Iran. Groundw. Sustain. Dev. 2019, 9, 100245–100258. [Google Scholar] [CrossRef]
- Patil, V.B.; Pinto, S.M.; Govindaraju, T.; Hebbalu, V.S.; Bhat, V.; Kannanur, L.N. Multivariate statistics and water quality index (WQI) approach for geochemical assessment of groundwater quality—A case study of Kanavi Halla Sub-Basin, Belagavi, India. Environ. Geochem. Health 2020, 1–18. [Google Scholar] [CrossRef]
- Patil, V.H.; Singh, S.N.; Mishra, S.; Donavan, D.T. Parallel Analysis Engine to Aid Determining Number of Factors to Retain (Computer software). Instruction and Research Server, University of Kansas. 2007. Available online: https://analytics.gonzaga.edu/parallelengine (accessed on 27 November 2019).
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.G.; Perera, B.J.C. Using the Analytic Hierarchy Process to identify parameter weights for developing a water quality index. Ecol. Indic. 2017, 75, 220–233. [Google Scholar] [CrossRef]
- Ustaoğlu, F.; Tepe, Y.; Taş, B. Assessment of stream quality and health risk in a subtropical Turkey river system: A combined approach using statistical analysis and water quality index. Ecol. Indic. 2019, 113, 105815–105826. [Google Scholar] [CrossRef]
- Wang, J. Statistical study on distribution of multiple dissolved elements and a water quality assessment around a simulated stackable fly ash. Ecotoxicol. Environ. Saf. 2018, 159, 46–55. [Google Scholar] [CrossRef]
- Liew, Y.S.; Sim, S.F.; Ling, T.Y.; Nyanti, L.; Grinang, J. Relationships between water quality and dissolved metal concentrations in a tropical river under the impacts of land use, incorporating multiple linear regression (MLR). AACL Bioflux 2020, 13, 470–480. [Google Scholar]
- Grzywna, A.; Bronowicka-Mielniczuk, U. Spatial and temporal variability of water quality in the bystrzyca river basin, Poland. Water 2020, 12, 190. [Google Scholar] [CrossRef]
- Abrahão, R.; Carvalho, M.; da Silva, W., Jr.; Machado, T.; Gadelha, C.; Hernandez, M. Use of index analysis to evaluate the water quality of a stream receiving industrial effluents. Water SA 2007, 33, 459–466. [Google Scholar] [CrossRef]
- Rabee, A.M.; Al-Fatlawy, Y.F.; Nameer, M. Using pollution load index (PLI) and geoaccumulation index (I-Geo) for the assessment of heavy metals pollution in Tigris river sediment in Baghdad Region. Al-Nahrain J. Sci. 2011, 14, 108–114. [Google Scholar]
- Rubio-Arias, H.; Contreras-Caraveo, M.; Quintana, R.M.; Saucedo-Teran, R.A.; Pinales-Munguia, A. An overall water quality index (WQI) for a man-made aquatic reservoir in Mexico. Int. J. Environ. Res. Public Health 2012, 9, 1687–1698. [Google Scholar] [CrossRef] [PubMed]
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.G.; Perera, B.J.C. Development of a water quality index for rivers in West Java Province, Indonesia. Ecol. Indic. 2018, 85, 966–982. [Google Scholar] [CrossRef]








| Variables a | Statistical Summary of Umgeni Water Quality Data | ||||||
|---|---|---|---|---|---|---|---|
| Minimum | Average | Maximum | Standard Deviation | Total Tests | Percentage of Missing Data | ||
| 1 | NH3 | 0.040 | 0.097 | 1.350 | 0.091 | 638 | 0.000% |
| 2 | Ca | 1.000 | 9.171 | 30.500 | 6.078 | 638 | 0.000% |
| 3 | Cl | 1.821 | 25.215 | 79.000 | 13.765 | 638 | 0.000% |
| 4 | Chl-a | 0.140 | 5.071 | 158.230 | 9.374 | 638 | 0.000% |
| 5 | EC | 6.220 | 19.398 | 144.400 | 9.840 | 638 | 0.000% |
| 6 | F | 0.100 | 0.136 | 0.544 | 0.048 | 638 | 0.000% |
| 7 | CaCO3 | 0.000 | 3.518 | 79.000 | 9.499 | 85 | 86.677% |
| 8 | Mg | 1.000 | 5.724 | 16.300 | 2.535 | 638 | 0.000% |
| 9 | Mn | 0.010 | 0.074 | 1.210 | 0.172 | 638 | 0.000% |
| 10 | NO3 | 0.050 | 0.571 | 19.900 | 0.984 | 638 | 0.000% |
| 11 | pH | 0.000 | 7.747 | 9.100 | 0.529 | 638 | 0.000% |
| 12 | SO4 | 0.160 | 7.497 | 24.200 | 5.980 | 638 | 0.000% |
| 13 | Turb | 0.430 | 15.019 | 367.000 | 29.638 | 638 | 0.000% |
| Sampling Station Identity | Identity Codes | Sampling Location Coordinates (DMS)* | |||
|---|---|---|---|---|---|
| Station | Catchment | Latitude | Longitude | ||
| 1 | Henley Dam | DHL003 | U20 | S 29° 37’ 25.734” | E 30° 14’ 49.754” |
| 2 | Hazelmere Dam | DHM003 | U30 | S 29° 35’ 53.722” | E 31° 02’ 32.121” |
| 3 | Inanda Dam 0.3 km | DIN003 | U20 | S 29° 42’ 27.403” | E 30° 52’ 03.352” |
| 4 | Inanda Dam 7.5 km | DIN013 | U20 | S 29° 40’ 37.002” | E 30° 49’ 52.881” |
| 5 | Inanda Dam 14 km | DIN017 | U20 | S 29° 40’ 11.420” | E 30° 48’ 45.824” |
| 6 | Midmar Dam | DMM003 | U20 | S 29° 29’ 47.332” | E 30° 12’ 05.655” |
| 7 | Umzinto Dam | DMZ009 | U80 | S 30° 18’ 40.676” | E 30° 35’ 34.580” |
| 8 | Nungwane Dam | DNW003 | U70 | S 30° 00’ 24.473” | E 30° 44’ 36.150” |
| Water Quality Variable | Symbol | Unit of Measure | Impact Ratings and Weightage Coefficients | ||||
|---|---|---|---|---|---|---|---|
| Delphi Rating | Literature Rating | Aggregated Impact (bi) | Weight Coefficients (wi) | ||||
| 1 | Ammonia | NH3 | mg/L | 4.3684 | 3.5033 | 3.9358 | 0.1035 |
| 2 | Calcium | Ca | mg/L | 3.5263 | 1.9961 | 2.7612 | 0.0726 |
| 3 | Chloride | Cl | mg/L | 3.7143 | 1.9249 | 2.8196 | 0.0742 |
| 4 | Chlorophyll-a | Chl-a | µg/L | 1.7222 | 1.0000 | 1.3611 | 0.0358 |
| 5 | Electrical Conductivity | EC | µS/m | 2.9474 | 2.3136 | 2.6305 | 0.0692 |
| 6 | Fluoride | F | mg/L | 3.7500 | 3.4619 | 3.6059 | 0.0949 |
| 7 | Hardness | CaCO3 | mg/L | 2.5714 | 1.8943 | 2.2329 | 0.0587 |
| 8 | Magnesium | Mg | mg/L | 3.4667 | 1.9334 | 2.7000 | 0.0710 |
| 9 | Manganese | Mn | mg/L | 3.8125 | 3.1093 | 3.4609 | 0.0910 |
| 10 | Nitrate | NO3 | mg/L | 3.9048 | 3.0072 | 3.4560 | 0.0909 |
| 11 | pondus Hydrogenium | pH | Unitless | 4.3333 | 2.5949 | 3.4641 | 0.0911 |
| 12 | Sulphate | SO4 | mg/L | 2.9167 | 2.9712 | 2.9439 | 0.0774 |
| 13 | Turbidity | Turb | NTU | 2.6667 | 2.6226 | 2.6446 | 0.0696 |
| Totals | 38.0167 | 1.0000 | |||||
| Variable | NH3 | Ca | Cl | Chl-a | EC | F | CaCO3 | Mg | Mn | NO3 | pH | SO4 | Turb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NH3 | 1.000 | ||||||||||||
| Ca | 0.077 | 1.000 | |||||||||||
| Cl | 0.092 | −0.012 | 1.000 | ||||||||||
| Chl-a | −0.090 | −0.061 | −0.178 | 1.000 | |||||||||
| EC | 0.359 | 0.186 | 0.153 | −0.078 | 1.000 | ||||||||
| F | 0.021 | −0.019 | −0.006 | −0.042 | 0.057 | 1.000 | |||||||
| CaCO3 | 0.066 | 0.998 | −0.005 | −0.071 | 0.170 | −0.028 | 1.000 | ||||||
| Mg | 0.050 | 0.987 | 0.003 | −0.086 | 0.149 | −0.041 | 0.995 | 1.000 | |||||
| Mn | 0.196 | −0.054 | 0.031 | 0.024 | 0.201 | −0.022 | −0.046 | −0.033 | 1.000 | ||||
| NO3 | 0.399 | −0.020 | 0.223 | −0.125 | 0.256 | 0.012 | −0.023 | −0.028 | −0.066 | 1.000 | |||
| pH | 0.006 | 0.032 | −0.194 | −0.018 | 0.070 | 0.034 | 0.024 | 0.014 | −0.170 | 0.012 | 1.000 | ||
| SO4 | 0.115 | 0.138 | 0.091 | −0.078 | 0.126 | 0.028 | 0.128 | 0.115 | −0.226 | 0.215 | 0.066 | 1.000 | |
| Turb | 0.173 | 0.113 | 0.191 | −0.090 | 0.183 | 0.272 | 0.109 | 0.101 | 0.125 | −0.006 | −0.070 | −0.134 | 1.000 |
| Kaiser-Meyer-Olkin (KMO) Measure of Sampling Adequacy | 0.510 | ||||||||||||
| Bartlett’s Test of Sphericity Significance | 0.000 | ||||||||||||
| Variable | Principal Components (PCs) a and Communalities | |||||
|---|---|---|---|---|---|---|
| PC 1 | PC 2 | PC 3 | PC 4 | PC 5 | Communalities | |
| Calcium (Ca) | 0.979 | −0.175 | 0.035 | −0.019 | −0.003 | 0.991 |
| Hardness (CaCO3) | 0.979 | −0.184 | 0.043 | −0.027 | −0.020 | 0.995 |
| Magnesium (Mg) | 0.972 | −0.194 | 0.053 | −0.035 | −0.043 | 0.987 |
| Ammonia (NH3) | 0.191 | 0.681 | −0.042 | −0.223 | 0.308 | 0.647 |
| Nitrate (NO3) | 0.080 | 0.636 | −0.428 | −0.124 | −0.012 | 0.609 |
| Electrical Conductivity (EC) | 0.313 | 0.593 | 0.029 | −0.120 | 0.321 | 0.569 |
| Sulphate (SO4) | 0.215 | 0.182 | −0.654 | 0.069 | −0.105 | 0.523 |
| Manganese (Mn) | −0.033 | 0.277 | 0.624 | −0.408 | 0.195 | 0.671 |
| Turbidity (Turb) | 0.188 | 0.372 | 0.522 | 0.472 | 0.008 | 0.669 |
| Floride (F) | 0.001 | 0.188 | 0.171 | 0.763 | 0.188 | 0.682 |
| Chloride (Cl) | 0.067 | 0.492 | 0.039 | 0.042 | −0.629 | 0.646 |
| pondus Hydrogenium (pH) | 0.042 | −0.110 | −0.395 | 0.261 | 0.610 | 0.610 |
| Chlorophyll-a (Chl-a) | −0.148 | −0.296 | 0.118 | −0.260 | 0.345 | 0.310 |
| Eigenvalues (>1.0) | 3.118 | 1.948 | 1.482 | 1.195 | 1.171 | |
| % Variance | 23.949 | 14.986 | 11.397 | 9.192 | 9.008 | |
| % Cumulative Variance | 23.949 | 38.935 | 50.332 | 59.525 | 68.533 | |
| Model | Multiple Linear Regression Coefficientsa | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Var. | Unstandardized Coefficients | Std. Coeff. | t | Sig. | 95% Confidence Interval for B | Correlations | Collinearity Statistics | ||||||
| B | Std. Error | Beta | Lower Bound | Upper Bound | Zero Order | Partial | Part | Tol. | VIF | ||||
| Proxy WQI(a) | Const. | 87.047 | 0.474 | 183.490 | 0.000 | 86.116 | 87.979 | ||||||
| Turb | −0.088 | 0.007 | −0.452 | −12.644 | 0.000 | −0.101 | −0.074 | −0.424 | −0.449 | −0.433 | 0.918 | 1.090 | |
| EC | −0.196 | 0.028 | −0.336 | −7.049 | 0.000 | −0.251 | −0.141 | −0.173 | −0.270 | −0.241 | 0.516 | 1.940 | |
| SO4 | 0.108 | 0.046 | 0.113 | 2.346 | 0.019 | 0.018 | 0.198 | −0.028 | 0.093 | 0.080 | 0.510 | 1.961 | |
| Chl-a | −0.042 | 0.021 | −0.069 | −1.978 | 0.048 | −0.084 | 0.000 | −0.152 | −0.078 | −0.068 | 0.963 | 1.038 | |
| Proxy WQI(b) | Const. | 85.273 | 2.969 | 28.726 | 0.000 | 79.444 | 91.102 | ||||||
| Chl-a | −0.042 | 0.022 | −0.068 | −1.921 | 0.055 | −0.084 | 0.001 | −0.152 | −0.076 | −0.066 | 0.946 | 1.057 | |
| EC | −0.151 | 0.020 | −0.259 | −7.375 | 0.000 | −0.191 | −0.111 | −0.173 | −0.281 | −0.254 | 0.959 | 1.043 | |
| pH | 0.224 | 0.378 | 0.021 | 0.593 | 0.553 | −0.518 | 0.966 | 0.003 | 0.024 | 0.020 | 0.977 | 1.024 | |
| Turb | −0.090 | 0.007 | −0.462 | −12.964 | 0.000 | −0.103 | −0.076 | −0.424 | −0.458 | −0.446 | 0.930 | 1.075 | |
| Sample Identity | Water Quality Index Results from Scenario-Based Analysis | |||||
|---|---|---|---|---|---|---|
| Ideal WQI Results | Proxy WQI(a) Results | Proxy WQI(b) Results | ||||
| Index Score | WQI Class | Index Score | WQI Class | Index Score | WQI Class | |
| Maximum | 100.00 | 1.00 | 85.09 | 1.00 | 85.44 | 1.00 |
| Average | 50.00 | 4.00 | 49.82 | 4.00 | 45.19 | 4.00 |
| 1 | 0.00 | 5.00 | 23.09 | 5.00 | 6.16 | 5.00 |
| 2 | 5.00 | 5.00 | 24.70 | 5.00 | 11.28 | 5.00 |
| 3 | 10.00 | 5.00 | 26.29 | 4.00 | 16.26 | 5.00 |
| 4 | 45.00 | 4.00 | 39.39 | 4.00 | 39.89 | 4.00 |
| 5 | 50.00 | 4.00 | 42.69 | 4.00 | 43.25 | 4.00 |
| 6 | 55.00 | 3.00 | 46.00 | 4.00 | 46.61 | 4.00 |
| 7 | 90.00 | 2.00 | 77.03 | 2.00 | 75.84 | 2.00 |
| 8 | 95.00 | 2.00 | 84.12 | 2.00 | 81.98 | 2.00 |
| 9 | 100.00 | 1.00 | 85.09 | 2.00 | 85.44 | 2.00 |
| ID | Water Quality Classification | |
|---|---|---|
| Description of Rank and Classification | Index Score | |
| 1 | Class 1—Good water quality Water quality is protected with a virtual absence of threat or impairment; conditions very close to natural or pristine levels | 95 < Index ≤ 100 |
| 2 | Class 2—Acceptable water quality Water quality is usually protected with only a minor degree of threat or impairment; conditions rarely depart from natural or desirable levels | 75 < Index ≤ 95 |
| 3 | Class 3—Regular water quality Water quality is usually protected but occasionally threatened or impaired; conditions sometimes depart from natural or desirable levels | 50 < Index ≤ 75 |
| 4 | Class 4—Bad water quality Water quality is frequently threatened or impaired; conditions often depart from natural or desirable levels | 25 < Index ≤ 50 |
| 5 | Class 5—Very bad water quality Water quality is almost always threatened or impaired; conditions usually depart from natural or desirable levels | 0 < Index ≤ 25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banda, T.D.; Kumarasamy, M. Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds. Water 2020, 12, 1584. https://doi.org/10.3390/w12061584
Banda TD, Kumarasamy M. Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds. Water. 2020; 12(6):1584. https://doi.org/10.3390/w12061584
Chicago/Turabian StyleBanda, Talent Diotrefe, and Muthukrishnavellaisamy Kumarasamy. 2020. "Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds" Water 12, no. 6: 1584. https://doi.org/10.3390/w12061584
APA StyleBanda, T. D., & Kumarasamy, M. (2020). Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds. Water, 12(6), 1584. https://doi.org/10.3390/w12061584






