Numerical and Observational Analysis of the Hydro-Dynamical Variability in a Small Lake: The Case of Lake Zirahuén, México

Abstract

Lake Zirahuén is one of the ecologically better preserved and small-sized lakes in Mexico. Observations revealed that Lake Zirahuén is subjected to a consistent diurnal wind because of the presence of a valley–mountain breeze that triggers semidiurnal and 3–8 h variability oscillations, with the latter among the natural frequencies of the lake, whereas the former and the principal forcing are in near resonance with the second vertical mode. The thermodynamic variability was greater in the metalimnion where the analysis of eigenfunctions shows that higher modes (>2) are important at depths below the thermocline. The numerical modeling adequately described the water temperature evolution and surface layer currents in an averaged manner. The daily observations showed drifts in surface currents, acquiring velocities of up to 0.1 m/s, owing to wind stress, which caused an increase in temperature at the northern section of the lake. Data averaged over three months revealed that the surface currents flow northward with an anticyclonic return to the east part and a pair of cyclonic returns to the northwestern and southwestern parts of the lake; whereas at the vertical, the structure showed two circular regions divided by the thermocline located at a depth of 15–20 m.

1. Introduction

Lakes, like every surface water source, play an important role in the availability and quality of clean water supplies. At present, clean water problem is one of the most important challenges for science and technology, owing to the rapid increase in population, the occurrence of extreme drought events, and the overexploitation and pollution of water bodies. A reliable supply of clean fresh water is essential for meeting the growing demands of the population for household use, recreation, irrigation, aquaculture, and habitat protection.

An important factor that has an immediate impact on lake water quality is climate change that causes an increase in water temperature. Water temperature increases with air temperature, promoting stronger vertical thermal gradients [1,2], which results in less vertical interchange during summer and less total vertical mixing during winter in tropical lakes. Changes in water temperature affect certain parameters that can be considered as climate change indicators, such as dissolved oxygen levels, chemical and biological processes, water density, and some aquatic species [3,4,5]. However, in addition to some effects of climate change, other local factors with multiple interacting stressors should be considered as equally important, such as land-use patterns, nutrient inputs, and sulfur and nitrogen oxide deposition [6,7,8,9,10].

Hence, interdisciplinary studies are required to completely understand the behavior of lakes and the changes in associated factors such as the physical, biological, and chemical properties, as well as climate and land use. Proper lake management is necessary to understand, maintain, and avoid adverse effects on the availability and quality of water [11,12,13,14,15,16].

Numerical models have been applied to better understand the physical, chemical, and biological processes in lakes to simulate water flow, sediment distribution, pollutant transport mechanisms, and environmental impacts. In particular, hydrodynamic models are valuable tools to provide crucial information concerning water quality processes [1,17,18]. This information is essential for the comprehensive planning of lake management and restoration [18,19,20,21], as well as an important tool for the prediction and management for algal blooms, or biological control management [22].

Hydrodynamic models applied to lakes ranging from large to small may be one- (1D) to three-dimensional (3D) multi-disciplinary models [23,24,25,26,27,28]. Initially, 1D vertical models were used to analyze the thermal evolution of the water column, disregarding the advective horizontal transport; the two-dimensional (2D) vertically integrated models focused on the horizontal distribution of temperature and velocity fields without considering the vertical processes in the water column. However, with the development of new numerical 3D models, recent studies have shown the complex dynamics generated using wind and heat fluxes [29]. The thermal profile generated by wind stress and heat flux exchanges with the lake is one of the most important characteristics that confine substances and nutrients of the lake within 2 or 3 layers—the epilimnion (the upper most, warmest and well oxygenated layer), the metalimnion (middle layer of a rapid change of temperature and oxygen concentrations), and the hypolimnion (bottom layer of colder water)—where the biogeochemical components are redistributed within the lake in different ways [1,30,31]. A model capable of reproducing these stratification characteristics is essential to completely understand the transport and fate of some tracers due to physical processes.

In comparison to most Mexican lakes that show an advanced state of desiccation, water pollution and eutrophication, Lake Zirahuén keeps having most of its parameters acceptable in a limnological way [3]. In recent years, however, signs of pollution have alerted the local authorities to the need for measurements regarding lake restoration [5]. A number of authors have previously reported findings on aspects related to the water quality of the lake; in particular, some studies have shown that the lake developed from oligotrophic to oligo-mesotrophic between 1988 and 2014. As a result, it is known that the main problems of Lake Zirahuén are related to agricultural pollution and household waste [5,32,33]. Those results show that the water quality of the lake is currently deteriorating. Although important things to notice in these studies are the lack in lake monitoring and the exclusion of the hydrodynamic circulation that may underestimate the pattern of dispersion of nutrients in the lake, hence the need to configure a hydrodynamical model.

To our knowledge, this is the first study to a) validate a high-resolution 3D hydrodynamic model allowing high-frequency measurements at Mexican lakes and b) calibrate using an inverse method for the optimal estimation of the wind drag coefficient (C_d). The model simulation was validated against current time series and water temperature data obtained during some field campaigns performed in 2018. The validated model was applied to investigate the thermally and wind-driven general circulation.

Study Area

Lake Zirahuén is one of the deepest and ecologically better-preserved lakes in Michoacán, Mexico (Figure 1). However, the accelerated change in the land use from forest to agriculture is deteriorating the environmental quality of this lake [34]. The climate, vegetation, and other important characteristics of the lake and basin have been widely described in the literature [4,5,32,33]. Lake Zirahuén is described as a warm monomictic, oligo-mesotrophic, and endorheic type with a mean water transparency of 3.8 m. It is located at 2080 m above sea level (a.s.l.) at 19.43° N and 101.74° W, with an area of almost 10 km². The lake is approximately 42 m deep, has a volume of 216,106 m³, and is almost rectangular in shape (rotated nearly 40° clockwise) with approximately 4.0 km in length × 3.5 km in width. Because the west-southwest side of Lake Zirahuén is surrounded by a mountain having height of 2200–2300 m a.s.l., the deepest portion of the lake is located to the left side as a continuation of the slope of the mountain. At the northwest and northeast of the lake, the mountains reach the height of above 2900 m a.s.l.; the shallower portion of the lake is located at the southeast side, where relative smaller and well-spaced mountains rise above the lake in the form of a valley (<2100 m a.s.l.). This topographic configuration generates a consistent pattern of wind called valley–mountain breeze that blows unequally between northward and southward during the day. A permanent run-off called “El silencio” is also located on the east side of the lake, carrying only a very small amount of water seasonally, <0.5 m³/s, but sufficiently to maintain the hydrological balance of the lake [4,5,34,35,36].

The thermal behavior of Lake Zirahuén is considered typical for tropical, deep lakes, with a well-mixed water column during winters where the lake reaches its minimum temperature of 16 °C. During spring, the heat transferred through the lake surface starts to develop a temperature profile; in summer a completely stratified configuration is reached (approximately 24 °C at the surface); during late summer and autumn, the surface begins to cool again (with the onset of the rainy season) reaching its maximum mixed layer at surface; finally, the lake again reaches its isothermal state at winter [4,5,34,35,36].

2. Materials and Methods

2.1. Field Campaigns of Measurements in 2018

The 3D hydrodynamic variability of Lake Zirahuén was analyzed in 2018 by conducting a series of eight field campaigns to sample the physical variables at the lake (Figure 2). The following instruments were used: weather station, Conductivity–Temperature–Depth (CTD) probe, series of thermistors, water-level sensor, current meter profiler, and sonar/GPS system. The dates and data were used according to the availability of instruments as follows in

Table 1. Dates and instruments used in each campaign.

	Weather Station	CTD	Thermistor Chain	Water Level	Acoustic Current Meter Profiler (ADP)
February
March
April			●
May			●
June			●
July
September			●
November

:

2.1.1. Weather Station

Wind and heat flux exchanges are the main factors that affect Lake Zirahuén. The meteorological parameters were monitored by installing a weather station (HOBO micro station logger H21-002; Onset Computer Corporation, Bourne, MA, USA) with sensors of air temperature and wind speed and direction (Davis anemometer; Davis Instruments, Hayward, CA, USA), which sampled every 15 min, during each field campaign: five times at the northeast rim of the lake during February–July, and one time in the northwest rim during November.

The data from another weather station located approximately 10 km to the south of the lake were also considered because that weather station includes measurements of more atmospheric parameters such as solar radiation and relative humidity, as well as air temperature, wind speed, and wind direction. This station provided data every 15 min from June to August 2018.

2.1.2. CTD Casts and Thermistor Chains

The thermal structure of Lake Zirahuén was measured using a CTD profiler XR-620 (RBR Ltd.; Ottawa, ON Canada) that was dropped manually from a boat, with a vertical speed of about 1 m/s and sampling rate of 1 data scan per second. The sampling was performed three times: February 17, May 13, and November 21–23. The data were treated and interpolated to a transect to obtain the spatial variability of temperature with depth and across the lake.

In order to continuously record temperature, a water thermistor chain was placed with 9 or 10 HOBO temperature loggers (Onset Computers Corporation, Bourne, MA, USA) that sampled at a rate of 5 min in the deepest part of the lake (depth, around 40 m) during four campaigns: about 5 days in April near the center of the lake, 1.5 months starting in May at the deepest part of the lake, and from 2 months during July to August and for 3 months from September to November, both near the coast around the deepest part of the lake. The chain location was changed to avoid its trapping in the fishing nets set by local fishermen.

2.1.3. Current Meter

An Acoustic Doppler current meter profiler (ADP, AquaPro, 400 kHz; Nortek USA Inc., Boston, MA, USA) was placed at the bottom of the lake for 2 months (from July to August) in the same place as the thermistor chain. It measured the vertical profile of three current speed components at a sampling rate of 5 min and discretization from the near bottom to surface of 1 m.

2.1.4. Bathymetry and GPS

Depth readings were obtained using a GPS-enabled electronic depth finder (Lowrance, Navico; Tusla, OK, USA) in order to improve the bathymetry estimation during each field campaign.

For all the temporal series data described in this section, a 2 h low-pass filter was applied in order to remove high frequency noise. For the CTD data a linear interpolation was done to smooth data around the thermocline by removing spikes due to sensor issues known as “align CTD” procedure. All data were visually inspected, in particular, incorrect readings from the echosounder were removed.

2.2. Numerical Model

The flow field at Lake Zirahuén was simulated by applying the Delft3D model version 7545 [37]. The Delft3D model is commonly used worldwide; it solves the Navier–Stokes equations for shallow water systems [38]. This model can be applied to simulate flows, sediment transport, morphology, waves, water quality, and ecology. This model has been successfully applied to simulate the hydrodynamics, sediment transport, and water quality of water bodies such as Lakes Naivasha, Taihu, Egirdir, Whangape, Constance, and Waahi [12,15,16,22,28,39,40,41].

The computational domain of 4.0 × 3.5 km was discretized into an irregular cartesian mesh with 56 × 54 nodes in the horizontal direction and a grid size resolution of about 70 m (Figure 2). The RGFGRID module of Delft3D was used to generate the grid file. The vertical domain of 42 m deep was discretized into 40 vertical layers of approximately 1 m thickness from the surface to the bottom. A Z-layers configuration was used in order to have a regular vertical grid on the surface. Bathymetry measurements obtained during the field campaigns were used to interpolate the depth file by using the QUICKIN module of Delft3D, a powerful tool able to handle various source of sample data of different time and quality, that can be interpolated by classical methods (triangular interpolation, simple mean average) depending on the density of data over the model area. The simulation reference date was 1 June 2018, and the model was run monthly (for intervals of 30 days, in order to save space) restarting with the last time of the previous simulation, except for the initial run where the initial condition was set from the thermal stratification of 1 June obtained from the thermistor data chain. Ten days were enough to warm up the model; in fact, at around half a day the thermal structure stabilizes, while for the currents takes about five days to reduce any noise and become stable. The allowable time step was 12 s in order to satisfy the Courant number [37]. Temperature and wind were the active physical processes. The other physical parameters had typical values such as: gravity, 9.81 m/s²; water density, 1000 kg/m³; air density, 1 kg/m³; uniform Chézy roughness, 65 m^1/2/s; and background horizontal and vertical eddy viscosity and diffusivity, 0 m²/s. The k-Epsilon model for 3D turbulence was used [42]. The Murakami model for heat flux was applied with the default values of 95% sky cloudiness and Dalton number of 0.0013; the Secchi depth was set to 3.8 m. Note that the short-wave radiation flux, relative humidity, and air temperature data were obtained from the weather station that was ~10 km away from the lake. The initial temperature profile and model calibration were based on the data obtained during May–June.

Wind stress plays an important role in the water movements and was therefore the principal parameter to calibrate the model. In the Delft3D model, the wind stress is parameterized based on the wind drag coefficient C_d [37]. In this study, the wind speed ranges from 0 to ~5 m/s, then a constant wind drag coefficient was considered according to [43].

Model Calibration

The calibration was achieved by using the parametric identification method based on nonlinear least squares [43]. In this case, the method involves the determination of the value of the parameter C_d by solving the inverse problem adjusting the model outputs with the observational values by minimizing the error between both. The sum of the squared error is the function that needs to be minimized, yielding an optimal solution after several model runs.

The implementation of this method is based on a trust-region-reflective algorithm, which is a subspace trust-region method with an interior-reflective Newton method described in [44]. Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradient [45].

2.3. Spectral Analysis

The power spectral density was used to evaluate the contribution from different frequency components $S_{11}\left(f\right)={{\displaystyle \int }}_{-\infty }^{\infty }{R}_{11}\left(\tau \right)e^{-i2\pi f\tau }d\tau$, where $R_{11}$ is the autocorrelation function of the time series 1 [46]. While the coherence between two time series was computed using the coherence spectrum ${\left|S_{12}\right|}^2/S_{11}{S}_{22}$, and the frequency response with the complex admittance function $H_{12}=S_{12}/S_{11}$, the gain or admittance amplitude is $\left|H_{12}\right|$, and the phase is given by $ta{n}^{-1} \left[img\left(H_{12}\right)/real\left(H_{12}\right)\right]$.

2.4. Metrics to Evaluate the Performance of the Hydrodynamical Model

To evaluate the performance of the model in the reproducibility of the observational data, the root mean square error, RMSE = ${\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(Mo{d}_i-Ob{s}_i\right)}^2\right]}^{1/2}$, was used as measurement of agreement between the model and observations; also the coefficient of determination R² = ${\left[\frac{{{\displaystyle \sum }}_{i=1}^n\left(Mo{d}_i-\overline{Mod}\right)\left(Ob{s}_i-\overline{Obs}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Mo{d}_i-\overline{Mod}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Ob{s}_i-\overline{Obs}\right)}^2}}\right]}^2$, was applied as the measure of the fraction of the variance in the observational data that can be explained by the numerical results. When the RMSE is small, close to 0, the agreement between the model and observational results will be better; and when R² becomes close to 1, the variance of the data is completely explained by the model results.

Other metrics were considered for assessing the agreement between the model and observations as part of the Taylor diagram [47]: the linear correlation coefficient (R), the standard deviation (std = $\sqrt{\frac{1}{n-1}{\displaystyle \sum }_{i=1}^n{\left(Mo{d}_i-\overline{Mod}\right)}^2}$), and the root mean squared error (RMSE).

2.5. Normal Modes of Oscillation

The theory of the three-layer system of continuum density [48], was applied to calculated the oscillation periods of the lake according to the formula $\left(2L/n\right)\left(h_1{\xi }_1\sqrt{\frac{a_1}{g}}\right)$, where L is the length of the lake (~4000 m), n = 1,2,…, are the basin modes of oscillation, $g$ (9.8 m/s²) is the acceleration due to gravity and ${\xi }_1$ is related with the positive root of the first vertical mode (n = 1). The width of the epilimnion is $h_1$ and $a_1$ is a constant length related to the slope of the surface density profile.

The vertical structure of the normal modes was obtained from solving numerically the equation $W{\left(z\right)}^{″}+m^{2}W\left(z\right)=0$, with boundary condition $W\left(z=0,H\right)=0$, and $m^2=k^2{N}^2\left(\frac{1+{\left(\frac{\omega }{N}\right)}^2}{{\omega }^2-f^2}\right)$, where $\left(k,m\right)$ is the wave number vector, $N\left(z\right)={\left[-\frac{g}{{\rho }_0}\frac{\partial \rho }{\partial z}\right]}^{1/2}$ is the continuous profile of Brunt-Väisälä frequency with $\rho$ and ${\rho }_0$ the water density and its reference value, respectively, $\omega$ is the frequency of the system and $f$ is the inertial frequency [49]. In the present case, it is considered $N\gg \omega$ and $f\to 0$, so the vertical wave number may be written as $m^2=\frac{k^2}{{\omega }^2}{N}^2={\alpha }^2{N}^2$, with $\alpha =\frac{1}{c}$ the eigenvalue of the corresponding differential equation and $c$ the phase speed.

3. Results and Discussion

3.1. Weather Parameters

From the weather station located at the rim of the lake (Figure 3), along the year, a persistent pattern in meteorological variables was noted with a well-defined diurnal variability. The weather was temperate with temperatures around 20 °C during daytime between 09:00 a.m. and 18:00 p.m. and below 15 °C at nighttime (Figure 3a). The wind tended to vary between calm (less than 0.5 m/s) and active periods of 3.5 m/s with gust of 6.5 m/s (Figure 3b,d). The wind direction for all sampling periods also tended to remain the same, with winds coming from the southwest or northeast (Figure 3c,d). This consistent pattern of wind is well defined and explained as a topographical effect because of the valley–mountain breeze (Figure 1).

As stated above, all meteorological variables showed well-defined diurnal variability. Nevertheless, at least for June 2018 (Figure 4), some peculiarities were noted for the region; for example, the onset of the cooling weather triggered by the start of the rainy season around day 11 of June, which lasted for at least 10 days. During this time, the maximum daily value of short-wave radiation drops down to around 300 W/m² (Figure 4b), and as a consequence of this the air temperature also decreased to below 15 °C (Figure 4a); although the wind speed did not vary considerably (Figure 4g), the relative humidity was practically saturated at 100% (Figure 4f). Even though the atmospheric variables showed always a typical behavior, the effect on the lake was extremely marked by a sudden drop in temperature that represent the onset of the mixing of the lake, as is discussed in the next section.

Additionally, a detailed analysis of the incoming shortwave radiation was performed classifying clear and cloudy days [50]. The selection was made following a simple method based on the incoming solar shortwave radiation at 13:00 p.m. local time: If the shortwave radiation at 13:00 and 15:00 p.m. is less than the average shortwave radiation at 13:00 p.m., then it is a cloudy day. If the data before 13:00 p.m. are monotonic ascendant and the data after 15:00 p.m. are monotonic descendant, then is a clear day. If the data do not satisfy these previous criteria, then is a partly cloudy day.

It was found that during this period, more cloudy days are present (77.6%) than clear days (22.4%), as seen in Figure 4d–f. The daily heating begins at around 8:00 a.m. local time and reaches its maximum peak around 14:00 p.m., except during cloudy days, where the solar radiation reaches its maximum peak around 12:00–13:00 p.m. On clear and partly cloudy days the solar radiation begins to decay smoothly during the afternoon till 21:00 p.m. (Figure 4d,e). The average of the shortwave radiation also presents this daily typical behavior. However, for the period from 12:00–15:00 p.m. it was found that the solar radiation was blocked by the clouds above the weather station during totally cloudy days (Figure 4f). As expected, the shortwave radiation spectra present a principal peak at the diurnal frequency, but due to some asymmetry on this time series (is a half-rectified-signal type) it has frequencies that do not have a physical interpretation in nature; for example, it is shown that, during one period of 12 h, its occurrence is impossible, as the Sun is not over the same point twice a day (Figure 4c).

Regarding to the average day of the wind speed, it was found that it reaches its maximum peak at 15:00 p.m., and another peak was found around 4:00 a.m., almost 12 h later (Figure 4i). This can be verified in the wind speed power spectra (Figure 4j). The wind direction is similar to the weather station located at the rim of the lake, with winds coming from the southwest or northeast (Figure 4k).

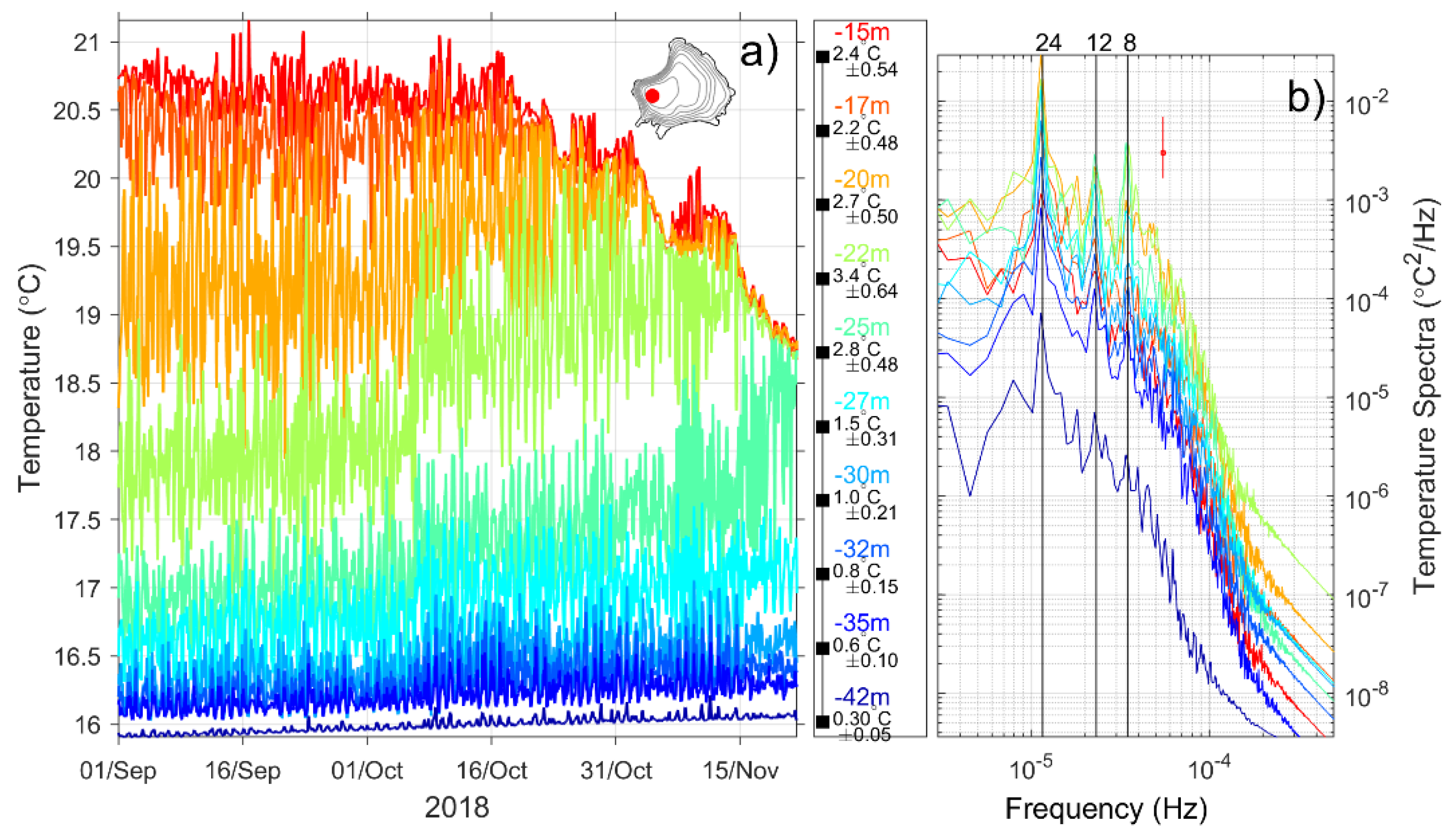
3.2. Hydrography from the Observational Thermistor Chain Data

From 14 April at 18:30 p.m. to 20 April at 03:00 a.m. (approximately five days; Figure 5), 10 thermistors (at depths of 3, 5, 8, 10, 13, 15, 20, 25, 28, and 30 m) were placed on a chain anchored at a depth of about 30 m, near the center of the lake. The four thermistors close to the surface showed a positive trend with temperatures ranging from 19 to 21 °C. The sensors showed a variability up to 1.4 °C with a maximum standard deviation (std) of 0.29 °C. The thermistors located between 13 and 15 m depth showed temperatures ranging from 17 to 18.5 °C without any marked trend; however, the vertical variability in this part of the water column was greater, which was almost 1.8 °C with a std of 0.39 °C. The thermocline was located at 15 m depth. Below the thermocline, the base of the metalimnion was located at about 20 m where the temperature was about 16.2 °C and showed a variability of 0.5 °C. From 25 to 30 m in depth, the temperature remained near 16 °C with a drop in the vertical variability to less than 0.3 °C and std of 0.06 °C.

Unfortunately, the chain was hooked in a fishing net from 20 April to 13 May. Then, from 13 May at 16:00 p.m. to 29 June at 11:00 a.m. (approximately 46 days; Figure 6), the 10 thermistors on the chain were relocated to a depth of about 40 m arranged at 13, 15, 18, 20, 23, 25, 28, 30, 33, and 40 m depth. The surface layer (apparently from surface to 13 m deep) was heated at a rate of 0.1 °C/d until 1 June (Figure 6a). For another 11 days, the temperature at this level oscillated at around 23 °C, and then a sudden cooling of −1.5 °C occurred during the rest of the month until 29 June. The thermistor located at 15 m depth suggested a positive trend during the first part of the time series with more variability (about 3.1 °C with a std of 0.65 °C), and then, on 17 June, the cooling started to influence at this level, and the sudden drop of temperature encompassed the upper layer. The layer at depths of 18, 20, 23, and 25 m can be considered a part of the metalimnion with a temperature range from 3.3 to 1.0 °C; no trend in time series variability was noted for this layer, except between 20 June and 29 June, when the variability increased across the entire water column. The thermocline during June was located at 18 m depth. Below 28 to 40 m, the temperature remained nearly above 16 °C, with a vertical variability of less than 0.6 °C and a std of 0.1 °C.

With longer time series, calculating the power spectrum to estimate the variability in the lake becomes possible. For these time series, the power spectrum clearly showed that the primary displacement of the isotherms in the lake was due to the diurnal forcing (Figure 6b). The power spectra also exhibited other discrete sets of overtones of a high-frequency variability at 12 h (principal period/2) and another at around 8 h (principal period/3). Notably, the 8- and 12-h periods were more intense around the thermocline depth and the base of the metalimnion, respectively. The periods that correspond to forced and free internal seiche modes of the lake will be determined using the numerical model later.

Between June 29 at 22:30 p.m. and 31 August at 13:00 p.m. (approximately 62 days; Figure 7), 9 thermistors were placed at a depth of about 37 m arranged at 11, 13, 16, 18, 21, 26, 28, 30, and 37 m depths (Figure 7a). The upper layer at 11, 13, and 16 m experienced cooling from 29 June to 20 July and from 3 August to the end of the recording at 31 August, and heating from 20 July to 3 August. The thermocline was located between the 18 and 21 m time series as they showed more variability of 3.2–3.4 °C than the rest of the water column. The base of the metalimnion also had a very distinctive signal within the time series of 26, 28, and 30 m where the temperature was around 16.5 °C. The 37-m time series was maintained below 16 °C, with a variability of less than 0.28 °C and a std of 0.05 °C. The power spectrum estimated from this period also clearly showed that the 24-h period was the primary variability in the lake (Figure 7b). The other two oscillation periods with the same characteristics as previously noted also appeared in the power spectrum: the 8-h period that was more intense around the thermocline depth, and the 12-h period that was more intense at the base on the metalimnion.

From 1 September at 12:00 p.m. to 22 November at 08:00 a.m. (approximately 81 days; Figure 8), the chain of 10 thermistors was placed at a depth of about 42 m arranged at 15, 17, 20, 22, 25, 27, 30, 33, 35, and 42 m depths (Figure 8a). The upper layer at 15 and 17 m underwent cooling during the entire period, more markedly at the end from 23 October to 22 November. Between the 20 and 22 m time series, the thermocline showed a variability of 2.7–3.4 °C. The base of the metalimnion was located around the arrangement formed by the time series at 25 and 27 m and by the group of the thermistors at 30, 32, and 35 m. The 42 m time series remained below 16 °C with a variability of less than 0.30 °C and a std of 0.05 °C. The peculiarities that occurred during this period were (i) the sudden rise of temperature in the metalimnion around 8 October, and (ii) the high variability of the 25 m time series in the final part of the period that seemed to squeeze the metalimnion. The power spectrum for this period clearly showed three more important periods of oscillation—24, 12, and 8 h—for the total water column, except at the very bottom where only the 24-h period was noted (Figure 8b).

3.3. Response Transfer Functions

The frequency response system between wind and/or shortwave radiation forcing (input signal) and water temperature (output signal) are presented based on the transfer functions: square coherence, admittance amplitude (the gain) and phase (Figure 9). Although the lake frequency response shows several resonant peaks with periods of 24, 12, and 8 h (Figure 9b,e), it is clear that the diurnal frequency response has the most significant correlation between the two series (Figure 9a,d). Note that the 12-h correlation between the water temperature and the shortwave radiation do not correspond to a physical interpretation.

The input force system response shows that in the surface layer it is more significant and has a phase delay of approximately 3 h (~−50°), while in the deeper layers there is an 6 h lag (~100°), as expected since forcing take place in the surface layer (Figure 9c,f).

3.4. CTD Data

The vertical distribution of temperature of the lake at specific transects is shown in Figure 10. The lake stratification characteristics noted around the year are clearly depicted: the epilimnion, metalimnion, and hypolimnion. Lake Zirahuén is considered as a tropical high mountain lake, with a well-mixed water column during winter where the lake reaches its minimum temperature of 16 °C (Figure 10a,b). During spring, the heat transferred through the lake surface starts to develop a temperature profile, and the epilimnion and metalimnion begin to widen. The epilimnion has a surface mixed layer of 5–7 m with temperature reaching 21 °C and continuing to rise up to early June where it becomes completed stratified (Figure 10d,e). Furthermore, the temperature and depth at the base of the metalimnion are 16 °C at 20 m, respectively, in a layer that spans nearly 10 m wide. The thermocline during May is shallower and is located at about 15 m depth. During autumn, surface cooling begins, and epilimnion development is completed at around 15 m depth (Figure 10g,h); the isothermal surface layer was at 19 °C in 2018. The metalimnion decreases to a 5-m-thick layer, with the thermocline at a lower level of 20 m depth, but with less strong thermal stratification with temperatures at the bottom of 16 °C and with surface temperatures around 19 °C than that during May where the temperatures at the bottom remain the same (16 °C) and the temperature at the surface is around 21 °C.

Notably, higher variability is noted in the epilimnion of the northwestern rim of the lake where the water temperature becomes slightly warmer, reaching 0.5–1 °C (Figure 10b,e,h).

The time average CTD profiles along with the continuous temperature profile during each field campaign is shown in Figure 11. The temperature profiles are separated by months. In addition to the stratification, the most uncommon characteristic was the difference between the CTD data and the monthly average value of temperature obtained during the period of heating in May and during one of the extreme cooling events at the end of November. However, note that a single CTD profile may not be representative and can introduce some bias, for example, a bias of nearly 4 °C in May (red thick line and dashed thin green line at about 15 m depth) was noted at the level of the thermocline; thus, taking one profile for this lake should be performed carefully, especially when the lake is stratifying or destratifying.

3.5. Water Level Chain

The lake oscillated at very distinctive frequencies after the forcing temporally ceased; these oscillations are called seiches. These seiches depend mainly on the ambient stratification and in the shape of the basin. They can be external and internal, forced or free. For instance, during the period of measurements obtained from 29 June to 31 August (Figure 12a), the power spectral showed that the primary water column variability in the lake was due to diurnal forcing and its overtone of 12-h resonant variability (Figure 12b). Notably, the 8-h period is not significant as the others since this one corresponds to an internal seiche mode of the lake.

Clearly shown in these time series are other atmospheric perturbations that also affect the lake (Figure 12a), but a detailed characterization of water supply of the lake is beyond the scope of the present study; however, it can be said that between June and September the water supply added to the lake by means of precipitation was about 200 mm per month, and decrease to about 70 mm during October [33].

3.6. Current Meter

From 29 June to 31 August (about 62 days), the current meter profiler was placed at a depth of about 34 m facing upward to obtain measurements at each meter, from approximately the bottom to the surface (Figure 13). In general, the data show higher current velocity near the surface due to the wind stress up to 0.4 m/s for horizontal components and 0.04 m/s for the vertical component (Figure 13a–c), whereas the intensity of the velocities remained nearly homogeneous below 0.1 m/s for the horizontal components and below 0.01 m/s for the vertical component.

The depth-average current velocity power spectrum (Figure 13d–f) estimated from this period also showed that the 24-h period is the primary variability in the lake. Notably, just in the north-south component spectra the other 12- and 8-h oscillation periods, and another high-frequency band within the 3- to 5-h oscillation periods, also appear in the power spectrum.

3.7. Numerical Model Results

We attempted to reproduce the characteristics of the lake described previously by using the numerical model Delft3D to obtain an integral representation of the hydrodynamic behavior of Lake Zirahuén. These numerical results, to our knowledge, are the first efforts on how Lake Zirahuén responds to atmospheric forcing. The model was run only from June to August 2018 because of the availability of atmospheric forcing. The model spin-up was obtained for 10 days; the model was calibrated on the next two days by using the same configuration as that described in the numerical model section.

3.7.1. Optimal Calibration

In this study, a set of two-day simulation runs were used to determine the optimal wind drag coefficient C_d (Figure 14). The model calibration was determined by comparing the std of the temperature time series from the observational data with that from the model simulations. The computational time and cost were further reduced by minimizing the error by considering only the temperature of one time series (Figure 14d). The black line represents the time series registered by the thermistor located at 18 m in June 2018.

An initial guess of C_d = 1.3 × 10⁻³ was used. Then, the algorithm evaluates around this point and moves forward or backward with an adequate step in order to make sure that the objective function decreases. In this case, the algorithm moved forward to a new local minimum value in C, slightly larger than B. Then, the algorithm keeps searching repeating this process until it converges to the minimum at K where no more minimum values are reached (Figure 14b).

The model prediction was quantified by performing statistical analysis. The overview of the model performance was provided using the Taylor diagram (Figure 14a). A total of 10 model simulations were run until the best value was found between the 18 m time series against model simulation output. The Taylor diagram shows three clusters of elements (represented by alphabetical letters) that were obtained after several simulations and revealed an acceptable correlation. In this diagram, the red A represents the observational data, and the other letters represent the 10 simulations grouped into three sets with each one characterized with a std, R, and RMSE. Group 1 of [B, C] and group 2 of [D, E] showed std of ~0.3 °C; a R of around 0.1 and 0.2, respectively, and an RMSE greater than 0.4 °C. Furthermore, group 3 of [F to K] shows considerable improvement of the correlation coefficient with the observational data greater than 0.5 °C and a better agreement with the observational data as the RMSE decreases close to 0.3 °C, along with a more similar std close to data A.

The simulation run performed using the Delft3D model default value of C_d = 6.3 × 10⁻⁴ (data not shown) always showed flat time series with a bad amplitude range and a different order of magnitude; the simulation run using the typical value for lakes (C_d = 1.3 × 10⁻³; green line in Figure 14d) represented an acceptable time series with an amplitude range in the order of the magnitude data, but with a low correlation coefficient (cluster of [B,C] in Figure 14a). With the optimal procedure, the best wind stress coefficient for Lake Zirahuén was found to be C_d = 4.5 × 10⁻³, which was almost three times greater than the typical value used for lakes and oceans (Figure 14c). Be aware, however, that the wind data used to force the model was obtained from a weather station located ~10 km southward of the lake, so the velocity wind acting in the numerical model might not be representative for the average wind velocity acting at the lake itself. Typically, above water, the wind speed is higher, which might explain why the high C_d value was obtained.

3.7.2. Model Validation

The hydrodynamic simulation of Lake Zirahuén was validated by comparing the model results with the observed data, from June 2018 in the case of the simulated water temperatures and from July 2018 for the horizontal velocity currents (Figure 15).

The model-predicted temperatures showed good agreement with the observations (Figure 15a,b), revealing mainly how the model temperature adequately reproduced the cooling at the surface layer around 11 June that lasted till the end of the month. Furthermore, the model adequately reproduced the corresponding variability at the epilimnion, metalimnion, and hypolimnion. Nonetheless, the model could not reproduce some peculiarities, as can be checked from the quantitative results of this comparison shown in

Table 2. Metrics considered to quantify the model prediction between the model and observations.

Temperature			Horizontal Velocity
Depth (m)	RMSE (°C)	R2	Depth (m)	RMSE		R2
				U (m/s)	V (m/s)	U	V
13	0.37	0.84	1	0.2	0.1	0.22	0.48
15	0.61	0.42	2	0.1	0.1	0.18	0.38
18	0.82	0.10	3	0.1	0.04	0.15	0.27
20	0.47	0.08	4	0.1	0.02	0.14	0.12
23	0.43	0.07	17	0.02	0.01	0.18	0.02
25	0.33	0.05	18	0.02	0.01	0.26	0.01
28	0.12	0.03	19	0.02	0.01	0.22	0.01
30	0.08	0.02	20	0.02	0.01	0.10	0.01

. As can be seen from the 13 m time series comparison, the time series shows better representation with a R² of 0.84 and RMSE of 0.37 °C. For the following time series (15 m), the RMSE and R² are reduced by 50%. At the thermocline level (18 m), the agreement of RMSE as well as R² is worse at the water column with R² of 0.10 and RMSE of 0.82 °C. However, starting from the thermocline (at about 18 m) to the base of the metalimnion (between 25 and 28 m), the agreement between the model and observations was improved again, remaining around 0.3–0.4 °C for the RMSE, but the R² was close to zero. For the time series at the hypolimnion, the RMSE and R² remained close to zero.

The horizontal velocities were compared only at some depths. For these variables, the model shows good visual agreement with observations at least for the second half of the period at the complete water column (Figure 15c–f). The RMSE is considerably homogenous (0.01–0.02 m/s) (Table 2). In the case of R², this decays rapidly from the surface, but have again an acceptable agreement between 17 and 25 m depth, which represents the thermocline and the base of the metalimnion.

Higher values of RMSE or lower values of R² are obtained because the model does not reproduce highly variable oscillations or due to some phase shift between the model and observational data. However, as long as the RMSE remains close to zero, the averaged quantities of the model prediction can be used to represent the mean behavior of the lake. This can be seen from Figure 15c, where in some intervals the series seem to match each other such as 23–27 July, and in other intervals seem out of phase such as 5–7 July. However, both series seem alike (Figure 13a,b and Figure 15e,f).

The temperature comparison—showing how the averaged quantities of the model can effectively reproduce the monthly thermal behavior of the lake, or how the numerical model reproduces particular days of heating or cooling events during some periods—is shown in Figure 16. In this figure, is clear that the mean behavior of the water column is reproduced in an acceptable way, from monthly mean (top row) to daily mean (middle and lower rows), even when the lake was cooling or heating.

In addition, Figure 16 shows how the water column can support higher oscillations up to 30 cycles per hour, particularly in the metalimnion layer, as expected from the observational data. The frequencies of oscillation were estimated from the Brunt–Väisälä frequency, $N$. It is worth mentioning that such higher frequencies are not the focus of this study, and here only long wave internal seiches are treated.

3.7.3. General Model Hydrography and Circulation

In general, the hydrodynamic modeling of Lake Zirahuén is described well in an averaged manner, in particular, with respect to the water temperature evolution. On the basis of these results, we describe the general circulation and hydrography pattern of the lake for a period of three months.

Figure 17 shows the composites of the simulated surface current velocity, water temperature and wind speed averaged for periods of 2 h, that is, the numerical results obtained for each pair of hours in a day were averaged. Thus, the regular surface hydrodynamics of the lake occurring on a daily basis is clearly noted: the diurnal heating, mountain and valley breeze, and back-and-forth surface currents.

Between 01:00 and 10:00 a.m., the surface temperature remained nearly homogenous, with the northern section being slightly warmer than the rest of the lake, except for the period from 09:00 to 10:00 a.m. where the lake presents the coldest surface temperature along the day (Figure 17, top row). The wind and currents are low and tend to move southwestward because of a moderate mountain breeze (about 0.7 m/s wind speed). From 07:00 to 10:00 a.m., the breeze intensifies slightly, but does not last for a long time. Around noon, the wind starts to change direction anticyclonically. The valley breeze begins at 13:00 and lasts till 20:00 p.m., with a mean wind speed of up to 1.5 m/s (Figure 17, middle row). During this period, the surface currents react to the wind stress and acquire greater speeds during the day (about 0.1 m/s), and then transport the temperature to the northern section of the lake. The wind suddenly stops around 21:00 p.m., and the inertia restores the currents and temperature fields (Figure 17, bottom row).

The vertical structure of the lake shows a very regular pattern in the entire water column that it is separated into two circular cells by the thermocline (Figure 18). The thermodynamic structure was completely characterized by the wind stress acting on the surface layer. From 11:00 a.m. to 18:00 p.m., the wind speed was higher (Figure 18, middle row); an upper layer cell generates a downwelling process at the northern section and an upwelling process at the southern section of the lake. The 22 °C isotherm tilts within the surface layer, but the other 18 and 20 °C isotherms barely oscillate. Below these isotherms, a counter-cell circulation is generated, but at a less intensity in the lower layer. Once the wind stress ceases, the inertia again tends to restore all the dynamic fields, and the circulation reverses in direction in both vertical cells (Figure 18, top and bottom rows).

The lake mainly tended to oscillate (Figure 19). With a simple implementation of an eigenvalue approach by using empirical orthogonal functions, the lake is found to have two horizontal modes of oscillation corresponding to the principal axes of the lake (Figure 19a,b). From the principal component of both the modes (Figure 19c,d), the oscillation periods forcing the lake are estimated to occur at the surface with perturbations that span for 24, 12, and 8 h and from 3 to 5 h (Figure 19e).

For the average of three months (Figure 19f), the depth-averaged currents presented a tendency to flow northward at the entire lake, with an anticyclonic return to the east part and a slightly cyclonic return to the northwestern and southwestern part, the water level shows a higher region in the northern section and is slightly lower at the southern portion of the lake.

3.7.4. Normal Basin and Vertical Modes of Oscillation, Free and Forced Seiches

The natural or free oscillation basin modes depend on the stratification and on the basin geometry, whereas the vertical modes depend only on the ambient stratification. For the data taken during June, July and August, the stratification of the lake presents a well-defined shape characterized by the buoyancy frequency of the Brunt–Väisälä N, which present a peak of 22–25 cph marking the thermocline depth (which remains between 18 and 25 m depth) and 5 cph elsewhere (Figure 16). According to those characteristics of the lake, the basin modes correspond to periods between (5.9–7.9), (3–4), (2–2.7) and (1.4–2.1) h, for each normal mode from mode-1 to mode-4 in this case, respectively, with the mode-1 representing the fundamental internal basin mode (see

Table 3. Periods of normal basin and vertical modes of oscillation. With n the normal mode and T₁ the fundamental basin mode.

Basin Modes Seiches
	External Mode [min]	Internal Modes [h]
		Mode-1	Mode-2	Mode-3	Mode-4
	Numerical Model with Flat Bottom at 40 m (Tn~T1/n, n > 1)
		n = 1	n = 2	n = 3	n = 4
	6.7	T1 = 7.9	4.0	2.7	2.1
	Numerical Model with Real Bathymetry
	7.4	T1 = 5.9	3.0	2.0	1.4
Vertical Modes
	Three Layers Model Continuous Density
		V Mode 1	V Mode 2	V Mode 3	V Mode 4
June	6.8	6.6/n	21.1/n	35.6/n	43.3/n
July	6.8	7.2/n	25.2/n	39.1/n	44.4/n
August	6.9	7.6/n	26.7/n	40.0/n	45.9/n
	Numerical Integration with N (z)
June		7.0/n	20.9/n	33.9/n	46.2/n
July		7.7/n	23.2/n	36.8/n	49.2/n
Augyst		8.0/n	22.3/n	35.2/n	47.4/n

). These data were obtained with spectral analysis from output of different configurations of the numerical model.

It is worth noting that those values match reasonably well with the theory of the three-layer system of continuum density. The width of the epilimnion and the constant length related to the slope of the surface density profile are shown in Figure 19e. Despite the fact that the theorical model does not take into account the bathymetry, the results show that the period of oscillation only deviate by less than 10% from the model data (see Table 3, column of mode 1).

Then, it is clear that the 24- along with the 12-h period (Figure 6, Figure 7 and Figure 8, Figure 12 and Figure 13) correspond to forced internal seiches, obviously caused by the wind and the shortwave radiation forcing (Figure 9), whereas part of the band around the 8-h oscillation period correspond to a mix of the basin modes of the lake and a resonance effect of the forced internal seiches, particularly around the thermocline depth, as can be seen in Figure 6, Figure 7 and Figure 8. However, exploring more on the three-layer model, it is shown that the lake is able to present a near resonant excitation on the vertical mode-2 (forced by the wind) around the 24- and 12-h oscillation period, considering the fundamental mode (n = 1) or its second overtone (n = 2), respectively (Table 3).

Considering the observed mean-average profile of N (z) during June, July, August (Figure 16), it was found that the vertical structure of the normal modes corresponds to those shown in Figure 20 with its corresponding periodicities shown in Table 3 for the first four normal modes.

As can be seen from Figure 6, Figure 7 and Figure 8 and Figure 20, the vertical modes 1 and 2 are responsible for the behavior at the metalimnion. One remarkable feature is the range between 15–25 m deep where the velocity components acquired their maximum values (Figure 15c–f), as theorical mode-2 and higher modes are suggesting. Depending on the basin mode selected (n = 1 or n = 2), vertical mode-2 will have a near excitation resonance around 24- and 12-h oscillation periods, as already seen in Figure 6, Figure 7 and Figure 8, Figure 11 and Figure 12.

4. Conclusions

From the observations obtained in 2018, Lake Zirahuén can be considered to be forced by a consistent northwestward wind owing to the topographic effect of a valley breeze. The wind starts at around noon and stops by afternoon at around 19:00 p.m. Like wind, all the meteorological variables showed a well-defined diurnal and seasonal variability. In particular, the vertical distribution of the temperature of the lake water column develops around the year because of the atmospheric forcing caused by the short-wave radiation. The complete development of the epilimnion, metalimnion, and hypolimnion occurs during spring; however, as the short-wave radiation begins to drop, the thermal stratification of the lake tends to disappear during late summer and autumn. Even though the forcing occurs at the surface, the lake presents more thermodynamic variability at the metalimnion with perturbations that span for 24, 12, and 8 h and from 3 to 5 h; these represent mainly a resonance response among forced and free oscillation modes of the lake.

The numerical modeling results are in reasonable agreement in an averaged manner; in particular, the water temperature evolution and currents at the surface layer. The behavior of Lake Zirahuén showed a surface current that reacts to wind stress daily and transports the temperature to the northern section of the lake. When the wind stops suddenly, the inertia restores the currents and temperature fields to their initial stage, starting the onset of the seiche modes. The three-month average showed a surface current flowing northward with an anticyclonic return to the east part and a pair of cyclonic return to the northwestern and southwestern parts of the lake; furthermore, the temperature field shows a warmer region on the northern section and a slight upwelling at the southern portion of the lake. The vertical structure shows two circular cells divided by the thermocline, which was positioned between 15 and 20 m depth, during the three-month period.

Finally, it is worth to mention that Lake Zirahuén has received little attention with regard to the physical importance of its hydrodynamics, in particular, the lack of numerical models to simulate the thermal- and wind-driven circulations and their subsequent transport processes. Remarkably, because of this thermal behavior of the lake, it is speculated that considerable bottom dissipation occurred at the shallower portion of the lake; for that reason, another experiment is currently being carried out using a cross-shaped polygon consisting of 12 thermistor chains with two thermistors in each line and a 10 thermistors chain located at the center of the lake. This experiment might last for a year. Therefore, this study and the perspective works are important for the approach of combining the use of modeling with the results of measured data for Lake Zirahuén that can be applied to other Mexican lakes as well.