Modeling Approaches for Determining Dripline Depth and Irrigation Frequency of Subsurface Drip Irrigated Rice on Different Soil Textures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Experiment
2.2. Simulations of Soil Water Dynamics
2.3. Validation of the Simulation Model
2.4. Water Balance Components
3. Results and Discussion
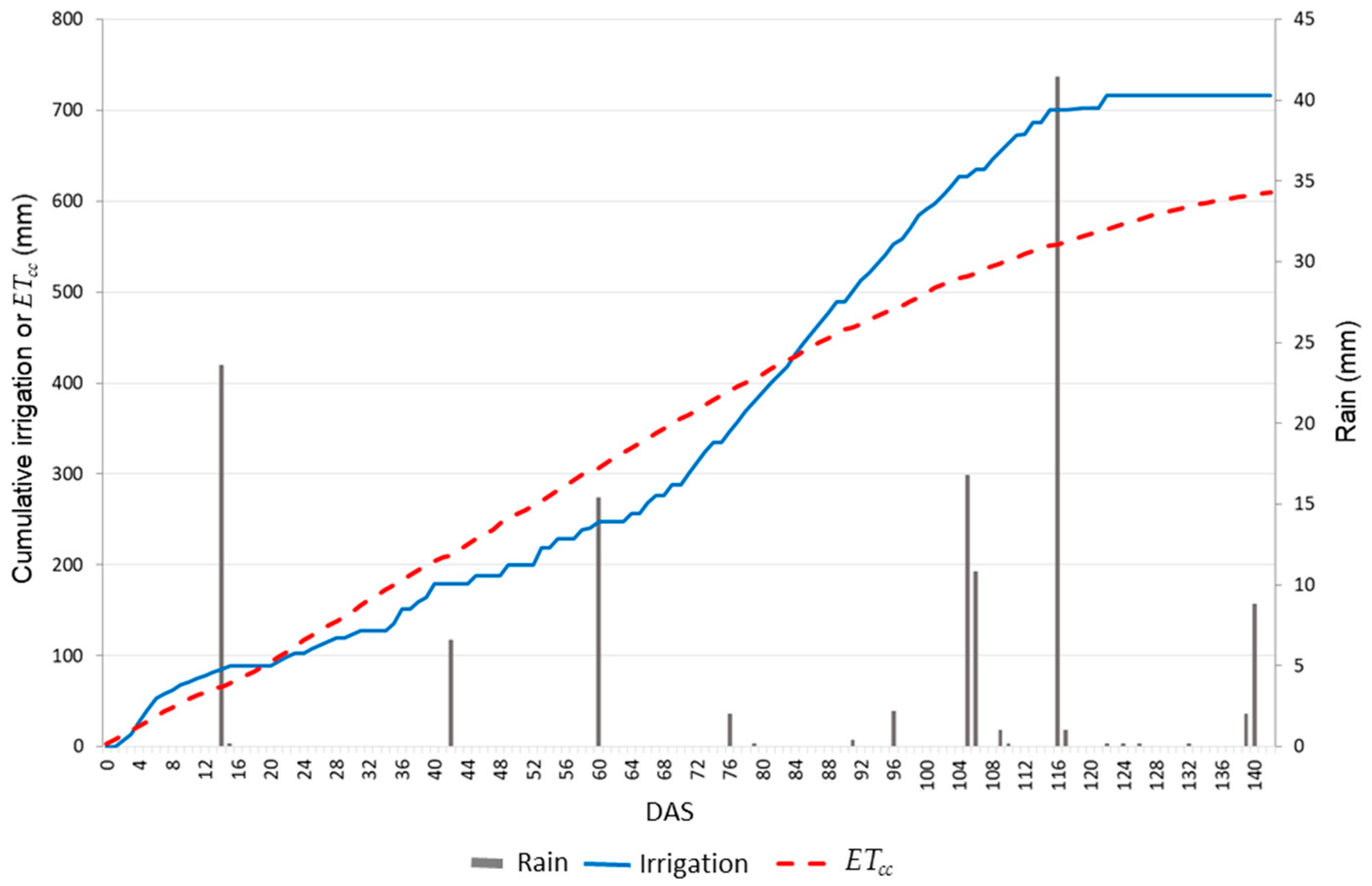
3.1. Irrigation Campaign in the Experimental Plot
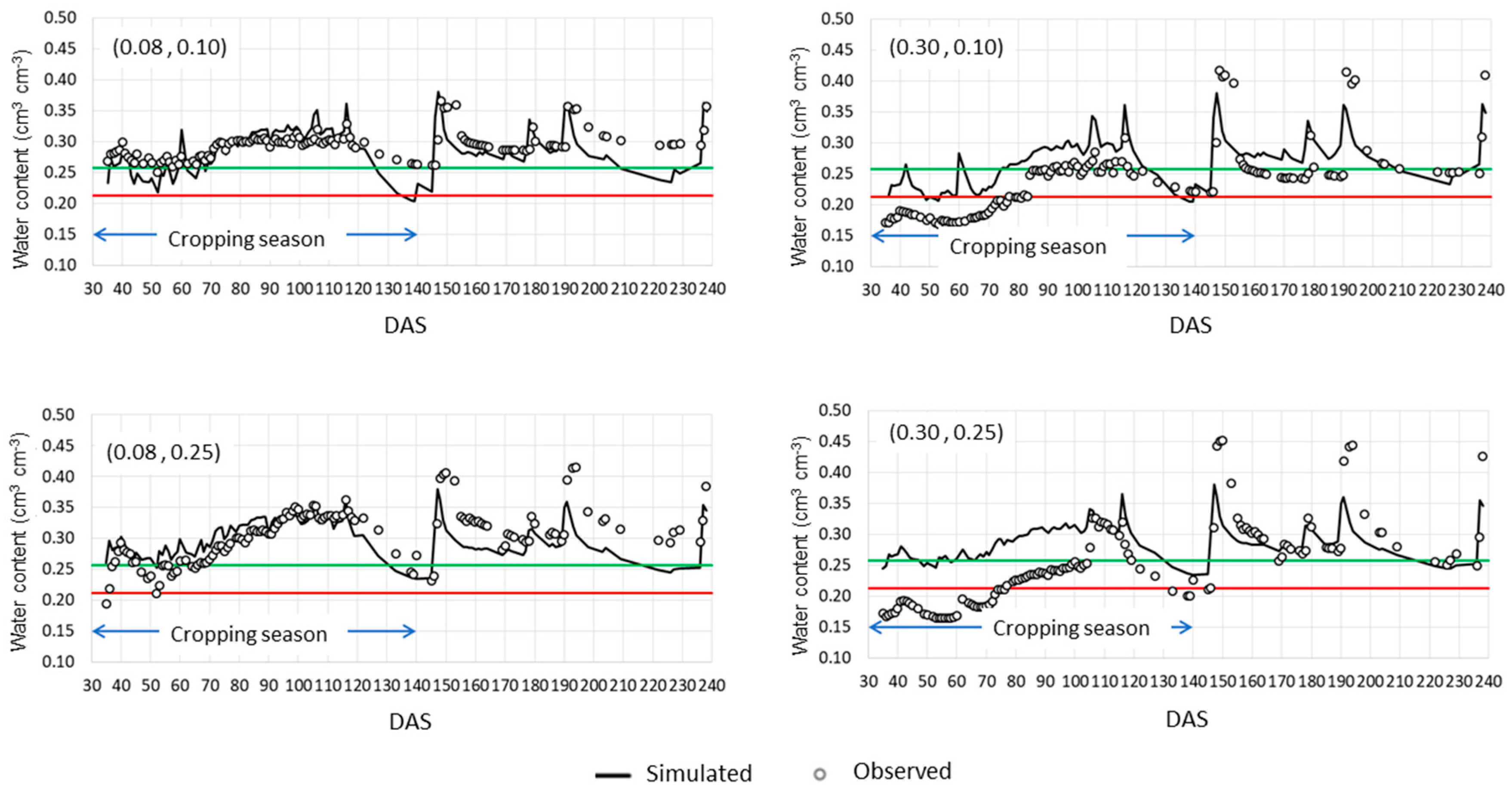
3.2. Validation of the Model
3.3. Components of Water Balance and Percolation Below 0.3 m Depth
3.4. Yield and Water Productivity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. FAOSTAT–Food and Agriculture Data. Available online: http://www.fao.org/faostat/en/#data (accessed on 5 May 2020).
- MAPA. Estadísticas de Superficies y Producciones Anuales de Cultivo en España; MAPA: Madrid, Spain, 2018. [Google Scholar]
- Maraseni, T.N.; Deo, R.C.; Qu, J.; Gentle, P.; Neupane, P.R. An international comparison of rice consumption behaviours and greenhouse gas emissions from rice production. J. Clean. Prod. 2018, 172, 2288–2300. [Google Scholar] [CrossRef]
- Maclean, J.L.; Dawe, D.C.; Hardy, B.; Hettel, G.P. Rice Almanac: Source Book for the Most Important Economic Activity on Earth, 4th ed.; International Rice Research Institute: Los Baños, Philippines, 2013. [Google Scholar]
- Zheng, J.; Wang, W.; Ding, Y.; Liu, G.; Xing, W.; Cao, X.; Chen, D. Assessment of climate change impact on the water footprint in rice production: Historical simulation and future projections at two representative rice cropping sites of China. Sci. Total Environ. 2020, 709, 136190. [Google Scholar] [CrossRef]
- Bouman, B.A.M.; Yang, X.; Wang, H.; Wang, Z.; Zhao, J.; Chen, B. Performance of aerobic rice varieties under irrigated conditions in North China. Field Crops Res. 2006, 97, 53–65. [Google Scholar] [CrossRef]
- Luo, L.; Mei, H.; Yu, X.; Xia, H.; Chen, L.; Liu, H.; Zhang, A.; Xu, K.; Wei, H.; Liu, G.; et al. Water-saving and drought-resistance rice: From the concept to practice and theory. Mol. Breed. 2019, 39. [Google Scholar] [CrossRef]
- He, H.; Ma, F.; Yang, R.; Chen, L.; Jia, B.; Cui, J.; Fan, H.; Wang, X.; Li, L. Rice performance and water use efficiency under plastic mulching with drip irrigation. PLoS ONE 2013, 8, e83103. [Google Scholar] [CrossRef] [Green Version]
- Parthasarathi, T.; Vanitha, K.; Mohandass, S.; Senthilvel, S.; Vered, E. Effects of impulse drip irrigation systems on physiology of aerobic rice. Indian J. Plant Physiol. 2015, 20, 50–56. [Google Scholar] [CrossRef]
- Arbat, G.; Parals, S.; Duran-Ros, M.; Pujol, J.; Puig-Bargués, J.; Ramírez de Cartagena, F. Dinámica del Agua en el Suelo, Productividad del Agua y Economía en Riego por Inundación y Goteo en Arroz; XXXVI Congreso Nacional de Riegos, AERYD: Valladolid, Spain, 2018; Volume 19, pp. 1–10. [Google Scholar]
- Lamm, F.R.; Rogers, D.H. Longevity and performance of a subsurface drip irrigation system. Trans. ASABE 2017, 60, 931–939. [Google Scholar] [CrossRef]
- Lamm, F.R.; Abou Kheira, A.A.; Trooien, T.P. Sunflower, Soybean, and Grain Sorghum Crop Production as Affected by Dripline Depth. Appl. Eng. Agric. 2010, 26, 873–882. [Google Scholar] [CrossRef]
- Rajwade, Y.A.; Swain, D.K.; Tiwari, K.N.; Bhadoria, P.B.S. Grain yield, water productivity, and soil nitrogen dynamics in drip irrigated rice under varying nitrogen rates. Agron. J. 2018, 110, 868–878. [Google Scholar] [CrossRef]
- Lamm, F.R.; Trooien, T.P. Dripline Depth Effects on Corn Production When Crop Establishment Is Nonlimiting. Appl. Eng. Agric. 2005, 21, 835–840. [Google Scholar] [CrossRef] [Green Version]
- Miyazaki, A.; Arita, N. Deep rooting development and growth in upland rice NERICA induced by subsurface irrigation. Plant Prod. Sci. 2020, 1–9. [Google Scholar] [CrossRef]
- Arbat, G.; Puig-Bargués, J.; Barragán, J.; Bonany, J.; Ramírez de Cartagena, F. Monitoring soil water status for micro-irrigation management versus modelling approach. Biosyst. Eng. 2008, 100, 286–296. [Google Scholar] [CrossRef]
- Mo’allim, A.A.; Kamal, M.R.; Muhammed, H.H.; Yahaya, N.K.E.; Man, H.B.; Wayayok, A. An assessment of the vertical movement of water in a flooded paddy rice field experiment using Hydrus-1D. Water 2018, 10, 783. [Google Scholar] [CrossRef] [Green Version]
- Rezayati, S.; Khaledian, M.; Razavipour, T.; Rezaei, M. Water flow and nitrate transfer simulations in rice cultivation under different irrigation and nitrogen fertilizer application managements by HYDRUS-2D model. Irrig. Sci. 2020. [Google Scholar] [CrossRef]
- Abrahamsen, P.; Hansen, S. Daisy: An open soil-crop-atmosphere system model. Environ. Model. Softw. 2000, 15, 313–330. [Google Scholar] [CrossRef]
- Jansson, P.E.; Moon, D.S. A coupled model of water, heat and mass transfer using object orientation to improve flexibility and functionality. Environ. Model. Softw. 2001, 16, 37–46. [Google Scholar] [CrossRef]
- van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Kroes, J.G. Advances of Modeling Water Flow in Variably Saturated Soils with SWAP. Vadose Zone J. 2008, 7, 640. [Google Scholar] [CrossRef]
- Ragab, R. Integrated Management Tool for Water, Crop, Soil and N-Fertilizers: The Saltmed Model. Irrig. Drain. 2015, 64, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, 2–25. [Google Scholar] [CrossRef] [Green Version]
- Karandish, F.; Šimůnek, J. A field-modeling study for assessing temporal variations of soil-water-crop interactions under water-saving irrigation strategies. Agric. Water Manag. 2016, 178, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Bristow, K.L.; Šimůnek, J.; Helalia, S.A.; Siyal, A.A. Numerical simulations of the effects furrow surface conditions and fertilizer locations have on plant nitrogen and water use in furrow irrigated systems. Agric. Water Manag. 2020, 232, 124. [Google Scholar] [CrossRef]
- Sanchez, C.A. Modeling Flow and Solute Transport in Irrigation Furrows. Irrig. Drain. Syst. Eng. 2014, 3, 124. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimian, H.; Liaghat, A.; Parsinejad, M.; Playán, E.; Abbasi, F.; Navabian, M. Simulation of 1D surface and 2D subsurface water flow and nitrate transport in alternate and conventional furrow fertigation. Irrig. Sci. 2013, 31, 301–316. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Šimůnek, J.; Mo, M.; Mccullough-Sanden, B.; Shahrokhnia, H.; Cherchian, S.; Wu, L. Assessing salinity leaching efficiency in three soils by the HYDRUS-1D and -2D simulations. Soil Tillage Res. 2019, 194, 104342. [Google Scholar] [CrossRef] [Green Version]
- Eltarabily, M.G.; Burke, J.M.; Bali, K.M. Effect of deficit irrigation on nitrogen uptake of sunflower in the low desert region of California. Water 2019, 11, 2340. [Google Scholar] [CrossRef] [Green Version]
- Naghedifar, S.M.; Ziaei, A.N.; Ansari, H. Simulation of irrigation return flow from a Triticale farm under sprinkler and furrow irrigation systems using experimental data: A case study in arid region. Agric. Water Manag. 2018, 210, 185–197. [Google Scholar] [CrossRef]
- Phogat, V.; Pitt, T.; Stevens, R.M.; Cox, J.W.; Šimůnek, J.; Petrie, P.R. Assessing the role of rainfall redirection techniques for arresting the land degradation under drip irrigated grapevines. J. Hydrol. 2020, 587, 125000. [Google Scholar] [CrossRef]
- Chen, N.; Li, X.; Šimůnek, J.; Shi, H.; Ding, Z.; Peng, Z. Evaluating the effects of biodegradable film mulching on soil water dynamics in a drip-irrigated field. Agric. Water Manag. 2019, 226, 105788. [Google Scholar] [CrossRef]
- Jin, X.; Chen, M.; Fan, Y.; Yan, L.; Wang, F. Effects of mulched drip irrigation on soil moisture and groundwater recharge in the Xiliao River Plain, China. Water 2018, 10, 1755. [Google Scholar] [CrossRef] [Green Version]
- Reyes-Esteves, R.G.; Slack, D.C. Modeling Approaches for Determining Appropriate Depth of Subsurface Drip Irrigation Tubing in Alfalfa. J. Irrig. Drain. Eng. 2019, 145, 04019021. [Google Scholar] [CrossRef]
- Grecco, K.L.; de Miranda, J.H.; Silveira, L.K.; van Genuchten, M.T. HYDRUS-2D simulations of water and potassium movement in drip irrigated tropical soil container cultivated with sugarcane. Agric. Water Manag. 2019, 221, 334–347. [Google Scholar] [CrossRef]
- Elasbah, R.; Selim, T.; Mirdan, A.; Berndtsson, R. Modeling of fertilizer transport for various fertigation scenarios under drip irrigation. Water 2019, 11, 893. [Google Scholar] [CrossRef] [Green Version]
- Skaggs, T.H.; Trout, T.J.; Simunek, J.; Shouse, P.J. Comparison of HYDRUS-2D Simulations of Drip Irrigation with Experimental Observations. J. Irrig. Drain. Eng. 2004, 130, 304–310. [Google Scholar] [CrossRef]
- Hanson, B.; Hopmans, J.W.; Šimůnek, J. Leaching with Subsurface Drip Irrigation under Saline, Shallow Groundwater Conditions. Vadose Zone J. 2008, 7, 810. [Google Scholar] [CrossRef] [Green Version]
- Phogat, V.; Skewes, M.A.; McCarthy, M.G.; Cox, J.W.; Šimůnek, J.; Petrie, P.R. Evaluation of crop coefficients, water productivity, and water balance components for wine grapes irrigated at different deficit levels by a sub-surface drip. Agric. Water Manag. 2017, 180, 22–34. [Google Scholar] [CrossRef] [Green Version]
- Bouman, B.A.M.; Peng, S.; Castañeda, A.R.; Visperas, R.M. Yield and water use of irrigated tropical aerobic rice systems. Agric. Water Manag. 2005, 74, 87–105. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Irrig. Drain. 1998, D05109. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587. [Google Scholar] [CrossRef] [Green Version]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef] [Green Version]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Belmans, C.; Wesseling, J.G.; Feddes, R.A. Simulation model of the water balance of a cropped soil: SWATRE. J. Hydrol. 1983, 63, 271–286. [Google Scholar] [CrossRef]
- Phogat, V.; Yadav, A.K.; Malik, R.S.; Kumar, S.; Cox, J. Simulation of salt and water movement and estimation of water productivity of rice crop irrigated with saline water. Paddy Water Environ. 2010, 8, 333–346. [Google Scholar] [CrossRef]
- Confalonieri, R.; Foi, M.; Casa, R.; Aquaro, S.; Tona, E.; Peterle, M.; Boldini, A.; De Carli, G.; Ferrari, A.; Finotto, G.; et al. Development of an app for estimating leaf area index using a smartphone. Trueness and precision determination and comparison with other indirect methods. Comput. Electron. Agric. 2013, 96, 67–74. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Willey & Sons: New York, NY, USA, 1978; ISBN 902200676X. [Google Scholar]
- Van Dam, J.C.; Malik, R.S. (Eds.) Water Productivity of Irrigated Crops in SIRSA District, India. INTEGRATION of Remote Sensing, Crop and Soil Models and Geographical Information Systems; WATPRO Final Report, Including CD-ROM; Haryana Agricultural University/IWMI/WaterWatch: Wageningen, The Netherlands, 2003; pp. 41–58. ISBN 90-6464-864-6. [Google Scholar]
- Li, Y.; Šimůnek, J.; Jing, L.; Zhang, Z.; Ni, L. Evaluation of water movement and water losses in a direct-seeded-rice field experiment using Hydrus-1D. Agric. Water Manag. 2014, 142, 38–46. [Google Scholar] [CrossRef] [Green Version]
- Bannayan, M.; Hoogenboom, G. Using pattern recognition for estimating cultivar coefficients of a crop simulation model. Field Crops Res. 2009, 111, 290–302. [Google Scholar] [CrossRef]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crops Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Wilcox, B.P.; Rawls, W.J.; Brakensiek, D.L.; Wight, J.R. Predicting runoff from Rangeland Catchments: A comparison of two models. Water Resour. Res. 1990, 26, 2401–2410. [Google Scholar] [CrossRef]
- Cabangon, R.; Lu, G.; Tuong, T.P.; Bouman, B.A.M.; Feng, Y.; Zhang, Z.C. Irrigation Management Effects on Yield and Water Productivity of Inbred and Aerobic Rice Varieties in Kaifeng. In Proceedings of the First International Yellow River Forum on River Basin Management, Zhengzhou, China, 12–15 May 2003; The Yellow River Conservancy Publishing House: Zhengzhou, China, 2003; pp. 65–75. [Google Scholar]
- Kandelous, M.M.; Šimůnek, J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation. Irrig. Sci. 2010, 28, 435–444. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Shao, D.; Liu, H. Simulating soil water regime in lowland paddy fields under different water managements using HYDRUS-1D. Agric. Water Manag. 2014, 132. [Google Scholar] [CrossRef]


| Property | Experimental Plot | Another Representative Soil Texture of the Area | |
|---|---|---|---|
| Texture | Sandy-loam | Loam | Silty-clay |
| Surface area of the plot (%) | 85.0 | 15.0 | - |
| Sand (%) | 64.9 | 47.4 | 6.5 |
| Silt (%) | 21.6 | 35.5 | 53.4 |
| Clay (%) | 13.5 | 17.1 | 40.1 |
| Bulk density (kg m−3) | 1530 | 1450 | 1260 |
| Soil water content at −33 kPa (m3 m−3) | 0.168 | 0.261 | 0.441 |
| Soil water content at −10 kPa (m3 m−3), field capacity | 0.257 | 0.313 | 0.490 |
| Soil water content at −1500 kPa (m3 m−3) | 0.061 | 0.131 | 0.252 |
| Parameters for Van Genuchten–Mualem Equations | Sandy-Loam Texture | Loam Texture | Silty-Clay Texture |
|---|---|---|---|
| Residual water content, θr (m3 m−3) | 0.048 | 0.048 | 0.094 |
| Saturated water content, θs (m3 m−3) | 0.384 | 0.396 | 0.522 |
| α (m−1) | 3.000 | 1.700 | 0.400 |
| n (-) | 1.389 | 1.335 | 1.416 |
| Saturated hydraulic conductivity, Ks (m day−1) | 0.323 | 0.204 | 0.157 |
| Statistic | Relative Positions (Horizontal; Depth) of the Soil Water Sensor | |||
|---|---|---|---|---|
| (0.08; 0,10) | (0.08; 0.25) | (0.30; 0.10) | (0.30; 0.25) | |
| RMSE (m3 m−3) | 0.028 | 0.034 | 0.048 | 0.064 |
| nRMSE (%) | 9.4 | 11.3 | 19.7 | 25.3 |
| R2 | 0.440 | 0.376 | 0.544 | 0.402 |
| E | −0.589 | 0.353 | 0.257 | 0.086 |
| Case | Texture | Dripline Depth | Irrigation Criteria | Irrigation Frequency | Inputs | Outputs | SS (mm) | BE (mm) | ETsim/(Irr + R) (%) | P0,3 m (mm) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Irr (mm) | R (mm) | ETsim (mm) | P1 m (mm) | |||||||||
| A | Sandy-Loam | 15 | Matric potential at −10 kPa | Variable | 739 | 129 | −489 | −337 | −45 | −2 | 56 | 370 |
| B | Loam | 15 | 740 | 129 | −520 | −324 | −29 | −4 | 60 | 339 | ||
| C | Silty-Clay | 15 | 740 | 129 | −545 | −368 | 39 | −5 | 63 | 339 | ||
| D | Sandy-Loam | 15 | ETc | Twice a day | 603 | 133 | −515 | −148 | −76 | −4 | 70 | 201 |
| E | Once a day | 603 | 132 | −511 | −148 | −77 | −2 | 70 | 201 | |||
| F | Every 4 days | 604 | 126 | −491 | −162 | −77 | −1 | 67 | 215 | |||
| G | 25 | Twice a day | 603 | 133 | −449 | −220 | −73 | −6 | 61 | 269 | ||
| H | Once a day | 602 | 132 | −444 | −221 | −72 | −3 | 60 | 271 | |||
| I | Every 4 days | 604 | 126 | −427 | −231 | −74 | −2 | 58 | 284 | |||
| J | Loam | 15 | Twice a day | 603 | 133 | −553 | −129 | −59 | −5 | 75 | 170 | |
| K | Once a day | 606 | 132 | −549 | −128 | −60 | 0 | 74 | 168 | |||
| L | Every 4 days | 604 | 126 | −533 | −137 | −60 | −1 | 73 | 178 | |||
| M | 25 | Twice a day | 603 | 133 | −511 | −176 | −57 | −8 | 70 | 213 | ||
| N | Once a day | 602 | 132 | −506 | −175 | −56 | −2 | 69 | 214 | |||
| O | Every 4 days | 604 | 126 | −492 | −181 | −58 | −1 | 67 | 222 | |||
| P | Silty-Clay | 15 | Twice a day | 603 | 133 | −544 | −221 | 17 | −12 | 74 | 209 | |
| Q | Once a day | 603 | 132 | −544 | −218 | 15 | −12 | 74 | 205 | |||
| R | Every 4 days | 604 | 126 | −537 | −213 | 15 | −5 | 74 | 201 | |||
| S | 25 | Twice a day | 603 | 133 | −536 | −229 | 17 | −12 | 73 | 214 | ||
| T | Once a day | 602 | 132 | −535 | −229 | 19 | −11 | 73 | 214 | |||
| V | Every 4 days | 604 | 126 | −531 | −219 | 16 | −4 | 73 | 209 | |||
| Irrigation System | Yield (kg ha−1) | WPIrr | WPIrr+R |
|---|---|---|---|
| SDI-2019 (2019 field test) | 5363 | 0.73 | 0.62 |
| DI-2017 [10] | 5565 | 0.72 | 0.60 |
| CFI-2017 [10] | 6486 | 0.46 | 0.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arbat, G.; Cufí, S.; Duran-Ros, M.; Pinsach, J.; Puig-Bargués, J.; Pujol, J.; Ramírez de Cartagena, F. Modeling Approaches for Determining Dripline Depth and Irrigation Frequency of Subsurface Drip Irrigated Rice on Different Soil Textures. Water 2020, 12, 1724. https://doi.org/10.3390/w12061724
Arbat G, Cufí S, Duran-Ros M, Pinsach J, Puig-Bargués J, Pujol J, Ramírez de Cartagena F. Modeling Approaches for Determining Dripline Depth and Irrigation Frequency of Subsurface Drip Irrigated Rice on Different Soil Textures. Water. 2020; 12(6):1724. https://doi.org/10.3390/w12061724
Chicago/Turabian StyleArbat, Gerard, Sílvia Cufí, Miquel Duran-Ros, Jaume Pinsach, Jaume Puig-Bargués, Joan Pujol, and Francisco Ramírez de Cartagena. 2020. "Modeling Approaches for Determining Dripline Depth and Irrigation Frequency of Subsurface Drip Irrigated Rice on Different Soil Textures" Water 12, no. 6: 1724. https://doi.org/10.3390/w12061724
APA StyleArbat, G., Cufí, S., Duran-Ros, M., Pinsach, J., Puig-Bargués, J., Pujol, J., & Ramírez de Cartagena, F. (2020). Modeling Approaches for Determining Dripline Depth and Irrigation Frequency of Subsurface Drip Irrigated Rice on Different Soil Textures. Water, 12(6), 1724. https://doi.org/10.3390/w12061724







