Medium-Term Rainfall Forecasts Using Artificial Neural Networks with Monte-Carlo Cross-Validation and Aggregation for the Han River Basin, Korea
Abstract
:1. Introduction
2. Data and Methods
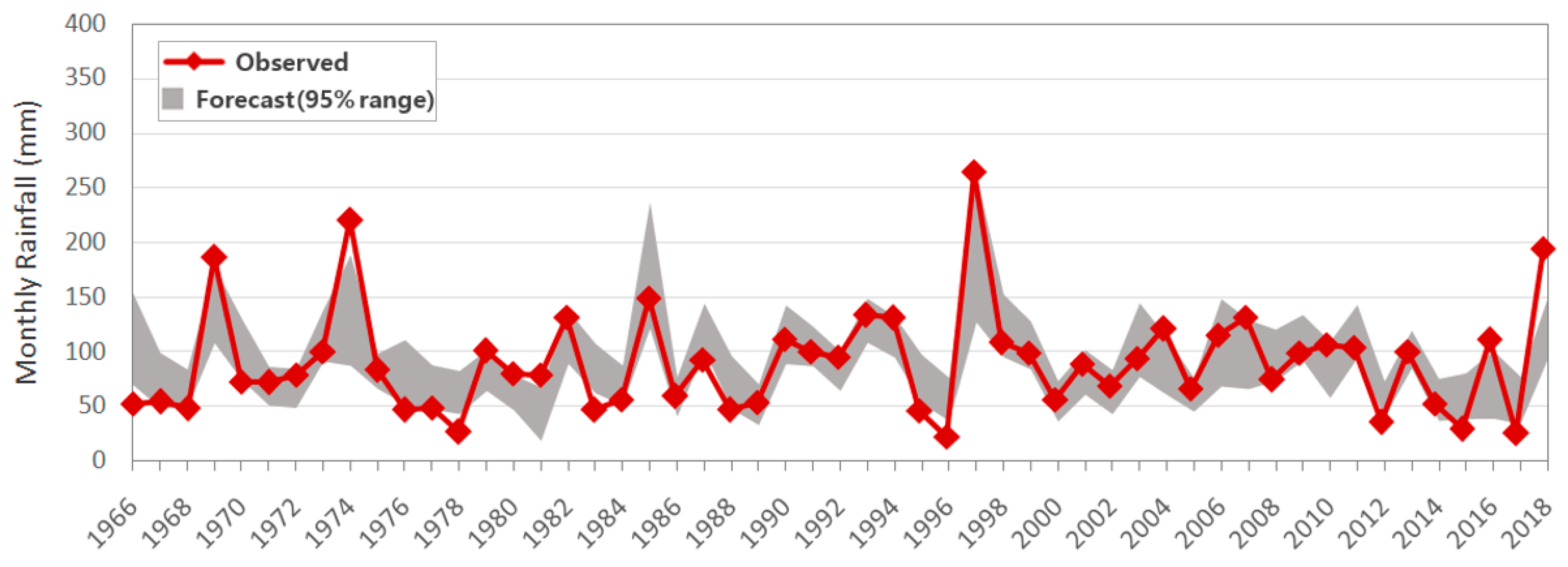
2.1. Data
2.2. Procedure of Artificial Neural Network (ANN) Model Development
2.3. Performance Evaluation of the Artificial Neural Network (ANN) Outputs
2.4. Uncertainty Analysis of the Artificial Neural Network (ANN) Outputs
3. Results and Discussion
3.1. Determination of the Preliminary Input Variables
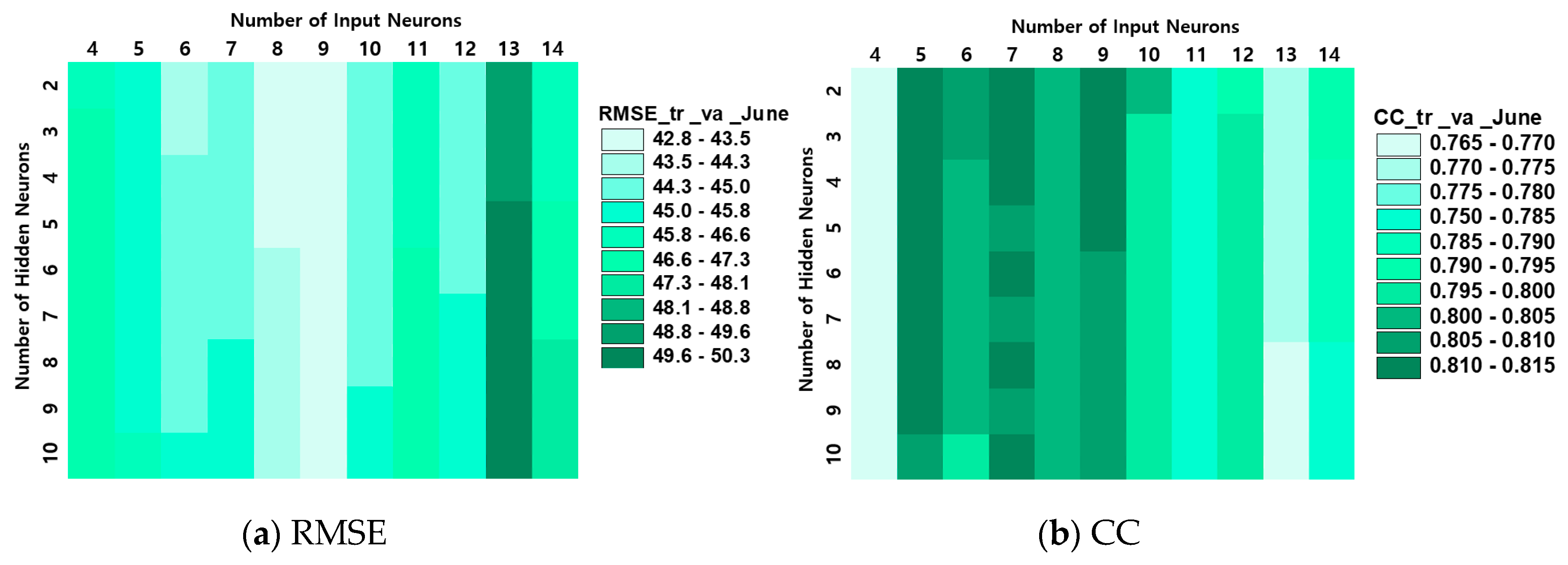
3.2. Performance of the Artificial Neural Network (ANN) Models
3.3. Uncertainty of the Artificial Neural Network (ANN) Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mekanik, F.; Imteaz, M.A.; Gato-Trinidad, S.; Elmahdi, A. Multiple regression and artificial neural network for long-term rainfall forecasting using large scale climate modes. J. Hydrol. 2013, 503, 11–21. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Darand, M. Forecasting precipitation with artificial neural networks (Case Study: Tehran). J. Appl. Sci. 2009, 9, 1786–1790. [Google Scholar] [CrossRef] [Green Version]
- Redmond, K.T.; Koch, R.W. Surface climate and streamflow variability in the western United States and their relationship to Large-Scale circulation Indices. Water Resour. Res. 1991, 27, 2381–2399. [Google Scholar] [CrossRef]
- Schepen, A.; Wang, Q.J.; Robertson, D. Evidence for using lagged climate indices to forecast Australian seasonal rainfall. J. Clim. 2012, 1230–1246. [Google Scholar] [CrossRef]
- Karabork, M.C.; Kahya, E.; Karaca, M. The influences of the Southern and North Atlantic Oscillations on climatic surface variables in Turkey. Hydrol. Process. 2005, 19, 1185–1211. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Application of artificial neural networks to rainfall forecasting in Queensland, Australia. Adv. Atmos. Sci. 2012, 29, 717–730. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Using lagged and forecast climate indices with artificial intelligence to predict monthly rainfall in the Brisbane Catchment, Queensland, Australia. Int. J. Sustain. Dev. Plan. 2015, 10, 29–41. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Forecasting of monthly rainfall in the Murray Darling Basin, Australia: Miles as a case study. WIT Trans. Ecol. Environ. 2015, 197, 149–159. [Google Scholar]
- Abbot, J.; Marohasy, J. Application of artificial neural networks to forecasting monthly rainfall one year in advance for locations within the Murray Darling basin, Australia. Int. J. Sustain. Dev. Plan. 2017, 12, 1282–1298. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.N.; Reddy, M.J.; Maity, R. Regional rainfall forecasting using large scale climate teleconnections and artificial intelligence techniques. J. Intell. Syst. 2007, 16, 307–322. [Google Scholar]
- Hartmann, H.; Becker, S.; King, L. Predicting summer rainfall in the Yangtze River basin with neural networks. Int. J. Climatol. 2008, 28, 925–936. [Google Scholar] [CrossRef]
- Yuan, F.; Berndtsson, R.; Uvo, C.B.; Zhang, L.; Jiang, P. Summer precipitation prediction in the source region of the Yellow River using climate indices. Hydrol. Res. 2016, 47, 847–856. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Kim, C.-G.; Lee, J.E.; Kim, N.W.; Kim, H. Application of Artificial Neural Networks to Rainfall Forecasting in the Geum River Basin, Korea. Water 2018, 10, 1448. [Google Scholar] [CrossRef] [Green Version]
- Zahmatkesh, Z.; Goharian, E. Comparing machine learning and decision making approaches to forecast long lead monthly rainfall: The city of Vancouver, Canada. Hydrology 2018, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Shao, J. Linear model selection by cross-validation. J. Am. Stat. Assoc. 1993, 88, 486–494. [Google Scholar] [CrossRef]
- Xu, Q.S.; Liang, Y.Z.; Du, Y.P. Monte Carlo cross-validation for selecting a model and estimating the prediction error in multivariate calibration. J. Chemom. 2004, 18, 112–120. [Google Scholar] [CrossRef]
- Barrow, D.K.; Crone, S.F. Cross-validation aggregation for combining autoregressive neural network forecasts. Int. J. Forecast. 2016, 32, 1120–1137. [Google Scholar] [CrossRef] [Green Version]
- WAMIS. Available online: https://web.archive.org/web/20200601094620/ (accessed on 31 May 2020).
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Kim, J.S.; Jain, S.; Yoon, S.K. Warm season streamflow variability in the Korean Han River Basin: Links with atmospheric teleconnections. Int. J. Climatol. 2012, 32, 635–640. [Google Scholar] [CrossRef]
- Kim, B.S.; Kim, B.K.; Kwon, H.H. Assessment of the impact of climate change on the flow regime of the Han River basin using indicators of hydrologic alteration. Hydrol. Processes 2011, 25, 691–704. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, Y.H.; Lee, W.S. Seasonal prediction of Korean regional climate from preceding large-scale climate indices. Int. J. Climatol. 2007, 27, 925–934. [Google Scholar] [CrossRef]
- CPC. Available online: https://psl.noaa.gov/data/climateindices/list/ (accessed on 31 May 2020).
- De Veaux, R.D.; Ungar, L.H. Multicollinearity: A Table of Two Nonparametric Regression; Springer: New York, NY, USA, 1994; pp. 393–402. [Google Scholar]
- Xu, L.; Chen, N.; Zhang, Z.; Chen, Z. A data-driven multi-model ensemble for deterministic and probabilistic precipitation forecasting at seasonal scale. Clim. Dyn. 2020, 54, 3355–3374. [Google Scholar] [CrossRef]
- Badr, H.S.; Zaitchik, B.F.; Guikema, S.D. Application of statistical models to the prediction of seasonal rainfall anomalies over the Sahel. J. Appl. Meteorol. Climatol. 2013, 53, 614–636. [Google Scholar] [CrossRef] [Green Version]
- Santos, T.S.; Mendes, D.; Torres, R.R. Artificial neural networks and multiple linear regression model using principal components to estimate rainfall over South America. Nonlinear Processes Geophys. 2016, 23, 13–20. [Google Scholar] [CrossRef]
- Ahmadi, A.; Han, D.; Lafdani, E.K.; Moridi, A. Input selection for long-lead precipitation prediction using large-scale climate variables: A case study. J. Hydroinform. 2015, 17, 114–129. [Google Scholar] [CrossRef]
- Lin, F.J. Solving multicollinearity in the process of fitting regression model using the nested estimate procedure. Qual. Quant. 2008, 42, 417–426. [Google Scholar] [CrossRef]
- Kim, T.W.; Valdes, J.B. Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Olden, J.D.; Joy, M.K.; Death, R.G. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecol. Model. 2004, 178, 389–397. [Google Scholar] [CrossRef]
- De Oña, J.; Garrido, C. Extracting the contribution of independent variables in neural network models: A new approach to handle instability. Neural Comput. Appl. 2014, 25, 859–869. [Google Scholar] [CrossRef]
- National Weather Service. Available online: https://www.weather.gov/mdl/verification_ndfd_public_scoredef#hss (accessed on 31 May 2020).
- Tokar, A.S.; Johnson, P.A. Rainfall-runoff modeling using artificial neural networks. J. Hydrol. Eng. 1999, 4, 232–239. [Google Scholar] [CrossRef]
- Singh, A.; Imtiyaz, M.; Isaac, R.K.; Denis, D.M. Assessing the performance and uncertainty analysis of the SWAT and RBNN models for simulation of sediment yield in the Nagawa watershed, India. Hydrol. Sci. J. 2014, 59, 351–364. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Boston, MA, USA, 1977. [Google Scholar]




| Abbreviation | Full name | Description |
|---|---|---|
| AAO | Antarctic Oscillation | The first leading mode from the Empirical Orthogonal Function (EOF) analysis of the monthly mean height anomalies at 700-hPa |
| AMM | Atlantic Meridional Mode | A climate mode associated with the cross-equatorial meridional gradient of the sea surface temperature anomaly (SSTA) in the tropical Atlantic |
| AMO | Atlantic Multidecadal Oscillation | A coherent mode of natural variability based upon the average anomalies of the sea surface temperatures (SST) in the North Atlantic basin, which is typically over 0–80° N |
| AO | Arctic Oscillation | The first leading mode from the Empirical Orthogonal Function (EOF) analysis of the monthly mean height anomalies at 1000-hPa |
| BEST | Bivariate ENSO Time series | Bivariate ENSO calculated by combining a standardized SOI and a standardized Niño 3.4 SST time series |
| CAR | Caribbean SST Index | The time series of the SST anomalies averaged over the Caribbean |
| EA | East Atlantic Pattern | The second prominent mode of the low-frequency variability over the North Atlantic, and it appears as a leading mode for all months |
| EAWR | East Atlantic/Western Russia Pattern | One of three prominent teleconnection patterns, which affects Eurasia throughout the year |
| EPNP | East Pacific/North Pacific Oscillation | A spring–summer–fall pattern with three main anomaly centers |
| GML | Global Mean Land Ocean Temperature Index | Anomaly index from the NASA Goddard Institute for Space Studies (GISS) |
| MEI.v2 | Multivariate ENSO Index version 2 | The multivariate ENSO index (MEI V2) time series is bimonthly so the Jan value represents the Dec-Jan value and it is centered between the months |
| NAO | North Atlantic Oscillation | One of the most prominent teleconnection patterns for all seasons |
| NINO1+2 | Extreme Eastern Tropical Pacific SST | Average sea surface temperature anomaly over 0–10° S, 90° W–80° W |
| NINO3 | Eastern Tropical Pacific SST | Average sea surface temperature anomaly over 5° N–5° S, 150° W–90° W |
| NINO3.4 | East Central Tropical Pacific SST | Average sea surface temperature anomaly over 5° N–5° S, 170–120° W |
| NINO4 | Central Tropical Pacific SST | Average sea surface temperature anomaly over 5° N–5° S, 160° E–150° W |
| NOI | Northern Oscillation Index | An index of the climate variability based on the difference in the SLP anomalies at the North Pacific High and near Darwin, Australia |
| NP | North Pacific Pattern | The area-weighted sea level pressure over the region 30° N–65° N, 160° E–140° W |
| Abbreviation | Full Name | Description |
| NTA | North Tropical Atlantic SST Index | The time series of the SST anomalies averaged over 60° W to 20° W, 6° N to 18° N and 20° W to 10° W, 6° N to 10° N |
| ONI | Oceanic Niño Index | The three-month running mean of the NOAA ERSST.V5 SST anomalies in the Niño 3.4 region |
| PDO | Pacific Decadal Oscillation | Pacific decadal oscillation over 7°0 N–60° S, 60° W–100° E The leading principal component (PC) of the monthly SST anomalies in the North Pacific Ocean |
| PNA | Pacific American Index | One of the most prominent modes of low-frequency variability in the Northern Hemisphere extratropics |
| POL | Polar/Eurasia Pattern | The most prominent mode of low-frequency variability during December and February |
| QBO | Quasi-biennial Oscillation | A quasi-periodic oscillation of the equatorial zonal wind between the easterlies and westerlies in the tropical stratosphere with a mean period of 28 to 29 months |
| SCAND | Scandinavia Pattern | A primary circulation center over Scandinavia, with weaker centers that have an opposite sign over western Europe and eastern Russia/western Mongolia |
| SLP_D | Darwin Sea Level Pressure | Sea level pressure at Darwin at 13° S, 131° E |
| SLP_E | Equatorial Eastern Pacific Sea Level Pressure | Standardized sea level pressure over the equatorial eastern Pacific region |
| SLP_I | Indonesia Sea Level Pressure | Standardized sea level pressure anomalies over the equatorial Indonesia region (5° N–5° S, 90° E–140° E) |
| SLP_T | Tahiti Sea Level Pressure | Sea level pressure at Tahiti at 18° S, 150° W |
| SOI | Southern Oscillation Index | Difference between the sea level pressure at Tahiti and Darwin |
| SOI_EQ | Equatorial SOI | The standardized anomaly of the difference between the area-average monthly sea level pressure in an area of the eastern equatorial Pacific (80° W–130° W, 5° N–5° S) and an area over Indonesia (90° E–140° E, 5° N–5° S) |
| SOLAR | Solar Flux | The 10.7 cm solar flux data provided by the National Research Council of Canada |
| TNA | Tropical Northern Atlantic Index | Tropical northern Atlantic SST over 25° N–5° N, 15° W–55° W Anomaly of the average of the monthly SST from 5.5° N to 23.5° N and 15° W to 57.5° W |
| TNI | Trans-Niño Index | Index of the El Niño evolution |
| TPI(IPO) | Tripole Index for Interdecadal Pacific Oscillation | The difference between the SSTA averaged over the central equatorial Pacific and the average of the SSTA in the Northwest and Southwest |
| TSA | Tropical Southern Atlantic Index | Tropical southern Atlantic SST over 0° S–20° S, 10° E–30° W Anomaly of the average of the monthly SST from Eq—20° S and 10° E–30° W |
| WHWP | Western Hemisphere Warm Pool | Monthly anomaly of the ocean surface area that is warmer than 28.5 °C in the Atlantic and the eastern North Pacific |
| WP | Western Pacific Index | A primary mode of low-frequency variability over the North Pacific for all months |
| May | June | ||||
|---|---|---|---|---|---|
| Climate Index | Time Lag | Correlation Coefficient | Climate Index | Time Lag | Correlation Coefficient |
| AO | 8 | −0.372 | AMM | 11 | 0.292 |
| AO | 10 | 0.218 | AMM | 12 | 0.311 |
| EAWR | 3 | 0.280 | AO | 6 | −0.292 |
| EAWR | 7 | −0.374 | EPNP | 2 | 0.279 |
| EAWR | 10 | −0.342 | EPNP | 7 | 0.246 |
| NOI | 12 | −0.173 | NAO | 6 | −0.450 |
| POL | 7 | 0.246 | PNA | 4 | −0.244 |
| POL | 12 | 0.186 | POL | 12 | 0.324 |
| QBO | 7 | −0.242 | SCAND | 3 | −0.327 |
| QBO | 8 | −0.242 | SCAND | 10 | −0.334 |
| SPI | 9 | −0.271 | SLP_E | 6 | 0.273 |
| WP | 5 | 0.279 | SLP_E | 3 | 0.246 |
| WP | 12 | −0.170 | WP | 4 | 0.292 |
| Han | 3 | 0.338 | Han | 4 | 0.356 |
| Noof Input | AO (8) | AO (10) | EAWR (3) | EAWR (7) | EAWR (10) | NOI (12) | POL (7) | POL (12) | QBO (7) | QBO (8) | SPI (9) | WP (5) | WP (12) | Han (3) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | −0.165 | 0.126 | 0.035 | −0.257 | −0.166 | −0.178 | 0.188 | 0.073 | −0.138 | −0.084 | −0.176 | 0.196 | −0.125 | 0.211 |
| 13 | −0.156 | 0.092 | −0.225 | −0.175 | −0.155 | 0.159 | 0.077 | −0.133 | −0.066 | −0.178 | 0.196 | −0.144 | 0.221 | |
| 12 | −0.157 | 0.133 | −0.248 | −0.173 | −0.172 | 0.171 | 0.062 | −0.185 | −0.189 | 0.197 | −0.139 | 0.209 | ||
| 11 | −0.170 | 0.147 | −0.242 | −0.187 | −0.211 | 0.197 | 0.069 | −0.212 | −0.208 | 0.179 | 0.242 | |||
| 10 | −0.178 | 0.144 | −0.232 | −0.193 | −0.179 | 0.196 | −0.193 | −0.203 | 0.174 | 0.245 | ||||
| 9 | −0.181 | −0.227 | −0.176 | −0.176 | 0.138 | −0.176 | −0.171 | 0.152 | 0.256 | |||||
| 8 | −0.173 | −0.221 | −0.181 | −0.150 | −0.178 | −0.150 | 0.158 | 0.271 | ||||||
| 7 | −0.192 | −0.188 | −0.215 | −0.183 | −0.176 | 0.1759 | 0.288 | |||||||
| 6 | −0.201 | −0.261 | −0.219 | −0.178 | 0.214 | 0.294 | ||||||||
| 5 | −0.241 | −0.234 | −0.213 | 0.198 | 0.288 | |||||||||
| 4 | −0.250 | −0.295 | −0.222 | 0.263 |
| No. of Input | AMM (11) | AMM (12) | AO (6) | EPNP (2) | EPNP (7) | NAO (6) | PNA (4) | POL (12) | SCAND (3) | SCAND (10) | SLP_E (6) | SLP_E (3) | WP (4) | Han (4) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14 | 0.043 | 0.254 | −0.113 | 0.289 | 0.226 | −0.218 | −0.040 | 0.183 | −0.239 | −0.279 | 0.111 | 0.187 | 0.023 | 0.366 |
| 13 | 0.051 | 0.275 | −0.132 | 0.309 | 0.221 | −0.220 | −0.040 | 0.169 | −0.244 | −0.323 | 0.100 | 0.174 | 0.340 | |
| 12 | 0.012 | 0.318 | −0.126 | 0.359 | 0.228 | −0.261 | 0.208 | −0.277 | −0.377 | 0.108 | 0.220 | 0.401 | ||
| 11 | 0.327 | −0.122 | 0.348 | 0.220 | −0.286 | 0.227 | −0.280 | −0.392 | 0.100 | 0.247 | 0.395 | |||
| 10 | 0.330 | −0.129 | 0.407 | 0.229 | −0.274 | 0.180 | −0.256 | −0.414 | 0.244 | 0.418 | ||||
| 9 | 0.388 | 0.365 | 0.228 | −0.416 | 0.218 | −0.300 | −0.443 | 0.304 | 0.449 | |||||
| 8 | 0.379 | 0.485 | 0.288 | −0.380 | −0.259 | −0.529 | 0.227 | 0.457 | ||||||
| 7 | 0.507 | 0.529 | 0.273 | −0.469 | −0.252 | −0.583 | 0.419 | |||||||
| 6 | 0.576 | 0.495 | 0.336 | −0.528 | −0.601 | 0.435 | ||||||||
| 5 | 0.717 | 0.665 | −0.706 | −0.679 | 0.452 | |||||||||
| 4 | 0.662 | 0.897 | −0.800 | −0.616 |
| Model | Statistics | RMSE (mm) | CC | ||||
|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | Training | Validation | Testing | ||
| mean | 27.4 | 33.6 | 39.5 | 0.809 | 0.725 | 0.641 | |
| ANN-M | median | 28.1 | 33.4 | 38.8 | 0.828 | 0.758 | 0.667 |
| standard deviation | 7.2 | 10.0 | 8.9 | 0.125 | 0.140 | 0.164 | |
| mean | 39.5 | 46.1 | 62.1 | 0.853 | 0.771 | 0.683 | |
| ANN-J | median | 38.2 | 44.1 | 61.6 | 0.893 | 0.825 | 0.714 |
| standard deviation | 13.6 | 14.6 | 14.6 | 0.143 | 0.196 | 0.170 | |
| Observed Category | Forecast Category | |||
|---|---|---|---|---|
| Below | Normal | Above | Total | |
| Below | 13 | 7 | 0 | 20 |
| Normal | 2 | 13 | 5 | 20 |
| Above | 0 | 5 | 8 | 13 |
| Total | 15 | 25 | 13 | 53 |
| Observed Category | Forecast Category | |||
|---|---|---|---|---|
| Below | Normal | Above | Total | |
| Below | 9 | 14 | 0 | 23 |
| Normal | 5 | 11 | 1 | 17 |
| Above | 0 | 4 | 9 | 13 |
| Total | 14 | 29 | 10 | 53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, C.-G.; Lee, J.E.; Kim, N.W.; Kim, H. Medium-Term Rainfall Forecasts Using Artificial Neural Networks with Monte-Carlo Cross-Validation and Aggregation for the Han River Basin, Korea. Water 2020, 12, 1743. https://doi.org/10.3390/w12061743
Lee J, Kim C-G, Lee JE, Kim NW, Kim H. Medium-Term Rainfall Forecasts Using Artificial Neural Networks with Monte-Carlo Cross-Validation and Aggregation for the Han River Basin, Korea. Water. 2020; 12(6):1743. https://doi.org/10.3390/w12061743
Chicago/Turabian StyleLee, Jeongwoo, Chul-Gyum Kim, Jeong Eun Lee, Nam Won Kim, and Hyeonjun Kim. 2020. "Medium-Term Rainfall Forecasts Using Artificial Neural Networks with Monte-Carlo Cross-Validation and Aggregation for the Han River Basin, Korea" Water 12, no. 6: 1743. https://doi.org/10.3390/w12061743
APA StyleLee, J., Kim, C.-G., Lee, J. E., Kim, N. W., & Kim, H. (2020). Medium-Term Rainfall Forecasts Using Artificial Neural Networks with Monte-Carlo Cross-Validation and Aggregation for the Han River Basin, Korea. Water, 12(6), 1743. https://doi.org/10.3390/w12061743





