Next Article in Journal
Experimental Characterization of the Hydraulic Jump Profile and Velocity Distribution in a Stilling Basin Physical Model
Previous Article in Journal
A Spatially Distributed Investigation of Stream Water Temperature in a Contemporary Mixed-Land-Use Watershed
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 12
Issue 6
10.3390/w12061757
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Variation in Runoff, Suspended Sediment Load, and Their Inter-Relationships in Response to Climate Change and Anthropogenic Activities Over the Last 60 Years: A Case Study of the Upper Fenhe River Basin, China

by
Luan Zhang
1,2,*,
Suqing Li
1,2,
Zhitao Wu
1,2,
Xiaohui Fan
1,2,
Hongjian Li
1,2,
Qi Meng
1,2 and
Jing Wang
3
1
Institute of Loess Plateau, Shanxi University, Taiyuan 030006, China
2
Shanxi Key Laboratory for Ecological Restoration of Loess Plateau, Taiyuan 030006, China
3
Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China
*
Author to whom correspondence should be addressed.
Water 2020, 12(6), 1757; https://doi.org/10.3390/w12061757
Submission received: 24 May 2020 / Revised: 14 June 2020 / Accepted: 15 June 2020 / Published: 20 June 2020
Browse Figures
Versions Notes

Abstract

:
The variation of river runoff (Q) and suspended sediment load (S), in addition to their influential factors, is an important area of focus in hydrological sciences. Here, Mann–Kendall tests and double mass curve analyses were used with hydrometric data from four hydrological stations in the upper Fenhe River Basin in China to evaluate temporal trends in annual Q (Qa) and S (Sa) values between 1955 and 2015. Based on the observed inflection points, three distinct periods were identified, namely, 1955–early 1980s (period I), the early 1980s–1996 (period II), and 1996–2015 (period III). The Qa and Sa values for the four stations, except for Qa values for the Jingle station, significantly decreased over the study period, with average reduction rates of 0.68–1.07 mm∙km−2∙a−1 and 9.24–54.39 t∙km−2∙a−1, respectively. Decreased rainfall, implementation of soil and water conservation program, and reservoir construction were primarily responsible for decreased Qa and Sa values for the three stations during period II, while the first two factors led to variation in Qa and Sa for the Jingle station during the same period. During period III, the Qa, Sa, and Qa–Sa relationships for the four stations were intensively affected by increased anthropogenic activities, including water diversion, cross-basin water transfers, soil and water conservation measures, revegetation efforts, and sand excavation. Further, the Qa, Sa, and Qa–Sa relationships at the Lancun station were affected by the construction of the No. 2 Fenhe Reservoir. Effective water use and supply strategies should be implemented in the future for the upper Fenhe River Basin.

1. Introduction

Climate change and increased anthropogenic activities in recent decades have introduced altered dynamics in river systems, including frequent occurrences of discontinuous flow [1], sharp decreases in suspended sediment loads (S) [2], increasingly strained water supplies [3], and deteriorated river ecologies [4]. Understanding these dynamics and their underlying factors have become areas of intense focus in hydrological research. Indeed, investigations of the variations in runoff (Q) and S have been conducted for large global rivers within recent decades, including the Mississippi [5], Nile [6], Amazon [7] Colorado [8], Yangtzi [9], and Yellow Rivers [10]. In addition, several studies have explored factors that influence Q and S. For example, Burn and HagElnur [11] evaluated 18 hydrological variables for 248 Canadian catchments and concluded that variation in hydrological variables was related to variation in meteorological variables. Additionally, Walling and Fang [12] demonstrated that reservoir construction was the primary factor underlying annual S reductions in about 50% of 145 major global rivers, excluding those in Africa and South America. Furthermore, Restrepo and Escobar [13] observed that dramatic increases in S in the Magdalena River and its tributaries during 1980–2010 were primarily attributed to marked increases in forest clearance.
The Yellow River is one of the most heavily sediment-laden rivers in the world and has been intensively affected by climate change and anthropogenic activities in recent decades [14,15]. The Middle Yellow River is the major sediment source for the Yellow River due to storms in summer, loose loess, hilly and gully landforms, poor vegetation, and unreasonable cultivation. Recently, dramatic changes in Q and S values in most of its tributaries have been observed [16]. Several factors have been implicated in the spatiotemporal changes of Q and S of the Middle Yellow River, including the El Nino/Southern Oscillation climate pattern [17], weakened summer monsoons [18], hydraulic engineering [19], soil and water conservation activities [14], water diversion, and sand excavation [20]. These factors may also alter the hydrologic response between Q and S (i.e., the Q–S relationship) that can be used to provide information to understand fluvial system behaviors and long-term trends, while also providing context for interpreting short-term events within a basin [21,22,23]. Scaling effects are some of the most important characteristics underlying fluvial system behaviors [7,24,25], where the dynamics of Q, S, and the Q–S interactions may vary across areas and among different periods in response to factors within tributary basins [26]. Consequently, it is necessary to investigate the basin-scale temporal variation in Q, S, and the Q–S relationships that are critical for predicting future trends in Q and S, in addition to informing effective management strategies for promoting river health and the sustainable utilization of water resources that is coordinated with economic development.
The Fenhe River is the second-largest tributary of the Yellow River, with a length of 710 km. The Fenhe River historically had appropriate conditions for boating and well-developed transportation activities. Indeed, its lower reaches were still viable for boating transport until 1929. However, discontinuous flow was first detected in the Middle Fenhe River in 1958 and has frequently occurred in various sections of the river in recent decades. By the end of the 1990s, critical water scarcity problems were occurring in the upper Fenhe River Basin [27]. Concomitantly, warming and drying climate trends were detected in this region during this period [28], while large reservoirs and several coal mining bases were established in the Fenhe River Basin. To alleviate serious soil erosion and improve the environment, the national level “Soil and Water Conservation,” “Natural Forest Protection,” and “Grain for Green” programs were successively implemented within the basin. Furthermore, a large-scale, cross-basin water transfer project was implemented in the early 21st century to meet the increasing water demands. Given these increasingly complex and interactive factors and processes in the basin, two essential questions have remained: How have Q and S values varied within the upper Fenhe River Basin over the past 60 years? Furthermore, how have Q and S, as well as the Q–S relationships, varied in response to climate change and anthropogenic disturbances? The present study addresses these questions using an in-depth analysis of annual Q (Qa) and S (Sa) datasets from 1955 to 2015 for four major hydrological stations in the upper Fenhe River Basin, which is a unique basin that is a water supply source for the provincial capital city with 4.46 million people and a large coal mining base in northern China, in addition to evaluating major factors that influence these metrics.

2. Study Area, Data Collection, and Methods

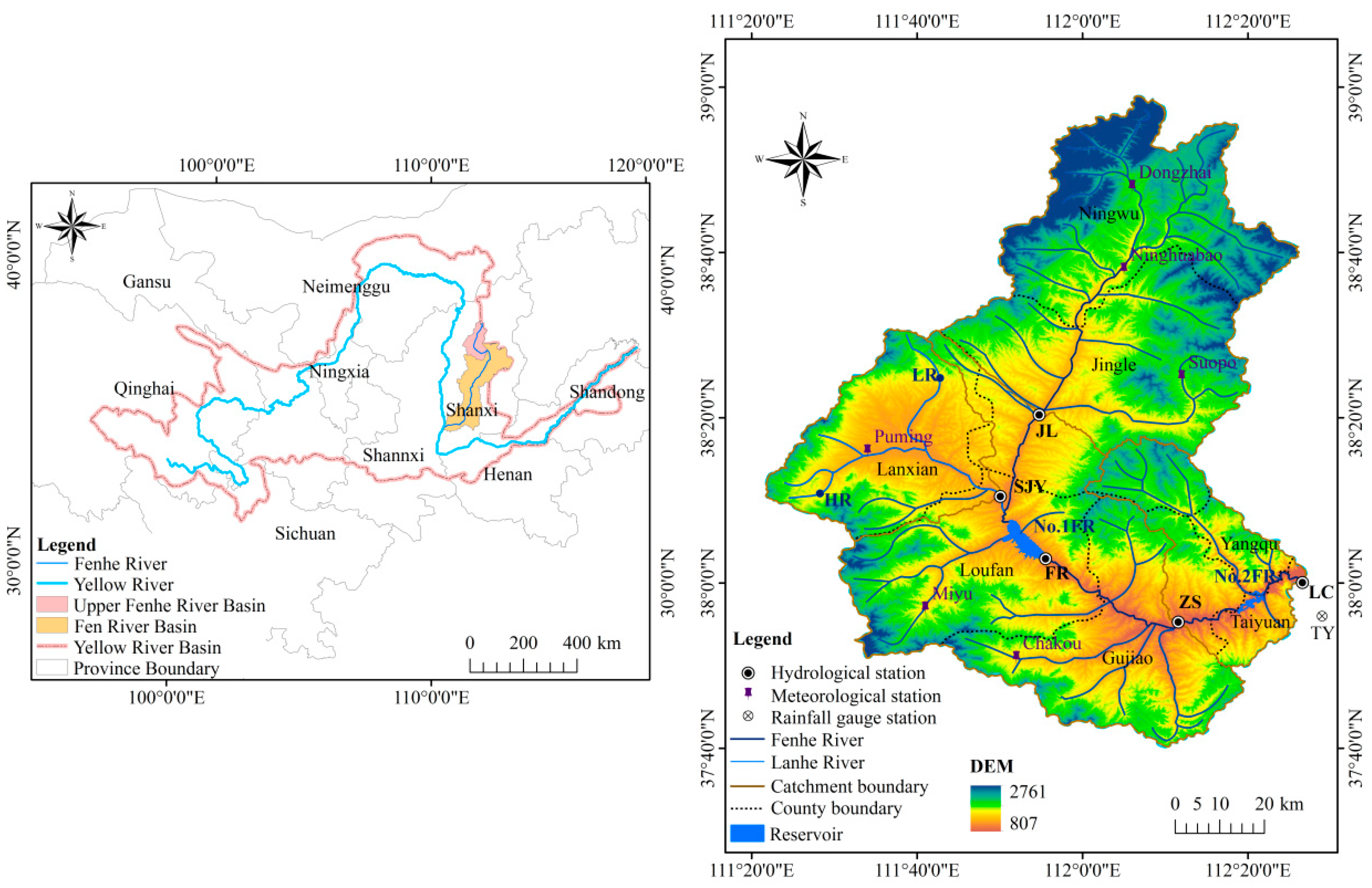
2.1. Study Area

The upper Fenhe River is about 217.3 km in length, with the Lancun hydrological station at the terminus. The river basin covers about 7705 km2 within the Ningwu, Jingle, Lanxian, Loufan, and Yangqu counties, in addition to Gujiao city and the Jiancaoping District of Taiyuan city, which is the capital city of the Shanxi Province [29]. The area is characterized by a temperate continental monsoon climate. The annual precipitation varies from 213 to 798 mm, more than 80% of which falls between June and September. The annual average temperature is 8.5–11.8 °C. The major topography of the basin is loess hilly-gully, rocky mountains, and riparian zone. Particularly, the loess hilly-gully area, which forms a severe erosion area in the basin with an average erosion modulus of 6700 ton·km−2·a−1, contributes about 70% of the erosion in the basin with less than 40% of the area [30]. The zonal vegetation is characterized as a temperate sub-humid deciduous broad-leaved forest [31]. The dominant plant species of the area include Quercus wutaishansea Mary, Pinus tabuliformis, Hippophae rhamnoides, and others. Agricultural cultivation was previously the primary source of economic income in the basin, where croplands accounted for more than 50% of the basin area at one point [32]. Following the implementation of China’s reform and opening-up policy in 1978, coal mining industries began to dominate economies in Ningwu county, Lanxian county, Gujiao city, and Taiyuan city, with some croplands and forestlands being converted to construction lands. Construction lands substantially expanded after 2000 with the rapid development of the economy and urbanization across the whole basin [33]. Concomitantly, vegetation coverage increased in the basin due to the implementation of the national level “Soil and Water Conservation” program for 20 years, beginning in 1988. Further, the initiation of the “Natural Forest Protection” and “Grain for Green” programs in the late 1990s and 2003, respectively, particularly promoted the restoration of native environments [33,34].
Hydrological stations and rainfall gauge stations were established by the Chinese Water Conservancy Department on the main stream of the upper Fenhe River and its major tributaries (e.g., the Lanhe River, which is the largest tributary of the upper Fenhe River) in the 1950s to monitor variations in hydrological characteristics. The No. 1 and No. 2 Fenhe reservoirs are present on the main stream of the upper Fenhe River and were completed in 1961 and 2000, respectively. The reservoirs have capacities of 7.12 × 108 and 1.33 × 108 m3, respectively, and are used for flood protection, water supplies, and electricity. In addition, the Lancheng and Hamashen reservoirs were built on the Lanhe River tributary in 1973 and 1975, respectively, and feature storage capacities of 6.0 × 106 and 6.24 × 106 m3, respectively [29]. Furthermore, a large-scale, cross-basin water transfer project, the Yellow River Water Transfer Project, was initiated in October 2003, primarily to alleviate intensified water scarcities in Taiyuan city, and exhibits an annual water transfer capacity of 640 million m3. The project transfers water from the Wanjiazhai Reservoir of the Yellow River via tunnels, aqueducts, pipelines, and a section of the upper Fenhe River channel to the No. 1 Fenhe Reservoir. The waters then supplement the Taiyuan city water supplies via underground pipelines from the reservoir [35].

2.2. Data and Methods

Annual Q (Qa) and S (Sa) data were collected from four hydrological stations in the upper Fenhe River Basin, representing the longest available time series (1955–2015) to investigate temporal variation in Qa and Sa values over those 60 years. The four hydrological stations included three stations on the main stream of the upper Fenhe River (Jingle, Zhaishang, and Lancun; referred to as JL, ZS, and LC, respectively) and one station (Shangjingyou, SJY) at the terminus of the Lanhe River.
Annual precipitation (Pa) data from the four hydrological stations, in addition to six other rainfall gauge stations (Dongzhai, Ninghuabao, Suopo, Puming, Miyu, and Chakou), from 1955 to 2015 were collected to explore the Qa and Sa values for JL, SJY, ZS, and LC in response to changes in the average Pa values (Pma) for individual catchments. All of the above data were collected from the Yellow River Water Conservancy Commission. The Pma values for the JL, SJY, ZS, and LC catchments (abbreviated as PmaJL for the JL catchment, for example) were calculated using the arithmetic mean of Pa for stations and rainfall gauges that were located within the catchments.
The annual average air temperature data for the Taiyuan meteorological station (TTY) from 1955 to 2015 were only collected due to the lack of such long-term time-series data at other meteorological stations. The TTY data were collected from the Shanxi Meteorological Information Center to explore variations in Qa and Sa values at the nearby LC station in response to air temperature changes. Variations of Pma for JL, SJY, ZS, and LC catchments and TTY during the different periods are provided in Table 1. Additional details for the above stations are provided in Figure 1.
The Qa data for the No. 1 Fenhe Reservoir hydrological station (FR) (QaFR) at the outlet of the reservoir was collected for the years 1962–2015 from the Yellow River Water Conservancy Commission to explore QaZS and QaLC changes in response to the construction of the No. 1 Fenhe Reservoir. Annual sediment deposition volume data for the No. 1 Fenhe Reservoir (DaFR) from 1963 to 2015 and cumulative sediment deposition volume from 1960 to 1962 were collected from the Fenhe Reservoir Administration Bureau to analyze the effect of the reservoir on SaZS and SaLC variations.
Monthly normalized difference vegetation index (NDVI) datasets, including the Global Inventory Modeling and Mapping Studies (GIMMS) NDVI3g dataset and the Terra Moderate Resolution Imaging Spectroradiometer (MODIS, NASA, Washington DC, USA) Vegetation Indices (MOD13Q1) dataset, were collected to analyze the relationships between vegetation coverage and Qa or Sa values over the study period. The GIMMS NDVI3g dataset was derived from the NOAA/AVHRR land dataset at a spatial resolution of 8 km in 15-day intervals from 1982 to 2015. The MODIS MOD13Q1 dataset exhibited a 250 m spatial resolution at 16-day intervals from 2000 to 2015, and was derived from the Earth Observing System of NASA [36]. Monthly NDVI values for the two datasets were first obtained using the maximum value composite method, which minimizes cloud contamination, atmospheric effects, and solar zenith angle effects [37]. The yearly NDVI value of each pixel was then calculated by computing the maximum values for the 12 monthly NDVI values. Finally, the annual regional values of GIMMS NDVI (NDVI8km) and MODIS NDVI (NDVI250m) for the JL, SJY, ZS, and LC catchments were separately calculated by computing the average yearly NDVI values for all grid cells within those catchments. Additionally, the annual floor space data for buildings under construction in Taiyuan city (FSBCTY) were collected for the years from 1996 to 2015 from the Shanxi Province Statistical Yearbook [38] to better understand the use of sand excavation and explore the associated impacts on Sa.
Autocorrelation was evaluated for the calculated metrics before analyzing the monotonic trends of the Qa and Sa time series for the JL, SJY, ZS, and LC stations, in addition to their respective Pma, NDVI8km, and NDVI250m values for the four respective catchments. Furthermore, autocorrelation was evaluated for the TTY, QaFR, and DaFR metrics [39]. The monotonic trends of the above variables were determined using nonparametric Mann–Kendall tests [40,41]. The magnitudes of the trends for the respective variables were indicated using Sen’s slopes [42]. The inflection points of the variables were identified based on the separate intersection of UF and UB curves from the Mann–Kendall tests within the confidence interval of [−0.01, 0.01] [43,44]. In addition, abrupt inflection points for Qa and Sa values for the four stations were detected from the variation in slope for straight lines that were fitted to double mass curves of Qa–Pma and Sa–Pma [45]. The abrupt inflection points obtained using the double mass curve method were used as nodes to divide periods (see Section 3.3) and further investigate changes in Qa, Sa, and the Qa–Sa relationships, in addition to their potential influential factors. The Qa–Sa relationships within different periods were analyzed using simple linear regression analyses. Linear regression models were tested using F tests to evaluate the statistical differences in relationships. Correlations between Qa or Sa and influential indicators (i.e., Pma, NDVI8km, NDVI250m, TTY, QaFR, and DaFR) were analyzed using Pearson correlation analysis.

3. Results

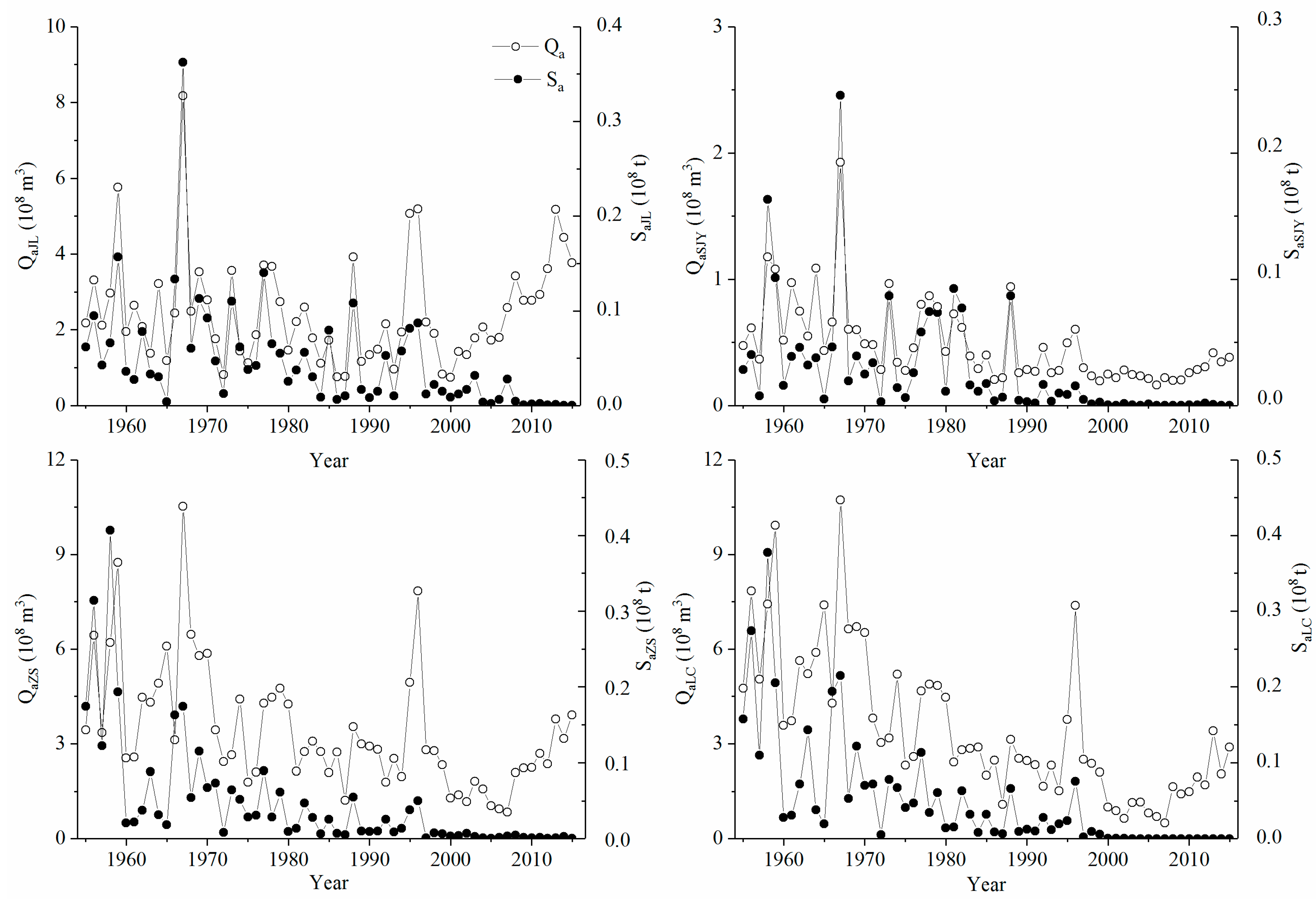
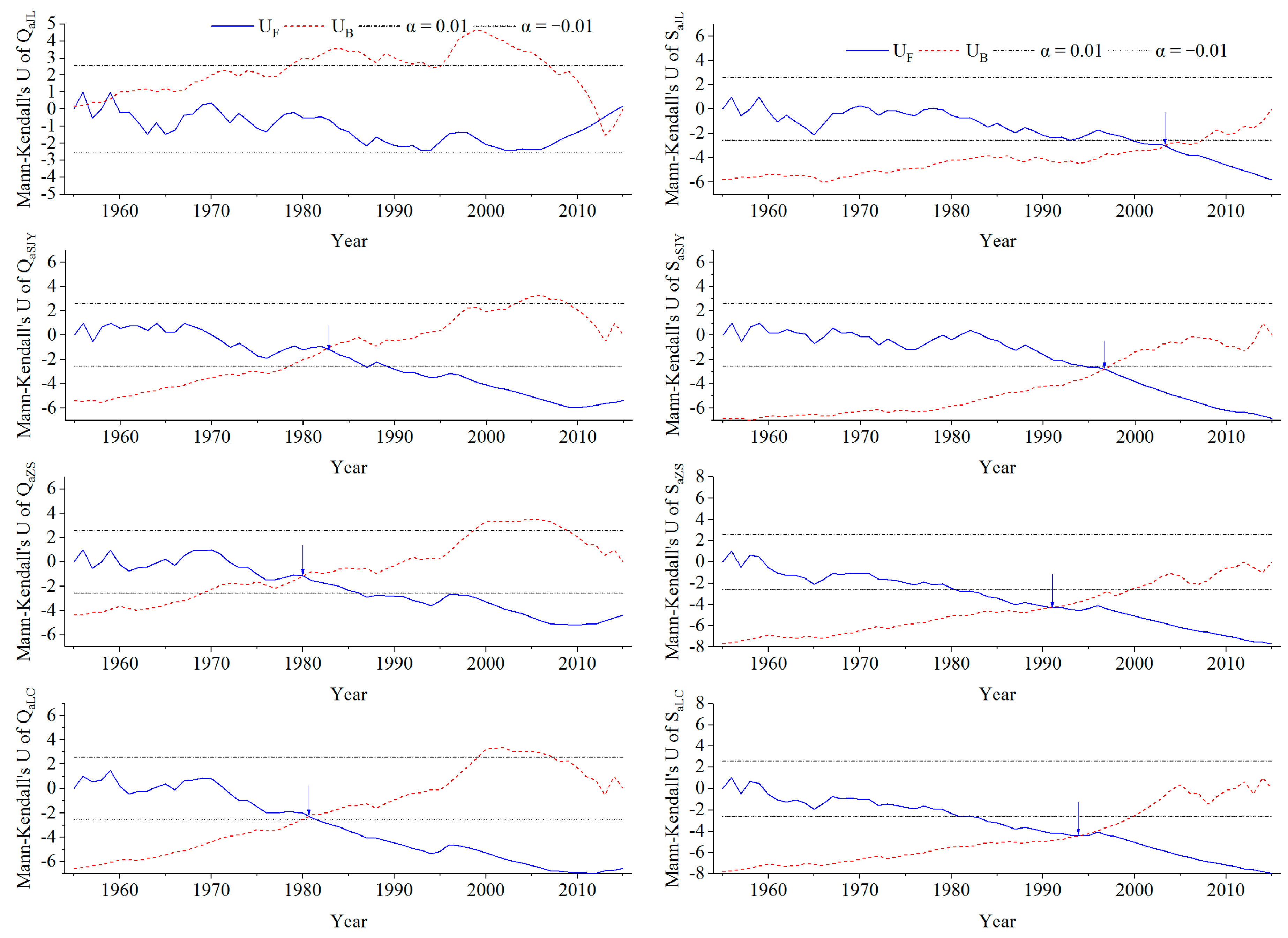
3.1. Temporal Variation in Qa and Sa Based on Mann–Kendall Tests

The temporal variation in Qa and Sa values for the JL, SJY, ZS, and LC stations from 1955 to 2015 is shown in Figure 2. The Qa variables, excluding QaJL, exhibited highly significant decreasing trends over the 60 years of the study, with average reduction rates of 0.68–1.07 mm∙km−2∙a−1 (p < 0.001) (Table 2). Sa values for the above four stations also exhibited significant decreasing trends over the same period, with average reduction rates of 9.24–54.39 t∙km−2∙a−1 (p < 0.001 or p < 0.01). The most significant decreases in the Qa and Sa rates were observed at LC and SJY, respectively. The inflection points for Qa were identified in 1983 for SJY, 1980 for ZS, and 1981 for LC, while the inflection points for Sa occurred in 2004 for JL, 1997 for SJY, 1991 for ZS, and 1994 for LC (Figure 3).

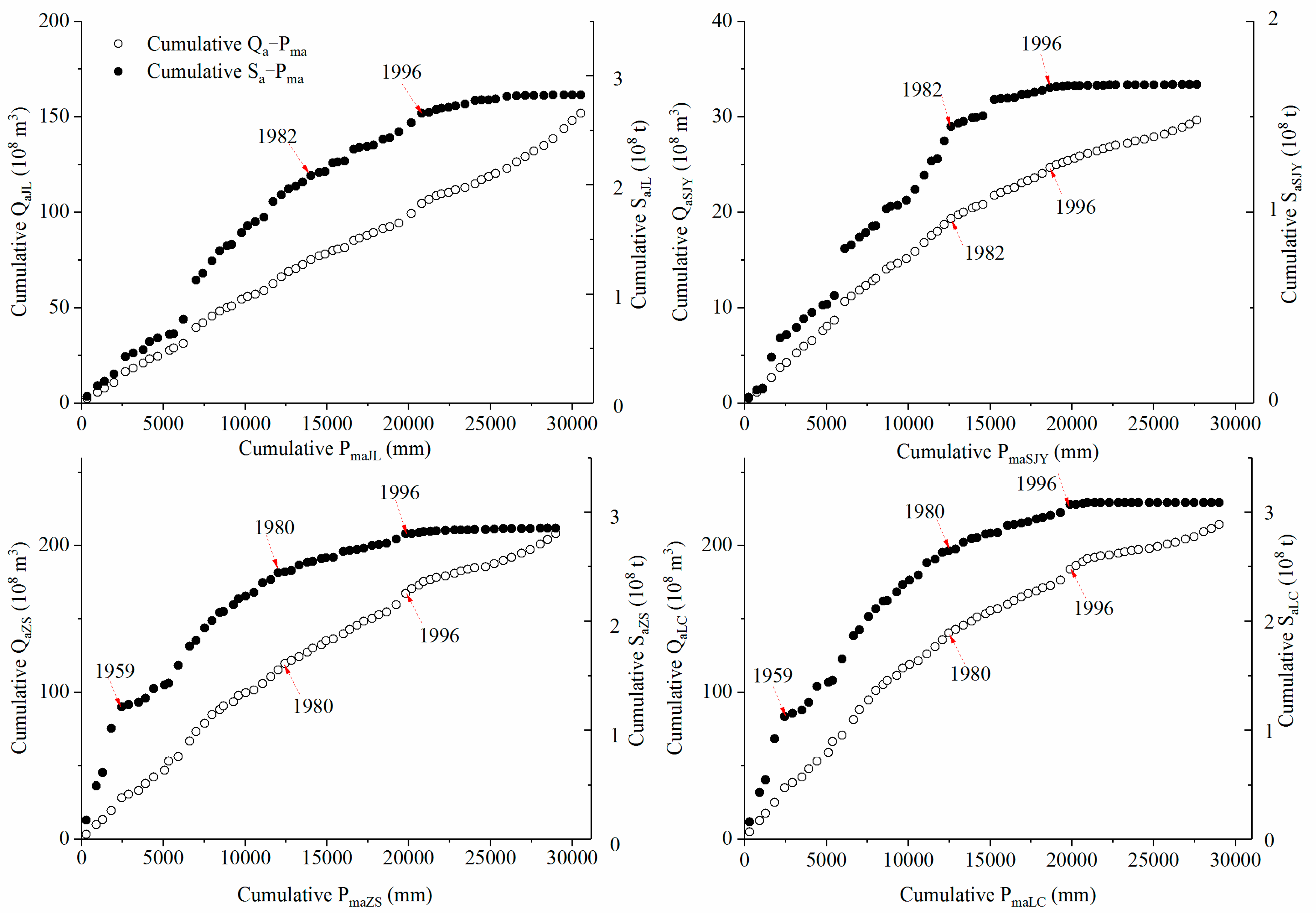
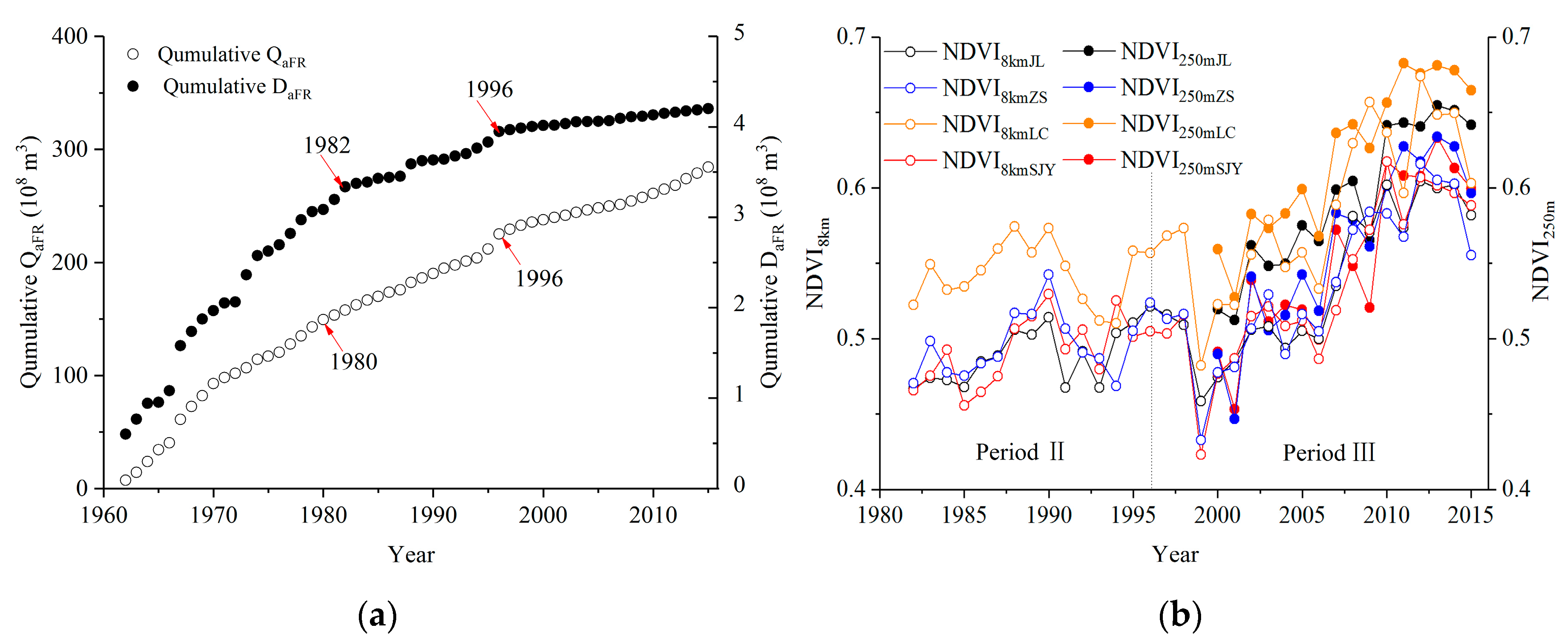
3.2. Temporal Variation of Qa–Pma and Sa–Pma Based on Double Mass Curves

Cumulative Qa and Sa values were plotted against cumulative Pma values for the four stations (Figure 4). Except for the double mass curve of QaJL−PmaJL, which manifested as a straight line without segmentation, the other double mass curves for SaJL−PmaJL, QaSJY−PmaSJY, and SaSJY−PmaSJY unanimously trended rightwards with abrupt inflection points occurring in 1982 and 1996. The double mass curves of Qa−Pma and Sa−Pma for ZS and LC, respectively, varied nearly synchronously, with the same abrupt inflection points occurring in 1980 and 1996, respectively, in the cumulative Qa−Pma curves and for the cumulative Sa−Pma curves in 1959, 1980, and 1996.

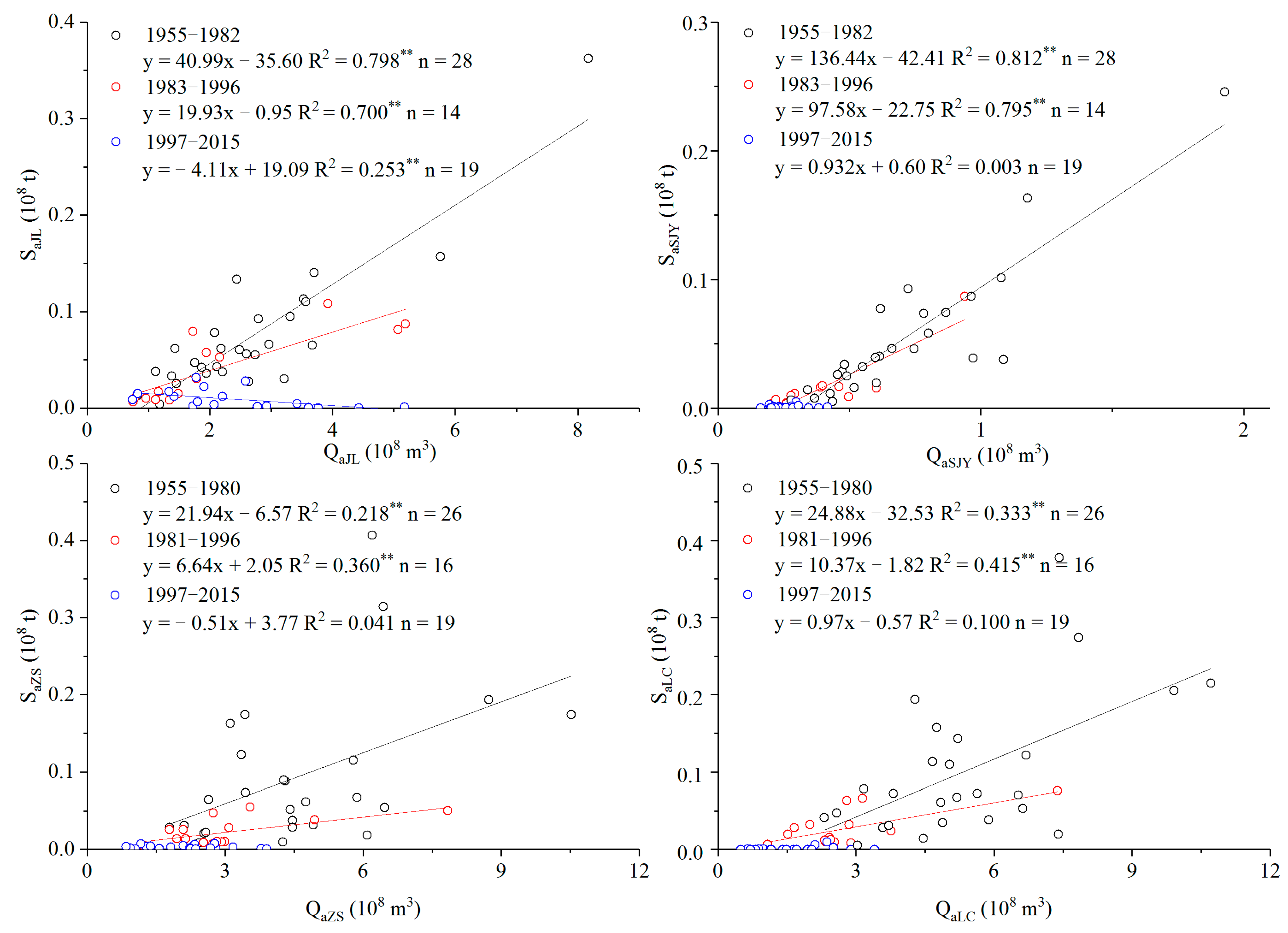
3.3. Changes in Average Qa, Sa, and the Qa–Sa Relationships during Three Separate Study Periods

Three periods were used to investigate changes in the Qa, Sa, and the Qa–Sa relationships, with 1982 and 1996 as the nodes of QaSJY and SaSJY, and 1980 and 1996 as the nodes of Qa and Sa for ZS and LC. To facilitate comparisons among the four stations, the QaJL and SaJL series were divided into three periods, with 1982 and 1996 as the nodes. Specifically, the three periods for Qa and Sa values of JL and SJY were defined as 1955–1982 (period I), 1983–1996 (period II), and 1997–2015 (period III). Likewise, the three periods for Qa and Sa values for ZS and LC were defined as 1955–1980 (period I), 1981–1996 (period II), and 1997–2015 (period III). The reductions in average Qa for the four stations during periods Ⅱ and III compared to period I were 21.77–49.46% and 7.25–70.35%, respectively (Table 3). The level of reduction in the average Sa was greater than that of Qa for the four stations, with average Sa values decreasing in periods II and III by 45.03–76.62% and 88.08–99.04%, respectively, when compared to period I.
The Qa–Sa relationships for JL, SJY, ZS, and LC during the three periods are shown in Figure 5. The simple linear regression lines, equations, and determination coefficients (R2) for all relationships are presented simultaneously for ease of interpretation, although some were not statistically significant. The Qa–Sa relationships for the four stations during periods I and II fit linear functions well, as indicated by the significant R2 values (p < 0.01). All of the regression lines for period II were below those of period I, indicating that the value of Sa decreased given the same values of Qa under such conditions. The slope of the QaJL–SaJL relationship regression line was negative during period III, contrasting with the positive slopes observed during the first two periods. Extremely low R2 values observed for SJY, ZS, and LC regressions during period III indicated the lack of significant correlations between Qa and Sa values for the three stations during this period.

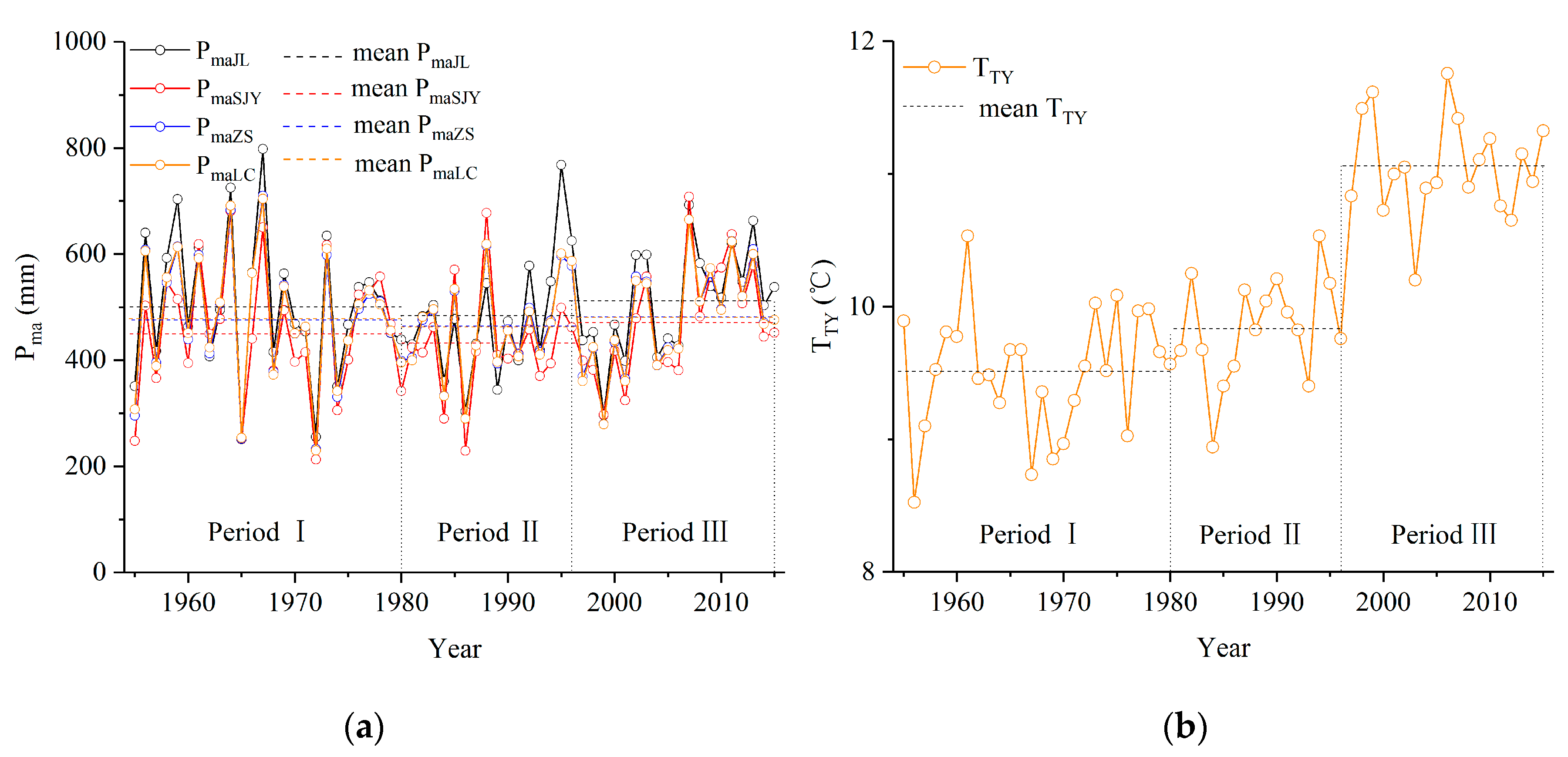
3.4. Temporal Variation in Potential Influential Variables

Trend-based analyses were conducted for representative environmental indicators in the study area, including Pma, NDVI8km, and NDVI250m metrics for the four catchments, in addition to the other environmental metrics TTY, QaFR, and DaFR. Significant changes were not observed for PmaJL, PmaSJY, PmaZS, and PmaLC from 1955 to 2015 (Table 4). However, average PmaJL, PmaSJY, PmaZS, and PmaLC values for period II (484.2, 432.5, 462.5, and 462.5 mm, respectively) were lower than those of period I (501.0, 450.8, 475.7, and 477.8 mm, respectively) and period III (512.0, 472.0, 481.6, and 480.0 mm, respectively) (Figure 6a). A significant increase in TTY values was observed from 1955 to 2015 with an average increasing rate of 0.36 °C (10 a)−1 (Z = 5.31, p < 0.001). Moreover, average TTY values for period III were clearly higher than those for the first two periods (Figure 6b). In contrast, a significant decrease was observed for QaFR values from 1962 to 2015 (Z = −2.75, p < 0.01; β = −7.80 × 106 m3∙a−1) and for DaFR from 1963 to 2015 (Z = −3.75, p < 0.001, β = −0.18 × 106 m3∙a−1). The abrupt inflection points for the cumulative QaFR curve occurred in 1980 and 1996, respectively, while those of the cumulative DaFR curve occurred in 1982 and 1996, respectively (Figure 7a). The NDVI8km values significantly increased from 1982 to 2015 in the four catchments (p < 0.05 or p < 0.01 or p < 0.001) (Table 4), with rapid increases after 2000 that were consistent with the variations in NDVI250m during the 2000–2015 period (p < 0.001) (Figure 7b).

3.5. Pearson’s Correlations between Qa, Sa, and Potential Influencing Variables

The Pearson’s correlation coefficients among Qa, Sa, and the potential influential factors for the JL, SJY, ZS, and LC stations were investigated for different periods (Table 5). Significant and positive correlations were observed between Qa and Sa values for the four stations over the first two periods (p < 0.01 or p < 0.05). In contrast, significant negative correlations for QaJL–SaJL (p < 0.05) and no significant correlations in the Qa–Sa relationships for the SJY, ZS, and LC stations were observed during period III. Significant and positive correlations were observed for the Qa−Pma values of JL during the three periods (p < 0.01 or p < 0.05) and for SJY during the first two periods (p < 0.01). In contrast, significant correlations were not observed for QaZS−PmaZS and QaLC–PmaLC during the three periods. Significant positive correlations were observed for the Sa−Pma values of the four stations during the first two periods (p < 0.01 or p < 0.05), except for SaZS−PmaZS during period I. Strongly positive and significant correlations were observed between Qa for the four stations and QaFR during the three periods (p < 0.01 or p < 0.05). Likewise, significant positive correlations were also observed for Sa−DaFR values of the four stations during the first two periods (p < 0.01). Significant positive correlations were observed for Qa−NDVI8km for the JL and ZS stations during period II (p < 0.05). Likewise, significant positive correlations were observed for JL, SJY, and ZS during period III (p < 0.01 or p < 0.05), in addition to similar relationships for Qa−NDVI250m for all four stations during period III (p < 0.01). In contrast, significant negative correlations were observed for Sa−NDVI8km values of JL and ZS, and for Sa−NDVI250m of LC over the same period (p < 0.05).

4. Discussion

The Mann–Kendall tests indicated that the Qa values for the SJY, ZS, and LC stations dramatically decreased, beginning in the early 1980s (Table 2 and Figure 3). This was further evinced from obvious rightward shifts of the double mass curves for Qa−Pma for the three stations around 1980 (Figure 4). A similar result was obtained by Zhang et al. [44] for the Qa series of the Fenhe River from 1957 to 2010. Average PmaSJY values during period II were lower than those of period I (Figure 6a), and significant positive correlations were observed for QaSJY−PmaSJY during the two periods (p < 0.01) (Table 5), indicating that the decreased PmaSJY values during period II could lead to reduced QaSJY values. Similarly, significant correlations in the SaSJY−PmaSJY and QaSJY−SaSJY relationships (p < 0.01) indicated that decreased PmaSJY and QaSJY during period II could have weakened sediment generation and carrying capacity, further reducing SaSJY. In addition to rainfall, other factors affected QaSJY and SaSJY during period II, as indicated by the obvious rightward deflection of the cumulative QaSJY−PmaSJY and SaSJY−PmaSJY curves around 1982. Qin [34] reported that the large-scale “Soil and Water Conservation” program was carried out in the upper Fenhe River Basin after 1988. Niu and Niu [46] further confirmed that 39 new check dams were built in the SJY catchment between 1983 and 1994, 33 of which were built after 1988, while only two reservoirs (the Lancheng and Hamashen reservoirs) and three check dams were built during period I. These check dams and reservoirs cumulatively controlled 50% of the drainage area in the loess hilly-gully areas of the SJY catchment, thereby effectively intercepting runoff and sediment, and dramatically reducing QaSJY and SaSJY during period II. The reduced rainfall and increased soil and water conservation measures were also responsible for the decreased QaJL and SaJL values observed for the same period. The QaJL and SaJL values had comparatively lower decreases than QaSJY and SaSJY during period II, respectively, when compared with the values for period I (Table 3). These differences may be related to different topographies among the two catchments. The SJY catchment is dominated by loess hilly-gully features that are more prone to soil erosion and more affected by soil and water conservation measures. In addition, the construction of two reservoirs in the SJY catchment could have also contributed to these observed differences.
Minimal Pma metric values were also observed for the ZS and LC catchments in the 1980s (Table 1 and Figure 6a), when the “Soil and Water Conservation” program was conducted in the two catchments after 1988. However, in contrast to the significant correlations in the QaSJY−PmaSJY and QaJL−PmaJL relationships observed during periods I and II (p < 0.01), significant correlations in the QaZS−PmaZS and QaLC−PmaLC relationships were not observed during the two periods. Likewise, significant correlations were not observed for the SaZS−PmaZS relationships during period I. These observations could be attributed to the regulation of runoff and sediment-intercepting effects of the No. 1 Fenhe Reservoir that is upstream of ZS. This supposition is supported by significant correlations in the QaZS−QaFR and QaLC−QaFR relationships during the three periods (p < 0.01), as well as the synchronous appearance of the first inflection points for the Qa data series of ZS, LC, and FR in 1980, and that of in the cumulative SaZS−PmaZS and SaLC−PmaLC curves in 1959 due to construction of the reservoir. The former occurred later than the latter, which was mainly due to differential effects of the reservoir on the regulation of gradual flows and complete sediment deposition. The reservoir mainly supported farmland irrigation but has continually supplied water for industrial activities in Gujiao city within the ZS catchment and the Taiyuan city downstream of the LC station since the 1980s [47]. Five large underground coal mines and associated coal preparation plants were successively built in Gujiao city during period II. By the end of this period, the annual coal output reached 16.5 million tons and the total industrial output value of the city increased 36.3 times over that of 1978 when China’s reform and opening-up policy was implemented [48]. Taiyuan city is an important industrial city in northern China and harbors industries with high water consumption (e.g., metallurgical, coal-fired, coking, and chemical industries) that accounted for 68.81% of the city’s industrial output value in the early 1990s [49]. Dramatic decreases in QaZS and QaLC over period II were the result of industrial development in the two cities and the reservoir filling, which led to the increased water diversion from rivers, coupled with reduced rainfall, reduced incoming flows upstream, and the implementation of soil and water conservation measures. Moreover, extensive goafs from Gujiao coal mining activities could have intensified the infiltration of flows in leakage areas, thereby resulting in decreased runoff [50], as was observed by Cravotta et al. [51] in the upper Schuylkill River of Pennsylvania. These factors also contributed to decreased SaZS and SaLC values, as indicated by the second abrupt inflection of cumulative SaZS−PmaZS and SaLC−PmaLC curves in 1980 and the significant correlations in the Qa–Sa relationships for the two stations over this period (p < 0.05 or p < 0.01).
The abrupt inflection points of cumulative Qa−Pma curves for the SJY, ZS, and LC stations and those of the cumulative Sa−Pma curves for the four stations coincidently occurred in 1996. Previous hydrological records [52] indicated that catastrophic flood events occurred in the upper Fenhe River Basin in 1996 due to an extreme precipitation event when rainfall lasted for 34 hours and 314 mm of accumulated rainfall was measured at the rainfall center. A persistent five-year drought subsequently occurred during 1997–2001, with an average annual Pma value for the five years of 280 mm, representing 78% of the average Pma for 1955–2015. These observations indicate that high magnitude flood events and climatic fluctuations are strongly coupled to fluxes in river discharge and sediment deposition [53]. However, significant correlations were not observed for the Qa−Pma relationships for the three stations during this period, except for QaJL−PmaJL of JL, nor for Sa−Pma at the four stations, or for QaLC−TTY and SaLC−TTY. These results could be primarily attributed to complex human activities that weaken the roles of climate change on the above values. As discussed earlier, 20 successive years of the “Soil and Water Conservation” program took place in the basin. By the end of 2007, 30341 hm2 of terraced fields, 131933 hm2 of afforestation and grass, and 118 check dams had been developed in the upper reaches of the No. 1 Fenhe Reservoir [34]. These data provide some evidence for the effects of soil and water conservation measures on reduced Qa and Sa values for JL and SJY during period III. Further evidence of this is given by the dramatic reduction in DaFR during this period (Figure 7a). The afforestation effects of the “Soil and Water Conservation,” “Natural Forest Protection,” and “Grain for Green” programs were confirmed by the significantly increased NDVI8km and NDVI250m values for the four catchments (p < 0.05 or p < 0.01 or p < 0.001). Moreover, the effects of sediment interception were represented by negative correlations for the SaJL−NDVI8kmJL, SaZS−NDVI8kmZS, and SaLC−NDVI250mLC relationships during this period (p < 0.05).
Booming industrial development and associated economies, along with urbanization, led to a continuous increase in water demand, thereby resulting in increased water diversion from rivers and dramatic decreases in runoff. The direct or indirect discharge of industrial wastewater and domestic sewage into rivers also led to the deterioration of water quality [47]. Consequently, severe water scarcity in industrial, agricultural, and domestic water occurred in Taiyuan city in the 1990s [54]. Concomitantly, over-exploitation of groundwater intensified, with the area of the deep groundwater depression cone near the lower reaches of LC station expanding by 44.8 km2 from 1990 to 2000 and central water levels dropping by 8.83 m [55]. As a result, the Yellow River Water Transfer Project was initiated in the basin, beginning in 2003, to primarily alleviate water scarcity in Taiyuan city. From 2003 to 2010, a total of 523 million m3 of Yellow River water had been supplied to Taiyuan city, and the annual water supply reached 320 million m3 by 2015 [56]. In addition, rapid urbanization development resulted in the development of a real estate industry. This was especially evident in the rapid development after 1998 upon implementation of China’s urban housing system reform, as indicated by the increased FSBCTY during 1996−2015 (Figure 8). The result caused an increased demand for river sand, thereby contributing to increased sand excavation along the river due to the lack of any policy forbidding sand excavation during that time, and decreased Sa values at the four stations. The above-mentioned factors profoundly influenced the spatiotemporal dynamics of rainfall-driven runoff generation and sediment delivery in the upper Fenhe River Basin, resulting in fundamentally changed Qa–Sa relationships at the four stations in period III (Figure 5). Similar results were reported by Xu [45] for the coarser sediment production area in the Middle Yellow River Basin. The comparably low reduction rate of QaJL in period III compared with that in period I (when compared to the other three stations) was due to the transferred Yellow River water that largely supplemented QaJL when passing through the river course upstream of the JL station. Conversely, the comparatively higher reduction of SaLC in period III than SaZS, when compared with values for period I, was caused by the construction of the No. 2 Fenhe Reservoir, which retained most of the sediments downstream of ZS after its commission in 2000.

5. Summary and Conclusions

In this study, temporal variation in Qa and Sa values, as well as the Qa–Sa relationships, were investigated for four stations (JL, SJY, ZS, and LC) in the upper Fenhe River Basin during the period encompassing 1955–2015. The primary results showed that:
(1) Qa values for SJY, ZS, and LC dramatically decreased with average reduction rates of 0.68−1.07 mm∙km−2∙a−1, and inflection points occurring around 1980, as shown using Mann–Kendall tests. The Sa values at the four stations also significantly decreased, with average reduction rates of 9.24−54.39 t∙km−2∙a−1. The inflection points of Sa occurred in 2004 for JL, 1997 for SJY, 1991 for ZS, and 1994 for LC.
(2) Decreased rainfall, soil and water conservation measures, and the construction of reservoirs were the primary factors underlying the decreased Qa and Sa values for SJY, ZS, and LC during period II. The first two processes were responsible for the variation in QaJL and SaJL during period II. Following 1997, dramatically decreased Qa and Sa values, in addition to fundamental changes in the Qa–Sa relationships for the four stations, were primarily caused by increased anthropogenic activities, including water diversion, a cross-basin water transfer project, soil and water conservation measures, revegetation efforts, and sand excavation. In addition, construction of the No. 2 Fenhe Reservoir was also responsible for variation in QaLC, SaLC, and the QaLC−SaLC relationship. In total, the influence of anthropogenic activities on Q and S was greater than that of climate change over the last 60 years in the upper Fenhe River Basin.
(3) The above results suggest that effective strategies should be stressed, including promoting the efficiency of water use, strengthening water resource management, etc., in order to adjust increasingly severe differences in water supplies and demands, as well as changed flow-sediment relationship in the upper Fenhe River Basin. In addition, the long-term impact of underground coal mining and a large-scale, cross-basin water transfer project on the environments of the upper Fenhe River should be an area of further concern and investigation.

Author Contributions

Conceptualization, L.Z. and S.L.; methodology, L.Z., Z.W., X.F., H.L., Q.M., and J.W.; writing and editing, L.Z. and S.L.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Foundation for Young Scientists of Shanxi Province (grant number 2013021031-3), the National Natural Science Foundation of China (grant numbers 41301609 and U1810101), and the Applied Basic Research of Shanxi Province (grant number 201901D111040).

Acknowledgments

We thank anonymous editors from Letpub for the English language editing. We thank the editors and anonymous reviewers for their professional comments, which have helped us greatly improve the manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Tang, Y.; Tang, Q.; Tian, F.; Zhang, Z.; Liu, G. Responses of natural runoff to recent climatic variations in the Yellow River basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 4471–4480. [Google Scholar] [CrossRef] [Green Version]
  2. Hestir, E.L.; Schoellhamer, D.H.; Morgan-King, T.; Ustin, S.L. A step decrease in sediment concentration in a highly modified tidal river delta following the 1983 El Nino floods. Mar. Geol. 2013, 345, 304–313. [Google Scholar] [CrossRef]
  3. Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Datsch Silveira, M.A.; Ribeiro, D.L.; Vieira, G.M.; Demarco, N.R.; Gregio d’Arce, L.P. Direct and Indirect Anthropogenic Contamination in Water Sources: Evaluation of Chromosomal Stability and Cytotoxicity Using the Allium cepa Test. Bull. Environ. Contam. Tox. 2018, 100, 216–220. [Google Scholar] [CrossRef] [PubMed]
  5. Ouyang, Y.; Leininger, T.D.; Moran, M. Impacts of reforestation upon sediment load and water outflow in the Lower Yazoo River Watershed, Mississippi. Ecol. Eng. 2013, 61, 394–406. [Google Scholar] [CrossRef]
  6. Gebremicael, T.G.; Mohamed, Y.A.; Betrie, G.D.; van der Zaag, P.; Teferi, E. Trend analysis of runoff and sediment fluxes in the Upper Blue Nile basin: A combined analysis of statistical tests, physically-based models and landuse maps. J. Hydrol. 2013, 482, 57–68. [Google Scholar] [CrossRef]
  7. Syvitski, J.P.M.; Cohen, S.; Kettner, A.J.; Brakenridge, G.R. How important and different are tropical rivers?—An overview. Geomorphology 2014, 227, 5–17. [Google Scholar] [CrossRef]
  8. Brusca, R.C.; Álvarez-Borrego, S.; Hastings, P.A.; Findley, L.T. Colorado River flow and biological productivity in the Northern Gulf of California, Mexico. Earth Sci. Rev. 2017, 164, 1–30. [Google Scholar] [CrossRef] [Green Version]
  9. Dai, Z.J.; Fagherazzi, S.; Mei, X.F.; Gao, J.J. Decline in suspended sediment concentration delivered by the Changjiang (Yangtze) River into the East China Sea between 1956 and 2013. Geomorphology 2016, 268, 123–132. [Google Scholar] [CrossRef] [Green Version]
  10. Gu, C.J.; Mu, X.M.; Gao, P.; Zhao, G.J.; Sun, W.Y. Changes in run-off and sediment load in the three parts of the Yellow River basin, in response to climate change and human activities. Hydrol. Process. 2019, 33, 585–601. [Google Scholar] [CrossRef]
  11. Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
  12. Walling, D.E.; Fang, D. Recent trends in the suspended sediment loads of the world’s rivers. Glob. Planet Chang. 2003, 39, 111–126. [Google Scholar] [CrossRef]
  13. Restrepo Juan, D.; Escobar Heber, A. Sediment load trends in the Magdalena River basin (1980–2010): Anthropogenic and climate-induced causes. Geomorphology 2018, 302, 76–91. [Google Scholar] [CrossRef]
  14. Peng, J.; Chen, S.L.; Ping, D. Temporal variation of sediment load in the Yellow River basin, China, and its impacts on the lower reaches and the river delta. Catena 2010, 83, 135–147. [Google Scholar] [CrossRef]
  15. Wei, Y.H.; Jiao, J.Y.; Zhao, G.J.; Zhao, H.K.; He, Z.; Mu, X.M. Spatial–temporal variation and periodic change in streamflow and suspended sediment discharge along the mainstream of the Yellow River during 1950–2013. Catena 2016, 140, 105–115. [Google Scholar] [CrossRef] [Green Version]
  16. Zhang, J.J.; Zhang, X.P.; Rui, L.; Chen, L.L.; Lin, P.F. Did streamflow or suspended sediment concentration changes reduce sediment load in the middle reaches of the Yellow River? J. Hydrol. 2017, 546, 357–369. [Google Scholar] [CrossRef]
  17. Xu, J.X.; Li, F.X. Response of lower Yellow River bank breachings to La Niña events since 924 CE. Catena 2019, 176, 159–169. [Google Scholar] [CrossRef]
  18. Xu, J.X. Response of land accretion of the Yellow River delta to global climate change and human activity. Quatern. Int. 2008, 186, 0–11. [Google Scholar] [CrossRef]
  19. Li, B.Q.; Liang, Z.M.; Bao, Z.X.; Wang, J.; Hu, Y.M. Changes in streamflow and sediment for a planned large reservoir in the middle Yellow River. Land Degrad. Dev. 2019, 30, 878–893. [Google Scholar] [CrossRef] [Green Version]
  20. Chen, K.; Su, J.L.; Wang, Y.G.; Chen, Y. Study on water-sediment relationship in the Yellow River. J. Sediment. Res. 2019, 44, 19–26. [Google Scholar]
  21. Gao, G.Y.; Fu, B.J.; Zhang, J.J.; Ma, Y.; Sivapalan, M. Multiscale temporal variability of flow-sediment relationships during the 1950s–2014 in the Loess Plateau, China. J. Hydrol. 2018, 563, 609–619. [Google Scholar] [CrossRef]
  22. Wang, S.; Fu, B.J.; Liang, W.; Liu, Y.; Wang, Y.F. Driving forces of changes in the water and sediment relationship in the Yellow River. Sci. Total. Environ. 2017, 576, 453–461. [Google Scholar] [CrossRef] [PubMed]
  23. Han, J.Q.; Gao, J.N.; Han, L. Changes and implications of the relationship between rainfall, runoff and sediment load in the Wuding River basin on the Chinese Loess Plateau. Catena 2019, 175, 228–235. [Google Scholar] [CrossRef]
  24. Walling, D.E. The sediment delivery problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
  25. Yan, Y.X.; Xu, J.X. A study of scale effect on specific sediment yield in the Loess Plateau, China. Sci. China 2007, 50, 102–112. [Google Scholar] [CrossRef]
  26. Zhao, G.J.; Mu, X.M.; Strehmel, A.; Tian, P. Temporal variation of streamflow, sediment load and their relationship in the Yellow River basin, China. PLoS ONE 2014, 9, e91048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Yang, J.S.; Liang, S.J.; Wang, J. Analysis of discontinuous flow of the Fenhe River. Yellow River 1998, 20, 3–6. [Google Scholar]
  28. Zuo, H.F. Response of runoff in mid and upper reaches of Fenhe River to climate changes during the last 50 years. J. China Hydrol. 2006, 26, 72–75. [Google Scholar]
  29. Department of Water Resources of Shanxi Province. Fenhe River Records; Shanxi People’s Publishing House: Taiyuan, China, 2006.
  30. Yao, W.X. Analysis on the sand production in the upstream basin of Fenhe reservoir. Shanxi Archit. 2007, 32, 361–362. [Google Scholar]
  31. Ma, Z.Q. Vegetation in Shanxi Province; Science and Technology Press: Beijing, China, 2001. [Google Scholar]
  32. Cui, W.; Wang, S.Y.; Zhang, H.; Ma, Y.J. Analysis on land-used cover change in the upper reaches of Fenhe River, China during 1976–1990. J. Shanxi Univer. Natur. Sci. Edit. 2008, 31, 141–146. [Google Scholar]
  33. Ma, Y.J.; Hou, Z.H.; Xu, X.L. The impact of land use change on ecology-economy harmony degree in the upper reaches of Fenhe River watershed. J. Desert Res. 2012, 32, 1803–1808. [Google Scholar]
  34. Qin, J.P. Effect of Soil and Water Conservation on Siltation in Upper Fenhe Reservoir Reaches. Soil Water Conserv. Sci. Tec. Shanxi 2016, 34–36. [Google Scholar]
  35. Li, Z.; Liu, Y.Z.; Yan, X.; Ren, G.P.; Wang, Y.Q. Summarization and application of high-tech in to Wanjiazhai Projects. Eng. Mech. 2007, 24 (Suppl. II), 21–32. [Google Scholar]
  36. NASA Modis Moderate Resolution Imaging Spectroradiometer. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod13.php (accessed on 20 June 2020).
  37. Holben, B. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
  38. Bureau of Statistics in Shanxi Province. Shanxi Province Statistical Yearbook; China Statistics Press: Beijing, China, 1996–2015.
  39. Fan, X.H.; Wang, Q.X.; Wang, M.B. Changes in temperature and precipitation extremes during 1959–2008 in Shanxi, China. Appl. Clim. 2012, 109, 283–303. [Google Scholar] [CrossRef]
  40. Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
  41. Mann, H.B. Nonparametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
  42. Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. Public Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
  43. Moraes, J.M.; Pellegrino, G.Q.; Bsllrdyrt, M.V.; Martinelli, L.A.; Victoria, R.L.; Krusche, A.V. Trends in Hydrological Parameters of a Southern Brazilian Watershed and its Relation to Human Induced Changes. Water Resour. Manag. 1998, 12, 295–311. [Google Scholar] [CrossRef]
  44. Zhang, D.; Liu, X.M.; Liu, C.M.; Peng, B. Responses of runoff to climatic variation and human activities in the Fenhe River, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1293–1301. [Google Scholar] [CrossRef]
  45. Xu, J.X. Trend of sediment yield in the coarser sediment producing area in the middle Yellow River basin in the period 1997–2007 and the formative cause. J. Soil Water Conserv. 2010, 24, 1–7. [Google Scholar]
  46. Niu, Q.S.; Niu, Y.J. Effect of construction of check dams and reservoirs in Lanhe River Basin, Lanxian County. Sci. Tec. Soil Water Conserv. Shanxi Pro. 1995, 1, 19–22. [Google Scholar]
  47. Li, J. Analysis on the Inflow and Outflow of Fenhe reservoir. Sci. Tech. Inf. Dev. Econ. 2010, 20, 165–167. [Google Scholar]
  48. History of Taiyuan. Available online: http://www.taiyuan.gov.cn/doc/2017/02/15/691195.shtml (accessed on 20 June 2020).
  49. Rong, L.; Li, S.R. Thinking about solving the shortage of water resources in Taiyuan. Mod. Urban Res. 1995, 2, 38–42. [Google Scholar]
  50. Ping, J.H.; Yan, S.Y.; Gu, P.; Wu, Z.N.; Hu, C.H. Application of MIKE SHE to study the impact of coal mining on river runoff in Gujiao mining area, Shanxi, China. PLoS ONE 2017, 12, e0188949. [Google Scholar] [CrossRef] [Green Version]
  51. Cravotta, C.A., III; Goode, D.J.; Bartles, M.D.; Risser, D.W.; Galeone, D.G. Surface water and groundwater interactions in an extensively mined watershed, upper Schuylkill River, Pennsylvania, USA. Hydrol. Process. 2014, 28, 3574–3601. [Google Scholar] [CrossRef]
  52. Li, Y.M. A Brief Record of Water Consevancy Important Events in Shanxi Province (1949–2002); Shanxi Science and Technology Press: Taiyuan, China, 2005. [Google Scholar]
  53. Syvitski, J.P.M.; Kettner, A. Sediment flux and the Anthropocene. Philos Trans. R. Soc. A 2011, 369, 957–975. [Google Scholar] [CrossRef]
  54. Ren, J.M.; Liu, Y.C.; Liang, A.Z. Influence of water resources on urban development of Taiyuan city and Countermeasures. Prod. Res. 2004, 2, 119–121. [Google Scholar]
  55. Wu, S.L. Analysis on the development of the depression cone of deep groundwater level in Taiyuan City in recent 25 years. Shanxi Hydrotech. 2018, 1, 68–70. [Google Scholar]
  56. Yuan, R.Q.; Zhang, W.X.; Wang, P.; Wang, S.Q. Impacts of water transfer from the Yellow River on water environment in the receiving area of the Fenhe River. J. Nat. Resour. 2018, 33, 1416–1426. [Google Scholar]
Water 12 01757 g001 550
Figure 1. Location of the Upper Fenhe River Basin and details: No. 1 FR: No. 1 Fenhe Reservoir; No. 2 FR: No. 2 Fenhe Reservoir; LR: Lancheng Reservoir; HR: Hamashen Reservoir.
Figure 1. Location of the Upper Fenhe River Basin and details: No. 1 FR: No. 1 Fenhe Reservoir; No. 2 FR: No. 2 Fenhe Reservoir; LR: Lancheng Reservoir; HR: Hamashen Reservoir.
Water 12 01757 g001
Water 12 01757 g002 550
Figure 2. Temporal variation in Qa and Sa values for four hydrological stations from 1955 to 2015. JL: Jingle, ZS: Zhaishang, LC: Lancun, SJY: Shangjingyou.
Figure 2. Temporal variation in Qa and Sa values for four hydrological stations from 1955 to 2015. JL: Jingle, ZS: Zhaishang, LC: Lancun, SJY: Shangjingyou.
Water 12 01757 g002
Water 12 01757 g003 550
Figure 3. Mann–Kendall tests of the Qa and Sa values for four hydrological stations from 1955 to 2015. The horizontal dashed lines represent the critical values corresponding to the 99% significance level. Solid blue arrow denotes inflection point years during the study period using Mann–Kendall tests.
Figure 3. Mann–Kendall tests of the Qa and Sa values for four hydrological stations from 1955 to 2015. The horizontal dashed lines represent the critical values corresponding to the 99% significance level. Solid blue arrow denotes inflection point years during the study period using Mann–Kendall tests.
Water 12 01757 g003
Water 12 01757 g004 550
Figure 4. Double-mass curves of Qa−Pma and Sa−Pma for four hydrological stations from 1955 to 2015. Dotted red arrows denote inflection point years during the study period using double mass curves.
Figure 4. Double-mass curves of Qa−Pma and Sa−Pma for four hydrological stations from 1955 to 2015. Dotted red arrows denote inflection point years during the study period using double mass curves.
Water 12 01757 g004
Water 12 01757 g005 550
Figure 5. Scatterplot distributions and regression equations for the Qa–Sa relationships for the four stations. ** Significant at p < 0.01.
Figure 5. Scatterplot distributions and regression equations for the Qa–Sa relationships for the four stations. ** Significant at p < 0.01.
Water 12 01757 g005
Water 12 01757 g006 550
Figure 6. Temporal variation in (a) PmaJL, PmaSJY, PmaZS, and PmaLC from 1955 to 2015; (b) TTY from 1955 to 2015.
Figure 6. Temporal variation in (a) PmaJL, PmaSJY, PmaZS, and PmaLC from 1955 to 2015; (b) TTY from 1955 to 2015.
Water 12 01757 g006
Water 12 01757 g007 550
Figure 7. Temporal variation in (a) cumulative QaFR from 1962 to 2015 and DaFR from 1960 to 2015; (b) NDVI8km from 1982 to 2015 and NDVI250m from 2000 to 2015.
Figure 7. Temporal variation in (a) cumulative QaFR from 1962 to 2015 and DaFR from 1960 to 2015; (b) NDVI8km from 1982 to 2015 and NDVI250m from 2000 to 2015.
Water 12 01757 g007
Water 12 01757 g008 550
Figure 8. Temporal variation in the annual floor space data for buildings under construction in Taiyuan city (FSBCTY) values from 1996 to 2015.
Figure 8. Temporal variation in the annual floor space data for buildings under construction in Taiyuan city (FSBCTY) values from 1996 to 2015.
Water 12 01757 g008
Table
Table 1. Variations of the average annual precipitation at four catchments and the annual average air temperature at Taiyuan meteorological station for the different periods.
Table 1. Variations of the average annual precipitation at four catchments and the annual average air temperature at Taiyuan meteorological station for the different periods.
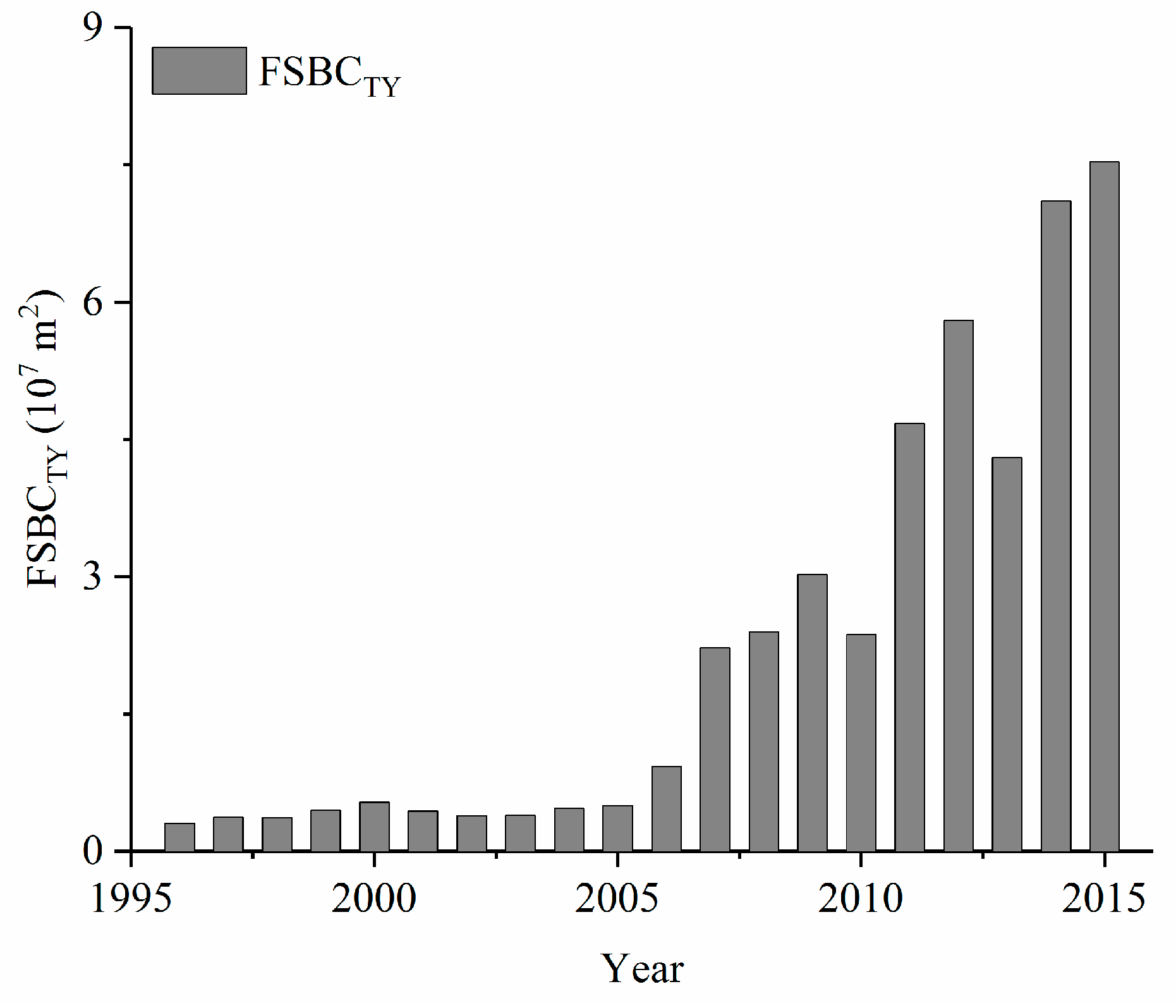
PeriodsPmaJLPmaSJYPmaZSPmaLCTTY
Mean (mm)CV (%)Mean (mm)CV (%)Mean (mm)CV (%)Mean (mm)CV (%)Mean (mm)CV (%)
1955–195954127.8043628.8749228.5949428.019.46.03
1960–196952930.2548427.6150927.7951027.439.55.31
1970–197946822.5744327.6044922.8745323.129.64.30
1980–198943217.6042430.5143721.9243722.279.73.95
1990–199950026.7340813.7745020.9344921.6610.47.11
2000–200951519.6046924.1648819.5848719.7811.03.72
2010–201556511.1053314.5353312.6753012.4311.02.51
Mean: arithmetic mean value of Pma during each period. CV: coefficient of variation of Pma during each period.
Table
Table 2. Qa and Sa trends revealed by the Mann–Kendall tests.
Table 2. Qa and Sa trends revealed by the Mann–Kendall tests.
StationsControlling Area (km2)Qa (1955–2015)Sa (1955–2015)
ZβZβ
(mm∙km−2∙a−1)(t∙km−2∙a−1)
JL27990.86 ns0.41−4.89 ***−34.66
SJY1140−5.05 ***−0.68−3.17 **−54.39
ZS6819−3.34 ***−0.73−2.62 **−9.24
LC7705−5.56 ***−1.07−3.72 ***−14.8
Z: Z value from the Mann–Kendall tests; β: Sen’s slope represents the average change rate; ns: no significant change; ** significant at p < 0.01; *** significant at p < 0.001.
Table
Table 3. Changes in average Qa and Sa values during different periods.
Table 3. Changes in average Qa and Sa values during different periods.
Variable1955–1982 (Period I)1983–1996 (Period II)1997–2015 (Period III)
Mean (108 m3)Mean (108 m3)Change Rate (%)Mean (108 m3)Change Rate (%)
QaJL 2.682.10−21.772.49−7.25
QaSJY0.690.38−44.530.26−62.29
Variable1955–1982 (Period I)1983–1996 (Period II)1997–2015 (Period III)
Mean (105 t)Mean (105 t)Change Rate (%)Mean (105 t)Change Rate (%)
SaJL74.3740.88−45.038.87−88.08
SaSJY51.7314.59−71.790.85−98.36
Variable1955–1980 (Period I)1981–1996 (Period II)1997–2015 (Period III)
Mean (108 m3)Mean (108 m3)Change Rate (%)Mean (108 m3)Change Rate (%)
QaZS4.593.01−34.552.13−53.65
QaLC5.392.73−49.461.60−70.35
Variable1955–1980 (Period I)1981–1996 (Period II)1997–2015 (Period III)
Mean (105 t)Mean (105 t)Change Rate (%)Mean (105 t)Change Rate (%)
SaZS94.2022.02−76.622.69−97.14
SaLC101.6626.45−73.990.98−99.04
Mean: arithmetic mean value of Qa or Sa during each period. Change rate: change rate of the mean value of Qa or Sa in periods II or III compared with that in period I.
Table
Table 4. Trends in influential variables revealed by the Mann–Kendall tests.
Table 4. Trends in influential variables revealed by the Mann–Kendall tests.
Stations Pma (1955–2015)NDVI8km (1982–2015)NDVI250m (2000–2015)
Zβ (mm∙(10a)−1)Zβ ((10a)−1)Zβ ((10a)−1)
JL0.13 ns0.902.96 **0.0334.36 ***0.097
SJY0.33 ns3.133.33 ***0.0363.56 ***0.101
ZS−0.15 ns−1.132.84 **0.0344.01 ***0.108
LC−0.27 ns−1.652.12 *0.0264.16 ***0.104
Z: Z value from the Mann–Kendall tests; β: Sen’s slope represents the average change rate; ns: no significant change; * significant at p < 0.05; ** significant at p < 0.01; *** significant at p < 0.001.
Table
Table 5. Pearson’s correlations between Qa, Sa, and potential influential variables.
Table 5. Pearson’s correlations between Qa, Sa, and potential influential variables.
CorrelationJLSJYZSLC
Period IPeriod IIPeriod IIIPeriod IPeriod IIPeriod IIIPeriod IPeriod IIPeriod IIIPeriod IPeriod IIPeriod III
1955–19821983–19961997–20151955–19821983–19961997–20151955–19801981–19961997–20151955–19801981–19961997–2015
rnrnrnrnrnrnrnrnrnrnrnrn
Qa−Pma★28★14◆19★28★14ns19ns26ns16ns19ns26ns16ns19
Qa−QaFR★21★14★19★21◆14★19★21★16★19★21★16★19
Qa−DaFR★20★14ns19★20★14ns19★20ns16ns19◆20ns16ns19
Qa−NDVI8km----◆14★19----ns14★19----◆15◆19----ns15ns19
Qa−NDVI250m--------★16--------★16--------★16--------★16
Qa–Sa★28★14◇19★28★14ns19◆26◆16ns19★26★16ns19
Sa−Pma★28★14ns19★28★14ns19ns26★16ns19◆26★16ns19
Sa−QaFR★21◆14◇19★21ns14ns19★21★16ns19◆21★16ns19
Sa−DaFR★20★14◆19★20★14ns19★20★16ns19★20★16ns19
Sa−NDVI8km----ns14◇19----ns14ns19----ns15◇19----ns15ns19
Sa−NDVI250m--------ns16--------ns16--------ns16--------◇16
r: Pearson’s correlation coefficients; n: number of variables; ★: distinctly significant positive correlation (p < 0.01); ◆: significant positive correlation (p < 0.05); ◇: significant negative correlation (p < 0.05); ns: no significant correlation; --: data is unavailable.

Share and Cite

MDPI and ACS Style

Zhang, L.; Li, S.; Wu, Z.; Fan, X.; Li, H.; Meng, Q.; Wang, J. Variation in Runoff, Suspended Sediment Load, and Their Inter-Relationships in Response to Climate Change and Anthropogenic Activities Over the Last 60 Years: A Case Study of the Upper Fenhe River Basin, China. Water 2020, 12, 1757. https://doi.org/10.3390/w12061757

AMA Style

Zhang L, Li S, Wu Z, Fan X, Li H, Meng Q, Wang J. Variation in Runoff, Suspended Sediment Load, and Their Inter-Relationships in Response to Climate Change and Anthropogenic Activities Over the Last 60 Years: A Case Study of the Upper Fenhe River Basin, China. Water. 2020; 12(6):1757. https://doi.org/10.3390/w12061757

Chicago/Turabian Style

Zhang, Luan, Suqing Li, Zhitao Wu, Xiaohui Fan, Hongjian Li, Qi Meng, and Jing Wang. 2020. "Variation in Runoff, Suspended Sediment Load, and Their Inter-Relationships in Response to Climate Change and Anthropogenic Activities Over the Last 60 Years: A Case Study of the Upper Fenhe River Basin, China" Water 12, no. 6: 1757. https://doi.org/10.3390/w12061757

APA Style

Zhang, L., Li, S., Wu, Z., Fan, X., Li, H., Meng, Q., & Wang, J. (2020). Variation in Runoff, Suspended Sediment Load, and Their Inter-Relationships in Response to Climate Change and Anthropogenic Activities Over the Last 60 Years: A Case Study of the Upper Fenhe River Basin, China. Water, 12(6), 1757. https://doi.org/10.3390/w12061757

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop