Experimental Investigation on Pouring Aggregate to Plug Horizontal Tunnel with Flow Water
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
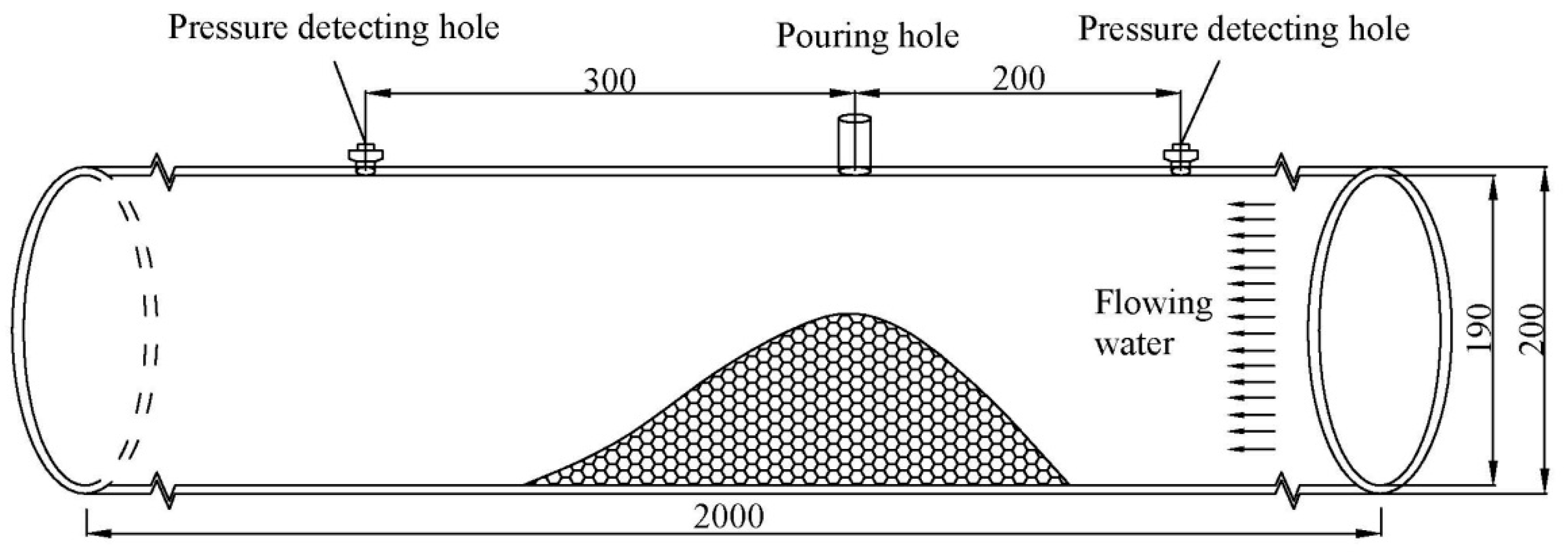
2.2. Experimental Set-Up
2.3. Experimental Design
3. Results
3.1. Shape of Deposited Aggregate
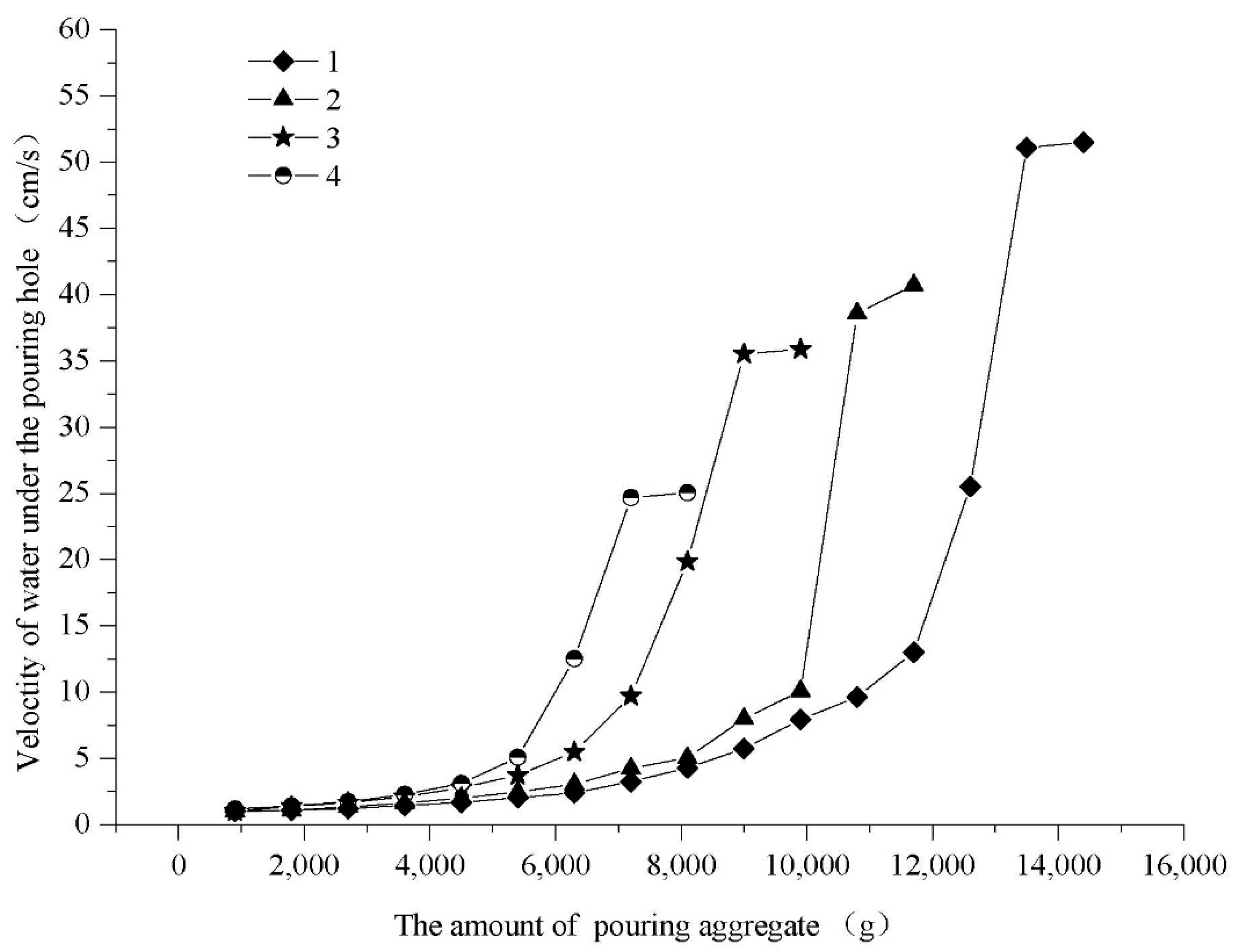
3.2. Formation Process of Deposition with Cone Shape
3.3. Factors that Influence Efficiency of Plugging
3.3.1. Efficiency of Plugging
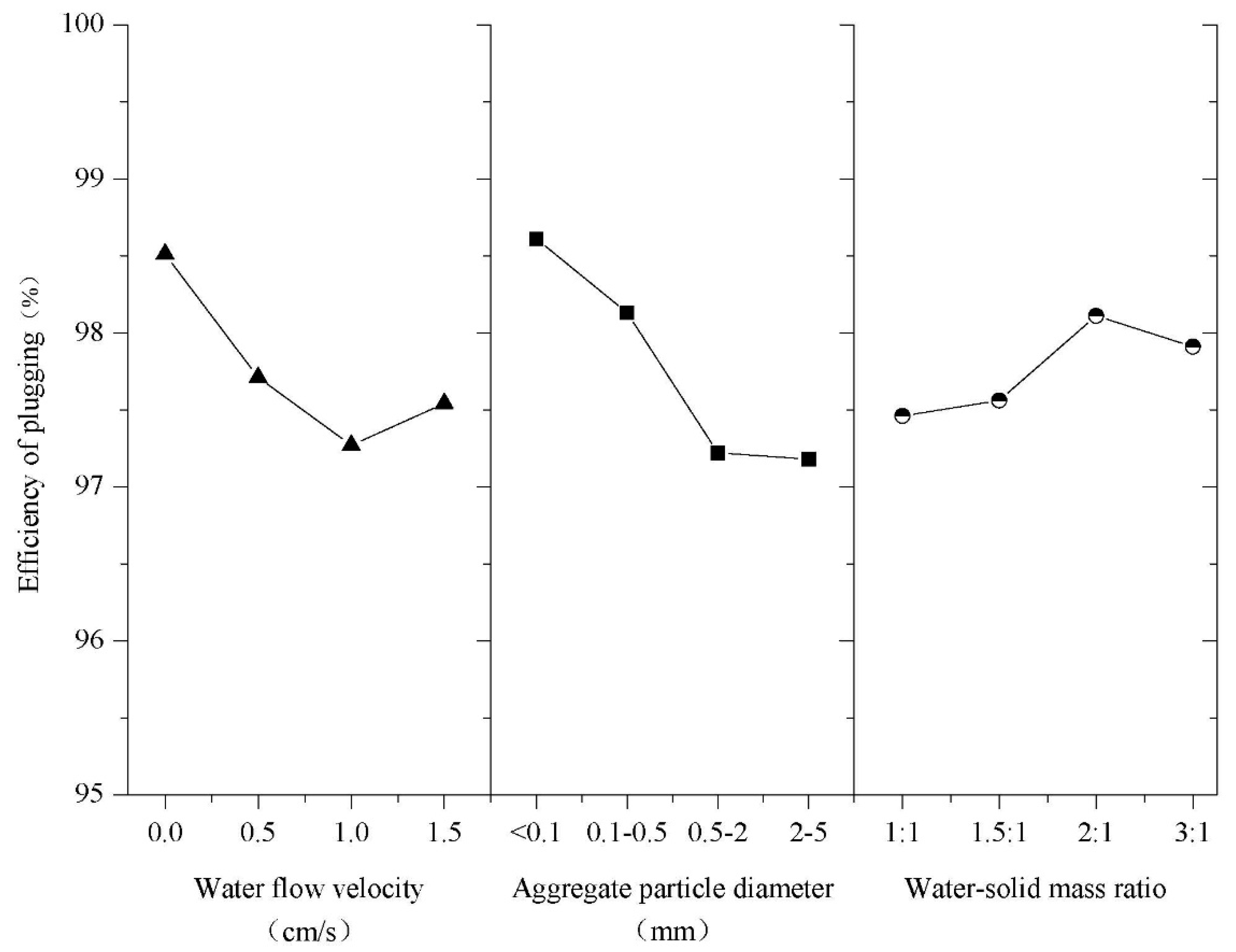
3.3.2. Main Effects
3.3.3. Aggregate Particle Size and Initial Velocity of Water Flow
3.3.4. Water–Solid Mass Ratio
4. Discussion
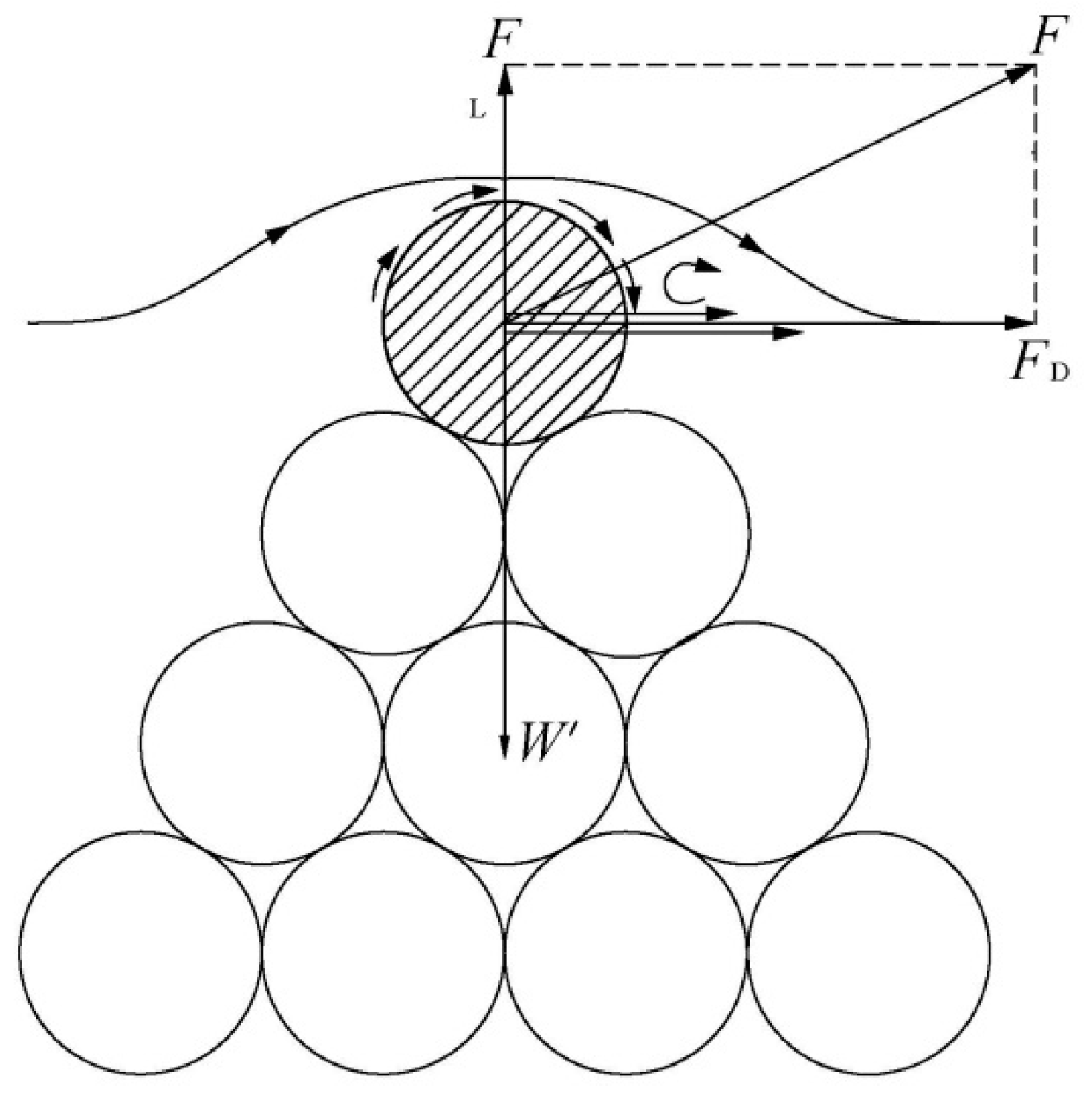
4.1. Criterion for Resistance to Flow
4.2. Optimal Spacing between Boreholes
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Durand, R. The Hydraulic Transportation of Coal and Other Materials in Pipes; Colloquium of National Coal Board: London, UK, 1952. [Google Scholar]
- Wasp, E.J.; Kenny, J.P.; Gandhi, R.L. Solid-Liquid Flow: Slurry Pipeline Transportation; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1977. [Google Scholar]
- Fei, X.J. Hydraulics of Slurry and Granular Material Transport; Tsinghua University Press: Beijing, China, 1994. [Google Scholar]
- Miedema, S.A. A head loss model for slurry transport in the heterogeneous regime. Ocean Eng. 2015, 106, 360–370. [Google Scholar] [CrossRef]
- Soepyan, F.B.; Cremaschi, S.; Sarica, C.; Subramani, H.J.; Kouba, G.E. Solids transport models comparison and fine-tuning for horizontal, low concentration flow in single-phase carrier fluid. AIChE J. 2013, 60, 76–122. [Google Scholar] [CrossRef]
- Zouaoui, S.; Djebouri, H.; Mohammedi, K.; Khelladi, S.; Aider, A.A. Experimental study on the effects of big particles physical characteristics on the hydraulic transport inside a horizontal pipe. Chin. J. Chem. Eng. 2016, 24, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Graf, W.H.; Robinson, M.; Yucel, O. The Critical Deposit Velocity for Solid-Liquid Mixtures. In Proceedings of 1st International Conference on the Hydraulic Transport of Solids in Pipes; BHRA Fluid Engineering: Cranfield, UK, 1970. [Google Scholar]
- Wasp, E.J.; Slatter, P.T. Deposition Velocities for Small Particles in Large Pipes. In Proceedings of the 12th International Conference on Transport & Sedimentation of Solid Particles, Prague, Czech Republic, 20–24 September 2004; pp. 20–24. [Google Scholar]
- Thomas, A. Predicting the deposit velocity for horizontal turbulent pipe flow of slurries. Int. J. Multiph. Flow 1979, 5, 113–129. [Google Scholar] [CrossRef]
- Pinto, T.S.; Júnior, D.D.M.; Slatter, P.; Filho, L.L. Modelling the critical velocity for heterogeneous flow of mineral slurries. Int. J. Multiph. Flow 2014, 65, 31–37. [Google Scholar] [CrossRef]
- Bratland, O. Pipe Flow 2: Multi-Phase Flow Assurance; Springer: New York, NY, USA, 2010; pp. 235–243. [Google Scholar]
- Kim, C.; Lee, M.; Han, C. Hydraulic transport of sand-water mixtures in pipelines Part I. Experiment. J. Mech. Sci. Technol. 2008, 22, 2534–2541. [Google Scholar] [CrossRef]
- Corredor, F.E.R.; Bizhani, M.; Kuru, E. Experimental investigation of cuttings bed erosion in horizontal wells using water and drag reducing fluids. J. Pet. Sci. Eng. 2016, 147, 129–142. [Google Scholar] [CrossRef]
- Ni, J.R.; Wang, G.Q.; Zhang, H.W. Basic Theory of Two-Phase Flow and Its Latest Application; Beijing Science Press: Beijing, China, 1989. [Google Scholar]
- Vlasák, P.; Kysela, B.; Chara, Z. Flow Structure of Coarse-Grained Slurry in A Horizontal Pipe. J. Hydrol. Hydromech. 2012, 60, 115–124. [Google Scholar] [CrossRef]
- Newitt, D.M.; Richardson, J.F.; Abbott, M.; Turtle, R.B. Hydraulic conveying of solids in horizontal pipes. Trans. Inst. Chem. Eng. 1955, 33, 93–110. [Google Scholar]
- Turian, R.M.; Yuan, T.-F. Flow of slurries in pipelines. AIChE J. 1977, 23, 232–243. [Google Scholar] [CrossRef]
- Turian, R.M.; Yuan, T.-F.; Mauri, G. Pressure drop correlation for pipeline flow of solid-liquid suspensions. AIChE J. 1971, 17, 809–817. [Google Scholar] [CrossRef]
- Miedema, S.A. The heterogeneous to homogeneous transition for slurry flow in pipes. Ocean Eng. 2016, 123, 422–431. [Google Scholar] [CrossRef] [Green Version]
- Allahvirdizadeh, P.; Kuru, E.; Parlaktuna, M. Experimental investigation of solids transport in horizontal concentric annuli using water and drag reducing polymer-based fluids. J. Nat. Gas Sci. Eng. 2016, 35, 1070–1078. [Google Scholar] [CrossRef]
- Duckworth, R.A.; Argyros, G. Influence of density ratio on the pressure gradient in pipes conveying suspensions of solids in liquids. In Proceedings of Hydrotransport 2: The 2nd International Conference on the Hydraulic Transport of Solids in Pipes; BHRA Fluid Engineering: New York, NY, USA, 1972. [Google Scholar]
- Kaushal, D.; Thinglas, T.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. CFD modeling for pipeline flow of fine particles at high concentration. Int. J. Multiph. Flow 2012, 43, 85–100. [Google Scholar] [CrossRef]
- Capecelatro, J.; Desjardins, O. Eulerian–Lagrangian modeling of turbulent liquid–solid slurries in horizontal pipes. Int. J. Multiph. Flow 2013, 55, 64–79. [Google Scholar] [CrossRef]
- Arolla, S.K.; Desjardins, O. Transport modeling of sedimenting particles in a turbulent pipe flow using Euler–Lagrange large eddy simulation. Int. J. Multiph. Flow 2015, 75, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Uzi, A.; Levy, A. Flow characteristics of coarse particles in horizontal hydraulic conveying. Powder Technol. 2018, 326, 302–321. [Google Scholar] [CrossRef]
- Ekambara, K.; Sanders, R.S.; Nandakumar, K.; Masliyah, J.H. Hydrodynamic Simulation of Horizontal Slurry Pipeline Flow Using ANSYS-CFX. Ind. Eng. Chem. Res. 2009, 48, 8159–8171. [Google Scholar] [CrossRef]
- Messa, G.V.; Malin, M.R.; Malavasi, S. Numerical prediction of fully-suspended slurry flow in horizontal pipes. Powder Technol. 2014, 256, 61–70. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. Improvements in the numerical prediction of fully-suspended slurry flow in horizontal pipes. Powder Technol. 2015, 270, 358–367. [Google Scholar] [CrossRef]
- Messa, G.V.; Matoušek, V. Analysis and discussion of two fluid modelling of pipe flow of fully suspended slurry. Powder Technol. 2020, 360, 747–768. [Google Scholar] [CrossRef]
- Sahai, Y.; Emi, T. Criteria for Water Modeling of Melt Flow and Inclusion Removal in Continuous Casting Tundishes. ISIJ Int. 1996, 36, 1166–1173. [Google Scholar] [CrossRef]
- Chanson, H. Turbulent air–water flows in hydraulic structures: Dynamic similarity and scale effects. Environ. Fluid Mech. 2008, 9, 125–142. [Google Scholar] [CrossRef] [Green Version]
- Mao, N. On the threshold velocity of silt-sand and gravel-stone. J. Yangtze River Sci. Res. Inst. 2011, 1, 6–11. [Google Scholar]
- Li, C.H. Interception-plugging technology for super giant water inrush laneway in mine. J. Xi’an Univ. Sci. Technol. 2010, 3, 305–308. [Google Scholar]
- Meng, Z.; Yang, W.J. Preliminary exploration of difference between submarine angle of repose and internal friction angle of sediment particles. J. Sediment Res. 2012, 4, 76–80. [Google Scholar]
- Wilson, K.C. Deposition-Limit Nomograms for Particles of Various Densities in Pipeline Flow. In Proceedings of the Hydrotransport 6; BHRA Fluid Engineering: Cranfield, UK, 1979; pp. 1–12. [Google Scholar]





| Coal Mine | Time | Groundwater Resource and Pathway | Treatment Measure and Material Consumption | Sealing Effect |
|---|---|---|---|---|
| Longmen coalmine, Henan | Groundwater inrush in 11 December 1994; Pouring aggregates from 20 June 1994 to 22 August, then grouting until 9 September. | Karst aquifer of the Cambrian limestone, through a pathway of geologic structure, with a pressure of 3 MPa and a flowrate of 2200 m3/h. | Pouring aggregates to control the speed of groundwater flow, then grouting to seal the remained flow; 3100.5 m3 of aggregates and 757 tons of cement. | 97.1% |
| Renlou coalmine, Anhui | Groundwater inrush in 4 March 1996; Pouring aggregates from 25 April to 25 May, then grouting until finishing. | Karst collapsed column of the Ordovician limestone, with a pressure of 5 MPa and a flowrate of 11,854–34,570 m3/h. | Pouring aggregates to plug the flow in tunnel first, and then sealing off the collapsed column; 129.88 m3 of aggregates, 15,032 tons of cement. | 85–90%, forming a plugging seal with a length of 60 m at a depth of 420–480 m in the column. |
| Wucun coalmine, Henan | Groundwater inrush in 15 November 1999; Pouring aggregates from 18 January 2000 to 10 March, then grouting until 11 April. | Aquifer of the Ordovician limestone intersected by faults and Karst collapsed column, with a steady flowrate of 2145 m3/h, a maximum of 2378 m3/h. | Pouring aggregates to plug the flow in tunnel first, and then sealing off the collapse column; 1535 m3 of aggregates, 3182.6 tons of cement. | 97–100%. |
| Dongpang coalmine, Hebei | Groundwater inrush in 12 April 2003; Pouring aggregates from 10 May to 11 June, then grouting until 23 September. | Karst collapsed column of the Ordovician limestone, with a pressure of 5 MPa and an average flowrate of 7000 m3/h. | Pouring aggregates to plug the flow in tunnel first, and then sealing off the collapse column; 42,837 m3 of aggregates, 26,396 tons of cement. | 98.71%, forming a plugging seal with a length of 105 m. |
| Sanshuping coalmine, Shaanxi | Groundwater inrush in 7 August 2003; Pouring aggregates from 15 October to 9 November, then grouting until 9 April 2012. | Karst aquifer of the Ordovician limestone, with a pressure of 3 MPa and an average flowrate of 8000 m3/, a maximum of 13,200 m3/h. | Pouring aggregates to plug the dynamic flow in tunnel, 25,716 m3 of aggregates, mainly fine sand, 60,383 tons of cement. | 98.71%, forming a plugging seal with a width of 23.5 m and a height of 3 m in the tunnel. |
| Panji coalmine No. 2, Anhui | Groundwater inrush in 25 May 2017; Pouring aggregates from 20 June to 27 July, then grouting until 16 August. | Karst collapsed column of the Ordovician limestone, with a flowrate of 3024 m3/h. | Pouring aggregates to plug the dynamic flow in tunnel, 21,141 m3 of aggregates, mainly fine sand, 15,349 tons of cement and fly ash. | 100%, forming a plugging seal with a length of 34 m. |
| Trial No. | Symbol for Trial | Initial Velocity of Water Flow (cm/s) A | Particle Size of Aggregate (mm) B | Water–Solid Mass Ratio C | Cross-Section Area of Residual Water Channel (mm2) | Efficiency of Plugging (%) PE |
|---|---|---|---|---|---|---|
| 1 | A1B1C1 | 0 | <0.1 | 1 | 271.05 | 99.04 |
| 2 | A1B2C2 | 0 | 0.1–0.5 | 1.5 | 332.44 | 98.83 |
| 3 | A1B3C3 | 0 | 0.5–2.0 | 2 | 491.11 | 98.27 |
| 4 | A1B4C4 | 0 | 2.0–5.0 | 3 | 592.13 | 97.91 |
| 5 | A2B1C2 | 0.5 | <0.1 | 1.5 | 553.32 | 98.05 |
| 6 | A2B2C1 | 0.5 | 0.1–0.5 | 1 | 577.92 | 97.96 |
| 7 | A2B3C4 | 0.5 | 0.5–2.0 | 3 | 770.98 | 97.28 |
| 8 | A2B4C3 | 0.5 | 2.0–5.0 | 2 | 695.35 | 97.55 |
| 9 | A3B1C3 | 1.0 | <0.1 | 2 | 379.39 | 98.66 |
| 10 | A3B2C4 | 1.0 | 0.1–0.5 | 3 | 634.79 | 97.76 |
| 11 | A3B3C1 | 1.0 | 0.5–2.0 | 1 | 1042.93 | 96.32 |
| 12 | A3B4C2 | 1.0 | 2.0–5.0 | 1.5 | 1034.04 | 96.35 |
| 13 | A4B1C4 | 1.5 | <0.1 | 3 | 371.72 | 98.69 |
| 14 | A4B2C3 | 1.5 | 0.1–0.5 | 2 | 577.35 | 97.96 |
| 15 | A4B3C2 | 1.5 | 0.5–2.0 | 1.5 | 851.84 | 97.00 |
| 16 | A4B4C1 | 1.5 | 2.0–5.0 | 1 | 991.38 | 96.50 |
| Four Levels | Average Efficiency of Plugging (%) for Factors | ||
|---|---|---|---|
| Initial Velocity of Water Flow (cm/s) A | Particle Size of Aggregate (mm) B | Water–Solid Mass Ratio C | |
| PE1 | 98.51 | 98.61 | 97.46 |
| PE2 | 97.71 | 98.13 | 97.56 |
| PE3 | 97.27 | 97.22 | 98.11 |
| PE4 | 97.54 | 97.18 | 97.91 |
| Range | 1.24 | 1.53 | 0.65 |
| Test Index | Variance Analysis Calculation | Value | |||
|---|---|---|---|---|---|
| Initial Velocity of Water Flow A | Particle Size of Aggregate B | Water–Solid Mass Ratio C | Correction Error | ||
| The cross-section area of the residual water channel (mm2) | Deviation sum of squares | 274,692.40 | 520,620.19 | 89,490.71 | 31,438.2 |
| Degree of freedom | 3 | 3 | 3 | 6 | |
| Mean square error | 91,564.13 | 173,540.06 | 29,830.24 | 5239.7 | |
| F ratio | 17.48 | 33.12 | 5.69 | -- | |
| Particle Size of Aggregate (mm) | umax (cm/s) | Calculation Results of Criterion for Plugging | Successful or not for Plugging in the Experiments | ||
|---|---|---|---|---|---|
| 2–5 | 25 | 30.0 | 89.0 | Y | Y |
| 0.5–2 | 35 | 58.8 | 35.6 | N | N |
| 0.1–0.5 | 40 | 115.2 | 8.9 | N | N |
| <0.1 | 50 | 600.0 | 1.8 | N | N |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Hui, S.; Li, W.; Sui, W. Experimental Investigation on Pouring Aggregate to Plug Horizontal Tunnel with Flow Water. Water 2020, 12, 1763. https://doi.org/10.3390/w12061763
Zhang G, Hui S, Li W, Sui W. Experimental Investigation on Pouring Aggregate to Plug Horizontal Tunnel with Flow Water. Water. 2020; 12(6):1763. https://doi.org/10.3390/w12061763
Chicago/Turabian StyleZhang, Gailing, Shuang Hui, Weixin Li, and Wanghua Sui. 2020. "Experimental Investigation on Pouring Aggregate to Plug Horizontal Tunnel with Flow Water" Water 12, no. 6: 1763. https://doi.org/10.3390/w12061763
APA StyleZhang, G., Hui, S., Li, W., & Sui, W. (2020). Experimental Investigation on Pouring Aggregate to Plug Horizontal Tunnel with Flow Water. Water, 12(6), 1763. https://doi.org/10.3390/w12061763





