Numerical Solution of the Two-Dimensional Richards Equation Using Alternate Splitting Methods for Dimensional Decomposition
Abstract
:1. Introduction
2. Richards Equation
3. Splitting Methods for Dimensional Decomposition
3.1. Godunov Method
3.2. Standard and Modified Strang Method
3.3. Alternate Splitting Method
4. Solution of 1D Equations
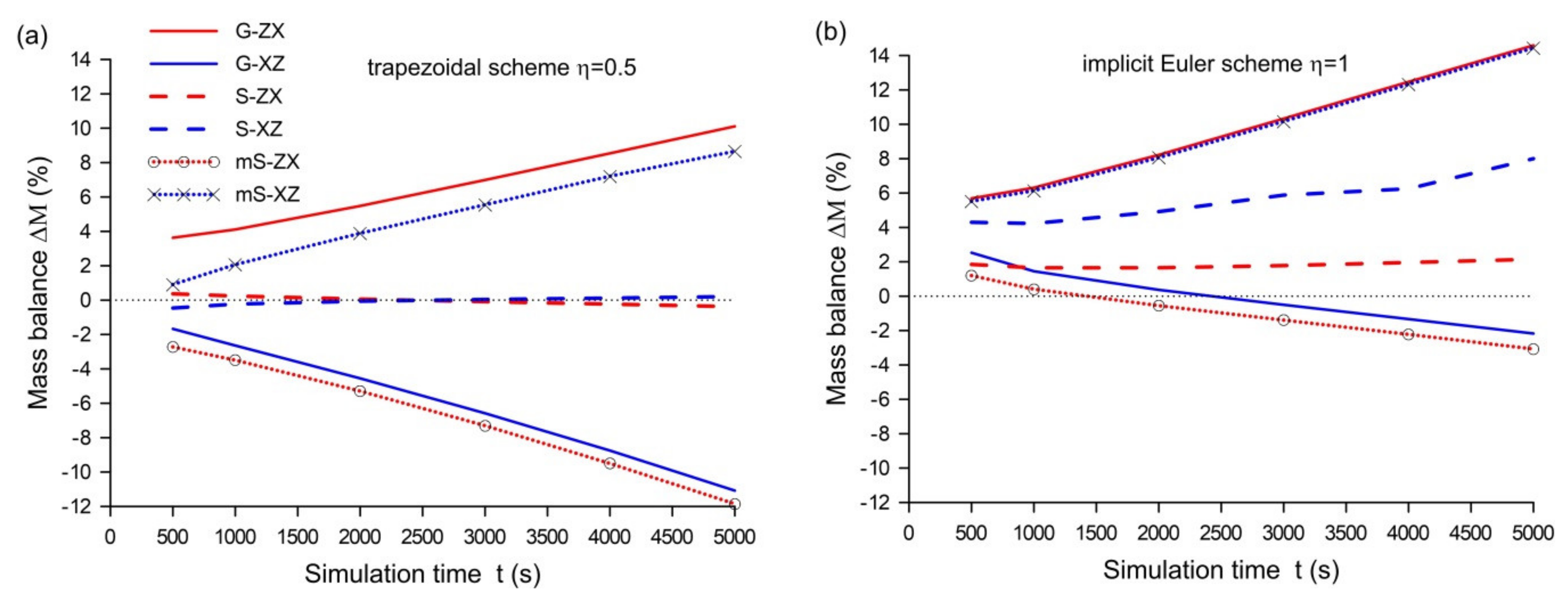
5. Numerical Tests
5.1. Test 1—Simulation of Infiltration Using the Gardner Model
5.2. Test 2—Simulation of Infiltration Using the Mualem–van Genuchten Model
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Farthing, M.W.; Ogden, F.L. Numerical solution of Richards’ equation: A review of advances and challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef] [Green Version]
- List, F.; Radu, F.A. A study on iterative methods for solving Richards’ equation. Comput. Geosci. 2016, 20, 341–353. [Google Scholar] [CrossRef] [Green Version]
- Clement, T.P.; Wise, W.R.; Molz, F.J. A physically based, two-dimensional, finite-difference algorithm for modeling variably saturated flow. J. Hydrol. 1994, 161, 71–90. [Google Scholar] [CrossRef]
- Dogan, A.; Motz, L.H. Saturated-unsaturated 3D groundwater model. I: Development. J. Hydrol. Eng. 2005, 10, 492–504. [Google Scholar] [CrossRef]
- Spanoudaki, K.; Stamou, A.I.; Nanou-Giannarou, A. Development and verification of a 3-D integrated surface water–groundwater model. J. Hydrol. 2009, 375, 410–427. [Google Scholar] [CrossRef]
- Simunek, J.; Huang, K.; Van Genuchten, M.T. The SWMS_3D code for simulating water flow and solute transport in three-dimensional variably-saturated media. US Salin. Lab. Agric. Res. Serv. 1995. [Google Scholar]
- Castanedo, V.; Saucedo, H.; Fuentes, C. Modeling two-dimensional infiltration with constant and time-variable water depth. Water 2019, 11, 371. [Google Scholar] [CrossRef] [Green Version]
- Šimunek, J.; Sejna, M.; van Genuchten, M. The HYDRUS-2D Software Package for Simulating the Two-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media, Version 2.0; International Ground Water Modeling Center, Colorado School of Mines: Golden, Co, USA, 1999. [Google Scholar]
- Manzini, G.; Ferraris, S. Mass-conservative finite volume methods on 2-D unstructured grids for the Richards’ equation. Adv. Water Resour. 2004, 27, 1199–1215. [Google Scholar] [CrossRef]
- Rees, I.; Masters, I.; Malan, A.G.; Lewis, R.W. An edge-based finite volume scheme for saturated–unsaturated groundwater flow. Comput. Methods Appl. Mech. Eng. 2004, 193, 4741–4759. [Google Scholar] [CrossRef]
- Szymkiewicz, A. Modelling Water Flow in Unsaturated Porous Media: Accounting for Nonlinear Permeability and Material Heterogeneity; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Svyatskiy, D.; Lipnikov, K. Second-order accurate finite volume schemes with the discrete maximum principle for solving Richards’ equation on unstructured meshes. Adv. Water Resour. 2017, 104, 114–126. [Google Scholar] [CrossRef] [Green Version]
- Panday, S.; Langevin, C.D.; Niswonger, R.G.; Ibaraki, M.; Hughes, J.D. MODFLOW–USG Version 1: An Unstructured Grid Version of MODFLOW for Simulating Groundwater Flow and Tightly Coupled Processes Using a Control Volume Finite-Difference Formulation; US Geological Survey: Reston, VA, USA, 2013.
- Bause, M.; Knabner, P. Computation of variably saturated subsurface flow by adaptive mixed hybrid finite element methods. Adv. Water Resour. 2004, 27, 565–581. [Google Scholar] [CrossRef]
- Belfort, B.; Ramasomanana, F.; Younes, A.; Lehmann, F. An efficient lumped mixed hybrid finite element formulation for variably saturated groundwater flow. Vadose Zone J. 2009, 8, 352–362. [Google Scholar] [CrossRef] [Green Version]
- Weill, S.; Mouche, E.; Patin, J. A generalized Richards equation for surface/subsurface flow modelling. J. Hydrol. 2009, 366, 9–20. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.; Lopez, L. A mixed MoL–TMoL for the numerical solution of the 2D Richards’ equation in layered soils. Comput. Math. Appl. 2020, 79, 1990–2001. [Google Scholar] [CrossRef]
- Suk, H.; Park, E. Numerical solution of the Kirchhoff-transformed Richards equation for simulating variably saturated flow in heterogeneous layered porous media. J. Hydrol. 2019, 579, 124213. [Google Scholar] [CrossRef]
- Berninger, H.; Kornhuber, R.; Sander, O. A multidomain discretization of the Richards equation in layered soil. Comput. Geosci. 2015, 19, 213–232. [Google Scholar] [CrossRef] [Green Version]
- Arrarás, A.; Portero, L.; Jorge, J.C. A combined mixed finite element ADI scheme for solving Richards’ equation with mixed derivatives on irregular grids. Appl. Numer. Math. 2009, 59, 454–467. [Google Scholar] [CrossRef]
- Deng, B.; Wang, J. Saturated-unsaturated groundwater modeling using 3D Richards equation with a coordinate transform of nonorthogonal grids. Appl. Math. Model. 2017, 50, 39–52. [Google Scholar] [CrossRef]
- Weeks, S.W.; Sander, G.C.; Braddock, R.D.; Matthews, C.J. Saturated and unsaturated water flow in inclined porous media. Environ. Modeling Assess. 2004, 9, 91–102. [Google Scholar] [CrossRef]
- An, H.; Ichikawa, Y.; Tachikawa, Y.; Shiiba, M. A new Iterative Alternating Direction Implicit (IADI) algorithm for multi-dimensional saturated–unsaturated flow. J. Hydrol. 2011, 408, 127–139. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin, Germnay, 1997. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002; Volume 31. [Google Scholar]
- Gąsiorowski, D. Analysis of floodplain inundation using 2D nonlinear diffusive wave equation solved with splitting technique. Acta Geophys. 2013, 61, 668–689. [Google Scholar] [CrossRef]
- Strang, G. On the construction and comparison of difference schemes. Siam J. Numer. Anal. 1968, 5, 506–517. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Tracy, F.T. Clean two-and three-dimensional analytical solutions of Richards’ equation for testing numerical solvers. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic Properties of Porous Media. Hydrol. Pap. Colo. State Univ. 1964, 24, 37. [Google Scholar]
- Strang, G.; MacNamara, S. Splitting methods in communication, imaging, science, and engineering. In Part of the Series Scientific Computation; Springer: Berlin, Germany, 2017. [Google Scholar]
- Helmig, R. Multiphase Flow and Transport Processes in the Subsurface: A Contribution to the Modeling of Hydrosystems; Springer: New York, NY, USA, 1997. [Google Scholar]
- Szymkiewicz, R. Numerical Modeling in Open Channel Hydraulics; Springer Science & Business Media: Berlin, Germany, 2010; Volume 83. [Google Scholar]
- Szymkiewicz, A. Approximation of internodal conductivities in numerical simulation of one-dimensional infiltration, drainage, and capillary rise in unsaturated soils. Water Resour. Res. 2009, 45, W10403. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Garcı, P.; Murillo, J. Verification, conservation, stability and efficiency of a finite volume method for the 1D Richards equation. J. Hydrol. 2013, 480, 69–84. [Google Scholar] [CrossRef]
- Gąsiorowski, D. Impact of diffusion coefficient averaging on solution accuracy of the 2D nonlinear diffusive wave equation for floodplain inundation. J. Hydrol. 2014, 517, 923–935. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Fletcher, C.A. Computational Techniques for Fluid Dynamics; Springer: Berlin, Germany, 1991. [Google Scholar]
- Artichowicz, W.; Gąsiorowski, D. Computationally efficient solution of a 2D diffusive wave equation used for flood inundation problems. Water 2019, 11, 2195. [Google Scholar] [CrossRef] [Green Version]
- Gąsiorowski, D.; Szymkiewicz, R. Mass and momentum conservation in the simplified flood routing models. J. Hydrol. 2007, 346, 51–58. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef] [Green Version]











| Soil | Ks (m/s) | θs (-) | θr (-) | α (m−1) | n (-) | Lx × Lz (m) | Δx = Δy (m) | Δtmin (s) | Δtmax (s) | T (h) |
|---|---|---|---|---|---|---|---|---|---|---|
| Sand | 8.25 × 10−5 | 0.43 | 0.045 | 14.5 | 2.68 | 1.0 × 1.2 | 0.02 | 10−5 | 50 | 2 |
| Loam | 2.89 × 10−6 | 0.43 | 0.078 | 3.6 | 1.56 | 1.0 × 1.0 | 0.02 | 10−2 | 200 | 35 |
| Soil | Splitting Algorithm | |||||||
|---|---|---|---|---|---|---|---|---|
| G-ZX | G-XZ | S-ZX | S-XZ | mod-ZX | mod-XZ | |||
| Sand | RMS | (m) | 1.62 | 1.62 | 1.37 | 1.45 | 1.01 | 1.01 |
| ΔM | (%) | 4.72 | −5.01 | −1.95 | 2.41 | 1.17 | 1.14 | |
| Niter | (×103) | 830.5 | 830.6 | 1087.8 | 1159.8 | 772.1 | 772.1 | |
| Ef | (×106 m−1) | 0.74 | 0.74 | 0.67 | 0.60 | 1.28 | 1.28 | |
| Loam | RMS | (m) | 7.15 | 7.15 | 7.16 | 7.16 | 7.17 | 7.17 |
| ΔM | (%) | 5.5 | −6.02 | −2.15 | 1.97 | 1.64 | 1.64 | |
| Niter | (×103) | 765.9 | 764.4 | 948.6 | 877.1 | 620.9 | 620.9 | |
| Ef | (×106 m−1) | 0.18 | 0.18 | 0.15 | 0.16 | 0.22 | 0.22 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gąsiorowski, D.; Kolerski, T. Numerical Solution of the Two-Dimensional Richards Equation Using Alternate Splitting Methods for Dimensional Decomposition. Water 2020, 12, 1780. https://doi.org/10.3390/w12061780
Gąsiorowski D, Kolerski T. Numerical Solution of the Two-Dimensional Richards Equation Using Alternate Splitting Methods for Dimensional Decomposition. Water. 2020; 12(6):1780. https://doi.org/10.3390/w12061780
Chicago/Turabian StyleGąsiorowski, Dariusz, and Tomasz Kolerski. 2020. "Numerical Solution of the Two-Dimensional Richards Equation Using Alternate Splitting Methods for Dimensional Decomposition" Water 12, no. 6: 1780. https://doi.org/10.3390/w12061780
APA StyleGąsiorowski, D., & Kolerski, T. (2020). Numerical Solution of the Two-Dimensional Richards Equation Using Alternate Splitting Methods for Dimensional Decomposition. Water, 12(6), 1780. https://doi.org/10.3390/w12061780






