An Alternative for Estimating the Design Flood Interval of Agricultural Reservoirs under Climate Change Using a Non-Parametric Resampling Technique
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Construction
2.1.1. Study Area
2.1.2. Design Criteria for Inflow Design Flood for Agricultural Reservoirs in South Korea
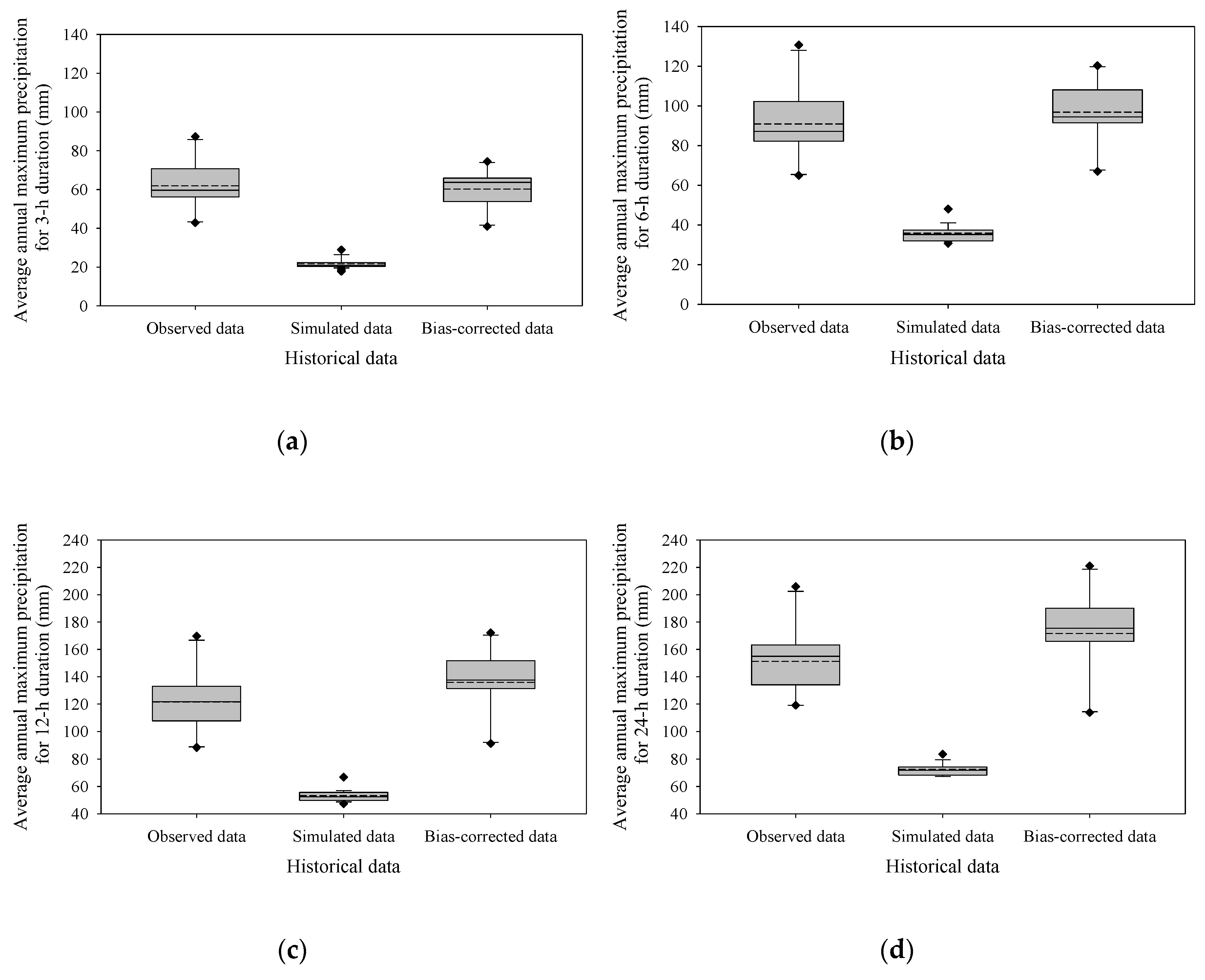
2.1.3. Climate Change Scenario and Bias-Correction
2.2. Interval Estimation of Design Flood Using a Non-Parametric Resampling Technique
2.2.1. Bootstrap Technique
2.2.2. Estimation of Probable Rainfall
2.2.3. Estimation of Inflow Design Flood
2.2.4. Interval Estimation of Inflow Design Flood Using the Bootstrap Technique
- Select B independent bootstrap samples , each consisting of n data values drawn with replacement from . The sample is the inflow design flood for a 24-h duration and a 200-y return period, the number of bootstrap samples (B) is 1000, and the sample size (n) is 30.
- Evaluate the bootstrap replication corresponding to each bootstrap sample, . is the mean of the bootstrap data set.
- Estimate the bias and standard error using Equations (1) and (2).
- Estimate the range of the inflow design flood using the BCa percentile method (Equations (3)–(7)). The confidence level is 95%.
- The first sample is the inflow design floods from 2034s (2005–2034). Repeat 1–4 until the last sample 2100s (2071–2100).
3. Results and Discussion
3.1. Bias-Corrected Climate Change Scenario
3.2. Estimation Result of Probable Rainfall
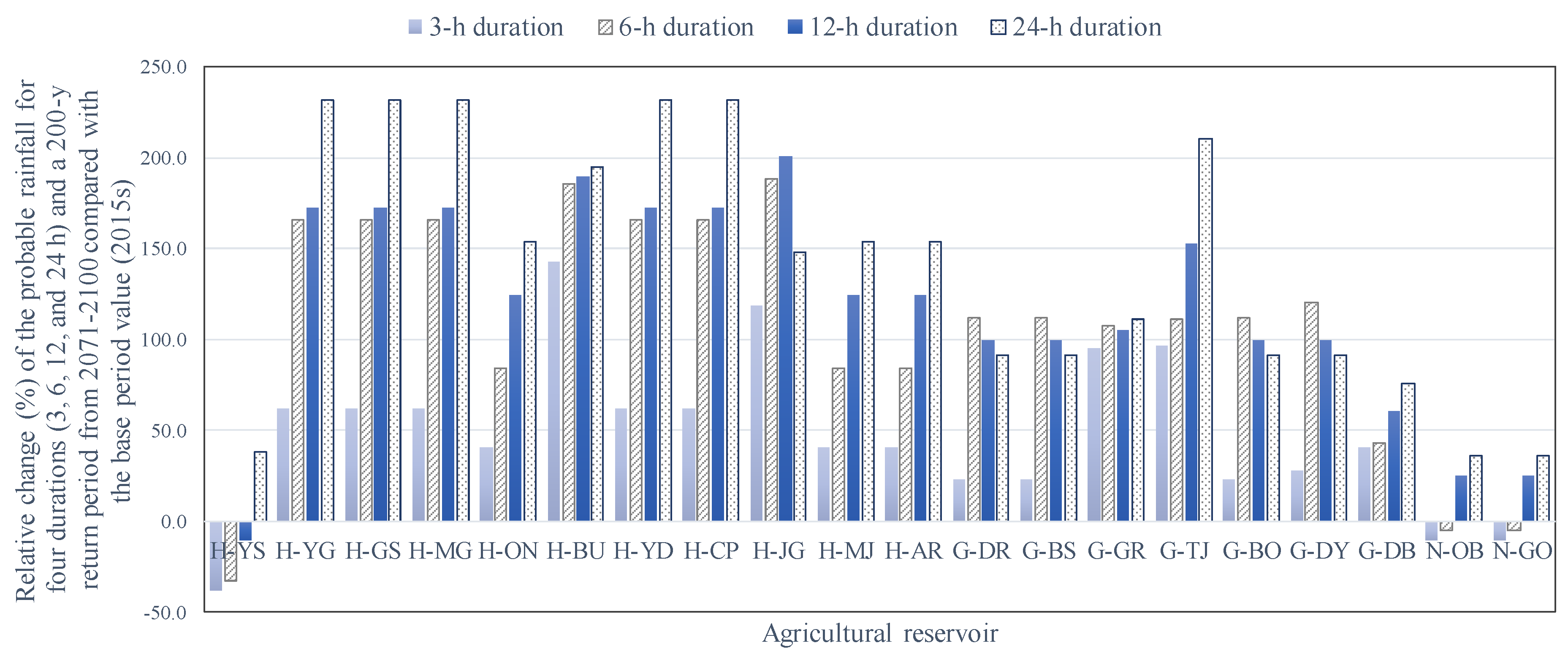
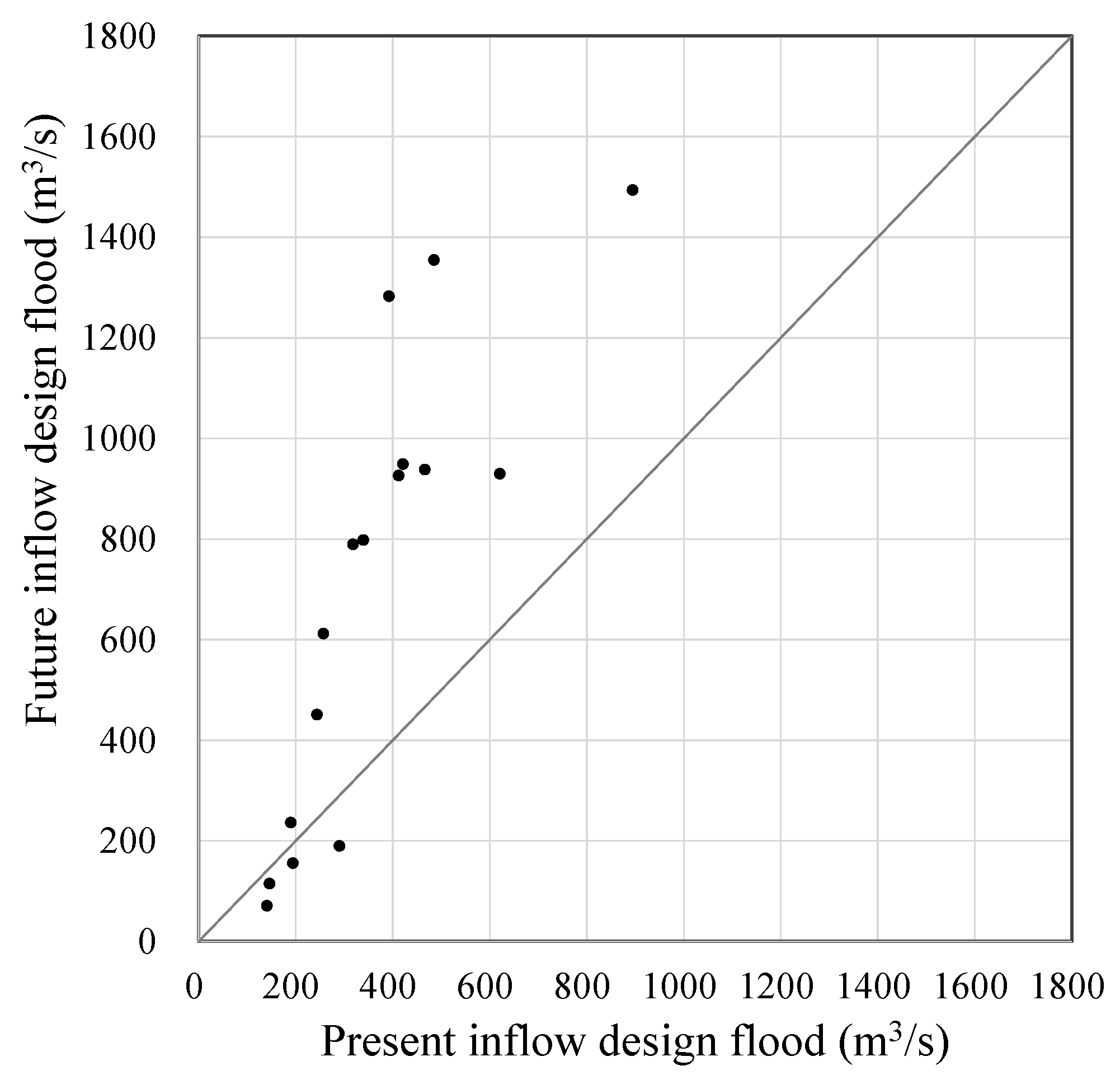
3.3. Change in Design Flood Due to Climate Change
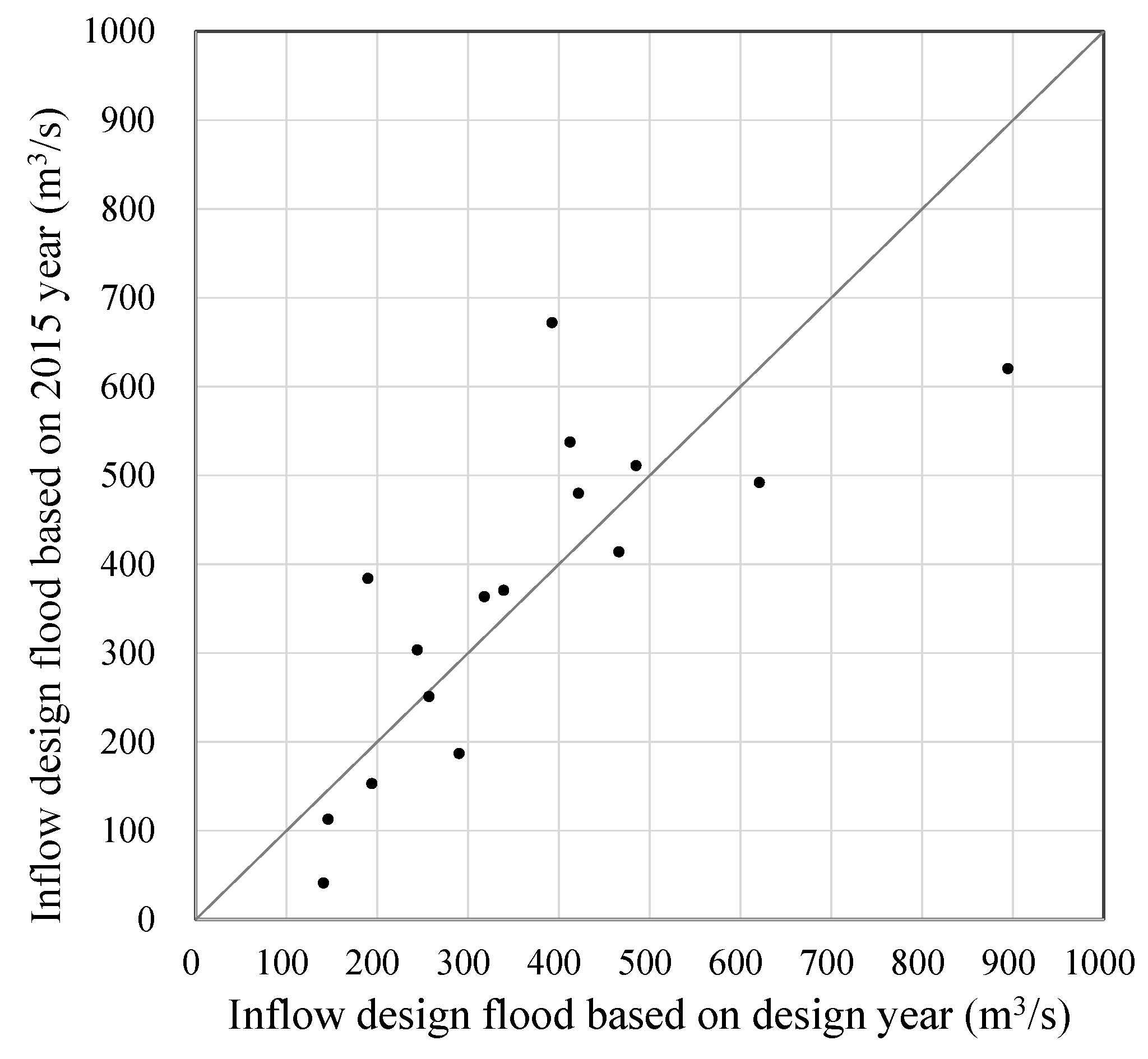
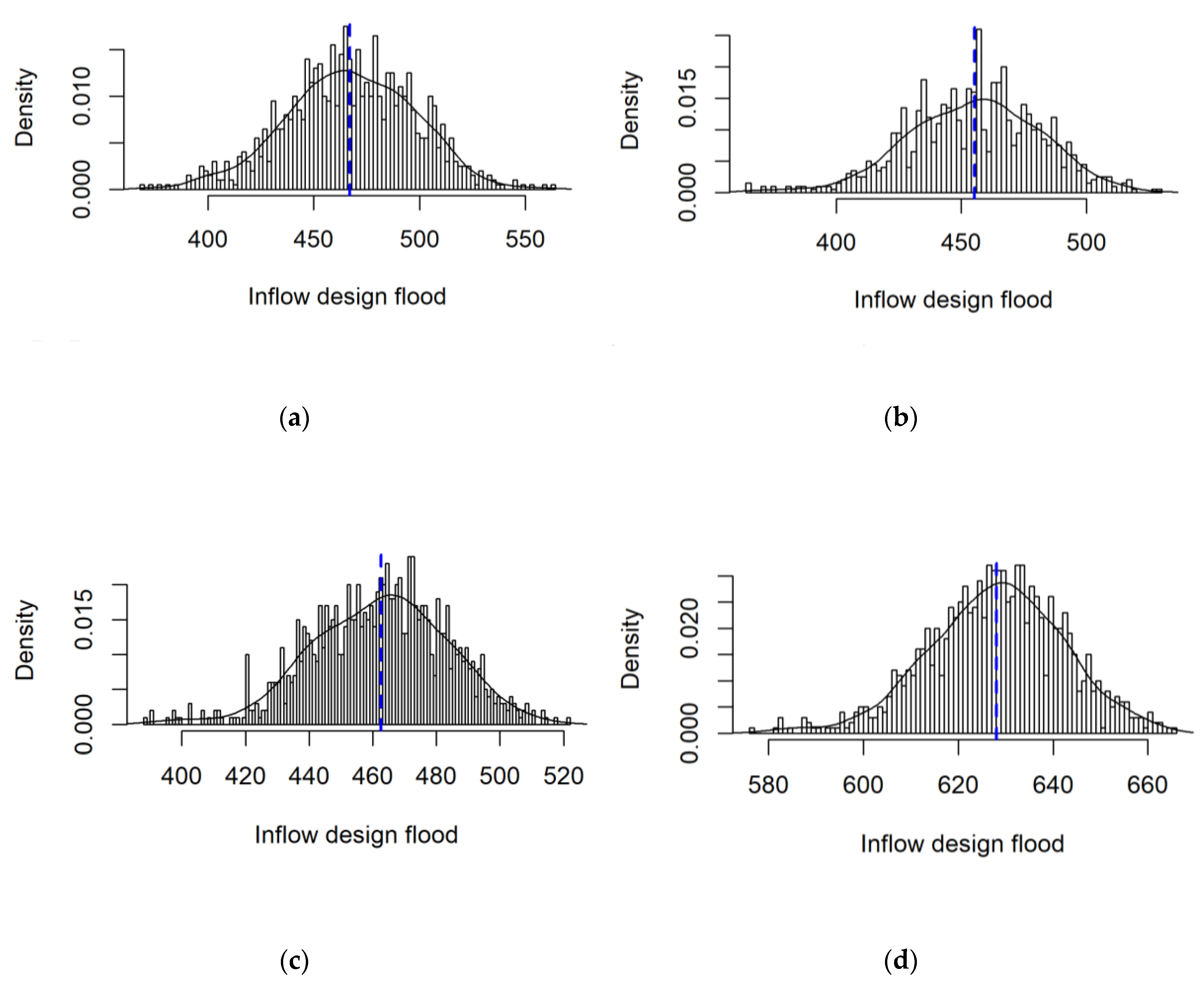
3.4. Bootstrap Result of Inflow Design Flood
3.5. Interval Estimation of Inflow Design Flood Using BCa Confidence Interval Considering Climate Change
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In IPCC, 2013: Climate Change 2013: The Physical Science Basis; Midgley, P.M., Ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Pachauri, R.K. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In IPCC, 2014: Climate Change 2014: Synthesis Report; Meyer, L.A., Ed.; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- United Nations Office for Disaster Risk Reduction (UNDRR). Available online: https://www.undrr.org (accessed on 20 January 2019).
- Ministry of Public Safety and Security (MPSS). Disaster Annual Report; MPSS: Seoul, Korea, 2014.
- Korea Meteorological Administration (KMA). Korea Peninsula Climate Change Projection Analysis; KMA: Seoul, Korea, 2018. [Google Scholar]
- Ministry of Agriculture, Food and Rural Affairs and Korea Rural Community Corporation (MAFRA and KRC). Statistical Yearbook of Land and Water Development for Agriculture. 2019. Available online: http://rawris.ekr.or.kr/stastics/pdf/2018.pdf (accessed on 25 August 2019).
- Smithers, J. Methods for design flood estimation in South Africa. Water SA 2012, 38, 633–646. [Google Scholar] [CrossRef]
- Kang, M.S.; Goo, J.H.; Song, I.; Chun, J.A.; Her, Y.G.; Hwang, S.W.; Park, S.W. Estimating design floods based on the critical storm duration for small watersheds. J. Hydro-Environ. Res. 2013, 7, 209–218. [Google Scholar] [CrossRef]
- Faulkner, D.; Warren, S.; Burn, D. Design floods for all of Canada. Can. Water Resour. J. 2016, 41, 398–411. [Google Scholar] [CrossRef]
- Gioia, A. Reservoir Routing on Double-Peak Design Flood. Water 2016, 8, 553. [Google Scholar] [CrossRef]
- Deng, X.; Ren, W.; Feng, P. Design flood recalculation under land surface change. Nat. Hazards 2016, 80, 1153–1169. [Google Scholar] [CrossRef]
- François, B.; Schlef, K.E.; Wi, S.; Brown, C.M. Design considerations for riverine floods in a changing climate—A review. J. Hydrol. 2019, 574, 557–573. [Google Scholar] [CrossRef]
- Tofiq, F.A.; Güven, A. Potential changes in inflow design flood under future climate projections for Darbandikhan Dam. J. Hydrol. 2015, 528, 45–51. [Google Scholar] [CrossRef]
- Tofiq, F.A.; Guven, A. Prediction of design flood discharge by statistical downscaling and General Circulation Models. J. Hydrol. 2014, 517, 1145–1153. [Google Scholar] [CrossRef]
- Kwon, H.H.; Sivakumar, B.; Moon, Y.I.; Kim, B.S. Assessment of change in design flood frequency under climate change using a multivariate downscaling model and a precipitation-runoff model. Stoch. Environ. Res. Risk Assess. 2011, 25, 567–581. [Google Scholar] [CrossRef]
- Botto, A.; Ganora, D.; Claps, P.; Laio, F. Technical note: Design flood under hydrological uncertainty. Hydrol. Earth Syst. Sci. 2017, 21, 3353–3358. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). Federal Guidelines for Dam Safety : Selecting and Accomodating Inflow Design Floods for Dams; FEMA: Washington, DC, USA, 2004.
- Vrijling, J.K.; Schweckendiek, T.; Kanning, W. Safety Standards of Flood Defenses. In Geotechnical Safety and Risk (ISGSR 2011); Bundesanstalt für Wasserba: Karlsruhe, Germany, 2011; pp. 67–84. [Google Scholar]
- Ministry of Agriculture, Food and Rural Affairs (MAFRA). Agricultural Infrastructure Design Standards. 2002. Available online: http://www.kcsc.re.kr (accessed on 25 August 2019).
- Communities and Local Government. Planning Policy Statement 25: Development and Flood Risk; The Stationery Office: London, UK, 2010.
- Vernieuwe, H.; Vandenberghe, S.; De Baets, B.; Verhoest, N.E.C. A continuous rainfall model based on vine copulas. Hydrol. Earth Syst. Sci. 2015, 19, 2685–2699. [Google Scholar] [CrossRef]
- Goodarzi, E.; Shui, L.T.; Ziaei, M. Risk and uncertainty analysis for dam overtopping—Case study: The Doroudzan Dam. Iran. J. Hydro-Environ. Res. 2014, 8, 50–61. [Google Scholar] [CrossRef]
- Blasone, R.S.; Madsen, H.; Rosbjerg, D. Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. J. Hydrol. 2008, 353, 18–32. [Google Scholar] [CrossRef]
- Blasone, R.S.; Vrugt, J.A.; Madsen, H.; Rosbjerg, D.; Robinson, B.A.; Zyvoloski, G.A. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov Chain Monte Carlo sampling. Adv. Water Resour. 2008, 31, 630–648. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Yoon, S.K.; Kim, J.S.; Moon, Y.-I. Urban stream overflow probability in a changing climate: Case study of the Seoul Uicheon Basin, Korea. J. Hydro-Environ. Res. 2016, 13, 52–65. [Google Scholar] [CrossRef]
- Weather Data Release Portal. Available online: https://data.kma.go.kr (accessed on 10 January 2019).
- Climate Information Portal. Available online: http://www.climate.go.kr (accessed on 10 January 2019).
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Dongbu); KRCC: Naju, Korea, 2006. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Onam, Maji, Aeryong); KRCC: Naju, Korea, 2007. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Bansan); KRCC: Naju, Korea, 2007. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Baegun, Yongseol); KRCC: Naju, Korea, 2008. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Yonggye, Mugeuk, Geumseok); KRCC: Naju, Korea, 2008. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Geumo, Daeseong, Obong, Dowon, Dalchang); KRCC: Naju, Korea, 2009. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Chupyeong); KRCC: Naju, Korea, 2009. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Dorim); KRCC: Naju, Korea, 2009. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Gyeryong); KRCC: Naju, Korea, 2009. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Boksim); KRCC: Naju, Korea, 2009. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Jamgok); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Junam, Gawol); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Dorim); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Gyeryong); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Boksim); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Yongdang); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Tapjeong); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Deokyong); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Damyang); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Gwangju); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Jangseong); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Suyang); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Master Plan (Naju); KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Reservoir Hydrological Research Synthesis Report; KRCC: Naju, Korea, 2010. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Yongdang); KRCC: Naju, Korea, 2011. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Chupyeong); KRCC: Naju, Korea, 2011. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Deokyong); KRCC: Naju, Korea, 2011. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Tapjeong); KRCC: Naju, Korea, 2012. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Damyang); KRCC: Naju, Korea, 2012. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Gwangju); KRCC: Naju, Korea, 2012. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Suyang); KRCC: Naju, Korea, 2012. [Google Scholar]
- Korea Rural Community Corporation (KRCC). Emergency Action Plan (Naju); KRCC: Naju, Korea, 2012. [Google Scholar]
- National Institute of Meteorological Sciences (NIMS). Climate Change Scenario Report for IPCC AR5; 11-1360395-000233-01; National Institute of Meteorological Research, Climate Research Division: Seoul, Korea, 2011. [Google Scholar]
- Park, J.; Kang, M.S.; Song, I. Bias correction of RCP-based future extreme precipitation using a quantile mapping method; for 20-weather stations of South Korea. J. Korean Soc. Agric. Eng. 2012, 54, 133–142. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Skaugen, T.E. Technical Note: Downscaling RCM precipitation to the station scale using quantile mapping—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap, Monograph in Applied Statistics and Probability, 57; Chapman and Hall/CRC: New York, NY, USA, 1994. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M.; Ryberg, K.R.; Archfield, S.A.; Gilroy, E.J. Statistical Methods in Water Resources: US Geological Survey Techniques and Methods; Book 4, Chapter A3; US Geological Survey: Reston, VA, USA, 2020.
- US Army Corps of Engineers (USACE). HEC-1 Flood Hydrograph Package. 1998. Available online: http://www.hec.usace.army.mil/publications/ComputerProgramDocumentation/HEC-1_UsersManual_(CPD-1a).pdf (accessed on 25 August 2019).
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Clark, C.O. Storage and the unit hydrograph. Trans. Am. Soc. Civil Eng. 1945, 110, 1419–1446. [Google Scholar]

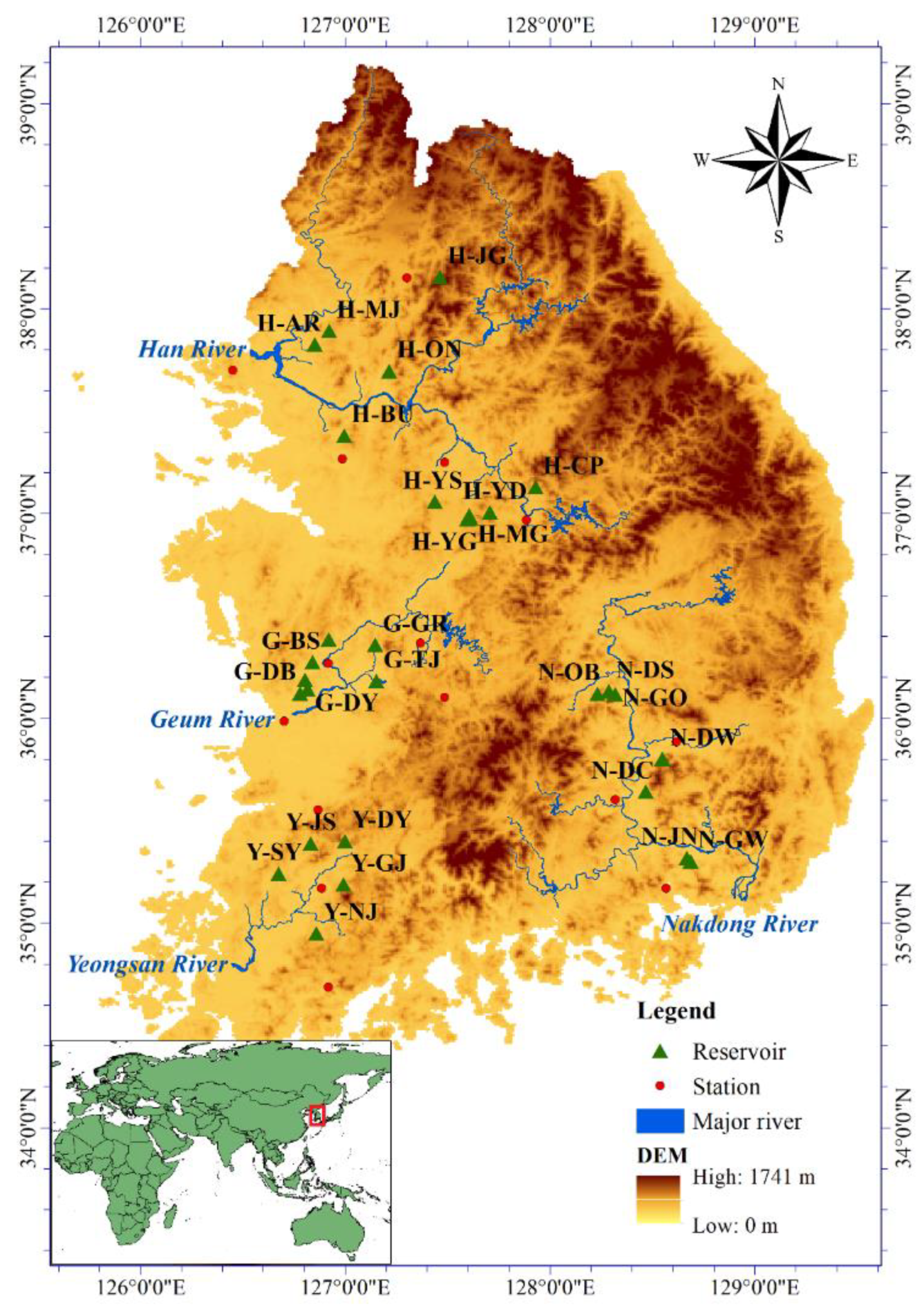



| Name of Reservoir | Watershed Area (ha) | Impervious (%) | Time of Concentration (h) | Watershed Length (km) | Total Storage Capacity (10,000 m3) | Effective Storage Capacity (10,000 m3) |
|---|---|---|---|---|---|---|
| H-YS | 790 | 1.85 | 0.38 | 2.19 | 302.0 | 293.2 |
| H-YG | 748 | 0.35 | 0.56 | 2.94 | 425.9 | 339.9 |
| H-GS | 717 | 1.26 | 0.42 | 2.96 | 383.8 | 330.9 |
| H-MG | 1315 | 2.05 | 0.67 | 3.75 | 306.8 | 279.1 |
| H-ON | 1552 | 0.79 | 0.70 | 4.68 | 271.0 | 271.0 |
| H-BU | 1020 | 2.44 | 0.47 | 3.19 | 138.0 | 137.9 |
| H-YD | 2873 | 8.27 | 1.22 | 6.30 | 692.9 | 683.0 |
| H-CP | 1610 | 2.08 | 0.76 | 5.40 | 493.3 | 455.5 |
| H-JG | 1970 | 0.21 | 0.40 | 3.78 | 436.4 | 427.9 |
| H-MJ | 1420 | 0.56 | 1.16 | 5.63 | 399.6 | 389.1 |
| H-AR | 890 | 1.62 | 0.99 | 4.52 | 103.0 | 98.4 |
| G-DR | 650 | 0.00 | 0.55 | 3.77 | 382.9 | 377.6 |
| G-BS | 1677 | 1.14 | 1.60 | 8.33 | 545.3 | 545.3 |
| G-GR | 1574 | 4.62 | 0.98 | 6.30 | 471.8 | 471.7 |
| G-TJ | 21,880 | 2.35 | 7.78 | 37.85 | 3842.3 | 3842.3 |
| G-BO | 1761 | 2.28 | 1.80 | 7.08 | 502.8 | 471.1 |
| G-DY | 1567 | 2.51 | 1.03 | 4.42 | 569.8 | 569.8 |
| G-DB | 2811 | 3.98 | 1.79 | 8.64 | 1218.2 | 1144.6 |
| N-OB | 1460 | 0.55 | 0.99 | 6.20 | 395.8 | 383.2 |
| N-GO | 1100 | 1.42 | 0.52 | 4.47 | 173.9 | 173.9 |
| N-DS | 1780 | 0.97 | 0.90 | 5.61 | 330.2 | 330.2 |
| N-DW | 576 | 1.02 | 0.61 | 4.23 | 140.4 | 140.4 |
| N-DC | 5630 | 1.65 | 3.85 | 12.72 | 878.8 | 864.9 |
| N-JN | 1173 | 3.48 | 1.52 | 3.18 | 1435.9 | 530.3 |
| N-GW | 3741 | 11.72 | 3.49 | 8.07 | 970.3 | 970.3 |
| Y-DY | 4720 | 1.07 | 0.95 | 12.00 | 7761.1 | 7667.0 |
| Y-GJ | 4130 | 1.62 | 0.81 | 10.20 | 2325.6 | 2108.5 |
| Y-JS | 12,280 | 1.37 | 1.55 | 15.48 | 10,388.0 | 9970.5 |
| Y-SY | 3300 | 6.71 | 0.94 | 11.90 | 1192.6 | 1183.3 |
| Y-NJ | 8460 | 1.33 | 1.25 | 15.70 | 10,780.9 | 10,654.4 |
| Name of Reservoir | Duration (h) | |||||||
|---|---|---|---|---|---|---|---|---|
| 2015s (1986–2015) | 2100s (2071–2100) | |||||||
| 3 | 6 | 12 | 24 | 3 | 6 | 12 | 24 | |
| H-YS | 256.7 | 425.0 | 561.6 | 586.6 | 159.7 | 286.0 | 502.0 | 809.1 |
| H-YG | 177.9 | 216.5 | 334.4 | 415.4 | 288.1 | 575.3 | 910.6 | 1378.8 |
| H-GS | 177.9 | 216.5 | 334.4 | 415.4 | 288.1 | 575.3 | 910.6 | 1378.8 |
| H-MG | 177.9 | 216.5 | 334.4 | 415.4 | 288.1 | 575.3 | 910.6 | 1378.8 |
| H-ON | 334.0 | 512.4 | 681.5 | 754.2 | 468.9 | 942.5 | 1529.4 | 1913.6 |
| H-BU | 201.6 | 301.6 | 402.2 | 494.7 | 490.0 | 861.9 | 1164.1 | 1460.3 |
| H-YD | 173.1 | 212.8 | 330.3 | 412.8 | 280.3 | 565.5 | 899.4 | 1370.1 |
| H-CP | 177.9 | 216.5 | 334.4 | 415.4 | 288.1 | 575.3 | 910.6 | 1378.8 |
| H-JG | 159.0 | 222.6 | 347.1 | 518.0 | 347.3 | 642.0 | 1043.7 | 1286.3 |
| H-MJ | 334.0 | 512.4 | 681.5 | 754.2 | 468.9 | 942.5 | 1529.4 | 1913.6 |
| H-AR | 334.0 | 512.4 | 681.5 | 754.2 | 468.9 | 942.5 | 1529.4 | 1913.6 |
| G-DR | 263.6 | 302.3 | 504.4 | 574.4 | 324.6 | 641.8 | 1007.1 | 1098.3 |
| G-BS | 263.6 | 302.3 | 504.4 | 574.4 | 324.6 | 641.8 | 1007.1 | 1098.3 |
| G-GR | 172.6 | 242.0 | 370.6 | 499.5 | 337.2 | 502.5 | 760.4 | 1054.0 |
| G-TJ | 99.9 | 154.5 | 208.9 | 257.9 | 196.6 | 326.3 | 528.7 | 801.8 |
| G-BO | 263.6 | 302.3 | 504.4 | 574.4 | 324.6 | 641.8 | 1007.1 | 1098.3 |
| G-DY | 243.2 | 278.6 | 490.3 | 559.0 | 311.4 | 613.8 | 978.7 | 1070.0 |
| G-DB | 132.8 | 249.4 | 417.0 | 469.0 | 187.2 | 357.7 | 669.4 | 823.0 |
| N-OB | 118.3 | 195.8 | 235.9 | 298.9 | 105.7 | 186.0 | 294.9 | 407.5 |
| N-GO | 118.3 | 195.8 | 235.9 | 298.9 | 105.7 | 186.0 | 294.9 | 407.5 |
| N-DS | 118.3 | 195.8 | 235.9 | 298.9 | 105.7 | 186.0 | 294.9 | 407.5 |
| N-DW | 99.0 | 120.6 | 178.8 | 277.3 | 103.5 | 218.9 | 323.3 | 393.3 |
| N-DC | 91.0 | 113.4 | 169.8 | 267.0 | 95.1 | 205.8 | 307.0 | 378.7 |
| N-JN | 198.5 | 333.9 | 363.7 | 335.8 | 159.1 | 271.6 | 352.9 | 401.1 |
| N-GW | 186.1 | 318.4 | 349.5 | 326.0 | 149.1 | 259.0 | 339.1 | 389.3 |
| Y-DY | 194.6 | 323.2 | 421.9 | 475.0 | 212.3 | 369.4 | 567.5 | 693.1 |
| Y-GJ | 161.2 | 251.7 | 365.9 | 457.1 | 325.4 | 601.8 | 889.2 | 1026.0 |
| Y-JS | 130.3 | 220.5 | 295.8 | 349.7 | 190.0 | 365.4 | 556.5 | 720.1 |
| Y-SY | 163.1 | 253.3 | 367.5 | 458.9 | 329.3 | 605.7 | 893.1 | 1030.0 |
| Y-NJ | 106.1 | 157.5 | 268.1 | 334.8 | 270.2 | 421.5 | 668.3 | 1062.6 |
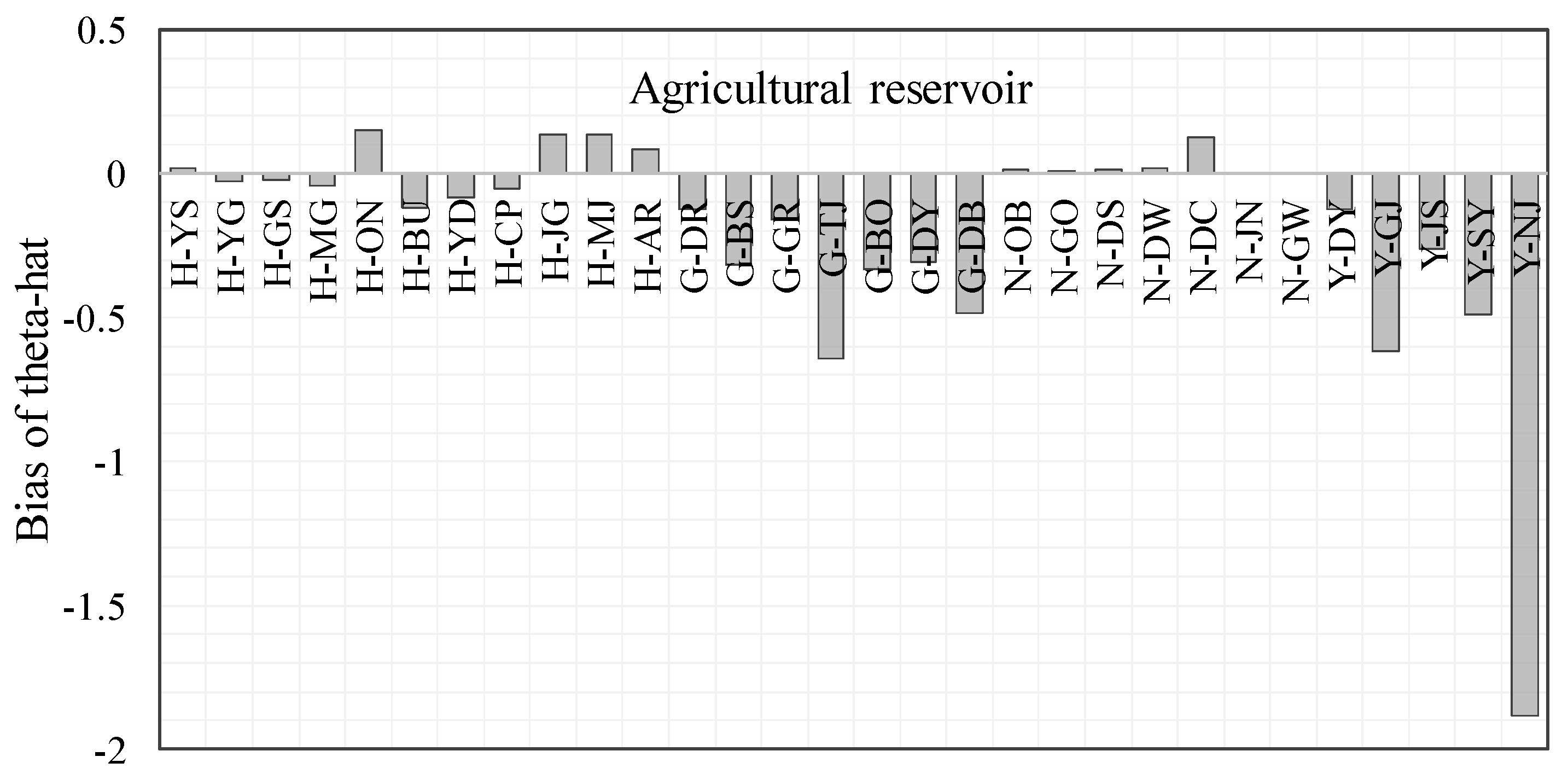
| ID | Name of Reservoir | Original of | Bias of | Standard Error of | (Bias-Correction) | (Acceleration) |
|---|---|---|---|---|---|---|
| 1 | H-YS | 111.0 | 0.0217 | 0.8 | −0.0451 | 0.0027 |
| 2 | H-YG | 161.2 | −0.0252 | 10.4 | −0.0075 | −0.0271 |
| 3 | H-GS | 155.0 | −0.0236 | 10.0 | −0.0050 | −0.0271 |
| 4 | H-MG | 282.6 | −0.0403 | 18.2 | −0.0025 | −0.0271 |
| 5 | H-ON | 467.1 | 0.1496 | 30.2 | 0.0075 | 0.0004 |
| 6 | H-BU | 190.0 | −0.1193 | 9.7 | −0.0326 | −0.0263 |
| 7 | H-YD | 605.8 | −0.0848 | 38.9 | −0.0025 | −0.0271 |
| 8 | H-CP | 344.2 | −0.0522 | 22.3 | 0.0000 | −0.0271 |
| 9 | H-JG | 408.0 | 0.1362 | 18.0 | 0.0150 | −0.0242 |
| 10 | H-MJ | 424.1 | 0.1374 | 27.2 | 0.0050 | 0.0004 |
| 11 | H-AR | 265.6 | 0.0855 | 17.1 | 0.0075 | 0.0004 |
| 12 | G-DR | 175.6 | −0.1243 | 10.2 | −0.0502 | −0.0254 |
| 13 | G-BS | 439.7 | −0.3189 | 25.6 | −0.0426 | −0.0255 |
| 14 | G-GR | 227.2 | −0.1564 | 7.9 | 0.0075 | −0.0151 |
| 15 | G-TJ | 852.4 | −0.6437 | 48.5 | −0.0326 | −0.0264 |
| 16 | G-BO | 455.4 | −0.3307 | 26.6 | −0.0451 | −0.0255 |
| 17 | G-DY | 401.7 | −0.3062 | 23.3 | −0.0426 | −0.0255 |
| 18 | G-DB | 462.6 | −0.4847 | 21.4 | −0.0351 | −0.0252 |
| 19 | N-OB | 86.3 | 0.0141 | 0.9 | −0.0602 | −0.0054 |
| 20 | N-GO | 62.0 | 0.0104 | 0.7 | −0.0301 | −0.0039 |
| 21 | N-DS | 104.7 | 0.0167 | 1.1 | −0.0301 | −0.0055 |
| 22 | N-DW | 40.3 | 0.0191 | 1.2 | −0.0502 | −0.0183 |
| 23 | N-DC | 276.0 | 0.1253 | 7.9 | −0.0602 | −0.0175 |
| 24 | N-JN | 83.6 | 0.0020 | 1.1 | 0.0050 | −0.0130 |
| 25 | N-GW | 195.3 | 0.0034 | 2.8 | 0.0075 | −0.0119 |
| 26 | Y-DY | 628.1 | −0.1250 | 14.3 | −0.0276 | −0.0240 |
| 27 | Y-GJ | 679.5 | −0.6172 | 27.2 | −0.0276 | −0.0148 |
| 28 | Y-JS | 1360.5 | −0.2596 | 49.8 | −0.0276 | −0.0202 |
| 29 | Y-SY | 546.1 | −0.4892 | 21.7 | −0.0326 | −0.0148 |
| 30 | Y-NJ | 1429.0 | −1.8847 | 96.9 | −0.0276 | −0.0198 |
| Name of Reservoir | Inflow Design Flood (m3/s) | |||||||
|---|---|---|---|---|---|---|---|---|
| Base Period Value (2015s) | Base Period Value (2015s) with the Safety Factor Applied | Interval Estimation (95% Non-Parametric Confidence Interval) | ||||||
| 2040s (2011–2040) | 2070s (2041–2070) | 2100s (2071–2100) | ||||||
| 0.025 | 0.975 | 0.025 | 0.975 | 0. 025 | 0.975 | |||
| H-YS | 111.0 | 133.2 | 109.5 | 112.5 | 102.9 | 112.3 | 147.7 | 163.4 |
| H-YG | 74.0 | 88.8 | 137.8 | 179.4 | 157.1 | 183.2 | 185.2 | 203.1 |
| H-GS | 71.0 | 85.2 | 132.5 | 172.4 | 150.7 | 175.9 | 177.8 | 194.8 |
| H-MG | 128.0 | 153.6 | 241.4 | 314.8 | 275.3 | 321.3 | 324.4 | 355.8 |
| H-ON | 279.0 | 334.8 | 403.7 | 522.9 | 457.2 | 551.7 | 487.8 | 561.2 |
| H-BU | 114.0 | 136.8 | 167.9 | 206.7 | 138.0 | 190.7 | 319.6 | 363.4 |
| H-YD | 277.0 | 332.4 | 518.2 | 674.4 | 589.6 | 688.0 | 694.8 | 761.9 |
| H-CP | 155.0 | 186.0 | 294.6 | 383.6 | 335.0 | 391.5 | 395.6 | 433.9 |
| H-JG | 238.0 | 285.6 | 370.0 | 440.5 | 339.8 | 403.2 | 595.3 | 649.4 |
| H-MJ | 255.0 | 306.0 | 367.1 | 474.3 | 415.1 | 499.9 | 442.7 | 509.0 |
| H-AR | 159.0 | 190.8 | 229.7 | 297.2 | 260.1 | 313.4 | 277.2 | 318.9 |
| G-DR | 90.0 | 108.0 | 151.4 | 192.5 | 118.2 | 156.3 | 200.2 | 224.3 |
| G-BS | 225.0 | 270.0 | 379.1 | 482.2 | 296.4 | 391.0 | 501.2 | 561.4 |
| G-GR | 179.0 | 214.8 | 210.0 | 242.2 | 285.1 | 360.8 | 368.1 | 399.1 |
| G-TJ | 452.0 | 542.4 | 739.5 | 933.3 | 1104.0 | 1334.0 | 1455.5 | 1553.7 |
| G-BO | 233.0 | 279.6 | 392.6 | 499.5 | 306.1 | 404.8 | 518.9 | 581.4 |
| G-DY | 208.0 | 249.6 | 346.3 | 440.4 | 270.7 | 357.3 | 457.3 | 513.1 |
| G-DB | 302.0 | 362.4 | 411.1 | 498.7 | 340.0 | 429.9 | 512.9 | 590.7 |
| N-OB | 90.0 | 108.0 | 84.4 | 88.0 | 103.3 | 121.6 | 131.6 | 137.8 |
| N-GO | 65.0 | 78.0 | 60.6 | 63.5 | 75.0 | 89.0 | 96.7 | 101.5 |
| N-DS | 110.0 | 132.0 | 102.4 | 107.0 | 125.4 | 147.7 | 160.1 | 167.8 |
| N-DW | 30.0 | 36.0 | 37.4 | 42.4 | 44.2 | 45.9 | 48.0 | 50.1 |
| N-DC | 212.0 | 254.4 | 257.2 | 289.5 | 302.1 | 312.9 | 327.2 | 340.6 |
| N-JN | 89.0 | 106.8 | 81.4 | 85.8 | 106.2 | 128.2 | 112.1 | 121.7 |
| N-GW | 208.0 | 249.6 | 190.1 | 200.5 | 249.5 | 301.9 | 263.0 | 286.1 |
| Y-DY | 504.0 | 604.8 | 595.3 | 653.5 | 590.9 | 669.9 | 761.7 | 824.2 |
| Y-GJ | 442.0 | 530.4 | 620.3 | 726.2 | 707.5 | 775.0 | 864.8 | 987.6 |
| Y-JS | 931.0 | 1117.2 | 1245.2 | 1450.4 | 1358.6 | 1571.0 | 1964.9 | 2200.5 |
| Y-SY | 357.0 | 428.4 | 498.9 | 583.3 | 568.4 | 622.5 | 694.0 | 792.1 |
| Y-NJ | 624.0 | 748.8 | 1218.1 | 1592.0 | 1310.9 | 1470.3 | 1289.3 | 1426.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Hwang, S.; Song, J.-H.; Kang, M.-S. An Alternative for Estimating the Design Flood Interval of Agricultural Reservoirs under Climate Change Using a Non-Parametric Resampling Technique. Water 2020, 12, 1894. https://doi.org/10.3390/w12071894
Park J, Hwang S, Song J-H, Kang M-S. An Alternative for Estimating the Design Flood Interval of Agricultural Reservoirs under Climate Change Using a Non-Parametric Resampling Technique. Water. 2020; 12(7):1894. https://doi.org/10.3390/w12071894
Chicago/Turabian StylePark, Jihoon, Syewoon Hwang, Jung-Hun Song, and Moon-Seong Kang. 2020. "An Alternative for Estimating the Design Flood Interval of Agricultural Reservoirs under Climate Change Using a Non-Parametric Resampling Technique" Water 12, no. 7: 1894. https://doi.org/10.3390/w12071894
APA StylePark, J., Hwang, S., Song, J.-H., & Kang, M.-S. (2020). An Alternative for Estimating the Design Flood Interval of Agricultural Reservoirs under Climate Change Using a Non-Parametric Resampling Technique. Water, 12(7), 1894. https://doi.org/10.3390/w12071894





