Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis
Abstract
1. Introduction
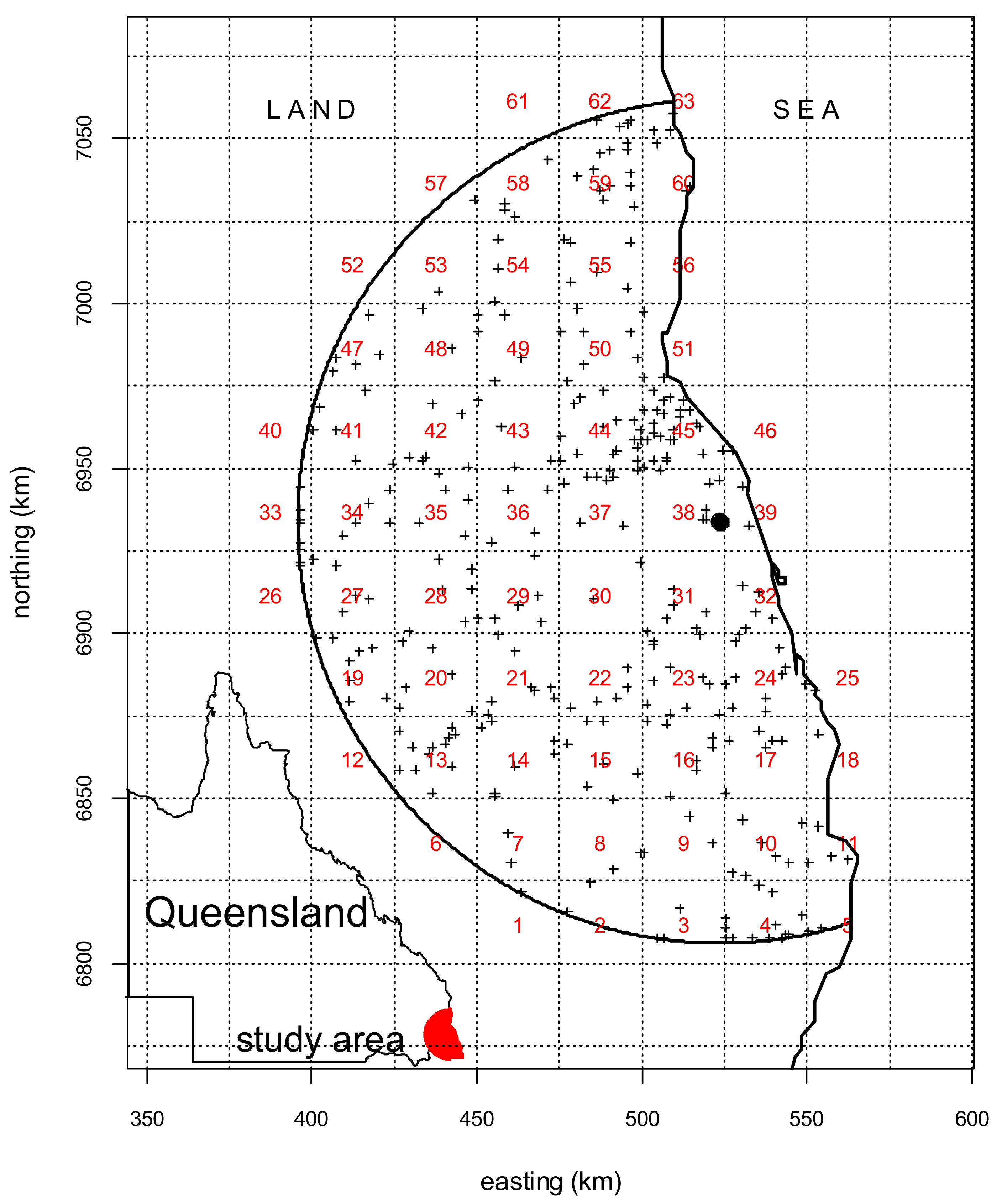
2. Study Area and Data
3. Methodology
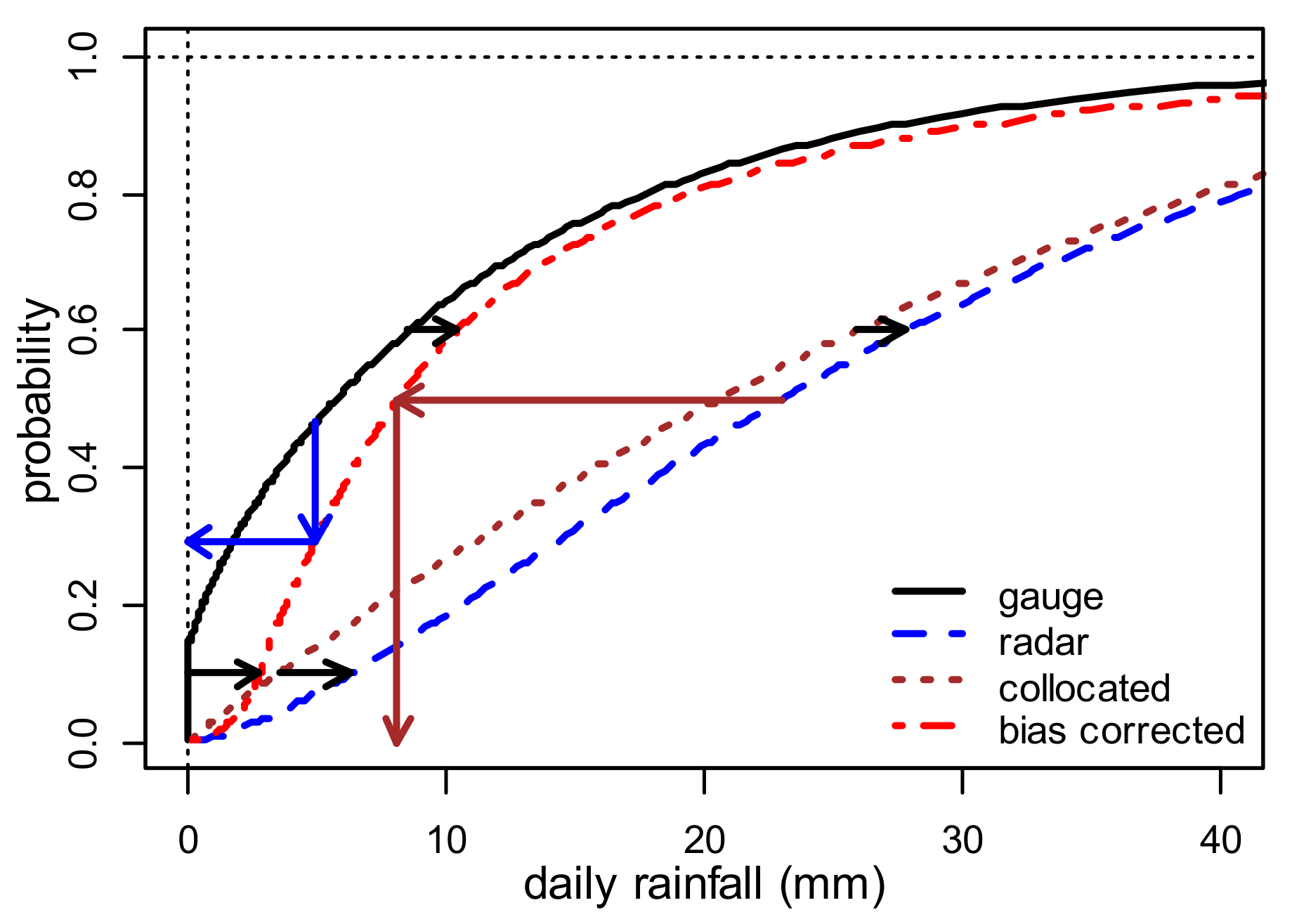
3.1. Marginal Distribution Fitting
3.2. Bias Correction
3.3. Spatial Structure Modelling
3.4. Stratified Sampling of Rain Gauge Locations
- Firstly, the study region was overlaid with a 25 km × 25 km grid, and the resulting 63 blocks within, or intersecting, the study region are labelled in Figure 1;
- Secondly, rain gauges within each grid were counted, and those blocks devoid of gauges were assigned a value of 0.5 times the fraction of the grid within the radar coverage, to allow for possible selection of gauges within the fractional grids, particularly for higher sampling numbers. The rain gauge network density of the grids varies from 1.7 to 48.6 gauges per 1000 km2, grid 45 recording the highest density;
- Thirdly, the observed rain gauge counts within the grids were used to develop the weights for the stratified sampling;
- Fourth, the number of rain gauges required were sampled with replacement from integers 1 to 63, representing the grids, in accordance with their weights;
- Finally, the numbers of samples from each grid from the previous step were sampled randomly, without replacement from the subset of the grid, noting that the subset of each grid is the number of 1-km2 radar grid centres it contains, which varies from 6 (grid 61) to 625 (the inner grids).
3.5. Performance Statistics
4. Results and Discussion
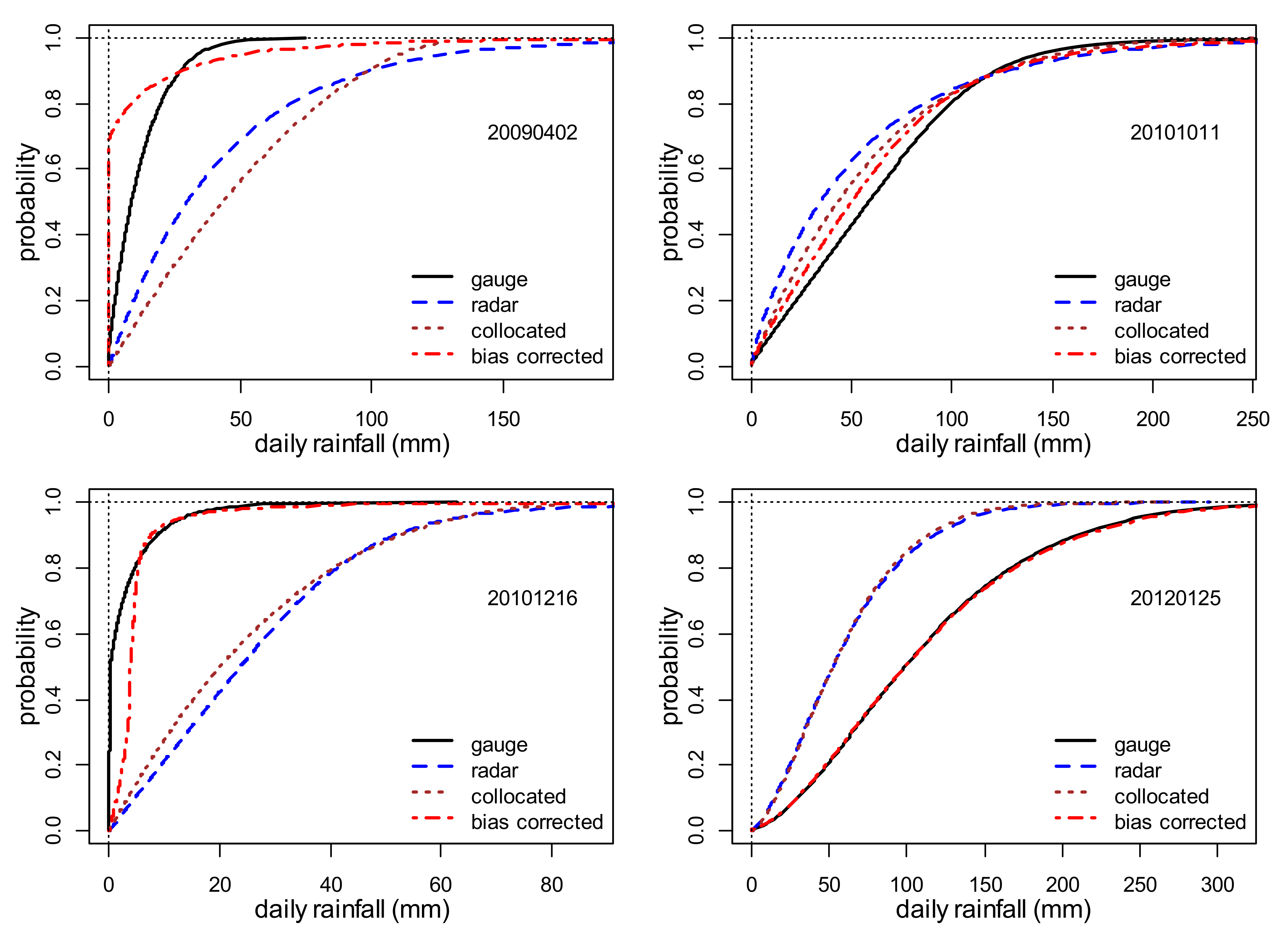
4.1. Marginal Distribution
4.2. Spatial Structure Parameters
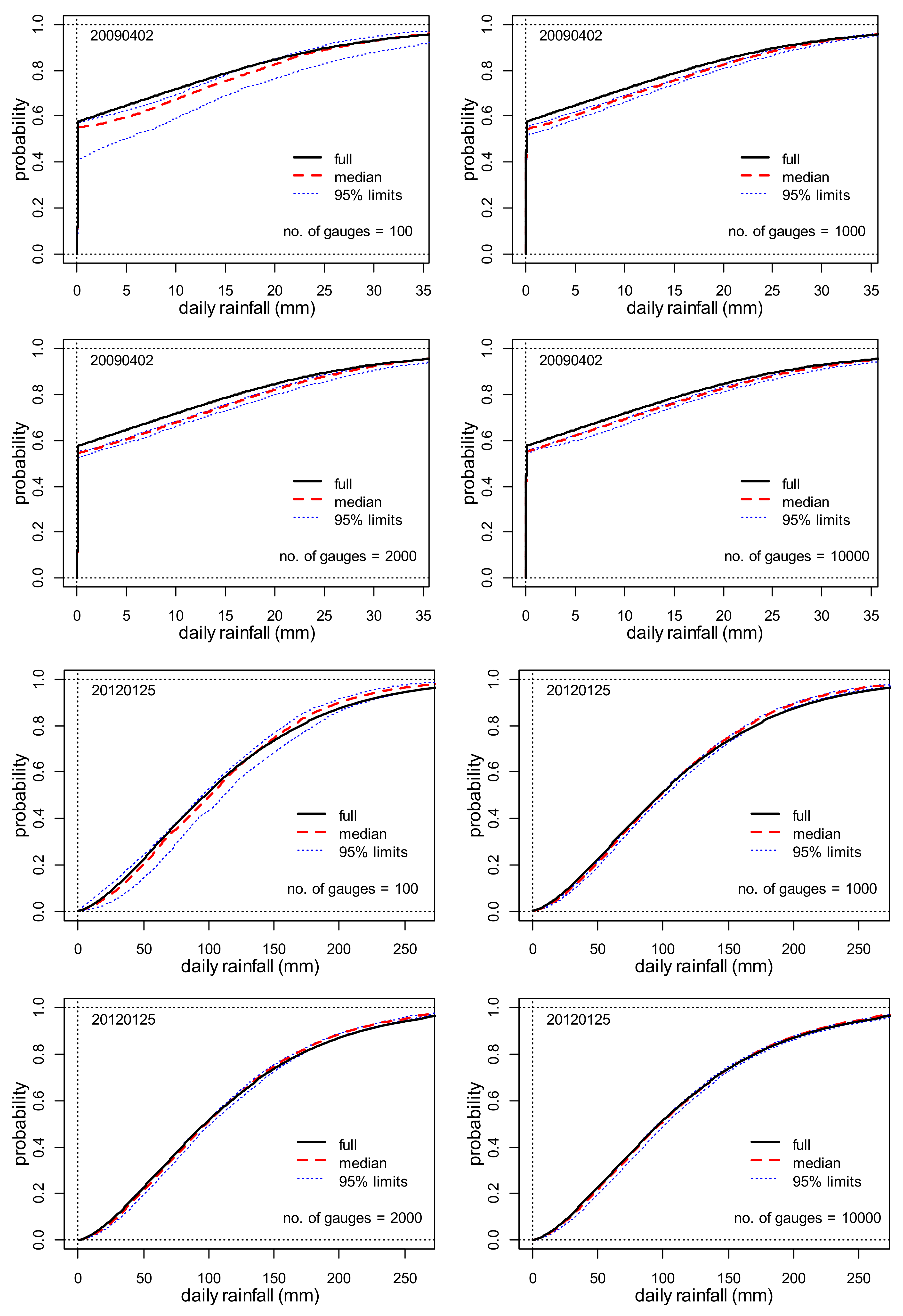
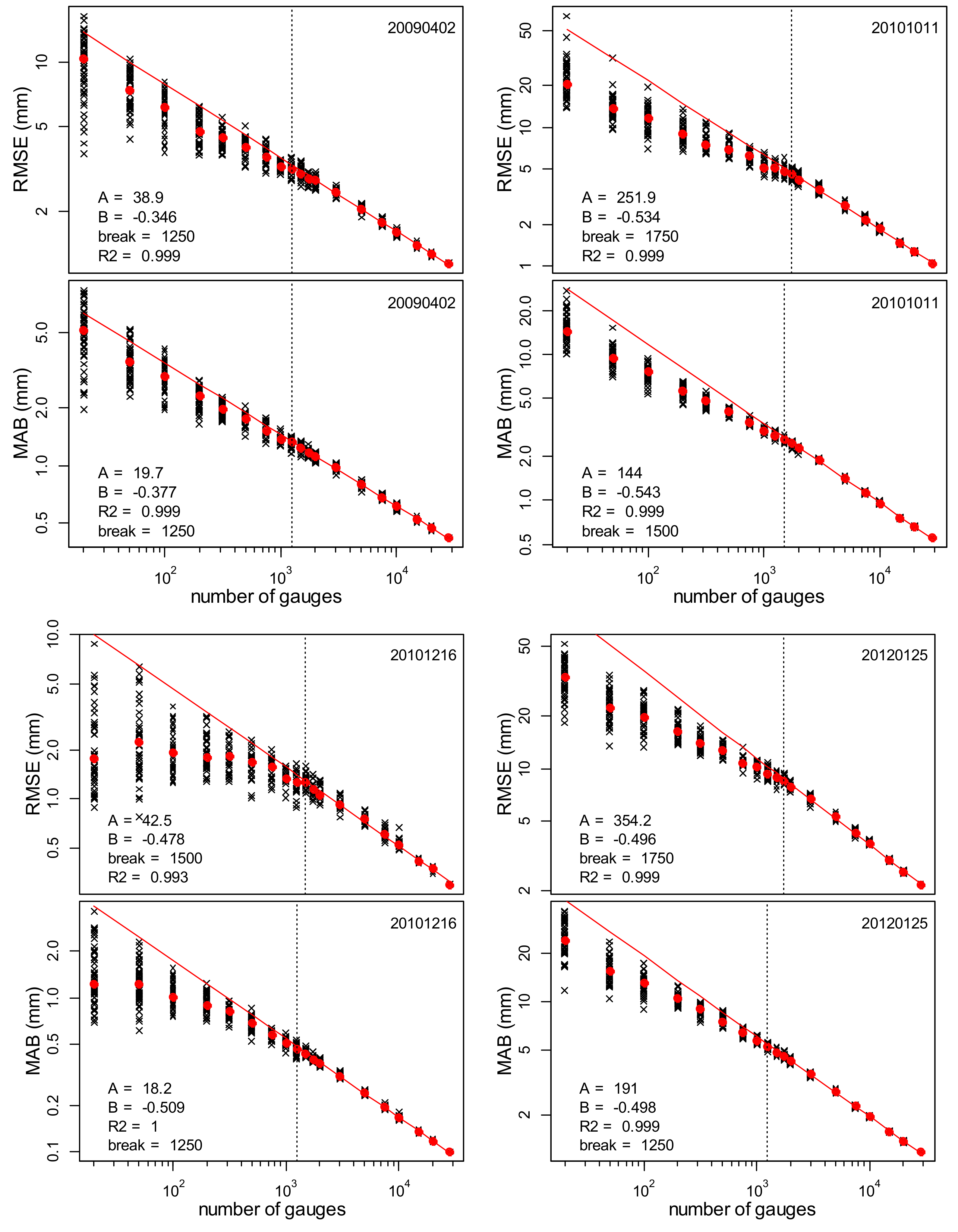
4.3. The Optimum Rain Gauge Network Density
5. Conclusions
Funding
Conflicts of Interest
References
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Huff, F.A. Time distribution characteristics of rainfall rates. Water Resour. Res. 1970, 6, 447–454. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Verbist, K.M.J. Bias adjustment of satellite-based precipitation estimation using gauge observations: A case study in Chile. J. Geophys. Res. Atmos. 2016, 121, 3790–3806. [Google Scholar] [CrossRef]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Q. J. Roy. Meteorol. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2013, 28, 3505–3520. [Google Scholar] [CrossRef]
- Collier, C.G. Accuracy of rainfall estimates by radar, part 1: Calibration by telemetering raingauges. J. Hydrol. 1986, 83, 207–223. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Sattari, M.-T.; Rezazadeh-Joudi, A.; Kusiak, A. Assessment of different methods for estimation of missing data in precipitation studies. Hydrol. Res. 2017, 48, 1032–1044. [Google Scholar] [CrossRef]
- St-Hilaire, A.; Ouarda, T.B.; Lachance, M.; Bobée, B.; Gaudet, J.; Gignac, C. Assessment of the impact of meteorological network density on the estimation of basin precipitation and runoff: A case study. Hydrol. Process. 2003, 17, 3561–3580. [Google Scholar] [CrossRef]
- Girons Lopez, M.; Wennerström, H.; Nordén, L.Å.; Seibert, J. Location and density of rain gauges for the estimation of spatial varying precipitation. Geogr. Ann. A 2015, 97, 167–179. [Google Scholar] [CrossRef]
- Maier, R.; Krebs, G.; Pichler, M.; Muschalla, D.; Gruber, G. Spatial Rainfall Variability in Urban Environments—High-Density Precipitation Measurements on a City-Scale. Water 2020, 12, 1157. [Google Scholar] [CrossRef]
- Faurès, J.-M.; Goodrich, D.C.; Woolhiser, D.A.; Sorooshian, S. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 1995, 173, 309–326. [Google Scholar] [CrossRef]
- Bárdossy, A.; Das, T. Influence of rainfall observation network on model calibration and application. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3691–3726. [Google Scholar] [CrossRef]
- Mishra, A.K. Effect of Rain Gauge Density Over the Accuracy of Rainfall: A Case Study over Bangalore, India; SpringerPlus: Berlin, Germany, 2013; Volume 2, p. 311. [Google Scholar] [CrossRef]
- Tesfagiorgis, K.; Mahani, S.E.; Krakauer, N.Y.; Khanbilvardi, R. Bias correction of satellite rainfall estimates using a radar-gauge product—A case study in Oklahoma (USA). Hydrol. Earth Syst. Sci. 2011, 15, 2631–2647. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.A. Resampling of regional climate model output for the simulation of extreme river flows. J. Hydrol. 2007, 332, 487–496. [Google Scholar] [CrossRef]
- Addor, N.; Seibert, J. Bias correction for hydrological impact studies-beyond the daily perspective. Hydrol. Process. 2014, 28, 4823–4828. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Downscaling RCM precipitation to the station scale using statistical transformations-a comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Clim. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Kim, K.B.; Bray, M.; Han, D. An improved bias correction scheme based on comparative precipitation characteristics. Hydrol. Process. 2015, 29, 2258–2266. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y.; Pegram, G. Interpolation of daily rainfall networks using simulated radar fields for realistic hydrological modelling of spatial rain field ensembles. J. Hydrol. 2014, 519, 777–791. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y. Assessment of radar based locally varying anisotropy on daily rainfall interpolation. Hydrol. Sci. J. 2016, 61, 1890–1902. [Google Scholar] [CrossRef][Green Version]
- Gyasi-Agyei, Y. Realistic sampling of anisotropic correlogram parameters for conditional simulation of daily rainfields. J. Hydrol. 2018, 556, 1064–1077. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y. Propagation of uncertainties in interpolated rainfields to runoff errors. Hydrol. Sci. J. 2019, 64, 587–606. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R package for fitting distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
- Aucoin, F. FAdist: Distributions That Are Sometimes Used in Hydrology. R package version 2.3. 2020. Available online: https://CRAN.R-project.org/package=FAdist (accessed on 1 May 2020).
- Shoji, T.; Kitaura, H. Statistical and geostatistical analysis of rainfall in central Japan. Comput. Geosci. 2006, 32, 1007–1024. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Karl, T.R.; Easterling, D.R.; Knight, R.W.; Jamason, P.F.; Hennessy, K.J.; Suppiah, R.; Page, C.M.; Wibig, J.; Fortuniak, K.; et al. Changes in the probability of heavy precipitation: Important indicators of climatic change. Clim. Chang. 1999, 42, 243–283. [Google Scholar] [CrossRef]
- Buishand, T.A. Some remarks on the use of daily rainfall models. J. Hydrol. 1978, 36, 295–308. [Google Scholar] [CrossRef]
- Ye, L.; Hanson, L.S.; Ding, P.; Wang, D.; Vogel, R.M. The probability distribution of daily precipitation at the point and catchment scales in the United States. Hydrol. Earth Syst. Sci. 2018, 22, 6519–6531. [Google Scholar] [CrossRef]
- Sharma, C.; Ojha, C.S.P. Changes of annual precipitation and probability distributions for different climate types of the World. Water 2019, 11, 2092. [Google Scholar] [CrossRef]
- Yao, T.; Journel, A.G. Automatic modeling of (cross) covariance tables using fast Fourier transform. Math. Geol. 1998, 30, 589–615. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Ly, S.; Charles, C.; Degre, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Austin, P.M. Relation between measured radar reflectivity and surface rainfall. Mon. Weather. Rev. 1987, 115, 1053–1070. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Villarini, G.; Smith, J.A. Radar-rainfall uncertainties. Bull. Am. Meteorol. Soc. 2010, 91, 87–94. [Google Scholar] [CrossRef]
- Rabiei, E.; Haberlandt, U. Applying bias correction for merging rain and radar data. J. Hydrol. 2015, 522, 544–557. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y.; de Troch, F.P.; Troch, P.A. A dynamic hillslope response model in a geomorphology based rainfall-runoff model. J. Hydrol. 1996, 178, 1–18. [Google Scholar] [CrossRef]
- Nguyen, P.; Shearer, E.J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS Data Portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.H.M.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]




| Date | MN | SD | WP | MAX | LX | LY | AR | AA |
|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (-) | (mm) | (km) | (km) | (-) | (degrees) | |
| 20090102 | 12.2 | 11.5 | 0.995 | 163.8 | 40.1 | 23.4 | 0.583 | 143.8 |
| 20090402 | 16.8 | 11.9 | 0.381 | 76.2 | 86.7 | 50.3 | 0.581 | 74.7 |
| 20090405 | 16.0 | 15.5 | 0.875 | 107.4 | 38.4 | 23.0 | 0.600 | 136.5 |
| 20090413 | 7.3 | 8.7 | 0.445 | 70.1 | 63.9 | 28.2 | 0.442 | 78.3 |
| 20101011 | 63.1 | 40.8 | 0.962 | 353.7 | 103.0 | 59.6 | 0.579 | 6.1 |
| 20101211 | 5.8 | 5.1 | 0.147 | 35.7 | 44.4 | 17.5 | 0.395 | 118.5 |
| 20101216 | 4.6 | 2.9 | 0.872 | 46.8 | 67.0 | 47.1 | 0.703 | 37.0 |
| 20110105 | 3.9 | 1.7 | 0.551 | 5.9 | 78.3 | 68.2 | 0.870 | 77.5 |
| 20110523 | 4.9 | 4.5 | 0.454 | 56.5 | 50.2 | 42.7 | 0.851 | 71.0 |
| 20110830 | 6.4 | 8.9 | 0.258 | 99.9 | 44.1 | 22.3 | 0.505 | 163.1 |
| 20111223 | 4.1 | 2.7 | 0.094 | 18.3 | 56.8 | 45.6 | 0.804 | 122.0 |
| 20120125 | 102.2 | 64.6 | 1.000 | 450.1 | 91.9 | 59.0 | 0.642 | 98.9 |
| 20121218 | 5.6 | 5.1 | 0.590 | 68.4 | 72.6 | 64.2 | 0.885 | 108.0 |
| 20130530 | 4.0 | 5.2 | 0.509 | 45.6 | 66.5 | 64.0 | 0.962 | 82.3 |
| 20130630 | 4.0 | 2.6 | 0.365 | 11.0 | 90.9 | 55.8 | 0.614 | 74.9 |
| 20140122 | 7.4 | 4.7 | 0.373 | 15.0 | 52.4 | 49.4 | 0.943 | 126.1 |
| 20140123 | 3.1 | 1.4 | 1.000 | 5.1 | 59.0 | 31.4 | 0.533 | 169.3 |
| 20140328 | 119.7 | 43.7 | 1.000 | 353.2 | 70.2 | 60.8 | 0.866 | 16.2 |
| 20141119 | 5.3 | 4.4 | 0.278 | 28.7 | 23.1 | 17.1 | 0.739 | 17.0 |
| 20141205 | 11.2 | 11.6 | 0.826 | 65.2 | 49.3 | 35.6 | 0.722 | 120.3 |
| 20141218 | 3.6 | 5.6 | 0.987 | 59.5 | 53.3 | 27.6 | 0.517 | 33.4 |
| 20150102 | 4.2 | 3.6 | 0.605 | 45.4 | 35.3 | 23.8 | 0.674 | 113.6 |
| 20150126 | 10.6 | 10.2 | 0.338 | 67.0 | 46.1 | 30.2 | 0.656 | 93.8 |
| 20150127 | 8.8 | 13.9 | 0.487 | 204.6 | 31.7 | 22.3 | 0.703 | 152.5 |
| Minimum | 3.1 | 1.4 | 0.094 | 5.1 | 23.1 | 17.1 | 0.395 | 6.1 |
| Average | 18.1 | 12.1 | 0.600 | 102.2 | 59.0 | 40.4 | 0.682 | 93.1 |
| Maximum | 119.7 | 64.6 | 1.000 | 450.1 | 103.0 | 68.2 | 0.962 | 169.3 |
| Date | RMSE | MAB | Average | |||||
|---|---|---|---|---|---|---|---|---|
| A | B | Break | A | B | Break | Break | ||
| 20090102 | 122.1 | −0.456 | 2000 | 57.4 | −0.494 | 1500 | 1750 | |
| 20090402 | 38.9 | −0.346 | 1250 | 19.7 | −0.377 | 1250 | 1250 | |
| 20090405 | 121.2 | −0.437 | 1000 | 58.8 | −0.422 | 500 | 750 | |
| 20090413 | 54.2 | −0.496 | 2000 | 16.4 | −0.476 | 1250 | 1625 | |
| 20101011 | 251.9 | −0.534 | 1750 | 144.0 | −0.543 | 1500 | 1625 | |
| 20101211 | 17.6 | −0.380 | 2000 | 7.8 | −0.420 | 2000 | 2000 | |
| 20101216 | 42.5 | −0.478 | 1500 | 18.2 | −0.509 | 1250 | 1375 | |
| 20110105 | 18.6 | −0.463 | 1500 | 9.1 | −0.456 | 750 | 1125 | |
| 20110523 | 23.3 | −0.387 | 1750 | 12.0 | −0.429 | 1000 | 1375 | |
| 20110830 | 34.6 | −0.390 | 2000 | 17.4 | −0.456 | 750 | 1375 | |
| 20111223 | 6.6 | −0.327 | 1500 | 3.6 | −0.378 | 1250 | 1375 | |
| 20120125 | 354.2 | −0.496 | 1750 | 191.0 | −0.498 | 1250 | 1500 | |
| 20121218 | 49.9 | −0.467 | 1000 | 13.7 | −0.438 | 750 | 875 | |
| 20130530 | 20.2 | −0.383 | 750 | 10.8 | −0.416 | 750 | 750 | |
| 20130630 | 12.8 | −0.491 | 1750 | 4.6 | −0.453 | 750 | 1250 | |
| 20140122 | 37.2 | −0.508 | 1000 | 11.3 | −0.466 | 1250 | 1125 | |
| 20140123 | 13.2 | −0.495 | 2000 | 7.0 | −0.496 | 1250 | 1625 | |
| 20140328 | 325.7 | −0.511 | 2000 | 153.9 | −0.505 | 1000 | 1500 | |
| 20141119 | 30.5 | −0.405 | 1000 | 10.2 | −0.388 | 500 | 750 | |
| 20141205 | 135.9 | −0.503 | 2000 | 43.9 | −0.473 | 750 | 1375 | |
| 20141218 | 48.2 | −0.443 | 1500 | 20.4 | −0.465 | 1000 | 1250 | |
| 20150102 | 34.9 | −0.446 | 2000 | 11.9 | −0.408 | 1000 | 1500 | |
| 20150126 | 95.1 | −0.479 | 1000 | 24.5 | −0.436 | 1750 | 1375 | |
| 20150127 | 70.2 | −0.354 | 750 | 27.5 | −0.388 | 750 | 750 | |
| Minimum | 6.6 | −0.534 | 750 | 3.6 | −0.543 | 500 | 750 | |
| Average | 81.6 | −0.445 | 1531 | 37.3 | −0.450 | 1073 | 1302 | |
| Maximum | 354.2 | −0.327 | 2000 | 191.0 | −0.377 | 2000 | 2000 | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gyasi-Agyei, Y. Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis. Water 2020, 12, 1906. https://doi.org/10.3390/w12071906
Gyasi-Agyei Y. Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis. Water. 2020; 12(7):1906. https://doi.org/10.3390/w12071906
Chicago/Turabian StyleGyasi-Agyei, Yeboah. 2020. "Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis" Water 12, no. 7: 1906. https://doi.org/10.3390/w12071906
APA StyleGyasi-Agyei, Y. (2020). Identification of the Optimum Rain Gauge Network Density for Hydrological Modelling Based on Radar Rainfall Analysis. Water, 12(7), 1906. https://doi.org/10.3390/w12071906





