Bimolecular Reactive Transport Experiments and Simulations in Porous Media
Abstract
1. Introduction
2. Materials and Methods
2.1. Laboratory Experiments
2.2. Numerical Simulation
2.2.1. CTRW-FEM Theory
2.2.2. Modeling Inputs and Simulation
3. Results and Discussion
3.1. Breakthrough Curves
3.2. Reactant Mixing and Anomalous Diffusion
3.3. Analysis of Parameters
3.4. Model Sensitivity Analysis
4. Conclusions
- (1)
- Breakthrough curves of product NQAB in the column-based and numerical experiments are indicative of incomplete mixing and non-Fickian behavior. The correlation coefficients are greater than 0.9. In general, CTRW-FEM can be used to solve over-estimated peak and tail problems in BTCs.
- (2)
- It was found that coarser particles can lead to enhanced true mixing. Non-Fickian behavior in sand columns for different particle sizes changes slightly.
- (3)
- β decreases with Pe and DL increases with Pe for the same Da; β and DL increase as Pe and Da grow together. There is a clear linear relationship between lg β and lg Pe or lg Da and lg Pe.
- (4)
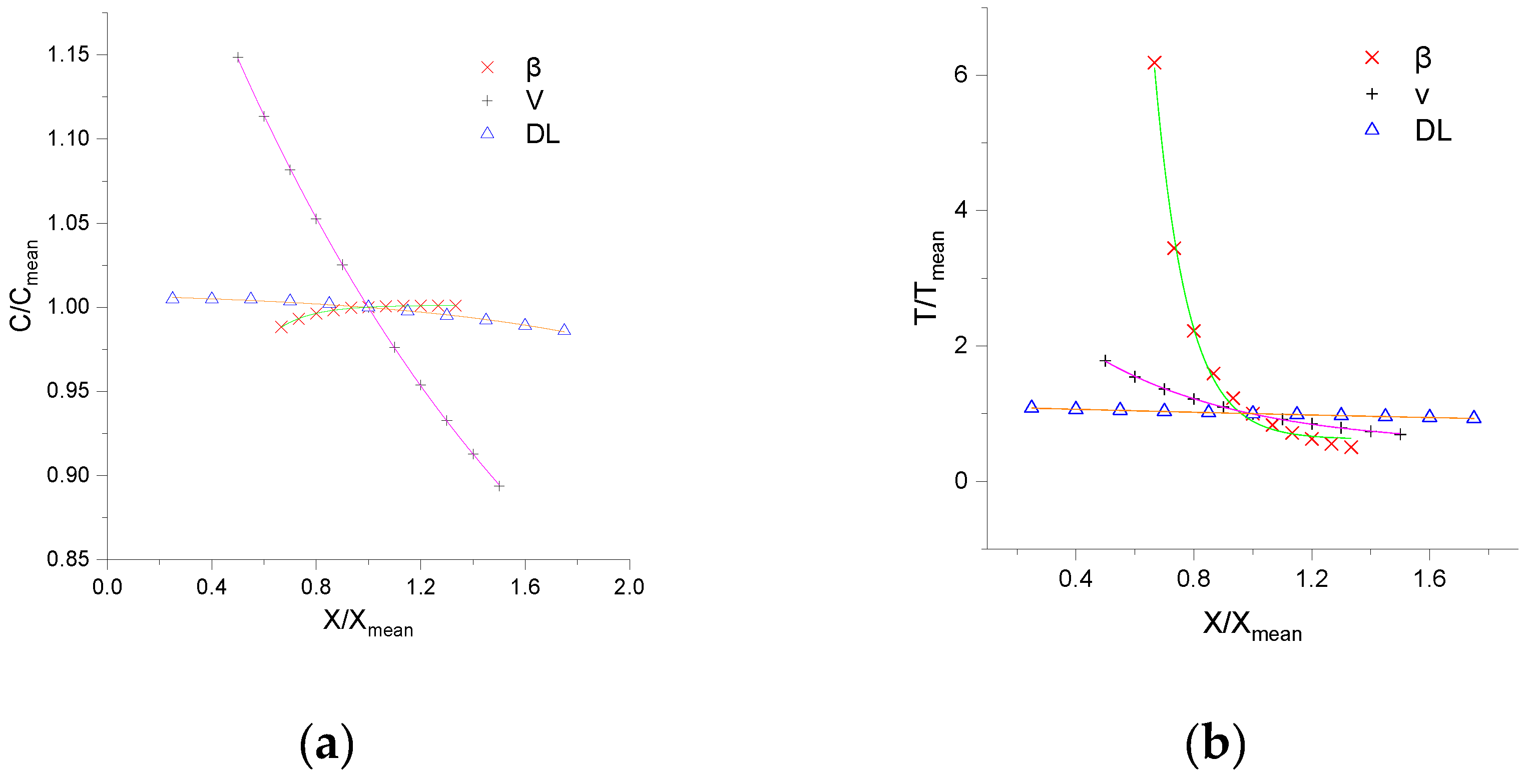
- The results of the sensitivity analysis show that peak concentration is most sensitive to V and the arrival peak time is most sensitive to β.
Author Contributions
Funding
Conflicts of Interest
References
- Brian, B.; Scher, H.; Cortis, A.; Dentz, M. Modeling Non-Fickian Transport in Geological Formations as a Continuous Time Random Walk. Rev. Geophys. 2006, 44. [Google Scholar] [CrossRef]
- Kang, P.K.; Le Borgne, T.; Dentz, M.; Bour, O.; Juanes, R. Impact of Velocity Correlation and Distribution on Transport in Fractured Media: Field Evidence and Theoretical Model. Water Resour. Res. 2015, 51, 940–959. [Google Scholar] [CrossRef]
- Lester, R.D.; Metcalfe, G.; Trefry, M.G. Anomalous Transport and Chaotic Advection in Homogeneous Porous Media. Phys. Rev. E 2014, 90, 063012. [Google Scholar] [CrossRef]
- Alina, T.; Dentz, M.; Kinzelbach, W.; Willmann, M. Mechanisms of Anomalous Dispersion in Flow through Heterogeneous Porous Media. Phys. Rev. Fluids 2016, 1, 074002. [Google Scholar]
- Hansen, K.S.; Berkowitz, B. Integrodifferential Formulations of the Continuous-Time Random Walk for Solute Transport Subject to Bimolecular a+B→0 Reactions: From Micro- to Mesoscopic. Phys. Rev. E 2015, 91, 032113. [Google Scholar] [CrossRef]
- Gabriele, C.; Bellin, A. Analytical Solution for Reactive Solute Transport Considering Incomplete Mixing within a Reference Elementary Volume. Water Resour. Res. 2013, 49, 2589–2600. [Google Scholar]
- Battiato, I.; Tartakovsky, D.M. Applicability Regimes for Macroscopic Models of Reactive Transport in Porous Media. J. Contam. Hydrol. 2011, 120, 18–26. [Google Scholar] [CrossRef]
- Battiato, I.; Tartakovsky, D.M.; Tartakovsky, A.M.; Scheibe, T. On Breakdown of Macroscopic Models of Mixing-Controlled Heterogeneous Reactions in Porous Media. Adv. Water Resour. 2009, 32, 1664–1673. [Google Scholar] [CrossRef]
- Ginn, T.R. Modeling Bimolecular Reactive Transport with Mixing-Limitation: Theory and Application to Column Experiments. Water Resour. Res. 2018, 54, 256–270. [Google Scholar] [CrossRef]
- Porta, M.G.; Ceriotti, G.; Thovert, J.F. Comparative Assessment of Continuum-Scale Models of Bimolecular Reactive Transport in Porous Media under Pre-Asymptotic Conditions. J. Contam. Hydrol. 2016, 185, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Porta, G.M.; Riva, M.; Guadagnini, A. Upscaling Solute Transport in Porous Media in the Presence of an Irreversible Bimolecular Reaction. Adv. Water Resour. 2012, 35, 151–162. [Google Scholar] [CrossRef]
- Sanchez-Vila, X.; Fernàndez-Garcia, D.; Guadagnini, A. Interpretation of Column Experiments of Transport of Solutes Undergoing an Irreversible Bimolecular Reaction Using a Continuum Approximation. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Hochstetler, L.D.; Kitanidis, P.K. The Behavior of Effective Rate Constants for Bimolecular Reactions in an Asymptotic Transport Regime. J. Contam. Hydrol. 2013, 144, 88–98. [Google Scholar] [CrossRef] [PubMed]
- Sherman, T.; Paster, A.; Porta, G.; Bolster, D. A Spatial Markov Model for Upscaling Transport of Adsorbing-Desorbing Solutes. J. Contam. Hydrol. 2019, 222, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Berkowitz, B.; Dror, I.; Hansen, S.K.; Scher, H. Measurements and Models of Reactive Transport in Geological Media. Rev. Geophys. 2016, 54, 930–986. [Google Scholar] [CrossRef]
- Noetinger, B.; Roubinet, D.; Russian, A.; le Borgne, T.; Delay, F.; Dentz, M.; de Dreuzy, J.; Gouze, P. Random Walk Methods for Modeling Hydrodynamic Transport in Porous and Fractured Media from Pore to Reservoir Scale. Transp. Porous Media 2016, 115, 345–385. [Google Scholar] [CrossRef]
- Boccardo, G.; Sokolov, I.M.; Paster, A. An Improved Scheme for a Robin Boundary Condition in Discrete-Time Random Walk Algorithms. J. Comput. Phys. 2018, 374, 1152–1165. [Google Scholar] [CrossRef]
- Edery, Y.; Dror, I.; Scher, H.; Berkowitz, B. Anomalous Reactive Transport in Porous Media: Experiments and Modeling. Phys. Rev. E 2015, 91, 052130. [Google Scholar] [CrossRef]
- Ding, D.; Benson, D.A.; Paster, A.; Bolster, D. Modeling Bimolecular Reactions and Transport in Porous Media Via Particle Tracking. Adv. Water Resour. 2013, 53, 56–65. [Google Scholar] [CrossRef]
- Nissan, A.; Dror, I.; Berkowitz, B. Time-Dependent Velocity-Field Controls on Anomalous Chemical Transport in Porous Media. Water Resour. Res. 2017, 53, 3760–3769. [Google Scholar] [CrossRef]
- Burnell, D.K.; Hansen, S.K.; Xu, J. Transient Modeling of Non-Fickian Transport and First-Order Reaction Using Continuous Time Random Walk. Adv. Water Resour. 2017, 107, 370–392. [Google Scholar] [CrossRef]
- Ben-Zvi, R.; Nissan, A.; Scher, H.; Berkowitz, B. A Continuous Time Random Walk (Ctrw) Integro-Differential Equation with Chemical Interaction. Eur. Phys. J. B 2018, 91, 1–8. [Google Scholar] [CrossRef]
- Ben-Zvi, R.; Scher, H.; Berkowitz, B. Bimolecular Reactive Transport in a Two-Dimensional Velocity Field in Disordered Media. J. Phys. A Math. Theor. 2019, 52, 424005. [Google Scholar] [CrossRef]
- Gramling, C.M.; Harvey, C.F.; Meigs, L.C. Reactive Transport in Porous Media: A Comparison of Model Prediction with Laboratory Visualization. Environ. Sci. Technol. 2002, 36, 2508–2514. [Google Scholar] [CrossRef] [PubMed]
- Raje, S.D.; Kapoor, V. Experimental Study of Bimolecular Reaction Kinetics in Porous Media. Environ. Sci. Technol. 2000, 34, 1234–1239. [Google Scholar] [CrossRef]
- Jose, S.C.; Cirpka, O.A. Measurement of Mixing-Controlled Reactive Transport in Homogeneous Porous Media and Its Prediction from Conservative Tracer Test Data. Environ. Sci. Technol. 2004, 38, 2089–2096. [Google Scholar] [CrossRef]
- Qian, J.; Zhan, H.; Zhang, Y.; Sun, P.; Liu, Y. Numerical Simulation and Experimental Study of Bimolecular Reactive Transport in Porous Media. Transp. Porous Media 2015, 109, 727–746. [Google Scholar] [CrossRef]
- Anna, P.; Jimenez-Martinez, J.; Tabuteau, H.; Turuban, R.; le Borgne, T.; Derrien, M.; Meheust, Y. Mixing and Reaction Kinetics in Porous Media: An Experimental Pore Scale Quantification. Environ. Sci. Technol. 2014, 48, 508–516. [Google Scholar] [CrossRef]
- Dentz, M.; PGouze; Carrera, J. Effective Non-Local Reaction Kinetics for Transport in Physically and Chemically Heterogeneous Media. J. Contam. Hydrol. 2011, 120, 222–236. [Google Scholar] [CrossRef]
- Liu, D.; Jivkov, A.P.; Wang, L.; Si, G.; Yu, J. Non-Fickian Dispersive Transport of Strontium in Laboratory-Scale Columns: Modelling and Evaluation. J. Hydrol. 2017, 549, 1–11. [Google Scholar] [CrossRef]
- Ben-Zvi, R.; Scher, H.; Berkowitz, B. Two-Dimensional Finite Element Method Solution of a Class of Integro-Differential Equations: Application to Non-Fickian Transport in Disordered Media. Int. J. Numer. Methods Eng. 2017, 112, 459–478. [Google Scholar] [CrossRef]
- Edery, Y.; Porta, G.M.; Guadagnini, A.; Scher, H.; Berkowitz, B. Characterization of Bimolecular Reactive Transport in Heterogeneous Porous Media. Transp. Porous Media 2016, 115, 291–310. [Google Scholar] [CrossRef]
- Navarre-Sitchler, A.; Jung, H. Complex Coupling of Fluid Transport and Geochemical Reaction Rates: Insights from Reactive Transport Models. Procedia Earth Planet. Sci. 2017, 17, 5–8. [Google Scholar] [CrossRef]
- Beisman, J.J.; Maxwell, R.M.; Navarre-Sitchler, A.K.; Steefel, C.I.; Molins, S. Parcrunchflow: An Efficient, Parallel Reactive Transport Simulation Tool for Physically and Chemically Heterogeneous Saturated Subsurface Environments. Comput. Geosci. 2015, 19, 403–422. [Google Scholar] [CrossRef]




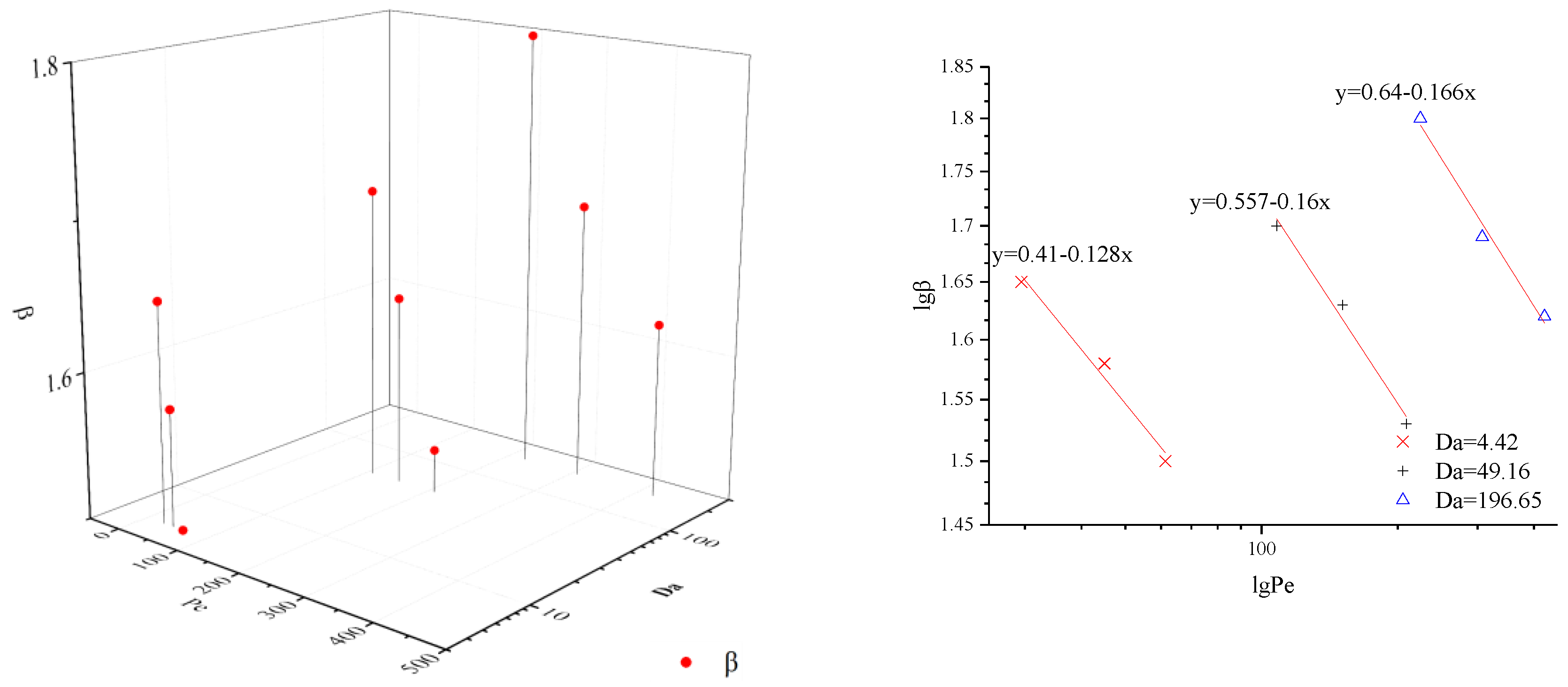
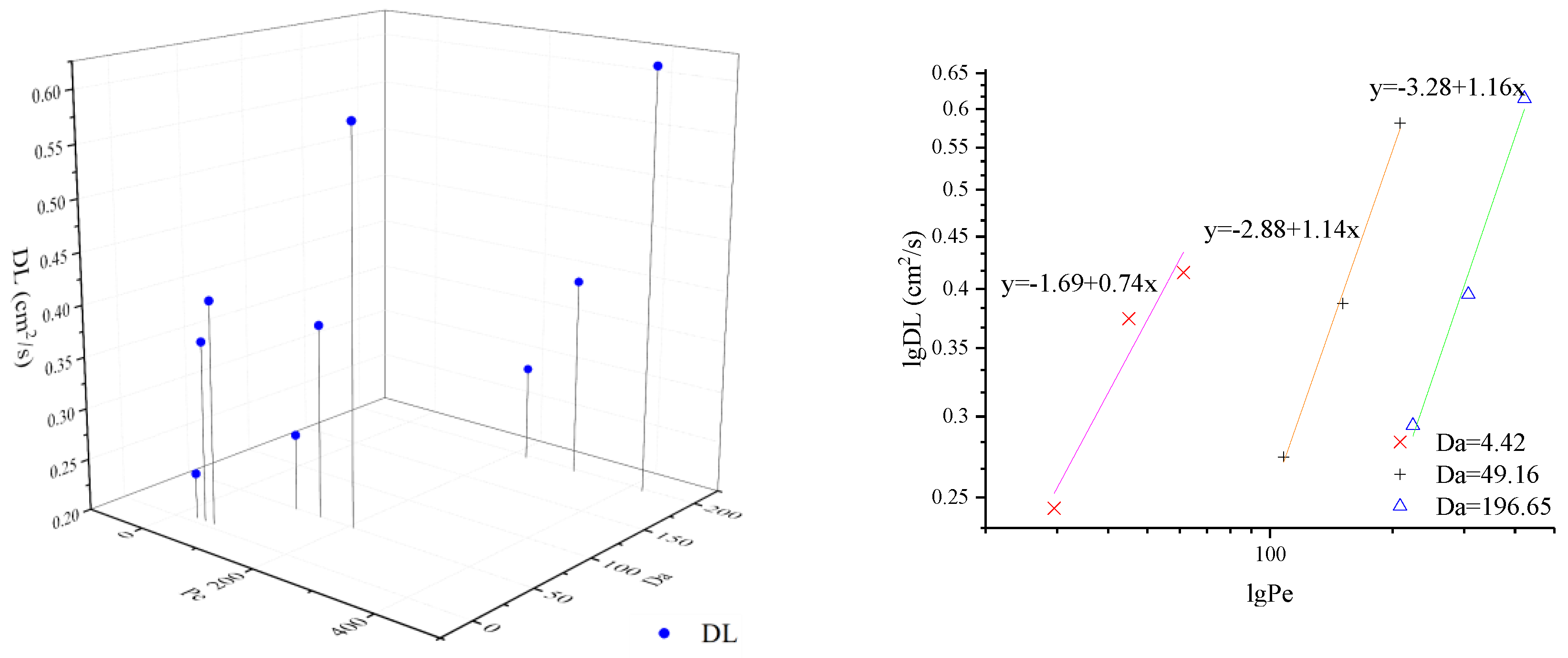
| Flow Rate (mL/min) | Media | Density (g/cm3) | V (cm/s) | Porosity | Da | Pe |
|---|---|---|---|---|---|---|
| 40.063 | fine | 1.64 | 0.131 | 0.406 | 4.42 | 29.48 |
| medium | 1.70 | 0.134 | 0.396 | 49.16 | 44.98 | |
| coarse | 1.76 | 0.137 | 0.389 | 196.65 | 61.31 | |
| 60.094 | fine | 1.64 | 0.200 | 0.406 | 4.42 | 108.00 |
| medium | 1.70 | 0.202 | 0.396 | 49.16 | 151.03 | |
| coarse | 1.76 | 0.205 | 0.389 | 196.65 | 208.78 | |
| 80.126 | fine | 1.64 | 0.261 | 0.406 | 4.42 | 224.40 |
| medium | 1.70 | 0.268 | 0.396 | 49.16 | 307.35 | |
| coarse | 1.76 | 0.273 | 0.389 | 196.65 | 422.00 |
| Flow Rate (mL/min) | Media | V(cm/s) | DL(cm2/s) | β | R2 | RMSE |
|---|---|---|---|---|---|---|
| 40.063 | fine | 0.131 | 0.244 | 1.65 | 0.991 | 0.0076 |
| medium | 0.134 | 0.274 | 1.7 | 0.993 | 0.0027 | |
| coarse | 0.137 | 0.294 | 1.8 | 0.992 | 0.0024 | |
| 60.094 | fine | 0.200 | 0.374 | 1.58 | 0.992 | 0.0023 |
| medium | 0.202 | 0.387 | 1.63 | 0.996 | 0.0024 | |
| coarse | 0.205 | 0.395 | 1.69 | 0.993 | 0.0030 | |
| 80.126 | fine | 0.261 | 0.415 | 1.5 | 0.907 | 0.0030 |
| medium | 0.268 | 0.581 | 1.53 | 0.994 | 0.0019 | |
| coarse | 0.273 | 0.614 | 1.62 | 0.999 | 0.0007 |
| Parameter | C/Cmean | T/Tmean |
|---|---|---|
| β | ||
| V | ||
| DL |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Bian, J.; Li, Y.; Zhang, C.; Ding, F. Bimolecular Reactive Transport Experiments and Simulations in Porous Media. Water 2020, 12, 1931. https://doi.org/10.3390/w12071931
Wang Q, Bian J, Li Y, Zhang C, Ding F. Bimolecular Reactive Transport Experiments and Simulations in Porous Media. Water. 2020; 12(7):1931. https://doi.org/10.3390/w12071931
Chicago/Turabian StyleWang, Qian, Jianmin Bian, Yihan Li, Chunpeng Zhang, and Fei Ding. 2020. "Bimolecular Reactive Transport Experiments and Simulations in Porous Media" Water 12, no. 7: 1931. https://doi.org/10.3390/w12071931
APA StyleWang, Q., Bian, J., Li, Y., Zhang, C., & Ding, F. (2020). Bimolecular Reactive Transport Experiments and Simulations in Porous Media. Water, 12(7), 1931. https://doi.org/10.3390/w12071931




