A Flow-Calibrated Method to Project Groundwater Infiltration into Coastal Sewers Affected by Sea Level Rise

Abstract

Collection systems in coastal cities are often below the groundwater table, leading to groundwater infiltration (GWI) through defects such as cracks and poor lateral connections. Climate-change-induced sea level rise (SLR) will raise groundwater levels, increasing the head and thus the inflow. A method has been developed to predict GWI when groundwater levels change using calibration with sewershed flow monitoring data. The calibration results in a parameter that characterizes the porosity of the collection system. A case study is presented for a coastal city with reliable flow monitoring data for eight days that resulted in a large range of effective defect sizes (minimum 0.0044 to maximum 0.338 radians), however, the range of predicted future GWI in currently submerged pipes varied by only 12% from the mean. The mean effective defect predicts 70 to 200% increases in GWI due to SLR of 0.3 to 0.9 m (1 to 3 ft), respectively, for currently submerged pipes. Predicted additional GWI for pipes that will become submerged due to SLR will increase GWI to values that approach or exceed the current average dry weather flow. This methodology can be used for planning of infrastructure improvements to enhance resiliency in coastal communities.

1. Introduction

The sea level has been rising due to ocean warming and expansion, and glaciers and polar ice caps melting [1]. This phenomenon has negatively impacted the quality of life in natural and human systems, and will continue to do so, by increasing erosion, submergence, and flooding of coastal land, loss of habitats and evacuation of homes, and saltwater intrusion and aquifer and soil contamination [2]. Sea level rise (SLR) projections by the National Oceanic and Atmospheric Administration (NOAA), range from a 0.3-m to 2.5-m rise in global mean sea level (MSL) by 2100 in the lower-bound and extreme upper-bound scenarios, respectively [3]. The 2017 NOAA projections, and earlier ones, were based on a constant SLR increase, however, the rate of SLR increases during the past few decades has been found to be accelerating at approximately 0.08 millimeters (mm) per year, each year, rather than steadily increasing as previously assumed at about 3 mm per year [4]. The new finding of accelerated SLR indicates that those projections may be underestimates which increases the concern in coastal areas, which are most affected.

In coastal communities, the groundwater table meets the sea surface at an interface and with SLR, the groundwater elevation also rises [5,6,7,8,9,10,11,12,13]. Groundwater impacts from SLR are substantial, occurring farther inland than surface water effects and causing flood volumes that rival those caused solely by surface flooding [7,10,13]. Wastewater sewer pipes located in groundwater (GW) are subject to infiltration as a function of depth below the GW table. This infiltration occurs through defects such as cracks, holes, and misaligned joints resulting from issues such as external pipe deterioration due to soil chemical composition, internal pipe crown deterioration due to sulfides, stresses from soil movement (soil shrink and swell), traffic loading, poor connections of laterals, and open laterals [14]. Sewer pipes currently located below the GW table will be subject to increased head with SLR and additional pipes will also become submerged. While a practical design criterion is to assume 10 to 25 percent (%) of domestic average dry weather flow (ADWF) as GW infiltration (GWI) [15], this value underestimates the actual amount of GWI that has been observed at many locations [16].

Increases in GWI lead to higher maintenance and treatment costs, and potentially more incidents of sanitary sewer overflows (SSOs) [17]. Planning and management tools are needed to predict increases in GWI and prioritize sanitary sewer rehabilitation. To quantify GWI, researchers have developed various methods, including GWI potential maps [18], fluid mechanics models with infiltration or permeability coefficients [16], and commercial software models [19,20,21,22]. However, these models use a general infiltration or permeability coefficient and do not account for changes in GW head. The present study used a two-dimensional (2-D) equation to estimate GWI into sanitary sewer pipes [23]. This equation uses commonly available data: surrounding soil hydraulic conductivity, groundwater elevation, pipe invert elevation, sewer pipe radius, defect position, and defect size. The equation calculates the GWI per unit length for a line defect running along the pipe wall. A previous study looked at the sensitivity of the various input variables and found that hydraulic conductivity and groundwater head are the most sensitive parameters [24]. That study also made future flow predictions based upon a defect severity matrix of hypothetical pipe conditions. In the present work, the 2-D equation was used to calculate GWI for a network of pipes for which flow monitoring data were available. A method was developed to calibrate the model with an equivalent uniform defect that results in flows that match the flow monitoring data. The calibrated model was then used to predict future GWI flows in the currently submerged pipes under conditions of SLR. The not yet submerged pipes will also experience GWI due to SLR and these flows can be predicted by either using the equivalent defect size or using the defect severity matrix.

2. Materials and Methods

The study area is a sanitary sewer network located 200 to 400 meters (m) from the coast in high-porosity soils on a tropical volcanic island that required anonymity. A flow and rainfall monitoring program was implemented for 10 consecutive weeks. Ten flow meters and two rain gauges were installed throughout nearly 9800 m of sanitary sewer lines. The flow meters logged level and velocity readings every five minutes, and the rain gauges recorded precipitation every five minutes. As part of quality control, weekly operation and maintenance visits and data downloads were performed. The flow meters were Teledyne Isco 2150 Area Velocity Modules and utilized continuous wave Doppler technology to measure content level and velocity (Teledyne ISCO, Lincoln NE). For this study, one flow meter location was selected that measured 1445 m of upstream sewer line. This meter was selected because some of the pipes are already submerged in groundwater, the location does not experience surcharging, and typical diurnal flow patterns were observed. This portion of the system experiences an ADWF of approximately 400 m³ d⁻¹ and has an estimated flow capacity of 4000 m³ d⁻¹. The groundwater level is continuously measured in a nearby U.S. Geological Survey (USGS) monitoring well which shows that the groundwater is affected by tides. The data from the USGS well and their published mean groundwater level contours for the whole city were used to estimate the groundwater elevation at the flow meter location and at every pipe in the upstream sewer lines.

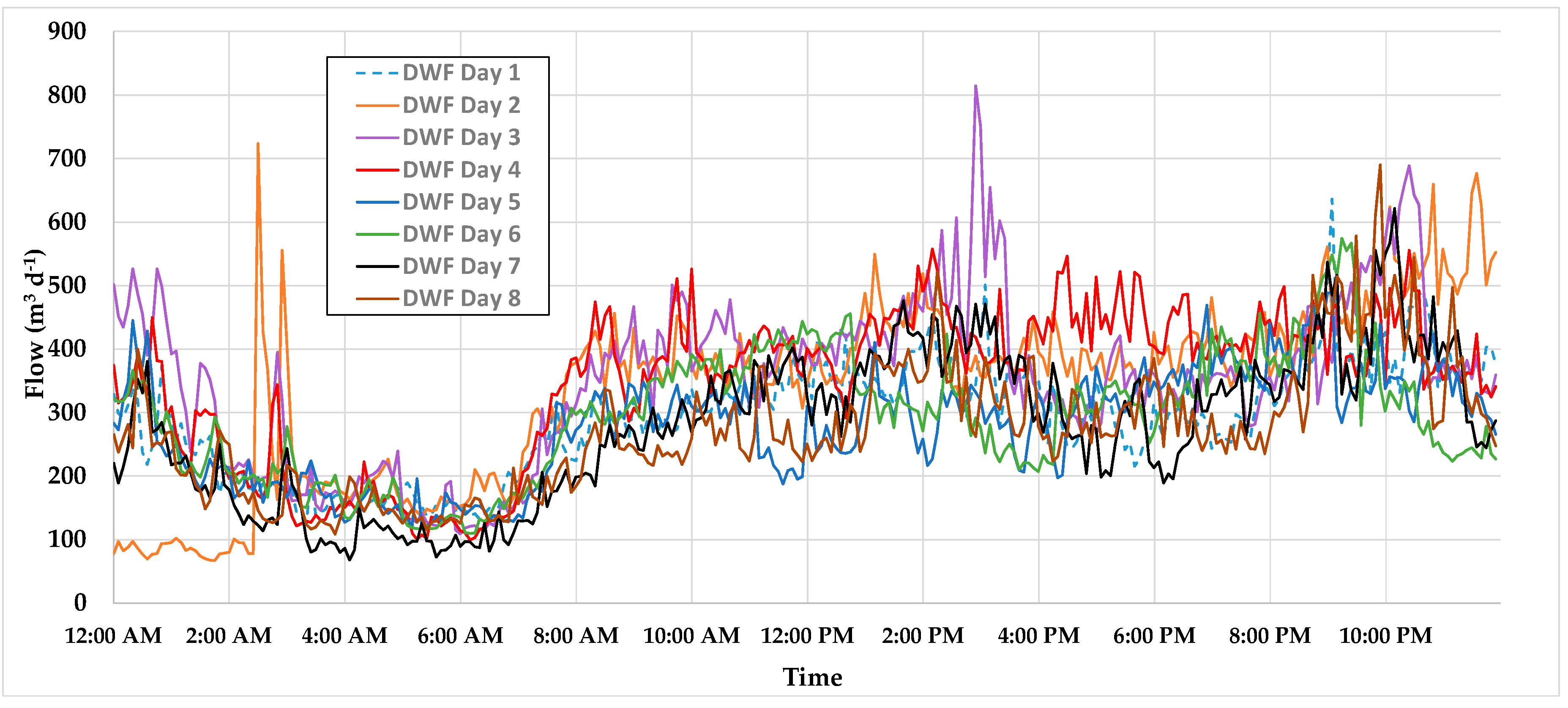
The U.S. Environmental Protection Agency’s Sanitary Sewer Overflow Analysis and Planning (SSOAP) software [25] was used to estimate GWI of the upstream pipes measured at the flow meter, which is noted herein as Q_{Actual, All Pipes}. SSOAP is a comprehensive tool that takes flow data and rainfall data and determines data suitability, dry weather flows, rainfall inflows, and GWI. Flow monitoring data and rainfall data were uploaded to SSOAP and GWI values were determined based on two criteria: (1) nighttime minimum flow and (2) dry weather flow (DWF) [25,26]. Days were selected as DWF days by SSOAP if the precipitation did not exceed a maximum amount of 2.54 mm over the preceding three days. For this study, eight dry weather flow (DWF) days met the criteria, and a Q_{Actual, All Pipes} was determined for each day using SSOAP to analyze the hydrographs which are shown in Figure 1. Flow measurement campaigns result in somewhat messy data, however, a previous study has shown that as long as eight different days of data are utilized, the uncertainty in the determined value of GWI is reduced threefold compared to a single day of data, and additional data points do not significantly further reduce uncertainty [27].

Statistical analysis of cross-correlation was used to compare the different time series among DWF Days 1–8 at various lags. The results allowed us to evaluate the strength between two series and determine the lag that maximized the correlation between them. The cross-correlation was calculated between flows on DWF Day 1 and each of the other DWF days.

Table 1. Summary of highest cross-correlations with DWF Day 1 data and the significance.

DWF Day	Highest Cross-Correlation			Significance at 95% Level of Confidence
	Lag τ	Cross-Correlation rτ	Period in Minutes	Observed t Value	Significant (>1.96)?
2	1	0.00005701	5	0.00096	No
3	1	0.0001975	5	0.0033	No
4	0	0.0001157	0	0.0020	No
5	0	0.00005764	0	0.00097	No
6	8	0.0001056	40	0.0018	No
7	0	0.0001482	0	0.0025	No
8	−1	0.0001052	5	0.0018	No

lists the highest cross-correlation r_τ and the lag τ at which they occur. Because the corresponding periods (Δt*τ) are near the time origin for each of these r_τ, the correlations are maximized close to the zero lag position, which confirms that the data sets are most similar when their time axes directly overlap.

The cross-correlations can also be tested in two-sided t-tests with the null hypothesis that the two compared series statistically have the same means at the 95% confidence level. Since n is large, our critical t is 1.96, based on the normal distribution. If the observed t statistic exceeds the critical t value, then we reject the null hypothesis and conclude that the two series are not the same. As shown in Table 1, each observed t statistic is less than the critical t value. Therefore, the null hypothesis cannot be rejected, and we conclude that the samples have the same statistical means at the 95% confidence level.

The GWI (Q_{Actual, All Pipes}) determined by SSOAP Toolbox is the sum of GWI in all upstream pipes.Therefore, a method was developed to calculate the GWI in each pipe segment. The 2-D model (Equation (1)) assumes the surrounding soil is homogeneous and isotropic with a constant hydraulic conductivity, and the groundwater table is horizontal [23]. The input parameters are sewer radius (r), sewer defect size (β), defect location on the pipe circumference (α), wastewater head above the pipe defect (P_i), groundwater head above pipe center (h), and hydraulic conductivity of the surrounding soil (K). This equation calculates the flow per unit length of pipe through a uniform crack along the length of the pipe [23].

$$\begin{gathered} \mathrm{Q}=2\mathsf{\pi }\mathrm{K}\left(\mathrm{h}\frac{1-{\lambda }^{\prime 2}}{1+{\lambda }^{\prime 2}}-{\mathrm{P}}_{\mathrm{i}}\right){\ln }^{-1}\left(\frac{2\mathsf{\pi }}{\mathsf{\beta }}\left(\frac{\mathrm{h}}{\mathrm{r}}-\sin \mathsf{\alpha }\right)\left(1+\sqrt{1-{\left(\frac{\mathsf{\beta }}{2\mathsf{\pi }\left(\frac{\mathrm{h}}{\mathrm{r}}-\sin \mathsf{\alpha }\right)}\right)}^2}\right)\right) \\ \mathrm{With}{\lambda }^{\prime }=\frac{2\mathsf{\pi }}{\mathsf{\beta }}\left(\frac{\mathrm{h}}{\mathrm{r}}-\sin \mathsf{\alpha }\right)-\sqrt{{\left(\frac{2\mathsf{\pi }}{\mathsf{\beta }}\left(\frac{\mathrm{h}}{\mathrm{r}}-\sin \mathsf{\alpha }\right)\right)}^2-1} \end{gathered}$$

(1)

where:

• Q = inflow rate per unit length of pipe (m³ d⁻¹ m⁻¹)
• K = hydraulic conductivity of the surrounding homogeneous soil (m d⁻¹)
• h = groundwater head above pipe centerline (m)
• P_i = internal pressure head due to depth of water above defect, equal to atmospheric pressure (P_ii = 0) when defect is above the content level or pipe is empty (m)
• β = defect size, expected to be small (0 − π/18) otherwise soil particles wash into
• pipe (0 − π/18) (radian)
• r = pipe radius (m)
• α = defect location (0 − 2π) (radian)

Available data were used for pipe radii 7.62 to 12.7 cm (6 to 10 in), hydraulic conductivity (K) of soil surrounding each pipe section (for most pipes = 0.000042 m s⁻¹, and for some pipes = 0.00014 m s⁻¹), pipe invert elevations (mean of upstream and downstream ends), and groundwater elevations (0.3 to 0.5 m above MSL in the study area). The h for each pipe was calculated by subtracting the mean pipe invert elevation and radius from the groundwater elevation. Structural analysis tests have found that line defects are usually generated at the crown, invert, and springlines: α = π/2, 3π/2, 0 and π, respectively [28,29]. When the defect is above the pipe content level (P_i = 0), then a crown defect (α = π/2) leads to the largest rates of GWI [23]. Thus the defect location was assumed at the crown which is the worst-case scenario. Defect size β was the target parameter for calibration.

The model GWI (Q_Model) was calculated for each 3.05 m (10 ft) section of pipe that is fully or partially submerged in the 1445 m pipe network upstream of the flow meter using an iteration procedure. An initial guess value of β is chosen, allowing calculation of GWI for each pipe segment (Q_{Model, Pipe Segment}) and these are summed to obtain a total (Q_{Model, All Pipes}). The proportioning in Equation (2) must be obeyed and thus an iteration test can be set up. From Equation (2), the estimated right-hand side values multiplied by the measured Q_{Actual, All Pipes} give a trial value of GWI for each pipe segment (Q_{Actual, Pipe Segment}). The value of β is iterated until all of the Q_{Model, Pipe Segment} and Q_{Actual, Pipe Segment} values match. This was completed in a spreadsheet, but could be coded in MatLab or made into a plug-in for other collection system software. The resulting calibrated value of β we call the “effective β” (Eβ), which can be thought of as the size of a single crack in every pipe in the network that would result in the measured amount of GWI. It is not an actual crack size, but the size of an equivalent crack that would account for all types of GWI such as cracks, holes, misaligned pipes, poor lateral connections, and so forth. It is a measure of the overall leakiness or porosity of the system. Once known, the Eβ can be used to calculate new values of GWI when the head (h) is increased due to SLR (or other causes).

$$\frac{{\mathrm{Q}}_{\mathrm{Model},\mathrm{Pipe}\mathrm{Segment}}}{{\mathrm{Q}}_{\mathrm{Model},\mathrm{All}\mathrm{Pipes}}}=\frac{{\mathrm{Q}}_{\mathrm{Actual},\mathrm{Pipe}\mathrm{Segment}}}{{\mathrm{Q}}_{\mathrm{Actual},\mathrm{All}\mathrm{Pipes}}}$$

(2)

The calibrated values of Eβ are used to calculate projected Q_{Model, Pipe Segment} values using Equation (1), which are summed to get the projected GWI. Although SLR-induced groundwater rise is not spatially uniform due to the heterogeneous depositional environmental and hydraulic properties of geologic materials [30], the study area described herein was in such close proximity to the coastline that spatial effects were negligible and a 1:1 ratio of groundwater rise to SLR was used. Although NOAA recommends that the extreme scenario be used to plan for infrastructure when there is low tolerance for risk [31], a range of SLRs were evaluated to expand the amount of potential projections. The study area has both a wet and dry season, and although the study took place in the wet season, selection criteria were used to identify and isolate days of DWF. Other factors that can play a role in GWI include ocean tides, seasonal recharge rates, and fluctuations in nearby rivers or bodies of water [6,16,17]. Tidal effects on groundwater elevations were included in the present study. The effect of tides were studied previously at a different location within 300 m of the coast where time-linked flow and tide data were available, and the daily tides caused groundwater fluctuations of +/− 0.1 m which resulted in GWI variations of +/− 4% in GWI [24].

3. Results

In the study area, approximately 6% (90 m) of the 1445 m of sewer lines (all of sizes 15, 20, and 25 cm; 6, 8, and 10 in), are currently located below the groundwater table and therefore affected by GWI. Based on monitoring data and SSOAP Toolbox analysis, there were eight days of data that met the quality requirements (

Table 2. Measured GWI and effective β calibration for each dry weather flow day.

DWF Day	Length Affected (m)	GWI Measured (m3 d−1)	GWI/ADWF (%)	Eβ (βi: π/18) (Radians)	Eβ (βi: π/32) (Radians)	Eβ (βi: π/90) (Radians)	Average Eβ (Radians)
1	101.3	156.3	39	0.180	0.182	0.186	0.183
2	101.3	80.6	20	0.0051	0.0043	0.0037	0.0044
3	98.3	154.8	39	0.206	0.209	0.213	0.209
4	95.2	138.5	34	0.153	0.155	0.158	0.156
5	86.1	145	36	0.313	0.321	0.331	0.321
6	86.1	142.7	35	0.295	0.303	0.312	0.303
7	86.1	99.2	25	0.062	0.062	0.063	0.062
8	83	140.4	35	0.332	0.337	0.344	0.338
AVG	92	132	33	0.193	0.197	0.201	0.197
Std Dev	8	27	7	0.12	0.12	0.13	0.12

), and the mean GWI was measured to be 132 m³ d⁻¹ with a standard deviation of 27 m³ d⁻¹. The values ranged from a low of 81 (39% lower than mean) to a high of 156 m³ d⁻¹ (18% higher than the mean). The differences are typical of sewer monitoring campaigns and can be caused by many factors, such as different days of the week, different numbers of residents and visitors, and accuracy of flow-measuring devices. In this study, we used all eight measured GWI flow values (Q_{Actual, All Pipes}) to observe the effects on calibration (Eβ) and future predictions. Table 2 shows that the mean groundwater elevation was not the same on each flow monitoring day due to tides which resulted in different lengths of sewer pipe affected. The fraction of GWI to ADWF is 20 to 39% for this section of sewer collection system.

The calibration procedure described above using Equations (1) and (2) was utilized to determine the Eβ values shown in Table 2. The average Eβs range from 0.0044 to 0.338 radians with a mean of 0.197 and standard deviation of 0.12. While this seems like a large range, it results in a reasonable range of predicted future flows resulting from SLR of 0.3 to 1.2 m (

Table 3. Projected GWI due to future SLR in currently submerged pipes.

SLR (m)	0	0.3	0.6	0.9	1.2
DWF Day	GWI (m3d−1)
1	156	255	353	447	538
2	81	200	281	358	433
3	155	253	351	445	537
4	139	208	291	372	449
5	145	246	340	432	521
6	143	236	328	417	503
7	99	207	291	371	449
8	140	208	291	372	449
Mean	132	227	316	402	485
Increase	0	72%	139%	204%	267%
% Dif. from Mean	Low	11.9	11.1	10.9	10.7
	High	12.3	11.7	11.2	10.9

). For each 0.3 m increment of SLR, the range of future flows predicted using the calibrated Eβs is such that the low and high values are only 11 to 12% smaller or greater than the mean predicted value. In the procedure, it was found that the initial guess of β has a minor effect on the determined values of Eβ (Table 2). For each DWF day, three different initial guess βs (π/18, π/32, and π/90) were used. For example, Table 2 shows that DWF Day 6 has calibrated βs of 0.295, 0.303, and 0.312 for initial βs of π/18, π/32, and π/90, respectively. Nevertheless, an overall mean of the calibrated βs, 0.197 radians, can be identified as the overall Eβ of this portion of the collection system. By the year 2100, the projected mean GWI is 227 m³d⁻¹ (72% increase) in a low-risk scenario of a 0.3 m rise in sea level, and GWI increases by 204% in an intermediate-risk scenario of about 0.9 m SLR (Table 3), which is equivalent in magnitude to the current ADWF (i.e., the ADWF is predicted to double when SLR is 0.9 m just considering the currently submerged pipes). Predictions can be made for greater amounts of SLR, however, the amount of unsaturated ground above the buried sewer pipes (space available for groundwater elevation rise due to SLR) is limited in coastal areas and thus predictions have been limited to SLR of 1.2 m herein.

The flows in Table 3 are the projections just for the currently submerged pipes that will experience greater groundwater head. As SLR occurs, additional upgradient sections of pipe will become submerged and contribute GWI (Figure 2). There are at least two ways to estimate the GWI for the pipes that will become submerged in the future as groundwater levels increase. First, if the nature of the pipes (materials, age, etc.) is similar to the downgradient pipes, the overall mean calibrated Eβ value or the full range of Eβs for different measured GWIs could be assumed to apply to the newly submerged pipes. Second, a hypothetical pipe condition approach (defect severity matrix) [24] could be used. Figure 3 shows the Eβ approach with the future submerged pipes represented in the upper curves (highest Eβ (0.338), mean Eβ (0.197), and the two lowest Eβs (0.0044 and 0.062) and the currently submerged pipes (alone) shown in the lower curves. Figure 3 indicates a scenario where the future submerged pipes have a much larger contribution than the currently submerged pipes because the percentage of pipes submerged (Figure 2) increases dramatically from the present 6% to approximately 30% in the future scenarios. Figure 3 shows the range of projections for SLR up to 1.2 m and

Table 4. Projected GWI flows for a range of effective β and SLR of 0.3 to 0.9 m.

		SLR (m)	0	0.3	0.9
WF Day	Pipes	β	GWI (m3d−1)
2	Existing Submerged Only	0.0044	81	200	358
	Existing + Future Submerged	0.0044		232	1182
	Increase Due to Future Pipes	0.0044		16%	230%
mean	Existing Submerged Only	0.197	132	227	402
	Existing + Future Submerged	0.197		431	2023
	Increase Due to Future Pipes	0.197		90%	403%
3	Existing Submerged Only	0.338	155	253	445
	Existing + Future Submerged	0.338		504	2280
	Increase Due to Future Pipes	0.338		99%	412%

shows the projected values of GWI for the cases of a low-risk scenario of a 0.3 m rise in sea level, and an intermediate-risk scenario of about 0.9 m SLR. Table 4 shows that the GWI for currently submerged pipes alone will almost double with 0.3 m of SLR and will approach or exceed the current ADWF (approximately 400 m³d⁻¹) with 0.9 m of SLR. This would be problematic, however, unless all the pipes not yet submerged are perfectly sealed and do not contribute any GWI (generally not possible), the future flows will be much larger. When considering the future submerged pipes, the magnitude of GWI will approach or exceed the current ADWF with SLR of just 0.3 m. The increase in GWI due to the future submerged pipes is 230 to 412% greater than the increase from the currently submerged pipes at 0.9 m of SLR. This situation is specific to this section of a case study collection system in which a large percentage of the pipes will become submerged and the currently submerged network is quite “leaky” or “porous” (GWI is over 30% of ADWF) compared to more typical ranges (10–15%) often assumed [15].

Table 5. Relationships between β (defect size) in radians and cm for different pipe sizes.

Diameter	Defect Size (cm)
cm (in)	β: π/90	β: π/32	β: π/18	β: 0.197	β: 0.0044	β: 0.062	β: 0.338
15 (6)	0.27	0.75	1.3	1.5	0.034	0.47	2.6
20 (8)	0.35	1.00	1.8	2.0	0.045	0.63	3.4
25 (10)	0.44	1.25	2.2	2.5	0.056	0.79	4.3

shows just how large (cm) the equivalent defect openings are for the various β values including calibrated values and assumed initial values.

Instead of using the calibrated Eβ for projecting future GWI values, a hypothetical range of pipe conditions can be investigated. A pipe defect severity matrix [24] was developed with 12 cases of varying degrees of defect size (from π/90 to π/18) and percent of sewer pipe length affected by GWI (5% to 100%) (see

Table 6. Defect severity cases for pipes newly submerged due to SLR.

Increasing % of Sewer Line Length Affected
Increasing Defect Size	Case 1 β = π/90 ≈ 0.035 % affected = 5%	Case 4 β = π/90 ≈ 0.035 % affected = 30%	Case 7 β = π/90 ≈ 0.035 % affected = 75%	Case 10 β = π/90 ≈ 0.035 % affected = 100%
	Case 2 β = π/32 ≈ 0.10 % affected = 5%	Case 5 β = π/32 ≈ 0.10 % affected = 30%	Case 8 β = π/32 ≈ 0.10 % affected = 75%	Case 11 β = π/32 ≈ 0.10 % affected = 100%
	Case 3 β = π/18 ≈ 0.17 % affected = 5%	Case 6 β = π/18 ≈ 0.17 % affected = 30%	Case 9 β = π/18 ≈ 0.17 % affected = 75%	Case 12 β = π/18 ≈ 0.17 % affected = 100%

). The columns (e.g., Cases 1–2–3) represent increasing defect size for a constant percentage of pipes affected, while the rows (e.g., Cases 1–4–7–10) represent increasing percentage of pipes affected for a constant defect size. The 12 cases can be grouped as follows: Cases 1-2-4 can be called “mild” porosity (green); Cases 3–5–6–7–8–10 can be considered “moderate” porosity (yellow); and Cases 9–11–12 can be considered “severe” porosity (red). The 12 cases can be used to make projections and investigate the possible range of resulting GWI, or a smaller set of cases can be examined based upon other potentially available information such as sewer system CCTV inspection videos to assign possible cases to sections of pipe or whole sewersheds. Figure 4 shows the projections for all 12 of the cases in Table 6 plus the projection using the average Eβ value (0.197 – black line) and the GWI projections for existing submerged pipes only (purple line).

Figure 4 shows that there is a larger effect of the percentage of pipes affected (with defects), compared to the defect size. For an SLR of 0.3 m, Case 1 projects GWI 224 m³ d⁻¹ for 5% of newly submerged pipes with a defect size of π/90, while Cases 4, 7, and 10 project GWI of 258 m³ d⁻¹, 320 m³ d⁻¹, and 354 m³ d⁻¹, respectively, for increasing percentages of affected pipes with the same defect size. Compared to Cases 2 and 3 with increasing defect sizes but the same percent affected, GWI rates are 226 m³ d⁻¹ and 227 m³ d⁻¹, respectively, which are much smaller increases. It is also noteworthy that the projections for the existing submerged pipes alone and the projections using the average calibrated Eβ (0.197) bracket all of the 12 defect severity cases.

4. Discussion

The magnitude of the increases in GWI due to future SLR determined herein (70% or 200%) may or may not be significant—that depends on the local conditions such as the current amount of GWI relative to ADWF, and the length of additional pipe that will be affected as SLR occurs. For the case study presented here, the amounts of future projected GWI are high (up to 100% or more) relative to the current ADWF of 400 m³d⁻¹, but still relatively small (about 10%) compared to the pipe capacity (estimated as 4000 m³d⁻¹). It is noted here that this study is for only one sewershed which represented about 15% (1445 m of 9800 m total) of the collection system for the wastewater treatment plant WWTP. In order to make projections for the whole system, the other parts of the collection system would also have to be monitored and calibrated using the same procedure. This would allow determination of which sewersheds contribute the most GWI presently and in the future and thus where rehabilitation/replacement should be focused in preparation for SLR. Our previous study [24] found that for a different large coastal city where a larger fraction (25%) of the submerged portion of the collection system was included, the GWI is currently approximately 7% of the 230,000 m³ d⁻¹ ADWF and future projections of SLR of 0.2 m, 0.4 m, and 0.9 m could result in ADWFs increasing by 3.5%, 8.7%, and 23.9%, respectively. That case showed that impacts will increase slowly, potentially for many years, but eventually these flows will be impactful. Other studies from around the world have found a wide range of GWI as a percentage of ADWF for current conditions for whole-system analyses (rather than individual sewersheds). Whittenberg and Askoy [15] note that often GWI is assumed to be approximately 10–25% of ADWF, while data they reviewed suggested an average of 27% in Seoul Korea, with evaluations in Germany, Italy, and Canada reporting values from 39% to 70%. Dirckx et al. [18] report GWI in the range of 40–50% of ADWF in Belgium. De Benedittis and Bertrand-Krajewski [27] reported GWI of about 20% of ADWF in Lyon, France. Liu et al. [17] summarized GWI ranges as: 73% in Nante, France, 108% in Rastatt, Germany, 39% in Zurich, Switzerland, 33% in Dresden, Germany, 14–50% in Rome, Italy, and 75% in Trondheim, Norway. The values reported in the present study are within the ranges reported in some of the prior studies.

Karpf et al. [16,19,21] have used a multiregression method to analyze inflow and infiltration (I/I) in Dresden, Germany. A series of 400 WWTP influent hydrographs were used to separate three forms of I/I: groundwater, surface water, and rainwater. They found that ADWF was about 72,000 m³ d⁻¹ and that GWI varied from about 9600 to 24,000 m³ d⁻¹ (13 to 33%). This method uses hydrographs at the WWTP and is not able to do predictions of GWI if groundwater levels change. Cahoon and Hanke [32] also used multiregression analyses of flow records to separate out ocean tide effects from total flows received at 19 WWTPs in coastal North Carolina. They found the effect of sea level (high tides) was from 5% to 35% of total flows to the treatment plants. Karpf and Krebs [22] used MODFLOW 3D simulations and a nonlinear infiltration equation which uses Darcy’s law to calculate GWI and came up with an infiltration factor K_IN and an area of leakage per unit length of sewer (A_L) and thus is similar to the approach here. Their method could be used to predict changes in GWI due to changes in groundwater head, but this was not an aspect of their research. Their method utilizes Monte Carlo simulations and sewer hydrographs and thus is more complicated than the approach herein. DeSilva et al. [14], Vollertsen and Hvitved-Jacobsen [33], and Rauch and Stegner [34] use Darcy’s law directly instead of the Guo [23] equation to calculate GWI. They define the area of flow as the defect area, the delta head as distance to GW table, and delta L as the thickness of the boundary layer which is set to 10 cm. They introduce a “leakage factor” k_f which has the same units as hydraulic conductivity and recommend values of 0.001 to 0.01 s⁻¹. Those works do not attempt to predict GWI when groundwater head changes.

Thorndahl et al. [20] coupled two commercial software models, MIKE SHE (groundwater transport) and MIKE MOUSE (sewer hydraulics), to model GWI. In their study area in Denmark, GWI is approximately 50% of ADWF. MIKE SHE was used to model groundwater elevations and was coupled to MIKE MOUSE with an equation that is based on Darcy’s law. They used the area of opening as 0.5 radians times pipe length (same as beta = π/6.3 or 0.5 radians), then used an infiltration coefficient (C_L) which is like an effective hydraulic conductivity. They report that C_L should be about 1 × 10⁻⁶ for separate wastewater collection systems, but use it as the adjustment parameter to calibrate to flow data. This approach is very similar to the approach herein, except that the Guo equation [23] uses the actual hydraulic conductivity of the surrounding soil, and the opening size is more realistic. The GWI values that were measured in our study are much larger than those found in the Thorndahl study [20]. Our GWI values result in C_L values of 2.5 to 4.3 × 10⁻⁴. The reason for this is that the rates of GWI are very different. The Thorndahl et al. study area has measured flows of approximately 45 m³ d⁻¹ km⁻¹. The study presented herein has much higher average measured GWI flows of 1435 m³ d⁻¹ km⁻¹, which is more than 30 times greater. The Thorndahl et al. method could be used to predict future flows due to SLR with the calibrated linked models, however, this was not a focus of their studies [20].

Here we introduce a new parameter related to the infiltration coefficients and leakage factors described above. The “leakage number” (LN) can characterize the overall porosity of the system (see Equation (3)).

$$\mathrm{LN}=\frac{{\mathrm{E}\mathsf{\beta }}_{\mathrm{Avg}}{\times \mathrm{r}}_{\mathrm{Avg}}{\times \mathrm{L}}_{\mathrm{pipe}\mathrm{affected}}{\times \mathrm{H}}_{\mathrm{Avg}}\times 86400}{\mathrm{GWI}}$$

(3)

where:

• LN = leakage number, s
• Eβ_avg = average Eβ from calibration, radians,
• r_avg = average radius of the submerged pipes, m,
• L_{pipe affected} = length of submerged pipes, m,
• H_avg = average groundwater head for submerged pipes, m
• 86,400 = s d⁻¹
• GWI = measured average GWI for the submerged pipes, m³ d⁻¹

Table 7. Calculated values of leakage number to characterize overall system porosity.

GWI (m3 d−1)	Eβ (Radians)	Lavg (m)	Havg (m)	LN (s)
80.6	0.0044	92	0.648	36
86.1	0.062	92	0.648	471
132	0.197	92	0.648	976
140.4	0.338	92	0.648	1575
132	π/180	92	0.648	86
132	π/90	92	0.648	173
132	π/32	92	0.648	486
132	π/18	92	0.648	865

shows the calculated values of LN which range from 36 to 1575 s. Calibration values of Eβ from the smallest values (0.0044 and 0.062) to the largest (0.338) are shown in the table. The overall average calibration Eβ is 0.197, which gives an LN value of 976. Portions of sewersheds with high porosity will have larger values of LN and larger values of GWI. Future studies of additional collection systems will provide additional values of LN and can be used to establish ranges that represent low, medium, and high porosity or leakiness.

5. Conclusions

This study developed and tested a procedure that uses flow and rainfall monitoring data to calibrate a model and project future GWI rates as groundwater head increases due to SLR. The calibration results in an effective defect size (Eβ) and a leakage number (LN) which are measures of the overall porosity of the collection system being modeled. It accounts for all the cracks, holes, misaligned pipes, leaky lateral connections, cave-ins, and other defects that allow GWI to occur. This same procedure can be used for any situation in which groundwater elevations change, for example, due to stormwater recharge, seasonal fluctuations in hydraulically connected water bodies (such as a lake or river), long-term unsustainable drawdown of potable water, or short-term excessive drawdown to meet drought demands. As shown, a flow monitoring campaign can result in multiple different measurements of actual GWI for a single flow monitoring location which will result in different Eβ calibrations. The calibration is only as good as the data, and the future predictions are only as good as the calibration. Thus, professional judgment and experience will be required to select the “official” calibration or a range of values that should be used. In a large-scale monitoring campaign, multiple sewersheds could be evaluated and Eβs determined and then these can be applied to other similar sewersheds that are not monitored. The flows in all sewershed contributing to a WWTP could be summed to estimate the overall impact of SLR. The individual sewershed results can be used to target rehabilitation/replacement projects in the most cost-effective manner. In the event that monitoring data is not available, the defect severity matrix can be applied to the sewer network as was done in Budd et al. [24]. It can also be tailored with system inspection knowledge to better select defect sizes and percent of lines affected for each case. Awareness of this issue followed by more detailed evaluations of affected areas can be a useful tool for use in sewer master planning and could potentially be a significant oversight if left out. SLR is here now, it is accelerating, and wastewater engineers designing long-lifespan infrastructure need to consider its effect on GWI.