Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments
Abstract
:1. Introduction
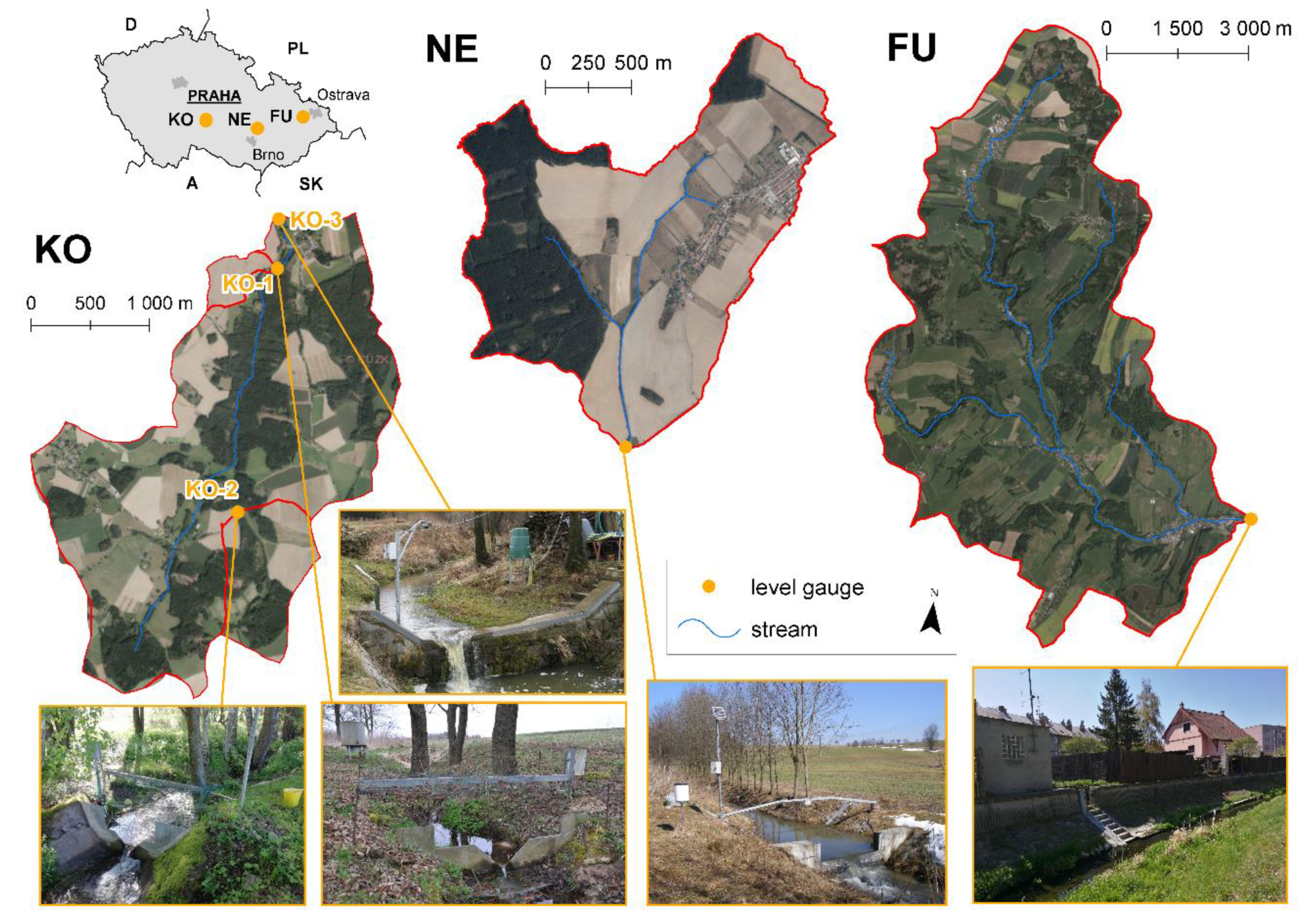
2. Study Area
2.1. Husí Creek Catchment (FU)
2.2. Suchý Creek Catchment (NE)
2.3. Kopaninský Creek Catchment (KO)
3. Materials and Methods
3.1. Data Collection
3.2. Estimate of CN Values
3.3. Events, Determination of λ
- precipitation level P (mm),
- rainfall event’s duration (h),
- maximum rain intensity imax (mm h−1),
- five- and 10-day rainfall accumulations P5d and P10d (mm),
- direct-runoff level Q was calculated (mm),
- initial abstraction Ia (mm), which was calculated as the rainfall level at the moment when direct runoff begins. Such a procedure has been used for instance in research by Shi et al. [11]. However, in large watersheds and/or in case of uneven spatial distribution of precipitation such a calculation of Ia might be problematic as the runoff needs some time to reach the watershed’s outlet [24].
3.3.1. Principal Component Analysis, Cluster Analysis
3.3.2. Modified λ with Tabulated CNs
Discrete λ
Interpolated λ
3.3.3. λ Modifications Not Dependent on Tabulated CNs
Event Analysis
- The total runoff Q and the initial abstraction Ia were calculated using the procedures described above (Section 3.3).
- The maximum potential retention, S, was an unknown parameter that was calculated using equation
- 3.
- The initial abstraction coefficient λ values were determined by dividing Ia by S for each rainfall-runoff event. Mean and median λ were calculated for each experimental watershed.
- 4.
- Regression of S, according to P10d, was calculated and used for the validation together with mean and median λ.
Model Fitting
3.4. Comparison of Estimated Runoff
3.5. HEC-HMS Simulations
4. Results
4.1. Influencing Parameters
4.1.1. Principal Component Analysis
4.1.2. Cluster Analysis
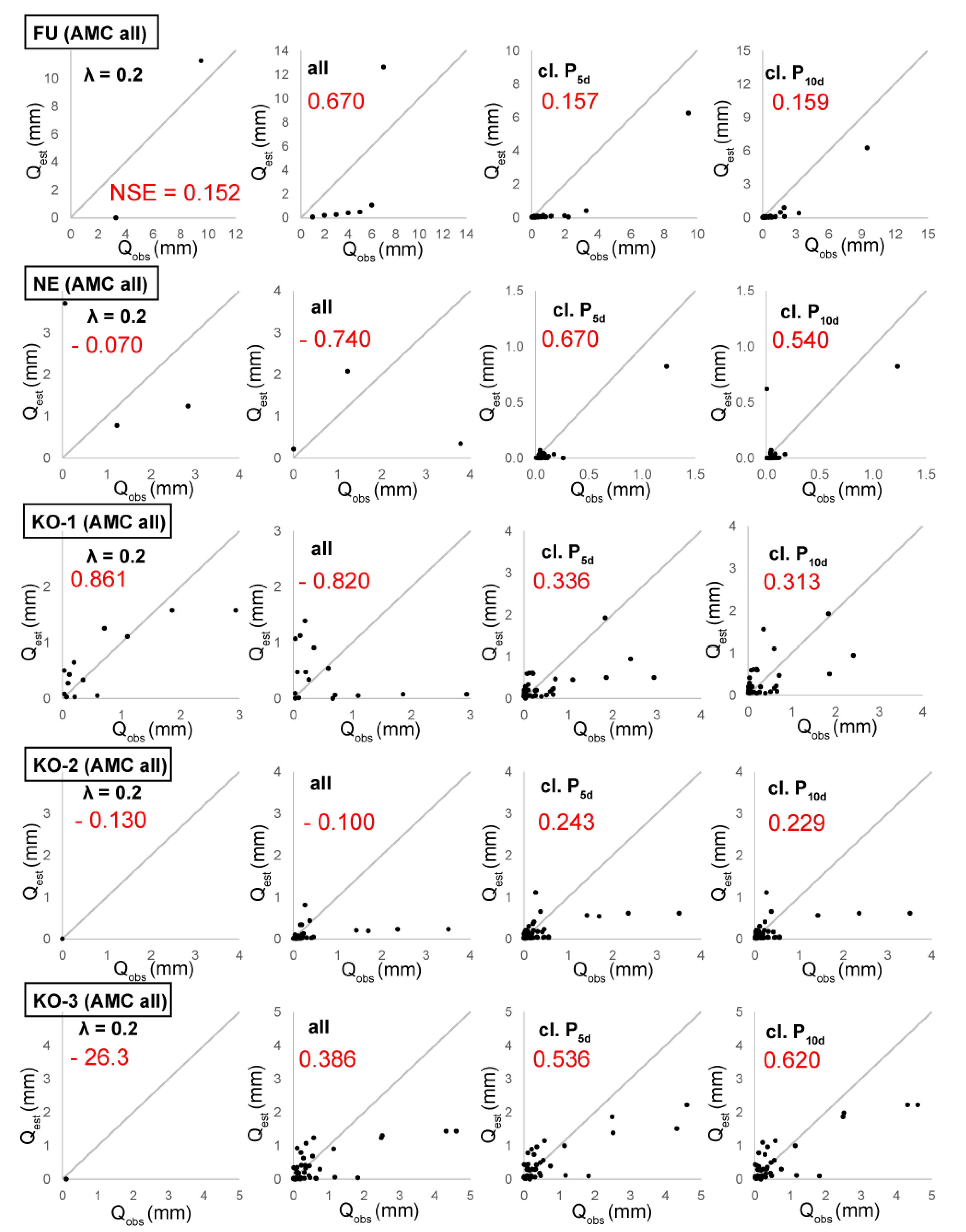
4.2. Tabulated CN-Based λ Modification
4.2.1. Discrete λ
4.2.2. Interpolated λ
4.3. Approaches Not Dependent on Tabulated CNs
4.3.1. Event Analysis
4.3.2. Model Fitting
4.4. HEC-HMS Simulations
5. Discussion and Conclusions
5.1. Tabulated CN, Discrete λ
5.2. Tabulated CN, Interpolated λ
5.3. Summary of Tabulated CN-Based Approaches
5.4. Tabulated CN-Independent Approaches
5.5. HEC-HMS Simulations Using Adjusted λ and CN
5.6. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonta, J.V. Determination of Watershed Curve Number Using Derived Distributions. J. Irrig. Drain. Eng. 1997, 123, 28–36. [Google Scholar] [CrossRef]
- Woodward, D.E.; Hawkins, R.H.; Jiang, R.; Hjelmfelt, A.T., Jr.; Van Mullem, J.A.; Quan, Q.D. Runoff curve number method: Examination of the initial abstraction ration. In Proceedings of the World Water and Environmental Resources Congress, Philadelphia, PA, USA, 23–26 June 2003; Bizier, P., De Barry, P., Eds.; pp. 691–700. [Google Scholar]
- USDA. Soil Conservation Service, National Engineering Handbook Supplement: Supplement A, Hydrology; USDA: Washington, DC, USA, 1956. [Google Scholar]
- USDA. Soil Conservation Service, National Engineering Handbook. Section 4: Hydrology; USDA: Washington, DC, USA, 1972; p. 762. [Google Scholar]
- USDA. Urban Hydrology for Small Watersheds, 2nd ed.; Technical Release 55; USDA: Washington, DC, USA, 1986; p. 164. [Google Scholar]
- USDA. National Engineering Handbook, Part 630, Hydrology; USDA: Washington, DC, USA, 2004. [Google Scholar]
- Hawkins, R.H.; Ward, T.J.; Woodwards, E.; Van Mullem, J.A. Continuing evolutioon of rainfall-runoff and the curve number precedent. In Proceedings of the 2nd Federal Inegracy Conference, Las Vegas, NV, USA, 27 June–1 July 2010. [Google Scholar]
- Mishra, S.K.; Vijay, P.; Singh, P.K. Revisiting the Soil Conservation Service curve number method. In Proceedings of the International Conference on Water, Environment, Energy and Society, Bhopal, India, 15–18 March 2016; Singh, V.P., Yadav, S., Yadava, R.N., Eds.; Springer: Singapore, 2018; pp. 667–693. [Google Scholar]
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Satheeshkumar, S.; Venkateswaran, S.; Kannan, R. Rainfall-runoff estimation using SCS-CN and GIS approach in the Pappiredipatti watershed of the Vaniyar sub basin, South India. Mod. Earth Sys. Environ. 2017, 3. [Google Scholar] [CrossRef]
- Shi, Z.H.; Chen, L.D.; Fang, N.F.; Qin, D.F.; Cai, C.F. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analywsis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- Jacobd, J.H.; Srinivasan, R. Effects of curve number modification on runoff estimation using WSR-88D raifall data in Texas watersheds. J. Soil Water Conserv. 2005, 60, 274–279. [Google Scholar]
- Lal, M.; Mishra, S.K.; Pandey, A. Physical verification of the effect of land features and antecedent moisture on runoff curve number. Catena 2015, 133, 318–327. [Google Scholar] [CrossRef]
- Springer, E.P.; McGurk, B.J.; Hawkins, R.H.; Coltharp, G.B. Curve numbers from watershed data. In Proceeding of the Symposium on Watershed Management, Boise, ID, USA, 21–23 July 1980; ASCE: New York, NY, USA, 1980; pp. 938–950. [Google Scholar]
- Mishra, S.K.; Chaudhary, A.; Shrestha, R.K.; Pandey, A.; Lal, M. Experimental Verification of the Effect and Land Use on SCS Runoff Curve Number. Water Resour. Manag. 2014, 28, 3407–3416. [Google Scholar]
- Hawkins, R.H.; Ward, T.J.; Woodwards, E.; Van Mullem, J.A. Curve Number Hydrology: State of the Practice; ASCE: Reston, VA, USA, 2009; p. 106. [Google Scholar]
- Jha, M.K.; Chovdary, V.M.; Kulkarni, Y.; Mal, B.C. Rainwater harvesting planning using geospatial techniques and multicriteria decision analysis. Res. Conserv. Recycl. 2014, 83, 96–111. [Google Scholar] [CrossRef]
- Sharpley, A.N.; Williams, J.R. EPIC Erosion/Productivity Impact Calculator: 1. Model Documentation. In USA Department of Agriculture Technical Bulletin No. 1768; Government Printing Office: Washington, DC, USA, 1990. [Google Scholar]
- Ajmal, M.; Moon, G.; Ahn, J.; Kim, T. Investigation of SCS-CN and its inspired modified models for runoff estimation in South Korean watersheds. J. Hydro-Environ. Res. 2015, 9, 592–603. [Google Scholar] [CrossRef]
- Ajmal, M.; Khan, T.A.; Kim, T.W. A CN-Based Ensembled Hydrological Model for Enhanced Watershed Runoff Prediction. Water 2016, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Singh, V.P. SCS-CN-based hydrologic simulation package. In Mathematical Models in Small Watershed Hydrology; Singh, V.P., Frevert, D.K., Eds.; Water Resources Publications: Littleton, CO, USA, 2002; pp. 391–464. [Google Scholar]
- Hjelmfelt, A.T. Ivestigation of curve number procedure. J. Hydraul. Eng. 1991, 117, 725–737. [Google Scholar] [CrossRef]
- Randusová, B.; Marková, R.; Kohnová, S.; Hlavčová, K. Comparison of cn estimation approaches. Int. J. Eng. Sci. 2015, 1, 34–40. [Google Scholar]
- Krajewski, A.; Sikorska-Senoner, A.E.; Hejduk, A.; Hejduk, L. Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment. Water 2020, 12, 471. [Google Scholar] [CrossRef] [Green Version]
- Hjelmfelt, A.T. Empirical investigation of curve number technique. J. Hydraul. Div. ASCE 1980, 106, 1471–1476. [Google Scholar]
- Hawkins, R.H. Discussion of ‘Empirical Ivestigation of Curve Number Technique’, by A. T. Hjelmfelt. J. Hydraul. Div. ASCE 1981, 107, 953–954. [Google Scholar]
- Hawkins, R.H.; Hjelmfelt, A.T.; Zevenbergen, A.W. Runoff probability, relative storm depth, and runoff curve numbers. J. Irrig. Drain. Eng. 1985, 111, 330–340. [Google Scholar] [CrossRef]
- Hawkins, R.H. 1993 Asymptotic determination of runoff curve numbers from data. J. Irrig. Dran. Div. ASCE 1993, 119, 334–345. [Google Scholar] [CrossRef]
- Ajmal, M.; Kim, T. Quantifying excess stormwater using SCS-CN-based rainfall runoff models and different curve number determination methods. J. Irrig. Drain. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogenous watersheds—The two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef] [Green Version]
- Soulis, K.X.; Valiantzas, J.D. Identification of the SCS-CN Parameter Spatial Distribution Using Rainfall-Runoff Data in Heterogenous Watersheds. Water. Resour. Manage. 2013, 27, 1737–1749. [Google Scholar] [CrossRef]
- Soulis, K.X. Estimation of SCS Curve Number variation following forest fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
- Rees, H.W.; Chow, T.L.; Gregorch, E.G. Soil and crop responses to long-term potato production at a benchmark site in northwestern New Brunswick. Can. J. Soil Sci. 1988, 88, 409–422. [Google Scholar] [CrossRef]
- Wang, X.; Liu, T.; Yang, W. Development of a robust runoff-prediction model by fusing the Rational Equation and modified SCS-CN method. Hydrol. Sci. J. 2012, 57, 1118–1140. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Pandey, R.P.; Jain, M.K.; Singh, V.P. A rain duration and modified AMC-dependent SCS-CN procedure for long duration rainfall-runoff events. Water Resour. Manag. 2008, 22, 861–876. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool (SWAT): Theoretical Documentation, Version 2000; Texas Water Resources Institute: College Station, TX, USA, 2002; p. 506. [Google Scholar]
- Sobhani, G. A Review of Selected Small Watershed Design Methods for Possible Adoption to Iranian Conditions. Master’s Thesis, Utah State University, Logan, UT, USA, 1975. [Google Scholar]
- Mishra, S.K.; Singh, V.P.; Sansalone, J.J.; Aravamuthan, V. A modified SCS-CN method: Characterization and testing. Water Resour. Manag. 2003, 17, 37–68. [Google Scholar] [CrossRef]
- Ponce, V.M. Engineering Hydrology, Principles and Practices; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; p. 640. [Google Scholar]
- Williams, J.R.; LaSeur, W.V. Water yield model using SCS curve numbers. J. Hydraul. Div. 1976, 102, 1241–1253. [Google Scholar]
- Hawkins, R.H. Runoff curve numbers with varying site moisture. J. Irrig. Drain. Div. 1978, 104, 389–398. [Google Scholar]
- Mishra, S.K.; Jain, M.K.; Singh, V.P. Evaluation of the SCS-CN-based model incorporating antecedent moisture. Water Resour. Manag. 2004, 18, 567–589. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. Long-term hydrological simulation based on the Soil Conservation Service curve number. Hydrol. Process. 2004, 18, 1291–1313. [Google Scholar] [CrossRef]
- Michel, C.; Andréassian, V.; Perrin, C. Soil Conservation Service Curve Number method: How to mend a wrong soil moisture accounting procedure? Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Jain, M.K.; Durbude, D.G.; Mishra, S.K. Improved CN-based long-term hydrologic simulation model. J. Hydrol. Eng. 2012, 17, 1204–1220. [Google Scholar] [CrossRef]
- Sahu, R.K.; Mishra, S.K.; Eldho, T.I.; Jain, M.K. An advanced soil moisture accounting, procedure for SCS curve number method. Hydrol. Process. 2007, 21, 2872–2881. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.K.; Berndtsson, R.; Jain, M.K.; Pandey, R.P. Development of modified SMA based MSCS-CN model for Runoff Estimation Water. Resour. Manag. 2015, 29, 4111–4127. [Google Scholar]
- Verma, S.; Mishra, S.K.; Singh, A.; Singh, P.K.; Verma, R.K. An enhanced SMA based SCS-CN inspired model for watershed runoff prediction. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Verma, S.; Singh, P.K.; Mishra, S.K.; Jain, S.K.; Berndtsson, R.; Singh, A.; Verma, R.K. Simplified SMA-inspired 1-parameter SCS-CN model for runoff estimation. Arab. J. Geosci. 2018, 11. [Google Scholar] [CrossRef]
- Desmukh, D.S.; Chaube, U.C.; Hailu, A.E.; Gudeta, D.A.; Kassa, M.T. Estimation and comparison of curve numbers based on dynamic land use cover change, observed rainfall-runoff data and land slope. J. Hydrol. 2013, 492, 89–101. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Wang, Z.; Goulet, M. A modification to the Soil Conservation Service curve number method for steep slopes in the Loess Plateau of China. Hydrol. Process. 2006, 20, 579–589. [Google Scholar] [CrossRef]
- Plummer, A.; Woodward, D.E. The origin and Derivation of Ia/S in the Runoff Curve Number System. In Proceedings of the International Water Resources Engineering Conference, Memphis, TN, USA, 3–7 August 1998; Abt, S.R., Yoing-Pezeshk, J., Watson, C.C., Eds.; ASCE: Reston, VA, USA, 1998; pp. 1260–1265. [Google Scholar]
- Fu, S.; Zhang, G.; Wang, N.; Luo, L. Initial abstraction ratio in the SCS-CN method in the Loess Plateau of China. Trans. ASABE 2011, 54, 163–169. [Google Scholar] [CrossRef]
- Fan, F.; Deng, Y.; Hu, X.; Weng, Q. Estimating Composite Curve Number Using an Improved SCS-CN Method with Remotely Sensed Variables in Guangzhou, China. Remote Sens. 2013, 5, 1425–1438. [Google Scholar] [CrossRef] [Green Version]
- Reistetter, J.A.; Russell, M. High-resolution land cover datasets, composite curve numbers, and storm water retention in the Tampa Bay, FL region. Appl. Geogr. 2011, 31, 740–747. [Google Scholar] [CrossRef]
- Mockus, V. Design Hydrographs. In National Engineering Handbook; Section 4, Hydrology; McKeever, V., Owen, W., Rallison, R., Eds.; Soil Conservation Service: Washington, DC, USA, 1972. [Google Scholar]
- Cazier, D.J.; Hawkins, R.H. Regional application of the curve number method. Water Today and Tomorrow. In Proceedings of the ASCE, Irrigation and Drainage Division Special Conference, Flagstaff, AZ, USA, 24–26 July 1984; Replogle, J.A., Ed.; ASCE: New York, USA, 1984. [Google Scholar]
- Mishra, S.K.; Singh, V.P. Another look at SCS-CN method. J. Hydrol. Eng. 1999, 4, 257–264. [Google Scholar] [CrossRef]
- Hawkins, R.H.; Khojeini, A.V. Initial Abstraction and Loss in the Curve Number Method Hydrol; Arizona-Nevada Academy of Science. Water Resour. Ariz. Southwest 2000, 30, 29–35. [Google Scholar]
- Jiang, R. Investigation of Runoff Curve Number Initial Abstraction Ratio. Master’s Thesis, The University of Arizona, Tucson, AZ, USA, 2001. [Google Scholar]
- Lim, K.J.; Engel, B.A.; Muthukrishnan, S.; Harbor, J. Effects of initial abstraction and urbanization of estimated runoff using CN technology. J. Am. Water Resour. Assoc. 2006, 42, 629–643. [Google Scholar] [CrossRef]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical Note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Sys. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef] [Green Version]
- Xiao, B.; Wang, Q.H.; Fan, J.; Han, F.P.; Dai, Q.H. Application of the SCS-CN model to runoff estimation on a small watershed with high spatial heterogeneity. Pedosphere 2011, 21, 738–749. [Google Scholar] [CrossRef]
- Yuan, Y.; Nie, W.; McCutcheon, S.C.; Taguas, E. Initial abstraction and curve numbers for semiarid watersheds in Southeastern Arizona. Hydrol. Process. 2014, 28, 774–783. [Google Scholar] [CrossRef]
- Janeček, M.; Dostál, T.; Dufková, J.K.; Dumbrovský, M.; Hůla, J.; Kadlec, V.; Konečná, J.; Kovář, P.; Krása, J.; Kubátová, E.; et al. Ochrana zemědělské půdy před erozí; Czech University of Life Sciences: Prague, Czech Republic, 2012; p. 113. [Google Scholar]
- Caletka, M.; Honek, D. Improving direct runoff estimations through modifying SCS-CN initial abstraction ratio in a catchment prone to flash floods. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management, lbena, Bulgaria, 28 June–7 July 2019; pp. 281–288. [Google Scholar]
- Caletka, M.; Michalková, M.Š. Determination of SCS-CN initial Abstraction ratio in a chatchment prone to flash floods. Pollack Per. 2020, 15, 112–123. [Google Scholar]
- Karabová, B. Testovanie možnosti regionalizácie vybraných parametrov metódy SCS-CN—Oblast nížin Slovenska. Acta Hydrol. Slovaca 2013, 15, 194–203. [Google Scholar]
- Kohnová, S.; Karabová, B.; Hlavčová, K. On the possibilities of watershed parametrization of extreme flow estimation on ungauged basins. In Proceedings of the Congress in Flood Risk and Precipitation in Catchments and Cities, Prague, Czech Republic, 22 June–2 July 2015; Chen, Y., Estupina, V.B., Schumann, A., Aksoy, H., Bloschl, G., Kooy, M., Rogger, M., Toth, E., Eds.; Copernicus GmbH: Göttingen, Germany, 2015; pp. 171–175. [Google Scholar]
- Kohnová, S.; Rutkowska, A.; Banasik, K.; Hlavčová, K. The L-moment based regional approach to curve numbers for Slovak and Polish Carpathian catchments. J. Hydrol. Hydromech. 2020, 68, 1–10. [Google Scholar] [CrossRef]
- Daňhelka, J.; Kubát, J. Vyhodnocení Povodní v Červnu a Červenci 2009 (Assessment of Floods in June and July 2009 in the Czech Republic); Ministry of Environment, CHMI: Prague, Czech Republic, 2009; p. 165. [Google Scholar]
- Šunka, Z. Vyhodnocení Povodní v Květnu a Červnu 2010 (Assessment of Floods in May and June 2010); Ministry of Environment, TGM WRI: Prague, Czech Republic, 2010; p. 172. [Google Scholar]
- Honek, D.; Michalková, M.Š.; Smetanová, A.; Sočuvka, V.; Velísková, Y.; Karásek, P.; Konečná, J.; Némethová, Z.; Danáčová, M. Estimating sedimentation rates in small reservoirs—Suitable approaches for local municipalities in central Europe. J. Environ. Manag. 2020, 261. [Google Scholar] [CrossRef] [PubMed]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Yang, K.; Cao, S.; Liu, X. Flow resistance and its precipitation methods in compound channels. Acta Mech. Sin. 2007, 23, 23–31. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means clustering. J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef] [Green Version]
- Dingman, S.L. Physical Hydrology, 2nd ed.; Macmillan Press Limited: New York, NY, USA, 2002; p. 646. [Google Scholar]
- Konečná, J.; Karásek, P.; Beitlerová, H.; Fučík, P.; Kapička, J.; Podhrázská, J.; Kvítek, T. Using WaTEM/SEDEM and HEC-HMS episodic models for the simulation of episodic hydrological and erosion events in a small agricultural catchment. Soil Water Res. 2019, 15, 18–29. [Google Scholar] [CrossRef]
- Muche, M.E.; Hutchinson, S.L.; Hutchinson, J.M.S.; Johnston, J.M. Phenology-adjusted dynamic curve number for improved hydrologic modelling. J. Environ. Manag. 2019, 235, 403–413. [Google Scholar] [CrossRef]







| Sub-Catchment | Area (km2) | Elevation (m) | Mean Slope (°) | Mean P (mm) | Mean Q (m3/s) | Mean T (°C) | |||
|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Annual | IV-IX | Annual | IV-IX | ||||
| FU | 57.8 | 282 | 563 | 6.1 | 675 | 450 | 0.350 | 8.0 | 13.5 |
| NE | 2.8 | 559 | 650 | 4.2 | 650 | 400 | 0.015 | 7.0 | 14.0 |
| KO-1 | 0.16 | 490 | 532 | 3.2 | 675 | 425 | 0.007 | 6.5 | 12.5 |
| KO-2 | 0.78 | 548 | 623 | 4.3 | 675 | 425 | 0.003 | 6.5 | 12.5 |
| KO-3 | 7.1 | 478 | 623 | 5.2 | 675 | 425 | 0.026 | 6.5 | 12.5 |
| Sub-Catchment | Percentage of Land Use Category (%) | ||||||||
| AL | BG | FO | GR | GA | GA | PA | SH | WA | |
| FU | 43.5 | 0.0 | 24.7 | 23.7 | 5.2 | 5.2 | 1.4 | 1.3 | 0.2 |
| NE | 50.9 | 0.2 | 31.8 | 5.2 | 5.4 | 5.4 | 3.1 | 3.4 | 0.0 |
| KO-1 | 97.3 | 0.0 | 0.1 | 0.0 | 1.3 | 1.3 | 0.7 | 0.6 | 0.0 |
| KO-2 | 52.2 | 0.0 | 44.4 | 1.1 | 0.6 | 0.6 | 0.1 | 1.5 | 0.0 |
| KO-3 | 41.8 | 0.0 | 37.9 | 8.0 | 6.1 | 6.1 | 0.9 | 5.2 | 0.1 |
| Sub-Catchment | Period | Number of Rain Gauges (Interval) | Level/Runoff Measurement (Interval) | Number of Events Chosen (Train./Valid.) |
|---|---|---|---|---|
| FU | 2008–2016 | 17 (10 min) | Level gauge (1 h) | 44/45 |
| NE | 2008–2017 | 1 (10 min) | Thomson weir (10 min) | 57/81 |
| KO-1 | 2005–2018 | 1 (10 min) | Thomson weir (10 min) | 56/52 |
| KO-2 | 2005–2018 | 1 (10 min) | Thomson weir (10 min) | 73/74 |
| KO-3 | 2005–2018 | 1 (10 min) | Cippoletti weir (10 min) | 80/60 |
| Method | Parameter | |
|---|---|---|
| Loss | SCS Curve Number | Initial abstraction (mm) |
| Curve Number (-) | ||
| Impervious (%) | ||
| Transform | Clark Unit Hydrograph | Time of concentration (hr) |
| Storage coefficient (hr) | ||
| Baseflow | Initial discharge (m3/s) | |
| Recession constant (-) | ||
| Ratio (-) | ||
| Sub-Catchment | FU | NE | KO-1 | KO-2 | KO-3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Explained Variability | PC 1 71.2% | PC 2 13.8% | PC 1 48.3% | PC 2 33.3% | PC 1 49.1% | PC 2 39.5% | PC 1 54.9% | PC 2 30.8% | PC 1 51.2% | PC 2 32.4% |
| P | −0.07 | 0.81 | −0.04 | 0.46 | 0.32 | 0.11 | −0.08 | 0.44 | −0.18 | 0.41 |
| duration | −0.02 | 0.47 | −0.01 | −0.02 | −0.02 | 0.00 | 0.02 | 0.00 | 0.02 | −0.01 |
| P5d | 0.45 | 0.32 | 0.51 | −0.04 | −0.25 | 0.56 | 0.59 | 0.09 | 0.50 | 0.20 |
| P10d | 0.89 | −0.09 | 0.85 | −0.09 | −0.34 | 0.71 | 0.77 | 0.24 | 0.77 | 0.34 |
| max. int. | −0.07 | 0.07 | 0.13 | 0.88 | 0.85 | 0.40 | −0.24 | 0.86 | −0.35 | 0.81 |
| Q | 0.04 | 0.11 | 0.01 | 0.03 | 0.00 | 0.00 | 0.00 | 0.01 | −0.01 | 0.04 |
| Ia | −0.01 | 0.01 | 0.00 | 0.02 | 0.00 | 0.01 | −0.01 | 0.02 | −0.05 | 0.11 |
| FU | NE | KO-1 | KO-2 | KO-3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Med. | Mean | Med. | Mean | Med. | Mean | Med. | Mean | Med. | ||||||
| duration | all (n = 45) | 12.02 | 10.00 | all (n = 81) | 3.62 | 2.67 | all (n = 56) | 4.00 | 2.92 | all (n = 73) | 3.50 | 2.67 | all (n = 80) | 3.47 | 2.75 |
| P | 17.4 | 14.0 | 10.8 | 6.9 | 17.1 | 11.5 | 13.9 | 10.0 | 14.3 | 10.0 | |||||
| P5d | 25.7 | 20.1 | 16.6 | 11.3 | 18.4 | 11.9 | 14.7 | 9.2 | 14.4 | 8.7 | |||||
| P10d | 42.9 | 35.3 | 30.1 | 22.2 | 28.8 | 21.2 | 25.0 | 18.8 | 27.2 | 19.9 | |||||
| max. int. | 10.68 | 8.30 | 14.40 | 7.80 | 23.12 | 13.80 | 19.11 | 12.60 | 19.88 | 12.30 | |||||
| Q | 1.830 | 0.337 | 0.448 | 0.076 | 0.316 | 0.081 | 0.293 | 0.069 | 0.567 | 0.101 | |||||
| Ia | 1.5 | 0.8 | 1.7 | 1.4 | 2.4 | 1.8 | 0.8 | 0.0 | 2.4 | 1.1 | |||||
| duration | cl. 1 (n = 31) | 12.03 | 9.00 | cl. 1 (n = 58) | 3.81 | 2.92 | cl. 1 (n = 48) | 3.69 | 2.92 | cl. 1 (n = 68) | 3.41 | 2.80 | cl. 1 (n = 52) | 3.37 | 2.67 |
| P | 18.5 | 14.1 | 11.3 | 7.1 | 17.8 | 11.4 | 14.0 | 10.0 | 16.3 | 10.8 | |||||
| P5d | 17.1 | 13.3 | 8.3 | 6.7 | 11.8 | 10.2 | 11.2 | 8.5 | 7.0 | 5.4 | |||||
| P10d | 26.2 | 26.4 | 18.1 | 17.0 | 22.4 | 18.8 | 21.8 | 17.2 | 13.7 | 13.7 | |||||
| max. int. | 11.43 | 8.90 | 13.70 | 7.80 | 24.40 | 14.40 | 19.43 | 12.90 | 22.80 | 12.60 | |||||
| Q | 1.152 | 0.301 | 0.319 | 0.065 | 0.308 | 0.056 | 0.246 | 0.052 | 0.633 | 0.090 | |||||
| Ia | 1.6 | 0.8 | 1.7 | 1.5 | 2.4 | 1.6 | 0.8 | 0.0 | 2.9 | 1.2 | |||||
| duration | cl. 2 (n = 14) | 12.00 | 10.50 | cl. 2 (n = 23) | 3.15 | 2.33 | cl. 2 (n = 8) | 5.81 | 5.17 | cl. 2 (n = 5) | 4.67 | 2.67 | cl. 2 (n = 28) | 3.67 | 2.83 |
| P | 15.1 | 12.4 | 9.7 | 5.5 | 12.9 | 11.7 | 12.5 | 10.8 | 10.5 | 8.8 | |||||
| P5d | 44.7 | 42.7 | 37.7 | 37.4 | 58.2 | 60.3 | 63.2 | 63.2 | 28.2 | 25.3 | |||||
| P10d | 79.9 | 76.6 | 60.4 | 59.5 | 67.5 | 67.4 | 68.0 | 69.9 | 52.3 | 42.5 | |||||
| max. int. | 9.03 | 7.00 | 16.17 | 9.00 | 15.60 | 7.80 | 14.90 | 10.80 | 14.55 | 11.40 | |||||
| Q | 3.332 | 2.406 | 0.773 | 0.097 | 0.361 | 0.208 | 0.925 | 0.514 | 0.444 | 0.178 | |||||
| Ia | 1.3 | 1.0 | 1.6 | 1.3 | 2.6 | 2.4 | 0.8 | 0.2 | 1.4 | 0.7 | |||||
| AMC All | AMC = II | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| λ | r2 | NSE | e | r2 | NSE | e | ||||
| FU | original | λ = 0.2 | 0.258 | 0.152 | −0.818 | 0.854 | 0.361 | −0.876 | ||
| median | all | 0.559 | 0.448 | −0.123 | 0.677 | 0.658 | +0.148 | |||
| P5d | ≤26 mm | >26 mm | 0.612 | 0.573 | −0.115 | 0.673 | 0.655 | +0.148 | ||
| P10d | ≤47 mm | >47 mm | 0.621 | 0.587 | −0.084 | 0.674 | 0.655 | +0.141 | ||
| mean | all | 0.413 | 0.282 | −0.591 | 0.763 | 0.663 | −0.489 | |||
| P5d | ≤26 mm | >26 mm | 0.563 | 0.516 | −0.532 | 0.671 | 0.627 | −0.400 | ||
| P10d | ≤47 mm | >47 mm | 0.57 | 0.527 | −0.512 | 0.673 | 0.627 | −0.404 | ||
| NE | original | λ = 0.2 | 0.01 | −0.071 | −0.298 | 0.781 | 0.388 | −0.253 | ||
| median | all | 0.671 | 0.668 | +0.052 | 0.684 | 0.465 | +0.173 | |||
| P5d | ≤39 mm | >39 mm | 0.676 | 0.676 | +0.017 | 0.675 | 0.436 | +0.192 | ||
| P10d | ≤39 mm | >39 mm | 0.68 | 0.68 | +0.012 | 0.677 | 0.442 | +0.188 | ||
| mean | all | 0.667 | 0.619 | −0.103 | 0.717 | 0.698 | −0.01 | |||
| P5d | ≤39 mm | >39 mm | 0.617 | 0.59 | −0.017 | 0.697 | 0.671 | +0.011 | ||
| P10d | ≤39 mm | >39 mm | 0.623 | 0.591 | −0.129 | 0.702 | 0.678 | +0.006 | ||
| KO-1 | original | λ = 0.2 | 0.685 | 0.861 | −0.033 | 0.635 | −16.769 | +1.087 | ||
| median | all | 0.590 | −3.286 | +0.827 | 0.567 | −21.898 | +1.781 | |||
| P5d | ≤35 mm | >35 mm | 0.601 | −4.208 | +0.855 | 0.569 | −31.133 | +1.700 | ||
| P10d | ≤42 mm | >42 mm | 0.532 | −7.993 | +0.597 | 0.541 | −25.939 | +1.597 | ||
| mean | all | 0.599 | 0.323 | +0.195 | 0.639 | −9.941 | +1.408 | |||
| P5d | ≤35 mm | >35 mm | 0.645 | −1.217 | +0.651 | 0.59 | −25.167 | +2.112 | ||
| P10d | ≤42 mm | >42 mm | 0.631 | −3.244 | +0.469 | 0.462 | −16.854 | +1.517 | ||
| KO-2 | original | λ = 0.2 | 0.973 | −0.133 | +1.234 | 0.845 | 0.365 | +0.501 | ||
| median | all | 0.656 | −0.012 | +0.256 | 0.659 | −5.681 | +0.835 | |||
| P5d | ≤41 mm | >41 mm | 0.654 | −0.093 | +0.273 | 0.621 | −11.888 | +1.002 | ||
| P10d | ≤50 mm | >50 mm | 0.656 | 0.083 | +0.211 | 0.638 | −10.24 | +0.933 | ||
| mean | all | 0.775 | 0.758 | +0.095 | 0.716 | −3.027 | +1.007 | |||
| P5d | ≤41 mm | >41 mm | 0.707 | 0.410 | +0.263 | 0.716 | −3.053 | +1.012 | ||
| P10d | ≤50 mm | >50 mm | 0.713 | 0.502 | +0.210 | 0.817 | −2.779 | +1.166 | ||
| KO-3 | original | λ = 0.2 | - | −26.299 | +0.263 | 0.888 | 0.869 | +0.057 | ||
| median | all | 0.661 | 0.525 | +0.170 | 0.663 | −1.663 | +0.716 | |||
| P5d | ≤20 mm | >20 mm | 0.649 | 0.501 | +0.180 | 0.644 | −1.779 | +0.754 | ||
| P10d | ≤28 mm | >28 mm | 0.649 | 0.533 | +0.161 | 0.647 | −1.509 | +0.719 | ||
| mean | all | 0.676 | 0.669 | +0.057 | 0.748 | −0.273 | +0.745 | |||
| P5d | ≤20 mm | >20 mm | 0.673 | 0.665 | +0.056 | 0.631 | −0.719 | +0.674 | ||
| P10d | ≤28 mm | >28 mm | 0.673 | 0.669 | +0.040 | 0.640 | −0.251 | +0.543 | ||
| AMC All | AMC = II | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r2 | NSE | e | r2 | NSE | e | ||||||
| FU | original | λ = 0.2 | 0.258 | 0.152 | −0.818 | 0.854 | 0.361 | −0.876 | |||
| int. | all | 0.920 | 0.670 | −0.430 | 0.633 | 0.600 | +0.035 | ||||
| P5d | ≤26 mm | >26 mm | 0.290 | 0.157 | −0.860 | 0.328 | 0.312 | +0.068 | |||
| P10d | ≤47 mm | >47 mm | 0.290 | 0.159 | −0.870 | 0.334 | 0.320 | +0.067 | |||
| NE | original | λ = 0.2 | 0.010 | −0.070 | −0.298 | 0.781 | 0.388 | −0.253 | |||
| int. | all | 0.120 | −0.740 | −0.110 | 0.688 | 0.263 | −0.197 | ||||
| P5d | ≤18 mm | >18 mm | 0.740 | 0.67 | −0.040 | 0.461 | 0.357 | −0.016 | |||
| P10d | ≤39 mm | >39 mm | 0.580 | 0.54 | −0.030 | 0.514 | 0.380 | −0.025 | |||
| KO-1 | original | λ = 0.2 | 0.010 | 0.861 | +0.005 | 0.635 | −16.789 | +1.087 | |||
| int. | all | 0.140 | −0.820 | −0.160 | 0.461 | 0.347 | −0.151 | ||||
| P5d | ≤35 mm | >35 mm | 0.390 | 0.336 | −0.120 | 0.427 | 0.333 | −0.141 | |||
| P10d | ≤42 mm | >42 mm | 0.350 | 0.313 | −0.010 | 0.427 | 0.339 | −0.138 | |||
| KO-2 | original | λ = 0.2 | 0.970 | −0.130 | +1.234 | 0.845 | 0.365 | +0.501 | |||
| int. | all | 0.070 | −0.100 | −0.330 | 0.58 | 0.322 | −0.890 | ||||
| P5d | ≤41 mm | >41 mm | 0.340 | 0.243 | −0.120 | 0.585 | 0.310 | −0.096 | |||
| P10d | ≤50 mm | >50 mm | 0.310 | 0.229 | −0.110 | 0.42 | 0.326 | −0.074 | |||
| KO-3 | original | λ = 0.2 | - | −26.300 | +0.263 | 0.882 | 0.876 | −0.095 | |||
| int. | all | 0.500 | 0.386 | −0.200 | 0.653 | 0.433 | −0.227 | ||||
| P5d | ≤20 mm | >20 mm | 0.630 | 0.536 | −0.130 | 0.566 | 0.507 | −0.109 | |||
| P10d | ≤28 mm | >28 mm | 0.690 | 0.620 | −0.110 | 0.555 | 0.452 | −0.144 | |||
| Catchment | λ | Regression of S | r2 | NSE | e | |
|---|---|---|---|---|---|---|
| FU | orig. | 0.2 | S = 13987.982 P10d−1.154 (r2 = 0.3731) | - | 0.129 | −0.820 |
| mean | 0.0183 | 0.84 | 0.683 | −0.120 | ||
| median | 0.0029 | 0.84 | 0.692 | +0.219 | ||
| NE | orig. | 0.2 | S = −318.995 ln (P10d) + 1584,638 (r2 = 0.3573) | 0.37 | 0.371 | −0.350 |
| mean | 0.0077 | 0.75 | 0.592 | +0.206 | ||
| median | 0.0026 | 0.74 | 0.636 | −0.100 | ||
| KO-1 | orig. | 0.2 | S = 9641.4 P10d−0.859 (r2 = 0.3473) | 0685 | 0.861 | −0.033 |
| mean | 0.0086 | 0.6 | 0.536 | −0.040 | ||
| median | 0.0012 | 0.67 | 0.511 | +0.070 | ||
| KO-2 | orig. | 0.2 | S = 1843.7 e−0.025 P10d (r2 = 0.1750) | - | −0.133 | +1.234 |
| mean | 0.0064 | 0.91 | 0.622 | −0.170 | ||
| median | 0.0 | 0.85 | 0.758 | −0.040 | ||
| KO-3 | orig. | 0.2 | S = 874.92 e−0.026 P10d (r2 = 0.2671) | - | −26.3 | +0.263 |
| mean | 0.0129 | 0.85 | 0.159 | −0.780 | ||
| median | 0.0010 | 0.77 | 0.521 | −0.260 | ||
| S (CN)/λ | ||||
|---|---|---|---|---|
| FU | all | 371.5 mm (40.64)/0.0 | ||
| cl. | P5d | ≤26 mm: 687.5 mm (26.98)/0.0 | >26 mm: 138.9 mm (64.65)/0.0 | |
| P10d | ≤47 mm: 596.9 mm (29.85)/0.0 | >47 mm: 97.9 mm (72.18)/0.0 | ||
| NE | all | 1093.0 mm (18.86)/0.0 | ||
| cl. | P5d | ≤18 mm: 1154.5 mm (18.03)/0.0 | >18 mm: 12.9 mm (95.17)/1.0 | |
| P10d | ≤39 mm: 1154.4 mm (10.03)/0.0 | >39 mm: 87.7 mm (74.33)/0.0667 | ||
| KO-1 | all | 3949.4 mm (6.04)/0.0 | ||
| cl. | P5d | ≤35 mm: 4015.7 mm (5.95)/0.0 | >35 mm: 909.9 mm (21.82)/0.0 | |
| P10d | ≤42 mm: 4152.3 mm (5.75)/0.0 | >42 mm: 1299.2 mm (16.35)/0.0 | ||
| KO-2 | all | 2967.0 mm (7.89)/0.0 | ||
| cl. | P5d | ≤41 mm: 3037.0 mm (7.72)/0.0 | >41 mm: 488.3 mm (34.22)/0.0 | |
| P10d | ≤50 mm: 3125.7 mm (7.52)/0.0 | >50 mm: 990.0 mm (20.42)/0.0 | ||
| KO-3 | all | 905.0 mm (21.92)/0.0 | ||
| cl. | P5d | ≤20 mm: 899.8 mm (22.01)/0.0 | >20 mm: 495.8 mm (33.88)/0.0 | |
| P10d | ≤28 mm: 923.3 mm (21.57)/0.0 | >28 mm: 501.0 mm (33.64)/0.0 | ||
| FU Catchment | NE Catchment | KO-1 Catchment | KO-2 Catchment | KO-3 Catchment | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All | cl. | All | cl. | All | cl. | All | cl. | All | cl. | ||||||
| P5d | P10d | P5d | P10d | P5d | P10d | P5d | P10d | P5d | P10d | ||||||
| r2 | 0.642 | 0.56 | 0.508 | 0.271 | 0.799 | 0.813 | 0.402 | 0.494 | 0.666 | 0.665 | 0.521 | 0.573 | 0.747 | 0.796 | 0.718 |
| NSE | 0.585 | 0.55 | 0.488 | 0.247 | 0.463 | 0.763 | 0.173 | 0.362 | 0.496 | 0.146 | 0.453 | 0.391 | 0.547 | 0.671 | 0.581 |
| e | −0.062 | −0.149 | +0.075 | −0.195 | +0.075 | −0.055 | −0.253 | −0.21 | −0.193 | −0.149 | −0.167 | −0.17 | +0.642 | −0.193 | −0.222 |
| Slower Onset | Rapid Onset | ||||||
|---|---|---|---|---|---|---|---|
| λ | Sub-Basin | Ia | CN | Tc | Ia | CN | Tc |
| 0.2 | NE-1 | 0.235 | 1.000 | 1.963 | 0.349 | 1.010 | 0.214 |
| NE-2 | 0.186 | 1.000 | 1.364 | 0.348 | 1.010 | 0.225 | |
| NE-3 | 0.192 | 1.000 | 3.284 | 0.353 | 1.325 | 0.307 | |
| 0.0142 | NE-1 | 0.778 | 1.015 | 1.136 | 0.134 | 0.670 | 0.210 |
| NE-2 | 0.778 | 1.015 | 0.794 | 0.136 | 0.669 | 0.147 | |
| NE-3 | 0.750 | 1.014 | 1.504 | 0.179 | 0.850 | 0.348 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caletka, M.; Šulc Michalková, M.; Karásek, P.; Fučík, P. Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments. Water 2020, 12, 1964. https://doi.org/10.3390/w12071964
Caletka M, Šulc Michalková M, Karásek P, Fučík P. Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments. Water. 2020; 12(7):1964. https://doi.org/10.3390/w12071964
Chicago/Turabian StyleCaletka, Martin, Monika Šulc Michalková, Petr Karásek, and Petr Fučík. 2020. "Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments" Water 12, no. 7: 1964. https://doi.org/10.3390/w12071964
APA StyleCaletka, M., Šulc Michalková, M., Karásek, P., & Fučík, P. (2020). Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments. Water, 12(7), 1964. https://doi.org/10.3390/w12071964





