Hydrochemical and Isotopic Assessment of Groundwater in the Goda Mountains Range System. Republic of Djibouti (Horn of Africa)
Abstract
1. Introduction
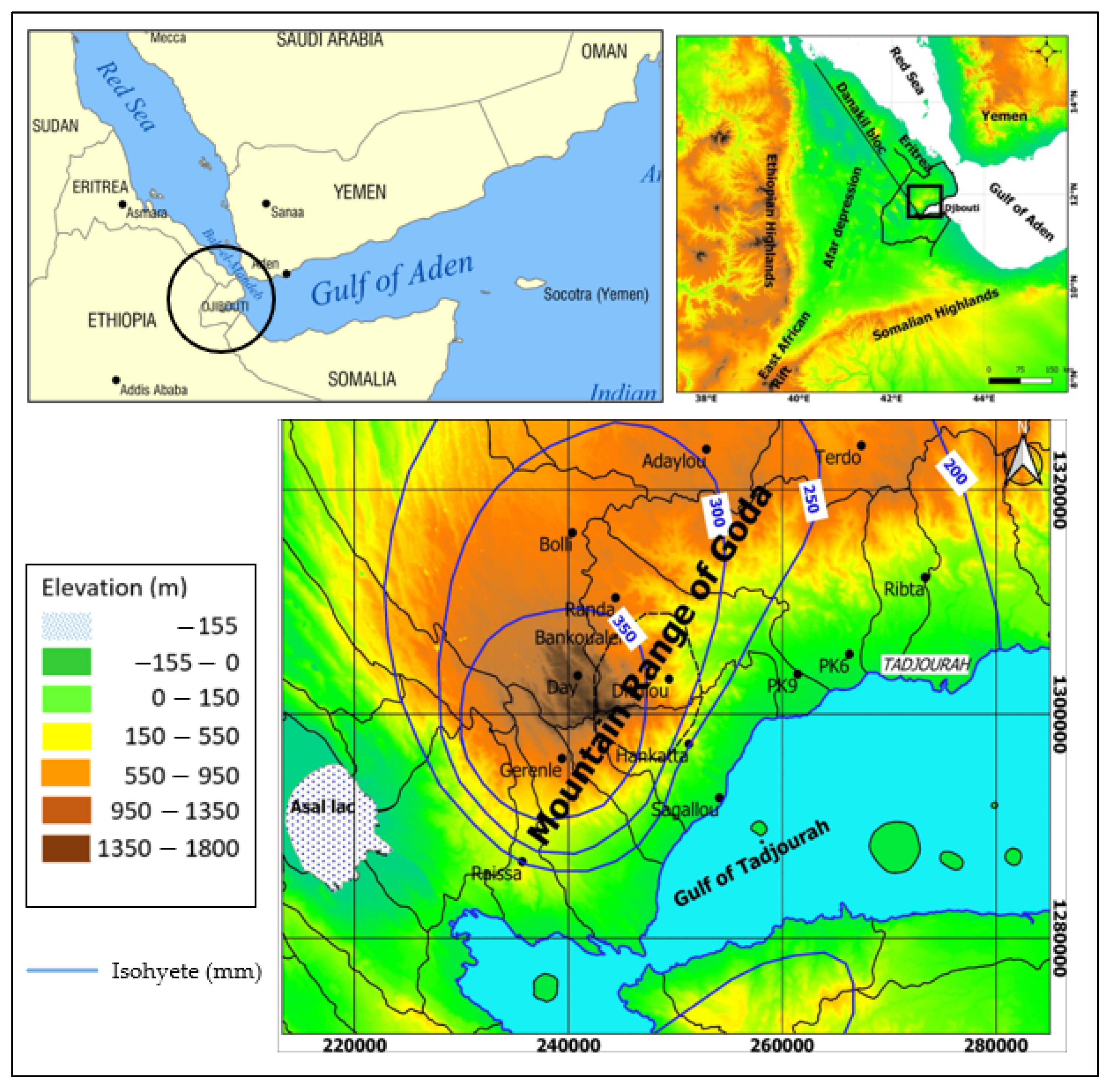
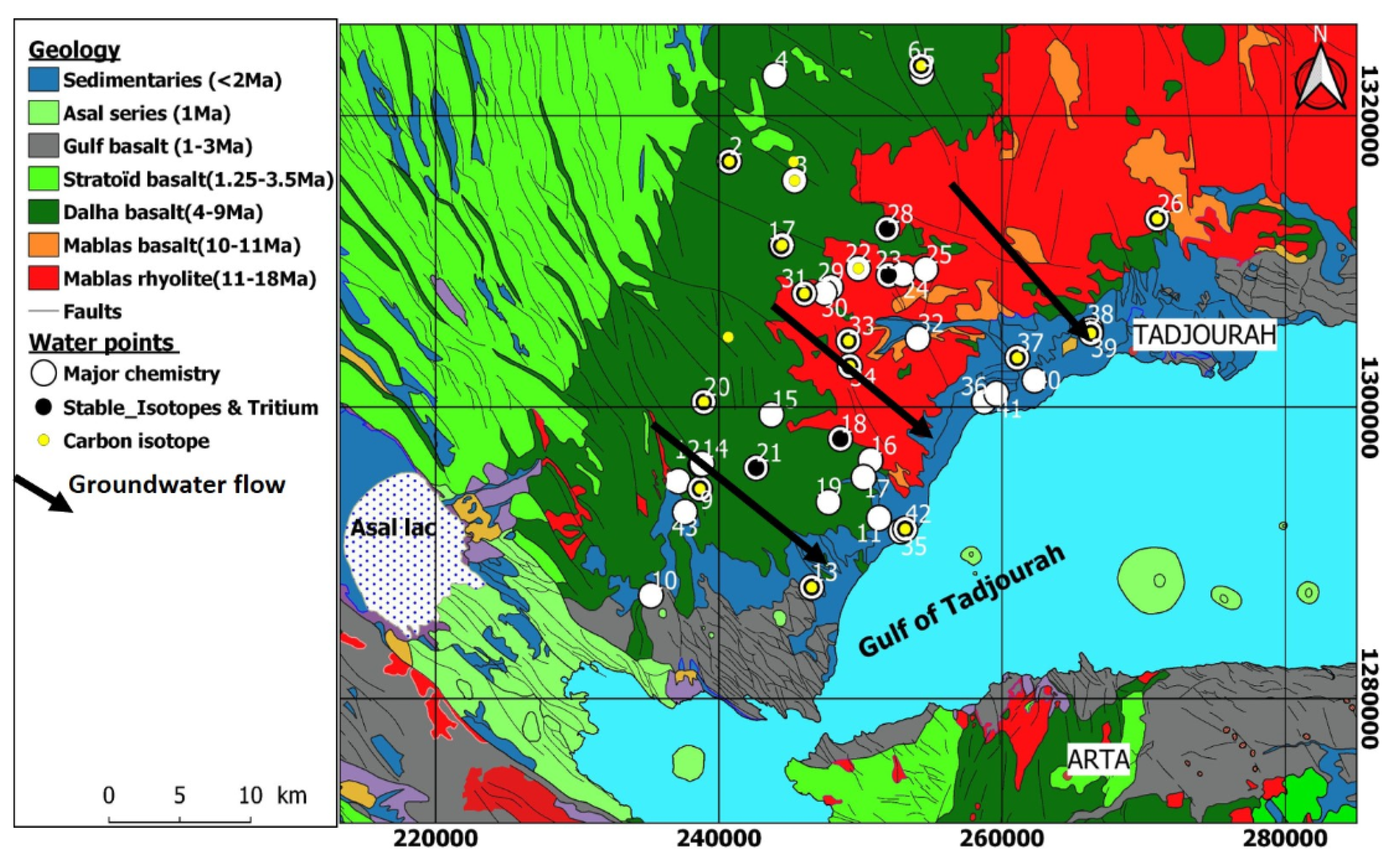
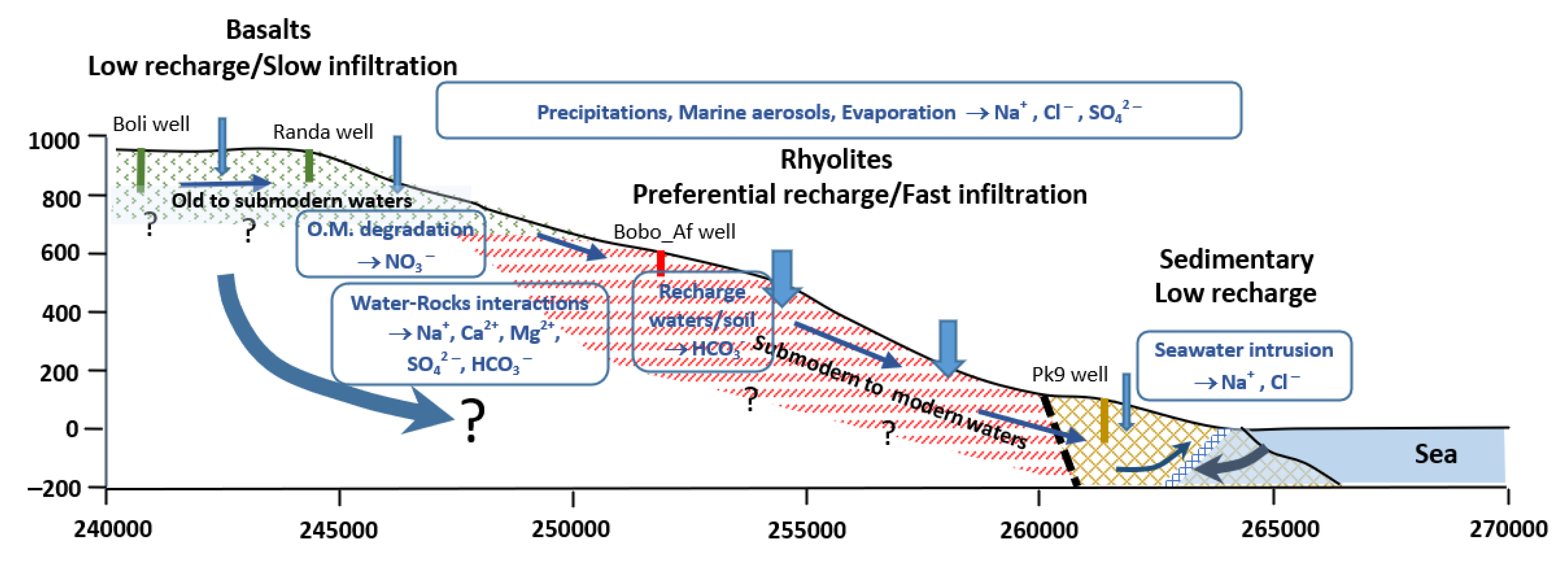
2. Geological, Geomorphological, and Hydrogeological Setting
3. Materials and Methods
4. Results and Discussion
4.1. Statistical Analysis
4.1.1. Descriptive Statistics
4.1.2. Correlation Matrix
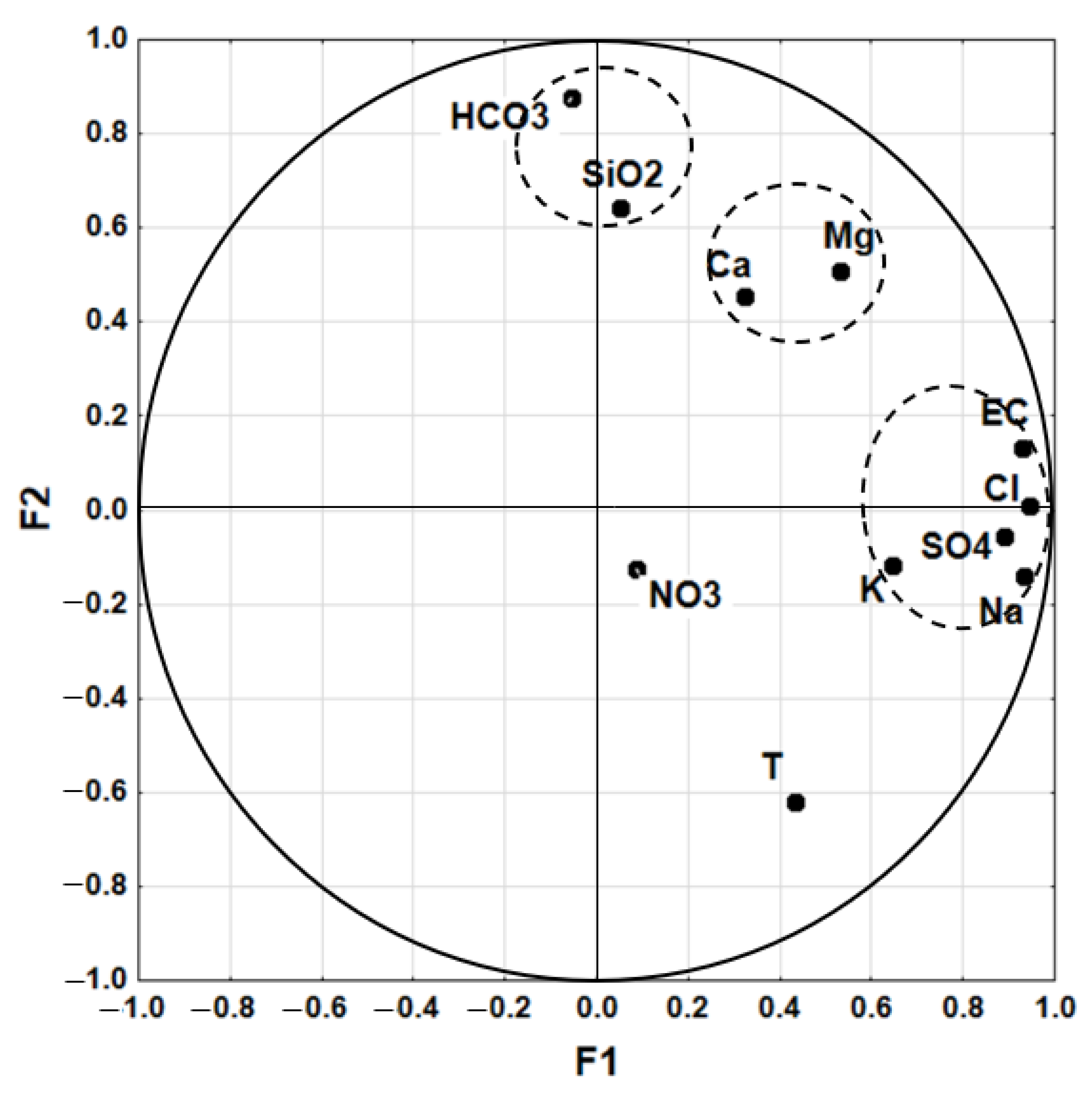
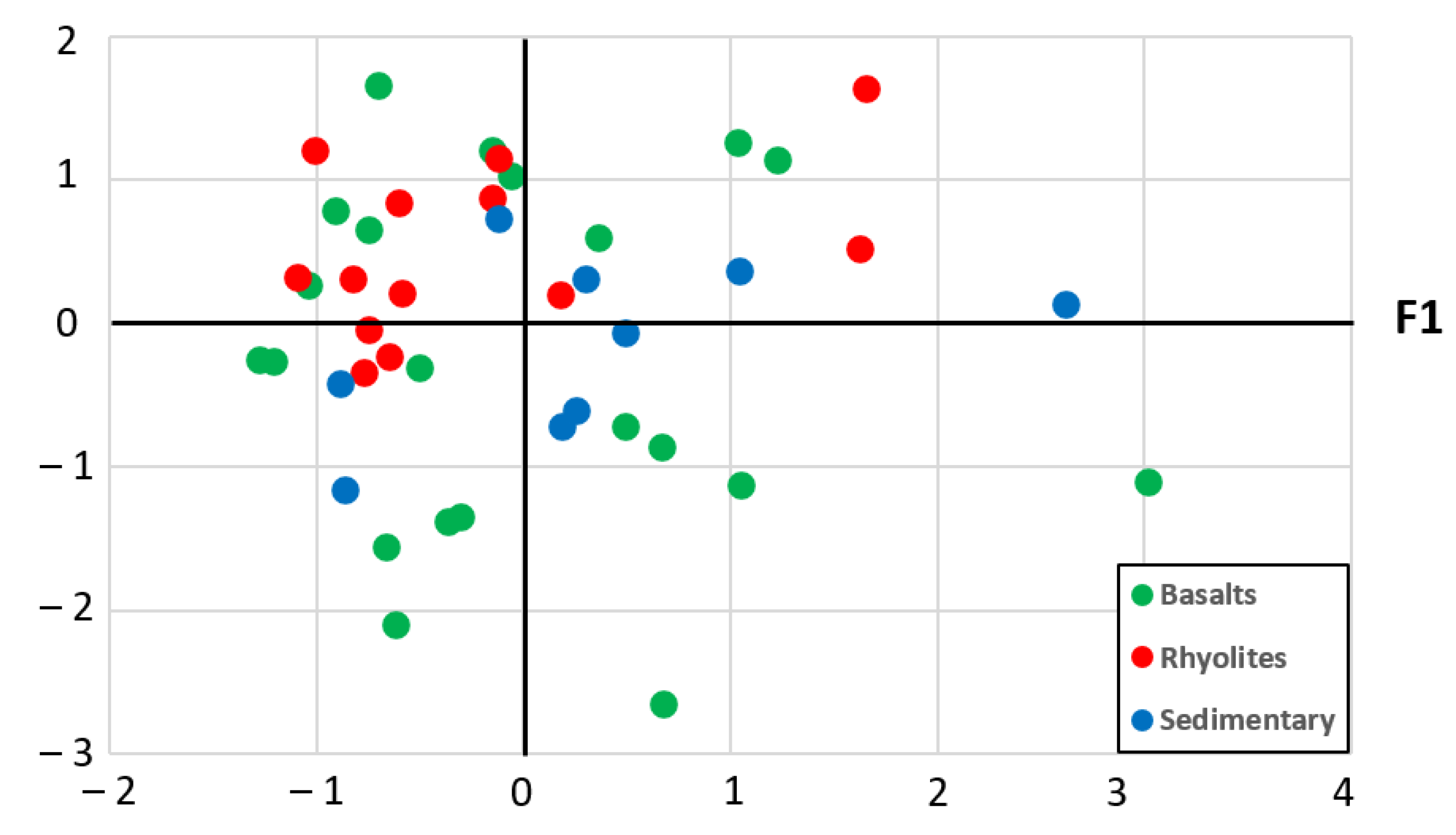
4.1.3. Principal Components Analysis
4.2. Water Types Classification and Hydrogeochemical Processes
4.2.1. Piper Diagram
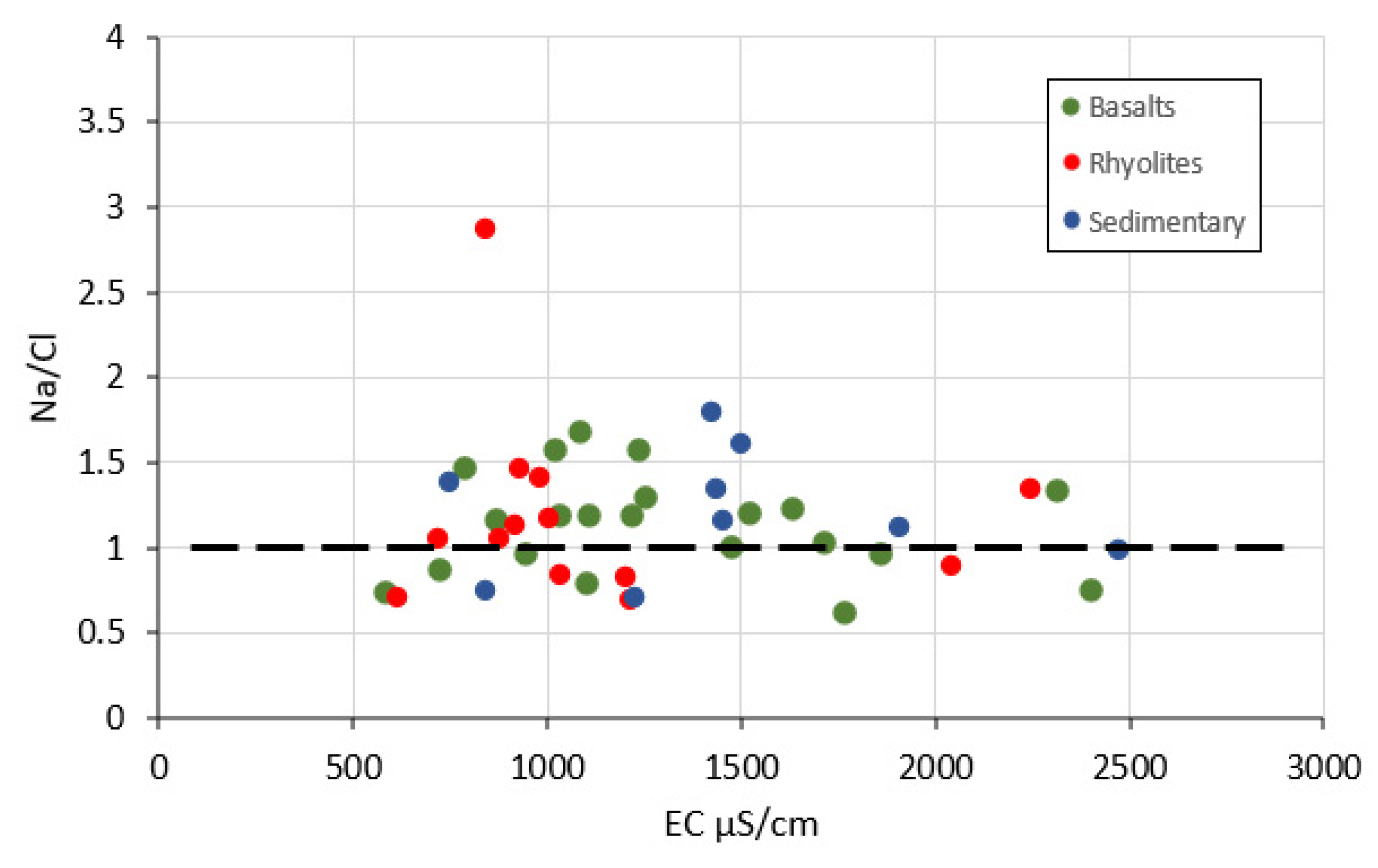
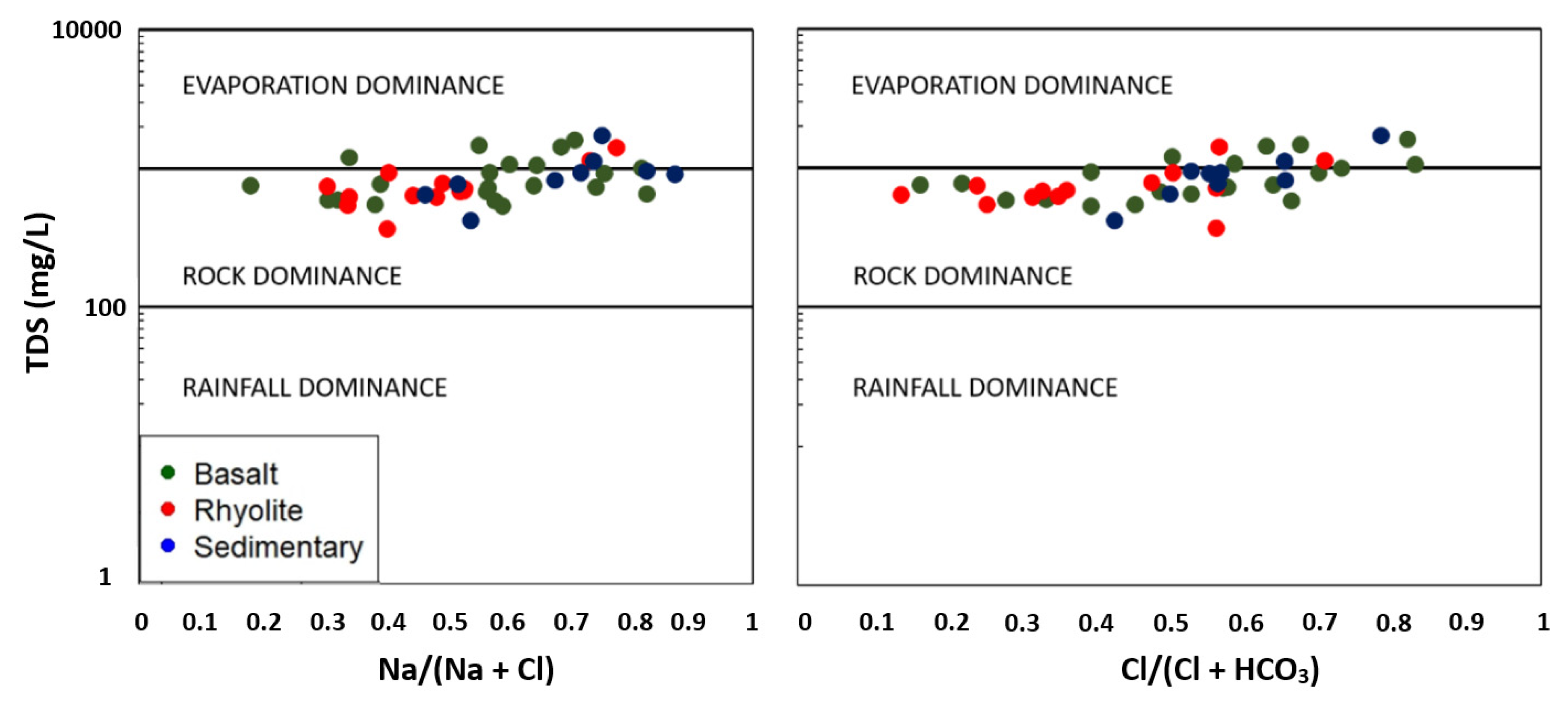
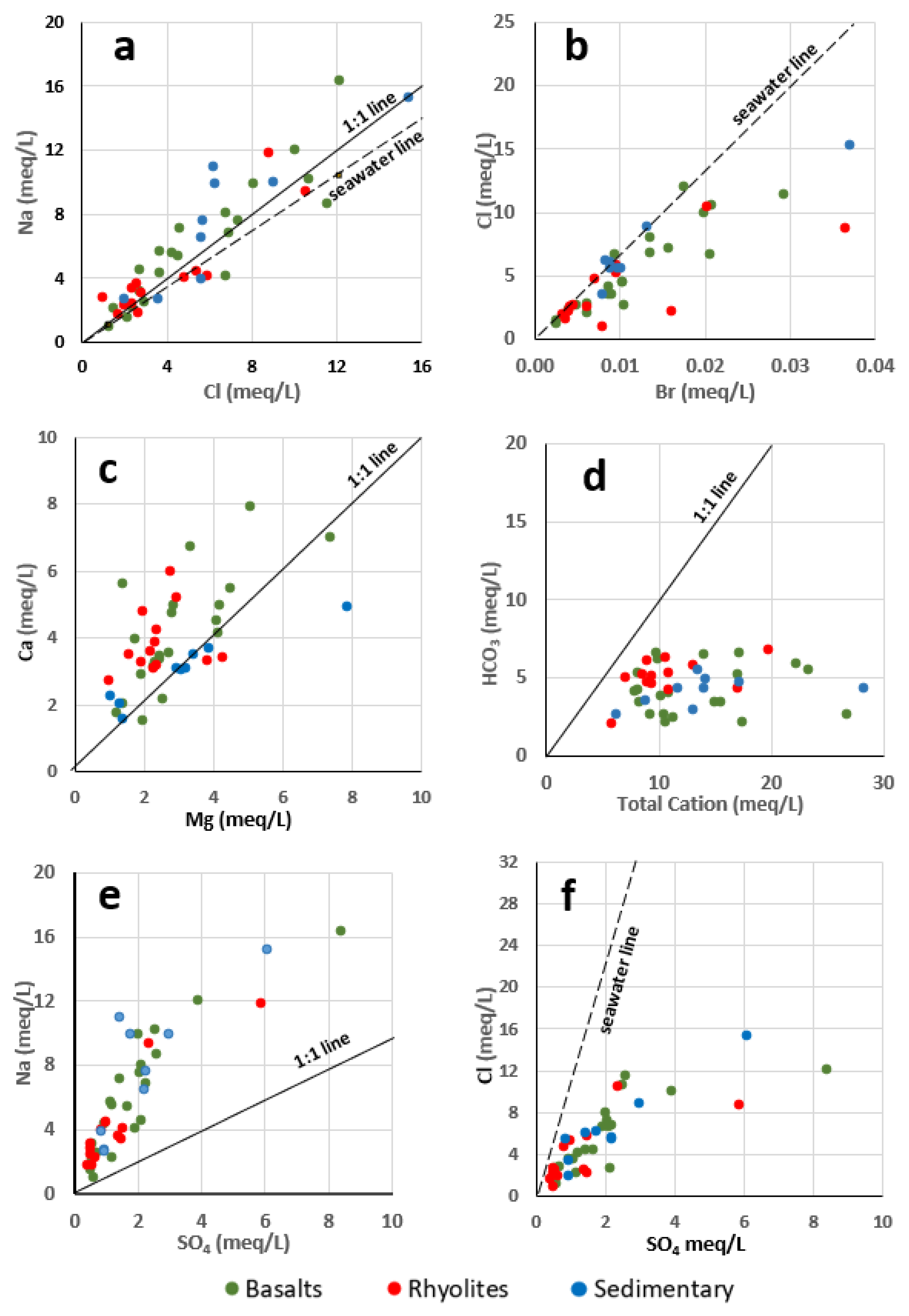
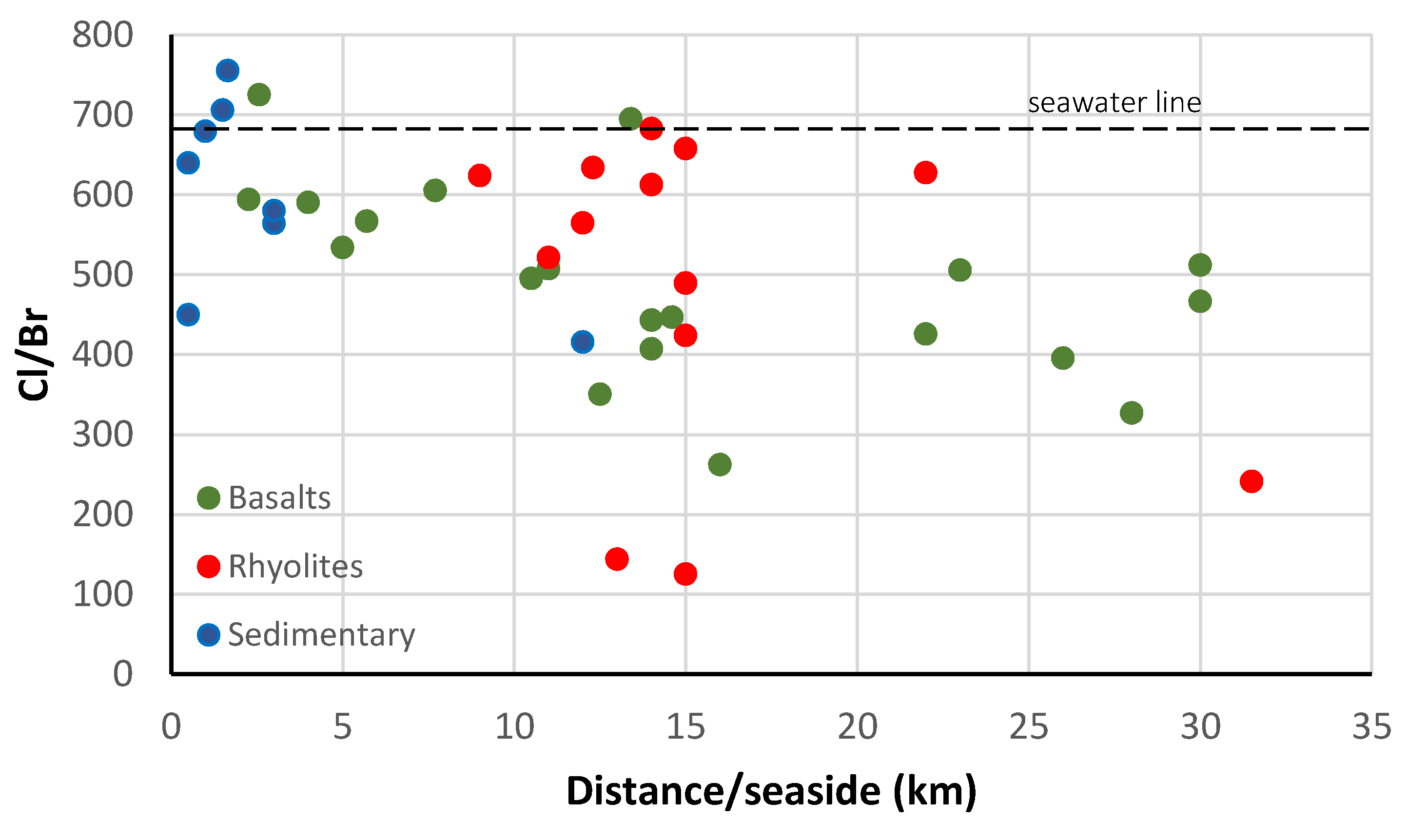
4.2.2. Hydrogeochemical Processes
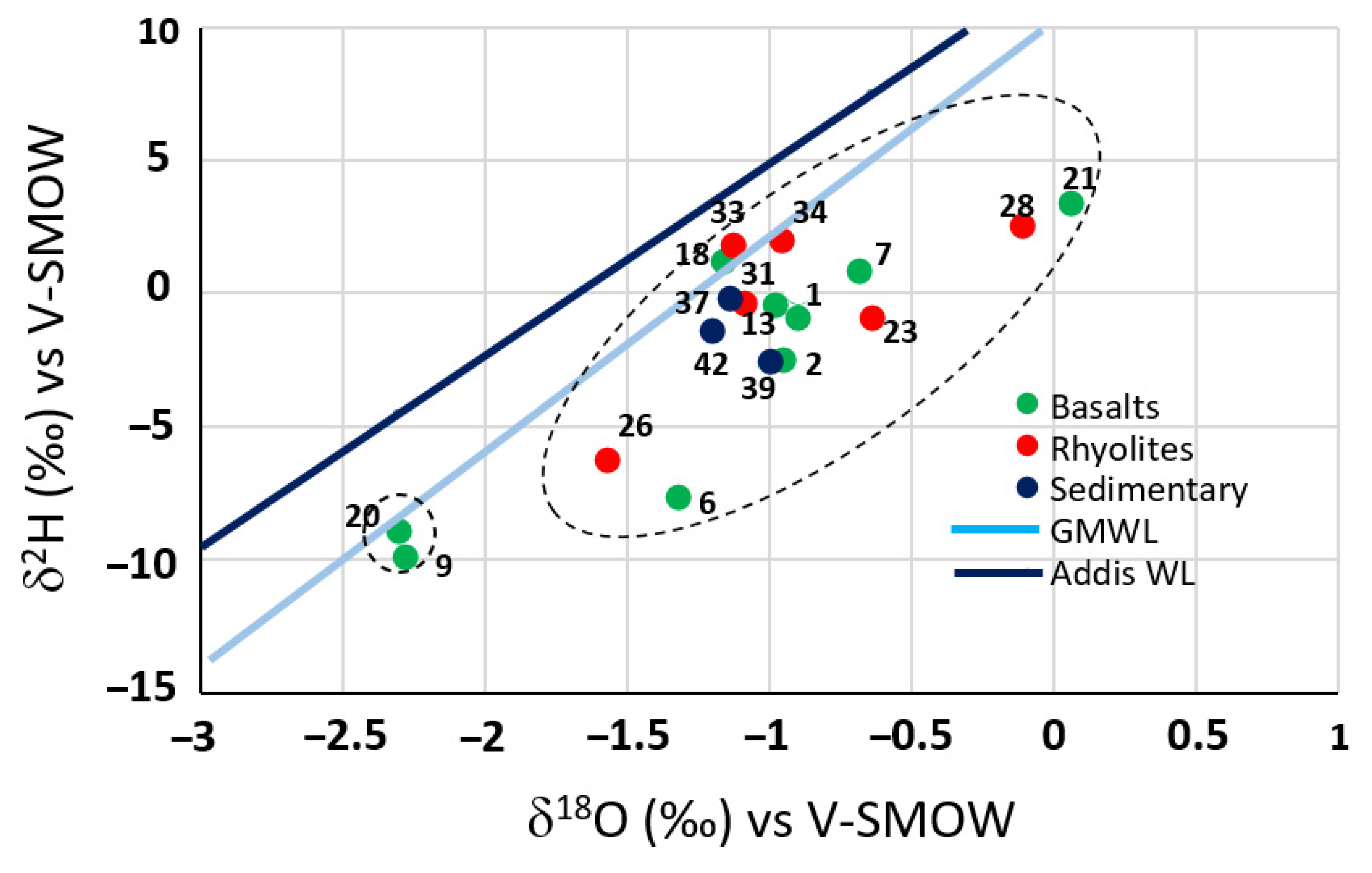
4.3. Isotope Investigations
4.3.1. Stable Isotopes
4.3.2. Radioactive Isotopes 3H and 14C
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ibrahim, M.; Le Coz, M.; Jalludin, M.; Sardini, P.; Razack, M. Assessment of groundwater resources in a complex volcanic reservoir with limited data sets in a semi-arid context using a novel stochastic approach. The Goda Volcanic Massif, Republic of Djibouti. J. Water Resour. Prot. 2017, 10, 106–120. [Google Scholar]
- Moya, C.E.; Raiber, M.; Taulis, M.; Cox, M.E. Hydrochemical evolution and groundwater flow processes in the Galilee and Eroman ga basins, great artesian Basin, Australia: A multivariate statistical approach. Sci. Total Environ. 2015, 508, 411–426. [Google Scholar] [CrossRef]
- Dogramaci, S.; Skrzypek, G.; Dodson, W.; Grierson, P. Stable isotopes and hydrochemical evolution of groundwater in the semi-arid Hamersley Basin of subtropical northwest Australia. J. Hydrol. 2012, 475, 281–293. [Google Scholar] [CrossRef]
- Bellia, C.; Gallardo, A.H.; Yasuhara, M.; Kazahaya, K. Geochemical Characterization of Groundwater in a Volcanic System. Resources 2015, 4, 358–377. [Google Scholar] [CrossRef]
- Bertrand, G.; Celle-Jeanton, H.; Huneau, F.; Loock, S.; Renac, C. Identification of different groundwater flowpaths within volcanic aquifers using natural tracers for the evaluation of the influence of lava flows morphology (Argnat basin, Chaîne des Puys, France). J. Hydrol. 2010, 391, 223–234. [Google Scholar] [CrossRef]
- Blasch, K.W.; Bryson, J.R. Distinguishing Sources of Ground Water Recharge by Using 2H and 18O. Ground Water 2007, 45, 294–308. [Google Scholar] [CrossRef]
- Cartwright, I.; Cendón, D.; Currell, M.; Meredith, K. A review of radioactive isotopes and other residence time tracers in understanding groundwater recharge: Possibilities, challenges, and limitations. J. Hydrol. 2017, 555, 797–811. [Google Scholar] [CrossRef]
- Appelo, C.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; Balkema Publishers: Leiden, The Netherlands, 2005; p. 615. [Google Scholar]
- Parisi, S.; Paternoster, M.; Kohfahl, C.; Pekdeger, A.; Meyer, H.; Hubberten, W.; Spilotro, G.; Mongelli, G. Groundwater recharge areas of a volcanic aquifer system inferred from hydraulic, hydrogeochemical and stable isotope data: Mount Vulture, southern Italy. Hydrogeol. J. 2011, 19, 133–153. [Google Scholar] [CrossRef]
- Aboubaker, M.; Jalludin, M.; Razack, M. Hydrochemistry of a complex volcano-sedimentary aquifer using major ions and environmental isotopes data: Dalha basalts aquifer, southwest of Republic of Djibouti. Environ. Earth Sci. 2013, 70, 3335–3349. [Google Scholar] [CrossRef]
- Mokadem, N.; Demdoumb, A.; Hamed, Y.; Bouri, S.; Rihab Hadji, R.; Boyced, A.; Laouar, R.; Sâad, A. Hydrogeochemical and stable isotope data of groundwater of a multi-aquifer system: Northern Gafsa basin—Central Tunisia. J. Afr. Earth Sci. 2016, 114, 174–191. [Google Scholar] [CrossRef]
- Cartwright, D.; Morgenstern, U. Constraining groundwater recharge and the rate of geochemical processes using tritium and major ion geochemistry: Ovens catchment, southeast Australia. J. Hydrol. 2012, 475, 137–149. [Google Scholar] [CrossRef]
- Subramani, T.; Rajmohan, N.; Elango, L. Groundwater geochemistry and identification of hydrogeochemical processes in a hard rock region, Southern India. Environ. Monit. Assess. 2010, 162, 123–137. [Google Scholar] [CrossRef] [PubMed]
- Rajmohan, N.; Elango, L. Identification and evolution of hydrogeochemical processes in the groundwater environment in an area of the Palar and Cheyyar River Basins, Southern India. Environ. Geol. 2004, 46, 47–61. [Google Scholar] [CrossRef]
- Matiatos, A.; Alexopoulos, A.; Godelitsas, A. Multivariate statistical analysis of the hydrogeochemical and isotopic composition of the groundwater resources in northeastern Peloponnesus (Greece). Sci. Total Environ. 2014, 476, 577–590. [Google Scholar] [CrossRef]
- Cloutier, V.; Lefebvre, R.; Therrien, R.; Savard, M. Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system. J. Hydrol. 2008, 353, 294–313. [Google Scholar] [CrossRef]
- Kolsi, S.H.; Bouri, S.; Hachicha, W.; Ben Dhia, H. Implementation and evaluation of multivariate analysis for groundwater hydrochemistry assessment in arid environments: A case study of Hajeb Elyoun–Jelma, Central Tunisia. Environ. Earth Sci. 2013, 70, 2215–2224. [Google Scholar] [CrossRef]
- Helena, B.; Pardo, R.; Vega, M.; Barrado, E.; Fernandez, J.M.; Fernandez, L. Temporal evolution of groundwater composition in an alluvial aquifer (Pisuerga River, Spain) by principal component analysis. Water Res. 2000, 34, 807–816. [Google Scholar] [CrossRef]
- Villegas, P.; Paredes, V.; Betancur, T.; Ribeiro, L. Assessing the hydrochemistry of the Urabá Aquifer, Colombia by principal component analysis. J. Geochem. Explor. 2013, 134, 120–129. [Google Scholar] [CrossRef]
- Güler, C.; Thyne, G.D.; McCray, J.E.; Turner, K.A. Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeol. J. 2002, 10, 455–474. [Google Scholar] [CrossRef]
- Abderamane, H.; Razack, M.; Vassolo, S. Hydrogeochemical and isotopic characterisation of the Groundwter in the Chari-Baguirmi depression. Republic of Chad. Environ. Earth Sci. 2013, 69, 2337–2350. [Google Scholar] [CrossRef]
- Nkotagu, H. Application of environmental isotopes to groundwater recharge studies in a semi-arid fractured crystalline basement area of Dodoma, Tanzania. J. Afr. Earth Sci. 1996, 22, 443–457. [Google Scholar] [CrossRef]
- De Vries, J.J.; Simmers, I. Groundwater recharge: An overview of processes and challenges. Hydrogeol. J. 2002, 1, 5–17. [Google Scholar] [CrossRef]
- Scanlon, B.; Keese, K.E.; Flint, A.; Flint, L.; Gaye, C.; Edmunds, W.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Chenini, M.; Msaddek, H.; Dlala, M. Hydrogeological characterization and aquifer recharge mapping for groundwater resources management using multicriteria analysis and numerical modeling: A case study from Tunisia. J. Afr. Earth Sci. 2019, 154, 59–69. [Google Scholar] [CrossRef]
- Clark, D. Groundwater Geochemistry and Isotopes; CRC Press: New York, NY, USA, 2015; p. 438. [Google Scholar]
- Négrel, P.; Petelet-Giraud, E. Geochemistry, isotopic composition (18O, 2H, 87Sr/86Sr, 143Nd/144Nd) in the groundwater of French Guiana as indicators of their origin, interrelations. Comptes Rendus Geosci. 2010, 342, 786–795. [Google Scholar] [CrossRef]
- Faure, H.; Fontes, J.-C.; Gischler, C.E.; Mook, W.G.; Vogel, J.C. Un exemple d’étude d’hydrogéologie isotopique en pays semi-aride, le bassin du Lac Tchad. J. Hydrol. 1970, 10, 141–150. [Google Scholar] [CrossRef]
- Eagles, G.; Gloaguen, R.; Ebinger, C. Kinematics of the Danakil microplate. Earth Planet. Sci. Lett. 2002, 203, 607–620. [Google Scholar] [CrossRef]
- Tazieff, H.; Varet, J.; Barberi, F.; Giglia, G. Tectonic Significance of the Afar (or Danakil) Depression. Nature 1972, 235, 144–147. [Google Scholar] [CrossRef]
- Courtillot, V.E. Opening of the Gulf of Aden and Afar by progressive tearing. Phys. Earth Planet. Inter. 1980, 21, 343–350. [Google Scholar] [CrossRef]
- Sichler, B. La biellette danakile: Un modèle pour l’évolution géodynamique de l’Afar. Bull. Soc. Géol. Fr. 1980, 22, 925–932. [Google Scholar] [CrossRef]
- Gadalia, A. Les Rhyolites du Stade Initial de L’ouverture d’un Rift: Exemple des Rhyolites Miocènes de l’Afar. Ph.D. Thesis, University Paris-Sud, Orsay, France, 1980; p. 406. [Google Scholar]
- Fournier, M.; Gasse, F.; Richard, O.; Ruegg, J.C. Notice Explicative: Carte Géologique de la République de Djibouti à 1/100 000: Tadjourah; ISERST, Ministère de la Coopération Française: Djibouti, Africa, 1985.
- Taylor, R.G.; Todd, M.C.; Kongola, L.; Maurice, L.; Nahozya, E.; Sanga, H.; MacDonald, A.M. Evidence of the dependence of groundwater resources on extreme rainfall in East Africa. Nat. Clim. Chang. 2013, 3, 374–378. [Google Scholar] [CrossRef]
- Moeck, C.; Grech-Cumbo, N.; Podgorski, J.; Bretzler, A.; Gurdak, J.J.; Berg, M.; Schirmer, M. A global-scale dataset of direct natural groundwater recharge rates: A review of variables, processes and relationships. Sci. Total Environ. 2020, 717, 137042. [Google Scholar] [CrossRef] [PubMed]
- Razack, M.; Jalludin, M.; Houmed-Gaba, A. Simulation of Climate Change Impact on a Coastal Aquifer under Arid Climate. The Tadjourah Aquifer (Republic of Djibouti, Horn of Africa). Water 2019, 11, 2347. [Google Scholar] [CrossRef]
- Thomas, B.F.; Ali Behrangi, A.; Famiglietti, J.S. Precipitation Intensity Effects on Groundwater Recharge in the Southwestern United States. Water 2016, 8, 90. [Google Scholar] [CrossRef]
- Le Gall, B.; Daoud, M.A.; Maury, R.; Gasse, F.; Rolet, J.; Jalludin, M.; Caminiti, A.M.; Moussa, N. Carte Géologique de la République de Djibouti, Echelle 1/200 000. (Geological Map of the Republic of Djibouti. Scale1/200000); Publisher CERD (Centre d’Etude et de Recherche de Djibouti) and CCGM (Commission de la Carte Géologique du Monde) Commission for the Geological Map of the World: Paris, France, 2015. [Google Scholar]
- Freeze, R.A.; Cheery, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979; p. 604. [Google Scholar]
- Ahmed, A.H.; Rayaleh, W.E.; Zghibi, A.; Ouddane, B. Assessment of chemical quality of groundwater in coastal volcanosedimentary aquifer of Djibouti, Horn of Africa. J. Afr. Earth Sci. 2017, 131, 284–300. [Google Scholar] [CrossRef]
- Barnes, C.J.; Jacobson, G.; Smith, G.D. The origin of high-nitrate ground waters in the Australian arid zone. J. Hydrol. 1992, 137, 181–197. [Google Scholar] [CrossRef]
- Heaton, T.H.E. Sources of the nitrate in phreatic groundwater in the western Kalahari. J. Hydrol. 1984, 67, 249–259. [Google Scholar] [CrossRef]
- Deans, J.; Edmunds, W.; Lindle, D.; Gaye, C.; BDreyfus, B.; Nizinski, J.; Neyra, M.; Ingleby, K.; Munro, R. Nitrogen in interstitial waters in the sahel: Natural baseline, pollutant or resource? Plant Soil 2005, 271, 47–62. [Google Scholar] [CrossRef]
- Hunter, R.B.; Romney, E.M.; Wallace, A. Nitrate Distribution in Mojave Desert Soils. Soil Sci. 1982, 134, 22–30. [Google Scholar] [CrossRef]
- Schwiede, M.; Duijnisveld, W.H.M.; Böttcher, J. Investigation of processes leading to nitrate enrichment in soils in the Kalahari Region, Botswana. Phys. Chem. Earth Parts A/B/C 2005, 30, 712–716. [Google Scholar] [CrossRef]
- Saporta, G. Probabilités, Analyse des Données et Statistiques, 3rd ed.; Technip: Paris, France, 2011; p. 656. [Google Scholar]
- Jollife, I.T. Principal Component Analysis; Springer: New York, NY, USA, 1986; p. 271. [Google Scholar]
- Meng, S.X.; Maynard, J.B. Use of statistical analysis to formulate conceptual models of geochemical behavior: Water chemical data from Butucatu aquifer in Sao Paulo State, Brazil. J. Hydrol. 2001, 250, 78–97. [Google Scholar] [CrossRef]
- Razack, M.; Dazy, J. Hydrochemical characterization of groundwater mixing in sedimentary and metamorphic reservoirs with a combined use of Piper’s principle and factor analysis. J. Hydrol. 1990, 114, 371–393. [Google Scholar] [CrossRef]
- Usunoff, E.J.; Guzman, A. Multivariate analysis in hydrochemistry: An example of the use of factor and correspondence analyses. Ground Water 1989, 27, 27–34. [Google Scholar] [CrossRef]
- Schoeller, H. Qualitative evaluation of groundwater resources. In Methods and Techniques of Groundwater Investigations and Development; UNESCO: Paris, France, 1965; pp. 54–83. [Google Scholar]
- Baird, C.; Cann, M. Chimie de L’environnement, 1st ed.; De Boeck: Paris, France, 2016; p. 832. [Google Scholar]
- Jankowski, J.; Acworth, R.I. Impact of depris-flow deposits on hydrogeochemical processes and the development of dryland salinity in the Yass River catchment, New South Wales, Australia. Hydrogeol. J. 1997, 5, 71–88. [Google Scholar] [CrossRef]
- Gibbs, R.J. Mechanisms controlling world water chemistry. Science 1970, 170, 1088–1090. [Google Scholar] [CrossRef]
- Adimalla, N.; Venkatayogi, S. Mechanism of fluoride enrichment in groundwater of hard rock aquifers in Medak, Telangana State, South India. Environ. Earth Sci. 2017, 76, 45. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Tziritis, E.; Fakhri, M.S.; Soltani, S. Identification of hydrogeochemical processes and pollution sources of groundwater resources in the Marand plain, northwest of Iran. Environ. Earth Sci. 2017, 76, 297. [Google Scholar] [CrossRef]
- Mayback, M. Global chemical weathering of surficial rocks estimated from river dissolved loads. Am. J. Sci. 1987, 287, 401–428. [Google Scholar] [CrossRef]
- Stumm, W.; Morgan, J.J. Aquatic Chemistry; Wiley-Interscience: New York, NY, USA, 1996; p. 780. [Google Scholar]
- Moller, D. The Na/Cl ratio in rainwater and the seasalt chloride cycle. Tellus 1990, 42B, 254–262. [Google Scholar] [CrossRef]
- Neal, C.; Kirchner, J.W. Sodium and chloride levels in rainfall, mist, streamwater and groundwater at the Plynlimon catchments, mid-Wales: Inferences on hydrological and chemical controls. Hydrol. Earth Syst. Sci. 2000, 4, 295–310. [Google Scholar] [CrossRef]
- Davis, S.N.; Whittemore, D.O.; Fabryka-Martin, J. Uses of Chloride/Bromide Ratios in Studies of Potable Water. Ground Water 1998, 36, 338–350. [Google Scholar] [CrossRef]
- Katz, B.G.; Eberts, S.M.; Kauffman, L.J. Using Cl/Br ratios and other indicators to assess potential impacts on groundwater quality from septic systems: A review and examples from principal aquifers in the United States. J. Hydrol. 2011, 397, 151–166. [Google Scholar] [CrossRef]
- Alcalá, F.J.; Custodio, E. Using the Cl/Br ratio as a tracer to identify the origin of salinity in aquifers in Spain and Portugal. J. Hydrol. 2008, 359, 189–207. [Google Scholar] [CrossRef]
- Richter, B.C.; Kreitler, C.W. Geochemistry of saltwater beneath the Rolling Plains, North-Central Texas. Ground Water 1986, 24, 735–742. [Google Scholar] [CrossRef]
- Morris, A.W.; Riley, J.P. The bromide/chlorinity and sulphate/chlorinity ratio in sea water. Deep Sea Res. Oceanogr. Abstr. 1966, 13, 699–705. [Google Scholar] [CrossRef]
- Möller, P.; Rosenthal, E.; Inbar, N.; Magri, F. Hydrochemical considerations for identifying water from basaltic aquifers: The Israeli experience. J. Hydrol. Reg. Stud. 2016, 5, 33–47. [Google Scholar] [CrossRef][Green Version]
- Gastmans, D.; Hutcheon, I.; Menegário, A.A.; Chang, H.K. Geochemical evolution of groundwater in a basaltic aquifer based on chemical and stable isotopic data: Case study from the Northeastern portion of Serra Geral Aquifer, São Paulo state (Brazil). J. Hydrol. 2016, 535, 598–611. [Google Scholar] [CrossRef]
- Rosentha, E. Chemical composition of rainfall and groundwater in recharge areas of the Bet Shean-Harod multiple aquifer system, Israel. J. Hydrol. 1987, 89, 329–352. [Google Scholar] [CrossRef]
- Rogers, R.J. Geochemical comparison of groundwater in areas of New England, New York and Pennsylvania. Ground Water 1989, 27, 690–712. [Google Scholar] [CrossRef]
- Mayo, A.L.; Loucks, M.D. Solute and isotopic geochemistry and ground water flow in the central Wasatch Range, Utah. J. Hydrol. 1995, 172, 31–59. [Google Scholar] [CrossRef]
- Katz, B.G.; Coplen, T.B.; Bullen, T.D.; Davis, J.H. Use of Chemical and Isotopic Tracers to Characterize the Interactions Between Ground Water and Surface Water in Mantled Karst. Ground Water 1997, 35, 1014–1028. [Google Scholar] [CrossRef]
- Jalludin, M. Propriétés Géométriques et Hydrodynamiques des Aquifères en Milieux Volcaniques Fissurés sous Climat Aride. République de Djibouti. Ph.D. Thesis, University of Poitiers, Poitiers, France, 1993. (In French). [Google Scholar]
- Kim, K. Long-term disturbance of groundwater chemistry following well installation. Ground Water 2003, 41, 780–789. [Google Scholar] [CrossRef] [PubMed]
- Bourgueil, B. Les carbonates et sulfates de sodium. In Rapport R 36299; BRGM: Orléans, France, 1992; p. 42. [Google Scholar]
- IAEA. Stable isotopes hydrology. In Technical Report Series No.210; IAEA: Vienna, Austria, 1992; p. 356. [Google Scholar]
- Craig, H. Isotopic Variations in Meteoric Waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
- Fontes, J.C. Dating of groundwater. In Guidebook on Nuclear Techniques in Hydrology, 1983 Edition. Technical Reports Series 91; IAEA: Vienna, Austria, 1983; pp. 285–317. [Google Scholar]
- IAEA. Isotope Methods for Dating Old Groundwater; IAEA: Vienna, Austria, 2013; p. 357. [Google Scholar]

| Water Point | ID | Type | Rock Type | X (m) | Y (m) | Z (m) | Depth (m) | P.L. (m) | T °C | EC µS/cm | pH | Ca2+ mg/L | Mg2+ mg/L | Na+ mg/L | K+ mg/L | HCO3−mg/L | Cl− mg/L | SO42− mg/L | NO3− mg/L | Br− mg/L | SiO2 mg/L | TDS mg/L | CA1 | CA2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Randa_S | 1 | S | Bas | 244,393 | 1,311,069 | 971 | - | - | 19 | 720 | 7.2 | 79.2 | 21 | 58.4 | 1.1 | 211.2 | 102.1 | 31.5 | 45.6 | 0.49 | 40.7 | 551 | 0.42 | 0.18 |
| Bolli | 2 | B | Bas | 240,731 | 1,316,866 | 950 | 151 | 820 | 26.7 | 2397 | 7.48 | 139.9 | 88.4 | 200.7 | 5.3 | 338.9 | 408.6 | 123.3 | 167.3 | 2.33 | 79.5 | 1477 | 0.5 | 0.44 |
| Magaleh | 3 | W | Bas | 245,340 | 1,315,551 | 960 | 11 | - | 23 | 1518 | 7.4 | 110.7 | 53.8 | 277.9 | 4 | 366.4 | 356.6 | 186.2 | 83.6 | 1.59 | 84.5 | 1443 | 0.21 | 0.14 |
| Essalou | 4 | B | Bas | 243,960 | 1,322,771 | 980 | 150 | - | 25 | 1762 | 7.23 | 158.5 | 60.5 | 95 | 1.6 | 405.8 | 238.9 | 90.6 | 151.8 | 1.65 | 63.6 | 1212 | 0.6 | 0.29 |
| Adaylou_P | 5 | W | Bas | 254,333 | 1,322,962 | 1030 | 14 | - | 25.1 | 1708 | 7.46 | 100.5 | 49.9 | 175.1 | 3.1 | 319 | 259.2 | 96.2 | 67.2 | 1.25 | 60.8 | 1075 | 0.31 | 0.2 |
| Adaylou_F | 6 | B | Bas | 254,277 | 1,323,430 | 1027 | 102 | 971 | 27 | 1857 | 7.86 | 112.9 | 16.2 | 236.1 | 6.9 | 132.8 | 377.8 | 119.8 | 60 | 1.66 | 37.4 | 1068 | 0.36 | 0.53 |
| Randa_F | 7 | B | Bas | 244,454 | 1,311,124 | 910 | 111 | 871 | 25.5 | 1029 | 7.6 | 66 | 27.6 | 99.9 | 4.1 | 238.1 | 129.4 | 44.5 | 67.5 | 0.69 | 62.2 | 681 | 0.2 | 0.09 |
| Marra | 8 | W | Bas | 237,136 | 1,294,913 | 866 | - | - | 31.2 | 1102 | 7.84 | 59 | 23 | 125 | 2.9 | 161.2 | 161 | 78.4 | 88.6 | 0.81 | 53.7 | 756 | 0.21 | 0.14 |
| Towele_F | 9 | B | Bas | 238,666 | 1,294,400 | 885 | 60 | 859 | 35 | 2313 | 7.61 | 134.5 | 39.9 | 376.1 | 10.3 | 163.4 | 429.8 | 401.8 | 48.2 | 1.39 | 39.5 | 1607 | 0.1 | 0.08 |
| Raïssa_P | 10 | W | Bas | 235,200 | 1,287,079 | 380 | 5 | 377 | 32 | 1476 | 7.67 | 99.5 | 33.9 | 159 | 5.7 | 214.9 | 243 | 105.3 | 57.3 | 1.08 | 48.5 | 926 | 0.32 | 0.24 |
| Sagallou_F | 11 | B | Bas | 251,301 | 1,292,382 | 70 | 120 | - | 36.8 | 1625 | 8.06 | 63.1 | 27.2 | 229.1 | 3 | 215.5 | 286.3 | 95.3 | 53.7 | 1.09 | 77.1 | 1006 | 0.19 | 0.17 |
| Gerenle2 | 12 | W | Bas | 238,693 | 1,296,061 | 1080 | 10 | 1070 | 28 | 1232 | 7.56 | 30.8 | 23.5 | 165.2 | 2.8 | 250 | 161.6 | 67.4 | 53.4 | 0.82 | 11.1 | 759 | −0.04 | −0.02 |
| Nghoubet | 13 | B | Bas | 246,547 | 1,287,646 | 123 | 183 | - | 47.1 | 1219 | 7.7 | 36.2 | 14.3 | 185.6 | 6.5 | 150.4 | 239.7 | 99 | 43.4 | 0.75 | 42 | 777 | 0.2 | 0.19 |
| Gerenlé_S | 14 | S | Bas | 238,800 | 1,296,117 | 1080 | - | - | 26 | 1015 | 7.69 | 40.8 | 16.6 | 132.4 | 2.3 | 162.8 | 128.8 | 52.2 | 54.7 | 0.71 | 21.2 | 592 | −0.05 | −0.03 |
| Wagile | 15 | W | Bas | 243,709 | 1,299,487 | 1275 | 3 | - | 22 | 582 | 7.4 | 71.3 | 32.1 | 35.9 | 1.4 | 254.7 | 74.6 | 22.6 | 40.1 | 0.48 | 32.7 | 534 | 0.5 | 0.13 |
| Hankata | 16 | W | Bas | 250,710 | 1,296,349 | 278 | 6 | 276 | 26.5 | 1100 | 7.37 | 90.5 | 49 | 23.2 | 2.3 | 400.9 | 45.5 | 26.5 | 18.6 | 0.19 | 97.6 | 657 | 0.44 | 0.05 |
| Gade | 17 | W | Bas | 250,214 | 1,295,180 | 270 | - | - | 25.4 | 785 | 7.5 | 67.8 | 29.3 | 50.2 | 1.7 | 325.2 | 52.4 | 23.9 | 30.7 | 0.20 | 56.5 | 584 | 0.01 | 0 |
| Masolay | 18 | S | Bas | 248,572 | 1,297,829 | 550 | - | - | 22.2 | 942 | 7.51 | 95.8 | 33.6 | 52.1 | 1.4 | 378.6 | 83 | 55.9 | 32.3 | 0.31 | 45.1 | 734 | 0.36 | 0.07 |
| Wea | 19 | W | Bas | 247,740 | 1,293,484 | 372 | - | - | 24.9 | 867 | 7.5 | 43.8 | 30.4 | 73.9 | 2.6 | 262.9 | 97.1 | 25.8 | 60 | 0.39 | 118.9 | 598 | 0.21 | 0.07 |
| Itki | 20 | B | Bas | 238,927 | 1,300,357 | 1459 | 252 | 1331 | 33 | 1077 | 7.8 | 69.6 | 29.3 | 105.4 | 3.8 | 131.1 | 96.9 | 101 | 184.1 | 0.83 | 44.7 | 723 | −0.13 | −0.05 |
| Illalou | 21 | S | Bas | 242,628 | 1,295,841 | 887 | - | - | 24.2 | 1251 | 7.7 | 83.6 | 49.4 | 127.9 | 5.3 | 400.2 | 151.3 | 56.2 | 60 | 0.69 | 64.2 | 937 | 0.12 | 0.04 |
| Amiso af | 22 | W | Rhy | 249,843 | 1,309,524 | 590 | 11 | 588 | 26 | 975 | 7.7 | 64.4 | 28.4 | 83.7 | 2.1 | 283.3 | 91.2 | 65.4 | 73.7 | 0.49 | 68.2 | 694 | 0.06 | 0.02 |
| Bobo af | 23 | B | Rhy | 251,972 | 1,309,060 | 610 | 60 | - | 26.7 | 928.8 | 8.206 | 61.9 | 27.1 | 78.1 | 3.8 | 287.5 | 82 | 69.7 | 73.3 | 1.29 | 59.6 | 687 | 0 | 0 |
| Akaabar | 24 | W | Rhy | 252,980 | 1,309,122 | 480 | 3 | - | 25.4 | 1202 | 7.69 | 78.1 | 27.6 | 102.3 | 7.9 | 258.6 | 190.2 | 46.1 | 5.9 | 0.76 | 63.7 | 719 | 0.42 | 0.26 |
| Affaloyna | 25 | W | Rhy | 254,607 | 1,309,449 | 460 | 7 | 458 | 25.9 | 916.7 | 7.73 | 65.7 | 23.1 | 72.4 | 4.5 | 317.5 | 99 | 23.2 | 19.3 | 0.35 | 59 | 626 | 0.22 | 0.06 |
| Daimoli_S | 26 | S | Rhy | 270,952 | 1,312,924 | 376 | - | - | 24.8 | 2041 | 7.83 | 67.1 | 45.5 | 217.1 | 11.3 | 266.5 | 373 | 112.2 | 42.4 | 1.61 | 80.3 | 1140 | 0.39 | 0.38 |
| Ayri | 27 | W | Rhy | 264,676 | 1,326,902 | 855 | 8 | 853 | 24 | 2246 | 7.796 | 68.9 | 51.2 | 272.8 | 3.6 | 417.1 | 312 | 281.5 | 9.8 | 2.92 | 87.2 | 1422 | 0.11 | 0.05 |
| Garassou_P | 28 | W | Rhy | 251,879 | 1,312,230 | 702 | 9 | 695 | 22.6 | 1000 | 7.39 | 104.1 | 35.2 | 53.9 | 0.9 | 384.7 | 71 | 30.1 | 64.7 | 0.26 | 77.6 | 746 | 0.23 | 0.04 |
| Biladita | 29 | W | Rhy | 247,909 | 1,308,228 | 623 | 3 | 622 | 24.3 | 1036 | 7.71 | 85 | 28 | 93.6 | 6.1 | 326.7 | 171.2 | 39.1 | 35.6 | 0.57 | 106.1 | 787 | 0.42 | 0.2 |
| Ounda ela | 30 | W | Rhy | 247,462 | 1,307,852 | 636 | 5 | 632 | 24.6 | 877 | 7.36 | 96.5 | 23.2 | 56.8 | 3.2 | 315.1 | 82.9 | 22.9 | 21.9 | 0.31 | 50 | 623 | 0.28 | 0.07 |
| Bankoualéh | 31 | S | Rhy | 246,030 | 1,307,794 | 722 | - | - | 22 | 840.5 | 7.69 | 72.8 | 26 | 65.9 | 7.2 | 376.2 | 35.4 | 22.6 | 32.5 | 0.64 | 64.7 | 642 | −1.06 | −0.09 |
| Dugum | 32 | W | Rhy | 254,044 | 1,304,711 | 331 | 8 | 325 | 27 | 1214 | 7.8 | 120 | 33 | 95.3 | 3 | 357.2 | 209 | 71.3 | 41.6 | 0.76 | 72.5 | 932 | 0.53 | 0.26 |
| Weer | 33 | S | Rhy | 249,148 | 1,304,548 | 611 | - | - | 21 | 609.5 | 7.24 | 55.1 | 11.8 | 42.7 | 5.7 | 128.2 | 93.4 | 24.8 | 7.4 | 0.32 | 77.5 | 370 | 0.48 | 0.29 |
| Tooha | 34 | S | Rhy | 249,246 | 1,302,815 | 609 | - | - | 19.5 | 719 | 7.85 | 70.7 | 18.5 | 41.7 | 3.4 | 307.8 | 60.8 | 18.9 | 24 | 0.28 | 46.7 | 547 | 0.26 | 0.05 |
| Nouro ela | 35 | W | Sed | 252,847 | 1,291,488 | 18 | 12 | 8 | 29.8 | 1223 | 7.31 | 74.2 | 46.3 | 91 | 3 | 270.2 | 198.7 | 39.5 | 53.2 | 0.70 | 114.1 | 778 | 0.53 | 0.34 |
| Andali | 36 | W | Sed | 258,716 | 1,300,405 | 10 | 9 | 1 | 30.5 | 1905 | 7.53 | 70.4 | 40.9 | 230.8 | 3.3 | 293.1 | 318.6 | 142.4 | 24.8 | 1.06 | 82.6 | 1128 | 0.27 | 0.19 |
| PK-9 | 37 | B | Sed | 261,069 | 1,303,387 | 115 | 135 | 5 | 29 | 746 | 7.81 | 45.8 | 12.3 | 63.1 | 2.6 | 164.9 | 70.2 | 44.6 | 18.6 | 0.01 | 50 | 423 | 0.06 | 0.02 |
| PK6-7 | 38 | B | Sed | 266,261 | 1,305,337 | 85 | 132 | 8 | 28.1 | 1435 | 7.54 | 61 | 36.5 | 176.1 | 7 | 268.7 | 201.7 | 105.4 | 73.6 | 0.81 | 75.6 | 933 | 0.09 | 0.05 |
| PK6-6 | 39 | B | Sed | 266,264 | 1,305,078 | 82 | 101 | 5 | 27.7 | 1447 | 7.67 | 62.4 | 38 | 149.8 | 4.8 | 180.7 | 198.7 | 104.2 | 79.8 | 0.77 | 60.4 | 821 | 0.22 | 0.15 |
| Ambabo_F | 40 | B | Sed | 262,279 | 1,301,844 | 30 | 60 | - | 29.2 | 1423 | 7.51 | 31.7 | 16.6 | 253.7 | 2.6 | 306.8 | 218.3 | 67.7 | 16.7 | 0.70 | 41.2 | 916 | −0.17 | −0.1 |
| Kalaf | 41 | W | Sed | 259,598 | 1,300,919 | 11 | 11 | 1 | 26 | 1496 | 7.9 | 41 | 15.7 | 229.4 | 3.1 | 340.2 | 220.2 | 82.2 | 25.8 | 0.66 | 75.8 | 959 | −0.06 | −0.03 |
| Chehem ela | 42 | W | Sed | 253,150 | 1,291,638 | 20 | 12 | 8 | 27.1 | 837.2 | 7.59 | 62 | 35 | 61.9 | 1.8 | 219.8 | 126.3 | 43.5 | 95.9 | 0.63 | 72.5 | 650 | 0.5 | 0.24 |
| Ideyta | 43 | W | Sed | 237,601 | 1,292,797 | 681 | 9 | 681 | 30.7 | 2470 | 7.1 | 99 | 94.3 | 351.3 | 5.7 | 263.8 | 545.3 | 290.9 | 75 | 2.96 | 44.8 | 1730 | 0.35 | 0.34 |
| Sample | ID | Water Point | Rock Type | δ18O V-SMOW | δ2H V-SMOW | 3H (TU) |
|---|---|---|---|---|---|---|
| Nghoubet | 13 | Borehole | Basalts | −0.98 | −0.5 | <0.8 ± 0.32 |
| Masolay | 18 | Spring | Basalts | −1.16 | 1.18 | <0.8 ± 0.30 |
| Randa | 1 | Spring | Basalts | −0.9 | −0.88 | <0.8 ± 0.34 |
| Boli | 2 | Borehole | Basalts | −0.95 | −2.44 | <0.8 ± 0.34 |
| Itki | 20 | Borehole | Basalts | −2.3 | −8.96 | <0.8 ± 0.32 |
| Illalou | 21 | Spring | Basalts | 0.06 | 3.38 | <0.8 ± 0.35 |
| Randaf | 7 | Borehole | Basalts | −0.69 | 0.81 | <0.8 ± 0.32 |
| Adailou | 6 | Borehole | Basalts | −1.32 | −7.66 | <0.8 ± 0.36 |
| Towele | 9 | Borehole | Basalts | −2.28 | −9.9 | <0.8 ± 0.32 |
| Garassou | 28 | Well | Basalts | −0.11 | 2.54 | <0.8 ± 0.34 |
| Bobo af | 23 | Borehole | Rhyolites | −0.64 | −0.93 | <0.8 ± 0.37 |
| Weer | 33 | Spring | Rhyolites | −1.13 | 1.85 | <0.8 ± 0.31 |
| Daimoli | 26 | Spring | Rhyolites | −1.57 | −6.25 | <0.8 ± 0.35 |
| Tooha | 34 | Spring | Rhyolites | −0.96 | 2.01 | <0.8 ± 0.32 |
| Bankoualé | 31 | Spring | Rhyolites | −1.09 | −0.38 | <0.8 ± 0.31 |
| PK6-6 | 39 | Borehole | Sedimentary | −1 | −2.53 | 1.0 ± 0.38 |
| PK9 | 37 | Borehole | Sedimentary | −1.14 | −0.19 | <0.8 ± 0.33 |
| Chehem | 42 | Well | Sedimentary | −1.2 | −1.46 | <0.8 ± 0.33 |
| Samples | ID | Water Point | Rock Type | 14C (pMC) (%) | Apparent Age Relative to 2015 (y) | Classification |
|---|---|---|---|---|---|---|
| Nghoubet | 13 | Borehole | Basalts | 64.43 | 3531 | Old |
| Magaleh | 3 | Borehole | Basalts | 100.71 | Modern | Modern |
| S_Randa | 1 | Spring | Basalts | 94.3 | 471 | Submodern |
| Bolli | 2 | Borehole | Basalts | 98.03 | 160 | Submodern |
| Itki | 20 | Borehole | Basalts | 85.85 | 1225 | Old |
| Day | 44 | Borehole | Basalts | 80.61 | 1731 | Old |
| Randa | 7 | Borehole | Basalts | 93.68 | 525 | Submodern |
| Adaylou | 6 | Borehole | Basalts | 85.9 | 1221 | Old |
| Towele | 9 | Borehole | Basalts | 73.36 | 2488 | Old |
| Hallu | 45 | Borehole | Basalts | 16.66 | 14,395 | Old |
| Amiso | 22 | Borehole | Rhyolites | 101.75 | Modern | Modern |
| Daimoli | 26 | Spring | Rhyolites | 92.46 | 630 | Submodern |
| Toha | 34 | Spring | Rhyolites | 98.03 | 160 | Submodern |
| Pk6-6 | 39 | Borehole | Sedimentary | 89.81 | 864 | Submodern |
| PK 9 | 37 | Borehole | Sedimentary | 87.59 | 1065 | Old |
| T °C | EC µS/cm | pH | Ca2+ | Mg2+ | Na+ | K+ | HCO3− | Cl− | SO42− | NO3− | Br− | SiO2 | TDS | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GMR system | Average | 26.9 | 1283 | 7.6 | 77 | 34 | 136 | 4 | 275 | 188 | 85 | 55 | 1 | 63 | 860 |
| SD | 4.9 | 497 | 0.2 | 29 | 18 | 88 | 2 | 83 | 120 | 78 | 39 | 1 | 23 | 315 | |
| CV (%) | 18 | 39 | 3 | 37 | 52 | 64 | 58 | 30 | 64 | 92 | 70 | 75 | 36 | 37 | |
| Minimum | 19.0 | 582 | 7.1 | 31 | 12 | 23 | 1 | 128 | 35 | 19 | 6 | 0 | 11 | 370 | |
| Maximum | 47.1 | 2470 | 8.2 | 159 | 94 | 376 | 11 | 417 | 545 | 402 | 184 | 3 | 119 | 1730 | |
| Basalts | Average | 27.9 | 1313 | 7.6 | 84 | 36 | 142 | 4 | 261 | 196 | 91 | 70 | 1 | 56 | 890 |
| SD | 6.3 | 491 | 0.2 | 35 | 18 | 88 | 2 | 95 | 120 | 82 | 44 | 1 | 25 | 321 | |
| CV (%) | 22 | 37 | 3 | 42 | 50 | 62 | 61 | 36 | 61 | 91 | 63 | 60 | 45 | 36 | |
| Minimum | 19.0 | 582 | 7.2 | 31 | 14 | 23 | 1 | 131 | 46 | 23 | 19 | 0 | 11 | 534 | |
| Maximum | 47.1 | 2397 | 8.1 | 159 | 88 | 376 | 10 | 406 | 430 | 402 | 184 | 2 | 119 | 1607 | |
| Rhyolites | Average | 24.1 | 1124 | 7.7 | 78 | 29 | 98 | 5 | 310 | 144 | 64 | 35 | 1 | 70 | 764 |
| SD | 2.3 | 484 | 0.2 | 19 | 10 | 69 | 3 | 72 | 103 | 71 | 24 | 1 | 16 | 270 | |
| CV (%) | 9 | 43 | 3 | 24 | 36 | 70 | 58 | 23 | 71 | 111 | 68 | 93 | 23 | 35 | |
| Minimum | 19.5 | 610 | 7.2 | 55 | 12 | 42 | 1 | 128 | 35 | 19 | 6 | 0 | 47 | 370 | |
| Maximum | 27.0 | 2246 | 8.2 | 120 | 51 | 273 | 11 | 417 | 373 | 282 | 74 | 3 | 106 | 1422 | |
| Sedimentary | Average | 28.7 | 1442 | 7.6 | 61 | 37 | 179 | 4 | 256 | 233 | 102 | 51 | 1 | 69 | 926 |
| SD | 1.6 | 521 | 0.2 | 20 | 25 | 98 | 2 | 58 | 135 | 79 | 31 | 1 | 23 | 362 | |
| CV (%) | 6 | 36 | 3 | 33 | 66 | 55 | 45 | 23 | 58 | 77 | 59 | 88 | 33 | 39 | |
| Minimum | 26.0 | 746 | 7.1 | 32 | 12 | 62 | 2 | 165 | 70 | 40 | 17 | 0 | 41 | 423 | |
| Maximum | 30.7 | 2470 | 7.9 | 99 | 94 | 351 | 7 | 340 | 545 | 291 | 96 | 3 | 114 | 1730 | |
| T | EC | pH | Ca2+ | Mg2+ | Na+ | K+ | HCO3− | Cl− | SO42− | NO3− | Br− | SiO2 | TDS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | 1 | |||||||||||||
| EC | 0.33 | 1 | ||||||||||||
| pH | 0.25 | −0.02 | 1 | |||||||||||
| Ca2+ | −0.15 | 0.44 | −0.31 | 1 | ||||||||||
| Mg2+ | −0.02 | 0.67 | −0.42 | 0.6 | 1 | |||||||||
| Na+ | 0.44 | 0.87 | 0.07 | 0.15 | 0.39 | 1 | ||||||||
| K+ | 0.25 | 0.46 | 0.22 | 0.13 | 0.12 | 0.47 | 1 | |||||||
| HCO3− | −0.46 | 0.1 | −0.17 | 0.35 | 0.42 | −0.11 | −0.24 | 1 | ||||||
| Cl− | 0.37 | 0.93 | −0.07 | 0.4 | 0.6 | 0.9 | 0.51 | −0.07 | 1 | |||||
| SO42− | 0.37 | 0.81 | −0.01 | 0.36 | 0.5 | 0.86 | 0.44 | −0.08 | 0.81 | 1 | ||||
| NO3− | 0.17 | 0.26 | −0.06 | 0.38 | 0.46 | 0.09 | −0.07 | −0.11 | 0.22 | 0.15 | 1 | |||
| Br− | 0.17 | 0.87 | −0.02 | 0.4 | 0.7 | 0.74 | 0.35 | 0.1 | 0.84 | 0.76 | 0.35 | 1 | ||
| SiO2 | −0.14 | 0.08 | −0.06 | 0.1 | 0.28 | −0.09 | 0.03 | 0.39 | 0.03 | −0.08 | −0.03 | 0.03 | 1 | |
| TDS | 0.25 | 0.94 | −0.1 | 0.55 | 0.74 | 0.86 | 0.39 | 0.22 | 0.92 | 0.86 | 0.31 | 0.87 | 0.09 | 1 |
| F1 | F2 | F3 | |
|---|---|---|---|
| T | 0.433 | −0.618 | 0.057 |
| EC | 0.930 | 0.133 | 0.221 |
| Ca2+ | 0.324 | 0.454 | 0.580 |
| Mg2+ | 0.531 | 0.508 | 0.548 |
| Na+ | 0.934 | −0.138 | −0.012 |
| K+ | 0.645 | −0.115 | −0.292 |
| HCO3− | −0.055 | 0.878 | 0.036 |
| Cl− | 0.946 | 0.010 | 0.169 |
| SO42− | 0.890 | −0.056 | 0.128 |
| NO3− | 0.088 | −0.126 | 0.903 |
| SiO2 | 0.053 | 0.642 | −0.147 |
| Expl.Var % | 42 | 21 | 12 |
| Cumulative % | 42 | 63 | 75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, I.M.; Jalludin, M.; Razack, M. Hydrochemical and Isotopic Assessment of Groundwater in the Goda Mountains Range System. Republic of Djibouti (Horn of Africa). Water 2020, 12, 2004. https://doi.org/10.3390/w12072004
Ahmed IM, Jalludin M, Razack M. Hydrochemical and Isotopic Assessment of Groundwater in the Goda Mountains Range System. Republic of Djibouti (Horn of Africa). Water. 2020; 12(7):2004. https://doi.org/10.3390/w12072004
Chicago/Turabian StyleAhmed, Ibrahim M., Mohamed Jalludin, and Moumtaz Razack. 2020. "Hydrochemical and Isotopic Assessment of Groundwater in the Goda Mountains Range System. Republic of Djibouti (Horn of Africa)" Water 12, no. 7: 2004. https://doi.org/10.3390/w12072004
APA StyleAhmed, I. M., Jalludin, M., & Razack, M. (2020). Hydrochemical and Isotopic Assessment of Groundwater in the Goda Mountains Range System. Republic of Djibouti (Horn of Africa). Water, 12(7), 2004. https://doi.org/10.3390/w12072004






