Assessment of Building Vulnerability with Varying Distances from Outlet Considering Impact Force of Debris Flow and Building Resistance
Abstract
1. Introduction
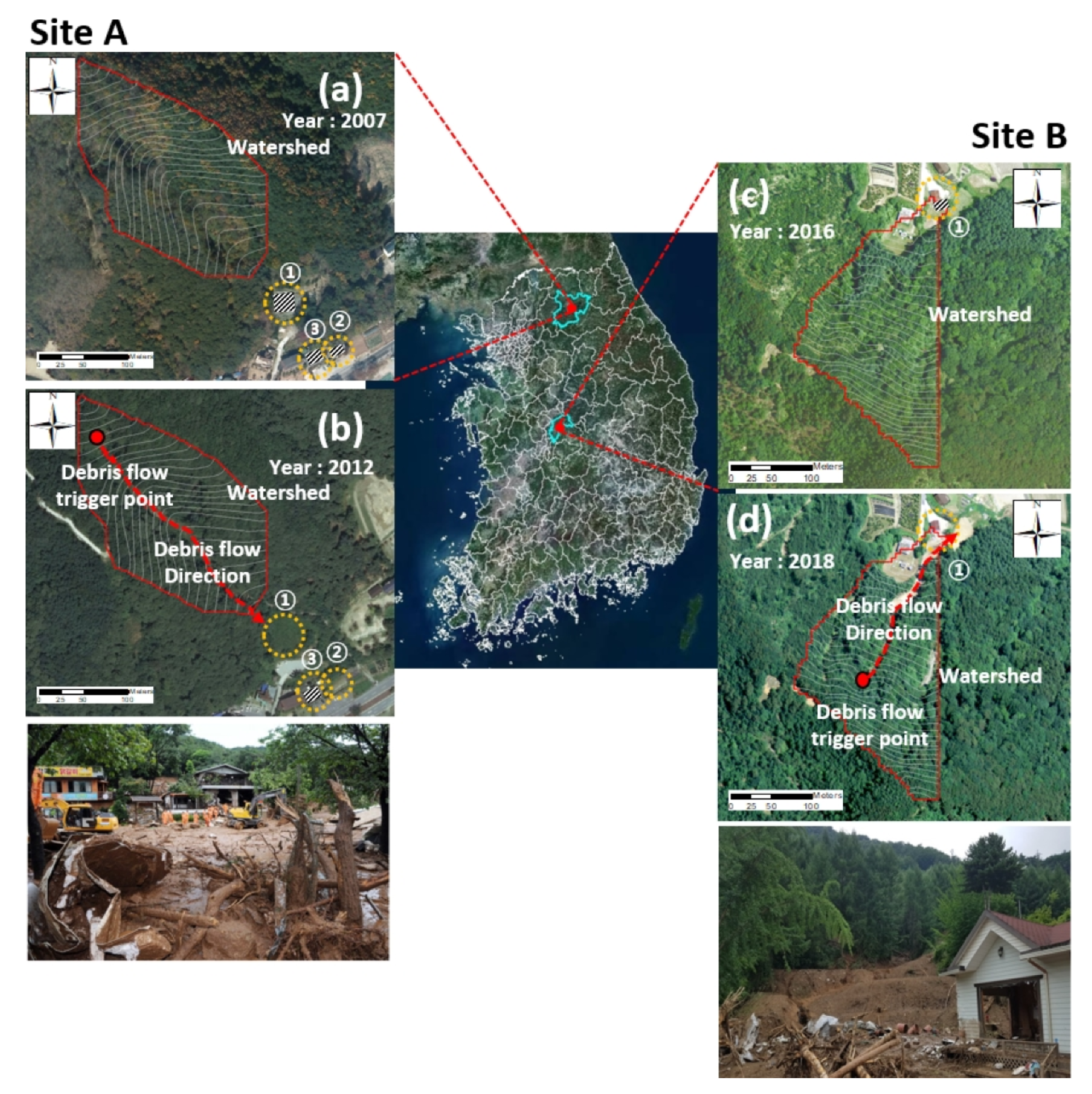
2. Study Area
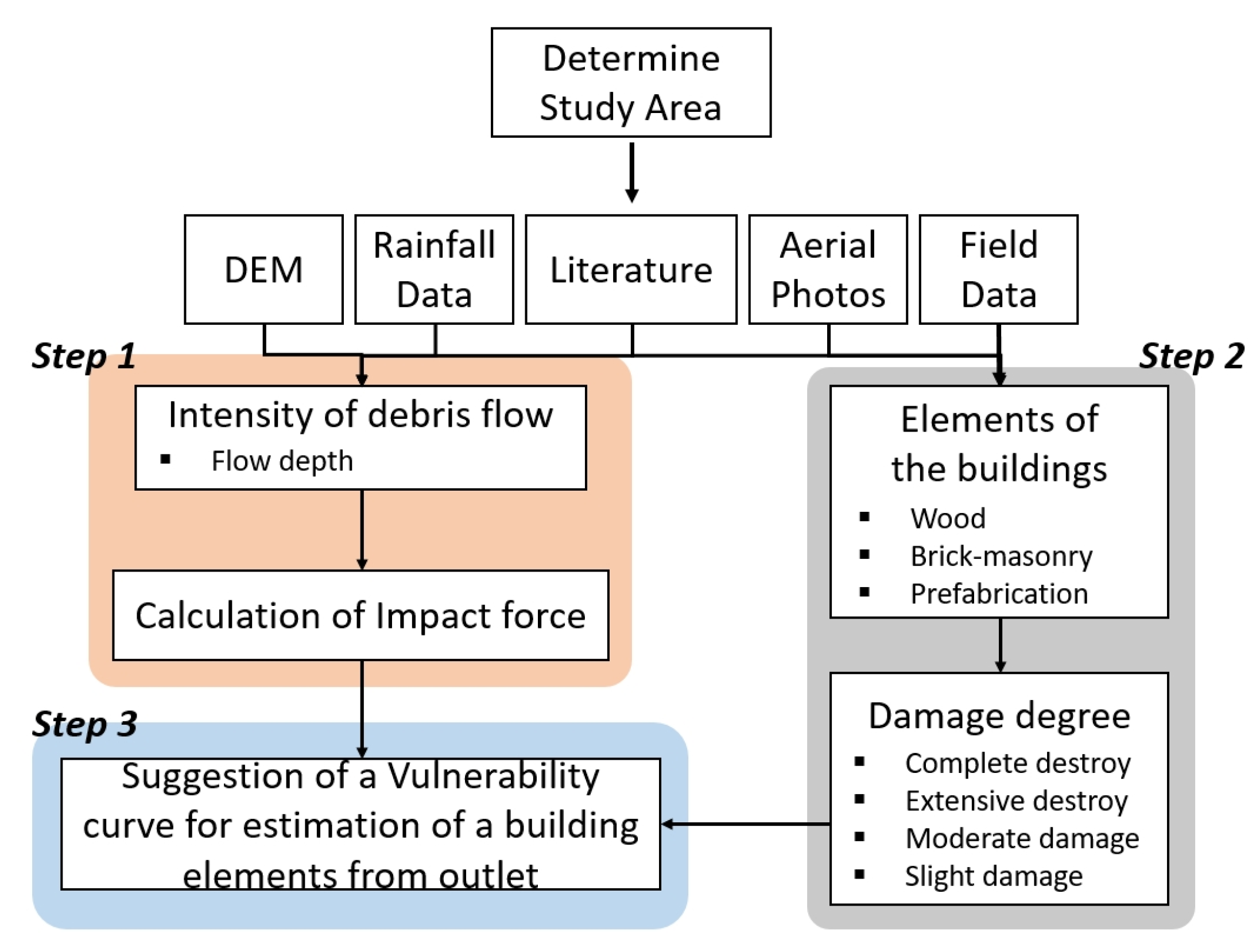
3. Methodology
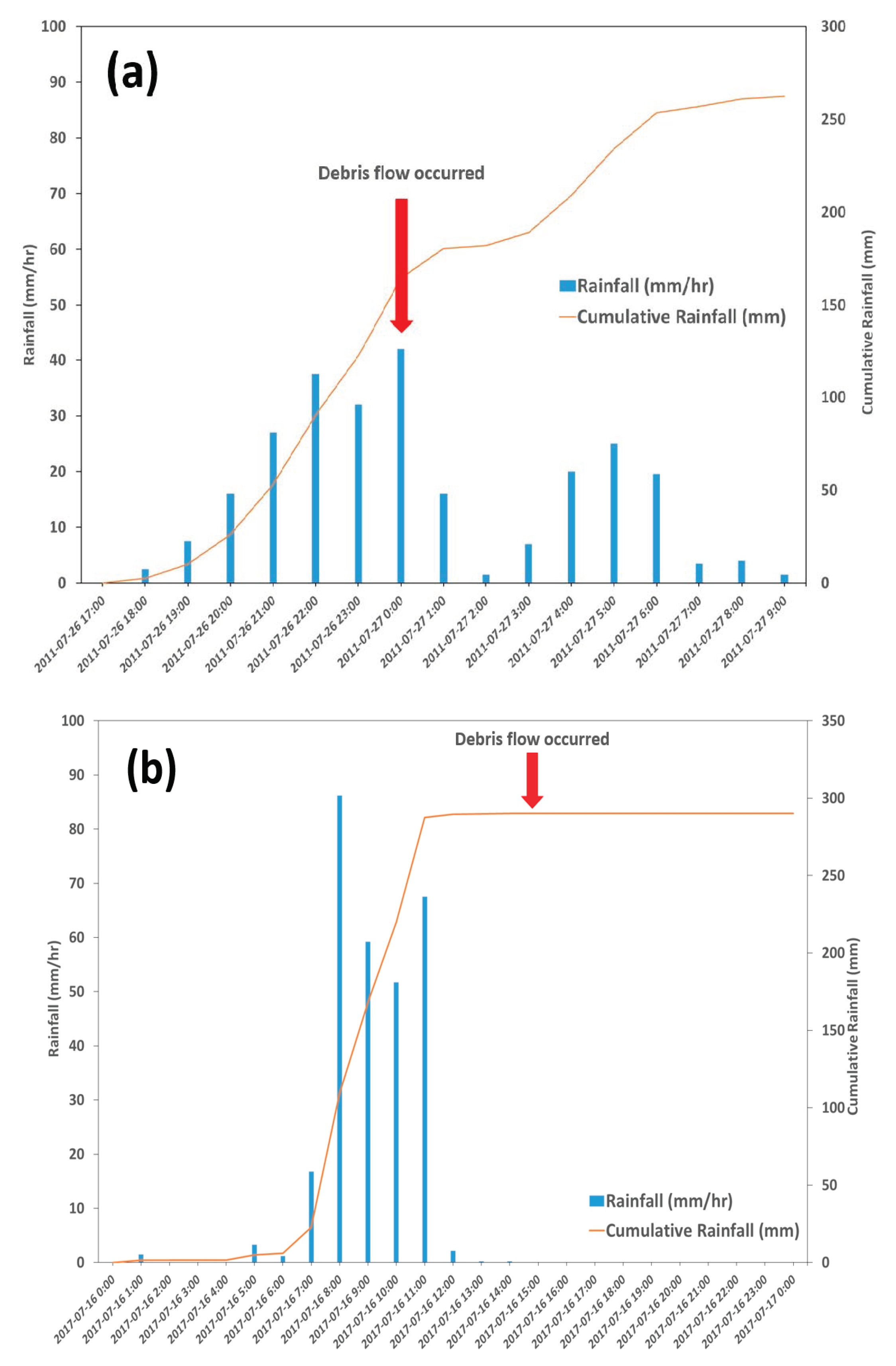
3.1. Assessment of Physical Characteristics of Debris Flows Using FLO-2D
3.2. Calculation of Impact Force of Debris Flow
3.3. Calculation of Resistance by Construction Material
3.4. Vulnerability by Building Material
4. Result
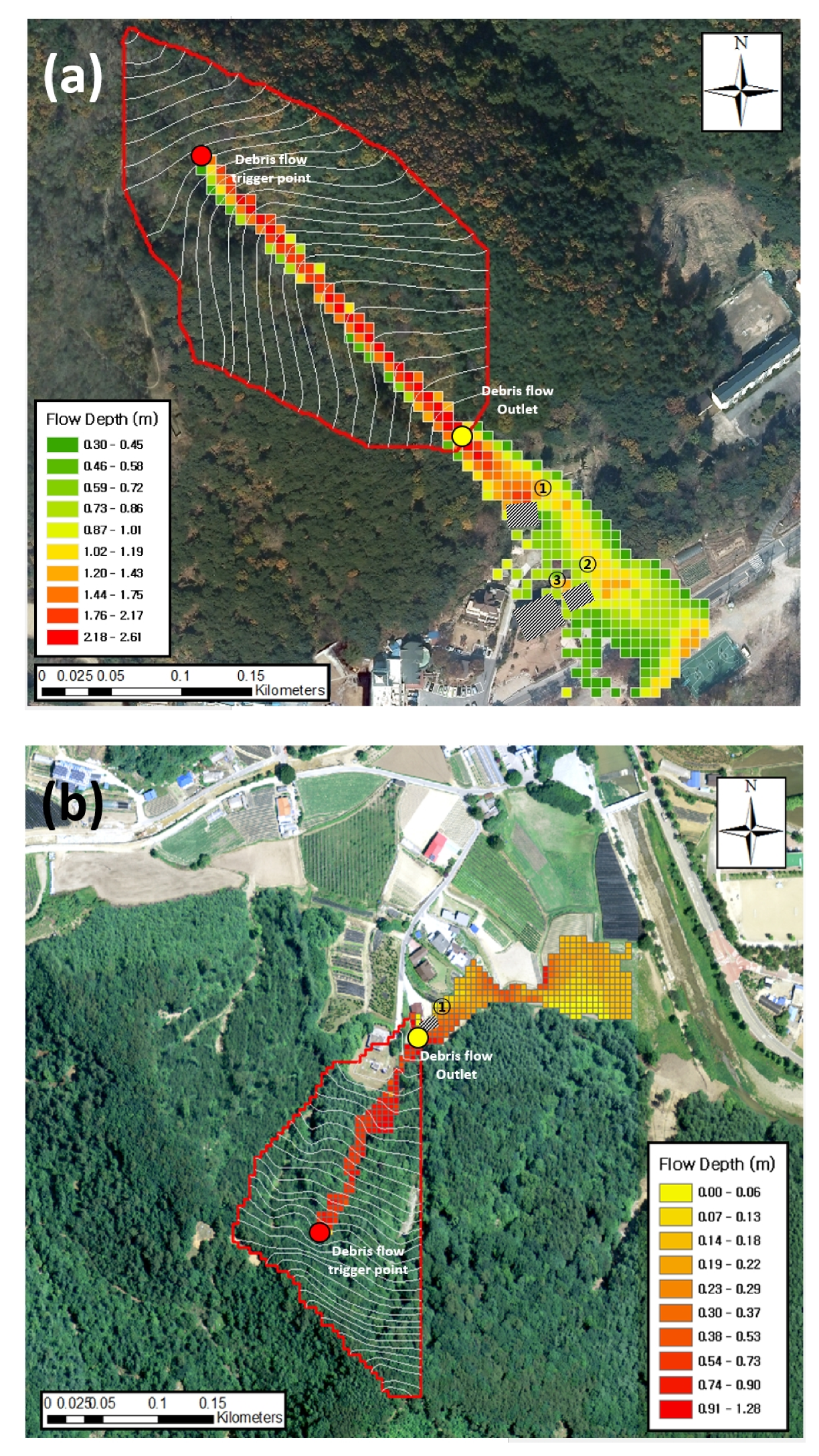
4.1. Analysis of Debris Flow Characteristics
4.2. Building Vulnerability Assessment by Distance From Outlet
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mousavi, M.E.; Irish, J.L.; Frey, A.E.; Olivera, F.; Edge, B.L. Global warming and hurricanes: The potential impact of hurricane intensification and sea level rise on coastal flooding. Clim. Chang. 2011, 104, 575–597. [Google Scholar] [CrossRef]
- Gallina, V.; Torresan, S.; Critto, A.; Sperotto, A.; Glade, T.; Marcomini, A. A review of multi-risk methodologies natual hazards: Consequences and challenges for a climate change impact assessment. J. Env. Manag. 2016, 168, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Solomon, S.; Qin, D.; Manning, M.; Chen, M.; Marquis, A.K.B.; Tignor, M.; Miller, H.L. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. IPCC, 2007; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2004; p. 996. [Google Scholar]
- Son, K.H.; Lee, B.J.; Bae, D.H. Assessment on flood characteristics changes using multi-GCMs climate scenario. J. Korea Water Resour. Assoc. 2010, 43, 789–799. [Google Scholar] [CrossRef]
- Lee, J.S.; Kang, H.S.; Suk, J.W.; Kim, Y.T. Development of hazard level-based rainfall threshold for prediction of rainfall-induced landslide occurrence in Korea. J. Korean Soc. Hazard Mitig. 2019, 19, 225–236, (In Korean with English abstract). [Google Scholar] [CrossRef]
- Kwak, J.H.; Kim, M.-I.; Lee, S.J. Landslide susceptibility assessment considering the saturation depth ratio by rainfall change. J. Eng. Geol. 2018, 28, 687–699, (In Korean with English abstract). [Google Scholar]
- O’Brien, J.S.; Julien, P.Y. Laboratory analysis of mudflow properties. J. Hydraul. Eng. 1988, 114, 877–887. [Google Scholar] [CrossRef]
- Tropeano, D.; Turconi, L. Geomorphic classification of alpine catchments for debris-flow hazard reduction. In Proceedings of the Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, Davos, Switzerland, 10–12 September 2003; pp. 1221–1232. [Google Scholar]
- Palladino, M.R.; Viero, A.; Turconi, L.; Brunetti, M.T.; Peruccacci, S.; Melillo, M.; Luino, F.; Deganutti, A.M.; Guzzetti, F. Rainfall thresholds for the activation of shallow landslides in the Italian Alps: The role of environmental conditioning factors. Geomorphology 2018, 303, 53–67. [Google Scholar] [CrossRef]
- Turconi, L.; Coviello, V.; Arattano, M.; Savio, G.; Tropeano, D. Monitoring Mud-Flows for Investigative and Warning Purposes: The Instrumented Catchment of Rio Marderello (North-Western Italy). Eng. Geol. Soc. Territ. 2015, 3, 85–90. [Google Scholar]
- Paranunzio, R.; Chiarle, M.; Laio, F.; Nigrelli, G.; Turconi, L.; Luino, F. New insights in the relation between climate and slope failures at high-elevation sites. Theor. Appl. Climatol. 2019, 137, 1765–1784. [Google Scholar] [CrossRef]
- Kang, H.S.; Kim, Y.T. Physical vulnerability function of building impacted by debris flow. J. Korean Soc. Hazard Mitig. 2014, 14, 133–143, (In Korean with English abstract). [Google Scholar] [CrossRef]
- Rickenmann, D.; Weber, D.; Stepanov, B. Erosion by debris flows in field and laboratory experiments. In Proceedings of the 3rd International Conference on Debris-Flow Hazards Mitigation and Assessment, Davos, Switzerland, 10–12 September 2003; pp. 883–894. [Google Scholar]
- Chen, J.; He, Y.P.; Wei, F.Q. Debris flow erosion and deposition in Jiangjia Gully, Yunnan, China. Environ. Geol. 2005, 48, 772–777. [Google Scholar] [CrossRef]
- Choi, S.K.; Lee, J.M.; Kwon, T.H. Effect of silt-type barrier on characteristics of water-dominant debris flows: Small-scale physical modeling. Landslides 2017, 15, 111–122. [Google Scholar] [CrossRef]
- Lee, S.G.; Winter, M.G. The effects of debris flow in the Republic of Korea and some issues for successful risk reduction. Eng. Geol. 2019, 251, 172–189. [Google Scholar] [CrossRef]
- Kim, S.E.; Paik, J.C.; Kim, K.S. Run-out Modeling of Debris Flows in Mt.Umyeon using FLO-2D. J. Korean Soc. Civ. Eng. 2013, 33, 965–974. [Google Scholar] [CrossRef]
- Papathoma-Kohle, M.; Kappes, M.; Keiler, M.; Glade, T. Physical vulnerability assessment for alpine hazards: State of the art and future needs. Nat. Hazards 2011, 58, 645–680. [Google Scholar] [CrossRef]
- Edisvig, U.M.K.; Papathoma-Köhle, M.; Du, J.; Glade, T.; Vangelsten, B.V. Quantification of model uncertainty in debris flow vulnerability assessment. Eng. Geol. 2014, 181, 15–26. [Google Scholar] [CrossRef]
- Marques, M.; Monteiro, R.; Delgado, R. An improved model for seismic risk assessment in Portugal. Int. J. Disaster Resil. Built Environ. 2016, 9, 70–83. [Google Scholar] [CrossRef]
- Li, D.Q.; Xiao, T.; Cao, Z.J.; Zhou, C.B.; Zhang, L.M. Enhancement of random finite element method in reliability analysis and risk assessment of soil slopes using Subset simulation. Landslides 2016, 13, 293–303. [Google Scholar] [CrossRef]
- Li, D.Q.; Zheng, D.; Cao, Z.J.; Tang, X.S.; Phoon, K.K. Response surface methods for slope reliability analysis: A review and comparison. Eng. Geol. 2016, 203, 3–14. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.M.; Chen, H.X.; Shen, P. Simulating debris flow mobility in urban settings. Eng. Geol. 2016, 214, 67–78. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.M.; Chen, H.X. Likely scenarios of natural terrain shallow slope failures on Hong Kong Island under extreme storms. Nat. Hazards Rev. 2017, 18, B4015001. [Google Scholar] [CrossRef]
- Pfurtscheller, C.; Genovese, E. The Felbertauern Landslide of 2013: Impact on Transport Networks, Effects on Regional Economy and Policy Decisions; SEEDS Working Paper; SEEDS: Ferrara, Italy, 2018; pp. 1–24. [Google Scholar]
- Jalayer, F.; Aronica, G.T.; Recupero, A.; Carozza, S.; Manfredi, G. Debris flow damage incurred to buildings: An in-situ back analysis. Flood Risk Manag. 2018, 11, 5646–5662. [Google Scholar] [CrossRef]
- Arattano, M.; Bertoldi, G.; Cavalli, M.; Comiti, F.; D’Agostino, V.; Theule, J. Comparison of Methods and Procedures for Debris-Flow Volume Estimation. In Engineering Geology for Society and Territory; Springer International Publishing: Cham, Switzerland, 2015; Volume 3, pp. 115–119. [Google Scholar]
- Coviello, V.; Arattano, M.; Turconi, L. Detecting torrential processes from a distance with a seismic monitoring network. J. Int. Soc. Prev. Mitig. Nat. Hazards 2015, 78, 2055–2080. [Google Scholar] [CrossRef]
- Fell, R.; Ho, K.K.S.; Lacasse, S.; Leroi, E. A framework for landslide risk assessment and management. In Landslide Risk Management; Hungr, O., Fell, R., Couture, R., Eberhardt, E., Eds.; Taylor & Francis: London, UK, 2005; pp. 533–541. [Google Scholar]
- Quan Luna, B.; Blahut, J.; van Westen, C.J.; Sterlacchini, S.; van Asch, T.W.J.; Akbas, S.O. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 2011, 11, 2047–2060. [Google Scholar] [CrossRef]
- Barbolini, M.; Cappabianca, F.; Sailer, R. Empirical estimate of vulnerability relations for use in snow avalanche risk assessment. In Risk Analysis IV; Brebbia, C., Ed.; WIT Press: Southampton, UK, 2004; pp. 533–542. [Google Scholar]
- Quan Luna, B.; Blahut, J.; Camera, C.; van Westen, C.; Apuani, T.; Jetten, V.; Sterlacchini, S. Physically based dynamic run-out modelling for quantitative debris flow risk assessment: A case study in Tresenda, Northern Italy. Environ. Earth Sci. 2014, 72, 645–661. [Google Scholar] [CrossRef]
- Kang, H.S.; Kim, Y.T. The physical vulnerability of different types of building structure to debris flow events. Nat. Hazards 2016, 80, 1475–1493. [Google Scholar] [CrossRef]
- Ciurean, R.L.; Hussin, H.; van Westen, C.J.; Jaboyedoff, M.; Nicolet, P.; Chen, L.; Frigerio, S.; Glade, T. Multi-scale debris flow vulnerability assessment and direct loss estimation of building in the Eastern Italian Alp. Nat. Hazards 2017, 85, 929–957. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Li, X.; Xu, Q. Physical vulnerability models for assessing building damage by debris flows. Eng. Geol. 2018, 247, 145–158. [Google Scholar] [CrossRef]
- Rickenmann, D.; Laigle, D.; McArdell, W.; Hübl, J. Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 2006, 10, 241–264. [Google Scholar] [CrossRef]
- Turconi, L.; Sunil, K.D.; Demurtas, F.; Demurtas, L.; Pendugiu, B.; Tropeano, D.; Savio, G. An analysis of debris-flow events in the Sardinia Island (Thyrrenian Sea, Italy). Environ. Earth Sci. 2013, 69, 1507–1521. [Google Scholar] [CrossRef]
- Comiti, F.; Marchi, L.; Macconi, P.; Arattano, M.; Bertoldi, G.; Broga, M.; Brardinoni, F.; Cavalli, M.; D’Agostino, V.; Penna, D.; et al. A new monitoring station for debris flows in the European Alps: First observations in the Gadria basin. Nat. Hazards 2014, 73, 1175–1198. [Google Scholar] [CrossRef]
- Revelliono, P.; Hungr, O.; Guadagno, F.M.; Evans, S.G. Velocity and runout simulation of destructive debris flows and debris avalanches in pyroclastic deposits, Campania region, Italy. Environ. Geol. 2004, 45, 295–311. [Google Scholar] [CrossRef]
- Aleotti, P.; Polloni, G.; Tropeano, D.; Turconi, L. Numerical Modeling to Determine Risk Scenarios in An Alpine Alluvial Fan. Risk Analysis IV 2004, 9, 153–162. [Google Scholar]
- Kim, M.-I.; Kwak, J.H.; Kim, B.-S. Assessment of dynamic impact force of debris flow in mountain torrent based on characteristics of debris flow. Environ. Earth Sci. 2018, 77, 538. [Google Scholar] [CrossRef]
- Julien, P.Y.; O’Brien, J.S. Selected Notes on Debris Flow Dynamics, Recent Developments on Debris Flows, Lecture Notes in Earth Sciences; Springer: Berlin, Germany, 1997; Volume 64, pp. 144–162. [Google Scholar]
- Hsu, S.M.; Chiou, L.B.; Lin, G.F.; Chao, C.H.; Wen, H.Y.; Ku, C.Y. Applications of simulation technique on debris flow hazard zone delineation: A case study in Hualien County, Taiwan. Nat. Hazards Earth Syst. Sci. 2010, 10, 535–545. [Google Scholar] [CrossRef]
- Li, M.N.; Sung, R.T.; Dong, J.J.; Lee, C.T.; Chen, C.C. The formation and breaching of a short-lived landslide dam at Hsiaolin Village, Taiwan-Part Ⅱ: Simulation of debris flow with landslide dam breach. Eng. Geol. 2011, 123, 66–71. [Google Scholar] [CrossRef]
- FLO-2D Software Inc. FLO-2D Reference Manual; FLO-2D Software Inc.: Nutrioso, AZ, USA, 2009. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Berti, M.; Genevois, R.; Simoni, A.; Tecca, P.R. Field observations of a debris flow event in the Dolomites. Geomorphology 1999, 29, 265–274. [Google Scholar] [CrossRef]
- Chen, J.-C.; Jan, C.-D.; Lee, M.-H. Reliability analysis of design discharge for mountainous gully flow. J. Hydraul. Res. 2008, 46, 835–838. [Google Scholar] [CrossRef]
- Chen, J.C.; Chuang, M.R. Discharge of landslide-induced debris flows: Case studies of Typhoon Morakot in southern Taiwan. Nat. Hazards Earth Syst. Sci. 2014, 14, 1719–1730. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transport. River Design Criteria; Korea Water Resources Association; MOLIT: Seoul, Korea, 2009; pp. 463–476.
- Zanchetta, G.; Sulpizio, R.; Pareschi, M.T.; Leoni, F.M.; Santacroce, R. Characteristics of May 5–6, 1998 volcaniclastic debris-flows in the Sarno area (Campania, Southern Italy): Relationships to structural damage and hazard zonation. J. Volcanol. Geotherm. Res. 2004, 133, 377–393. [Google Scholar] [CrossRef]
- Okuda, S.; Okunishi, K.; Suwa, H. Observation of debris flow at Kamikamihori Valley of Mt. Yakedake. In Proceedings of the Third meeting of the IGU Commission on Field Experiments in Geomorphology, Kyoto, Japan, 24–30 August 1980; pp. 116–139. [Google Scholar]
- Hu, K.H.; Cui, P.; Zhang, J.Q. Characteristics of damage to buildings by debris flows on 7 August 2010 in Zhouqu, Western China. Nat. Hazards Earth Syst. Sci. 2012, 12, 2209–2217. [Google Scholar] [CrossRef]
- Steel Panel for Wall in Buildings; KS F 4724; Korean Standards Association: Seoul, Korea, 2017.
- Scheidl, C.; Chiari, M.; Kaitna, R.; Müllegger, M.; Krawtschuk, A.; Zimmermann, T.; Proske, D. Analysing Debris-flow impact models, based on small scale modelling approach. Surv. Geophys. 2013, 34, 121–140. [Google Scholar] [CrossRef]
- Cui, P.; Zeng, C.; Lei, Y. Experimental analysis on the impact force of viscous debris flow. Earth Surf. Process. Landf. 2015, 40, 1644–1655. [Google Scholar] [CrossRef]
- Fuchs, S.; Heiss, K.; Hübl, J. Towards an empirical vulnerability function for use in debris flow risk assessment. Nat. Hazards Earth Syst. Sci. 2007, 7, 495–506. [Google Scholar] [CrossRef]
- Jakob, M.; Stein, D.; Ulmi, M. Vulnerability of buildings to debris flow impact. Nat. Hazards 2012, 60, 241–261. [Google Scholar] [CrossRef]
- Hürlimann, M.; Coviello, V.; Bel, C.; Guo, X.; Berti, M.; Graf, C.; Hübl, J.; Miyata, S.; Smith, B.D.; Yin, H.Y. Debris-flow monitoring and warning: Review and example. Earth Sci. Rev. 2019, 199, 102981. [Google Scholar] [CrossRef]
| Manning Coefficient | Limiting Froude Number | Viscosity | Yield Stress | Sediment Concentration | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α1 | α2 | β1 | β2 | α1 | α2 | β1 | β2 | |||
| 0.15 | 0.8 | 0.0014 | 0.0046 | 23.0 | 20.044 | 0.0383 | 0.0043 | 19.6 | 23.775 | 0.56 |
| Site A Chuncheon-Shi Area | Site B Cheongju-Shi Area | ||||||
|---|---|---|---|---|---|---|---|
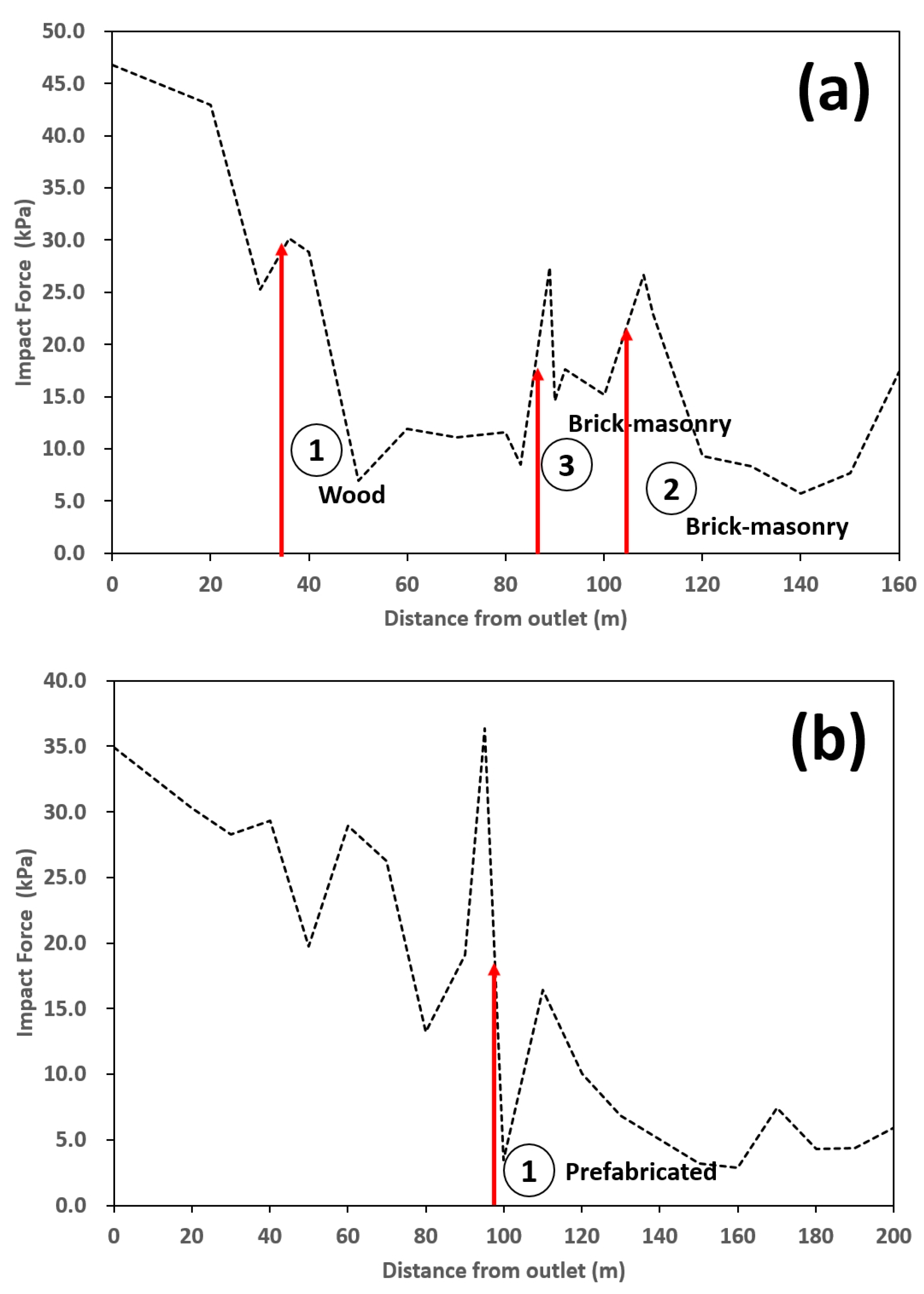
| Distance from Outlet (m) | Impact Force (kPa) | Structural Type | Damage Grade | Distance from Outlet (m) | Impact Force (kPa) | Structural Type | Damage Grade |
| 20 | 42.99 | 20 | 30.33 | ||||
| 30 | 25.25 | 30 | 28.28 | ||||
| 36 | 30.14 | Wood | Complete | 40 | 29.32 | ||
| 40 | 28.90 | 50 | 19.77 | ||||
| 50 | 6.96 | 60 | 28.94 | ||||
| 60 | 11.93 | 70 | 26.26 | ||||
| 70 | 11.14 | 80 | 13.26 | ||||
| 80 | 11.59 | 90 | 19.07 | ||||
| 89 | 27.39 | Brick masonry | Slight | 95 | 36.36 | Prefabricated | Complete |
| 90 | 14.57 | 100 | 3.44 | ||||
| 100 | 15.18 | 110 | 16.44 | ||||
| 108 | 26.63 | Brick masonry | Complete | 120 | 10.02 | ||
| 110 | 22.94 | 130 | 6.83 | ||||
| 120 | 9.34 | 140 | 5.03 | ||||
| 130 | 8.32 | 150 | 3.22 | ||||
| 140 | 5.71 | 160 | 2.90 | ||||
| 150 | 7.69 | 170 | 7.42 | ||||
| 160 | 17.36 | 180 | 4.32 | ||||
| 190 | 4.36 | ||||||
| 200 | 5.92 | ||||||
| Site A Chuncheon-Shi Area | Site B Cheongju-Shi Area | ||||||
|---|---|---|---|---|---|---|---|
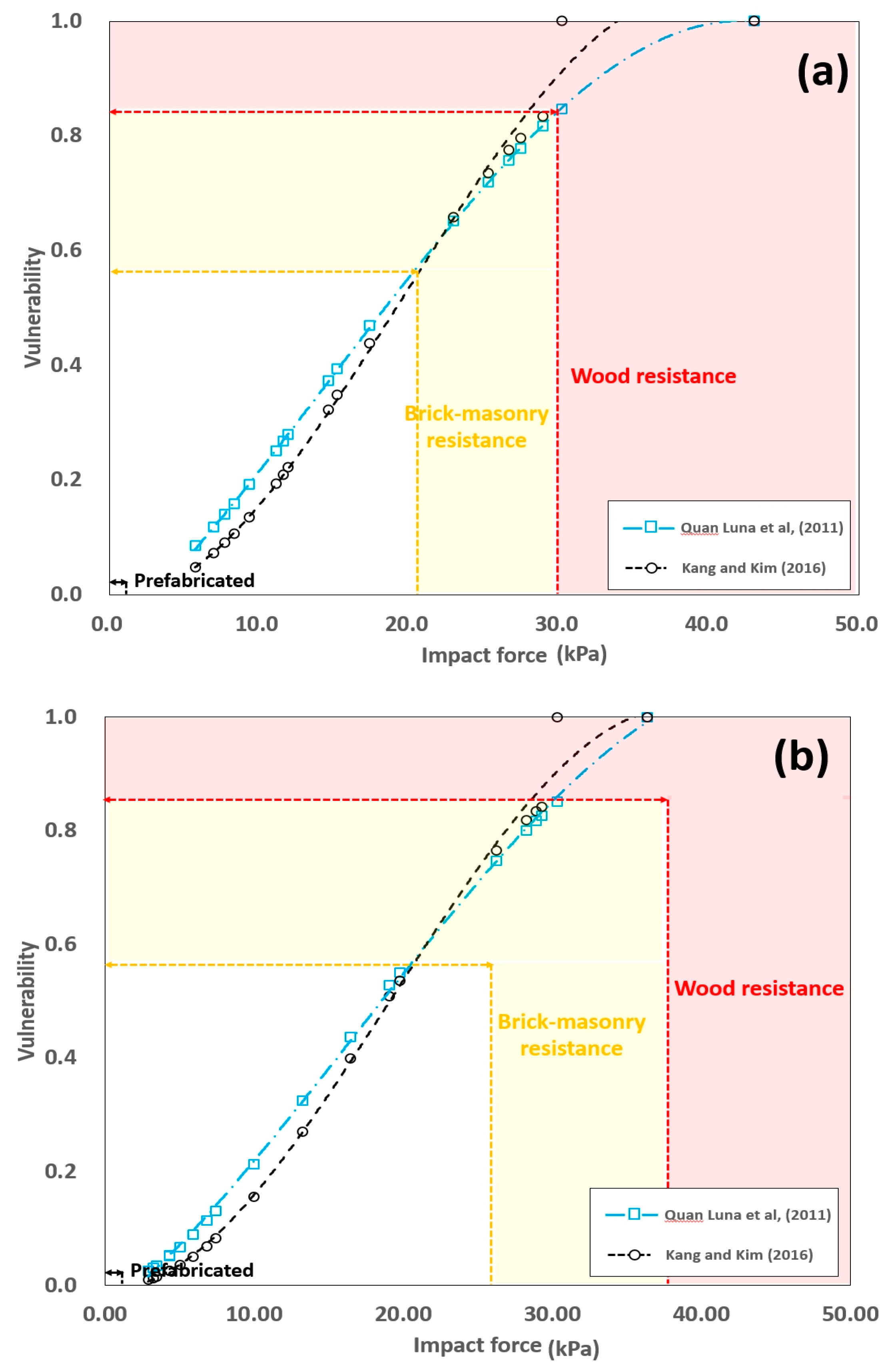
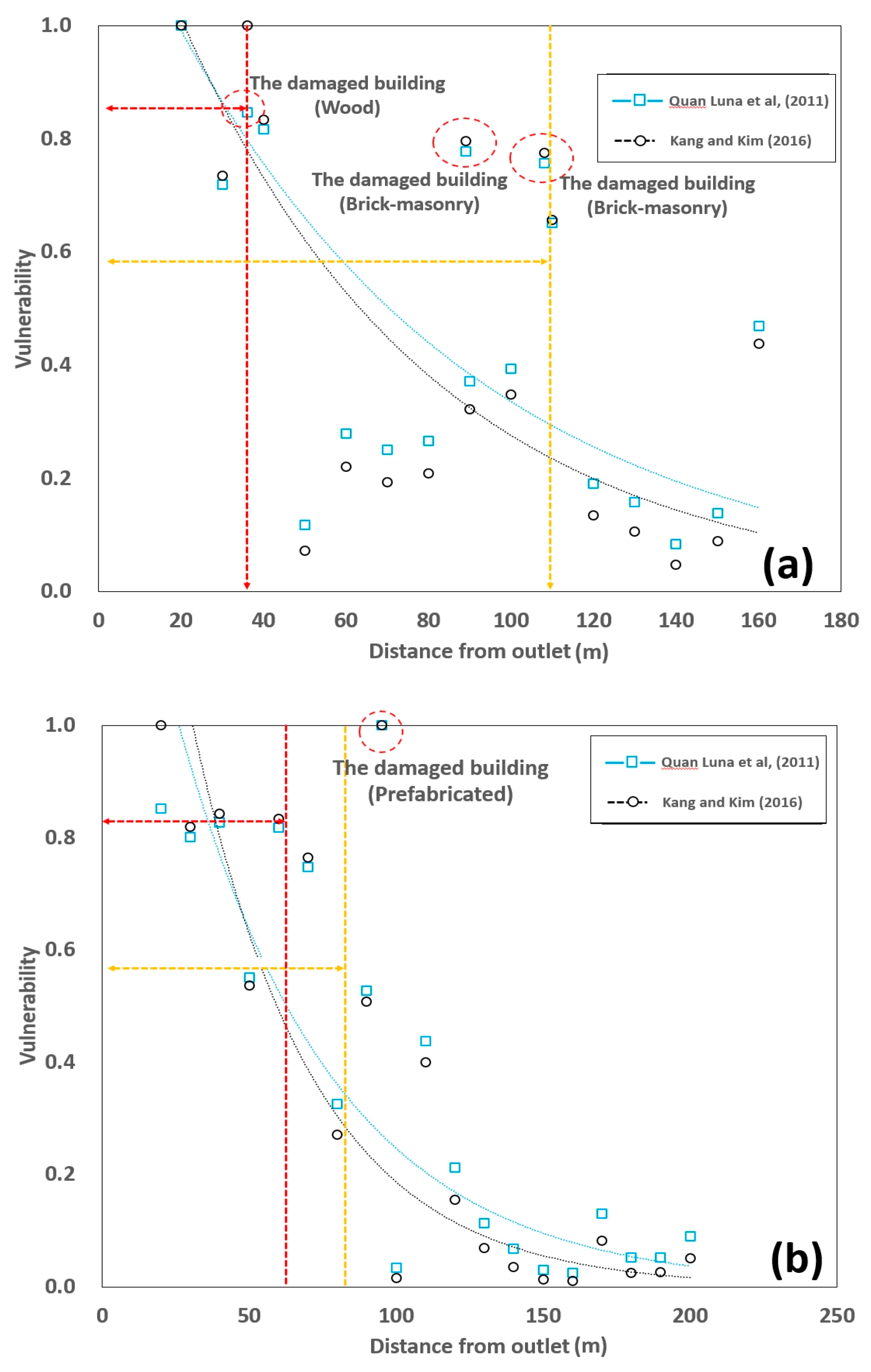
| Distance from Outlet (m) | Impact Force (kPa) by Kim et al. [41] | Vulnerability Index | Distance from Outlet (m) | Impact Force (kPa) by Kim et al. [41]) | Vulnerability Index | ||
| Quan Luna et al. [30] | Kang and Kim [33] | Quan Luna et al. [30] | Kang and Kim [33] | ||||
| 20 | 42.99 | 1.00 | 1.00 | 20 | 30.33 | 0.85 | 1.00 |
| 30 | 25.25 | 0.72 | 0.73 | 30 | 28.28 | 0.80 | 0.82 |
| 36 | 30.14 | 0.85 | 1.00 | 40 | 29.32 | 0.83 | 0.84 |
| 40 | 28.90 | 0.82 | 0.83 | 50 | 19.77 | 0.55 | 0.54 |
| 50 | 6.96 | 0.12 | 0.07 | 60 | 28.94 | 0.82 | 0.83 |
| 60 | 11.93 | 0.28 | 0.22 | 70 | 26.26 | 0.75 | 0.76 |
| 70 | 11.14 | 0.25 | 0.19 | 80 | 13.26 | 0.33 | 0.27 |
| 80 | 11.59 | 0.27 | 0.21 | 90 | 19.07 | 0.53 | 0.51 |
| 89 | 27.39 | 0.78 | 0.80 | 95 | 36.36 | 1.00 | 1.00 |
| 90 | 14.57 | 0.37 | 0.32 | 100 | 3.44 | 0.03 | 0.02 |
| 100 | 15.18 | 0.39 | 0.35 | 110 | 16.44 | 0.44 | 0.40 |
| 108 | 26.63 | 0.76 | 0.78 | 120 | 10.02 | 0.21 | 0.16 |
| 110 | 22.94 | 0.65 | 0.66 | 130 | 6.83 | 0.11 | 0.07 |
| 120 | 9.34 | 0.19 | 0.13 | 140 | 5.03 | 0.07 | 0.04 |
| 130 | 8.32 | 0.16 | 0.11 | 150 | 3.22 | 0.03 | 0.01 |
| 140 | 5.71 | 0.08 | 0.05 | 160 | 2.90 | 0.03 | 0.01 |
| 150 | 7.69 | 0.14 | 0.09 | 170 | 7.42 | 0.13 | 0.08 |
| 160 | 17.36 | 0.47 | 0.44 | 180 | 4.32 | 0.05 | 0.03 |
| 190 | 4.36 | 0.05 | 0.03 | ||||
| 200 | 5.92 | 0.09 | 0.05 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-I.; Kwak, J.-H. Assessment of Building Vulnerability with Varying Distances from Outlet Considering Impact Force of Debris Flow and Building Resistance. Water 2020, 12, 2021. https://doi.org/10.3390/w12072021
Kim M-I, Kwak J-H. Assessment of Building Vulnerability with Varying Distances from Outlet Considering Impact Force of Debris Flow and Building Resistance. Water. 2020; 12(7):2021. https://doi.org/10.3390/w12072021
Chicago/Turabian StyleKim, Man-Il, and Jae-Hwan Kwak. 2020. "Assessment of Building Vulnerability with Varying Distances from Outlet Considering Impact Force of Debris Flow and Building Resistance" Water 12, no. 7: 2021. https://doi.org/10.3390/w12072021
APA StyleKim, M.-I., & Kwak, J.-H. (2020). Assessment of Building Vulnerability with Varying Distances from Outlet Considering Impact Force of Debris Flow and Building Resistance. Water, 12(7), 2021. https://doi.org/10.3390/w12072021





