Wave Energy Assessment in the Bohai Sea and the Yellow Sea Based on a 40-Year Hindcast
Abstract
:1. Introduction
2. Methodology
2.1. Model Description
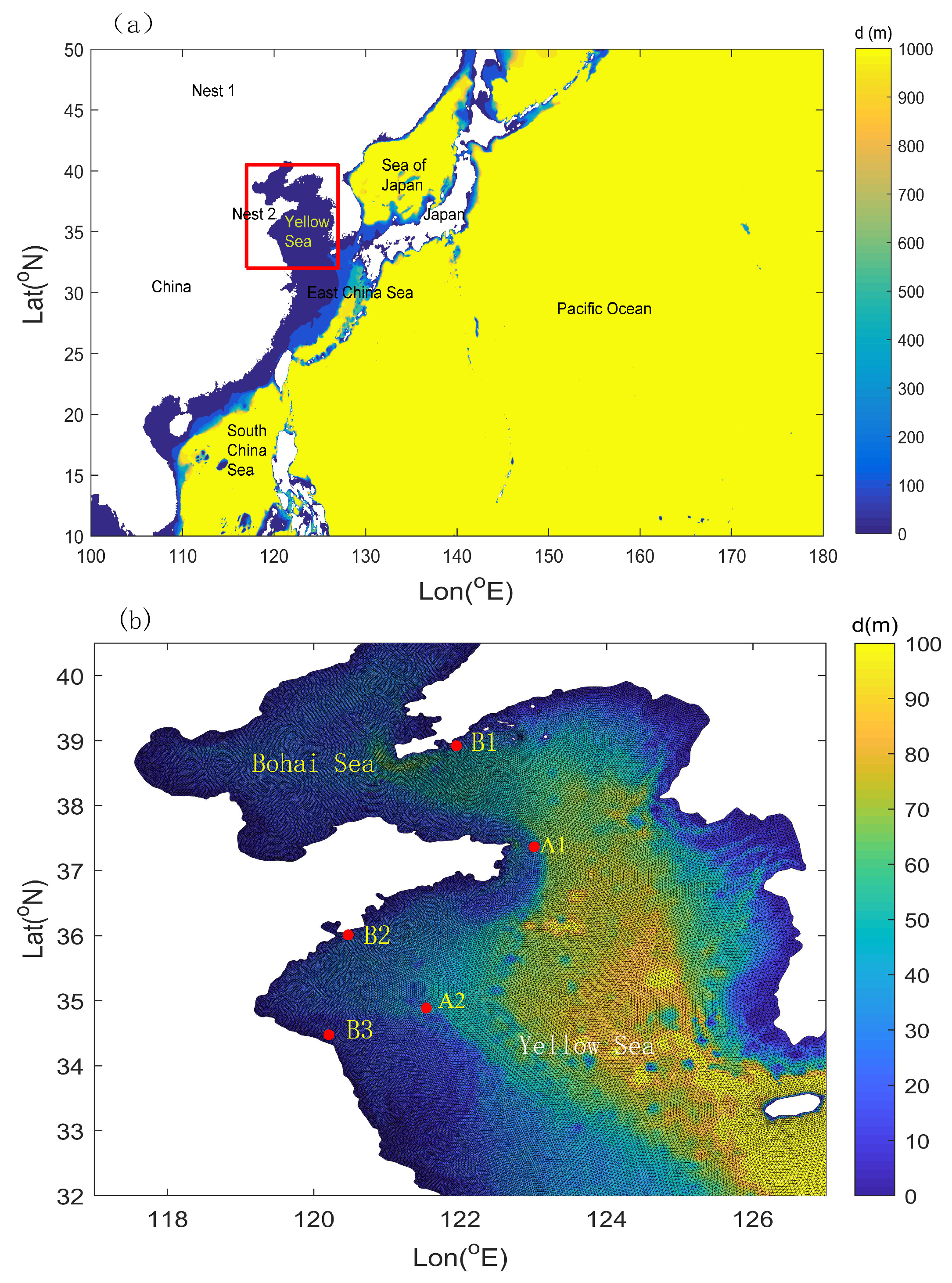
2.2. Model Setup
2.3. Error Index
2.4. Wave Energy Calculation
2.5. Definition of Exploitable Wave Energy
3. Results
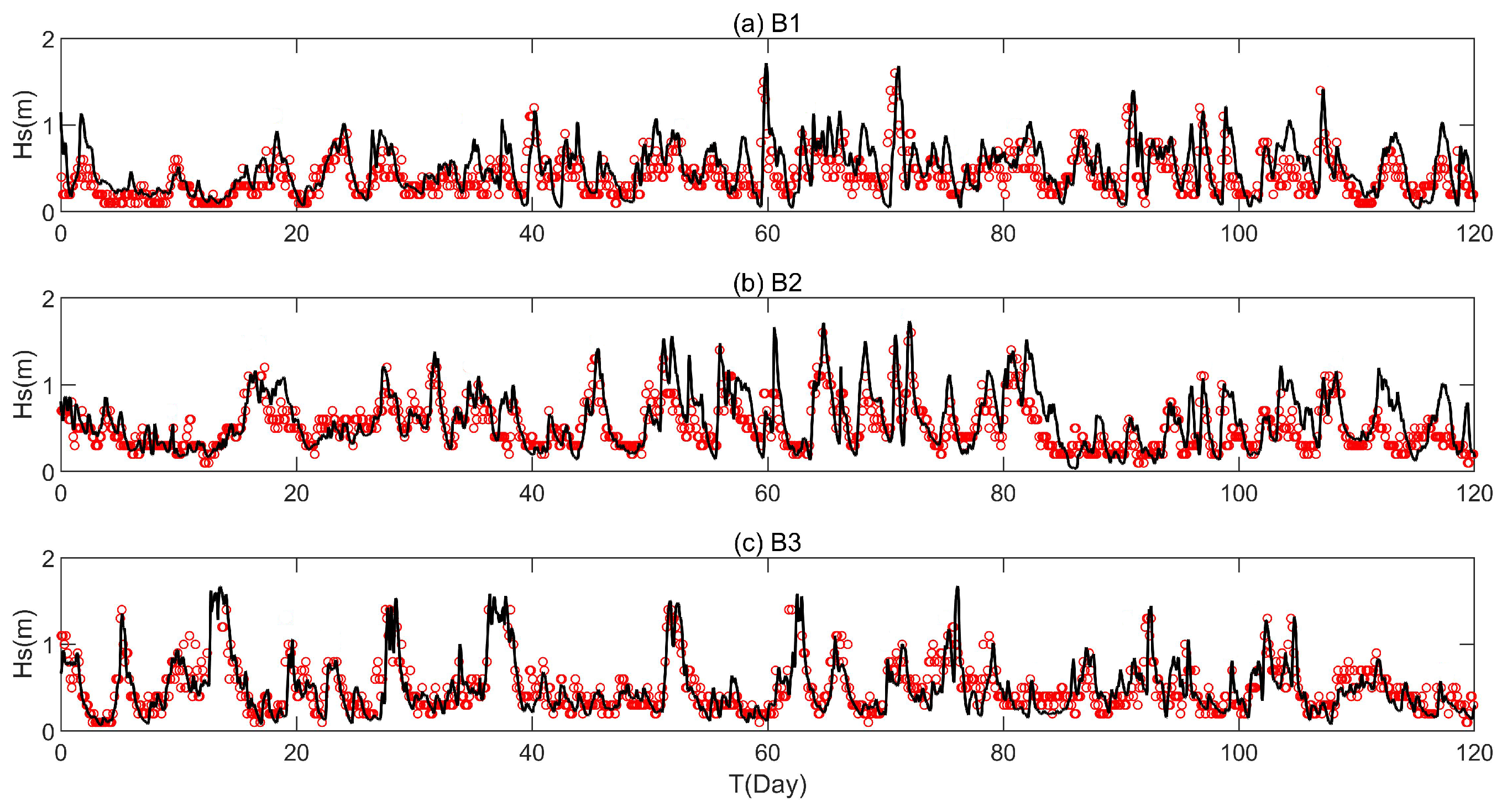
3.1. Validation
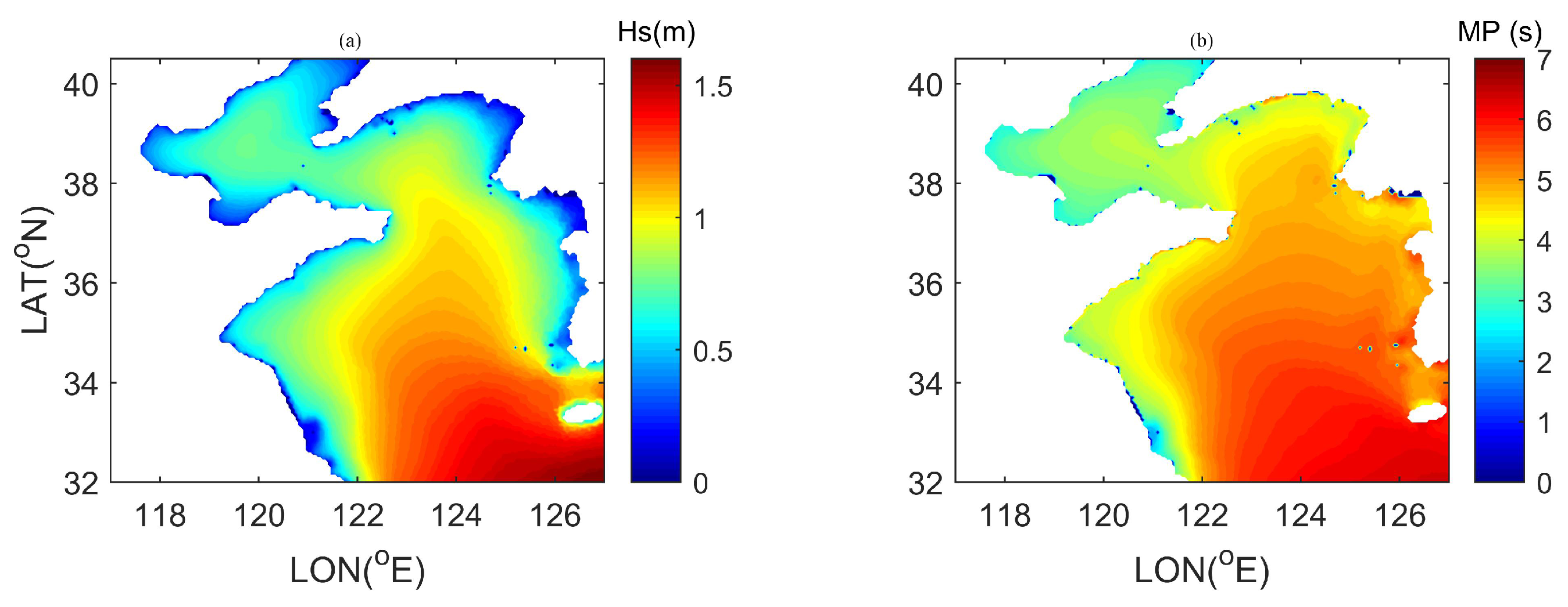
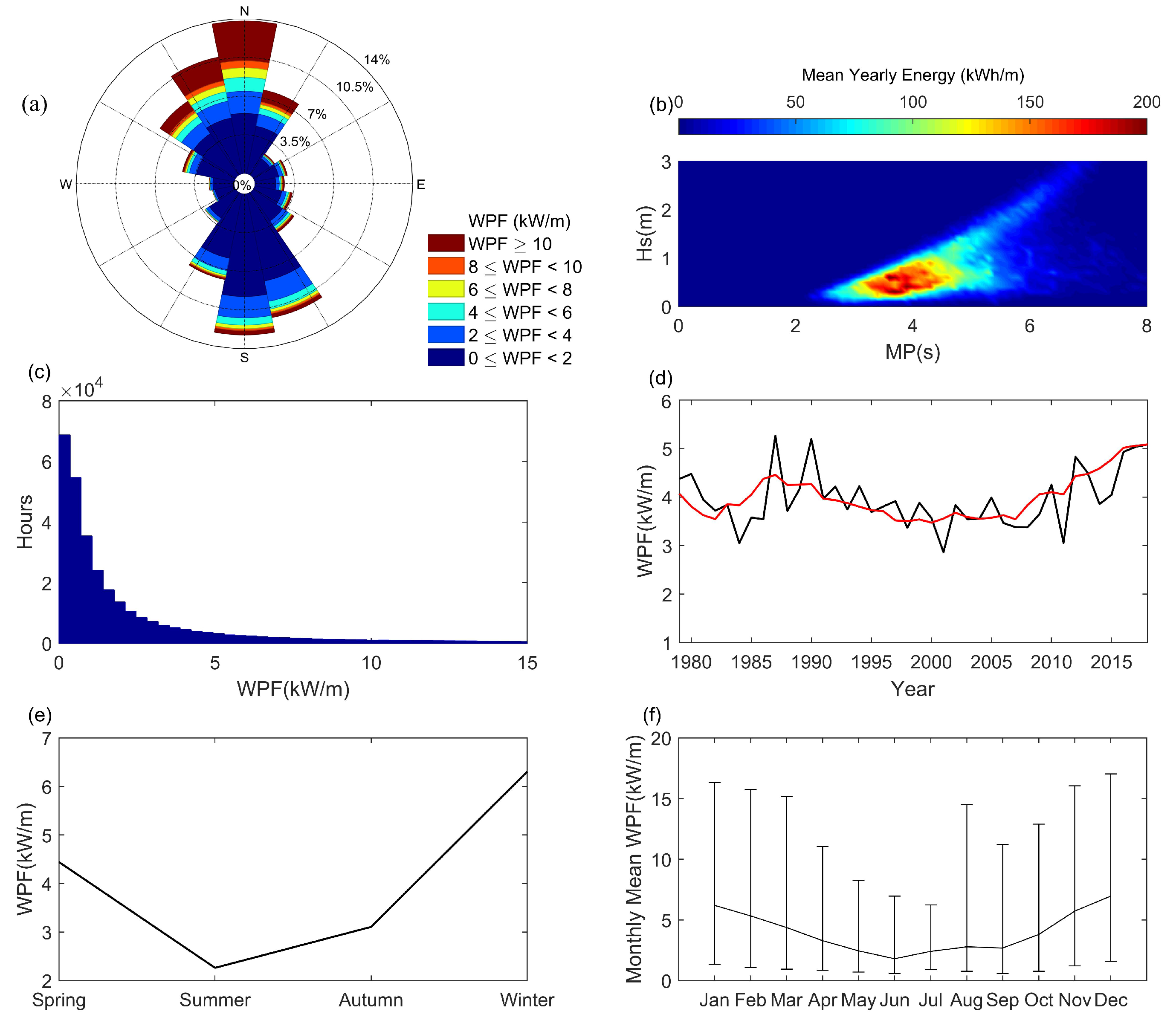
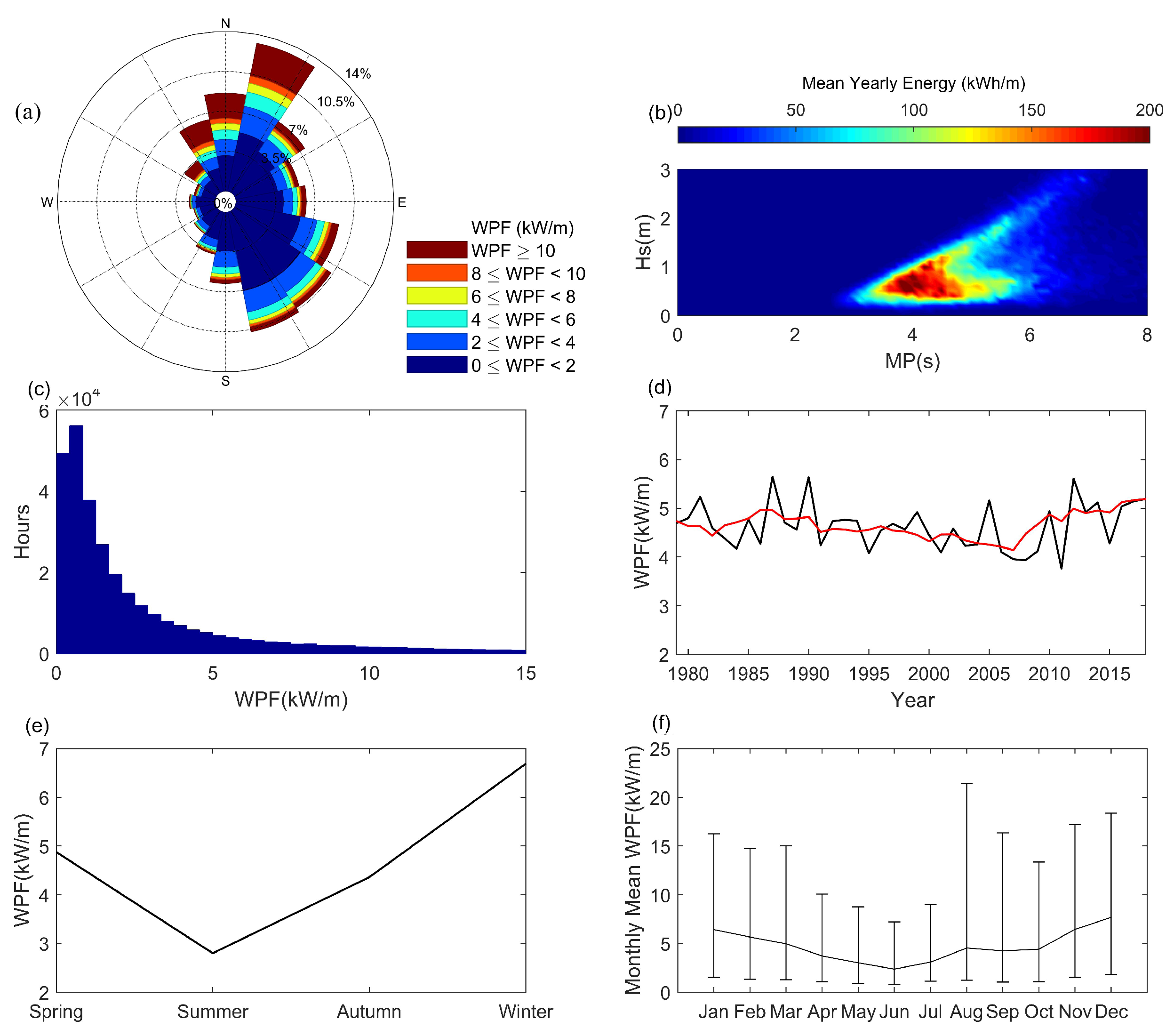
3.2. Mean Wave Characteristics in the BS and YS
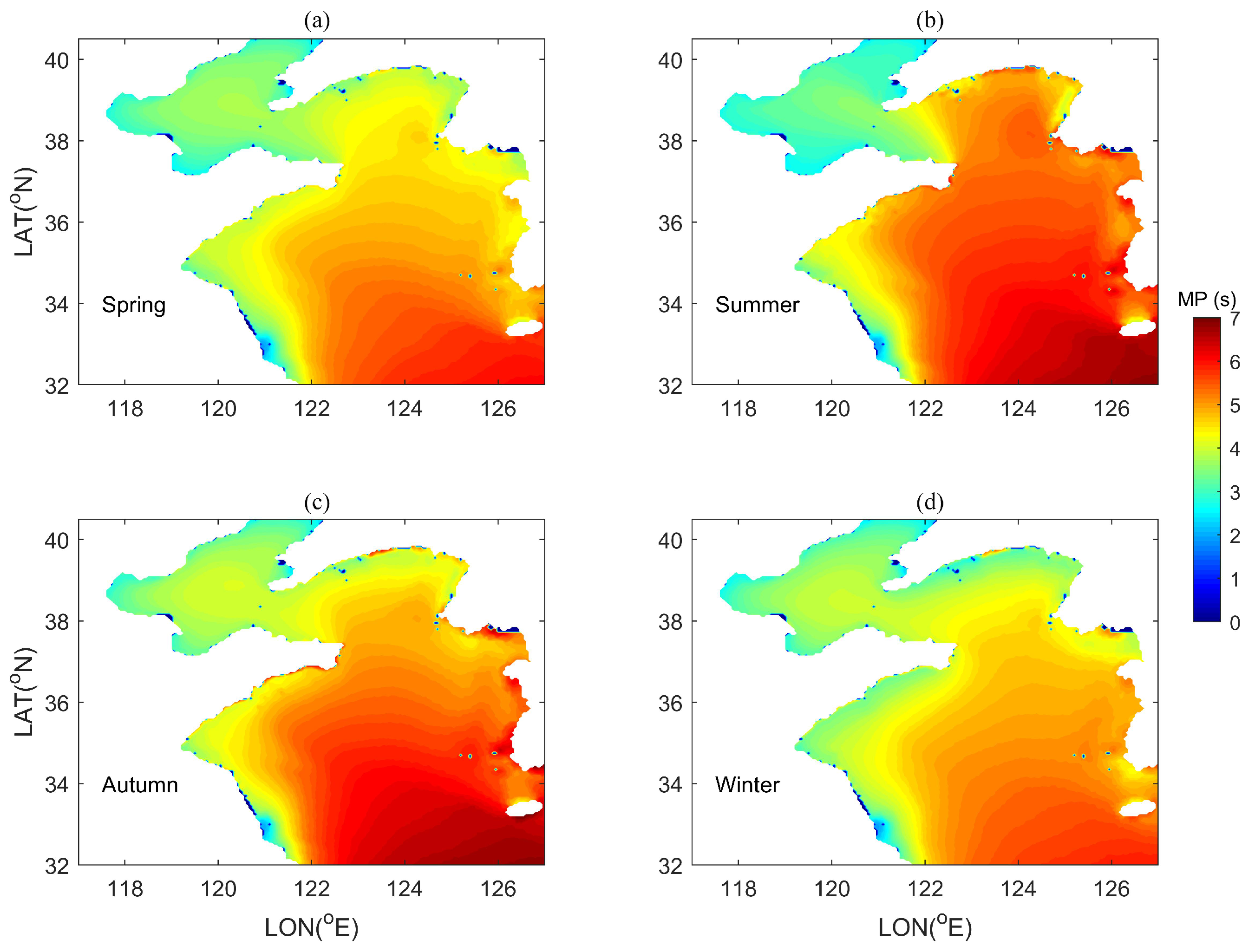
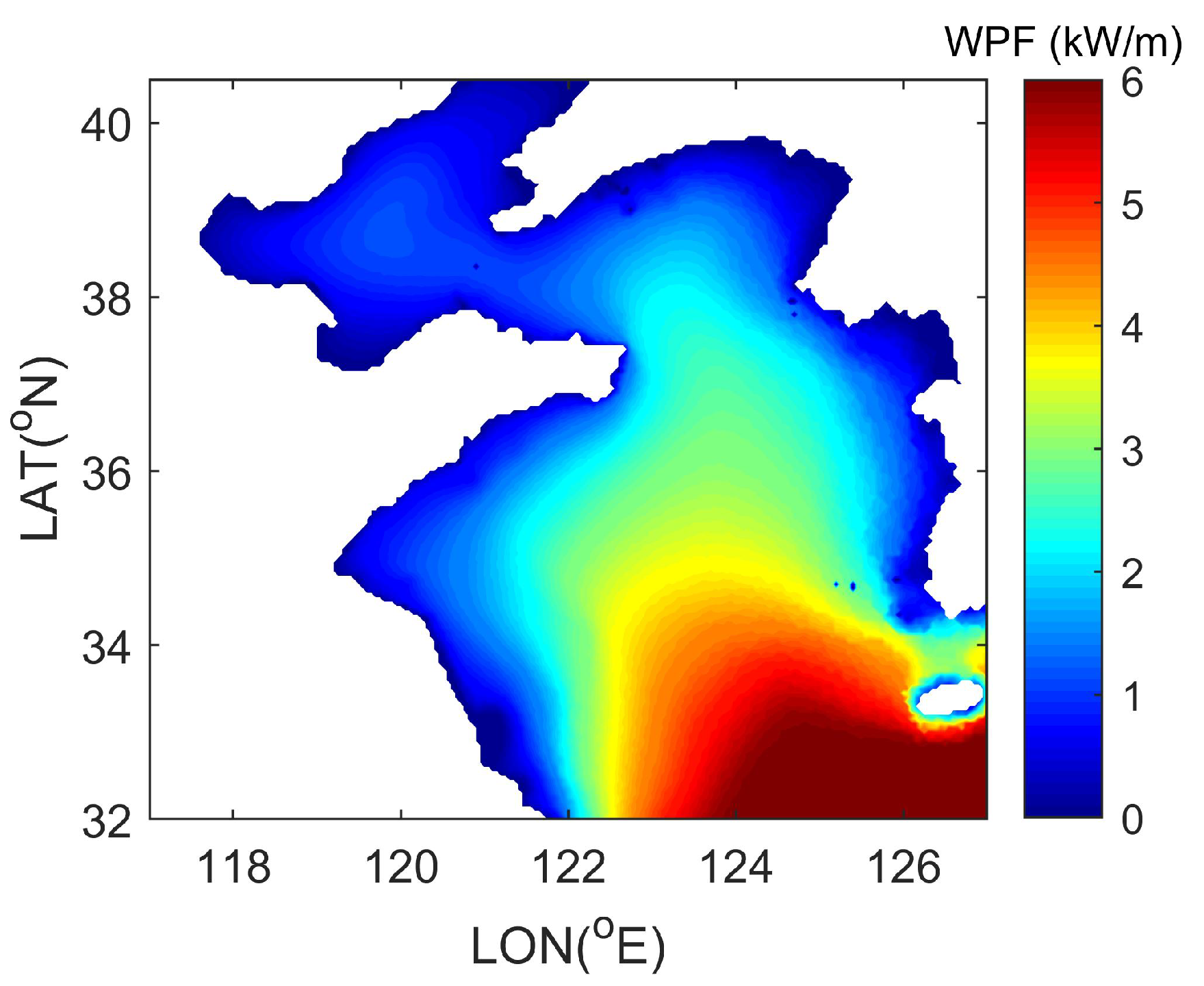
3.3. Spatial and Temporal Distributions of the Wave Energy Potential
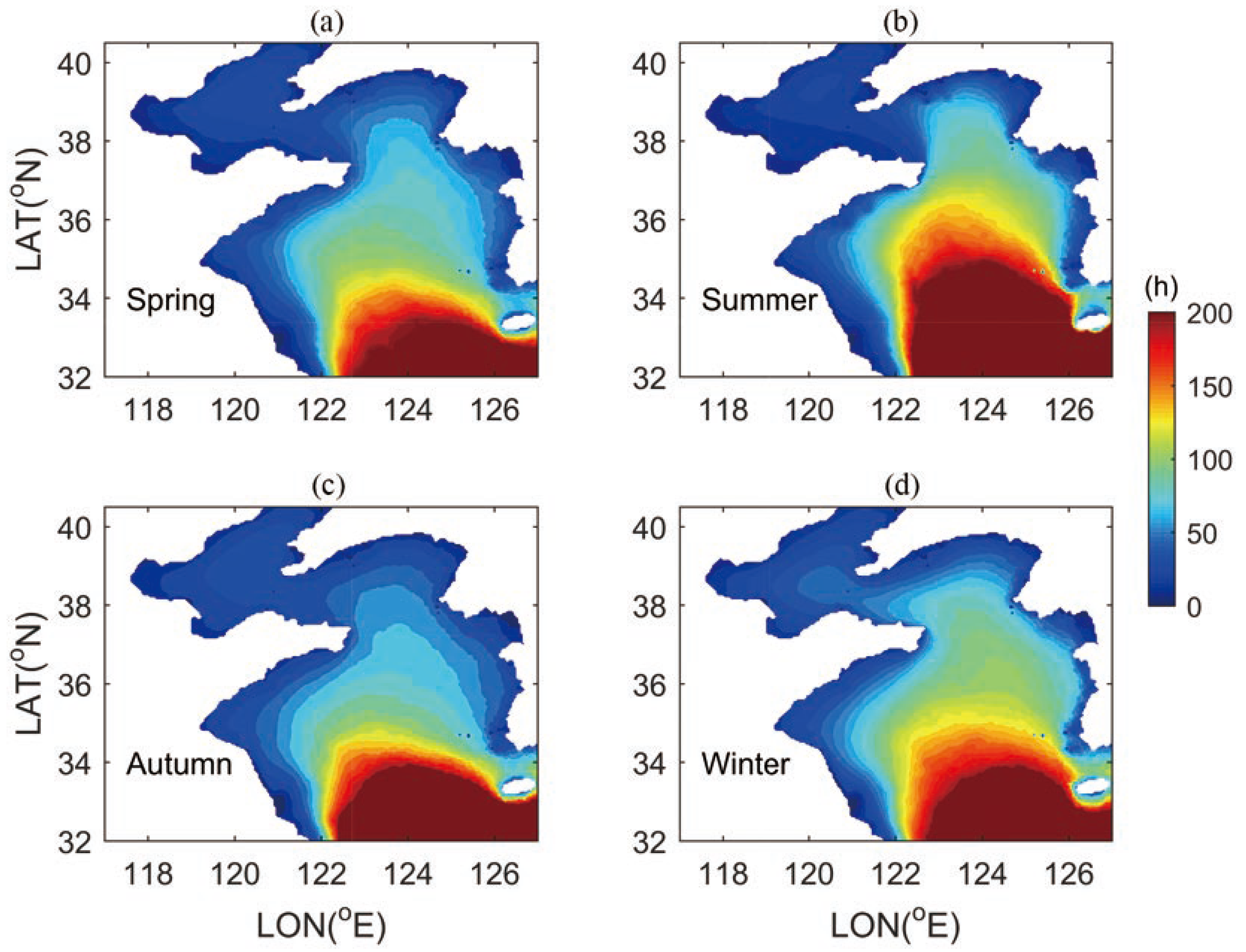
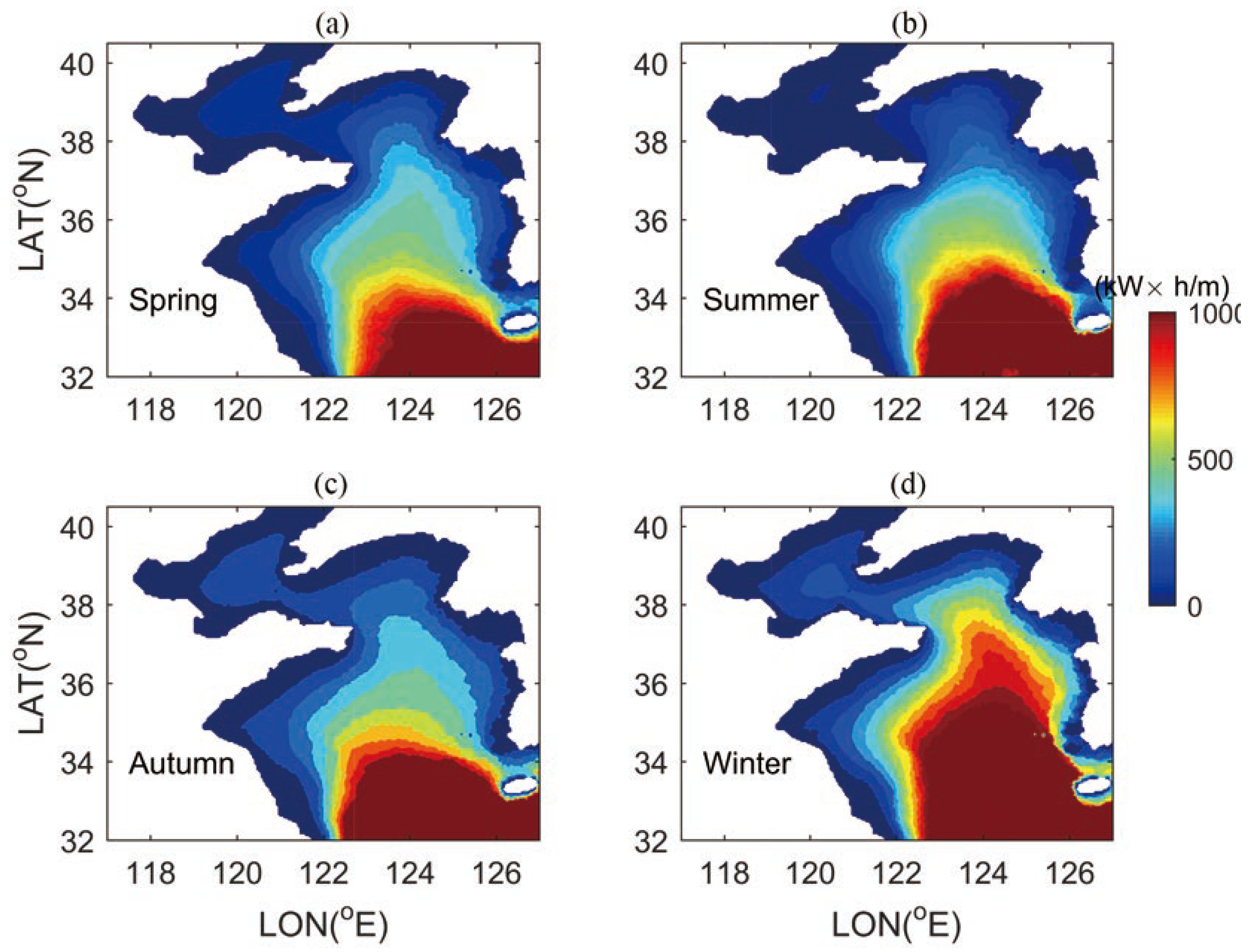
4. Exploitable Wave Energy
5. Wave Energy Assessment on Location Scale
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Silva, D.; Martinho, P.; Soares, C.G. Wave energy distribution along the portuguese continental coast based on a thirty three years hindcast. Renew. Energy 2018, 127, 1064–1075. [Google Scholar] [CrossRef]
- Haces-Fernandez, F.; Hua, L.; Ramirez, D. Wave energy characterization and assessment in the u.s. gulf of mexico, east and west coasts with energy event concept. Renew. Energy 2018, 123, 312–322. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.; Ahmed, Y.M.; Rheem, C.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Lopez, I.; Andreu, J.; Ceballos, S.; Martinez de Alegria, I.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Liberti, L.; Carillo, A.; Sannino, G. Wave energy resource assessment in the mediterranean, the italian perspective. Renew. Energy 2013, 50, 938–949. [Google Scholar] [CrossRef]
- Lanfredi, N.W.; Pousa, J.L.; Mazio, C.A.; Dragani, W.C. Wave-power potential along the coast of the province of buenos aires, argentina. Energy 1992, 17, 997–1006. [Google Scholar] [CrossRef]
- Liang, B.; Fan, F.; Liu, F.; Gao, S.; Zuo, H. 22-year wave energy hindcast for the china east adjacent seas. Renew. Energy 2014, 71, 200–207. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Q.; Zheng, J.; Demirbilek, Z. Parameterization of nearshore wave front slope. Coast. Eng. 2017, 127, 80–87. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, C.; Demirbilek, Z.; Lin, L. Numerical study of sandbar migration under wave-undertow interaction. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 146–159. [Google Scholar] [CrossRef] [Green Version]
- The Wamdi Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef] [Green Version]
- Tolman, H. A third-generation model for wind waves on slowly varying unsteady, and inhomogeneous depths and current. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L. A third-generation wave model for coastal regions, Part 1, Model description and validation. J. Phys. Oceanogr. 1999, 104, 7649–7666. [Google Scholar]
- Benoit, M.; Marcos, F.; Becq, F. Development of a third generation shallow-water wave model with unstructured spatial meshing. In Proceedings of the 25th Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; pp. 465–478. [Google Scholar]
- Sterl, A.; Komen, G.; Cotton, P. Fifteen years of global wave hindcasts using winds from the European Centre for Medium—Range Weather Forecasts reanalysis: Validating the reanalyzed winds and assessing wave climate. J. Geophys. Res. 1998, 103, 5477–5492. [Google Scholar] [CrossRef]
- Cox, A.T.; Swail, V.R. A global wave hindcast over the period 1958–1997: Validation and climate assessment. J. Geophys. Res. Ocean. 2001, 106, 2313–2329. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. 100-year return value estimates for ocean wind speed and significant wave height from the ERA-40 data. J. Clim. 2005, 18, 1032–1048. [Google Scholar] [CrossRef]
- Kaas, E.; Li, T.S.; Schmith, T. Statistical hindcast of wind climatology in the North Atlantic and northwestern European region. Clim. Res. 1996, 7, 97–110. [Google Scholar] [CrossRef] [Green Version]
- Soares, C.G.; Weisse, R.; Carretero, J.C.; Alvarez, E. A 40 year hindcast of wind, sea level and waves in European waters. In Proceedings of the OMAE 2002: 21st International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, 23–28 June 2002; pp. 669–675. [Google Scholar]
- Wang, X.; Swail, V. Trends of atlantic wave extremes as simulated in a 40-yr wave hindcast using kinematically reanalyzed wind fields. J. Clim. 2002, 15, 1020–1035. [Google Scholar] [CrossRef]
- Arkhipkin, V.S.; Gippius, F.N.; Koltermann, K.P.; Surkova, G.V. Wind waves in the Black Sea: Results of a hindcast study. Nat. Hazards Earth Syst. Sci. 2014, 14, 2883–2897. [Google Scholar] [CrossRef] [Green Version]
- Reistad, M.; Breivik, Ø.; Haakenstad, H.; Aarnes, O.J.; Furevik, B.R.; Bidlot, J.R. A high-resolution hindcast of wind and waves for the North Sea, the Norwegian Sea, and the Barents Sea. J. Geophys. Res. Oceans 2011, 116, C05019. [Google Scholar] [CrossRef] [Green Version]
- Liang, B.; Gao, H.; Shao, Z. Characteristics of global waves based on the third-generation wave model swan. Mar. Struct. 2019, 64, 35–53. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, J.; Zhang, C.; Joly, A.; Zhang, W.; Xu, P.; Sui, T.; Chen, T. A 39-year high resolution wave hindcast for the Chinese coast: Model validation and wave climate analysis. Ocean Eng. 2019, 183, 224–235. [Google Scholar] [CrossRef]
- Bozzi, S.; Archetti, R.; Passoni, G. Wave electricity production in Italian offshore: A preliminary investigation. Renew. Energy 2014, 62, 407–416. [Google Scholar] [CrossRef]
- Lo Re, C.; Manno, G.; Ciraolo, G.; Besio, G. Wave Energy Assessment around the Aegadian Islands (Sicily). Energies 2019, 12, 333. [Google Scholar]
- Roger, B. Wave Energy Forecasting Accuracy as a Function of Forecast Time Horizon; Electric Power Research Institute: Palo Alto, CA, USA, 2009. [Google Scholar]
- Zheng, C.W.; Pan, J.; Li, J.X. Assessing the China Sea wind energy and wave energy resources from 1988 to 2009. Ocean Eng. 2013, 65, 39–48. [Google Scholar] [CrossRef]
- Besio, G.; Mentaschi, L.; Mazzino, A. Wave energy resource assessment in the Mediterranean Sea on the basis of a 35-year hindcast. Energy 2016, 94, 50–63. [Google Scholar] [CrossRef]
- Folley, M.; Whittaker, T.J.T. Analysis of the nearshore wave energy resource. Renew. Energy 2009, 34, 1709–1715. [Google Scholar] [CrossRef]
- Gaeta, M.G.; Samaras, A.G.; Federico, I.; Archetti, R.; Maicu, F.; Lorenzetti, G. A coupled wave-3-d hydrodynamics model of the taranto sea (italy): A multiple-nesting approach. Nat. Hazards Earth Syst. Sci. 2016, 16, 2017–2083. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Hanna, S.R.; Heinold, D.W. Development and Application of a Simple Method for Evaluating Air Quality Models; Technical Report; American Petroleum Institute: Washington, DC, USA, 1985. [Google Scholar]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch III in the Mediterranean Sea. Ocean Model. 2015, 90, 82–94. [Google Scholar] [CrossRef]
- He, H.; Song, J.; Bai, Y.; Xu, Y.; Wang, J.; Bi, F. Climate and extrema of ocean waves in the East China Sea. Sci. China Earth Sci. 2018, 61, 980–994. [Google Scholar] [CrossRef]
- Liang, B.; Liu, X.; Li, H.; Wu, Y.; Lee, D. Wave Climate Hindcasts for the Bohai Sea, Yellow Sea, and East China Sea. J. Coast. Res. 2014, 32, 172–180. [Google Scholar]





| Station | Hs | MP |
|---|---|---|
| 0.04 0.18 | −0.05 0.17 | |
| 0.03 0.19 | −0.03 0.15 | |
| −0.02 0.17 | −0.03 0.16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Shi, J.; Zhao, J.; Zhang, C.; Xu, H. Wave Energy Assessment in the Bohai Sea and the Yellow Sea Based on a 40-Year Hindcast. Water 2020, 12, 2087. https://doi.org/10.3390/w12082087
Dong J, Shi J, Zhao J, Zhang C, Xu H. Wave Energy Assessment in the Bohai Sea and the Yellow Sea Based on a 40-Year Hindcast. Water. 2020; 12(8):2087. https://doi.org/10.3390/w12082087
Chicago/Turabian StyleDong, Jie, Jian Shi, Jianchun Zhao, Chi Zhang, and Haiyan Xu. 2020. "Wave Energy Assessment in the Bohai Sea and the Yellow Sea Based on a 40-Year Hindcast" Water 12, no. 8: 2087. https://doi.org/10.3390/w12082087
APA StyleDong, J., Shi, J., Zhao, J., Zhang, C., & Xu, H. (2020). Wave Energy Assessment in the Bohai Sea and the Yellow Sea Based on a 40-Year Hindcast. Water, 12(8), 2087. https://doi.org/10.3390/w12082087





