Features and Control of Submerged Horizontal Vortex in Stepped Dissipation Wells
Abstract
:1. Introduction
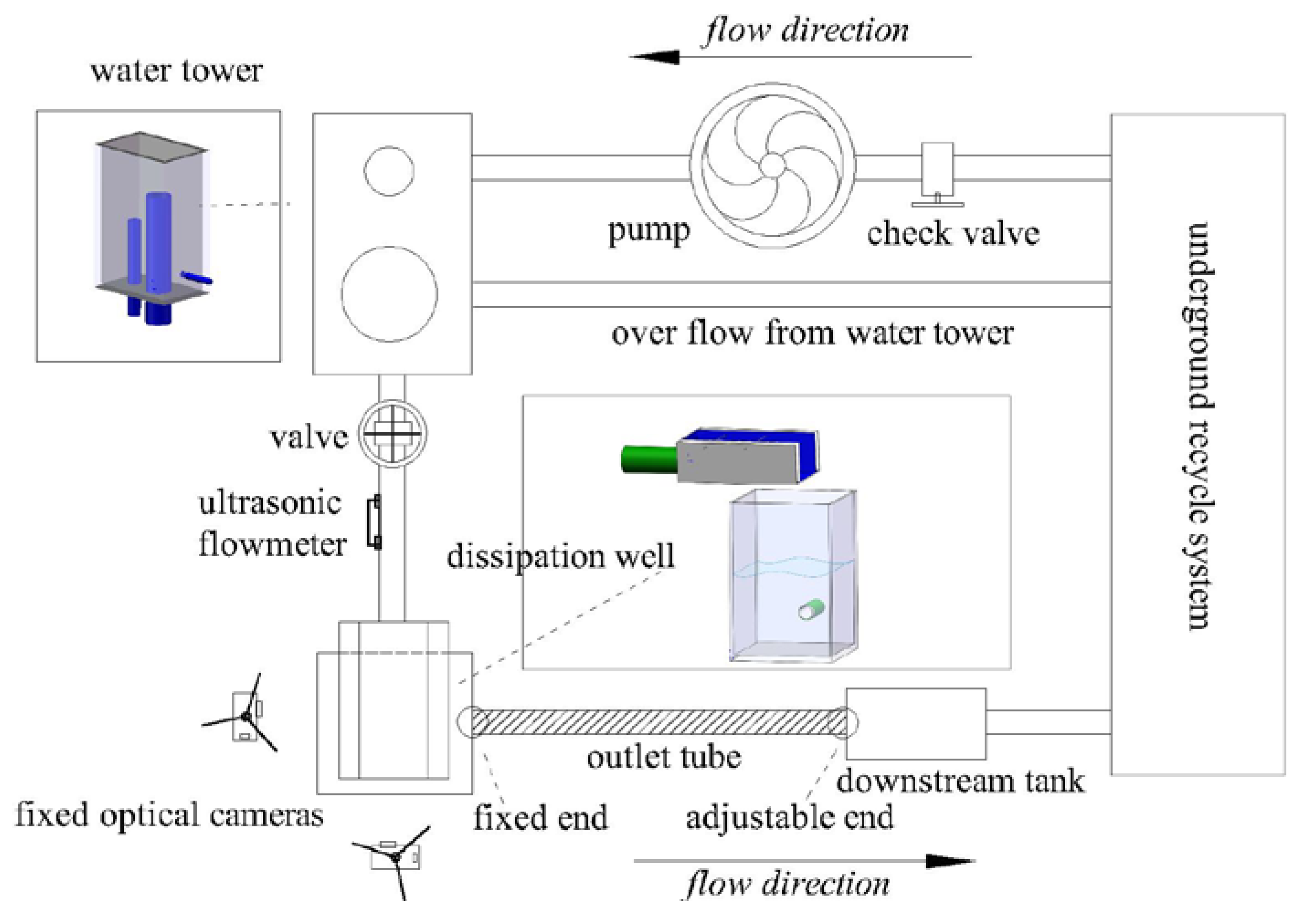
2. Experiment Platform Setup
3. Experimental Results and Analysis
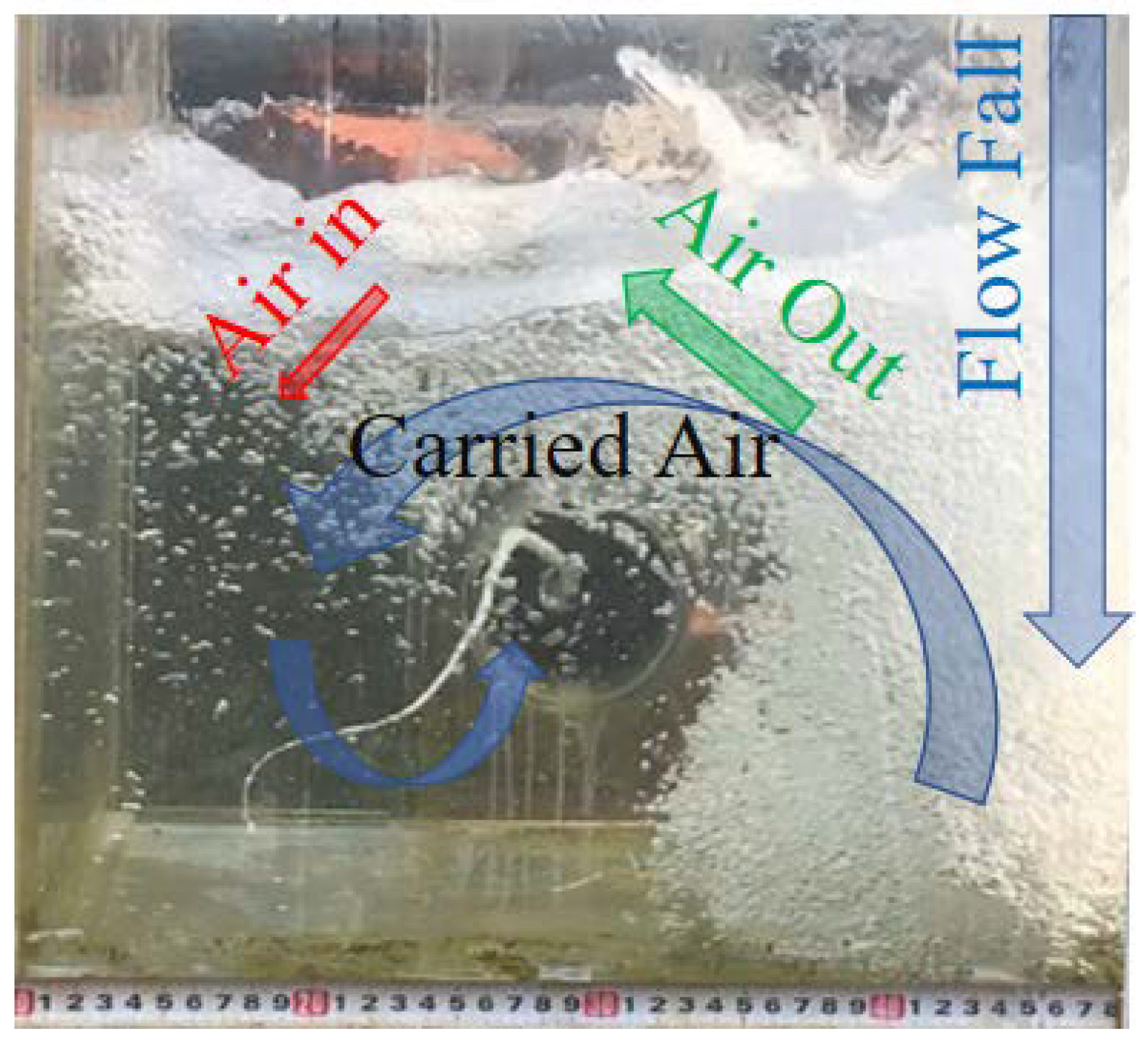
3.1. Formation and Collapse
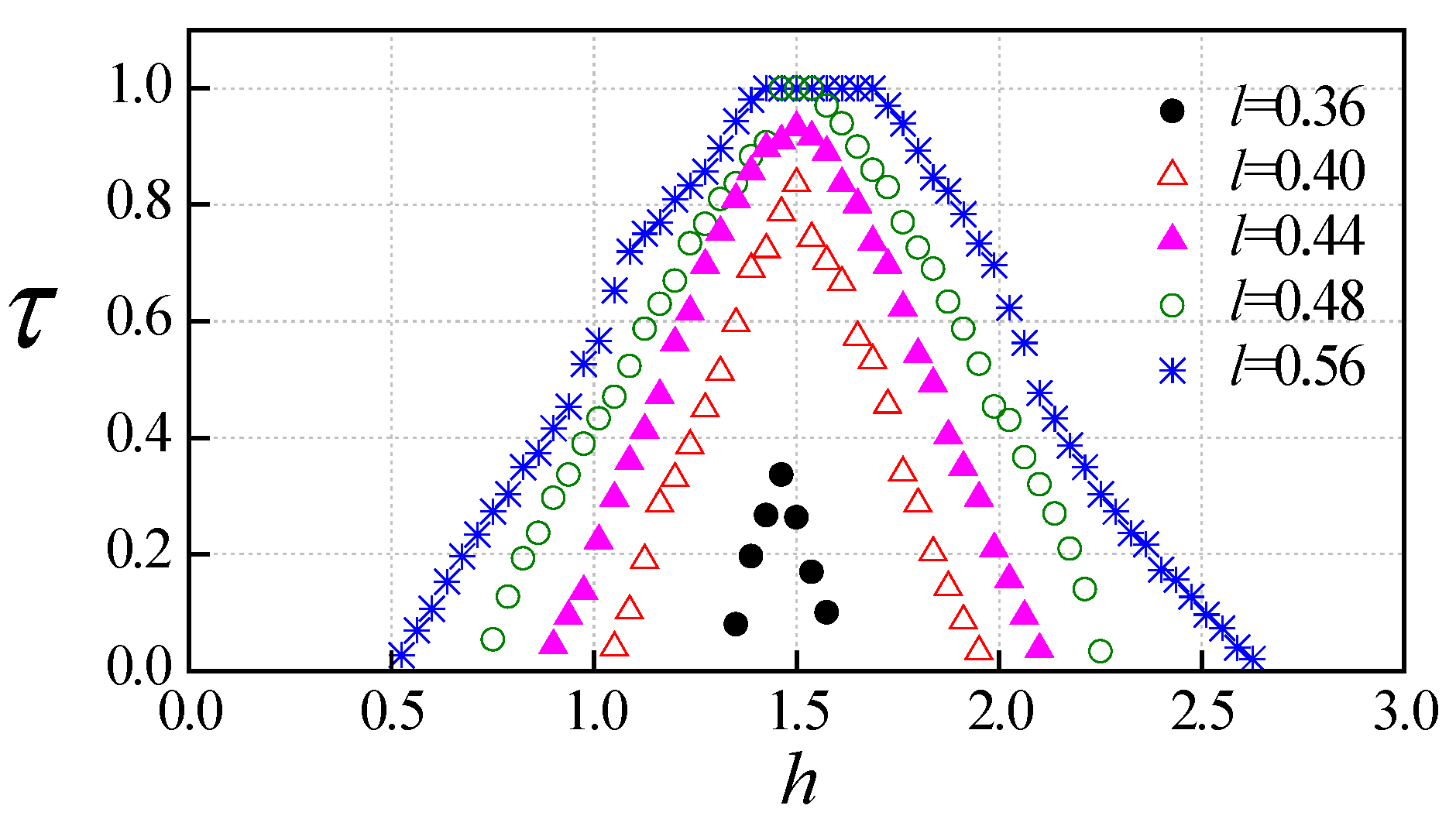
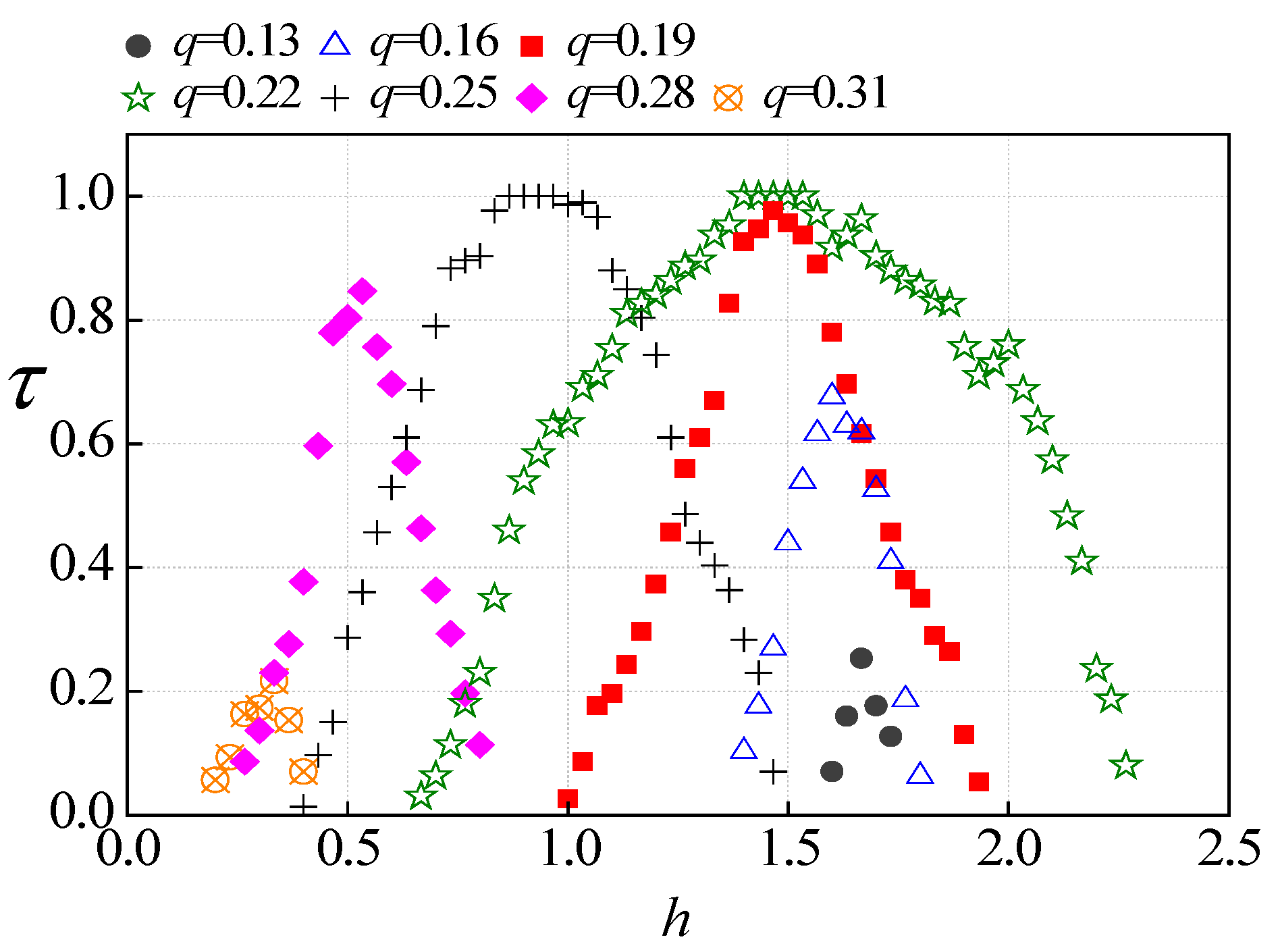
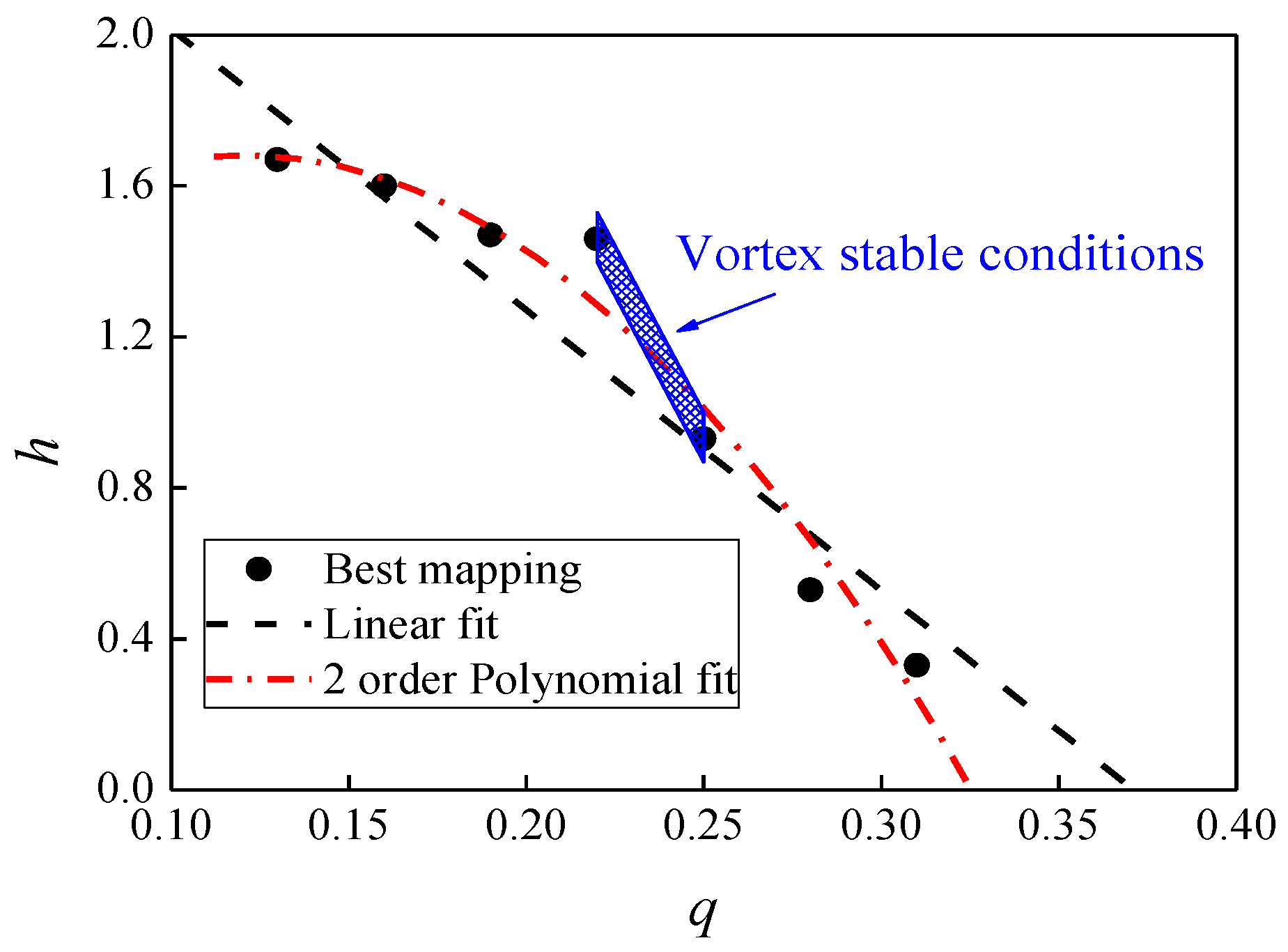
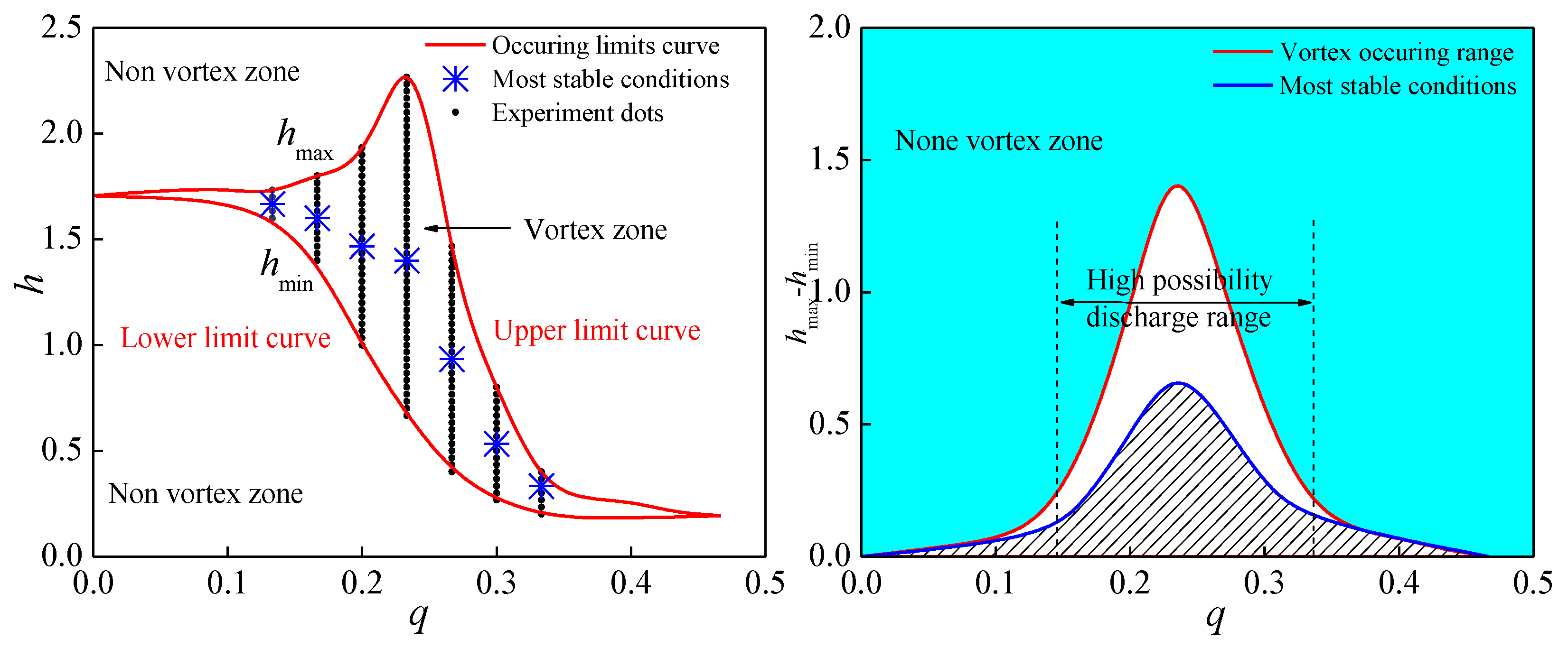
3.2. Formation Requirement Analysis
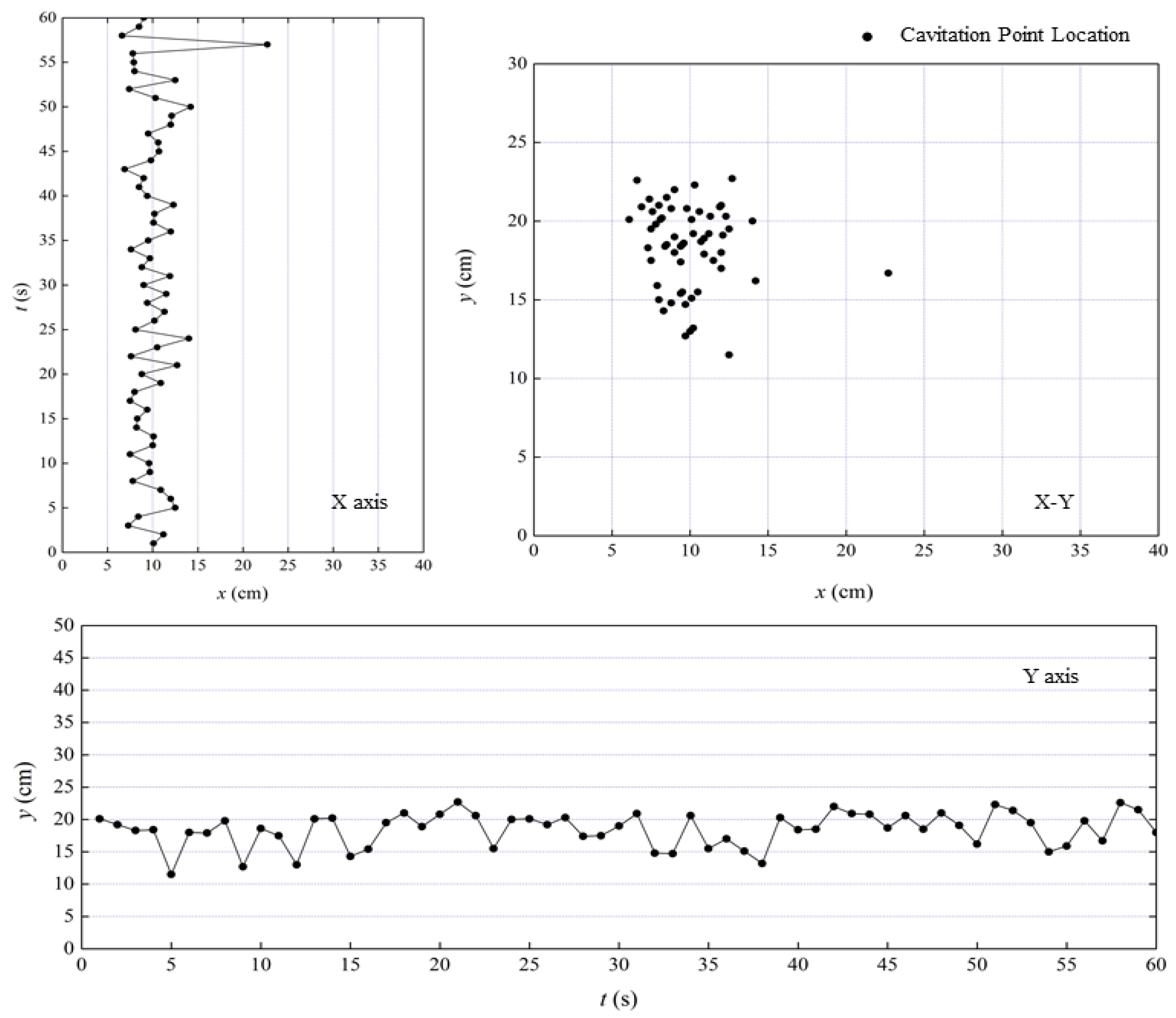
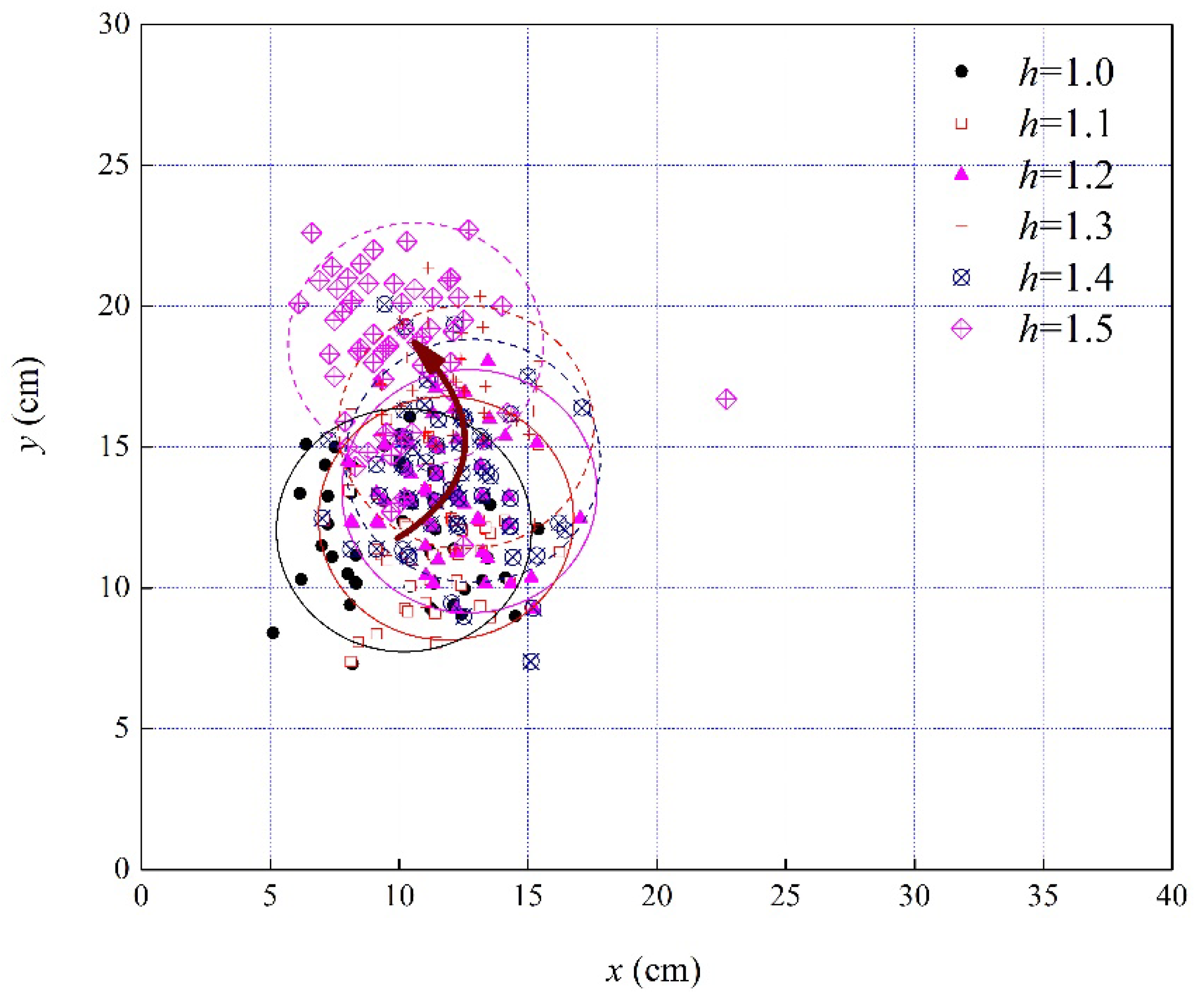
3.3. The Motion of Cavitation Point
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| t | time (s) |
| lA | the width between the two adjustable boards (cm) |
| lA0 | the width between the two fixed boards (cm) |
| DI | the diameter of the inlet pipe (cm) |
| dA | the length of the adjuster bottom board (cm) |
| hW | the height of the well (cm) |
| hV | the height of the water volume inside the well (cm) |
| dW | the width of the well (cm) |
| lW | the length of the well (cm) |
| hE | the height of the exit hole (cm) |
| DE | the diameter of the outlet pipe (cm) |
| T | initial time point (s) |
| DT | time step (s) |
| the possibility of vortices occurring | |
| q | the dimensionless discharge |
| l | the dimensionless width of the inlet fall |
| h | the dimensionless height |
| tV | the time duration of maintaining the vortex (s) |
| tR | the time duration of the whole record (s) |
| Δh | the hydraulic head difference (m) |
References
- Agee, E.; Church, C.; Morris, C.; Snow, J. Some synoptic aspects and dynamic features of vortices associated with tornado outbreak of 3 april 1974. Mon. Weather Rev. 1975, 103, 318–333. [Google Scholar] [CrossRef] [Green Version]
- Agee, E.M.; Snow, J.T.; Clare, P.R. Multiple vortex features in tornado cyclone and occurrence of tornado families. Mon. Weather Rev. 1976, 104, 552–563. [Google Scholar] [CrossRef] [Green Version]
- Onishchenko, O.; Fedun, V.; Horton, W.; Pokhotelov, O.; Verth, G. Dust Devils: Structural Features, Dynamics and Climate Impact. Climate 2019, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Zwicky, F. Some novel features of the whirlpool nebula as revealed by composite analytical photography. Publ. Astron. Soc. Pac. 1955, 67, 232. [Google Scholar] [CrossRef] [Green Version]
- Weissmann, S.; Pinkall, U.; Schroder, P. Smoke Rings from Smoke. ACM Trans. Graph. 2014, 33, 8. [Google Scholar] [CrossRef]
- Cao, L.K.; Li, D.X.; Chen, H.; Liu, C.J. Spatial relationship between energy dissipation and vortex tubes in channel flow. J. Hydrodyn. 2017, 29, 575–585. [Google Scholar] [CrossRef]
- Feng, S.; Graham, A.L.; Abbott, J.R.; Brenner, H. Antisymmetric stresses in suspensions: Vortex viscosity and energy dissipation. J. Fluid Mech. 2006, 563, 97–122. [Google Scholar] [CrossRef]
- Serfaty, S. Vortex collisions and energy-dissipation rates in the Ginzburg-Landau heat flow Part II: The dynamics. J. Eur. Math. Soc. 2007, 9, 383–426. [Google Scholar] [CrossRef] [Green Version]
- Kwon, T.S.; Song, C.H.; Baek, W.P. Advanced DVI for ECC direct bypass mitigation. Nucl. Eng. Des. 2009, 239, 1095–1102. [Google Scholar] [CrossRef]
- Zhang, Y.; Kennedy, A.B.; Tomiczek, T.; Donahue, A.; Westerink, J.J. Validation of Boussinesq-Green-Naghdi modeling for surf zone hydrodynamics. Ocean Eng. 2016, 111, 299–309. [Google Scholar] [CrossRef] [Green Version]
- Iga, K.; Yokota, S.; Watanabe, S.; Ikeda, T.; Niino, H.; Misawa, N. Various phenomena on a water vortex in a cylindrical tank over a rotating bottom. Fluid Dyn. Res. 2014, 46, 031409. [Google Scholar] [CrossRef]
- Lin, J.C.; Ozgoren, M.; Rockwell, D. Space-time development of the onset of a shallow-water vortex. J. Fluid Mech. 2003, 485, 33–66. [Google Scholar] [CrossRef]
- Ward, N.B. The exploration of certain features of tornado dynamics using a laboratory model. J. Atmos. Sci. 1972, 29, 1194–1204. [Google Scholar] [CrossRef]
- Zipser, E.J.; Golden, J.H. Summertime tornado outbreak in colorado—Mesoscale environment and structural featuRES. Mon. Weather Rev. 1979, 107, 1328–1342. [Google Scholar] [CrossRef]
- Akbulut, M.; Hwang, J.; Kimpel, F.; Gupta, S.; Verdun, H. Pulsed coherent fiber lidar transceiver for aircraft in-flight turbulence and wake-vortex hazard detection. In Laser Radar Technology and Applications XVI; Turner, M.D., Kamerman, G.W., Eds.; SPIE Defense, Security, and Sensing: Orlando, FL, USA, 2011; Volume 8037. [Google Scholar] [CrossRef]
- Harris, M.; Young, R.I.; Kopp, F.; Dolfi, A.; Cariou, J.P. Wake vortex detection and monitoring. Aerosp. Sci. Technol. 2002, 6, 325–331. [Google Scholar] [CrossRef]
- Janic, M. Toward Time-Based Separation Rules for Landing Aircraft. Transp. Res. Rec. 2008, 2052, 79–89. [Google Scholar] [CrossRef]
- Rennich, S.C.; Lele, S.K. Method for accelerating the destruction of aircraft wake vortices. J. Aircr. 1999, 36, 398–404. [Google Scholar] [CrossRef]
- Rossow, V.J. Lift-generated vortex wakes of subsonic transport aircraft. Prog. Aerosp. Sci. 1999, 35, 507–660. [Google Scholar] [CrossRef]
- Schwarz, C.W.; Hahn, K.U. Full-flight simulator study for wake vortex hazard area investigation. Aerosp. Sci. Technol. 2006, 10, 136–143. [Google Scholar] [CrossRef]
- Lee, C.B. New features of CS solitons and the formation of vortices. Phys. Lett. A 1998, 247, 397–402. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Finlay, W.H.; Fields, W.A.; Fuqua, S.J.; Subramanian, C.S. Features of wavy vortices in a curved channel from experimental and numerical-studies. Phys. Fluids A Fluid Dyn. 1992, 4, 695–709. [Google Scholar] [CrossRef]
- Das, Y. Parametric modeling of tropical cyclone wind fields in India. Nat. Hazards 2018, 93, 1049–1084. [Google Scholar] [CrossRef]
- Hrabovsky, M.; Konrad, M.; Kopecky, V.; Sember, V. Processes and properties of electric arc stabilized by water vortex. IEEE Trans. Plasma Sci. 1997, 25, 833–839. [Google Scholar] [CrossRef]
- Travis, Q.B.; Mays, L.W. Prediction of Intake Vortex Risk by Nearest Neighbors Modeling. J. Hydraul. Eng. 2011, 137, 701–705. [Google Scholar] [CrossRef]
- Chen, J.G.; Chen, X.Q.; Li, Y.; Wang, F. An experimental study of dilute debris flow characteristics in a drainage channel with an energy dissipation structure. Eng. Geol. 2015, 193, 224–230. [Google Scholar] [CrossRef]
- Gens, A.; Alonso, E.E. Aznalcollar dam failure. Part 2: Stability conditions and failure mechanism. Geotechnique 2006, 56, 185–201. [Google Scholar] [CrossRef] [Green Version]
- Bennacer, R.; Sefiane, K. Vortices, dissipation and flow transition in volatile binary drops. J. Fluid Mech. 2014, 749, 649–665. [Google Scholar] [CrossRef] [Green Version]
- Monshizadeh, M.; Tahershamsi, A.; Rahimzadeh, H.; Sarkardeh, H. Vortex Dissipation Using a Hydraulic-Based Anti-Vortex Device at Intakes. Int. J. Civ. Eng. 2018, 16, 1137–1144. [Google Scholar] [CrossRef]
- Seol, D.G.; Jirka, G.H. Quasi-two-dimensional properties of a single shallow-water vortex with high initial Reynolds numbers. J. Fluid Mech. 2010, 665, 274–299. [Google Scholar] [CrossRef]
- Kessal, M.; Amaouche, M. Numerical simulation of transient vaporous and gaseous cavitation in pipelines. Int. J. Numer. Methods Heat Fluid Flow 2001, 11, 121–137. [Google Scholar] [CrossRef]
- Wan, W.Y.; Zhang, B.R. Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank. Energies 2018, 11, 1450. [Google Scholar] [CrossRef] [Green Version]
- Wan, W.Y.; Zhang, B.R.; Chen, X.Y. Investigation on Water Hammer Control of Centrifugal Pumps in Water Supply Pipeline Systems. Energies 2019, 12, 108. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.R.; Wan, W.Y.; Shi, M.S. Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment. Water 2018, 10, 928. [Google Scholar] [CrossRef] [Green Version]
- Meng, W.W.; Cheng, Y.G.; Wu, J.Y.; Yang, Z.Y.; Zhu, Y.X.; Shang, S. GPU Acceleration of Hydraulic Transient Simulations of Large-Scale Water Supply Systems. Appl. Sci. 2019, 9, 91. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.D.; Yang, X.W.; Zhang, J. Stability analysis of hydro-turbine governing system including surge tanks under interconnected operation during small load disturbance. Renew. Energy 2019, 133, 1426–1435. [Google Scholar] [CrossRef]
- Triki, A.; Fersi, M. Further investigation on the water-hammer control branching strategy in pressurized steel-piping systems. Int. J. Press. Vessel. Pip. 2018, 165, 135–144. [Google Scholar] [CrossRef]
- Triki, A.; Chaker, M.A. Compound technique-based inline design strategy for water-hammer control in steel pressurized-piping systems. Int. J. Press. Vessel. Pip. 2019, 169, 188–203. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S. A Generalized Procedure for Pipeline Hydraulic Components in Quasi-Two-Dimensional Unsteady Flow Analysis. J. Fluids Eng. Trans. ASME 2019, 141, 061107. [Google Scholar] [CrossRef]
- Wan, W.Y.; Shi, M.S.; Zhang, B.; Fan, L.L. Experimental investigation on characteristics of horizontal vortex column in side-flow energy dissipation well. J. Zhejiang Univ. 2018, 52, 2083–2091. [Google Scholar]
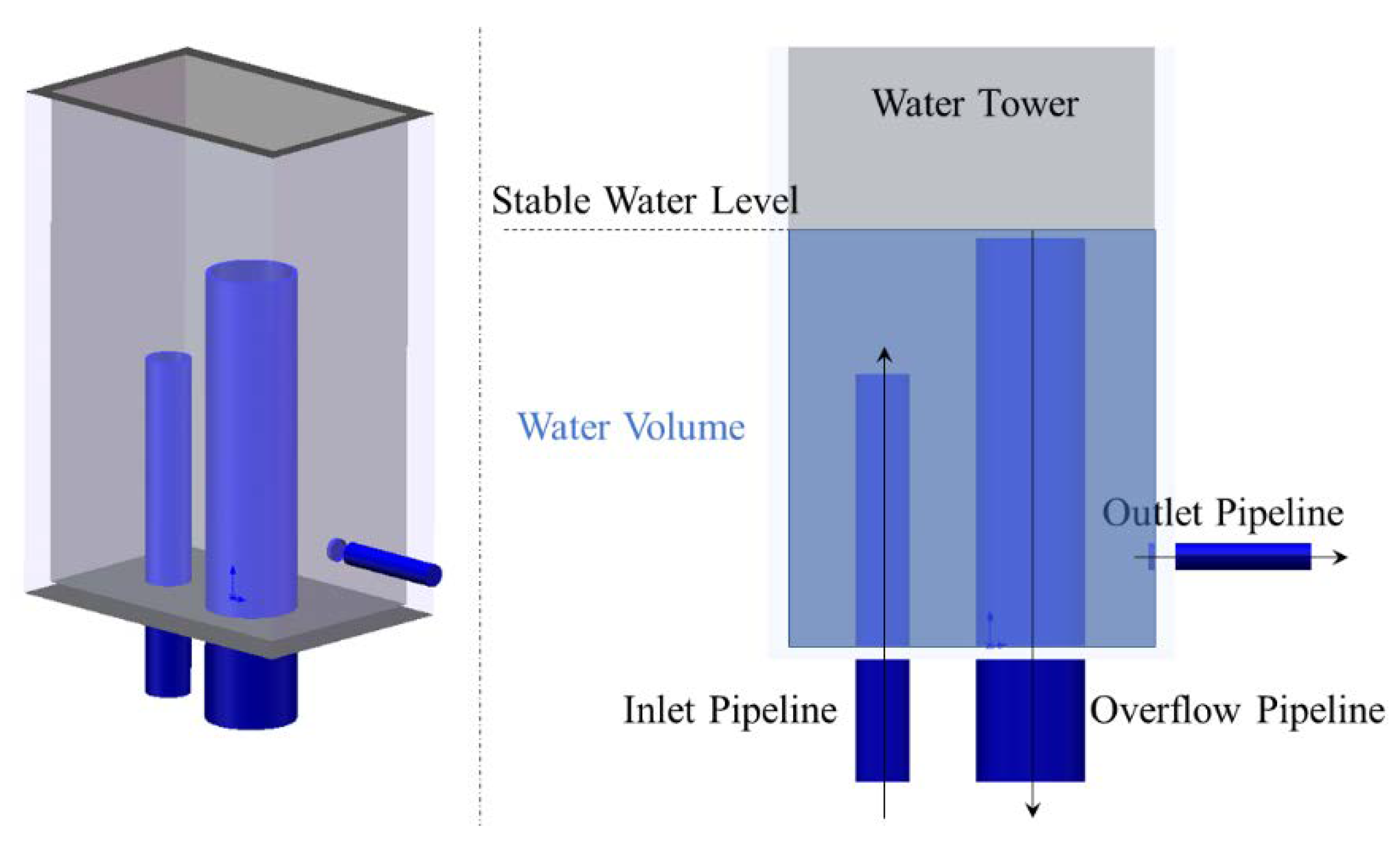
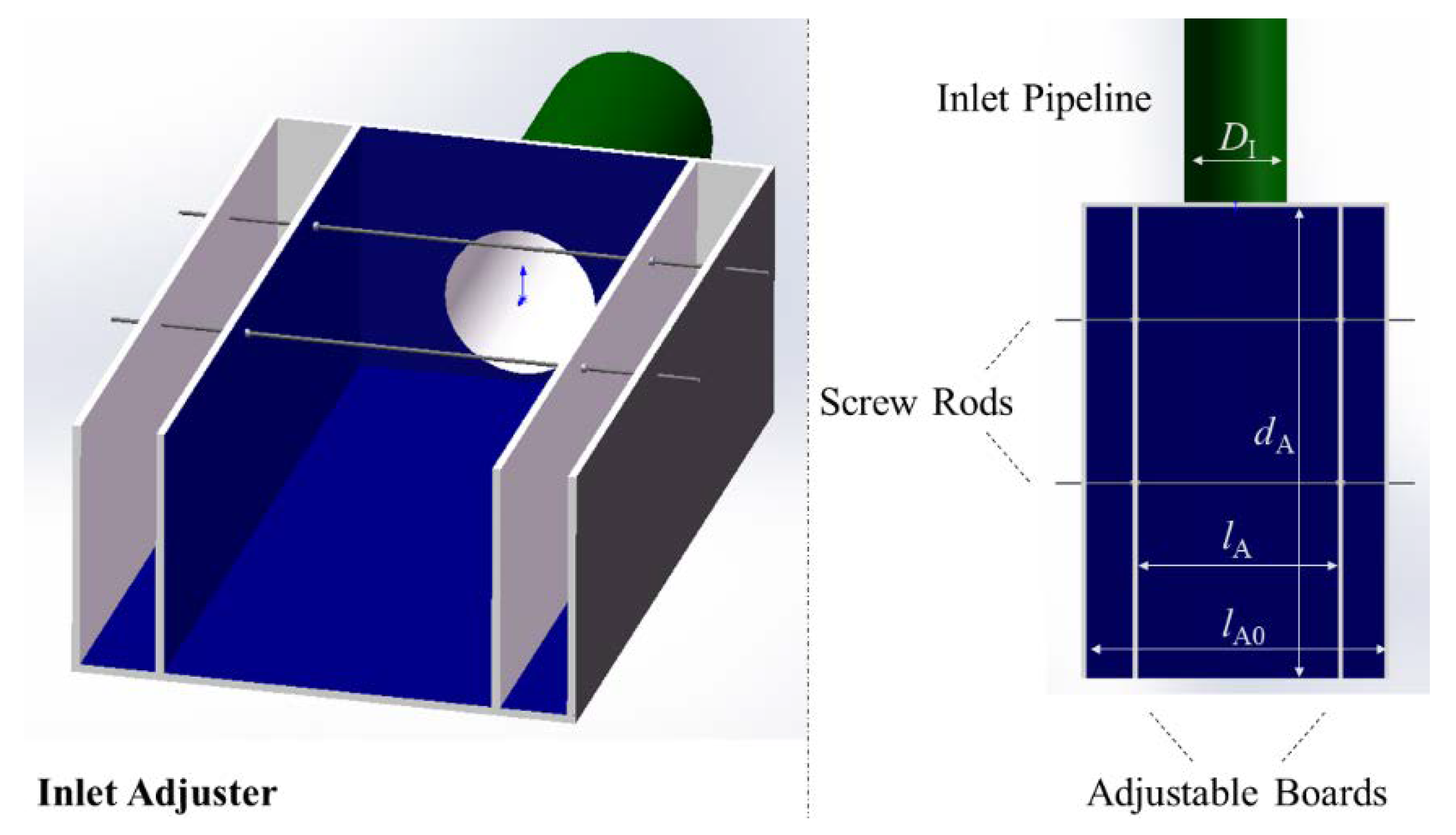
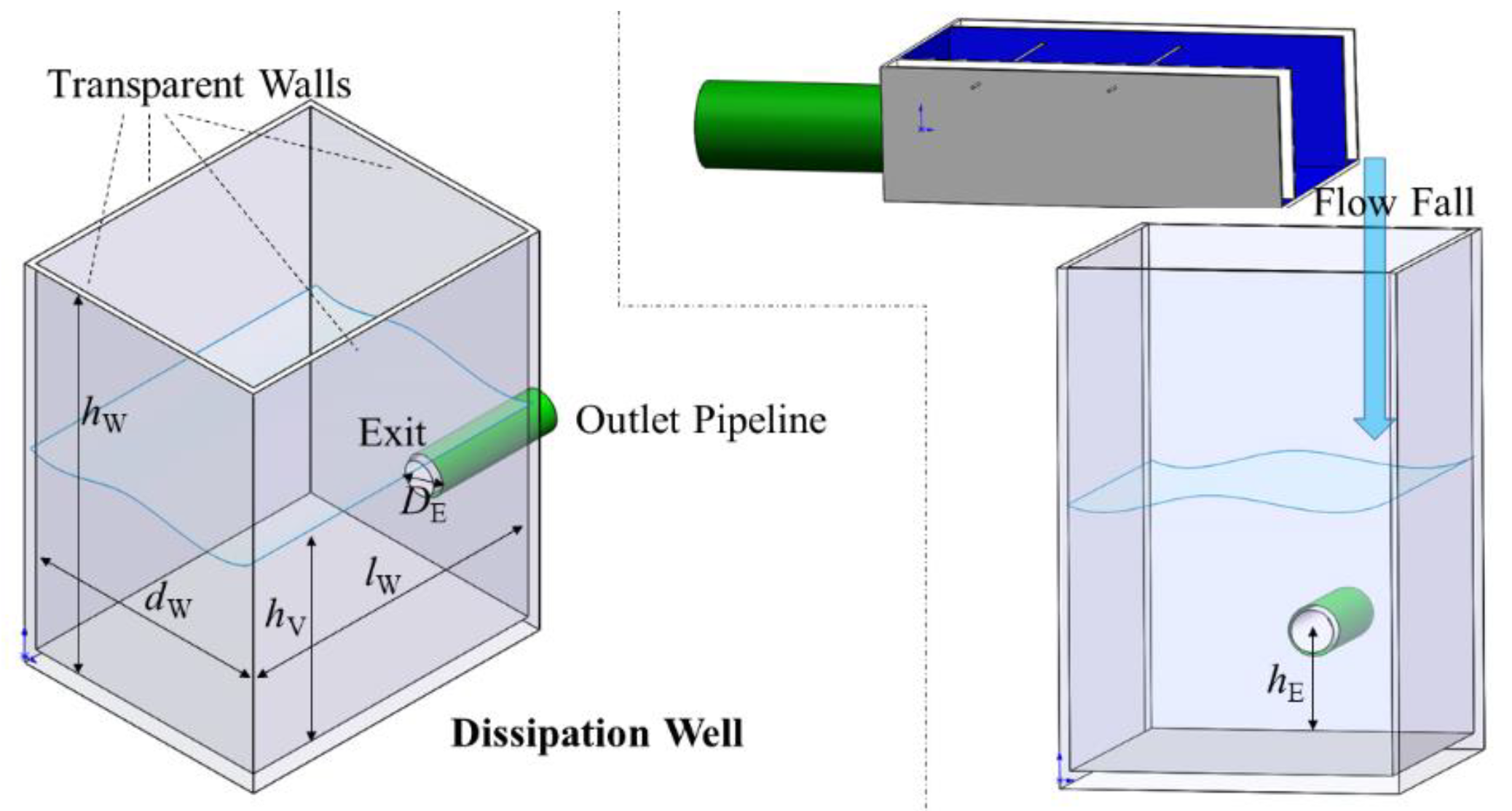


| Inlet Adjuster | Dissipation Well | Pipes | |||||
|---|---|---|---|---|---|---|---|
| lA0 | dA | hW | dW | lW | hE | DI | DE |
| 30 | 70 | 80 | 40 | 50 | 15 | 10 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Shi, M.; Yao, L.; Wan, W. Features and Control of Submerged Horizontal Vortex in Stepped Dissipation Wells. Water 2020, 12, 2117. https://doi.org/10.3390/w12082117
Zhang B, Shi M, Yao L, Wan W. Features and Control of Submerged Horizontal Vortex in Stepped Dissipation Wells. Water. 2020; 12(8):2117. https://doi.org/10.3390/w12082117
Chicago/Turabian StyleZhang, Boran, Mengshan Shi, Lvtan Yao, and Wuyi Wan. 2020. "Features and Control of Submerged Horizontal Vortex in Stepped Dissipation Wells" Water 12, no. 8: 2117. https://doi.org/10.3390/w12082117
APA StyleZhang, B., Shi, M., Yao, L., & Wan, W. (2020). Features and Control of Submerged Horizontal Vortex in Stepped Dissipation Wells. Water, 12(8), 2117. https://doi.org/10.3390/w12082117






