Numerical Simulation of the Flow Field Characteristics of Stationary Two-Pipe Vehicles under Different Spacings
Abstract
:1. Introduction
2. Mathematical Formulations
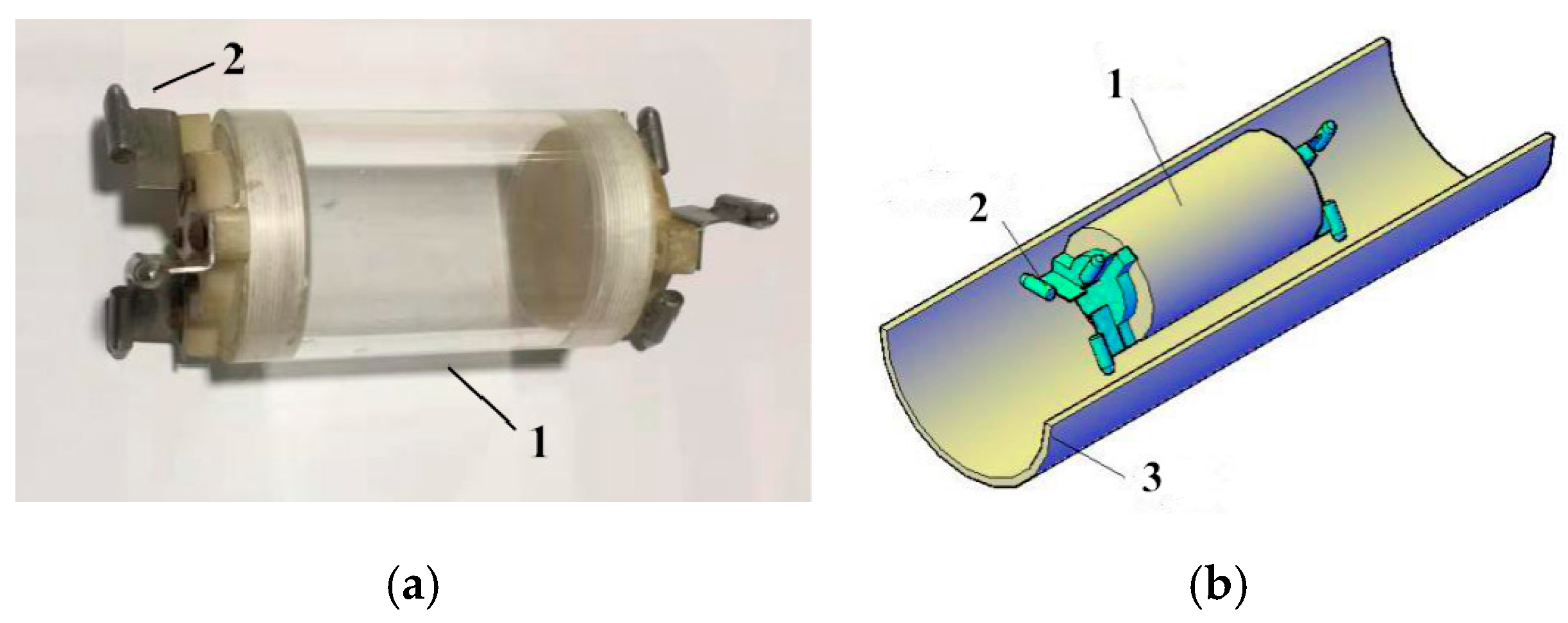
2.1. Geometric Model
2.2. Governing Equations and Turbulence Model
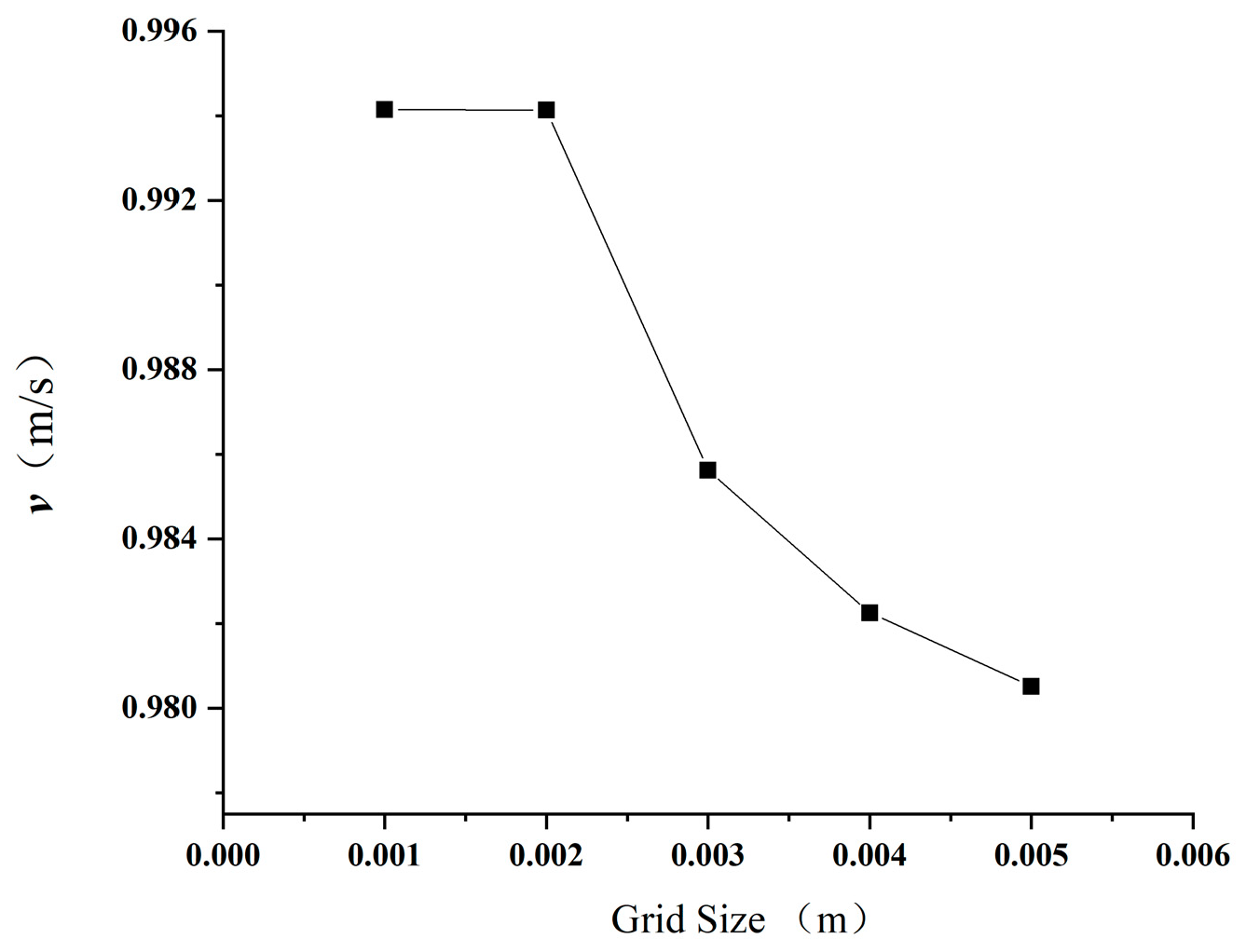
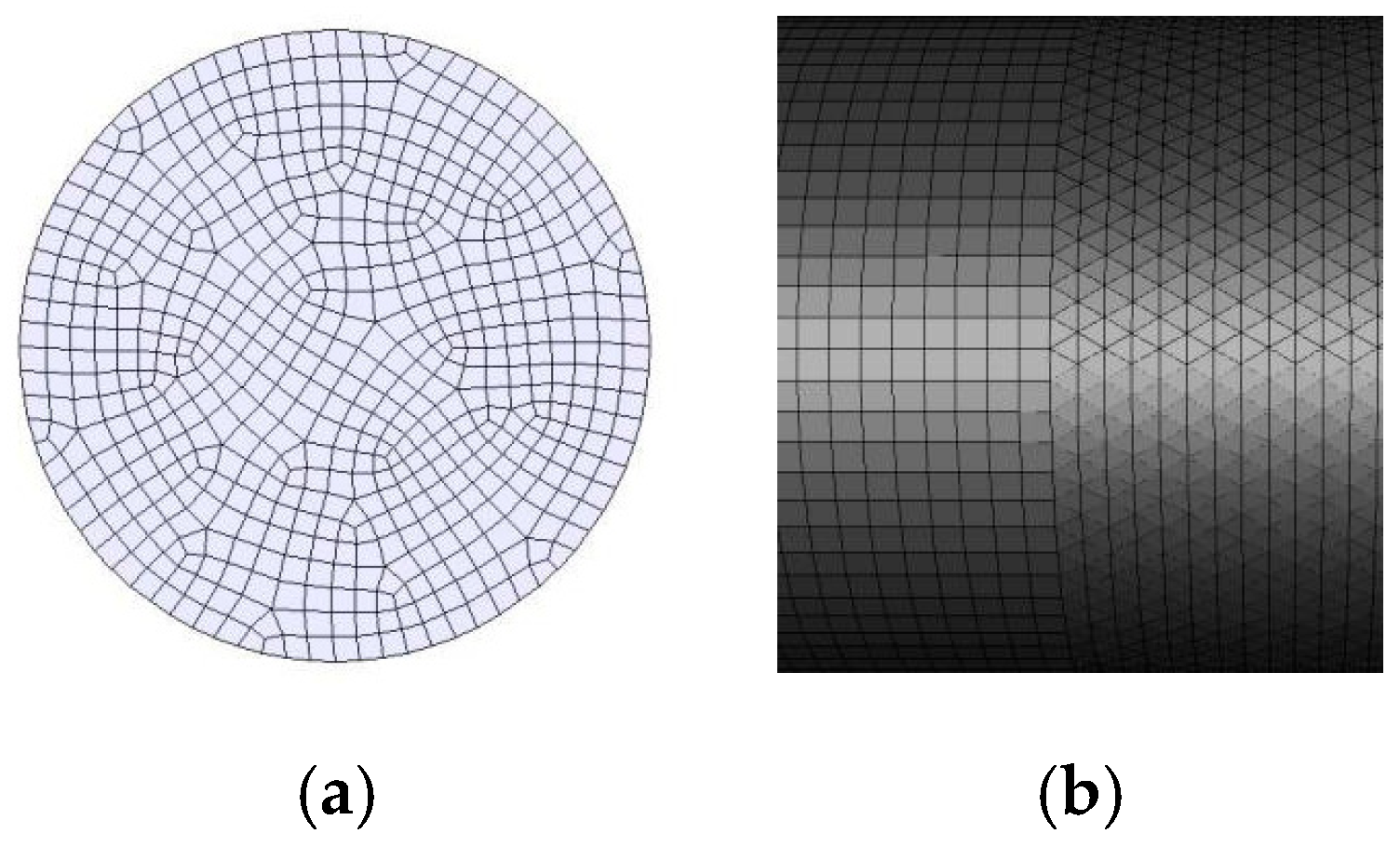
2.3. Mesh
2.4. Boundary Conditions and Algorithms
- The pipeline inlet boundary was set as the “velocity inlet” condition. The liquid medium in the pipeline was water, and the density was 1000 kg/m3 with a dynamic viscosity of 1.062 × 10−3 Pa·s (water temperature was 18 °C). The measured velocity was used in order to define the distributions of the flow velocity at the inlet cross-section. The parameters of the “velocity inlet” were calculated by Equations (13)–(17), and the specific calculation results are shown in Table 1.where ρ is the water density; η is dynamic viscosity; l0 is turbulence length; I represents turbulence intensity; k is the turbulent kinetic energy; ε is the turbulent dissipation rate; Cμ is the empirical constant of the turbulent model, generally taking 0.09; Vp is the average flow velocity in the pipeline; and Dp is the pipe diameter.
- The outlet boundary was set as a “pressure outlet” condition. The measured pressure was used to define the pressure distributions at the outlet boundary of the mathematical model. The outlet pressure value was obtained through physical experiment; the pressure was set to 6000 Pa.
- The wall boundary included the wall surface of the two-pipe vehicles and the pipeline wall, which was set as a “no-slip” condition. The pipeline wall and two-pipe vehicle wall were considered to be hydrodynamically smooth, with a wall roughness constant of zero.
3. Experimental Methods
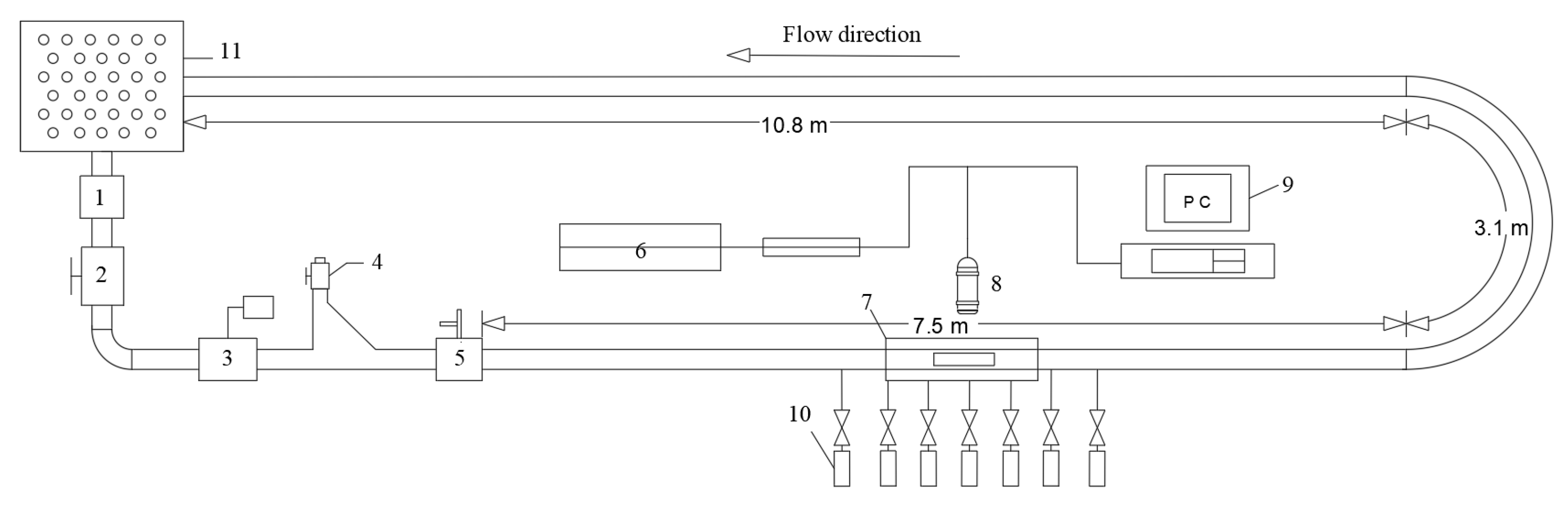
3.1. Experimental System and Procedures
3.2. Experiment Plan
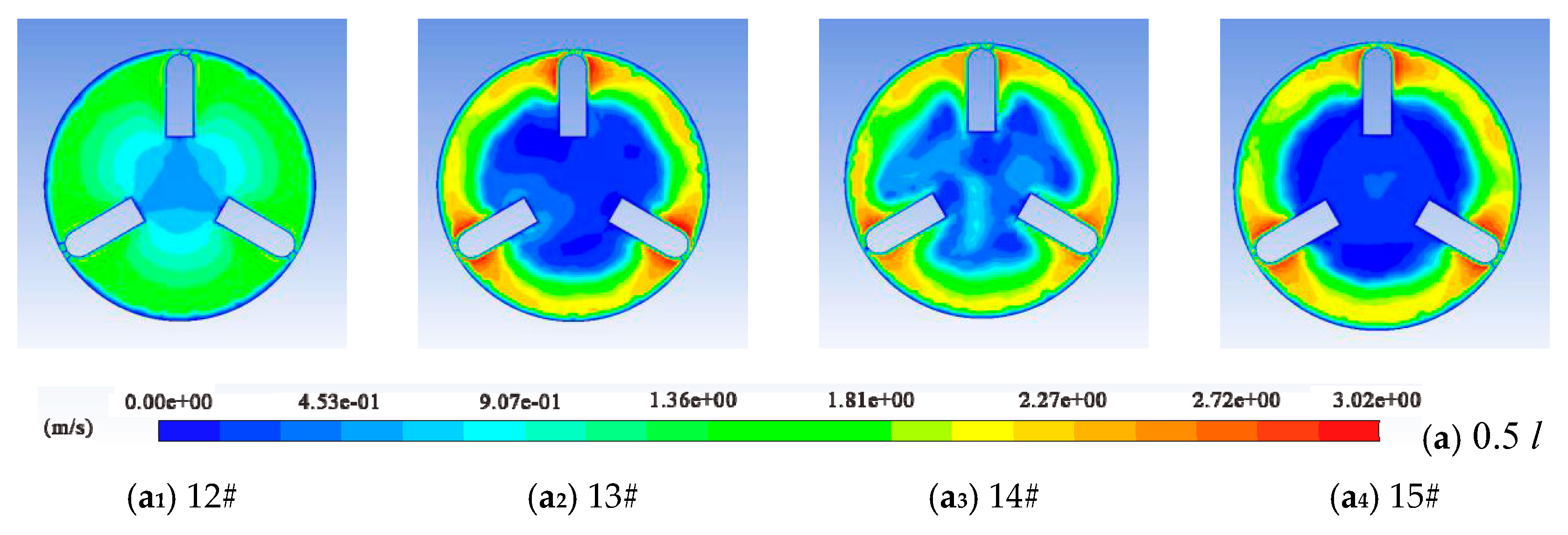
3.3. Section Selection and Measuring Point Arrangement
4. Simulation Results and Discussion
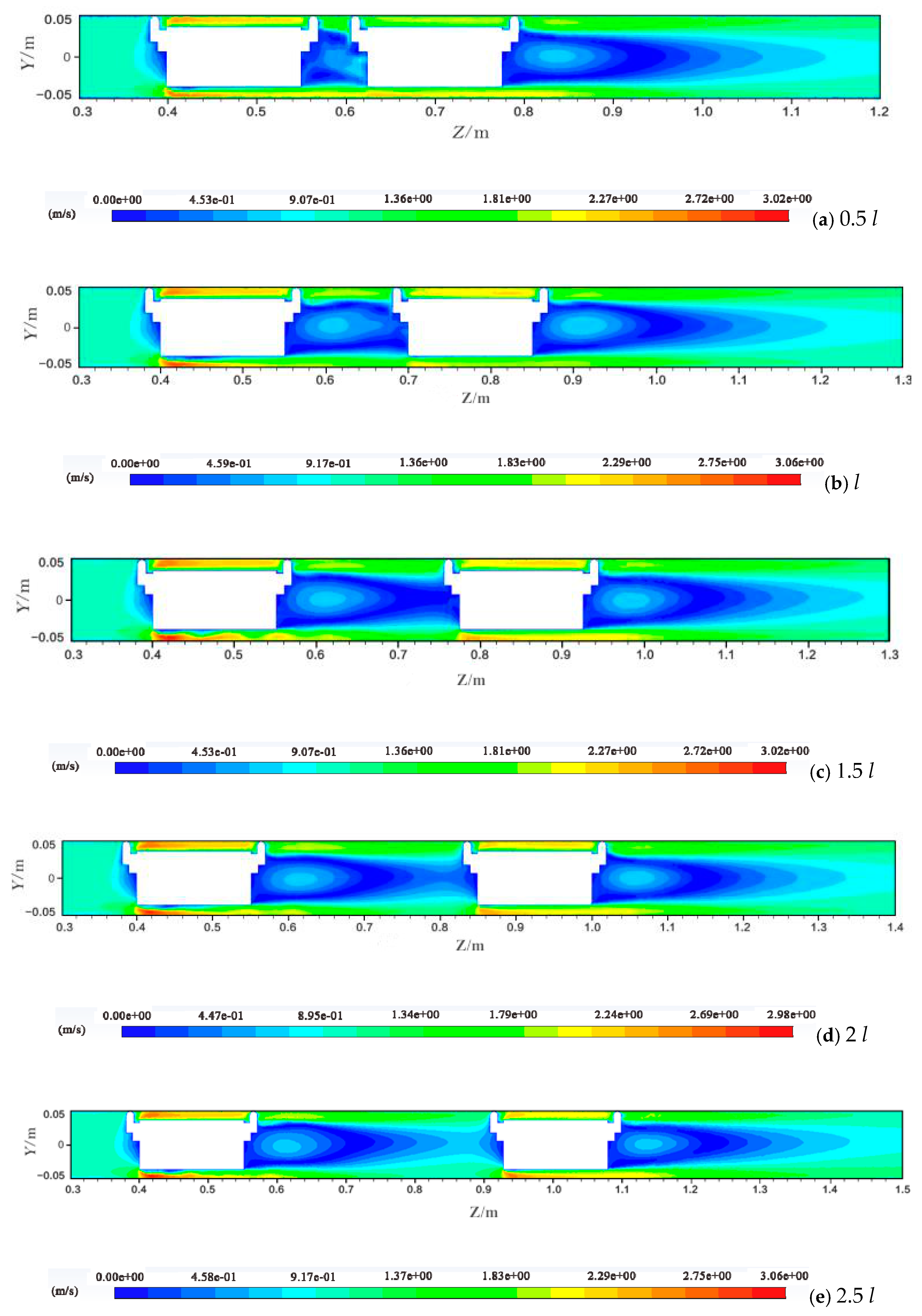
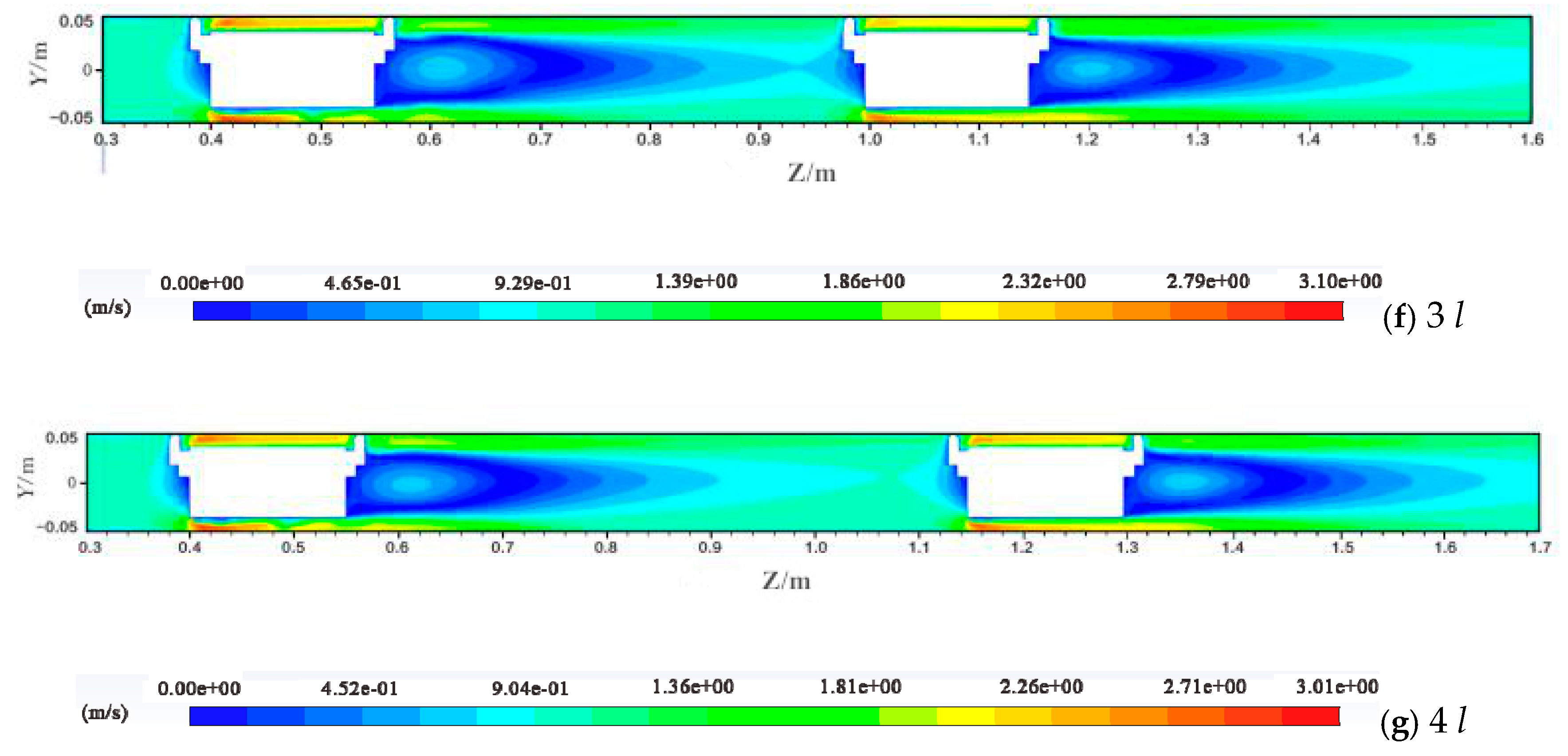
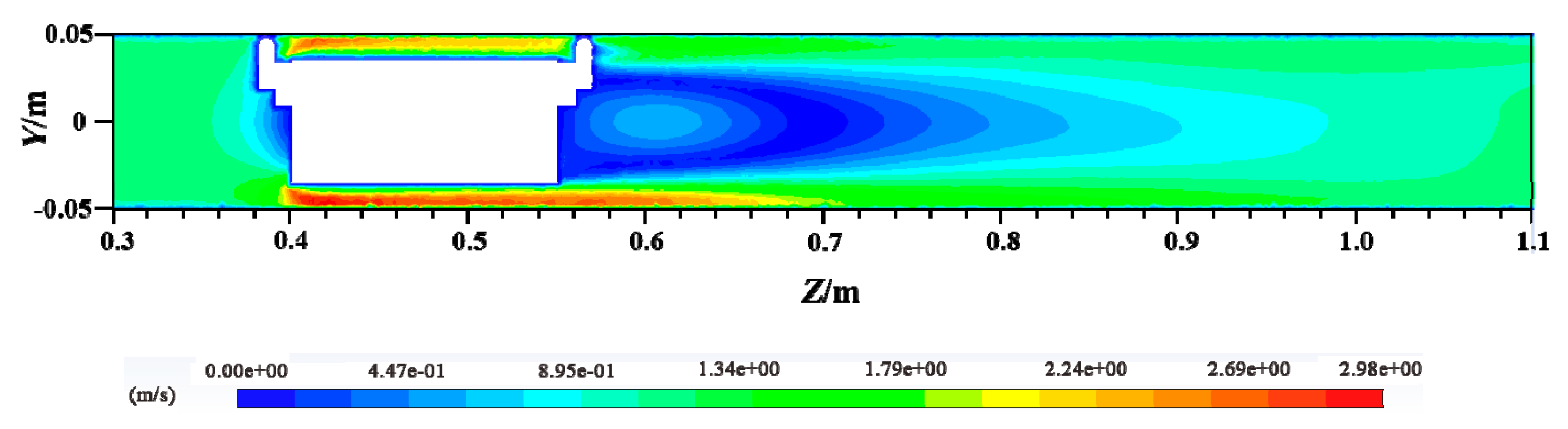
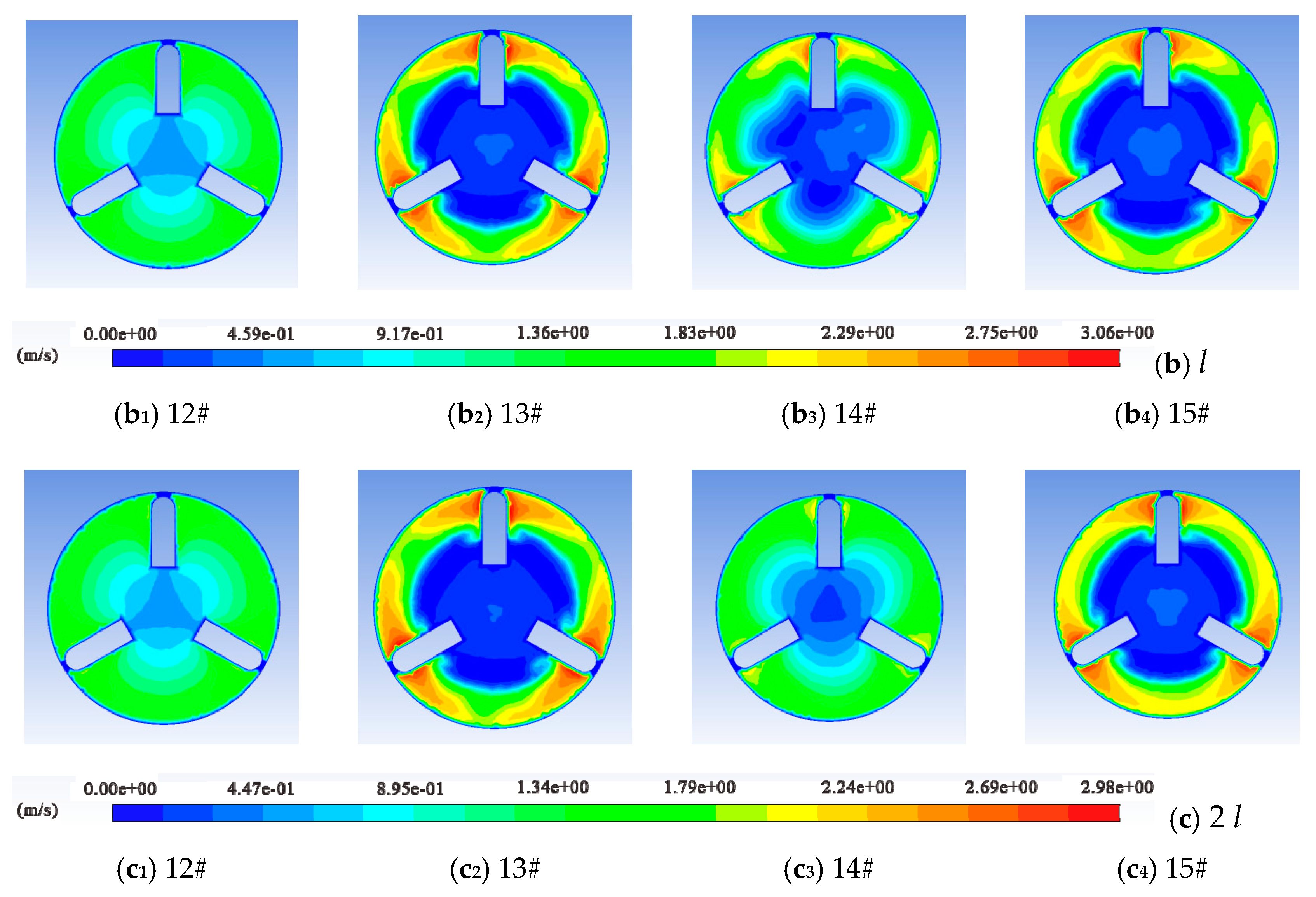
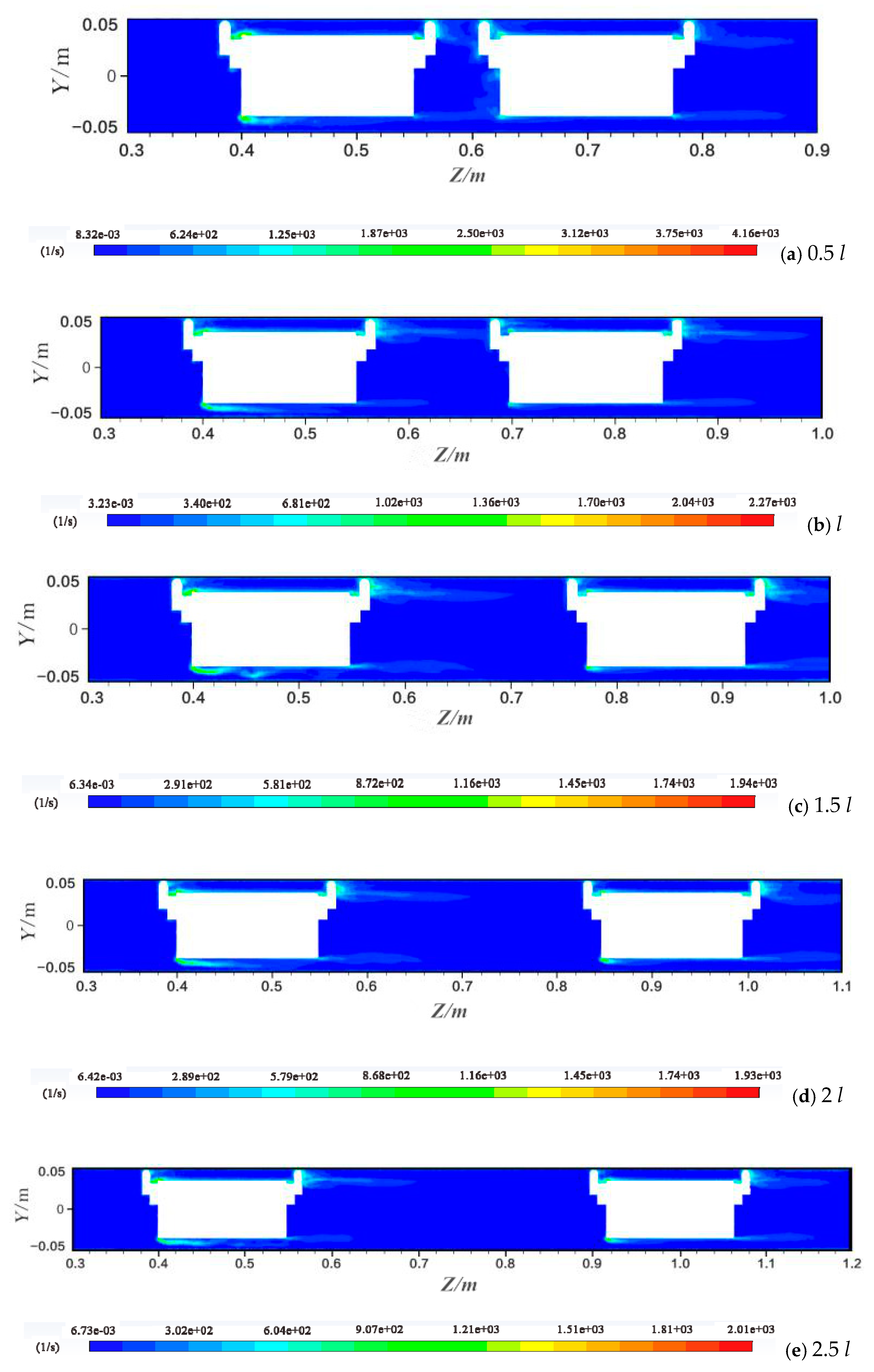
4.1. Distribution of Velocity Magnitude
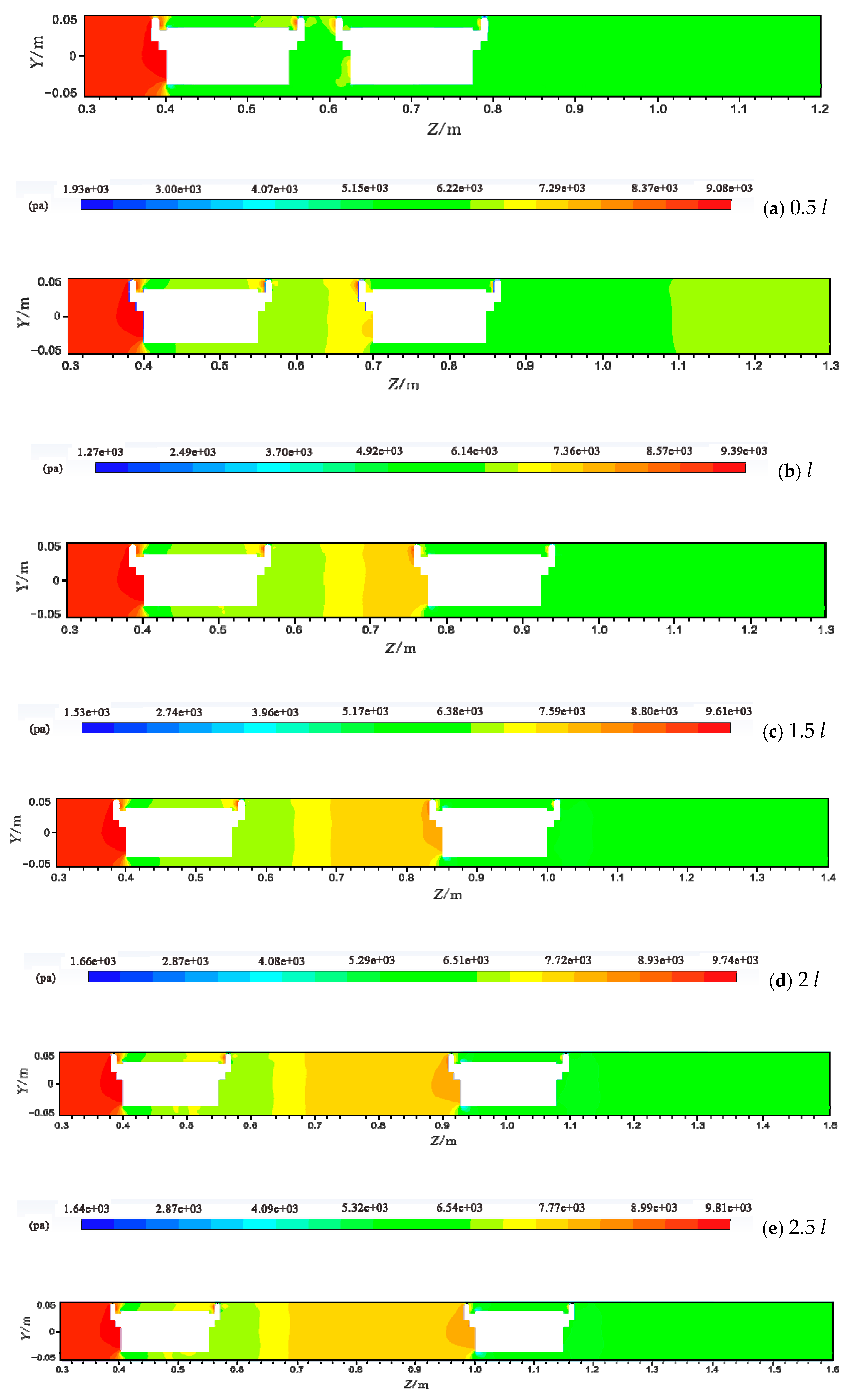
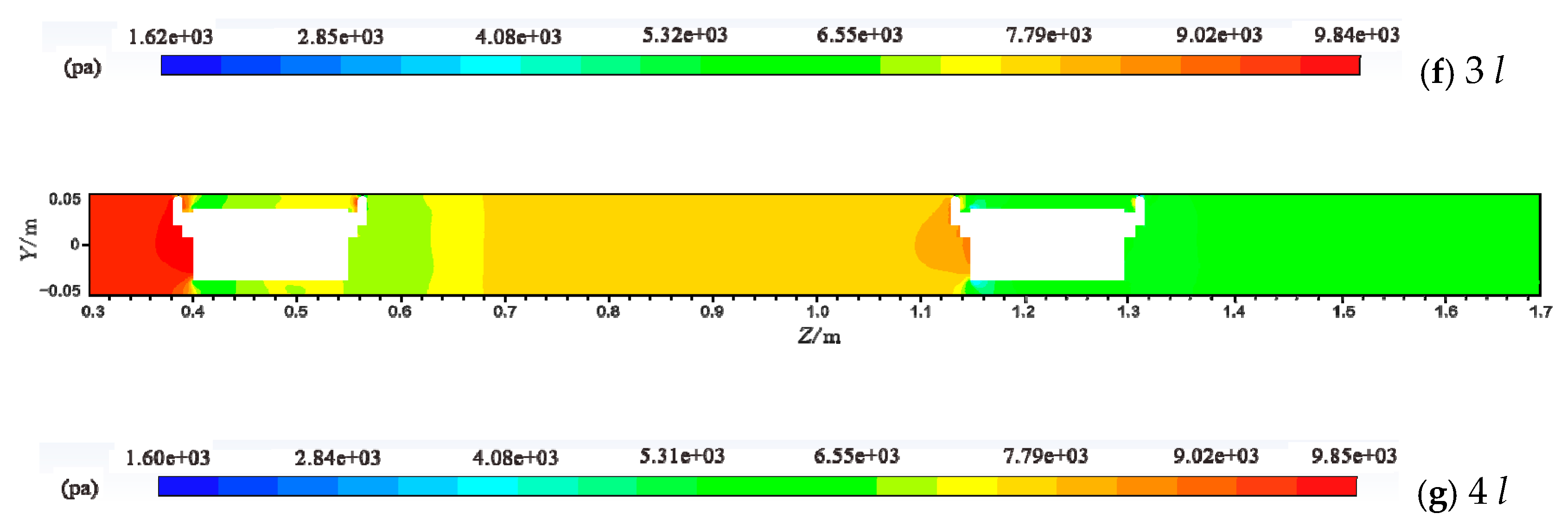
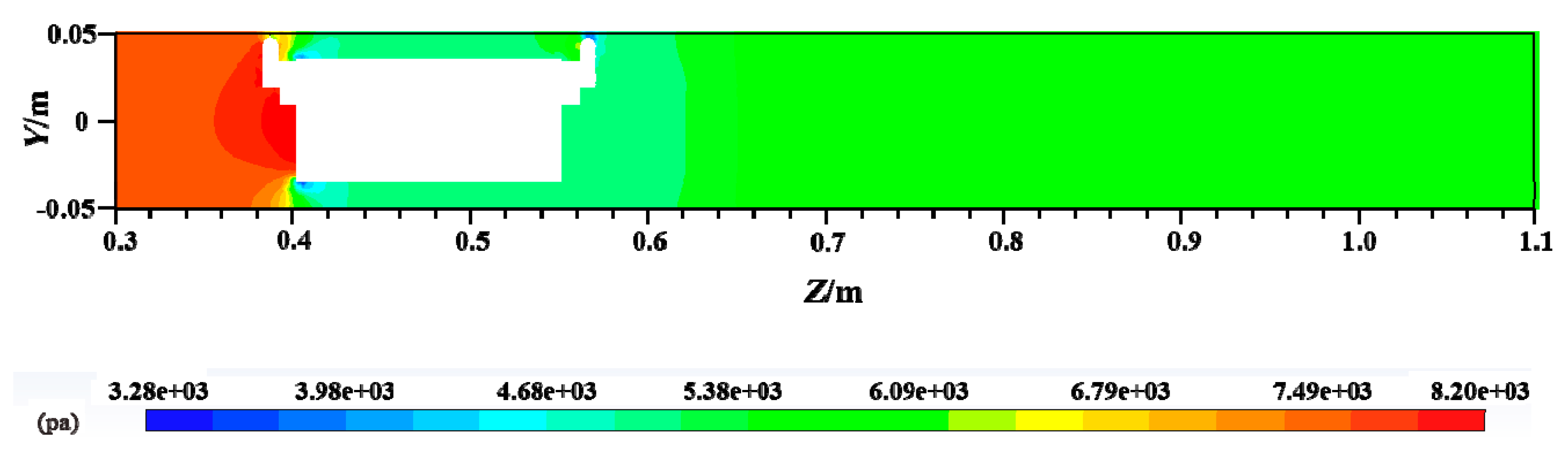
4.2. Distribution of Pressure
- (1)
- The pipeline inlet region was from the pipeline entrance to the left annular gap entrance, and the pressure showed a trend of decreasing first and then increasing. This was mainly due to the fact that the average water velocity in the pipeline was almost the same before the water flow contacted the left pipe vehicle. According to the energy equation, when the kinetic energy and potential energy were unchanged, the pressure energy was reduced due to the existence of the drag loss along the path, so the pressure value was reduced accordingly. When the water flow approached the pipe vehicle, the water flow velocity blocked by the pipe vehicle decreased rapidly and part of the kinetic energy was converted into pressure energy, so the pressure increased.
- (2)
- In the left annular gap region, the pressure along the positive direction of the Z-axis showed a trend of first decreasing and then increasing, but in the right annular gap, the pressure value gradually decreased. This was mainly because the water flow was blocked by the end face of the pipe vehicle at the entrance of the annular gap, so the pressure value was high. Constrained by the annular gap, the velocity of the water flow in the annular gap was relatively stable; that is, the kinetic energy change was relatively small. However, due to the influence of the viscous resistance near the pipe vehicle wall and the pipeline wall, the total energy of the water flow was reduced, meaning that the pressure energy was reduced, and the pressure gradually decreased. The blocking effect of the right pipe vehicle affected the pressure field near the exit of the left annular gap, and the pressure value at the exit of the left annular gap therefore increased. However, the water flowing out of the right annular gap was no longer blocked by obstacles, and so there was no pressure increase at the outlet of the right annular gap.
- (3)
- In the two-pipe vehicle spacing region, the pressure change was small when the two-pipe vehicles spacing was 0.5 l. With the increase of the vehicle spacing, the pressure in the two-pipe vehicles spacing showed a gradually increasing trend along the positive direction of the Z-axis. According to the above analysis, it can be determined that the change of the water flow velocity in the spacing was small when the distance between the two-pipe vehicles was 0.5 l, the change in kinetic energy was relatively small, and the change in pressure energy was also small, and so the pressure change in the two-pipe vehicle was small. When the vehicle spacing was greater than 0.5 l, the water flow velocity gradually decreased along the positive direction of the Z-axis due to the blocking effect of the right-hand pipe vehicle, the kinetic energy was gradually converted into pressure energy and the pressure gradually increased. Therefore, the pressure in the workshop gradually increased along the positive direction of the Z-axis.
- (4)
- The pipeline exit region was from the right annular gap exit to the pipeline outlet, and the pressure showed a trend of increasing first and then decreasing along the positive direction of the Z-axis. This was mainly due to the flow of water from the right annular gap forming a high-speed backflow region near the end face of the pipe vehicle. The backflow region had a higher water flow velocity, so the kinetic energy was larger and the pressure energy was correspondingly lower. The backflow region expanded downstream and the water flow velocity decreased, so the kinetic energy decreased and the corresponding pressure energy increased. When it was sufficiently far away from the right pipe vehicle, the water flow gradually stabilized and the velocity value remained unchanged; that is, the kinetic energy remained unchanged, but the simultaneous loss of resistance gradually reduced the pressure energy, and so the pressure decreased accordingly.
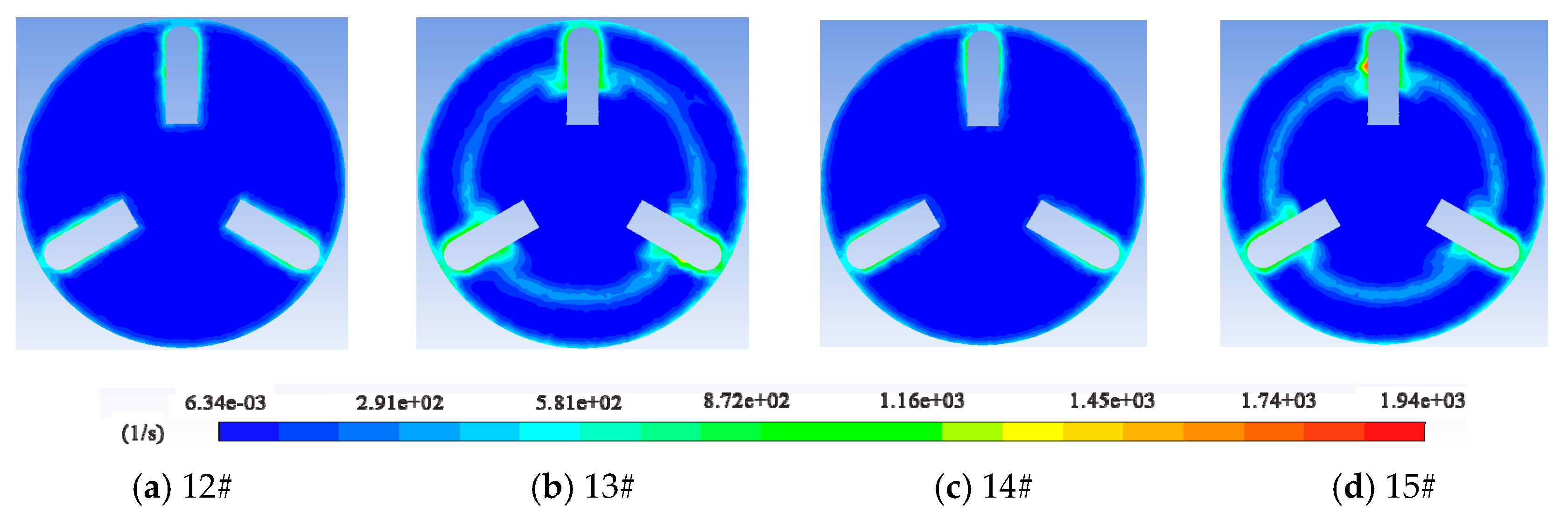
4.3. Distribution of Vorticity
5. Verification of the Simulated Results
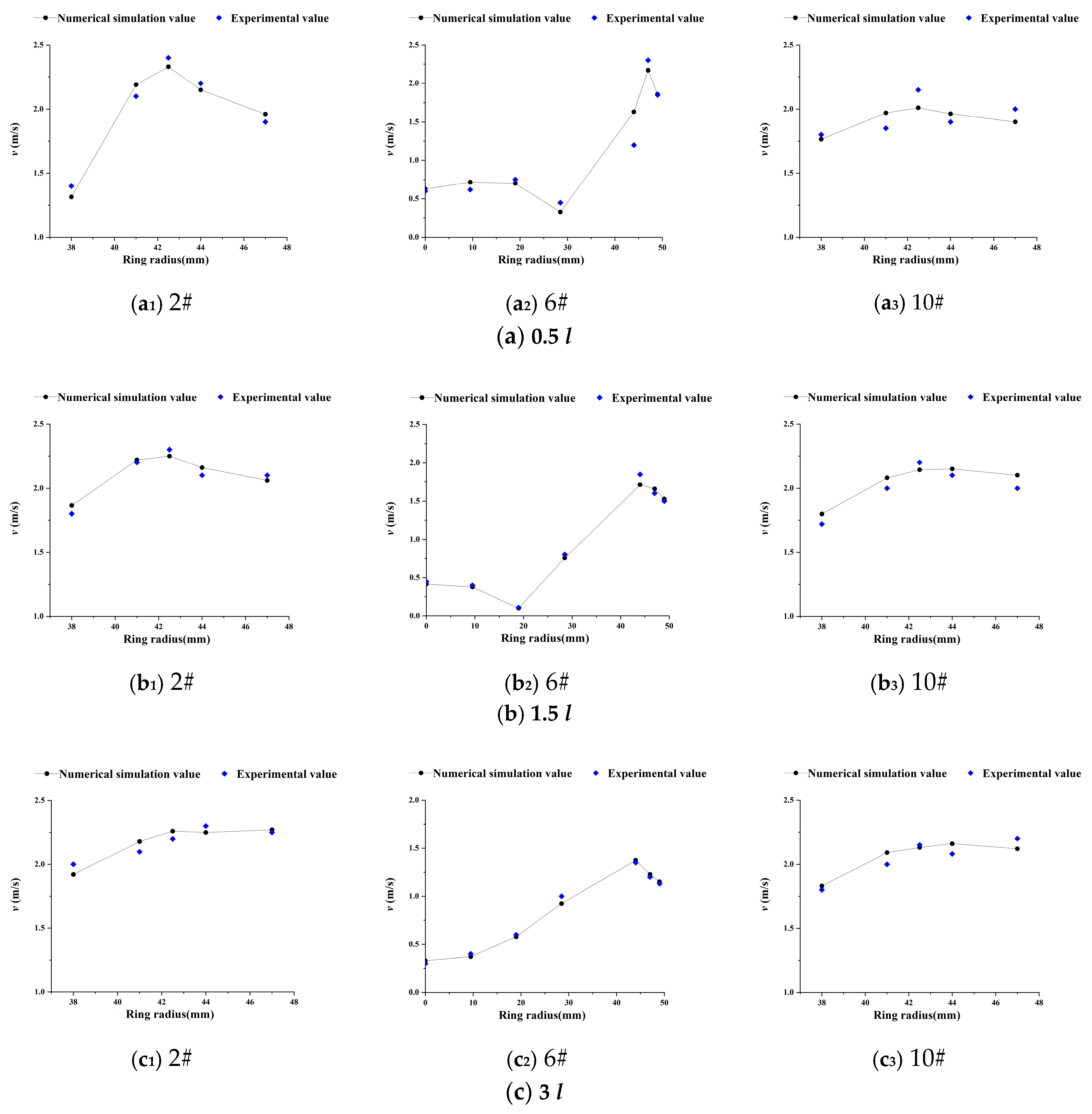
5.1. Velocity Distribution
5.2. Pressure Distribution
6. Conclusions
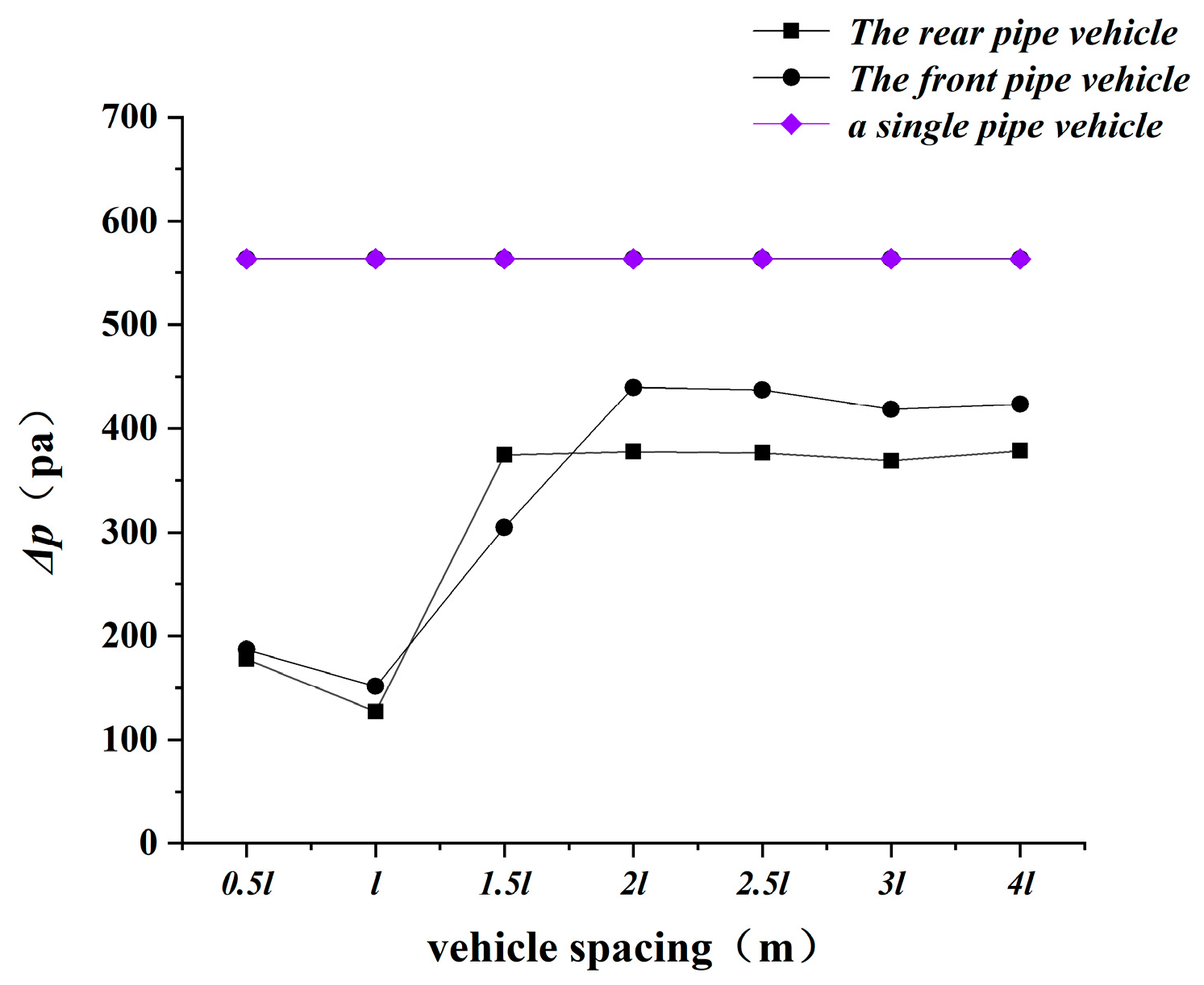
- Compared with a single-pipe vehicle, the water flow and pressure change rules of the pipeline inlet region, annular gap region and the pipeline outlet region of the two-pipe vehicles are the same. With the increase of the number of pipe vehicles, the change of the water flow velocity value is relatively small, and the change of the internal pressure value of the pipeline is large. This provides a certain reference for future research on the changes of water flow and pressure distribution when multiple vehicles are stationary in the pipeline.
- Under different vehicle spacing conditions, the velocity of the annular gap along the direction of water flow shows a trend of increasing first, then decreasing and finally increasing; from the pipe vehicle wall to the pipe wall, the water flow velocity shows an increase and then a decrease. As the vehicle spacing gradually increases, the flow field in the spacing is gradually weakened by the influence of the two-pipe vehicles. When the vehicle spacing reaches 4 l, the interaction between the two-pipe vehicles is negligible.
- The pressure changes in the pipeline along the water flow direction are approximately the same under different vehicle spacing conditions. In the pipeline inlet region, the pressure gradually decreases along with the pipe vehicle. In the annular gap of the rear pipe vehicle, the pressure shows a trend of decreasing first and then increasing, but in the annular gap of the front pipe vehicle, the pressure showed a gradually decreasing trend. When the vehicle spacing is 0.5 l, the pressure change in the spacing is small. As the vehicle spacing gradually increases, the pressure appears to gradually increase along the direction of the water flow. In the pipeline outlet region, the pressure shows a trend of increasing first and then decreasing.
- As the vehicle spacing increases, the pressure difference decreases first and then increases and finally gradually stabilizes. The change law of the starting acceleration of the two-pipe vehicles under different vehicle spacings is consistent with the change law of pressure difference.
- The vorticity value is large near the entrance and exit of the annular gap and around the support bodies, and there is no vortex shedding in the pipeline under different vehicle spacings. The generation and dissipation of vortices can be reduced by simplifying the support body structure and optimizing the shape of the end face of the pipe vehicle.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hodgson, G.W.; Charles, M.E. The pipeline flow of capsules. Can. J. Chem. Eng. 1963, 42, 43–45. [Google Scholar]
- Kruyer, J.; Redberger, P.G.; Ellis, H.S. The pipeline flow of capsules. J. Fluid Mech. 1967, 30, 513–531. [Google Scholar] [CrossRef]
- Brown, R.A.S. Capsule pipeline research at the Alberta Research Council, 1985–1978. J. Pipeline 1987, 6, 75–82. [Google Scholar]
- Charles, M.E. Theoretical analysis of the concentric flow of cylindrical forms. Can. J. Chem. Eng. 1963, 41, 46–51. [Google Scholar]
- Ellis, H.S. An experimental investigation of the transport by water of single cylindrical and spherical capsules with density equal to that of the water. Can. J. Chem. Eng. 1964, 42, 1–8. [Google Scholar] [CrossRef]
- Van den Kroonenberg, H.H. A Mathematical Model for Concentric Horizontal Capsule Transport. Can. J. Chem. Eng. 1978, 56, 538–543. [Google Scholar] [CrossRef] [Green Version]
- Latto, B.; Chow, K.W. Hydrodynamic transport of cylindrical capsules in a vertical pipeline. Can. J. Chem. Eng. 1982, 60, 713–722. [Google Scholar] [CrossRef]
- Liu, H.; Graze, H.R. Lift and drag on stationary capsule in pipeline. J. Hydraul. Eng. 1983, 109, 28–47. [Google Scholar] [CrossRef]
- Liu, H.; Noble, J.S.; Wu, J.; Zuniga, R. Economics of coal log pipeline for transporting coal. Transp. Res. 1998, 32, 377–391. [Google Scholar] [CrossRef]
- Liu, H.; Wu, J.P. Economic Feasibility of Using Hydraulic Pipeline to Transport Grain in the Midwest of the United States; Freight Pipeline (Proc. 6th Int. Symp, on Freight Pipelines); Hemisphere Publishing Corp: New York, NY, USA, 1990; pp. 135–140. [Google Scholar]
- Liu, H.; Richards, J. Hydraulics of stationary capsule in pipe. J. Hydraul. Eng. 1994, 120, 22–40. [Google Scholar] [CrossRef]
- Tomita, Y.; Yamamoto, M.; Funatsu, K. Motion of a single capsule in a hydraulic pipeline. J. Fluid Mech. 1986, 171, 495–508. [Google Scholar] [CrossRef]
- Lenau, C.W.; El-Bayya, M.M. Unsteady flow in hydraulic capsule pipeline. J. Fluid Eng. 1996, 122, 1168–1173. [Google Scholar] [CrossRef]
- Vlasak, P. An experimental investigation of capsules of anomalous shape conveyed by liquid in a pipe. Powder Technol. 1999, 104, 207–213. [Google Scholar] [CrossRef]
- Quadrio, M.; Luchini, P. Direct numerical simulation of the turbulent flow in a pipe with annular cross section. Eur. J. Mech. 2002, 21, 413–427. [Google Scholar] [CrossRef]
- Mohamed, F.; Khalil, S.Z.; Kassab, I.G. Turbulent flow around single concentric long capsule in a pipe. Appl. Math. Model 2009, 34, 2000–2017. [Google Scholar]
- Asim, T.; Mishra, R. Computational fluid dynamics based optimal design of hydraulic capsule pipelines transporting cylindrical capsules. Powder Technol. 2016, 295, 180–201. [Google Scholar] [CrossRef] [Green Version]
- Asim, T.; Mishra, R. Development of a design methodology for hydraulic pipelines carrying rectangular capsules. Int. J. Press. Ves. Pip. 2016, 146, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Asim, T.; Mishra, R. Optimal design of hydraulic capsule pipeline transporting spherical capsules. Can. J. Chem. Eng. 2016, 94, 966–979. [Google Scholar] [CrossRef]
- Zhang, X.L.; Sun, X.H.; Li, Y.Y. 3-D numerical investigation of the wall-bounded concentric annulus flow around a cylindrical body with a special array of cylinders. J. Hydrodyn. 2015, 27, 120–130. [Google Scholar] [CrossRef]
- Sun, X.H.; Li, Y.Y.; Yan, Q.F. Experimental study on starting conditions of the hydraulic transportation on the piped carriage. In Proceedings of the 20th National Conference on Hydrodynamics, Taiyuan, China, 23–25 August 2007; pp. 425–431. [Google Scholar]
- Wang, R.; Sun, X.H.; Li, Y.Y. Transportation characteristics of piped carriage with different Reynolds numbers. J. Drain Irrig. Mach. Eng. 2011, 29, 343–346. [Google Scholar]
- Li, Y.Y.; Sun, X.H. Mathematical model of the piped vehicle motion in piped hydraulic transportation of tube-contained raw material. Math. Probl. Eng. 2019, 2019, 1023–1033. [Google Scholar] [CrossRef]
- Wang, J.; Sun, X.H.; Li, Y.Y. Analysis of pressure characteristics of tube-contained raw material pipeline hydraulic transportation under different discharges. In Proceedings of the International Conference on Electrical, Mechanical and Industrial Engineering (ICEMIE), Phuket, Thailand, 24–25 April 2016; pp. 44–46. [Google Scholar]
- Li, Y.Y.; Sun, X.H.; Yan, Y.X. Hydraulic characteristics of tube-contained raw material hydraulic transportation under different loads on the piped carriage. Trans. Chin. Soc. Agric. Mach. 2008, 39, 93–96. [Google Scholar]
- Jing, Y.H. Characteristics of Slit Flow Velocity by the Formation of Stable Moving Piped Carriage with Different Diameter in Straight Piped Segments. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2014. [Google Scholar]
- Yang, X.N. Study on the Character of Spiral Flow Caused by Different Length Guide Vanes. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2013. [Google Scholar]
- Zhang, C.J.; Sun, X.H.; Li, Y.Y. Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines. Water 2018, 10, 1378. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.F. Research on the Numerical Simulation of the Velocity of the Concentric Annular Gap Spiral Flow around the Stationary Column in the Horizontal Straight Pipeline. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2018. [Google Scholar]
- Zhang, X.L.; Sun, X.H.; Li, Y.Y.; Xi, X.N.; Guo, F.; Zheng, L.J. Numerical investigation of the concentric annulus flow around a cylindrical body with contrasted effecting factors. J. Hydrodyn. 2015, 27, 273–285. [Google Scholar] [CrossRef]
- Li, Y.Y.; Sun, X.H.; Xu, F. Numerical simulation on the piped hydraulic transportation of tube-contained raw material based on FLOW-3D. Syst. Eng.-Theory Pract. 2013, 33, 262–266. [Google Scholar]
- Feng, J.; Huang, P.Y.; Joseph, D.D. Dynamic simulation of the motion of capsules in pipelines. J. Fluid Mech. 1995, 286, 201–227. [Google Scholar] [CrossRef]
- Zhang, C.J.; Sun, X.H.; Li, Y.Y.; Zhang, X.L.; Zhang, X.Q.; Yang, X.N.; Li, F. Hydraulic Characteristics of Transporting a Piped Carriage in a Horizontal Pipe Based on the Bidirectional Fluid-Structure Interaction. Math. Probl. Eng. 2018, 2018, 43–60. [Google Scholar] [CrossRef]
- Bearman, P.W.; Wadcock, A.J. The interaction between a pair ofcircular cylinders normal to a stream. J. Fluids Struct. 1973, 61, 499–511. [Google Scholar]
- Zdravkovich, M.M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Cui, W.Z.; Zhang, X.T.; Li, Z.X.; Li, H.; Liu, Y. Three-dimensional numerical simulation of flow around combined pier based on detached eddy simulation at high Reynolds numbers. Int. J. Heat Technol. 2017, 35, 91–96. [Google Scholar] [CrossRef]
- Alam, M.M. Lift Forces Induced by the Phase Lag Between the Vortex Sheddings from Two Tandem Bluff Bodies. J. Fluid Struct. 2016, 65, 217–237. [Google Scholar] [CrossRef]
- Carmo, B.S.; Meneghini, J.R. Numerical investigation of the flow around two circular cylinders in tandem. J. Fluid Struct. 2006, 22, 979–988. [Google Scholar] [CrossRef]
- Rahimi, H.; Schepers, J.G.; Shen, W.Z.; Ramos García, N.; Schneider, M.S.; Micallef, D.; Simao Ferreira, C.J.; Jost, E.; Klein, L.; Herráez, I. Evaluation of different methods for determining the angle of attack on wind turbine blades with CFD results under axial inflow conditions. Renew. Energy 2018, 125, 866–876. [Google Scholar] [CrossRef] [Green Version]
- Magdalena, T.; Jarosław, B. The Impact of the Strength of Roof Rocks on the Extent of the Zone with a High Risk of Spontaneous Coal Combustion for Fully Powered Longwalls Ventilated with the Y-Type System—A Case Study. Appl. Sci. 2019, 9, 53152019. [Google Scholar]
- Magdalena, T.; Jarosław, B. Analysis of the Impact of Auxiliary Ventilation Equipment on the Distribution and Concentration of Methane in the Tailgate. Energies 2018, 11, 3076. [Google Scholar]
- Wojciech, S. The basic equations of fluid mechanics in form characteristic of the finite volume method. Technol. Sci. 2011, 14, 299–313. [Google Scholar]
- Yakhot, V.; Orzag, S.A. Renormalization group analysis of turbulence: Basic theory. J. Sci. Comput. 1986, 1, 3–11. [Google Scholar] [CrossRef]






| Velocity Inlet (m/s) | Re | k (m2/s2) | ε (m2/s3) | I | l0 (m) |
|---|---|---|---|---|---|
| 1.03 | 115,513 | 0.0024 | 0.0028 | 0.0378 | 0.007 |
| Rear Pipe Vehicle l (mm) × Dc (mm) | Front Pipe Vehicle l (mm) × Dc (mm) | Q (m3/h) | L (mm) | Condition |
|---|---|---|---|---|
| 150 × 70 | 150 × 70 | 30 | 0.5 l/l/1.5 l/2 l/2.5 l/3 l/4 l | Static |
| L (mm) | Fitting Formula | R2 |
|---|---|---|
| 0.5 l | Z = −0.0316Y2 + 2.7482Y − 57.47 | 0.9458 |
| 1.5 l | Z = −0.0133Y2 + 1.509Y − 22.601 | 0.9211 |
| 3 l | Z = −0.0073Y2 + 0.6558Y − 12.94 | 0.9823 |
| L (mm) | Fitting Formula | R2 |
|---|---|---|
| 0.5 l | Z = −0.008Y2 + 0.6942Y − 13.039 | 0.9552 |
| 1.5 l | Z = −0.0094Y2 + 0.8295Y − 16.179 | 0.9947 |
| 3 l | Z = −0.009Y2 + 0.7957Y − 15.38 | 0.9791 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Sun, X.; Li, Y. Numerical Simulation of the Flow Field Characteristics of Stationary Two-Pipe Vehicles under Different Spacings. Water 2020, 12, 2158. https://doi.org/10.3390/w12082158
Jia X, Sun X, Li Y. Numerical Simulation of the Flow Field Characteristics of Stationary Two-Pipe Vehicles under Different Spacings. Water. 2020; 12(8):2158. https://doi.org/10.3390/w12082158
Chicago/Turabian StyleJia, Xiaomeng, Xihuan Sun, and Yongye Li. 2020. "Numerical Simulation of the Flow Field Characteristics of Stationary Two-Pipe Vehicles under Different Spacings" Water 12, no. 8: 2158. https://doi.org/10.3390/w12082158
APA StyleJia, X., Sun, X., & Li, Y. (2020). Numerical Simulation of the Flow Field Characteristics of Stationary Two-Pipe Vehicles under Different Spacings. Water, 12(8), 2158. https://doi.org/10.3390/w12082158




