A New Set of Local Indices Applied to a Water Network through Demand and Pressure Driven Analysis (DDA and PDA)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Local Performance Indices
2.2. Hydraulic Software Solvers
2.2.1. Demand Driven Analysis
2.2.2. Pressure Driven Analysis
2.2.3. Simulation Settings and Hypotheses
3. Results and Discussion
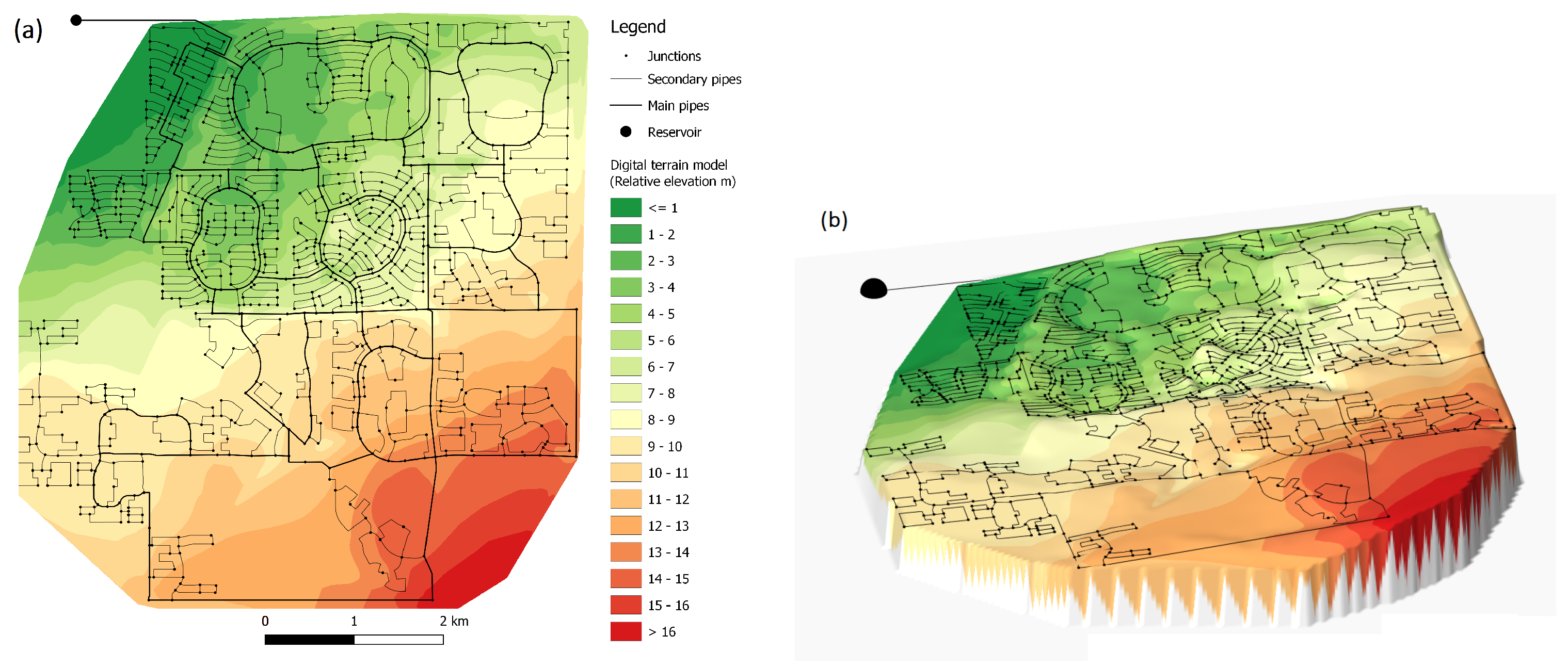
3.1. Test Network and Requested Condition
3.2. Peak Coefficients
3.3. Simulation Results
- The network is subjected to stress for which it is not designed for, and it works in conditions of excessive demand and, consequently, pressure deficit.
- The required conditions are too stringent and far from reality.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cervarolo, G.; Mendicino, G.; Senatore, A. Re-modulating water allocation in a complex multi-reservoir system under current and climate change scenarios. Eur. Water 2012, 37, 47–57. [Google Scholar]
- Maiolo, M.; Mendicino, G.; Pantusa, D.; Senatore, A. Optimization of Drinking Water Distribution Systems in Relation to the Effects of Climate Change. Water 2017, 9, 803. [Google Scholar] [CrossRef]
- Davis, M.J.; Janke, R. Patterns in potential impacts associated with contamination events in water distribution systems. J. Water Resour. Plan. Manag. 2011, 137, 1–9. [Google Scholar] [CrossRef]
- Gheisi, A.; Forsyth, M.; Naser, G. Water distribution systems reliability: A review of research literature. J. Water Resour. Plann. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Loucks, D.P. Quantifying System Sustainability Using Multiple Risk Criteria: Risk, Reliability, Uncertainty, and Robustness of Water Resources Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Maiolo, M.; Pantusa, D. A methodological proposal for the evaluation of potable water use risk. Water Pract. Technol. 2015, 10, 152–163. [Google Scholar] [CrossRef]
- Maiolo, M.; Pantusa, D.; Chiaravalloti, F.; Carini, M.; Capano, G.; Procopio, A. A New Vulnerability Measure for Water Distribution Network. Water 2019, 10, 1005. [Google Scholar] [CrossRef] [Green Version]
- Maiolo, M.; Pantusa, D. Infrastructure vulnerability index of drinking water supply systems to possible terrorist attacks. Cogent Eng. 2018, 5, 1456710. [Google Scholar] [CrossRef]
- Maiolo, M.; Pantusa, D. Combined reuse of wastewater and desalination for the management of water systems in conditions of scarcity. Water Ecol. 2017, 72, 116–126. [Google Scholar]
- Maiolo, M.; Pantusa, D. A proposal for multiple reuse of urban wastewater. J. Water Reuse Desalin. 2018, 8, 468–478. [Google Scholar] [CrossRef] [Green Version]
- Böhringer, C.; Jochem, P.E. Measuring the immeasurable—A survey of sustainability indices. Ecol. Econ. 2007, 63, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Maiolo, M.; Carini, M.; Capano, G.; Piro, P. Synthetic sustainability index (SSI) based on life cycle assessment approach of low impact development in the Mediterranean area. Cogent Eng. 2017, 4, 1410272. [Google Scholar] [CrossRef]
- Maiolo, M.; Martirano, G.; Morrone, P.; Pantusa, D. Assessment criteria for a sustainable management of water resources. Water Pract. Technol. 2006, 1. [Google Scholar] [CrossRef]
- Maiolo, M.; Pantusa, D. An optimization procedure for the sustainable management of water resources. Water Sci. Technol. Water Supply 2016, 16, 61–69. [Google Scholar] [CrossRef]
- Maiolo, M.; Pantusa, D. Sustainable Water Management Index, SWaM_Index. Cogent Eng. 2019, 6, 1603817. [Google Scholar] [CrossRef]
- Agathokleous, A.; Christodoulou, C.; Christodoulou, S.E. Topological Robustness and Vulnerability Assessment of Water Distribution Networks. Water Resour. Manag. 2017, 31, 4007–4021. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G.C.; Maier, H.R. Improved genetic algorithm optimization of water distribution system design by incorporating domain knowledge. Environ. Model. Softw. 2015, 69, 370–381. [Google Scholar] [CrossRef]
- Bragalli, C.; Fortini, M.; Todini, E. Data assimilation in water distribution systems. Procedia Eng. 2017, 186, 506–513. [Google Scholar] [CrossRef]
- Candelieri, A.; Giordani, I.; Archetti, F. Supporting Resilience Management of Water Distribution Networks through Network Analysis and Hydraulic Simulation. In Proceedings of the 21st International Conference on Control Systems and Computer Science, Bucharest, Romania, 29–31 May 2017. [Google Scholar]
- Candelieri, A.; Soldi, D.; Archetti, F. Network analysis for resilience evaluation in water distribution networks. Environ. Eng. Manag. J. 2015, 14, 1261–1270. [Google Scholar] [CrossRef]
- Dai, J.; Wu, S.; Han, G.; Weinberg, J.; Xie, X.; Wu, X.; Song, X.; Jia, B.; Xue, W.; Yang, Q. Water-energy nexus: A review of methods and tools for macro-assessment. Appl. Energy 2018, 210, 393–408. [Google Scholar] [CrossRef]
- D’Ambrosio, C.; Lodi, A.; Wiese, S.; Bragalli, C. Mathematical programming techniques in water network optimization. Eur. J. Oper. Res. 2015, 243, 774–788. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Complex network and fractal theory for the assessment of water distribution network resilience to pipe failures. Water Sci. Technol. Water Supply 2017, 18, 767–777. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.; Venticinque, S. An automated tool for smart water network partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Eliades, D.G.; Kiriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar]
- Ferrari, G.; Savíc, D.; Becciu, G. Graph-theoretic approach and sound engineering principles for design of district metered areas. J. Water Resour. Plann. Manag. 2014, 140, 04014036. [Google Scholar] [CrossRef] [Green Version]
- Hamiche, A.M.; Stambouli, A.B.; Flazi, S. A review of the water-energy nexus. Renew. Sustain. Energy Rev. 2016, 65, 04016047. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. A Graph-Theoretic Framework for Assessing the Resilience of Sectorised Water Distribution Networks. Water Resour. Manag. 2016, 30, 319–331. [Google Scholar] [CrossRef] [Green Version]
- Jayaram, N.; Srinivasan, K. Performance-based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Sa Marques, A. Technical performance evaluation of water distribution networks based on EPANET. Procedia Eng. 2014, 70, 1201–1210. [Google Scholar] [CrossRef] [Green Version]
- Prasad, T.D.; Park, N.S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Sharif, M.N.; Haider, H.; Farahat, A.; Hewage, K.; Sadiq, R. Water Energy Nexus for Water Distribution Systems: A Literature Review. Environ. Rev. 2019. [Google Scholar] [CrossRef]
- Crotty, P.A. Selection and Definition of Performance Indicators for Water and Wastewater Utilities; American Water Works Association: Washington, DC, USA, 2004. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.; Tzatchkov, V.; Alcocer-Yamanaka, V. Performance indices for water network partitioning and sectorization. Water Sci. Technol. Water Supply 2014, 15, 499–509. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.; Tzatchkov, V.; Alcocer-Yamanaka, V. Water Network Sectorization Based on Graph Theory and Energy Performance Indices. J. Water Resour. Plan. Manag. Optim. 2014, 140, 620–629. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J. Water Distribution System Design to Minimize Costs and Maximize Topological and Hydraulic Reliability. J. Water Resour. Plan. Manag. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Mori, K.; Christodoulou, A. Review of sustainability indices and indicators: Towards a new City Sustainability Index (CSI). Environ. Impact Assess. Rev. 2011. [Google Scholar] [CrossRef]
- Shin, S.; Lee, S.; Judi, D.; Parvania, M.; Goharian, E.; McPherson, T.; Burian, S. A systematic review of quantitative resilience measures for water infrastructure systems. Water 2018, 10, 164. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, B.; Lansey, K.; Kang, D. Resilience/availability analysis of municipal water distribution system incorporating adaptive pump operation. J. Hydraul. Eng. 2012, 139, 527–537. [Google Scholar] [CrossRef]
- Caldarola, F.; Maiolo, M. Local indices within a mathematical framework for urban water distribution systems. Cogent Eng. 2019, 6, 1643057. [Google Scholar] [CrossRef]
- Bonora, M.; Caldarola, F.; Maiolo, M.; Muranho, J.; Sousa, J. The new set up of local performance indices into WaterNetGen and applications to Santarèm’s network. Environ. SCI. Proc. 2020, in press. [Google Scholar]
- Bonora, M.; Caldarola, F.; Muranho, J.; Sousa, J.; Maiolo, M. Numerical experimentations for a new set of local indices of a water network. In Proceedings of the 3rd International Conference “Numerical Computations: Theory and Algorithms”; Lecture Notes in Computer Science; Sergeyev, Y.D., Kvasov, D.E., Eds.; Springer: Cham, Switzerland, 2020; Volume 11973. [Google Scholar] [CrossRef]
- Caldarola, F.; Maiolo, M. Algebraic tools and new local indices for water networks: Some numerical examples. In Proceedings of the 3rd International Conference “Numerical Computations: Theory and Algorithms”; Lecture Notes in Computer Science; Sergeyev, Y., Kvasov, D., Eds.; Springer: Cham, Switzerland, 2020; Volume 11973. [Google Scholar] [CrossRef]
- Todini, E. Looped water distribution networks design using a resilience index based on heuristic approach. Urban Water 2000, 12, 115–122. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Rodriguez Varela, J.; Santonastaso, G.; Simone, A.; Tzatchkov, V. Redundancy features of water distribution systems. Procedia Eng. 2017, 186, 412–419. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M. A heuristic design support methodology based on graph theory for district metering of water supply networks. Eng. Optim. 2011, 12, 193–211. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M. A design support metodology for district metering of water supply networks. Presented at the WSDA 12th International Conference, Dothan, AB, USA, 21 December 2011. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G. Individuazione dei settori idrici isolati di una rete idrica di distribuzione con una metodologia basata sulla teoria dei grafi. In La Gestione Delle Reti Idriche, Atti del Convegno “Le Reti Acquedottistiche e di Drenaggio: Progettazione, Manutenzione e Sostenibilità alla Luce Degli Aspetti Economico-Normativi”, Ferrara, Italy, 24 Maggio 2012; Angeli, F., Ed.; Franco Angeli: Milan, Italy. (In Italian)
- Di Nardo, A.; Di Natale, M.; Santonastaso, G. A comparison between different techniques for water network sectorization. Water Sci. Technol. Water Supply 2014, 14, 961–970. [Google Scholar] [CrossRef]
- Caldarola, F.; Maiolo, M. A mathematical investigation on the invariance problem of some hydraulic indices. 2020. Submitted. [Google Scholar]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Sa Marques, A. WaterNetGen—An EPANET extension for automatic water distribution network models generation and pipe sizing. Water Sci. Technol. Water Supply 2012, 12, 117–123. [Google Scholar] [CrossRef]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Sa Marques, A. Pressure Dependent Demand and Leakage Modelling with an EPANET Extension—WaterNetGen. Procedia Eng. 2014, 89, 632–639. [Google Scholar] [CrossRef] [Green Version]
- Wagner, J.M.; Shamir, U.; Mark’s, D.H. Water Distribution Reliability: Simulation Methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef] [Green Version]
- Rossman, L.A. EPANET 2: Users Manualus Environmental Protection Agency; Water Supply and Water Resources Division, National Risk Management Research Laboratory: Cincinnati, OH, USA, 2000. [Google Scholar]
- Kang, D.; Lansey, K.E. Revisiting optimal water-distribution system design: Issues and a heuristic hierarchical approach. J. Water Resour. Plan. Manag. 2012, 138, 208–217. [Google Scholar] [CrossRef]
- Lamberti, P.; Maiolo, M.; Mazzola, R.; Veltri, P. Rapporto sui consumi idropotabili sul finire degli anni ’80. In I Quaderno del Gruppo Nazionale “Consumi idropotabili”; Taglialatela, L., Bertola, P., Eds.; CUEN Editrice: Napoli, Italy, 1994. (In Italian) [Google Scholar]

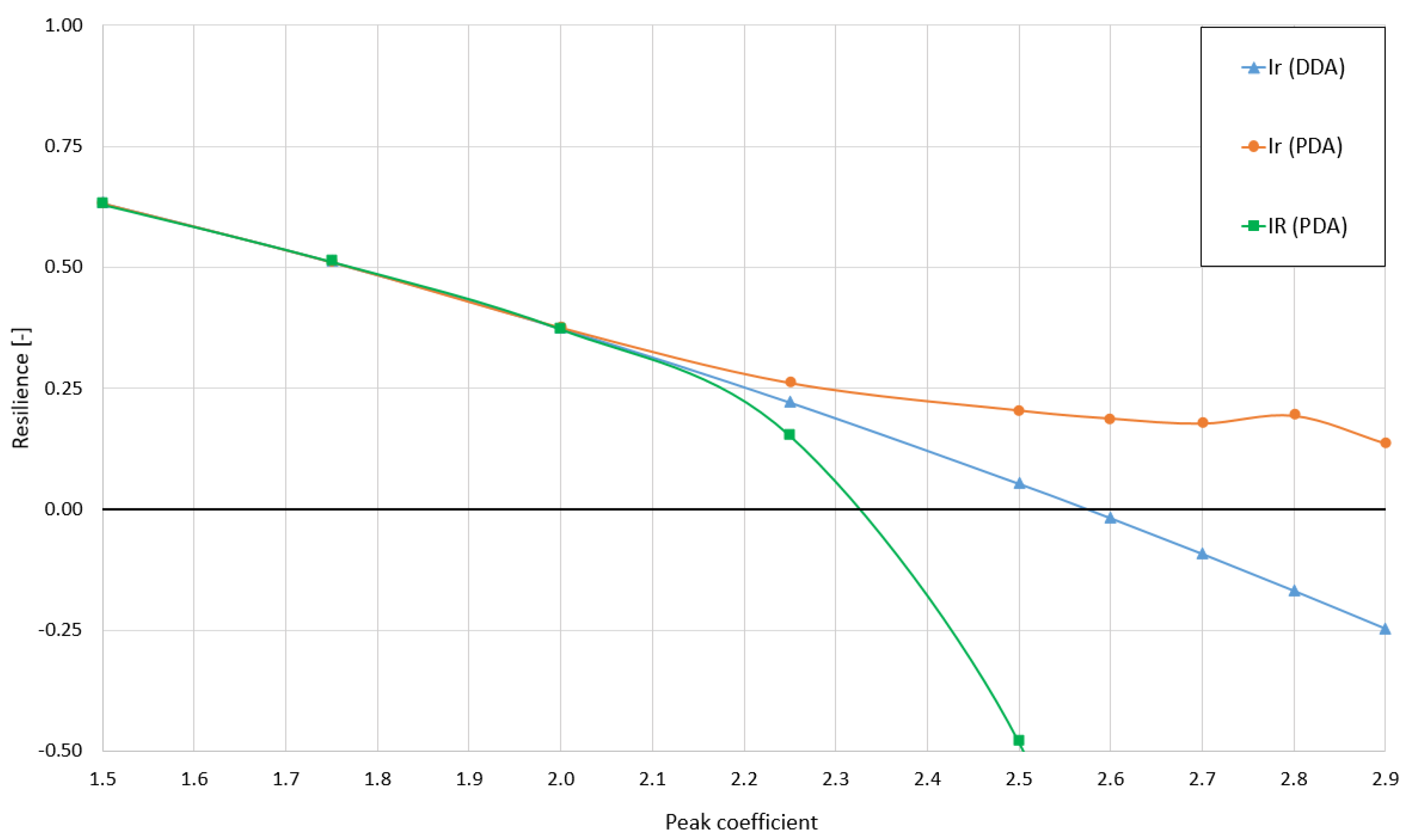




| by DDA | by PDA | by PDA | |
|---|---|---|---|
| 1.50 | 0.632 | 0.632 | 0.629 |
| 1.75 | 0.511 | 0.511 | 0.511 |
| 2.00 | 0.373 | 0.375 | 0.371 |
| 2.25 | 0.221 | 0.261 | 0.152 |
| 2.50 | 0.053 | 0.204 | −0.482 |
| 2.60 | −0.018 | 0.187 | −1.134 |
| 2.70 | −0.092 | 0.177 | −2.842 |
| 2.80 | −0.168 | 0.193 | −17.969 |
| 2.90 | −0.247 | 0.135 | 7.503 |
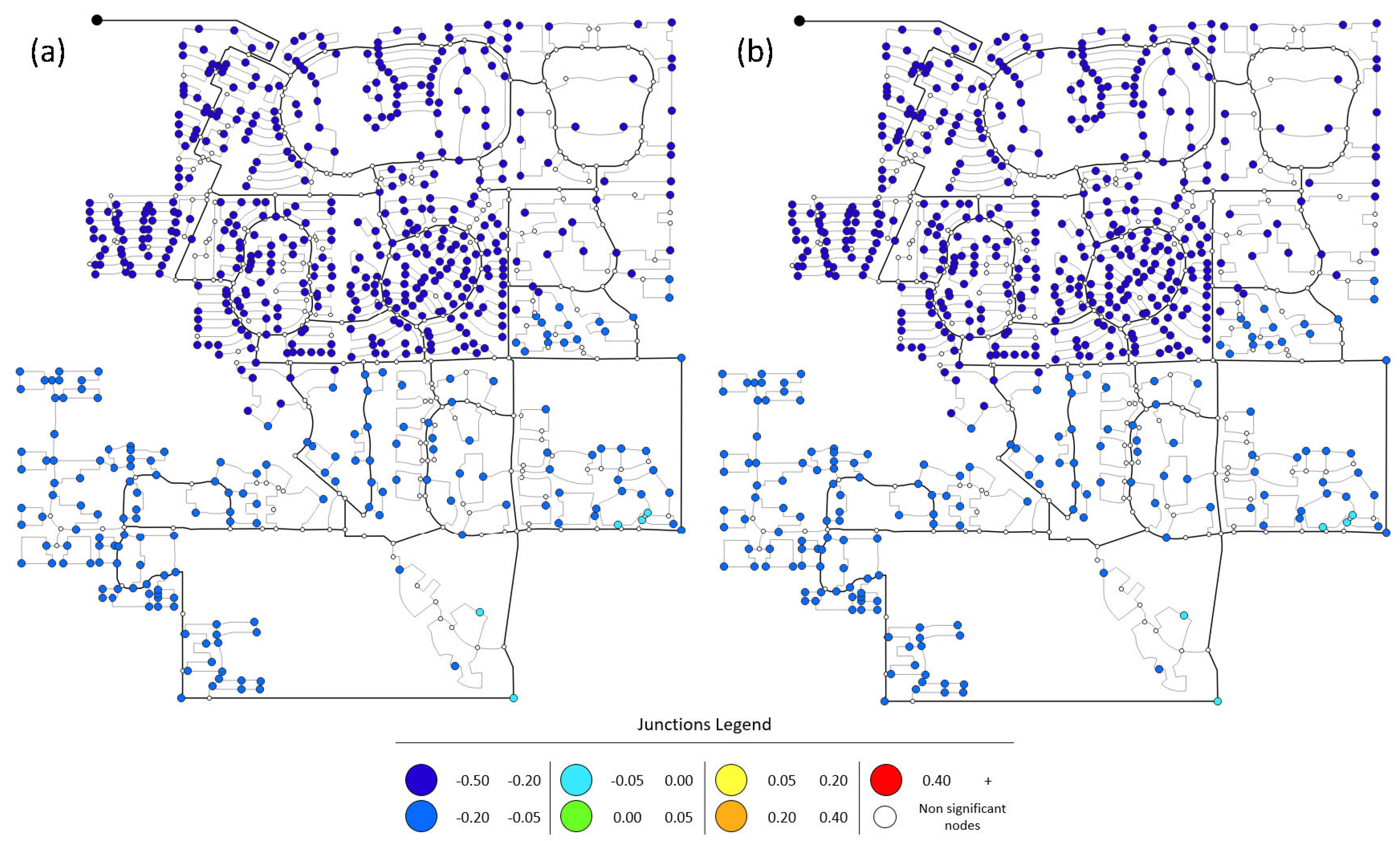
| Range | 1.75, DDA | 1.75, PDA | 2.00, DDA | 2.00, PDA |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 7 | 6 | |
| 5 | 5 | 140 | 141 | |
| 174 | 174 | 203 | 203 | |
| 444 | 444 | 272 | 272 | |
| Not significant | 312 | 312 | 312 | 312 |
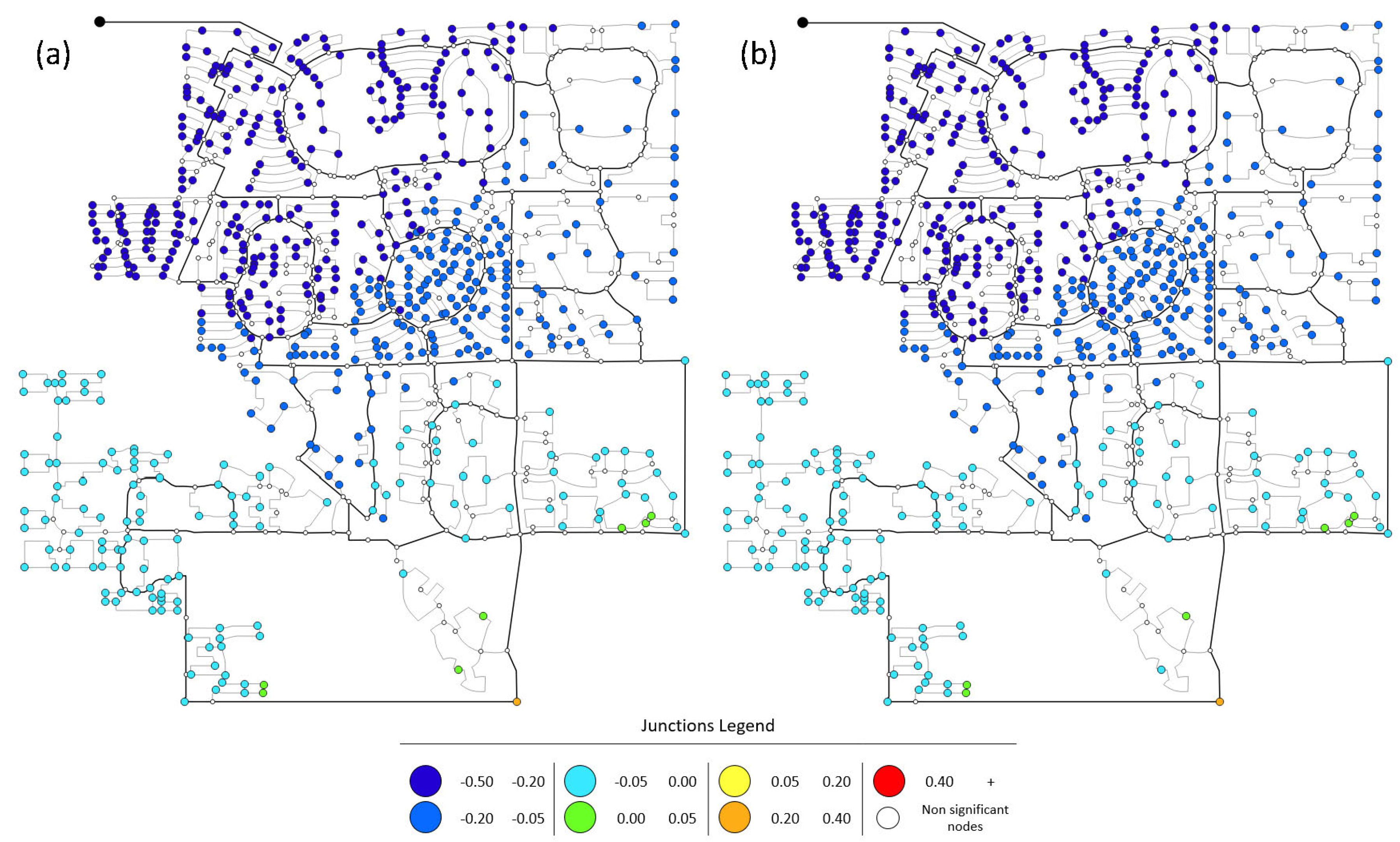
| Range | 2.25, DDA | 2.25, PDA | 2.50, DDA | 2.50, PDA |
|---|---|---|---|---|
| 1 | 1 | 135 | 56 | |
| 69 | 62 | 80 | 120 | |
| 67 | 63 | 75 | 26 | |
| 28 | 32 | 56 | 78 | |
| 148 | 140 | 129 | 159 | |
| 202 | 201 | 81 | 113 | |
| 108 | 124 | 67 | 71 | |
| Not significant | 312 | 312 | 312 | 312 |
| Range | 1.75 | 2.00 | 2.25 | 2.50 |
|---|---|---|---|---|
| 0 | 0 | 1 | 62 | |
| 0 | 0 | 21 | 86 | |
| 0 | 1 | 55 | 39 | |
| 0 | 0 | 40 | 6 | |
| 623 | 622 | 506 | 430 | |
| Not significant | 312 | 312 | 312 | 312 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonora, M.A.; Caldarola, F.; Maiolo, M. A New Set of Local Indices Applied to a Water Network through Demand and Pressure Driven Analysis (DDA and PDA). Water 2020, 12, 2210. https://doi.org/10.3390/w12082210
Bonora MA, Caldarola F, Maiolo M. A New Set of Local Indices Applied to a Water Network through Demand and Pressure Driven Analysis (DDA and PDA). Water. 2020; 12(8):2210. https://doi.org/10.3390/w12082210
Chicago/Turabian StyleBonora, Marco Amos, Fabio Caldarola, and Mario Maiolo. 2020. "A New Set of Local Indices Applied to a Water Network through Demand and Pressure Driven Analysis (DDA and PDA)" Water 12, no. 8: 2210. https://doi.org/10.3390/w12082210







