Quantitative Analysis of the Impact of Meteorological Factors on Reference Evapotranspiration Changes in Beijing, 1958–2017
Abstract
1. Introduction
2. Materials and Methods
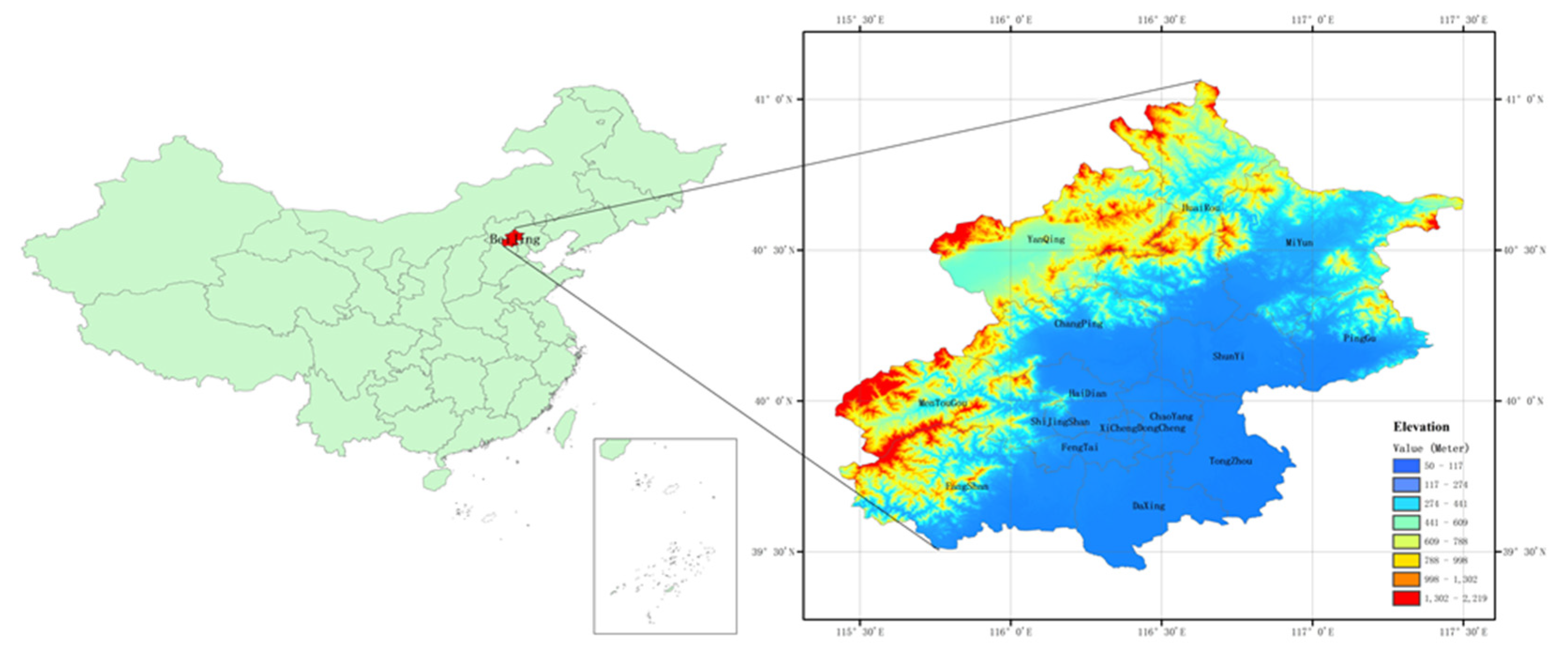
2.1. Study Area
2.2. Calculation of Reference Evapotranspiration
2.3. Sensitivity Analysis
2.4. Determination of Contributions
3. Results
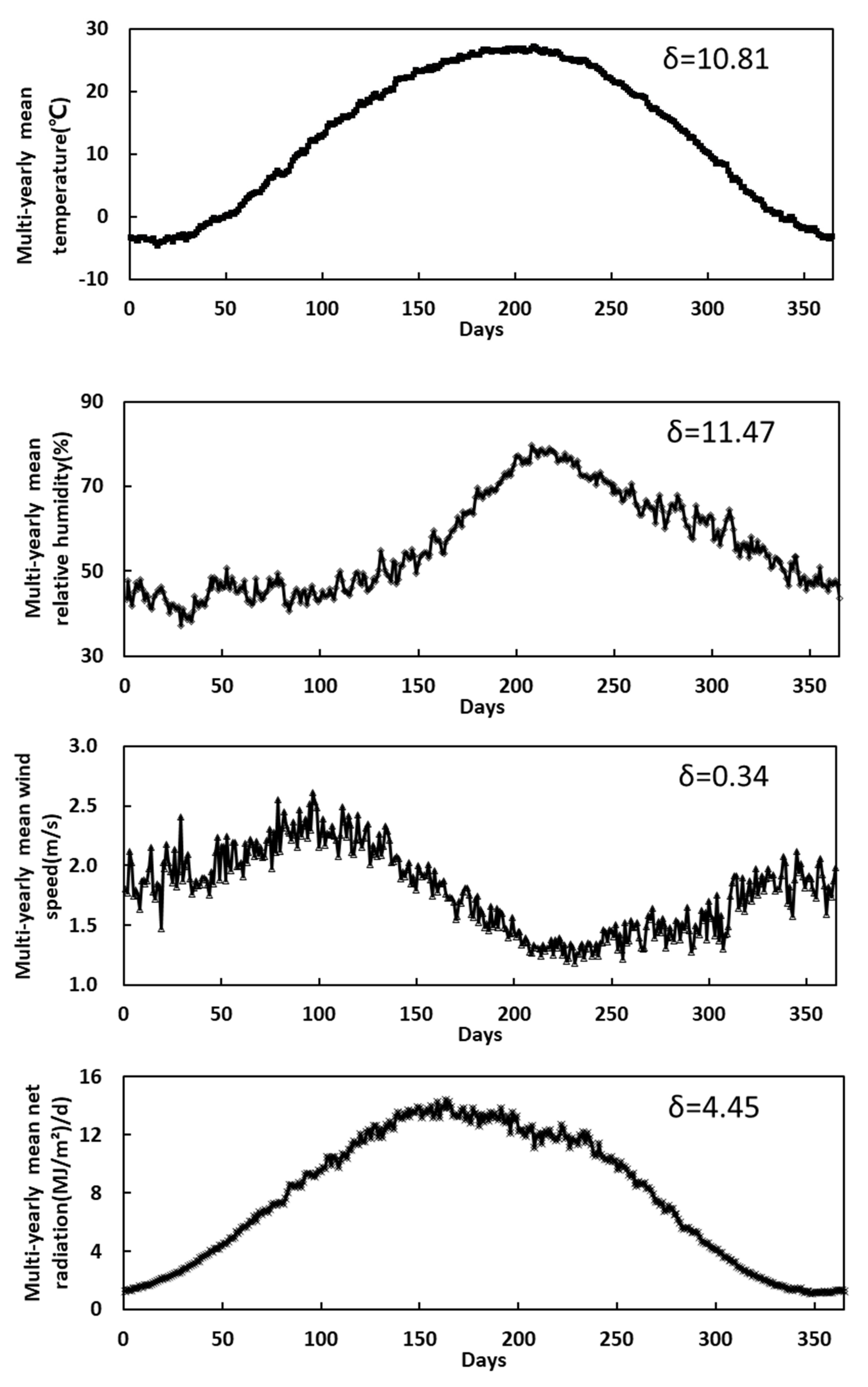
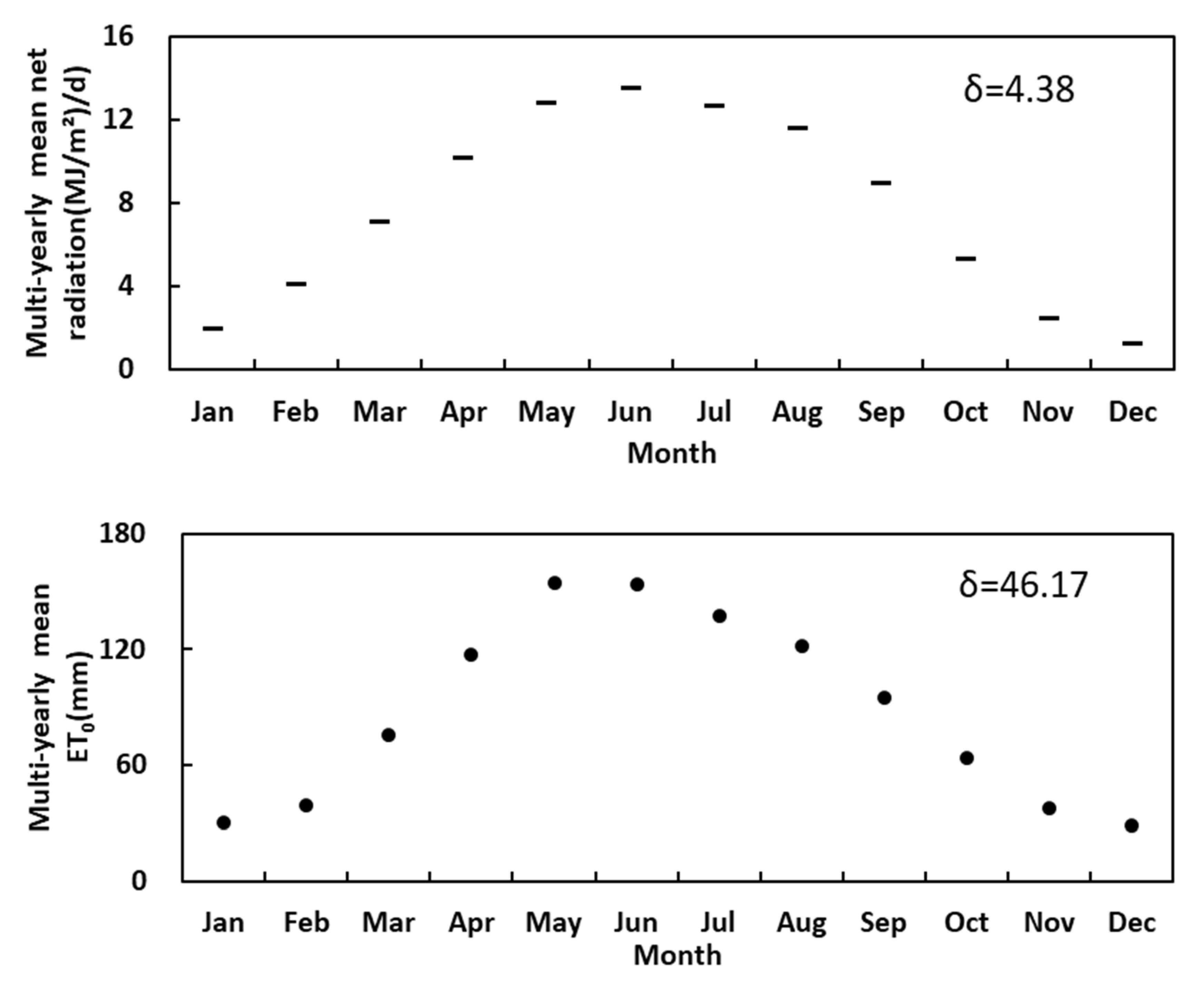
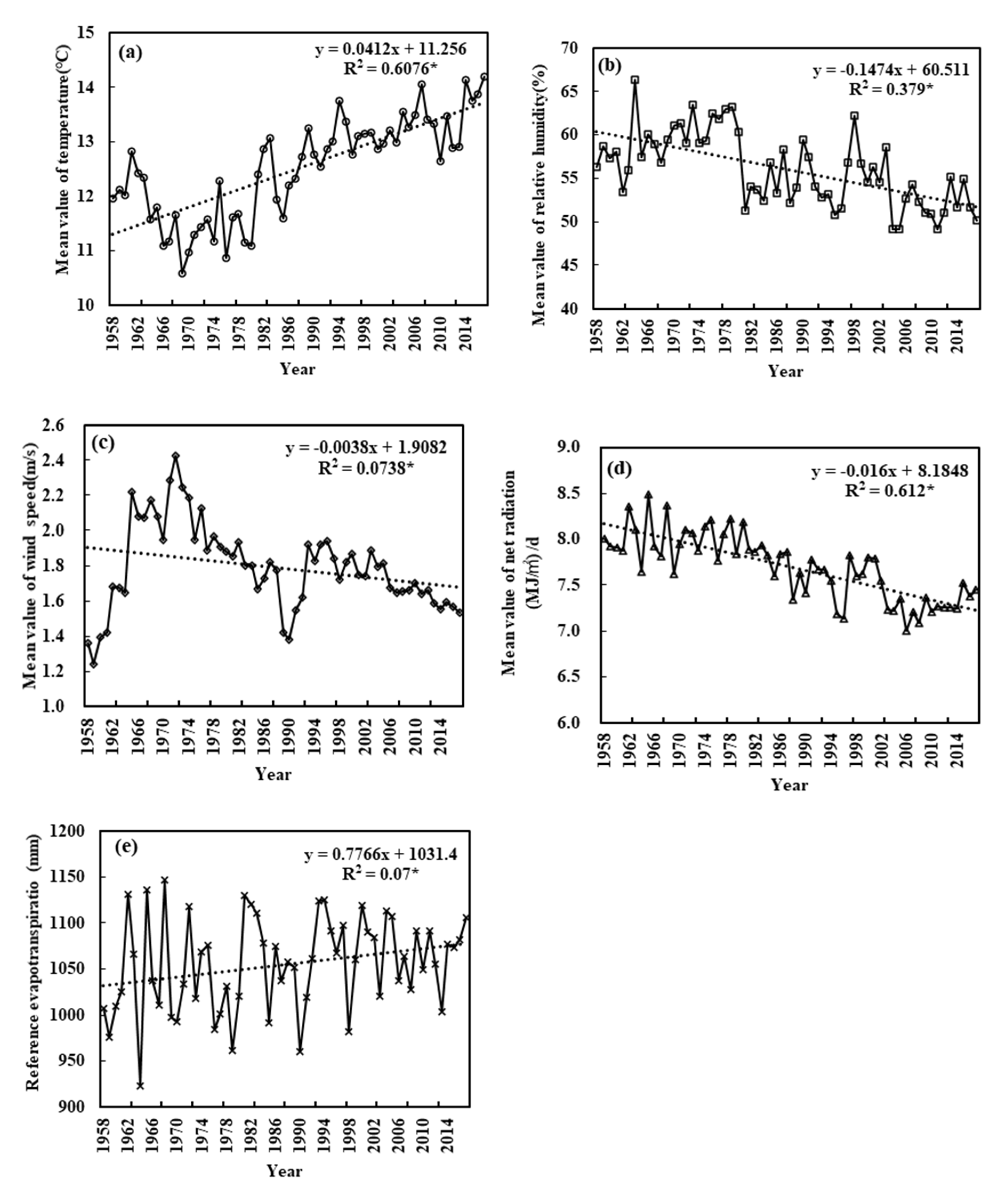
3.1. Changes in Meteorological Factors and ET0 at Different Time Scales
3.1.1. Intra-Annual Variations
3.1.2. Interannual Variations
3.2. Variations in the Sensitivity Coefficients of Meteorological Factors
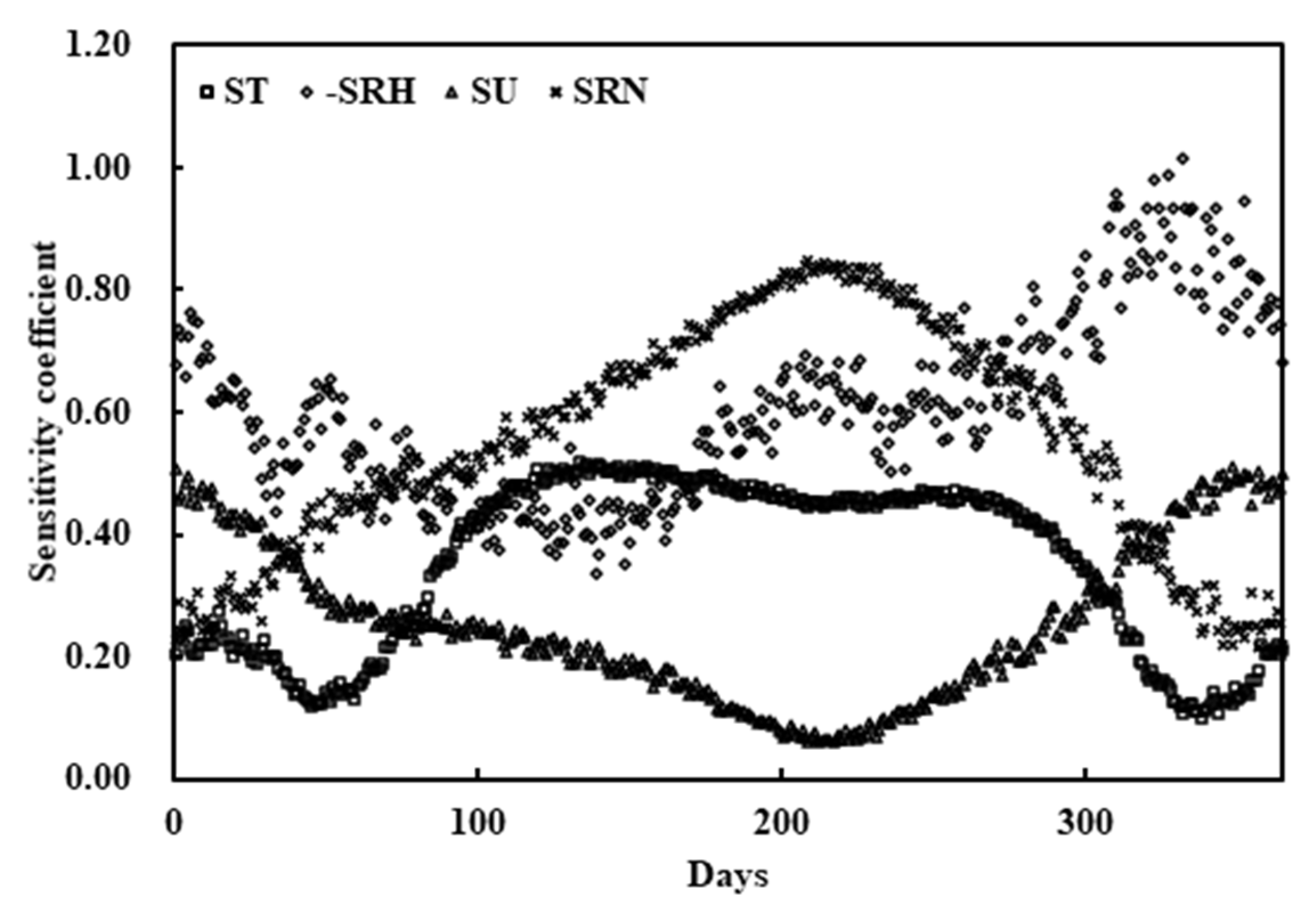
3.2.1. Intra-Annual Variations in Sensitivity Coefficients
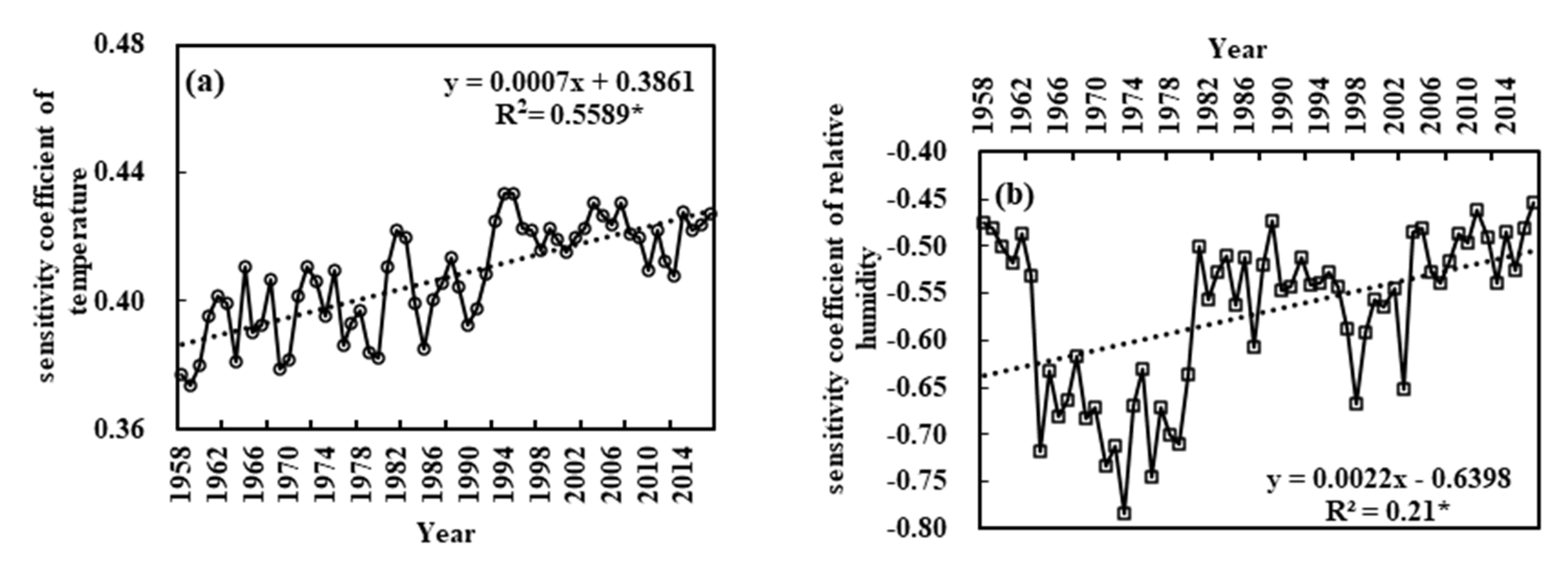
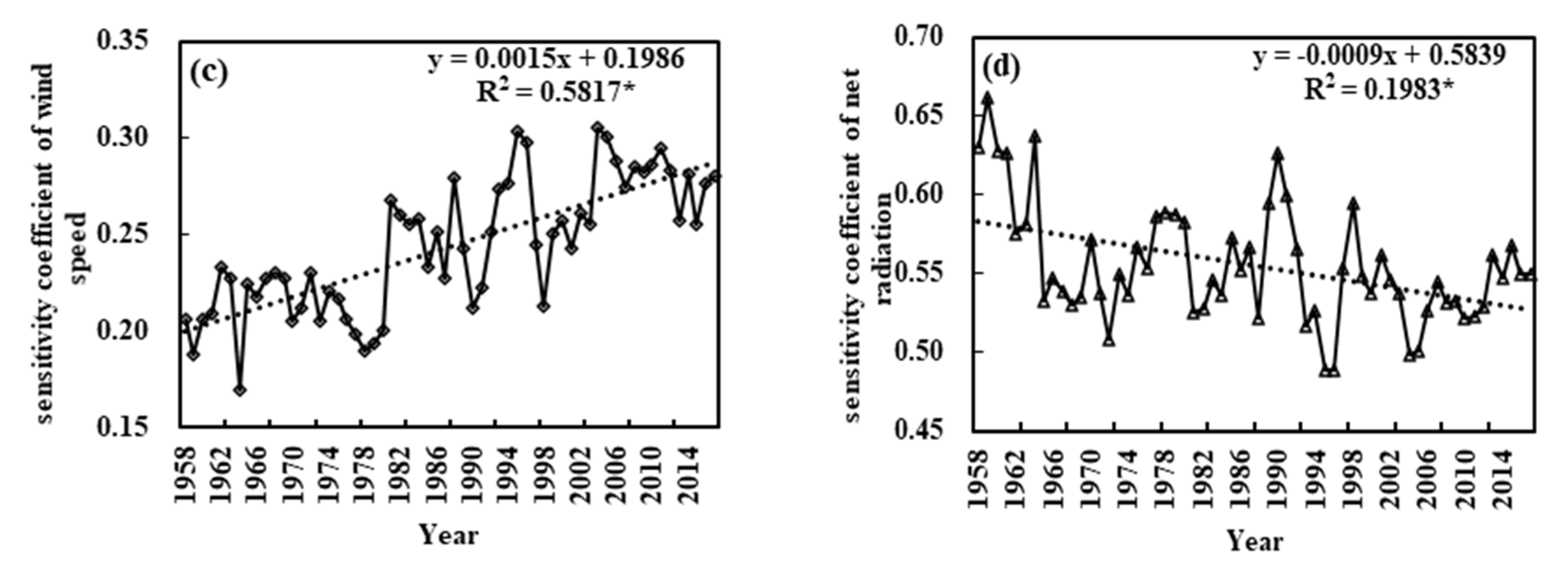
3.2.2. Interannual Variation of Sensitivity Coefficients
3.3. Contributions of Meteorological Factors to Variation in Potential Evapotranspiration
3.3.1. Daily Time Scales
3.3.2. Monthly and Seasonal TIME Scales
3.4. Discussion
4. Conclusions
- (1)
- Over the last 60 years, RH, U and RN values have all declined, and only T has continued to rise. The rise in T and decline in RH are the main reasons underlying the ET0 increase. However, the decline in U and RN hinder further increases of ET0 in Beijing, with RN being the most inhibitory in summer. Determining the main control factors of ET0 change on different time scales will provide a theoretical basis for water resources regulation, irrigation system design and crop water management in Beijing.
- (2)
- The variations of sensitivity coefficients of the four meteorological factors over different time scales has resulted in variation in the main sensitivity factor affecting ET0. Over the course of 1 year, the sensitivity coefficients of four meteorological factors fluctuated greatly, with RH and RN being alternately the most sensitive factor. Between 1958 and 1979, RH was the most sensitive factor, but it has since become RN.
- (3)
- The contributions of the four meteorological factors to ET0 varied on different time scales, reflecting their annual fluctuations. The contributions of T and U were large at the start and the end of the year, while the contributions of RH and RN were dominant mid-year. On interannual scales, the main contributing factors were RH and T.
- (4)
- A limitation of this research is that the application of contribution rate analysis method was only done for Beijing, also, the ET0 response to climate change will differ by region and season because of the large spatiotemporal variability of the sensitivity coefficients and relative change rate. Thus, an important focus area for research will be analyzing the contribution of meteorological factors to changes in ET0 on larger spatial scales and different temporal scales. Meanwhile, it is worth noting that the applicability of the contribution rate method in different climate zones still needs to be discussed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, S.J.; Zhang, B.Z. Advances of evapotranspiration research based on the Penman approach and complementary principle. J. Hydraul. Eng. 2018, 49, 1158–1168. [Google Scholar]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.Q.; De, J.R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. 1948, A193, 120–146. [Google Scholar]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Area from Climatological Irrigation Data; Techical Paper No 1998; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1950; Volume 96, p. 48.
- Taikan, O.; Shinjiro, K. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar]
- Xu, Z.X.; Li, J.Y. A distributed approach for estimating basin evapotranspiration: Comparison of the combination equation and the complementary relationship approaches. Hydrol. Process 2003, 17, 1509–1523. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V.P. Evaluation of three complementary relationship evapotranspiration models by water balance approach to estimate actual regional evapotranspiration in different climatic regions. J. Hydrol. 2005, 308, 105–121. [Google Scholar] [CrossRef]
- Zhang, B.Z.; Xu, D.; Liu, Y.; Chen, H. Review of multi-scale evapotranspiration estimation and spatio-temporal scale expansion. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2015, 31, 8–16. [Google Scholar]
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef]
- Pan, S.F.; Tian, H.Q.; Dangal, S.R.S.; Yang, Q.C.; Yang, J.; Lu, C.Q.; Tao, B.; Ren, W.; Ouyang, Z.Y. Response of global terrestrial evapotranspiration to climate change and increasing atmospheric CO2 in the 21st century. Earth’s Future 2015, 3, 15–35. [Google Scholar] [CrossRef]
- Shukla, J.; Mintz, Y. Influence of land-surface evapotranspiration on the earth’s climate. Science 1982, 215, 1498–1501. [Google Scholar] [CrossRef]
- Haskett, J.D.; Pachepsky, Y.A.; Acock, B. Effect of climate and atmospheric change on soybean water stress: A study of Iowa. Ecol. Model. 2000, 135, 277. [Google Scholar] [CrossRef]
- Zuo, D.P.; Xu, Z.X.; Yang, H. Spatiotemporal variations and abrupt changes of potential evapotranspiration and its sensitivity to key meteorological variables in the Wei River basin, China. Hydrol. Process. 2012, 26, 1149–1160. [Google Scholar] [CrossRef]
- Han, S.J.; Hu, H.P. Spatial variations and temporal changes in potential evaporation in the Tarim Basin, northwest China (1960-2006): Influenced by irrigation? Hydrol. Process. 2012, 26, 3041–3051. [Google Scholar] [CrossRef]
- Huang, H.P.; Cao, M.M.; Song, J.X.; Han, Y.P.; Chen, S.S. Temporal and spatial changes of potential evapotranspiration and its influencing factors in China from 1957 to 2012. J. Nat. Resour. 2015, 30, 315–326. [Google Scholar]
- Liu, C.M.; Zhang, D. Temporal and spatial change analysis of the sensitivity of potential evapotranspiration to meteorological influencing factors in China. J. Geogr. Sci. 2011, 66, 579–588. [Google Scholar]
- Li, Y.Z.; Liang, K.; Bai, P.; Feng, A.Q.; Liu, L.F.; Dong, G.T. The spatiotemporal variation of reference evapotranspiration and the contribution of its climatic factors in the Loess Plateau, China. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Ni, G.H.; Li, X.H.; Cong, Z.T.; Sun, F.B.; Liu, Y. Temporal and spatial characteristics of reference evapotranspiration in China. J. Agric. Eng. 2006, 22, 1–4. [Google Scholar]
- Thomas, A. Spatial and temporal characteristics of potential evapotranspiration trends over China. Int. J. Climatol. 2015, 20, 381–396. [Google Scholar] [CrossRef]
- Yang, H.B.; Yang, D.W. Climatic factors influencing changing pan evaporation across China from 1961 to 2001. J. Hydrol. 2012, 414–415, 183–193. [Google Scholar] [CrossRef]
- Guo, D.L.; Westra, S.; Maier, H.R. Sensitivity of potential evapotranspiration to changes in climate variables for different Australian climatic zones. Hydrol. Earth Syst. Sci. 2017, 21, 2107–2126. [Google Scholar] [CrossRef]
- Liang, L.Q.; Li, L.J.; Zhang, L.; Li, J.Y.; Jang, D.J.; Xu, M.X.; Song, W.X. Sensitivity of the reference crop evapotranspiration in growing season in the West Songnen Plain. J. Agric. Eng. 2008, 18, 340–347. [Google Scholar]
- Yang, L.S.; Li, C.B.; Wang, S.B. Sensitive analysis of potential evapotranspiration to key climatic factors in Taohe River Basin. Trans. Chin. Soc. Agric. Eng. 2014, 30, 102–109. [Google Scholar]
- McCuen, R.H. A sensitivity analysis of procedures used for estimating evaporation. Water Resour. Bull. 1974, 10, 486–497. [Google Scholar] [CrossRef]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, 190. [Google Scholar] [CrossRef]
- Gong, L.B.; Xu, C.Y.; Chen, D.L.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2012, 329, 620–629. [Google Scholar] [CrossRef]
- Saxton, K.E. Sensitivity analyses of the combination evapotranspiration equation. Agric. Meteorol. 1975, 15, 343–353. [Google Scholar] [CrossRef]
- Ren, J.L.; Li, Q.F.; Yu, M.X.; Li, H.Y. Variation trends of meteorological variables and their impacts on potential evaporation in Hailar region. Water Sci. Eng. 2012, 5, 137–144. [Google Scholar]
- Sergio, M.; Vicente, S.; Cesar, A.M.; Arturo, S.L.; Arturo SLJesús, R.; Enrique, M.T.; Juan, I.L.M.; Francisco, E. Sensitivity of reference evapotranspiration to changes in meteorological parameters in Spain (1961–2011). Water Resour. Res. 2014, 50, 8458–8480. [Google Scholar]
- Sharifi, A.; Dinpashoh, Y. Sensitivity analysis of the Penman-Monteith reference crop evapotranspiration to climatic variables in Iran. Water Resour. Manag. 2014, 28, 5465–5476. [Google Scholar] [CrossRef]
- Yang, Y.G.; Cui, N.B.; Hu, X.T.; Gong, D.Z. Spatio-Temporal variability and cause analysis of reference crop evapotranspiration in the main grain producing areas of China. Chin. Agric. Meteorol. 2018, 39, 245–255. [Google Scholar]
- Zhao, J.; Xu, Z.X.; Zuo, D.P.; Wang, X.M. Temporal variations of reference evapotranspiration and its sensitivity to meteorological factors in Heihe River Basin, China. Water Sci. Eng. 2015, 8, 1–8. [Google Scholar] [CrossRef][Green Version]
- Gao, G.; Chen, D.L.; Ren, G.Y.; Chen, Y. Spatial and temporal variations and controlling factors of potential evapotranspiration in China: 1956–2000. J. Geogr. Sci. 2006, 16, 3–12. [Google Scholar] [CrossRef]
- Ma, N.; Wang, N.A.; Wang, P.L.; Sun, Y.M.; Dong, C.Y. Temporal and spatial variation characteristics and quantification of the affect factors for reference evapotranspiration in Heihe River Basin. J. Nat. Resour. 2012, 27, 975–989. [Google Scholar]
- Kang, N.J.; Batur, B.; Luo, N.N.; Xue, Y.R.; Wang, M.H. Spatio-Temporal variation and influencing factors of reference crop evapotranspiration at different time scales in Altay region. Chin. Agric. Meteorol. 2018, 39, 502–511. [Google Scholar]
- Huan, H.J.; Yang, Z.Q.; Liu, Y.; Xia, F.H. Temporal and spatial variation of reference crop evapotranspiration and contribution of main factors in the middle area of Shandong province. Chin. Agric. Meteorol. 2015, 36, 692–698. [Google Scholar]
- Zou, H.P.; Chen, H.L.; Tian, G.H.; Chen, X.M.; Bai, R.; Tong, J.H. Spatiotemporal change characteristics and causes analysis of reference crop evapotranspiration in Hainan Island. Chin. Agric. Meteorol. 2018, 39, 18–26. [Google Scholar]
- Liu, C.; Zhang, X.; Zhang, Y. Determination of daily evaporation and evapotranspiration of winter wheat and maize by large-scale weighing lysimeter and micro-lysimeter. Agric. For. Meteorol. 2002, 111, 109–120. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, S.; Sun, H.; Shao, L.; Wang, Y. Changes in evapotranspiration over irrigated winter wheat and maize in North China Plain over three decades. Agric. Water Manag. 2011, 98, 1097–1104. [Google Scholar] [CrossRef]
- Yin, Y.H.; Wu, S.H.; Dai, E.F. Determining factors in potential evapotranspiration changes over China in the period 1971–2008. Chin. Sci. Bull. 2010, 55, 3329–3337. [Google Scholar] [CrossRef]
- Yin, Y.H.; Wu, S.H.; Chen, G.; Dai, E.F. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Liu, H.J.; Li, Y.; Josef, T. Quantitative estimation of climate change effects on potential evapotranspiration in Beijing during 1951–2010. Sci. Press 2014, 24, 93–112. [Google Scholar] [CrossRef]
- Liu, S.Y.; Wang, H.X.; Wang, Y.Y.; Ye, W. Variation characteristic analysis of time series of potential evapotranspiration in Beijing. South-to-North Water Transf. Water Sci. Technol. 2013, 11, 13–16. [Google Scholar]
- Zhao, L.L.; Xia, J.; Wang, Z.G.; Li, Z.L. The Inter-Intra annual climatic pattern of potential evaporation in Beijing and attribution. J. Nat. Resour. 2013, 28, 1911–1921. [Google Scholar]
- Suat, I.; José, O.P.; Derrel, L.M.; Ayse, I.; Terry, A.H. Sensitivity analyses and sensitivity coefficients of standardized daily ASCE-Penman-Monteith equation. J. Irrig. Drain. Eng. 2006, 24, 564–578. [Google Scholar]
- Hupet, F.; Vanclooster, M. Effect of the sampling frequency of meteorological variables on the estimation of the reference evapotranspiration. J. Hydrol. 2001, 243, 192–204. [Google Scholar] [CrossRef]
- Liu, X.M.; Zheng, H.X.; Liu, C.M.; Cao, Y.J. Sensitivity of the potential evapotranspiration to key climatic variables in the Haihe River Basin. Resour. Sci. 2009, 31, 1470–1476. [Google Scholar]


| Time Scale | Meteorological Trend Rate | Sensitivity Coefficient (%) | Sensitive Factor | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TrendT (°C/10a) | TrendRH (%/10a) | TrendU (m/s)/10a | TrendRN ((MJ/m2)/d/10a) | TrendET0 (mm/10a) | ST | SRH | SU | SRN | ||
| Jan | 0.43 | 0.40 | −0.13 | −0.01 | −0.40 | 20.2 | −63.1 | 49.6 | 20.7 | RH |
| Feb | 0.58 | −1.20 | −0.09 | −0.06 | 0.82 | 9.2 | −55.2 | 36.5 | 34.5 | |
| Mar | 0.65 | −2.90 | −0.07 | −0.11 | 2.83 | 25.0 | −47.4 | 28.5 | 44.1 | |
| Apr | 0.49 | −1.50 | −0.09 | −0.08 | 1.67 | 45.9 | −42.2 | 25.5 | 51.2 | RN |
| May | 0.37 | −1.30 | −0.04 | −0.21 | 0.91 | 51.3 | −40.2 | 21.3 | 60.7 | |
| Jun | 0.23 | −0.60 | −0.01 | −0.42 | −2.08 | 50.0 | −45.2 | 16.4 | 69.9 | |
| Jul | 0.31 | −2.20 | 0.05 | −0.35 | 0.31 | 46.8 | −55.6 | 9.4 | 79.8 | |
| Aug | 0.40 | −2.50 | 0.08 | −0.22 | 1.86 | 45.8 | −56.2 | 8.4 | 81.3 | |
| Sept | 0.44 | −1.70 | 0.02 | −0.24 | 0.65 | 46.7 | −61.1 | 16.3 | 70.6 | |
| Oct | 0.38 | −1.70 | −0.02 | −0.14 | 0.76 | 40.7 | −75.0 | 28.0 | 55.0 | RH |
| Nov | 0.27 | −1.50 | −0.09 | −0.04 | 0.20 | 19.5 | −92.1 | 45.6 | 30.6 | |
| Dec | 0.39 | −0.90 | −0.09 | −0.03 | 0.24 | 9.3 | −81.4 | 55.2 | 16.6 | |
| Spring | 0.50 | −1.90 | −0.07 | −0.14 | 0.09 | 44.4 | −42.9 | 24.6 | 52.5 | RN |
| Summer | 0.32 | −1.80 | 0.04 | −0.33 | 1.62 | 47.6 | −52.8 | 11.5 | 76.9 | |
| Autumn | 0.36 | −1.70 | −0.03 | −0.14 | −0.02 | 40.2 | −74.4 | 27.4 | 54.8 | RH |
| Winter | 0.47 | −0.50 | −0.10 | −0.06 | 7.77 | 10.9 | −64.3 | 47.0 | 24.1 | |
| Annual mean | 0.41 | −1.47 | −0.04 | −0.16 | 0.77 | 34.2 | −59.6 | 28.4 | 51.3 | RH |
| Time Scale | Contribution of Meteorological Elements on ET0 (mm) | ΔET0 (mm) | Main Control Factor | ||||
|---|---|---|---|---|---|---|---|
| GT | GRH | GU | GRN | Gsum | |||
| Jan | 4.38 | −1.03 | −6.16 | −0.22 | −3.04 | −2.41 | U |
| Feb | 7.38 | 3.36 | −4.02 | −1.26 | 5.46 | 4.93 | T |
| Mar | 12.05 | 13.92 | −4.00 | −3.11 | 18.86 | 16.96 | RH |
| Apr | 11.17 | 10.06 | −7.15 | −2.93 | 11.15 | 9.99 | T |
| May | 8.46 | 9.62 | −3.51 | −9.37 | 5.19 | 5.46 | RH |
| Jun | 4.27 | 3.87 | −0.57 | −19.93 | −12.36 | −12.45 | RN |
| Jul | 4.55 | 13.56 | 2.76 | −18.33 | 2.54 | 1.84 | RN |
| Aug | 5.35 | 13.62 | 3.97 | −11.08 | 11.86 | 11.16 | RH |
| Sep | 5.77 | 8.82 | 1.54 | −10.61 | 5.52 | 3.93 | RN |
| Oct | 4.51 | 7.96 | −1.21 | −5.38 | 5.89 | 4.57 | RH |
| Nov | 2.63 | 5.58 | −5.24 | −1.21 | 1.76 | 1.19 | RH |
| Dec | 3.91 | 2.74 | −4.66 | −0.65 | 1.36 | 1.43 | U |
| Spring | 34.08 | 36.51 | −15.28 | −14.83 | 40.47 | 32.41 | RH |
| Summer | 14.61 | 32.95 | 8.22 | −49.67 | 6.11 | 0.54 | RN |
| Autumn | 13.63 | 23.29 | −5.63 | −16.02 | 15.27 | 9.70 | RH |
| Winter | 15.52 | 4.53 | −15.36 | −3.77 | 0.91 | 3.95 | TU |
| seasonal mean | 19.46 | 24.32 | −7.01 | −21.07 | 15.69 | 11.65 | RH |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhang, B.; Han, S. Quantitative Analysis of the Impact of Meteorological Factors on Reference Evapotranspiration Changes in Beijing, 1958–2017. Water 2020, 12, 2263. https://doi.org/10.3390/w12082263
Liu W, Zhang B, Han S. Quantitative Analysis of the Impact of Meteorological Factors on Reference Evapotranspiration Changes in Beijing, 1958–2017. Water. 2020; 12(8):2263. https://doi.org/10.3390/w12082263
Chicago/Turabian StyleLiu, Wenhui, Baozhong Zhang, and Songjun Han. 2020. "Quantitative Analysis of the Impact of Meteorological Factors on Reference Evapotranspiration Changes in Beijing, 1958–2017" Water 12, no. 8: 2263. https://doi.org/10.3390/w12082263
APA StyleLiu, W., Zhang, B., & Han, S. (2020). Quantitative Analysis of the Impact of Meteorological Factors on Reference Evapotranspiration Changes in Beijing, 1958–2017. Water, 12(8), 2263. https://doi.org/10.3390/w12082263







