A Compound Approach for Monthly Runoff Forecasting Based on Multiscale Analysis and Deep Network with Sequential Structure
Abstract
1. Introduction
2. Materials and Methods
2.1. Time-Varying Filtering-Based Empirical Mode Decomposition (TVFEMD)
- Step 1:
- Locate the maximum timing of the given signal x(t).
- Step 2:
- Seek out the intermittence ui satisfying , and then define ej, = ui, j = 1, 2, ….
- Step 3:
- Determine the status of ej according to the relationship between and , i.e., corresponds to rising edge, corresponds to the falling edge, and the remaining ones correspond to peaks.
- Step 4:
- Access the ultimate local cut-off frequency based on the interpolation achieved among the peaks.
2.2. Sample Entropy (SE)
- Step 1:
- Reconstruct the given time series into a m-dimensional matrix Xi = [xi, xi+1, …, xi+m−1], where i = 1, 2, … N − m + 1.
- Step 2:
- Find out the maximum difference of the components between Xi and Xj, which is defined as .
- Step 3:
- Calculate the ratio corresponding to the total number of for the i-th vector, after which the mean value of is defined as .
- Step 4:
- Given a new dimension as m + 1, deduce by repeating Step 1 to Step 3.
- Step 5:
- For the given bounded time series, the se value can be expressed as follows:where the calculated se value can be defined as se(N, m, r), N is the length of the series, m represents the embedded dimension, and r is the similarity tolerance set in the scope of [0.1SD, 0.25SD] (SD indicates the standard deviation of the time series) [32].
2.3. Convolutional Neural Network (CNN)
2.4. Gated Recurrent Unit Network (GRU)
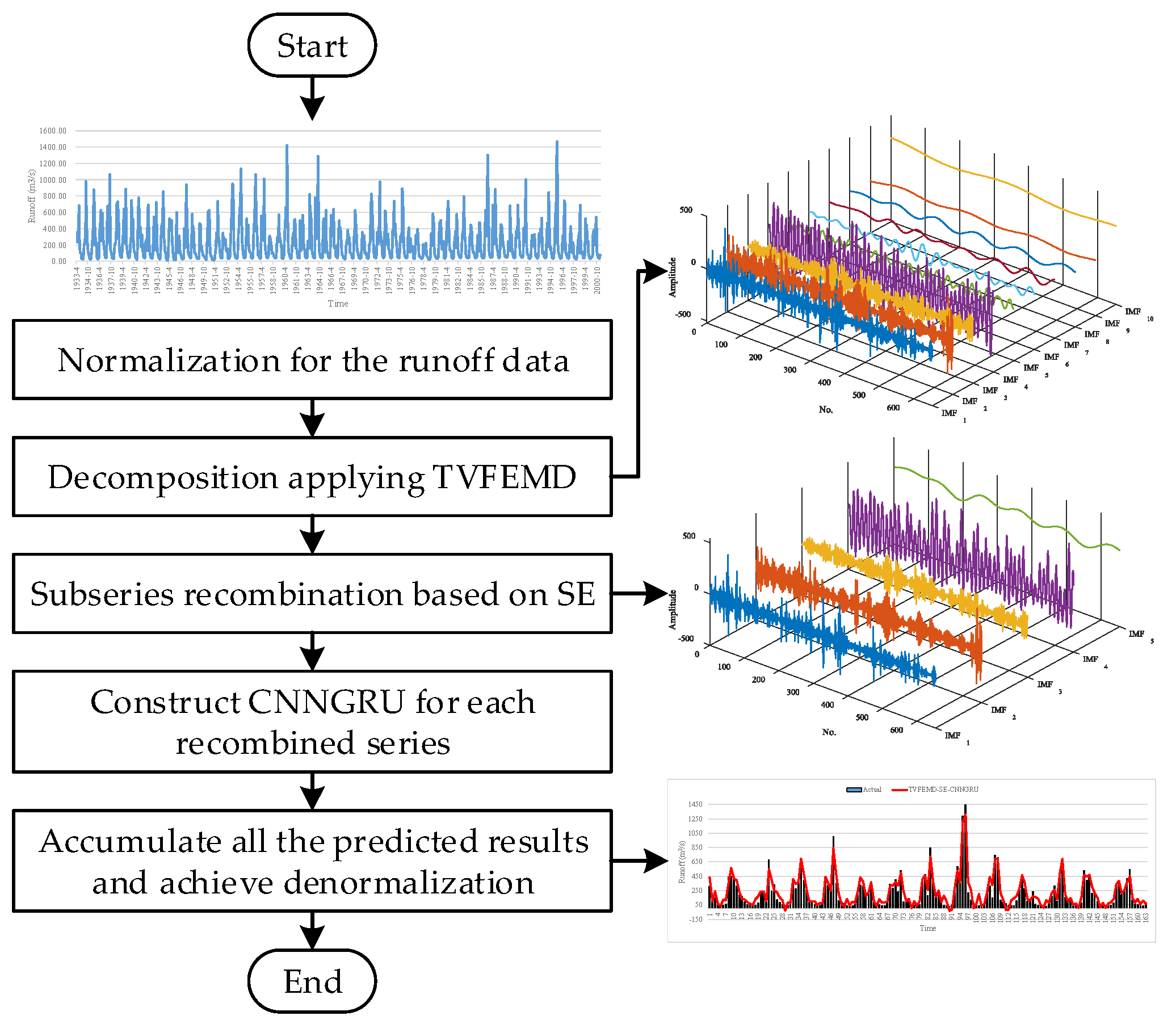
3. The Proposed Approach
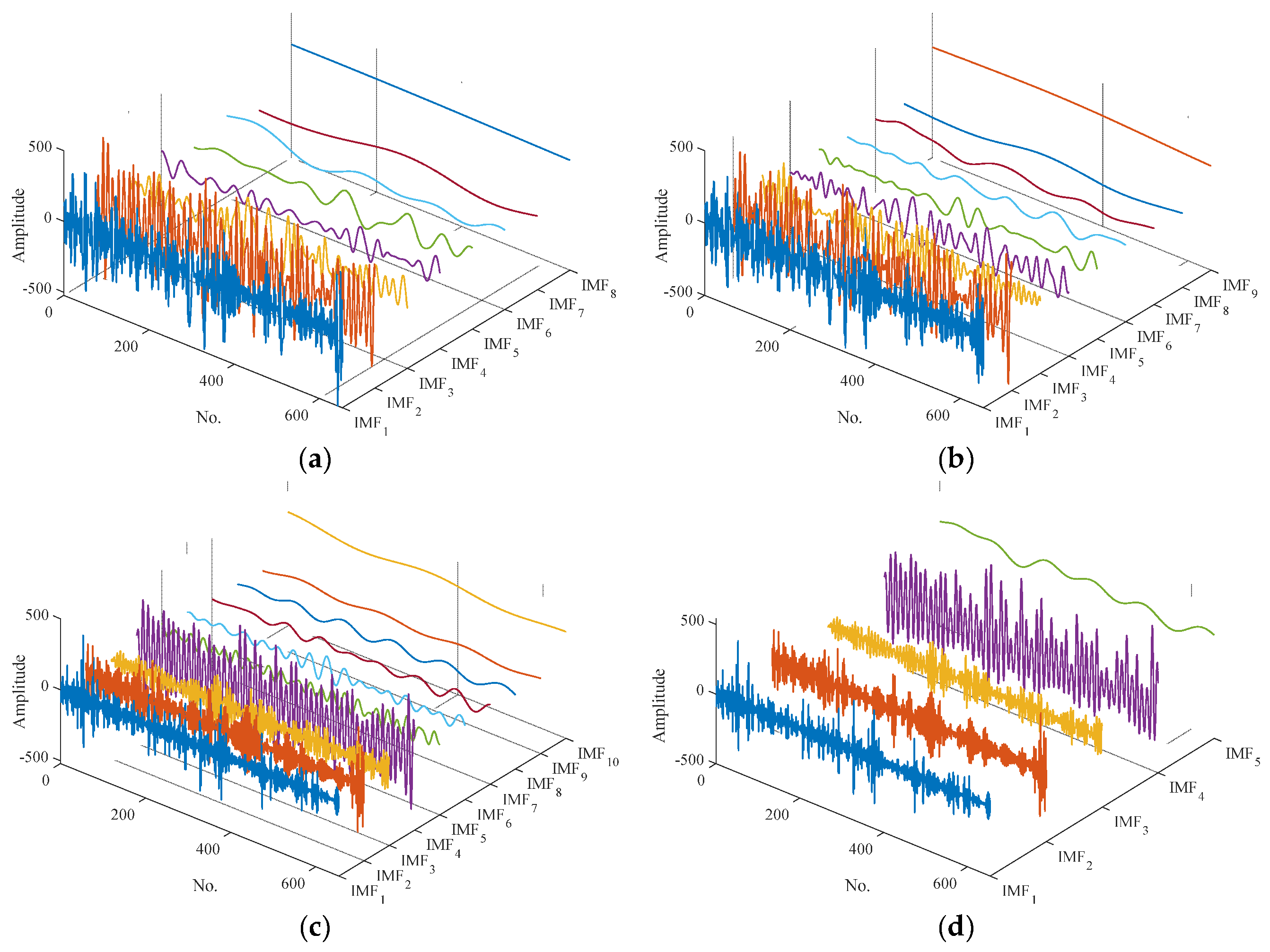
3.1. SE-Based Subseries Recombination for TVFEMD
3.2. CNN Incorporated into GRU with Deep Sequential Structure (CNNGRU)
3.3. Specific Procedures of the Proposed Compound Approach
- Step 1.
- Normalize the collected runoff dataset and divide it into training and testing sets.
- Step 2.
- Decompose the normalized runoff data into a series of IMFs with TVFEMD, applying appropriate parameters.
- Step 3.
- Calculate the SE value for each IMF, and adaptively recombine the IMFs based on the recombination criterion.
- Step 4.
- Construct CNNGRU to predict each recombined subseries.
- Step 5.
- Accumulate all the prediction results of the recombined subseries and implement denormalization to deduce the ultimate prediction results of the collected runoff series.
4. Experimental Design
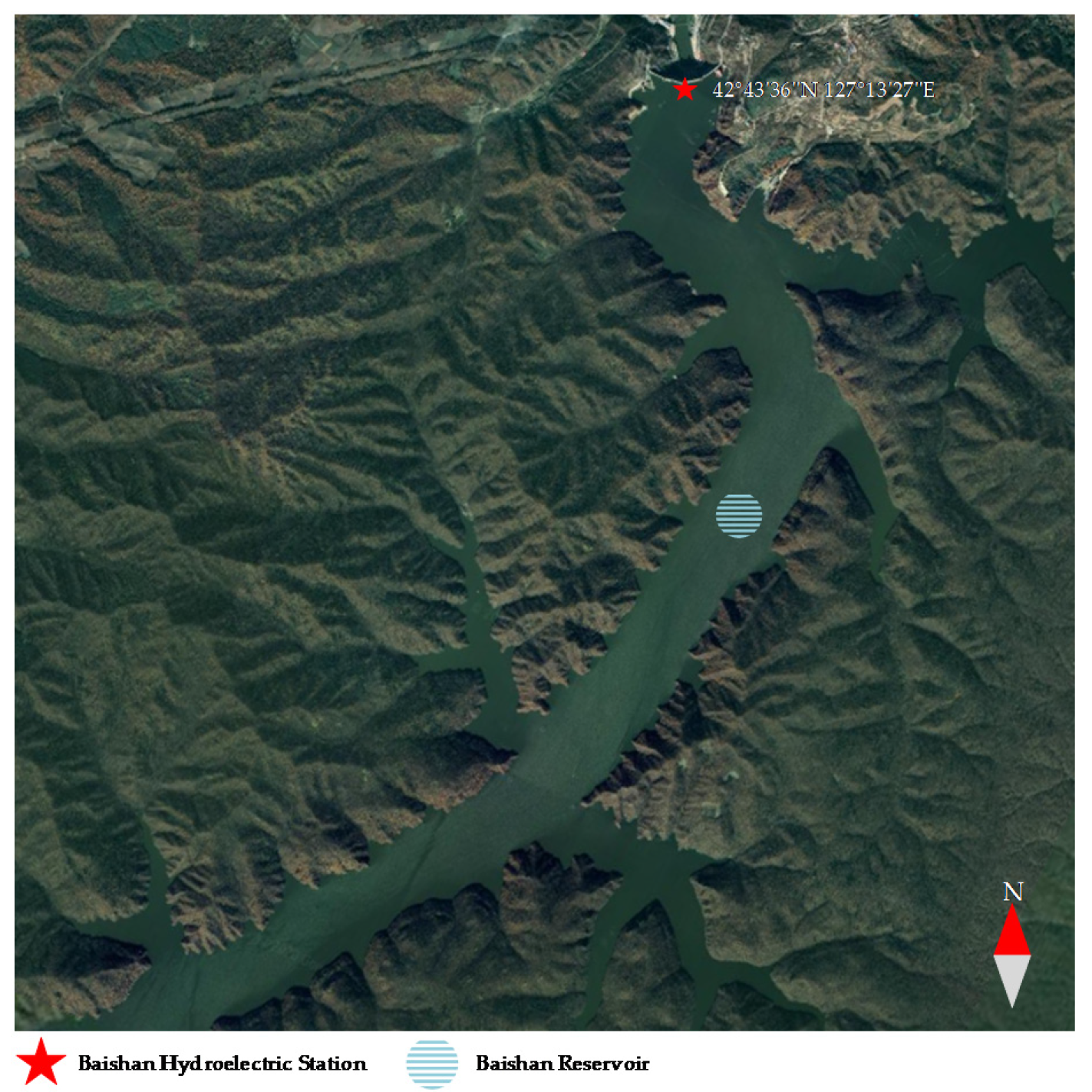
4.1. Study Area and Data
4.2. Experimental Description
4.3. Contrastive Analyses
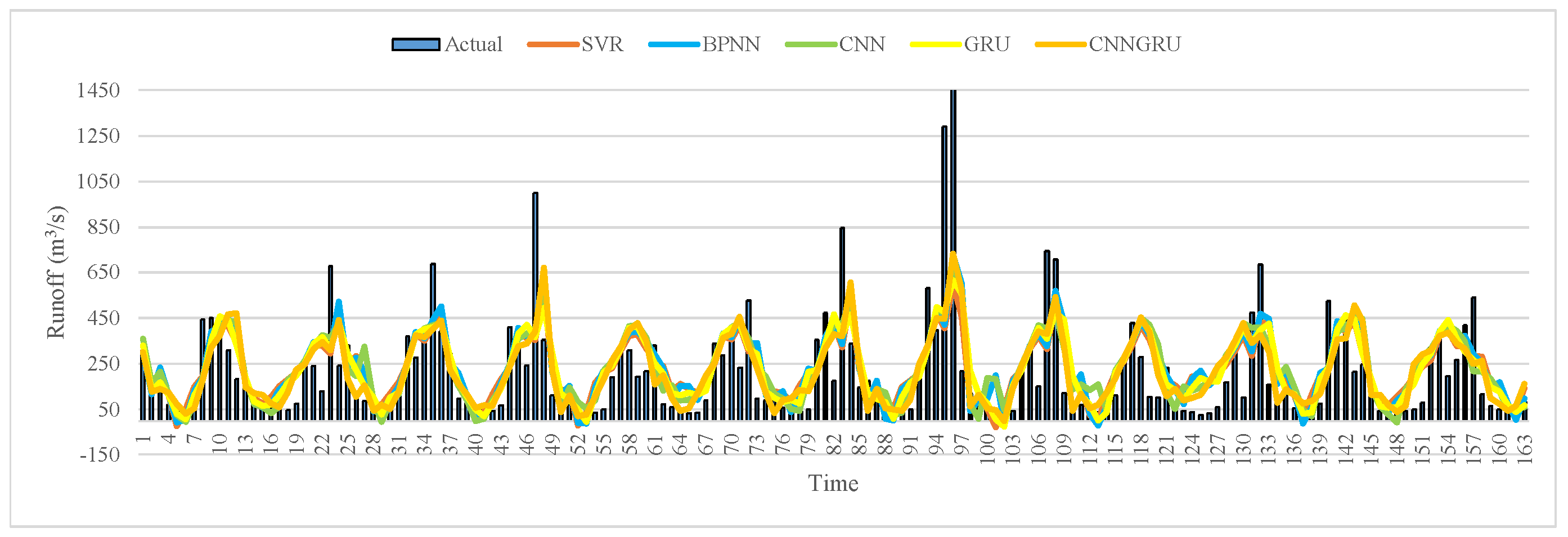
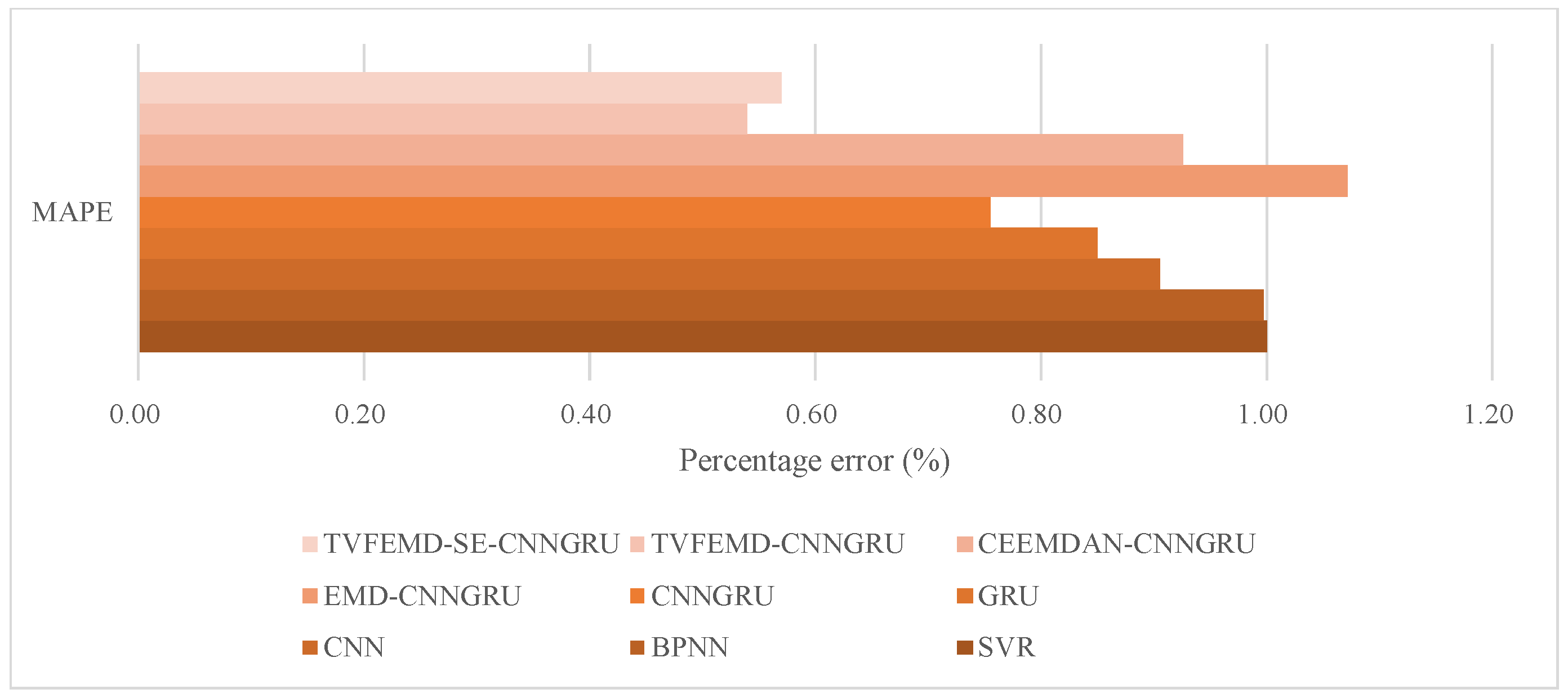
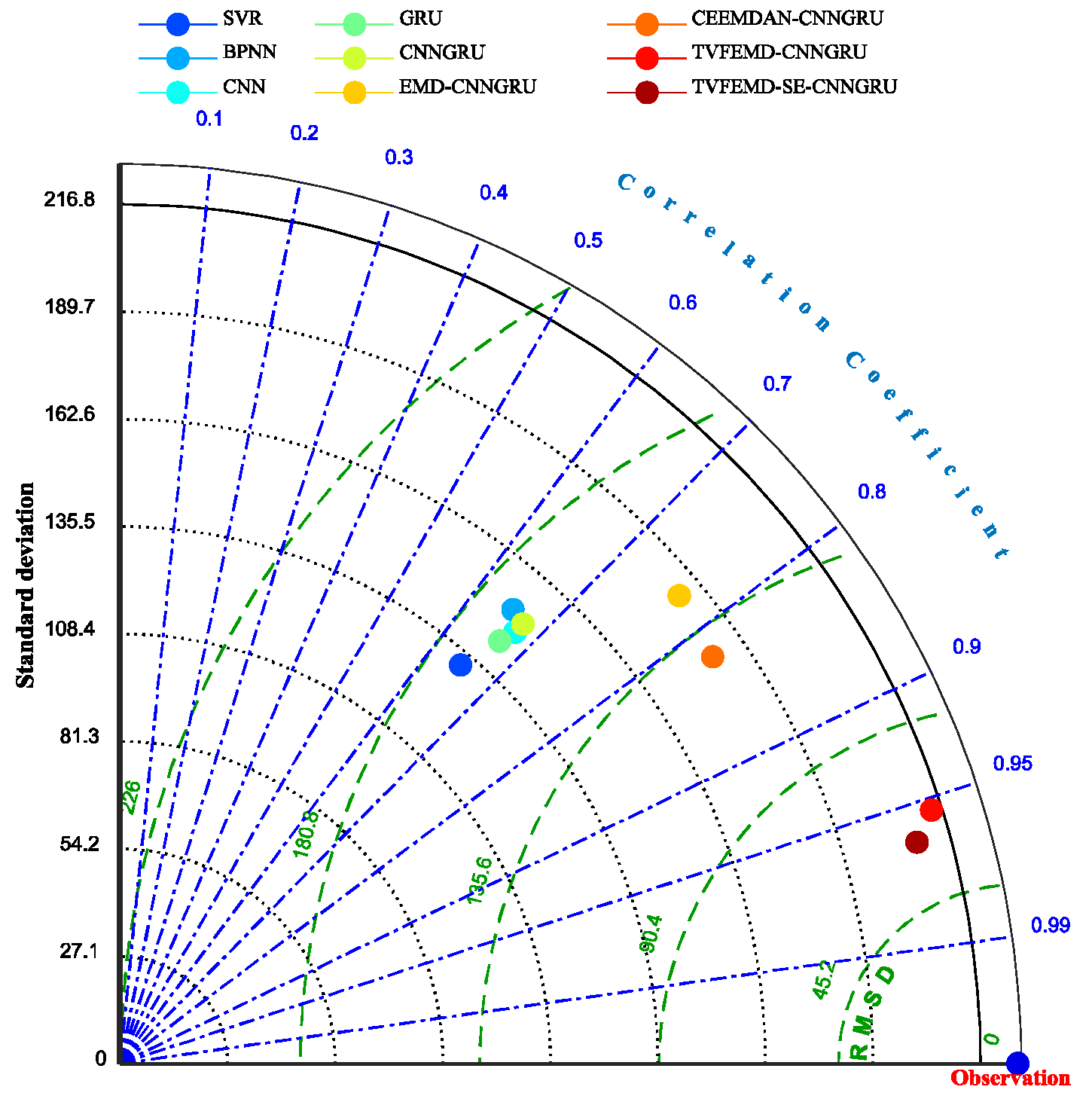
- Focusing on the comparisons among SVR, BPNN, CNN, GRU, and CNNGRU, it can be observed that the newly developed CNNGRU achieves the minimum indicator values in terms of RMSE, MAE, and MAPE as 167.3551, 108.9287 and 0.7550, while the corresponding correlation coefficient R2 of CNNGRU is the maximum at 0.6752. Hence, it can be affirmed that preferable forecasting performance can be obtained by the newly constructed CNNGRU. However, compared to the remaining single models, the average decline ratios of RMSE, MAE, and MAPE, obtained by CNNGRU, are 2.44%, 5.74%, and 19.13%, respectively. Similarly, the metric CE obtained by CNNGRU is 0.4528, which achieves an average improvement of 6.14% compared with the remaining single models, thus indicating that the performance gaps among the single models are not significant. A reasonable hypothesis to interpret the phenomenon could be inferred, namely, that the forecasting capability of the aforementioned individual models would be significantly restricted by the volatility of the runoff series.
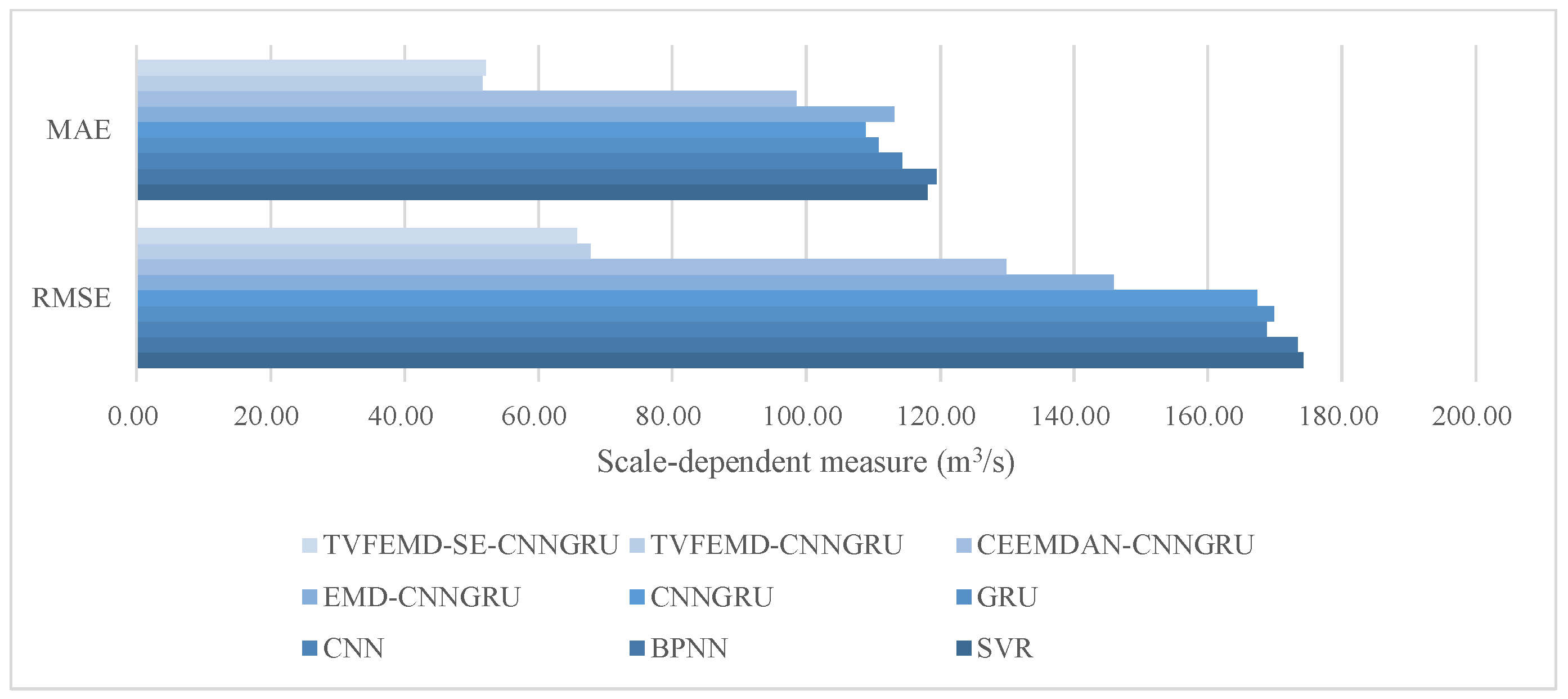
- Further contrasting the evaluation results obtained by CNNGRU, EMD-CNNGRU, CEEMDAN-CNNGRU, and TVFEMD-CNNGRU, it can be found that the forecasting accuracy can be markedly enhanced by adopting the decomposition techniques, except for EMD. Specifically, compared with EMD-CNNGRU, the CEEMDAN-based model possesses better forecasting performance in terms of RMSE, MAE, and MAPE, where the corresponding decline rates are 11.01%, 12.91%, and 13.63%, respectively. Additionally, the indicators RMSE, MAE, and MAPE of TVFEMD-CNNGRU are 67.7378, 51.5727, and 0.5395, which are the minimum values, and achieve the averaged descents of 53.65%, 51.59%, and 39.97% compared with CNNGRU, EMD-CNNGRU, and CEEMDAN-CNNGRU. It can be found that the TVFEMD-based model estimates more significant index decline rates, which can be attributed to the fact that the modal-aliasing existing in EMD and CEEMDAN can be effectively handled by TVFEMD, thus completing the superior decomposition performance.
- On the basis of TVFEMD-CNNGRU, the SE-based subseries recombination is introduced in the proposed model, with which the number of decomposed subsequences can be significantly reduced. The metrics of RMSE, MAE, and MAPE, obtained by the proposed model, are 65.6926, 52.1495, and 0.5697, which are close to the metrics obtained by TVFEMD-CNNGRU. It can be observed that the metrics MAE and MAPE of the proposed model are slightly more extensive than those of TVFEMD-CNNGRU, while the metrics R2 and CE of the proposed model is the maximum among all the models at 0.9633 and 0.9157. Additionally, considering the same networks applied for the preprocessed subseries in both TVFEMD-based models, the proposed model, adopting the SE-based subseries recombination, possesses fewer subseries to be predicted, thus achieving less computational complexity compared with TVFEMD-CNNGRU. Furthermore, it can be observed from the results of the DM test illustrated in Table 6 that all the values are larger than 2.5800, which practically corresponds to the critical value of significance level 1%, except for TVFEMD-CNNGRU, with which it can be concluded that the proposed model achieves a significant promotion in forecasting accuracy, as well as a reduction of the computational cost, without significantly reducing prediction accuracy when compared with TVFEMD-CNNGRU.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AE | Approximate entropy |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| AR | Autoregressive |
| ARIMA | Autoregressive integrated moving average |
| ARMA | Autoregressive moving average |
| BPNN | Back propagation neural network |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CNN | Convolutional neural network |
| CNNGRU | Convolutional neural network incorporated into gated recurrent unit network |
| DM | Diebold-Mariano |
| EMD | Empirical mode decomposition |
| GRU | Gated recurrent unit network |
| IMF | Intrinsic mode function |
| LSTM | Long short-term memory network |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| ReLU | Rectified linear unit |
| RMSD | Root mean square difference |
| RMSE | Root-mean-square error |
| SE | Sample entropy |
| SVR | Support vector regression |
| tanh | Hyperbolic tangent |
| TVF | Time-varying filter |
| TVFEMD | Time-varying filtering-based empirical mode decomposition |
References
- Feng, Z.; Niu, W.; Zhou, J.; Cheng, C. Linking Nelder-Mead Simplex Direct Search Method into Two-Stage Progressive Optimality Algorithm for Optimal Operation of Cascade Hydropower Reservoirs. J. Water Resour. Plan. Manag. 2020, 146, 4020019. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Tang, Z.-Y.; Jiang, Z.-Q.; Xu, Y.; Liu, Y.; Zhang, H. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Li, P.; Zuo, G.; Xie, J. A Hybrid Model Based on Variational Mode Decomposition and Gradient Boosting Regression Tree for Monthly Runoff Forecasting. Water Resour. Manag. 2020, 34, 865–884. [Google Scholar] [CrossRef]
- Chang, F.J.; Guo, S. Advances in hydrologic forecasts and water resources management. Water 2020, 12, 1819. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in Surface Water Hydrology and Hydraulics: A Review of Two Decades Retrospective, Current Status and Future Prospects. J. Hydrol. 2020, 125085. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Fu, W. Streamflow forecasting using empirical wavelet transform and artificial neural networks. Water 2017, 9, 406. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, T.; Zhang, C.; Sun, N. Data pre-analysis and ensemble of various artificial neural networks for monthly streamflow forecasting. Water 2018, 10, 628. [Google Scholar] [CrossRef]
- Napolitano, G.; Serinaldi, F.; See, L. Impact of EMD decomposition and random initialisation of weights in ANN hindcasting of daily stream flow series: An empirical examination. J. Hydrol. 2011, 406, 199–214. [Google Scholar] [CrossRef]
- Sun, Y.; Niu, J.; Sivakumar, B. A comparative study of models for short-term streamflow forecasting with emphasis on wavelet-based approach. Stoch. Environ. Res. Risk Assess. 2019, 33, 1875–1891. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Parviz, L.; Rasouli, K. Development of Precipitation Forecast Model Based on Artificial Intelligence and Subseasonal Clustering. J. Hydrol. Eng. 2019, 24, 1–13. [Google Scholar] [CrossRef]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional neural network coupled with a transfer-learning approach for time-series flood predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J.; Yang, S.N.; Kao, I.F.; Ku, Y.Y.; Kuo, C.L.; Amin, I.M.Z.b.M. Building an intelligent hydroinformatics integration platform for regional flood inundation warning systems. Water 2018, 11, 9. [Google Scholar] [CrossRef]
- Lee, D.; Lee, G.; Kim, S.; Jung, S. Future Runoff Analysis in the Mekong River Basin under a Climate Change Scenario Using Deep Learning. Water 2020, 12, 1556. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Bojang, P.O.; Yang, T.C.; Pham, Q.B.; Yu, P.S. Linking singular spectrum analysis and machine learning for monthly rainfall forecasting. Appl. Sci. 2020, 10, 3224. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, F.; Yang, Z. Comparative analysis of ANN and SVM models combined with wavelet preprocess for groundwater depth prediction. Water 2017, 9, 781. [Google Scholar] [CrossRef]
- Kao, I.-F.; Zhou, Y.; Chang, L.-C.; Chang, F.-J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, EMNLP, Doha, Qatar, 26–28 October 2014; pp. 1724–1734. [Google Scholar]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.W. Comparative analysis of recurrent neural network architectures for reservoir inflow forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y.; Duan, Z.; Xu, Y. Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, convolutional Gated Recurrent Unit network and Support Vector Regression. Renew. Energy 2019, 143, 842–854. [Google Scholar] [CrossRef]
- Tan, Q.F.; Lei, X.H.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Lu, H.; Niu, T.; Du, P. Hybrid wind energy forecasting and analysis system based on divide and conquer scheme: A case study in China. J. Clean. Prod. 2019, 222, 942–959. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Yin, Z.; Yang, L.; Singh, V.P. Two-phase extreme learning machines integrated with the complete ensemble empirical mode decomposition with adaptive noise algorithm for multi-scale runoff prediction problems. J. Hydrol. 2019, 570, 167–184. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Mo, W. A time varying filter approach for empirical mode decomposition. Signal Process. 2017, 138, 146–158. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Qin, L.; An, X. Deterministic and probabilistic interval prediction for short-term wind power generation based on variational mode decomposition and machine learning methods. Energy Convers. Manag. 2016, 112, 208–219. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y. Multi-step ahead wind speed prediction based on optimal feature extraction, long short term memory neural network and error correction strategy. Appl. Energy 2018, 230, 429–443. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Yang, Q.; Yan, Z.; Zhang, C. A novel probabilistic wind speed prediction approach using real time refined variational model decomposition and conditional kernel density estimation. Energy Convers. Manag. 2019, 185, 758–773. [Google Scholar] [CrossRef]
- Zhou, K.-B.; Zhang, J.-Y.; Shan, Y.; Ge, M.-F.; Ge, Z.-Y.; Cao, G.-N. A Hybrid Multi-Objective Optimization Model for Vibration Tendency Prediction of Hydropower Generators. Sensors 2019, 19, 2055. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y. Short-term wind speed forecasting based on fast ensemble empirical mode decomposition, phase space reconstruction, sample entropy and improved back-propagation neural network. Energy Convers. Manag. 2018, 157, 1–12. [Google Scholar] [CrossRef]
- Ding, L.; Fang, W.; Luo, H.; Love, P.E.D.; Zhong, B.; Ouyang, X. A deep hybrid learning model to detect unsafe behavior: Integrating convolution neural networks and long short-term memory. Autom. Constr. 2018, 86, 118–124. [Google Scholar] [CrossRef]
- Mi, X.; Liu, H.; Li, Y. Wind speed prediction model using singular spectrum analysis, empirical mode decomposition and convolutional support vector machine. Energy Convers. Manag. 2019, 180, 196–205. [Google Scholar] [CrossRef]
- Chai, J.; Wang, Y.; Wang, S.; Wang, Y. A decomposition–integration model with dynamic fuzzy reconstruction for crude oil price prediction and the implications for sustainable development. J. Clean. Prod. 2019, 229, 775–786. [Google Scholar] [CrossRef]
- Zheng, W.; Peng, X.; Lu, D.; Zhang, D.; Liu, Y.; Lin, Z.; Lin, L. Composite quantile regression extreme learning machine with feature selection for short-term wind speed forecasting: A new approach. Energy Convers. Manag. 2017, 151, 737–752. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Fan, W.; Ma, P. A new chaotic time series hybrid prediction method of wind power based on EEMD-SE and full-parameters continued fraction. Energy 2017, 138, 977–990. [Google Scholar] [CrossRef]
- Gemperline, P.J.; Long, J.R.; Gregoriou, V.G. Nonlinear multivariate calibration using principal components regression and artificial neural networks. Anal. Chem. 1991, 63, 2313–2323. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]


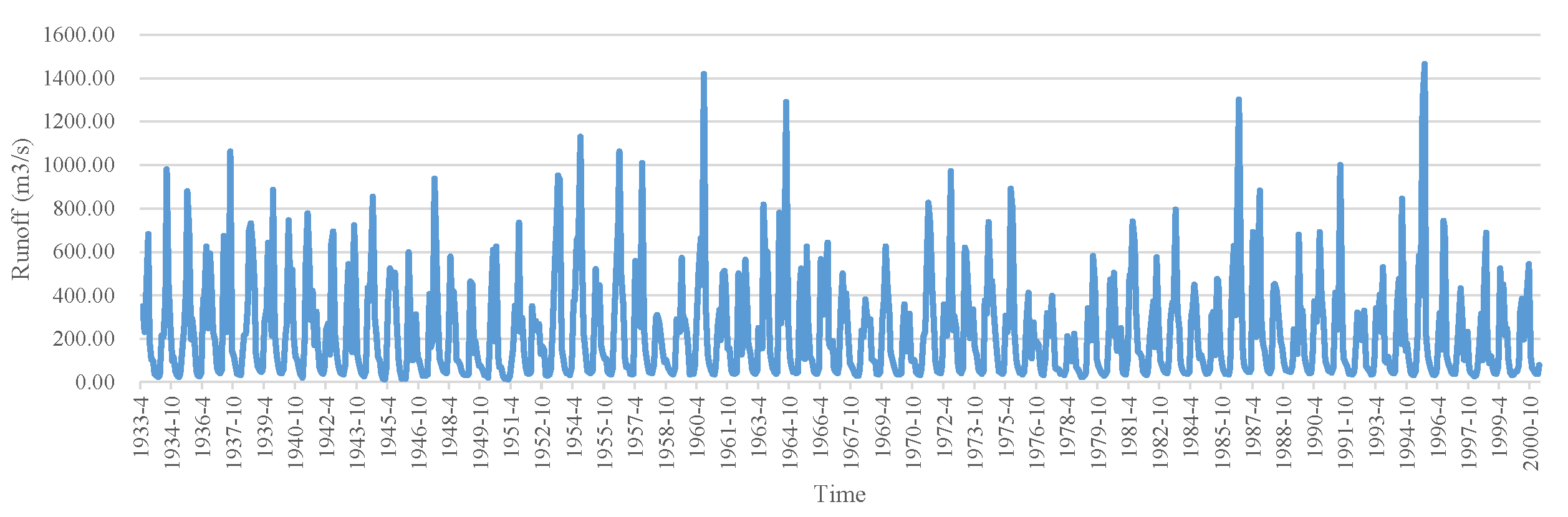



| Datasets | Mean (m3/s) | Max. (m3/s) | Min. (m3/s) | Std. |
|---|---|---|---|---|
| Baishan | 229.98 | 1466.00 | 12.60 | 232.08 |
| Models | Parameter | Setting Values |
|---|---|---|
| SE | Tolerance | 0.2 times the standard deviation of the series |
| Scale factor | 1 | |
| Vector dimension | 3 | |
| CEEMDAN | Standard deviation of the added white noise | 0.05 |
| Number of realizations | 500 | |
| The allowed maximum number of sifting iterations | 5000 | |
| TVF-EMD | B-spline order n | 26 |
| Bandwidth threshold ξ | 0.2 | |
| SVR | Regularization coefficient c | [2−10, 210] |
| Kernel parameter g | [2−10, 210] | |
| BPNN | Number of hidden layer nodes | 32 |
| Number of hidden layers | 1 | |
| Size of batch | 128 | |
| Epochs of training | 500 | |
| Activation function | hyperbolic tangent (tanh) | |
| CNN | Number of kernels | 32 |
| Size of max-pooling | 2 | |
| Kernel size | 3 | |
| Size of batch | 128 | |
| Epochs of training | 500 | |
| Activation function | ReLU | |
| GRU | Number of hidden layer nodes | 32 |
| Number of hidden layers | 1 | |
| Size of batch | 128 | |
| Epochs of training | 500 | |
| Activation function | tanh | |
| CNNGRU | Number of kernels | 3 |
| Kernel size | 16 | |
| Size of max-pooling | 2 | |
| Number of hidden layer nodes | 32 | |
| Number of hidden layers | 1 | |
| Size of batch | 128 | |
| Epochs of training | 500 | |
| Activation function | RuLU (CNN)/tanh (GRU) |
| Indicators | Explanation | Representation |
|---|---|---|
| RMSE | Root-mean-square error (m3/s) | |
| MAE | Mean absolute error (m3/s) | |
| MAPE | Absolute percentage error (%) | |
| R2 | Correlation coefficient | |
| CE | Nash–Sutcliffe efficiency coefficient |
| Indicators | Explanation | Representation |
|---|---|---|
| Decline ratio of RMSE | ||
| Decline ratio of MAE | ||
| Decline ratio of MAPE |
| Models | RMSE (m3/s) | MAE (m3/s) | MAPE (%) | R2 | CE |
|---|---|---|---|---|---|
| SVR | 174.2332 | 118.1611 | 0.9999 | 0.6488 | 0.4069 |
| BPNN | 173.3733 | 119.4081 | 0.9974 | 0.6539 | 0.4127 |
| CNN | 168.8239 | 114.2668 | 0.9054 | 0.6748 | 0.4431 |
| GRU | 169.8721 | 110.8002 | 0.8497 | 0.6674 | 0.4362 |
| CNNGRU | 167.3551 | 108.9287 | 0.7550 | 0.6752 | 0.4528 |
| EMD-CNNGRU | 145.9209 | 113.1712 | 1.0718 | 0.7665 | 0.5840 |
| CEEMDAN-CNNGRU | 129.8612 | 98.5647 | 0.9257 | 0.8241 | 0.6705 |
| TVFEMD-CNNGRU | 67.7378 | 51.5727 | 0.5395 | 0.9544 | 0.9104 |
| TVFEMD-SE-CNNGRU | 65.6926 | 52.1495 | 0.5697 | 0.9633 | 0.9157 |
| Models | PRMSE (%) | PMAE (%) | PMAPE (%) | DM test |
|---|---|---|---|---|
| SVR | 61.12 | 56.35 | 46.04 | 3.5571 *** |
| BPNN | 60.93 | 56.81 | 45.90 | 4.0079 *** |
| CNN | 59.88 | 54.87 | 40.41 | 3.8229 *** |
| GRU | 60.12 | 53.45 | 36.50 | 3.6708 *** |
| CNNGRU | 59.52 | 52.65 | 28.54 | 3.8433 *** |
| EMD-CNNGRU | 53.58 | 54.43 | 49.66 | 4.6821 *** |
| CEEMDAN-CNNGRU | 47.84 | 47.68 | 41.72 | 4.3568 *** |
| TVFEMD-CNNGRU | 3.02 | −1.12 | −5.59 | 0.5830 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Dong, S.; Cao, Z.; Guo, J. A Compound Approach for Monthly Runoff Forecasting Based on Multiscale Analysis and Deep Network with Sequential Structure. Water 2020, 12, 2274. https://doi.org/10.3390/w12082274
Chen S, Dong S, Cao Z, Guo J. A Compound Approach for Monthly Runoff Forecasting Based on Multiscale Analysis and Deep Network with Sequential Structure. Water. 2020; 12(8):2274. https://doi.org/10.3390/w12082274
Chicago/Turabian StyleChen, Shi, Shuning Dong, Zhiguo Cao, and Junting Guo. 2020. "A Compound Approach for Monthly Runoff Forecasting Based on Multiscale Analysis and Deep Network with Sequential Structure" Water 12, no. 8: 2274. https://doi.org/10.3390/w12082274
APA StyleChen, S., Dong, S., Cao, Z., & Guo, J. (2020). A Compound Approach for Monthly Runoff Forecasting Based on Multiscale Analysis and Deep Network with Sequential Structure. Water, 12(8), 2274. https://doi.org/10.3390/w12082274






