New Method for Estimating Roughness Coefficient for Debris Flows
Abstract
1. Introduction
2. Method for Estimating the Roughness Coefficient of Debris Flows
2.1. Factors Influencing the Manning Roughness Coefficient
- (1)
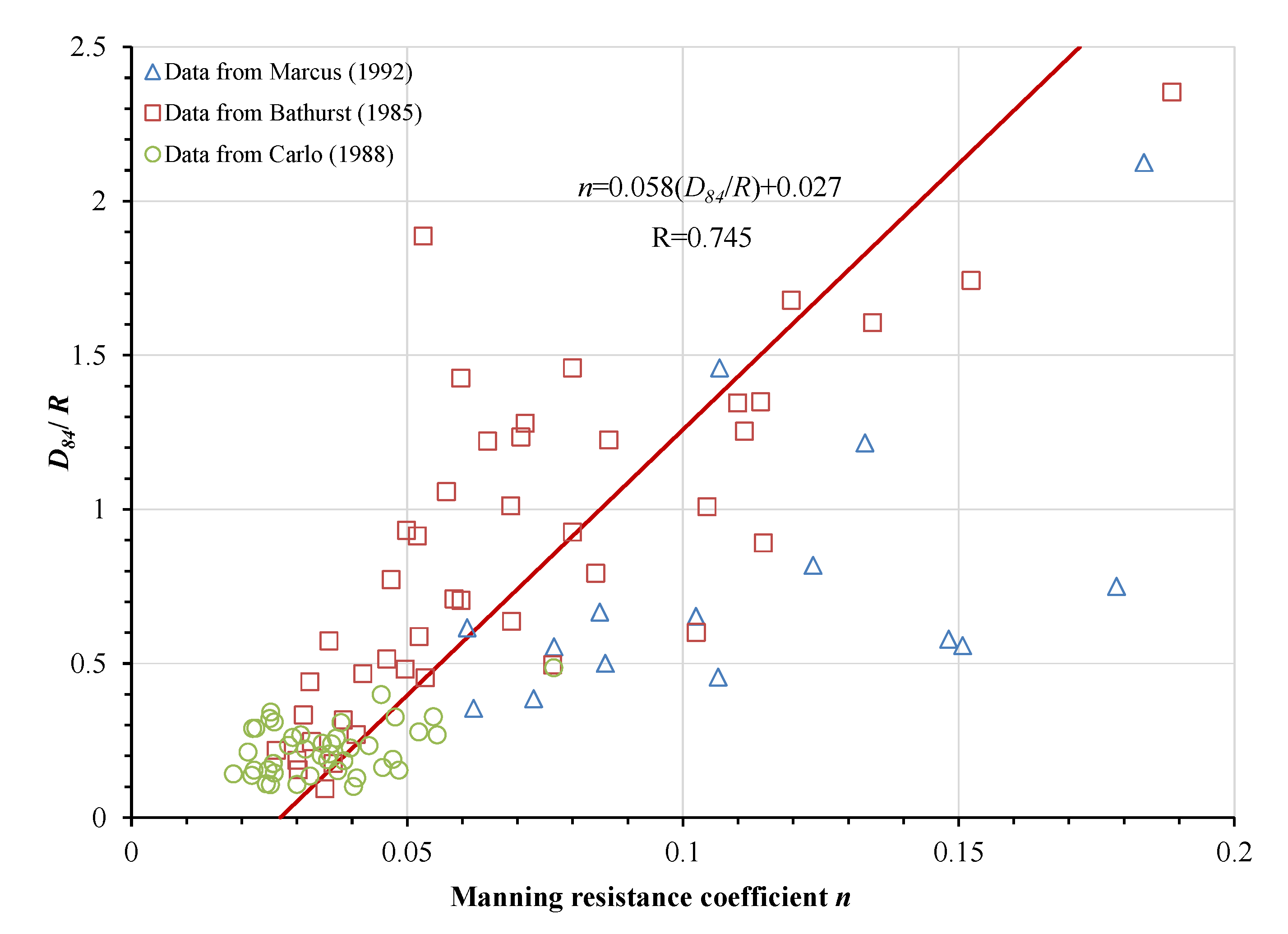
- Roughness of the channel bed. The channel bed roughness is primarily determined by the particle size composition of the bed. Many scholars have tried to establish a relationship between the roughness coefficient and the representative particle size of the channel bed material [11,23,24,25,26]. The influence of particle size on roughness can be so great in some situations that many field techniques will use sediment size to estimate flow resistance [8,23,27,28,29]. A rougher bed surface provides a greater roughness coefficient. However, there are varying opinions in terms of the representative particle size to use, with the most commonly used representative particle sizes being D90, D84, and D50.
- (2)
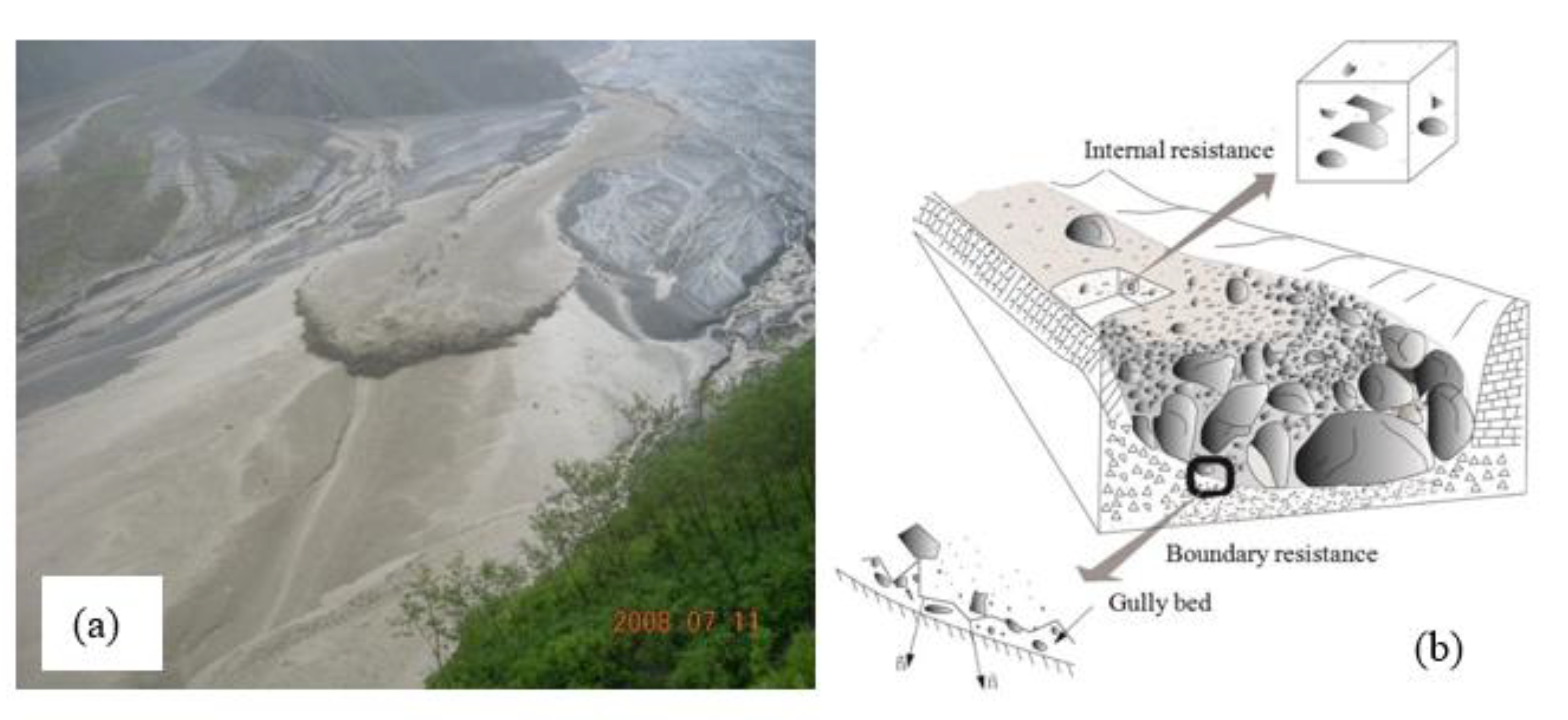
- Cross section geometry. In general, a larger contact area between the debris flow and the channel boundary will result in a greater resistance to movement of the debris flow [30]. The wetted perimeter is typically used to reflect the size of the contact area between a fluid and the boundary, with a larger wetted perimeter creating more resistance. In addition, if an irregular section appears in a channel, or the cross-section changes locally, local head loss will occur that will also reflect an increase in roughness. Due to the randomness of an irregular cross section, the local head loss caused by debris flows through an irregular section is very complicated [1]. Therefore, it is easier to select a straight section of channel as much as possible when measuring the roughness coefficient of a debris flow.
- (3)
- (4)
- Solid volume concentration of the debris flow. A debris flow is a special solid-liquid two-phase fluid [14,32] where the liquid phase is mainly a slurry mixed with water and fine particles and the solid phase is mainly large stones and gravel. During movement of a viscous debris flow there is a significant relative motion between the solid and liquid phases. In addition to the viscous resistance of the slurry, the internal resistance also includes the collision and frictional resistance between particles and the resistance generated by the relative motion between the solid and liquid phases [33,34,35]. Takahashi [36] pointed out that the internal resistance of a two-phase flow was dominated by particle collisions, while Iverson [37] believed that the friction between particles was more important. In general, the magnitude of the collision resistance and the frictional resistance are inextricably linked to the content of the solid particles of the debris flow.
- (5)
- Particle composition of solid materials in the debris flow. The gradation of solid phase particles is always wide in a debris flow, which makes the resistance characteristics very complicated. The fine particles increase the effective viscosity of the liquid slurry [38], which inhibits the fluid turbulence to a certain extent and thereby reduces energy loss during debris flow movement. In addition, the coarse particles in a debris flow will undergo forceful collisions with the raised sand bed at the boundary of the channel and thereby increase movement resistance.
2.2. The Roughness Coefficient of Debris Flows
3. The External Resistance of a Debris Flow
3.1. Expression of External Roughness
3.2. Determine the Unknown Coefficient of the Expression
4. The Internal Resistance of Debris Flow
4.1. Expression of Internal Roughness
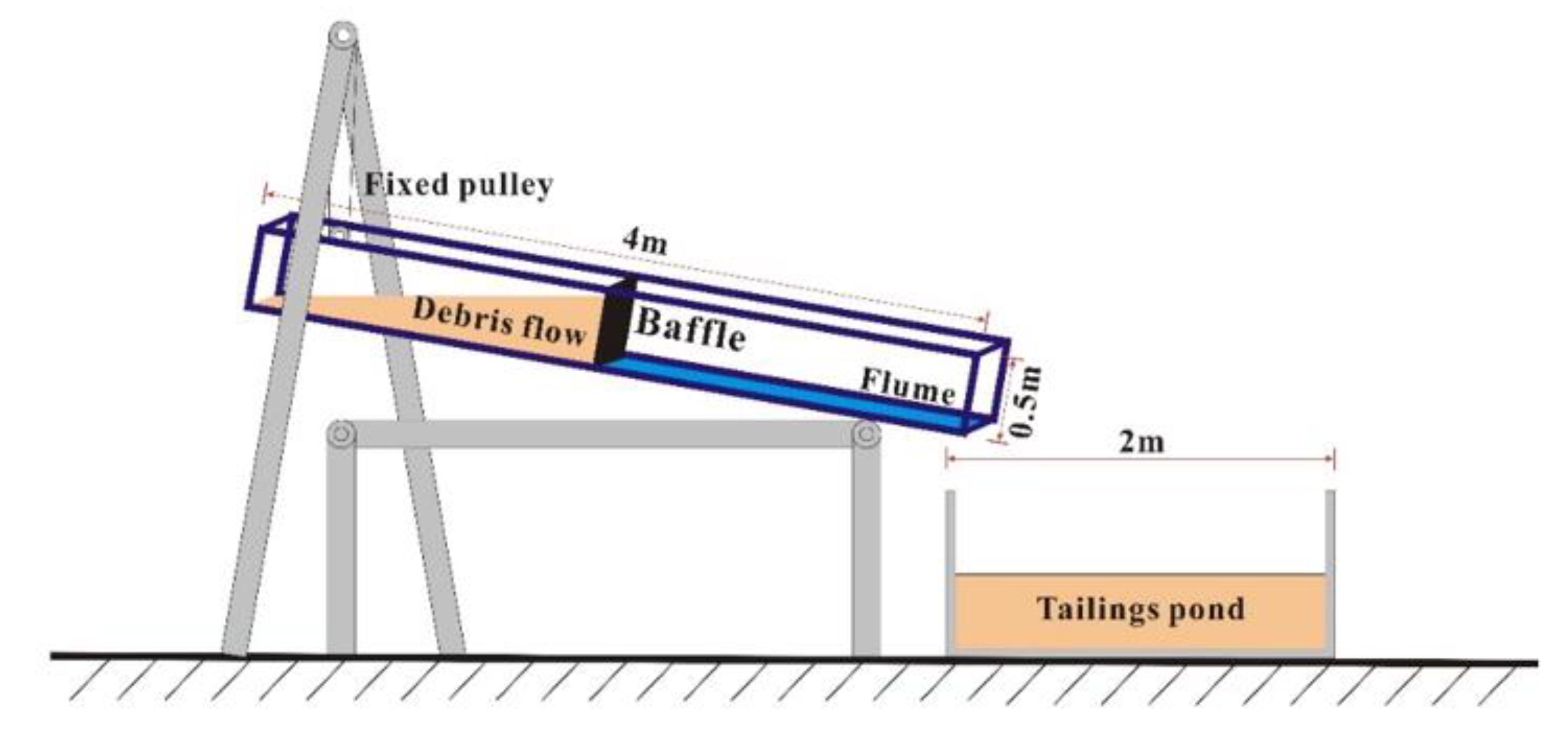
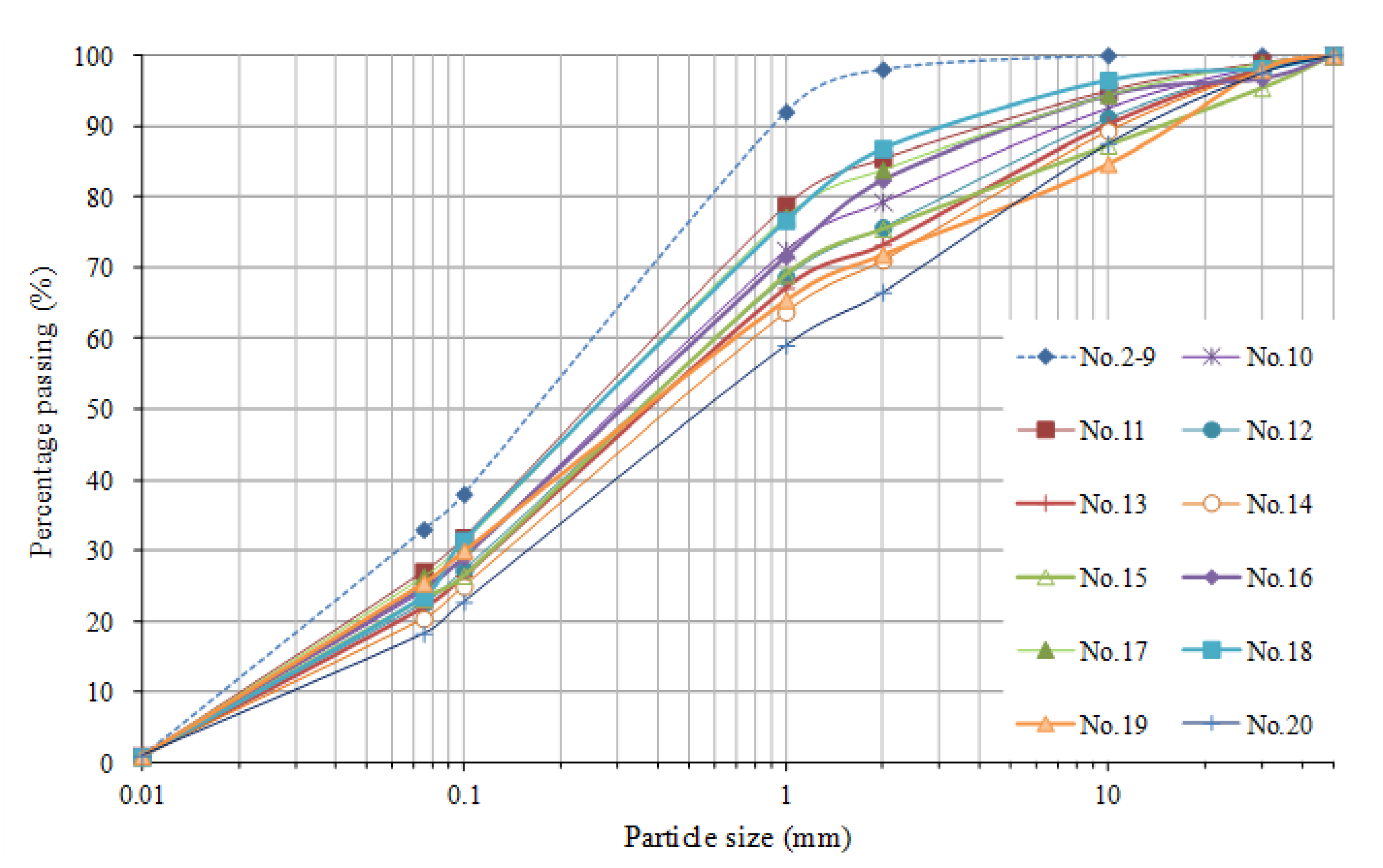
4.2. Experimental Methods
4.3. Calibration of Undetermined Coefficient
5. Verification of Manning’s Roughness Coefficient
6. Conclusions
- (1)
- The Manning’s roughness coefficient of a debris flow is composed of the external roughness coefficient n1 and the internal roughness coefficient n2, and is significantly different from the roughness coefficient of a mountain river.
- (2)
- Dimensionless factors affecting n1 and n2 with precise physical meanings were proposed, with a calculation method for Manning’s roughness coefficient fitted and analyzed based on observation data from published research papers. The analysis results showed that the external resistance coefficient is closely related to the dimensionless factor D84/R in the debris flow channel. The external roughness n2 has the best correlation with Sv, a weak positive correlation with H/D50 and J, and a very weak negative correlation with D16/D50.
- (3)
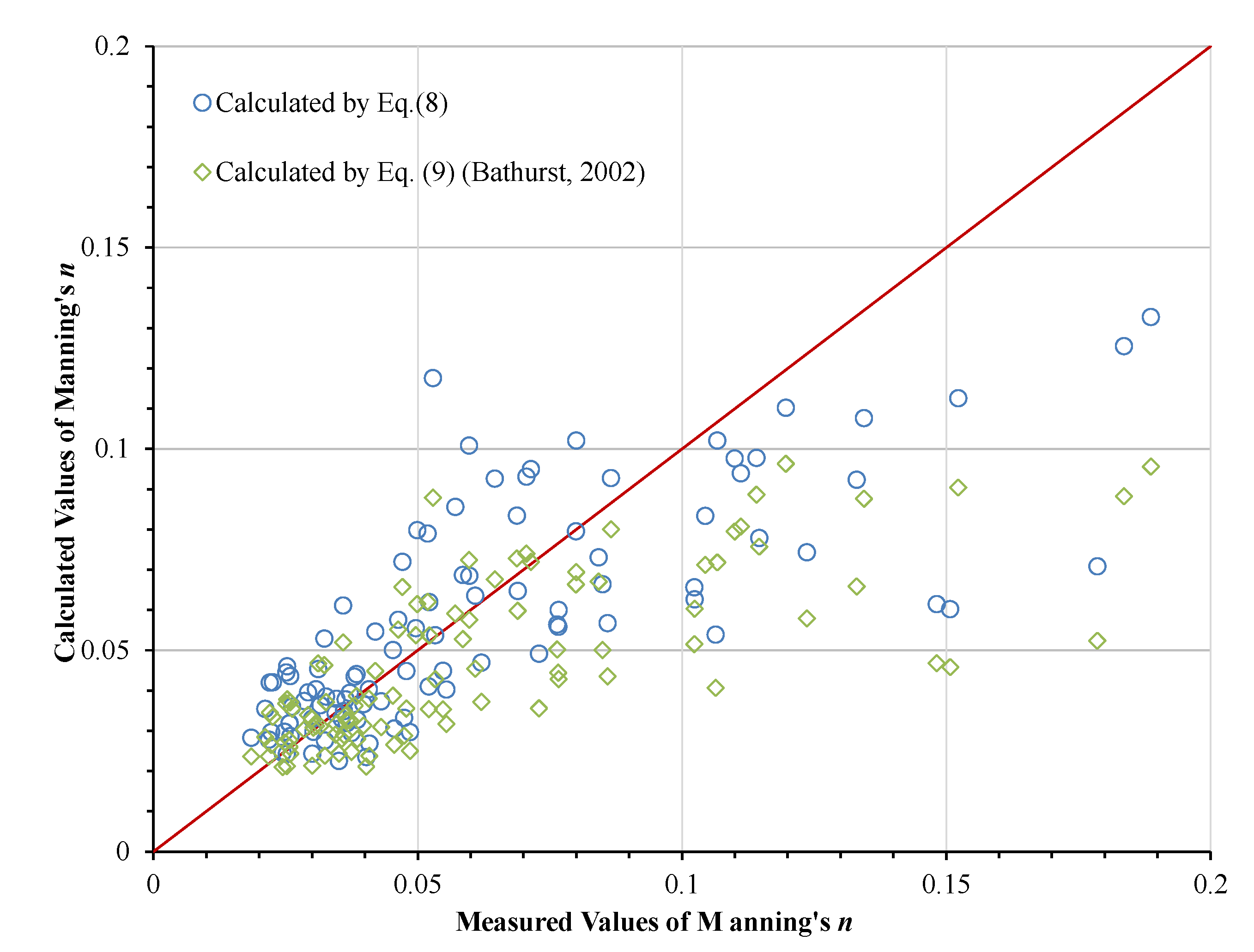
- The expression of external roughness n1 is calibrated based on the observation data of 102 cross-sections listed in previous works, and the internal roughness n2 is calibrated by 20 experimental model tests. Finally, the mathematical expression of Manning’s roughness coefficient is proposed and verified based on 24 groups of observation data from Dongchuan Debris Flow Observation Station in China. Equation (15) is generally satisfactory but still does not truly reflect the importance of some key parameters, as the calculated values have certain errors compared with the observation values.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Powell, D.M. Flow resistance in gravel-bed rivers: Progress in research. Earth Sci. Rev. 2014, 136, 301–338. [Google Scholar] [CrossRef]
- Ferguson, R.I. Time to abandon the Manning equation? Earth Surf. Process. Landf. 2010, 35, 1873–1876. [Google Scholar] [CrossRef]
- Tian, M.; Hu, K.H.; Ma, C.; Lei, F.H. Effect of Bed Sediment Entrainment on Debris-Flow Resistance. J. Hydraul. Eng. 2014, 140, 115–120. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; Mc Graw Hill: New York, NY, USA, 1959; p. 680. [Google Scholar]
- Dalrymple, T.; Benson, M.A. Measurement of Peak Discharge by Slope Area Method; Techniques of Water Resources Investigations, 03-A2; U.S. Department of the Interior: Washington, DC, USA, 1967; pp. 12–16. [CrossRef]
- Jarrett, R.D. Hydraulics of High-Gradient Streams. J. Hydraul. Eng. 1984, 110, 1519–1539. [Google Scholar] [CrossRef]
- Marcus, W.A.; Roberts, K.; Harvey, L.; Tackman, G. An evaluation of methods for estimating Manning’s n in small mountain streams. Mt. Res. Dev. 1992, 12, 227–239. [Google Scholar] [CrossRef]
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering, and Straight; United States Geological Survey: Reston, VA, USA, 1957; p. 85.
- Rouse, H. Critical analysis of open-channel flow resistance. J. Hydraul. Div. 1965, 91, 1–25. [Google Scholar]
- Hey, R.D. Flow resistance in gravel-bed rivers. J. Hydraul. Div. 1979, 105, 365–379. [Google Scholar]
- Bathurst, J.C. Flow resistance of large scale roughness. J. Hydraul. Div. 1978, 104, 1587–1603. [Google Scholar]
- Rickenmann, D. An alternative equation for the mean velocity in gravel bed rivers and mountain torrents. In Hydraulic Engineering; ASCE: Buffalo, NY, USA, 1994; pp. 672–676. [Google Scholar]
- Rickenmann, D. Empirical Relationships for Debris Flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Cui, P. Study on conditions and mechanisms of debris flow initiation by means of experiments. Chin. Sci. Bull. 1992, 37, 759–763. (In Chinese) [Google Scholar]
- Yan, Y.; Cui, Y.; Tian, X.; Hu, S.; Guo, J.; Wang, Z.; Yin, S.; Liao, L. Seismic signal recognition and interpretation of the 2019 “7.23” Shuicheng landslide by seismogram stations. Landslides 2020, 17, 1–16. [Google Scholar] [CrossRef]
- Jin, M.; Fread, D.D.L. 1D Modeling of Mud/Debris Unsteady Flows. J. Hydraul. Eng. 1999, 125, 827–834. [Google Scholar] [CrossRef]
- Hu, K.; Tian, M.; Li, Y. Influence of Flow Width on Mean Velocity of Debris Flows in Wide Open Channel. J. Hydraul. Eng. 2013, 139, 65–69. [Google Scholar] [CrossRef]
- Cui, P.; Tang, J.B.; Lin, P.Z. Research progress of resistance character of debris flow. J. Sichuan Univ. 2016, 48, 1–11. (In Chinese) [Google Scholar]
- Kang, Z.C. A Velocity Analysis of Viscous Debris Flow at Jiangjia Gully of Dongchuan in Yunnan; Science Press: Beijing, China, 1985; pp. 97–100. (In Chinese) [Google Scholar]
- Fei, X.J. Velocity and solid transportation concentration of viscous debris flow. J. Hydraul. Eng. 2003, 2, 15–18. (In Chinese) [Google Scholar]
- Qian, N.; Wan, Z.H. The Dynamic Theory of Sedimentation; The Science Publishing Company: Beijing, China, 1983. (In Chinese) [Google Scholar]
- Cowan, W.L. Estimating Hydraulic Roughness Coefficients. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Bray, D.I. Estimating average velocity in gravel-bed rivers. J. Hydraul. Div. 1979, 105, 1103–1122. [Google Scholar]
- Griffiths, G.A. Flow Resistance in Coarse Gravel Bed Rivers. J. Hydraul. Eng. 1981, 107, 899–918. [Google Scholar]
- Graf, W.H.; Cao, H.H.; Suszka, L. Hydraulics of steep mobile-bed channels. In Proceedings of the 20th Congress of the IAHR, Moscow, Russia, 5–9 September 1983; pp. 301–305. [Google Scholar]
- Oubanas, H.; Gejadze, I.; Malaterre, P.O.; Durand, M.; Wei, R.; Frasson, R.; Domeneghetti, A. Discharge Estimation in Ungauged Basins Through Variational Data Assimilation: The Potential of the SWOT Mission. Water Resour. Res. 2018, 54, 2405–2423. [Google Scholar] [CrossRef]
- Strickler, A. Contributions to the Question of a Velocity Formula and Roughness Data for Streams, Channels and Closed Pipelines; Mitteilungen des Eidgenossischen Amtes fur Wasserwirtschaft: Bern, Switzerland, 1923. [Google Scholar]
- Boyer, M.C. Estimating the Manning coefficient from average bed roughness in open channels. Eos Trans. AGU 1954, 35, 957–961. [Google Scholar] [CrossRef]
- Limerinos, J.T. Determination of the Manning Coefficient from Measured Bed Roughness in Natural Channels; US Geological Survey: Reston, VA, USA, 1898; p. 47.
- Yen, B.C. Open Channel Flow Resistance. J. Hydraul. Eng. 2002, 128, 20–39. [Google Scholar] [CrossRef]
- Du, R.H.; Kang, Z.C.; Chen, X.Q.; Zhu, P.Y. Comprehensive Investigation and Control Planning for Debris Flow in the Xiaojiang River Basin of Yunan Province; Science and technology literature press: Chongqing Branch, Chongqing, China, 1987; pp. 145–150. (In Chinese) [Google Scholar]
- Major, J.; Iverson, R.M. Debris-flow deposition: Effects of pore-fluid pressure and friction concentrated at flow margins. Geol. Soc. Am. Bull. 1999, 111, 1424–1434. [Google Scholar] [CrossRef]
- Pitman, E.B.; Le, L. A two-fluid model for avalanche and debris flows. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 363, 1573–1601. [Google Scholar] [CrossRef] [PubMed]
- Berzi, D.; Jenkins, J.T. A theoretical analysis of free-surfaceflows of saturated granular-liquid mixtures. J. Fluid Mech. 2008, 608, 393–410. [Google Scholar]
- Pudasaini, S.P. A general two-phase debris flow model. J. Geophys. Res. Space Phys. 2012, 117, 131–144. [Google Scholar] [CrossRef]
- Takahashi, T. Mechanical characteristics of debris flow. J. Hydraul. Div. 1978, 104, 1153–1169. [Google Scholar]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J. Influence of size disparity on small-strain shear modulus of sand-fines mixtures. Soil Dyn. Earthq. Eng. 2018, 115, 217–224. [Google Scholar] [CrossRef]
- Soto, A.U.; Madrid-Aris, M. Roughness coefficient in Mountain rivers. In Hydraulic Engineering; Cotroneo, G., Rumer, R., Eds.; American Society of Civil Engineering: New York, NY, USA, 1994. [Google Scholar]
- Shu, A.P.; Fei, X.J. Calculation for velocity and discharge of the viscous debris flow. J. Sediment Res. 2003, 3, 7–11. (In Chinese) [Google Scholar]
- Wiberg, P.L.; Smith, J.D. Velocity distribution and bed roughness in high-gradient streams. Water Resour. Res. 1991, 27, 825–838. [Google Scholar] [CrossRef]
- Colosimo, C.; Copertino, V.A.; Veltri, M. Friction Factor Evaluation in Gravel-Bed Rivers. J. Hydraul. Eng. 1988, 114, 861–876. [Google Scholar] [CrossRef]
- Bagnold, R.A. Experiments on a gravity free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1954, 225, 49–63. [Google Scholar]
- Kang, Z.C.; Cui, P.; Wei, F.Q.; He, S.F. Observational Experimental Data Collection of the Dongchuan Debris Flow Observation and Research Station of the Chinese Academy of Sciences (1961–1984); Science Press: Beijing, China, 2006; pp. 254–257. (In Chinese) [Google Scholar]
- Pähtz, T.; Kok, J.F.; Parteli, E.J.; Herrmann, H.J. Flux Saturation Length of Sediment Transport. Phys. Rev. Lett. 2013, 111, 218002. [Google Scholar] [CrossRef] [PubMed]
- Pähtz, T.; Parteli, E.J.; Kok, J.F.; Herrmann, H.J. Analytical model for flux saturation in sediment transport. Phys. Rev. E 2014, 89, 052213. [Google Scholar] [CrossRef]



| No | Fluid Type | ρs (kg/m3) | V (m/s) | α (°) | Sv | H (m) | R (m) | D16 (mm) | D50 (mm) | D84 (mm) | n | n2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | pure water | 1000 | 2.41 | 18° | 0.000 | 0.019 | 0.017 | 0.000 | 0.000 | 0.000 | 0.016 | 0.000 |
| 2. | single-phase flow | 1270 | 2.02 | 15° | 0.159 | 0.041 | 0.032 | 0.026 | 0.170 | 0.700 | 0.026 | 0.010 |
| 3. | single-phase flow | 1320 | 2.09 | 18° | 0.188 | 0.058 | 0.042 | 0.026 | 0.170 | 0.700 | 0.033 | 0.017 |
| 4. | single-phase flow | 1550 | 1.27 | 15° | 0.324 | 0.055 | 0.040 | 0.026 | 0.170 | 0.700 | 0.048 | 0.032 |
| 5. | single-phase flow | 1720 | 0.93 | 18° | 0.424 | 0.061 | 0.043 | 0.026 | 0.170 | 0.700 | 0.076 | 0.060 |
| 6. | single-phase flow | 1420 | 1.49 | 20° | 0.247 | 0.059 | 0.042 | 0.026 | 0.170 | 0.700 | 0.049 | 0.034 |
| 7. | single-phase flow | 1530 | 1.28 | 14° | 0.312 | 0.063 | 0.044 | 0.026 | 0.170 | 0.700 | 0.049 | 0.033 |
| 8. | single-phase flow | 1630 | 1.08 | 16° | 0.371 | 0.051 | 0.038 | 0.026 | 0.170 | 0.700 | 0.056 | 0.041 |
| 9. | single-phase flow | 1670 | 1.02 | 18° | 0.394 | 0.045 | 0.035 | 0.026 | 0.170 | 0.700 | 0.059 | 0.044 |
| 10. | two-phase flow | 1370 | 2.19 | 18° | 0.218 | 0.065 | 0.045 | 0.042 | 0.310 | 4.100 | 0.033 | 0.018 |
| 11. | two-phase flow | 1550 | 1.46 | 15° | 0.324 | 0.069 | 0.047 | 0.038 | 0.240 | 2.000 | 0.046 | 0.031 |
| 12. | two-phase flow | 1630 | 1.45 | 18° | 0.371 | 0.068 | 0.047 | 0.051 | 0.350 | 5.600 | 0.051 | 0.035 |
| 13. | two-phase flow | 1680 | 1.31 | 15° | 0.400 | 0.055 | 0.040 | 0.047 | 0.340 | 6.100 | 0.046 | 0.031 |
| 14. | two-phase flow | 1700 | 1.43 | 18° | 0.412 | 0.051 | 0.038 | 0.058 | 0.430 | 7.700 | 0.045 | 0.030 |
| 15. | two-phase flow | 1730 | 1.37 | 16° | 0.429 | 0.063 | 0.044 | 0.039 | 0.370 | 9.100 | 0.049 | 0.033 |
| 16. | two-phase flow | 1760 | 1.12 | 14° | 0.447 | 0.057 | 0.041 | 0.041 | 0.310 | 2.400 | 0.053 | 0.038 |
| 17. | two-phase flow | 1770 | 1.11 | 18° | 0.453 | 0.049 | 0.037 | 0.038 | 0.260 | 2.600 | 0.057 | 0.041 |
| 18. | two-phase flow | 1810 | 1.01 | 15° | 0.476 | 0.048 | 0.036 | 0.042 | 0.250 | 1.500 | 0.056 | 0.041 |
| 19. | two-phase flow | 1830 | 1.23 | 20° | 0.488 | 0.052 | 0.039 | 0.034 | 0.430 | 14.400 | 0.056 | 0.040 |
| 20. | two-phase flow | 1850 | 1.32 | 18° | 0.500 | 0.041 | 0.032 | 0.061 | 0.550 | 8.100 | 0.044 | 0.028 |
| No | D-M-Y | ρS | SV | U | H | R | J | D84 | D50 | D16 | n | n0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | 29 June 1974 | 1.57 | 0.34 | 3.98 | 0.17 | 0.17 | 0.055 | 2.500 | 0.700 | 0.010 | 0.018 | 0.019 |
| 2. | 29 June 1974 | 1.83 | 0.50 | 3.67 | 0.17 | 0.17 | 0.055 | 5.000 | 1.800 | 0.010 | 0.020 | 0.022 |
| 3. | 16 July 1974 | 2.08 | 0.65 | 8.94 | 1.70 | 1.57 | 0.060 | 22.000 | 5.000 | 0.028 | 0.037 | 0.043 |
| 4. | 16 July 1974 | 2.20 | 0.72 | 8.84 | 1.50 | 1.40 | 0.063 | 34.000 | 7.000 | 0.045 | 0.035 | 0.041 |
| 5. | 16 July 1974 | 2.21 | 0.73 | 7.36 | 2.00 | 1.82 | 0.063 | 50.000 | 9.000 | 0.051 | 0.051 | 0.043 |
| 6. | 16 July 1974 | 2.25 | 0.75 | 7.89 | 2.00 | 1.82 | 0.063 | 43.000 | 11.000 | 0.100 | 0.047 | 0.039 |
| 7. | 16 July 1974 | 2.16 | 0.70 | 10 | 0.95 | 0.87 | 0.063 | 17.000 | 4.100 | 0.021 | 0.023 | 0.040 |
| 8. | 16 July 1974 | 2.25 | 0.75 | 7.36 | 0.55 | 0.52 | 0.063 | 22.000 | 6.000 | 0.032 | 0.022 | 0.033 |
| 9. | 16 July 1974 | 2.07 | 0.64 | 7.63 | 1.10 | 1.01 | 0.063 | 19.000 | 4.500 | 0.026 | 0.033 | 0.038 |
| 10. | 16 July 1974 | 2.19 | 0.71 | 7.63 | 1.00 | 0.93 | 0.063 | 40.000 | 7.000 | 0.040 | 0.031 | 0.037 |
| 11. | 16 July 1974 | 2.21 | 0.72 | 7.32 | 0.90 | 0.84 | 0.063 | 28.000 | 7.500 | 0.050 | 0.031 | 0.033 |
| 12. | 16 July 1974 | 2.19 | 0.71 | 6.63 | 0.70 | 0.65 | 0.063 | 30.000 | 7.000 | 0.048 | 0.029 | 0.033 |
| 13. | 16 July 1974 | 2.09 | 0.65 | 7.63 | 1.27 | 1.16 | 0.063 | 16.000 | 4.000 | 0.026 | 0.036 | 0.042 |
| 14. | 8 July 1982 | 2.15 | 0.69 | 5.87 | 0.90 | 0.86 | 0.060 | 16.000 | 3.500 | 0.006 | 0.038 | 0.042 |
| 15. | 8 July 1982 | 2.24 | 0.74 | 6.29 | 1.20 | 1.15 | 0.060 | 40.000 | 11.000 | 0.220 | 0.043 | 0.033 |
| 16. | 8 July 1982 | 2.33 | 0.80 | 7.33 | 1.80 | 1.70 | 0.060 | 35.000 | 9.000 | 0.055 | 0.048 | 0.043 |
| 17. | 8 July 1982 | 2.15 | 0.69 | 5.5 | 0.80 | 0.76 | 0.060 | 18.000 | 5.400 | 0.014 | 0.037 | 0.032 |
| 18. | 8 July 1982 | 2.21 | 0.73 | 8.8 | 2.20 | 2.14 | 0.060 | 24.000 | 7.000 | 0.026 | 0.046 | 0.047 |
| 19. | 8 July 1982 | 2.24 | 0.74 | 7.33 | 1.50 | 1.46 | 0.060 | 33.000 | 9.000 | 0.056 | 0.043 | 0.037 |
| 20. | 8 July 1982 | 2.09 | 0.65 | 6.29 | 1.00 | 0.95 | 0.060 | 18.000 | 4.000 | 0.010 | 0.038 | 0.039 |
| 21. | 8 July 1982 | 2.14 | 0.68 | 3.62 | 0.40 | 0.39 | 0.063 | 28.000 | 7.600 | 0.020 | 0.037 | 0.030 |
| 22. | 8 July 1982 | 1.89 | 0.55 | 4.94 | 1.30 | 1.28 | 0.063 | 22.000 | 5.500 | 0.014 | 0.060 | 0.032 |
| 23. | 8 July 1982 | 2.29 | 0.77 | 4.54 | 1.20 | 1.18 | 0.063 | 22.000 | 6.400 | 0.020 | 0.062 | 0.041 |
| 24. | 8 July 1982 | 1.72 | 0.43 | 3.26 | 0.30 | 0.29 | 0.063 | 40.000 | 5.000 | 0.010 | 0.034 | 0.034 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Liu, B.; Liu, Y. New Method for Estimating Roughness Coefficient for Debris Flows. Water 2020, 12, 2341. https://doi.org/10.3390/w12092341
Zhu X, Liu B, Liu Y. New Method for Estimating Roughness Coefficient for Debris Flows. Water. 2020; 12(9):2341. https://doi.org/10.3390/w12092341
Chicago/Turabian StyleZhu, Xinghua, Bangxiao Liu, and Yue Liu. 2020. "New Method for Estimating Roughness Coefficient for Debris Flows" Water 12, no. 9: 2341. https://doi.org/10.3390/w12092341
APA StyleZhu, X., Liu, B., & Liu, Y. (2020). New Method for Estimating Roughness Coefficient for Debris Flows. Water, 12(9), 2341. https://doi.org/10.3390/w12092341






