Development and Sensitivity Analysis of an Empirical Equation for Calculating the Amplitude of Pressure Head Loss of Oscillating Water Flow in Different Types of Pipe
Abstract
:1. Introduction
2. Material and Methods
2.1. Experiments
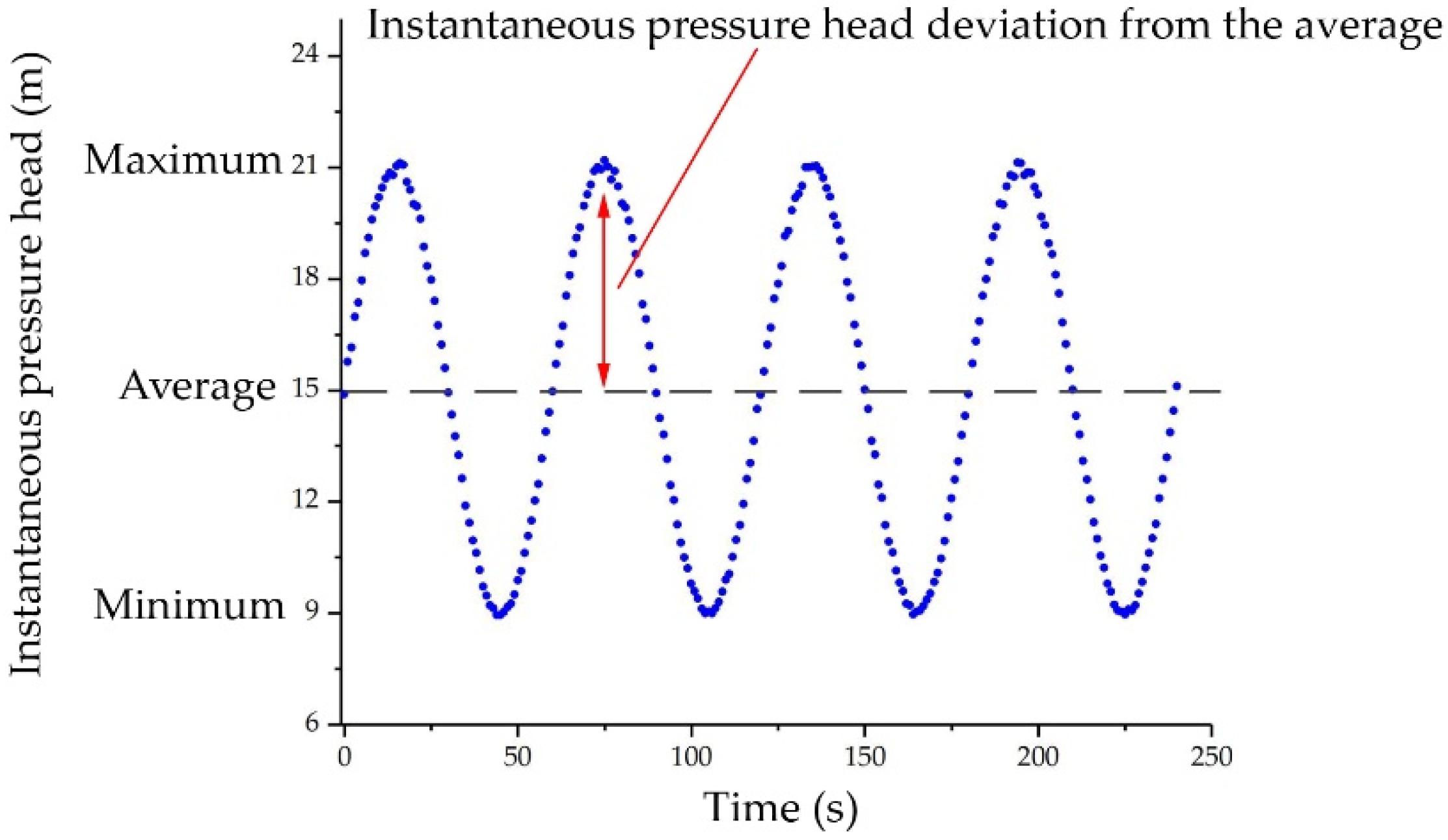
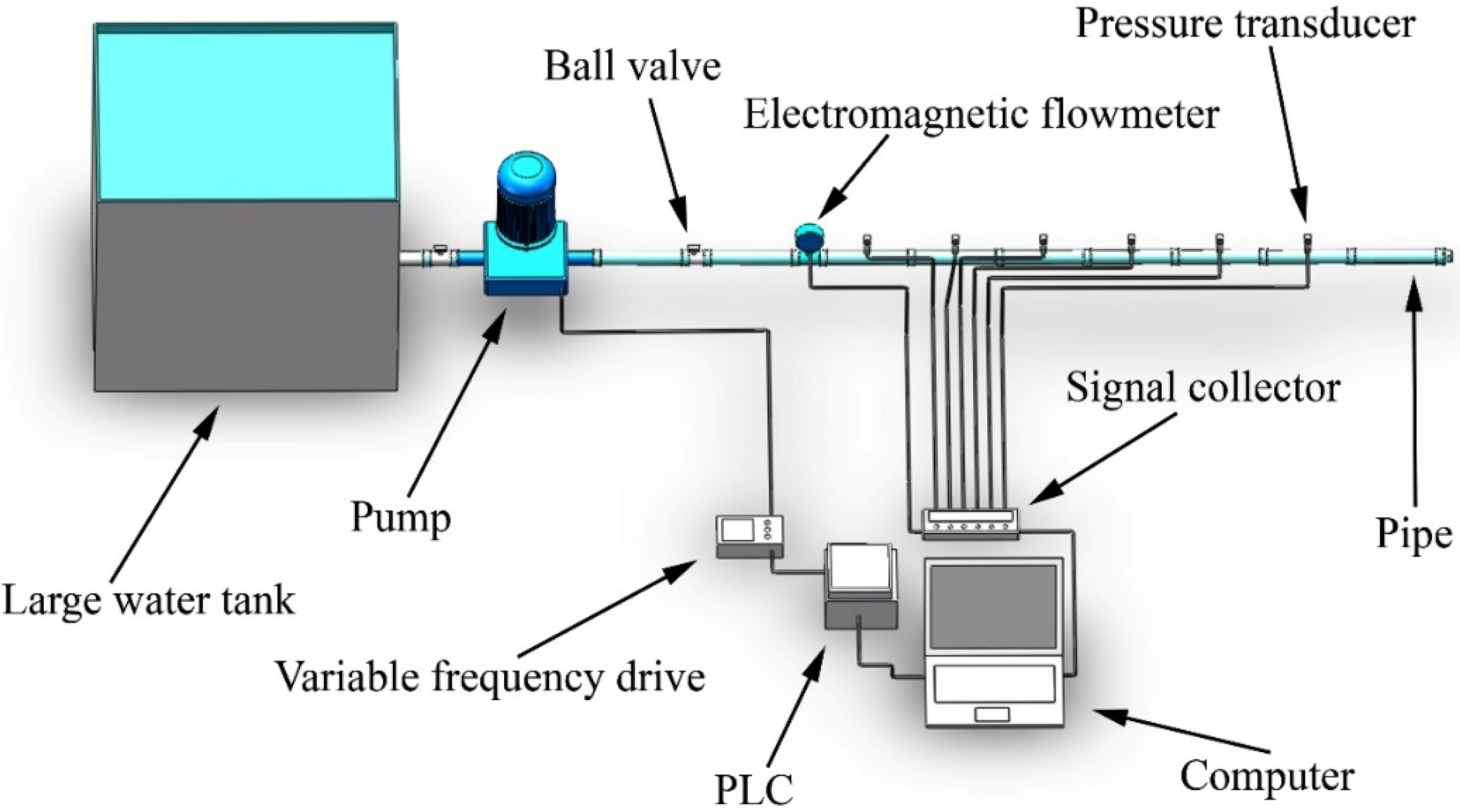
2.1.1. Experimental Equipment and Procedure
2.1.2. Experimental Setup
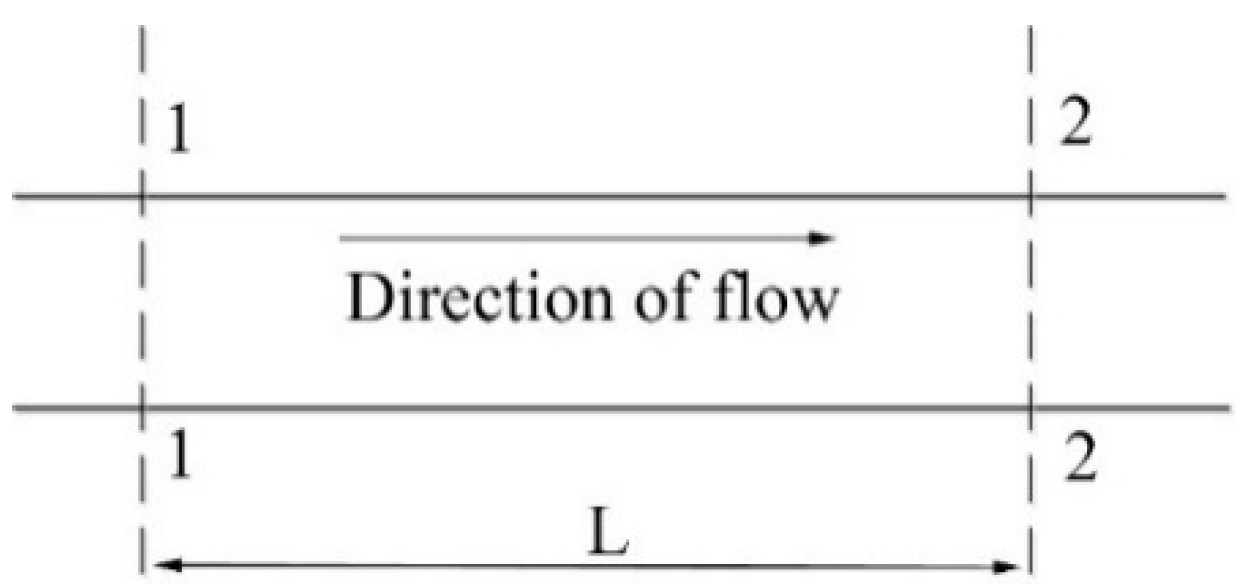
2.2. Calculation Model
2.3. Dimensional Analysis
2.4. Statistical Tests of Data
2.4.1. Multicollinearity Test
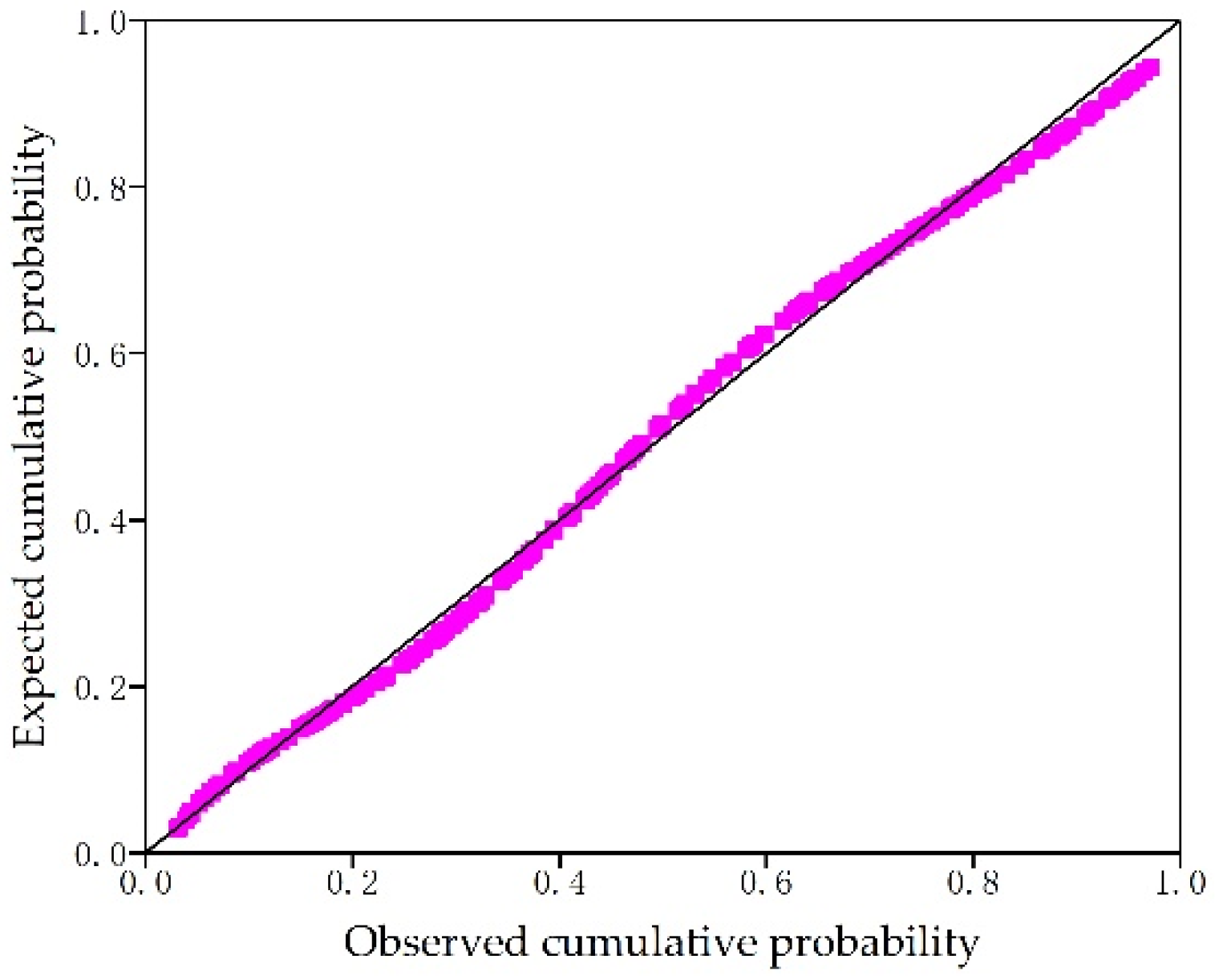
2.4.2. Normality Test
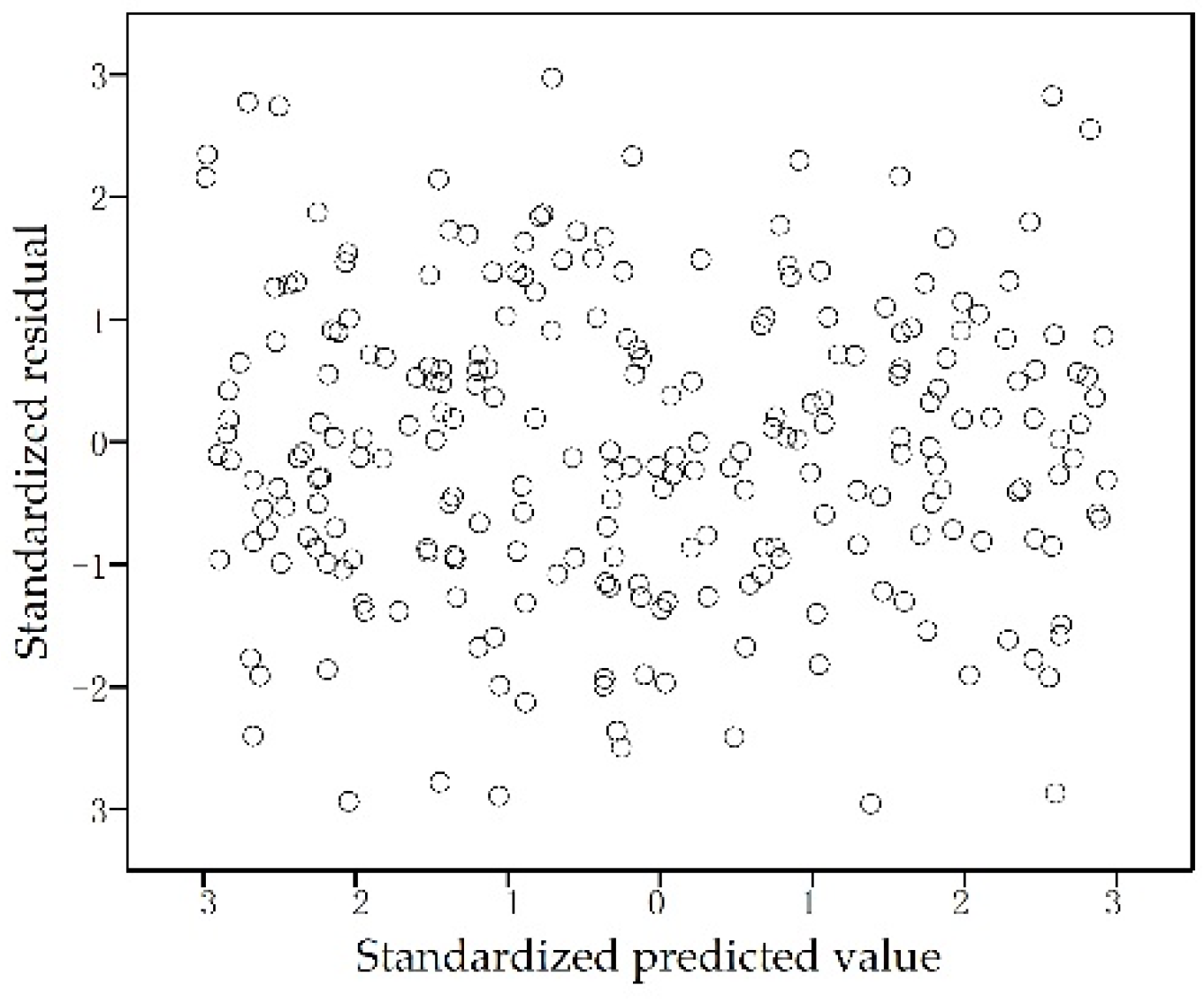
2.4.3. Heteroscedasticity Test
2.5. The Relative Error and Sensitivity Coefficient
3. Results and Discussion
3.1. Results
3.1.1. Validation of the Empirical Equation
3.1.2. Sensitivity Analysis of Empirical Equation
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Woltering, L.; Ibrahim, A.; Pasternak, D.; Ndjeunga, J. The economics of low pressure drip irrigation and hand watering for vegetable production in the Sahel. Agric. Water Manag. 2011, 99, 67–73. [Google Scholar] [CrossRef] [Green Version]
- Marsh, B.; Dowgert, M.; Hutmacher, R.; Phene, C.J. Low-pressure drip system in reduced tillage cotton. WIT Ecol. Environ. 2007, 103, 73–80. [Google Scholar]
- Kranz, W.L.; Eisenhauer, D.E.; Retka, M.T. Water and energy-conservation using irrigation scheduling with center-pivot irrigation systems. Agric. Water Manag. 1992, 22, 325–334. [Google Scholar] [CrossRef]
- O’Shaughnessy, S.A.; Evett, S.R.; Andrade, M.A.; Workneh, F.; Price, J.A.; Rush, C.M. Site-specific variable-rate irrigation as a means to enhance water use efficiency. Trans. ASABE 2016, 59, 239–249. [Google Scholar]
- Singh, A.K.; Sharma, S.P.; Upadhyaya, A.; Rahman, A.; Sikka, A.K. Performance of low energy water application device. Water Resour. Manag. 2010, 24, 1353–1362. [Google Scholar] [CrossRef]
- Masseroni, D.; Arbat, G.; de Lima, I.P. Editorial—Managing and Planning Water Resources for Irrigation: Smart-Irrigation Systems for Providing Sustainable Agriculture and Maintaining Ecosystem Services. Water 2020, 12, 263. [Google Scholar] [CrossRef] [Green Version]
- Wei, Q.S.; Lu, G.; Liu, J.; Shi, Y.S.; Dong, W.C.; Huang, S.H. Evaluations of emitter clogging in drip irrigation by two-phase flow simulations and laboratory experiments. Comput. Electron. Agric. 2008, 63, 294–303. [Google Scholar]
- Oron, G.; Demalach, J.; Hoffman, Z.; Cibotaru, R. Subsurface microirrigation with effluent. J. Irrig. Drain. Eng. ASCE 1991, 117, 25–36. [Google Scholar] [CrossRef]
- Zhai, G.L.; Lv, M.C.; Wang, H.; Xiang, H.A. Plugging of microirrigation system and its prevention. Trans. Chin. Soc. Agric. Eng. 1999, 15, 144–147. [Google Scholar]
- Shamshery, P.; Winter, A.G. Shape and form optimization of on-line pressure-compensating drip emitters to achieve lower activation pressure. J. Mech. Des. 2018, 140, 035001. [Google Scholar] [CrossRef] [Green Version]
- Sayyadi, H.; Nazemi, A.H.; Sadraddini, A.A.; Delirhasannia, R. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler. Biosyst. Eng. 2014, 119, 13–24. [Google Scholar] [CrossRef]
- Seginer, I.; Kantz, D.; Nir, D. The distortion by wind of the distribution patterns of single sprinklers. Agric. Water Manag. 1991, 19, 341–359. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, J.D.; Alam, M.; Zhao, G.Y. Influence of geometrical parameters of labyrinth flow path of drip emitters on hydraulic and anti-clogging performance. Trans. ASABE 2006, 49, 637–643. [Google Scholar] [CrossRef]
- Yu, L.M.; Li, N.; Liu, X.G.; Yang, Q.L.; Li, Z.Y.; Long, J. Influence of dentation angle of labyrinth channel of drip emitters on hydraulic and anti-clogging performance. Irrig. Drain. 2019, 68, 256–267. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.H.; Tang, Y.P.; Lu, B.H. Anti-clogging performance evaluation and parameterized design of emitters with labyrinth channels. Comput. Electron. Agric. 2010, 74, 59–65. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.H.; Tang, Y.P.; Lu, B.H. Structural optimization of labyrinth-channel emitters based on hydraulic and anti-clogging performances. Irrig. Sci. 2011, 29, 351–357. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, S.; Li, H.; Zhu, X. Combination uniformity improvement of impact sprinkler. Trans. Chin. Soc. Agric. Eng. 2011, 27, 107–111. [Google Scholar]
- Li, H.; Jiang, Y.; Xu, M.; Li, Y.; Chen, C. Effect on hydraulic performance of low-pressure sprinkler by an intermittent water dispersion device. Trans. ASABE 2016, 59, 521–532. [Google Scholar]
- Yuan, S.; Wei, Y.; Li, H.; Xiang, Q. Structure design and experiments on the water distribution of the variable-rate sprinkler with non-circle nozzle. Trans. Chin. Soc. Agric. Eng. 2010, 26, 149–153. [Google Scholar]
- Zhang, L.; Wu, P.; Zhu, D.; Zheng, C. Effect of oscillating pressure on labyrinth emitter clogging. Irrig. Sci. 2017, 35, 267–274. [Google Scholar] [CrossRef]
- Zheng, C.; Wu, P.T.; Zhang, L.; Zhu, D.L.; Zhao, X.; An, B.D. Particles movement characteristics in labyrinth channel under different dynamic water pressure modes. Trans. Chin. Soc. Agric. Mach. 2017, 48, 294–301. [Google Scholar]
- Yu, L.M.; Li, N.; Liu, X.G.; Yang, Q.L.; Long, J. Influence of flushing pressure, flushing frequency and flushing time on the service life of a labyrinth-channel emitter. Biosyst. Eng. 2018, 172, 154–164. [Google Scholar] [CrossRef]
- Zhang, K.; Song, B.; Zhu, D. The influence of sinusoidal oscillating water flow on sprinkler and impact kinetic energy Intensities of laterally-moving sprinkler irrigation systems. Water 2019, 11, 1325. [Google Scholar] [CrossRef] [Green Version]
- Hills, D.J.; Silveira, R.C.M.; Wallender, W.W. Oscillating pressure for improving application uniformity of spray emitters. Trans. ASABE 1986, 29, 1080–1085. [Google Scholar] [CrossRef]
- Hills, D.J.; Gu, Y.P.; Wallender, W.W. Sprinkler uniformity for oscillating low water-pressure. Trans. ASABE 1987, 30, 729–734. [Google Scholar] [CrossRef]
- Buchin, A.F.; Pons, S.J.; Hills, D.J.; Abudu, S. Improving Water Application Efficiency in the Landscape through Pressure Oscillation. April 2004. Available online: https://www.researchgate.net/publication/237342500 (accessed on 1 April 2019).
- Tijsseling, A.S. Water hammer with fluid–structure interaction in thick-walled pipes. Comput. Struct. 2007, 85, 844–851. [Google Scholar] [CrossRef] [Green Version]
- Ghidaoui, M.S.; Mansour, S.G.S.; Zhao, M. Applicability of quasisteady and axisymmetric turbulence models in water hammer. J. Hydraul. Eng. 2002, 128, 917–924. [Google Scholar] [CrossRef]
- Zhang, B.; Wan, W.; Shi, M. Experimental and numerical simulation of water hammer in gravitational pipe flow with continuous air entrainment. Water 2018, 10, 928. [Google Scholar] [CrossRef] [Green Version]
- Kochupillai, J.; Ganesan, N.; Padmanabhan, C. A new finite element formulation based on the velocity of flow for water hammer problems. Int. J. Press. Vessel. Pip. 2005, 82, 1–14. [Google Scholar] [CrossRef]
- Besharat, M.; Teresa, V.M.; Ramos, H. Experimental study of air vessel behavior for energy storage or system protection in water hammer events. Water 2017, 9, 63. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Zhou, J.; Li, Y.; Guan, X.; Liu, D.; Zhang, J. Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer. Water 2020, 12, 1025. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Song, B.; Zhu, D. The Development of a Calculation Model for the Instantaneous Pressure Head of Oscillating Water Flow in a Pipeline. Water 2019, 11, 1583. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G. Relating the Hazen-Williams and Darcy-Weisbach friction loss equations for pressurized irrigation. Appl. Eng. Agric. 1996, 12, 685–694. [Google Scholar] [CrossRef]
- Haktanır, T.; Ardıc¸lıog˘lu, M. Numerical modeling of Darcy–Weisbach friction factor and branching pipes problem. Adv. Eng. Softw. 2004, 35, 773–779. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. Harmony search optimization: Application to pipe network design. Int. J. Simul. Model. 2002, 22, 125–133. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Modified Hazen–Williams and Darcy–Weisbach equations for friction and local head losses along irrigation laterals. J. Irrig. Drain. Eng. ASCE 2005, 131, 342–350. [Google Scholar] [CrossRef]
- Yurdem, H.; Demir, V.; Degirmencioglu, A. Development of a mathematical model to predict clean water head losses in hydrocyclone filters in drip irrigation systems using dimensional analysis. Biosyst. Eng. 2010, 105, 495–506. [Google Scholar] [CrossRef]
- Zitterell, D.B.; Frizzone, J.A.; Neto, O.R. Dimensional analysis approach to estimate local head losses in microirrigation connectors. Irrig. Sci. 2014, 32, 169–179. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, D.; Zhang, L.; Zhu, S. Simulation of Local Head Loss in Trickle Lateral Lines Equipped with In-line Emitters Based on Dimensional Analysis: Local head loss in trickle laterals lines. Irrig. Drain. 2018, 67, 572–581. [Google Scholar] [CrossRef]
- Sreen, N.; Purbey, S.; Sadarangani, P. Impact of culture, behavior and gender on green purchase intention. J. Retail. Consum. Serv. 2018, 41, 177–189. [Google Scholar] [CrossRef]
- Olive, D.J. Linear Regression; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Henderson, A.R. Testing experimental data for univariate normality. Clin. Chim. Acta 2006, 366, 112–129. [Google Scholar] [CrossRef] [PubMed]
- Bakar, S.A.; Nadarajah, S.; Adzhar, Z.A. Loss modeling using Burr mixtures. Empir. Econ. 2018, 54, 1503–1516. [Google Scholar]
- Sun, R.; Yuan, H.; Liu, X. Effect of heteroscedasticity treatment in residual error models on model calibration and prediction uncertainty estimation. J. Hydrol. 2017, 554, 680–692. [Google Scholar] [CrossRef]
- Cleasby, I.R.; Nakagawa, S. Neglected biological patterns in the residuals. Behav. Ecol. Sociobiol. 2011, 65, 2361–2372. [Google Scholar] [CrossRef]
- Sang, X.; Zhou, Z.; Wang, H.; Qin, D.; Zhai, Z.; Chen, Q. Development of Soil and Water Assessment Tool Model on Human Water Use and Application in the Area of High Human Activities, Tianjin, China. J. Irrig. Drain. Eng. ASCE 2010, 136, 23–30. [Google Scholar] [CrossRef]
- Wang, X.; Kang, F.; Li, J.; Wang, X. Inverse Parametric Analysis of Seismic Permanent Deformation for Earth-Rockfill Dams Using Artificial Neural Networks. Math. Probl. Eng. 2012, 2012, 1–19. [Google Scholar] [CrossRef]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Scaloppi, E.J. Adjusted F factor for multiple-outlet pipes. J. Irrig. Drain. Eng. 1988, 114, 169–174. [Google Scholar] [CrossRef] [Green Version]
- Anwar, A.A. Factor G for pipelines with equally spaced multiple outlets and outflow. J. Irrig. Drain. Eng. 1999, 125, 34–38. [Google Scholar] [CrossRef]
- Ju, X.; Weckler, P.R.; Wu, P.; Zhu, D.; Wang, X.; Li, Z. New Simplified Approach for Hydraulic Design of Micro-Irrigation Paired Laterals. Trans. ASABE 2015, 58, 1521–1534. [Google Scholar]


| Case | P(s) | D(m) | L(m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C1-1 | 3.92 | 2.48 | 0.6 | 0.25 | 30 | 0.8 | 0.0274 | 0.0003 | 48 |
| C1-2 | 5.17 | 3.36 | 0.72 | 0.35 | 43 | 0.8 | 0.0312 | 0.0004 | 48 |
| C1-3 | 8.69 | 1.99 | 1.2 | 0.12 | 36 | 0.8 | 0.0392 | 0.0004 | 48 |
| C1-4 | 7.67 | 5.2 | 1.18 | 0.6 | 55 | 0.8 | 0.047 | 0.0005 | 48 |
| C1-5 | 10.21 | 4.49 | 1.48 | 0.5 | 70 | 0.8 | 0.049 | 0.0005 | 48 |
| C1-6 | 11.76 | 4.86 | 1.68 | 0.5 | 78 | 0.8 | 0.0616 | 0.0007 | 48 |
| C1-7 | 13.36 | 5.39 | 2.32 | 0.48 | 65 | 0.8 | 0.0734 | 0.0008 | 48 |
| C1-8 | 8.18 | 3.17 | 1.82 | 0.52 | 86 | 0.8 | 0.0784 | 0.0008 | 48 |
| C2-1 | 24.11 | 12.32 | 1.21 | 0.67 | 89 | 1.7 | 0.0206 | 0.0022 | 48 |
| C2-2 | 25.3 | 19.4 | 1.53 | 1.12 | 63 | 1.7 | 0.027 | 0.0025 | 48 |
| C2-3 | 21.02 | 8.25 | 1.74 | 0.56 | 70 | 1.7 | 0.034 | 0.003 | 48 |
| C2-4 | 14.38 | 4.95 | 1.69 | 0.31 | 49 | 1.7 | 0.0434 | 0.0033 | 48 |
| C2-5 | 13.06 | 3.4 | 2.07 | 0.36 | 35 | 1.7 | 0.0654 | 0.0048 | 48 |
| C2-6 | 8.89 | 7.67 | 1.94 | 0.76 | 58 | 1.7 | 0.079 | 0.0055 | 48 |
| C2-7 | 5.18 | 4.25 | 1.51 | 0.79 | 43 | 1.7 | 0.0884 | 0.0058 | 48 |
| C2-8 | 3.87 | 2.81 | 1.4 | 0.6 | 80 | 1.7 | 0.098 | 0.006 | 48 |
| C3-1 | 37.15 | 10.34 | 1.67 | 0.47 | 51 | 2.6 | 0.021 | 0.002 | 48 |
| C3-2 | 26.3 | 15.34 | 1.93 | 0.76 | 43 | 2.6 | 0.028 | 0.002 | 48 |
| C3-3 | 24.84 | 8.63 | 1.92 | 0.55 | 60 | 2.6 | 0.036 | 0.002 | 48 |
| C3-4 | 13.31 | 10.48 | 1.50 | 0.93 | 85 | 2.6 | 0.0452 | 0.0024 | 48 |
| C3-5 | 13.64 | 6.33 | 2.05 | 0.67 | 76 | 2.6 | 0.057 | 0.003 | 48 |
| C3-6 | 9.59 | 7.42 | 2.04 | 0.87 | 69 | 2.6 | 0.0814 | 0.0043 | 48 |
| C3-7 | 5.43 | 3.55 | 1.61 | 0.73 | 95 | 2.6 | 0.0916 | 0.0042 | 48 |
| C3-8 | 3.32 | 2.54 | 1.33 | 0.48 | 34 | 2.6 | 0.1016 | 0.0042 | 48 |
| C4-1 | 37.54 | 10.29 | 1.68 | 0.39 | 54 | 5 | 0.021 | 0.002 | 48 |
| C4-2 | 25.27 | 20.34 | 1.54 | 1.08 | 72 | 5 | 0.028 | 0.002 | 48 |
| C4-3 | 27.41 | 4.59 | 2.12 | 0.3 | 93 | 5 | 0.0364 | 0.0018 | 48 |
| C4-4 | 14.28 | 12.16 | 2.01 | 1.03 | 31 | 5 | 0.058 | 0.0025 | 48 |
| C4-5 | 8.84 | 6.72 | 1.66 | 1.07 | 84 | 5 | 0.069 | 0.003 | 48 |
| C4-6 | 8.23 | 4.22 | 1.73 | 0.45 | 47 | 5 | 0.074 | 0.003 | 48 |
| C4-7 | 12.47 | 4.1 | 2.39 | 0.42 | 62 | 5 | 0.083 | 0.0035 | 48 |
| C4-8 | 6.78 | 3.95 | 1.85 | 0.38 | 41 | 5 | 0.092 | 0.004 | 48 |
| C5-1 | 29.44 | 25.62 | 1.41 | 0.99 | 79 | 6 | 0.0224 | 0.0013 | 48 |
| C5-2 | 17.86 | 15.81 | 1.6 | 1.2 | 71 | 6 | 0.037 | 0.0015 | 48 |
| C5-3 | 14.83 | 7.91 | 1.7 | 0.49 | 36 | 6 | 0.046 | 0.002 | 48 |
| C5-4 | 21.78 | 4.6 | 2.54 | 0.33 | 54 | 6 | 0.058 | 0.0025 | 48 |
| C5-5 | 16.63 | 12.59 | 2.47 | 1.29 | 87 | 6 | 0.0696 | 0.0027 | 48 |
| C5-6 | 9.47 | 5.22 | 2.07 | 0.48 | 45 | 6 | 0.084 | 0.003 | 48 |
| C5-7 | 4.52 | 3.91 | 1.48 | 0.61 | 30 | 6 | 0.093 | 0.0035 | 48 |
| C5-8 | 3.58 | 1.56 | 1.41 | 0.29 | 65 | 6 | 0.103 | 0.0035 | 48 |
| Type of Physical Parameter | Symbol | Parameter | Dimension | Unit |
|---|---|---|---|---|
| Dependent variable | Amplitude of the pressure head loss between Cross-section 1-1 and Cross-section 2-2 along the pipe | L | m | |
| Independent variables | Average velocity at Cross-section 1-1 | |||
| Amplitude of velocity at Cross-section 1-1 | ||||
| Period of oscillating water flow | T | s | ||
| g | Acceleration due to gravity | |||
| Kinematic viscosity of water | ||||
| Density of water | ||||
| E | Modulus of elasticity of the pipe material | |||
| D | Internal pipe diameter | L | m | |
| Thickness of the pipe wall | L | m | ||
| L | Length of pipe between Cross-section 1-1 and Cross-section 2-2 | L | m |
| Pi Term | π1 | π2 | π3 | π4 | π5 | π6 | π7 | π8 |
|---|---|---|---|---|---|---|---|---|
| Expression |
| Pi term | |||||||
|---|---|---|---|---|---|---|---|
| VIF | 2.713 | 2.504 | 3.287 | 3.098 | 4.182 | 1.689 | 1.690 |
| Term in Equation (14) | Coefficient | Standard Deviation | T test | p-Value |
|---|---|---|---|---|
| Constant | 0.00938 | 0.076 | −26.688 | |
| 0.847 | 0.027 | 31.576 | ||
| 1.034 | 0.017 | 60.56 | ||
| −0.035 | 0.025 | −1.404 | ||
| −1.063 | 0.024 | −43.525 | ||
| −0.012 | 0.014 | −0.822 | ||
| −0.022 | 0.015 | −1.464 | ||
| 1.013 | 0.013 | 77.786 |
| Case | P(s) | D(m) | L(m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| T1 | 5.12 | 2.27 | 0.61 | 0.26 | 43 | 0.8 | 0.0246 | 0.0002 | 48 |
| T2 | 13.9 | 9.11 | 1.87 | 0.80 | 59 | 1.7 | 0.0544 | 0.0043 | 48 |
| T3 | 11.88 | 10.83 | 1.98 | 1.09 | 30 | 2.6 | 0.0678 | 0.0036 | 48 |
| T4 | 23.20 | 11.51 | 2.15 | 0.98 | 92 | 5 | 0.046 | 0.002 | 48 |
| T5 | 46.49 | 8.27 | 2.44 | 0.35 | 76 | 6 | 0.029 | 0.0015 | 48 |
| Case | Item | Location Along Pipe (m) | |||||
|---|---|---|---|---|---|---|---|
| 8 | 16 | 24 | 32 | 40 | 48 | ||
| T1 | Calculated amplitude (m) | 0.13 | 0.27 | 0.41 | 0.54 | 0.68 | 0.82 |
| Measured amplitude (m) | 0.12 | 0.29 | 0.46 | 0.5 | 0.81 | 0.88 | |
| Relative error (%) | 8.33 | 6.90 | 10.87 | 8.00 | 16.05 | 6.82 | |
| T2 | Calculated amplitude (m) | 0.37 | 0.75 | 1.13 | 1.52 | 1.9 | 2.29 |
| Measured amplitude (m) | 0.41 | 0.7 | 0.98 | 1.38 | 1.89 | 2.71 | |
| Relative error (%) | 9.76 | 7.14 | 15.31 | 10.14 | 0.53 | 15.50 | |
| T3 | Calculated amplitude (m) | 0.42 | 0.85 | 1.28 | 1.71 | 2.14 | 2.57 |
| Measured amplitude (m) | 0.38 | 1.01 | 1.46 | 1.85 | 1.93 | 2.3 | |
| Relative error (%) | 10.53 | 15.84 | 12.33 | 7.57 | 10.88 | 11.74 | |
| T4 | Calculated amplitude (m) | 0.63 | 1.27 | 1.92 | 2.57 | 3.22 | 3.87 |
| Measured amplitude (m) | 0.74 | 1.16 | 1.66 | 2.33 | 3.12 | 4.51 | |
| Relative error (%) | 14.86 | 9.48 | 15.66 | 10.30 | 3.21 | 14.19 | |
| T5 | Calculated amplitude (m) | 0.43 | 0.87 | 1.31 | 1.76 | 2.21 | 2.65 |
| Measured amplitude (m) | 0.39 | 1.01 | 1.56 | 1.95 | 2.43 | 2.36 | |
| Relative error (%) | 10.26 | 13.86 | 16.03 | 9.74 | 9.05 | 12.29 | |
| Parameter | Initial Value | Value Range of Each Parameter |
|---|---|---|
| Average velocity at Cross-section 1-1 () | 3.24 | 1.62–4.86 |
| Amplitude of velocity at Cross-section 1-1 () | 0.62 | 0.31–0.93 |
| Period of oscillating water flow (P) | 60.32 | 30.16–90.48 |
| Modulus of elasticity of the pipe material (E) | 3.18 | 1.59–4.77 |
| Internal pipe diameter (D) | 0.056 | 0.0280–0.0840 |
| Thickness of the pipe wall () | 0.0026 | 0.0013–0.0038 |
| Length of pipe between Cross-section 1-1 and Cross-section 2-2 (L) | 28.46 | 14.23–42.69 |
| Sensitivity classification | highly sensitive | sensitive | medium sensitive | insensitive |
| Parameter | Sensitivity Coefficient | Sensitivity Classification |
|---|---|---|
| Average velocity at Cross-section 1-1 () | 0.85 | sensitive |
| Amplitude of velocity at Cross-section 1-1 () | 1.03 | highly sensitive |
| Period of oscillating water flow (P) | −0.37 | sensitive |
| Modulus of elasticity of the pipe material (E) | −0.22 | sensitive |
| Internal pipe diameter (D) | −1.55 | highly sensitive |
| Thickness of the pipe wall () | −0.13 | medium sensitive |
| Length of pipe between Cross-section 1-1 and Cross-section 2-2 (L) | 1.01 | highly sensitive |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zhang, B.; Zhu, D. Development and Sensitivity Analysis of an Empirical Equation for Calculating the Amplitude of Pressure Head Loss of Oscillating Water Flow in Different Types of Pipe. Water 2020, 12, 2421. https://doi.org/10.3390/w12092421
Zhang K, Zhang B, Zhu D. Development and Sensitivity Analysis of an Empirical Equation for Calculating the Amplitude of Pressure Head Loss of Oscillating Water Flow in Different Types of Pipe. Water. 2020; 12(9):2421. https://doi.org/10.3390/w12092421
Chicago/Turabian StyleZhang, Kai, Baoxu Zhang, and Delan Zhu. 2020. "Development and Sensitivity Analysis of an Empirical Equation for Calculating the Amplitude of Pressure Head Loss of Oscillating Water Flow in Different Types of Pipe" Water 12, no. 9: 2421. https://doi.org/10.3390/w12092421
APA StyleZhang, K., Zhang, B., & Zhu, D. (2020). Development and Sensitivity Analysis of an Empirical Equation for Calculating the Amplitude of Pressure Head Loss of Oscillating Water Flow in Different Types of Pipe. Water, 12(9), 2421. https://doi.org/10.3390/w12092421





