Geomorphologic Analysis of Small River Basin within the Framework of Fractal Tree
Abstract
:1. Introduction
2. Theoretical Background
2.1. Horton’s Law
- Channels that originate at a source are defined to be the first-order streams.
- When two streams of order join a stream of order is generated.
- When two streams of different orders join, the channel segment immediately downstream has the higher order of the two combining streams.
2.2. Hack’s Law
2.3. Fractal Tree
3. Methodology
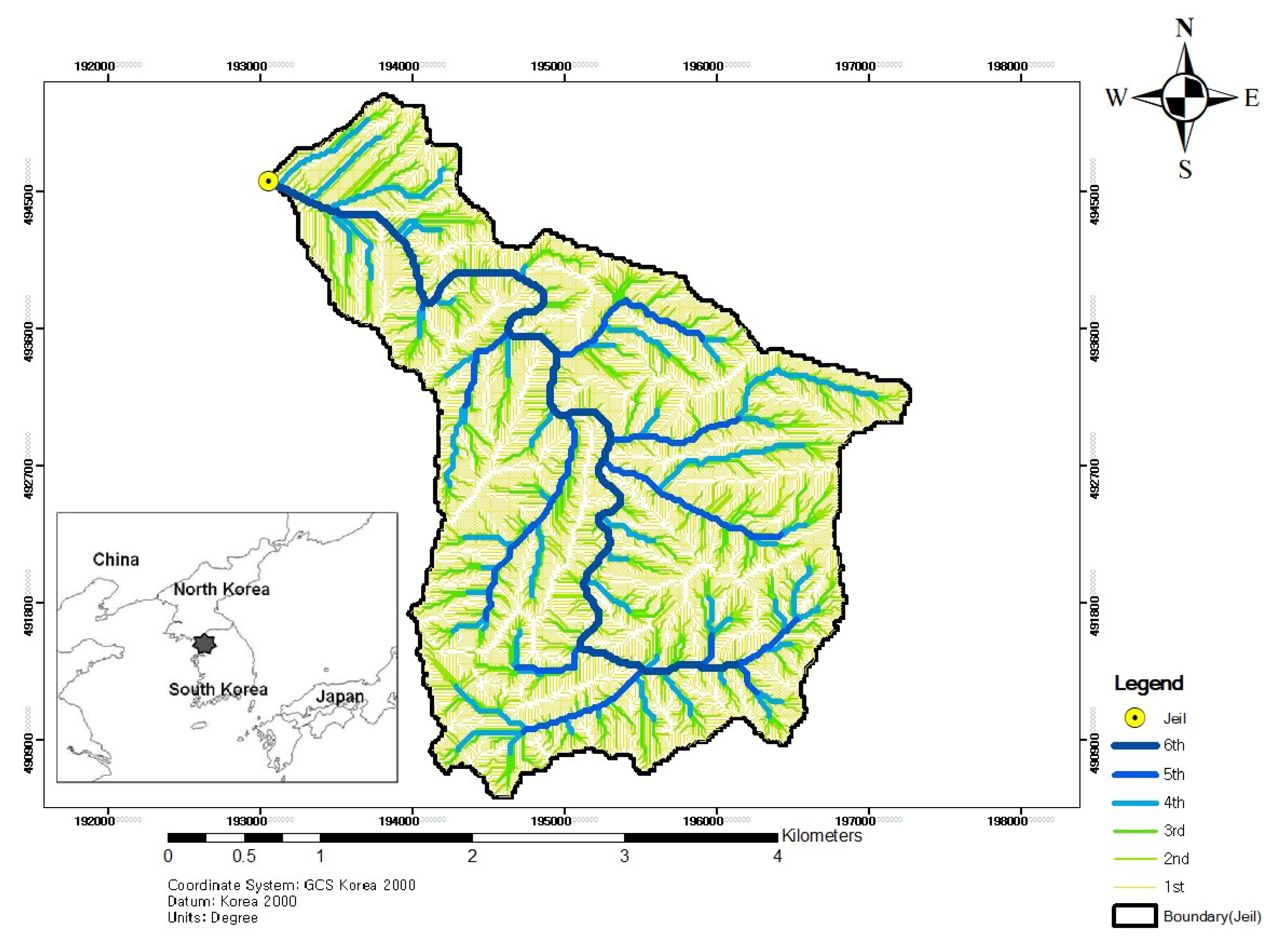
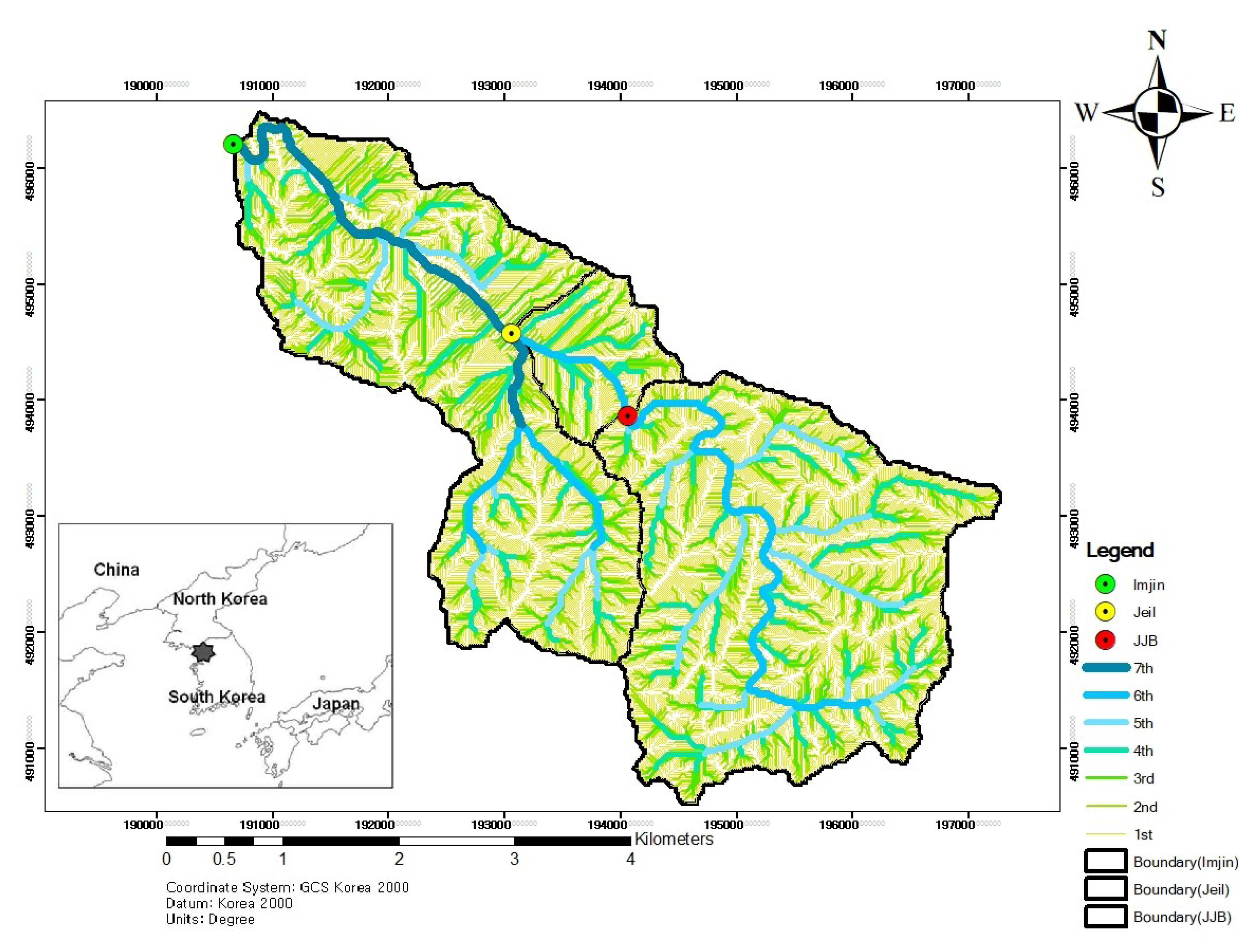
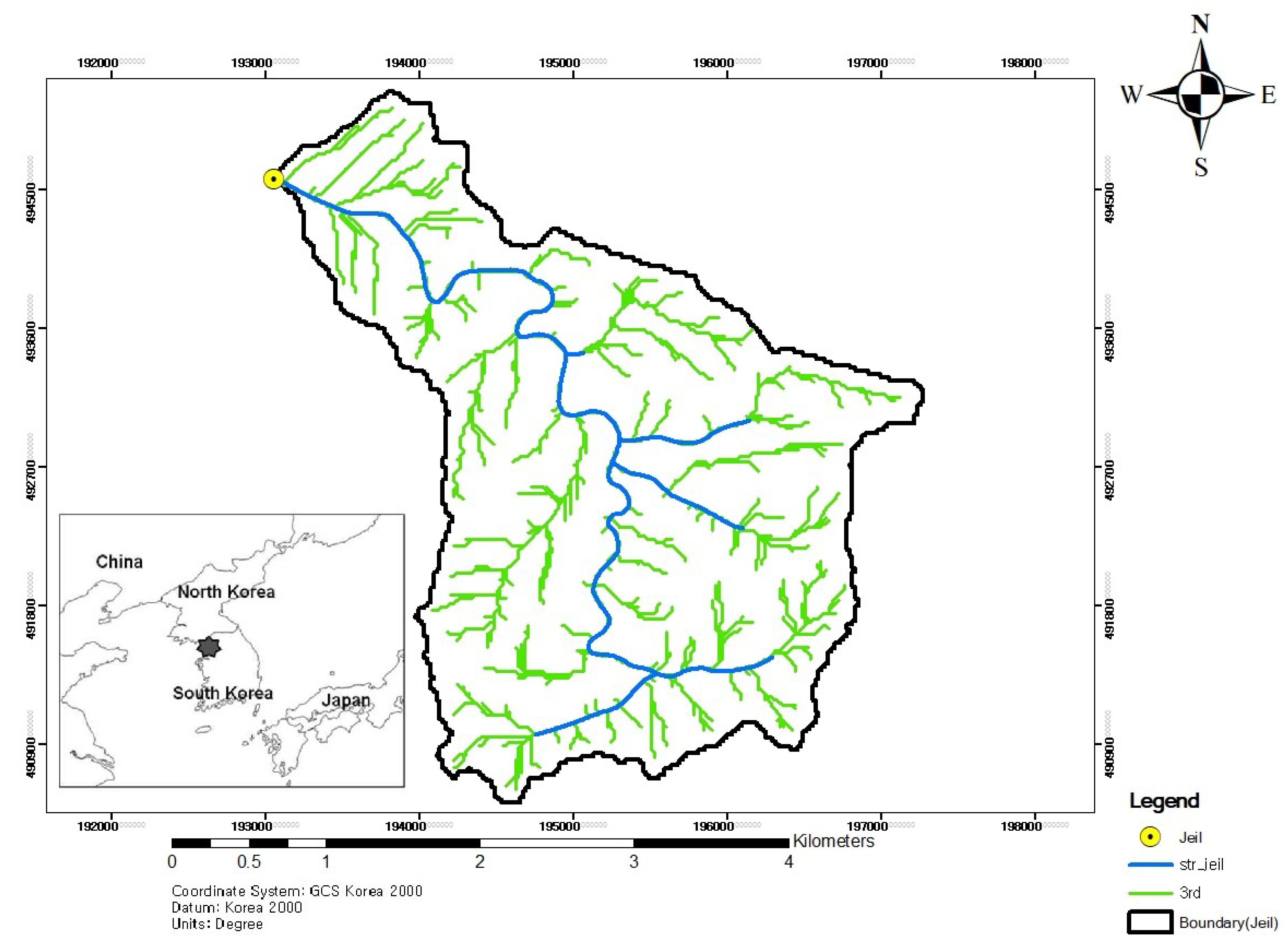
3.1. Study Site
3.2. Geomorphologic Analysis
3.3. Scaling Relations
4. Results and Discussion
4.1. Construction of Fractal Tree
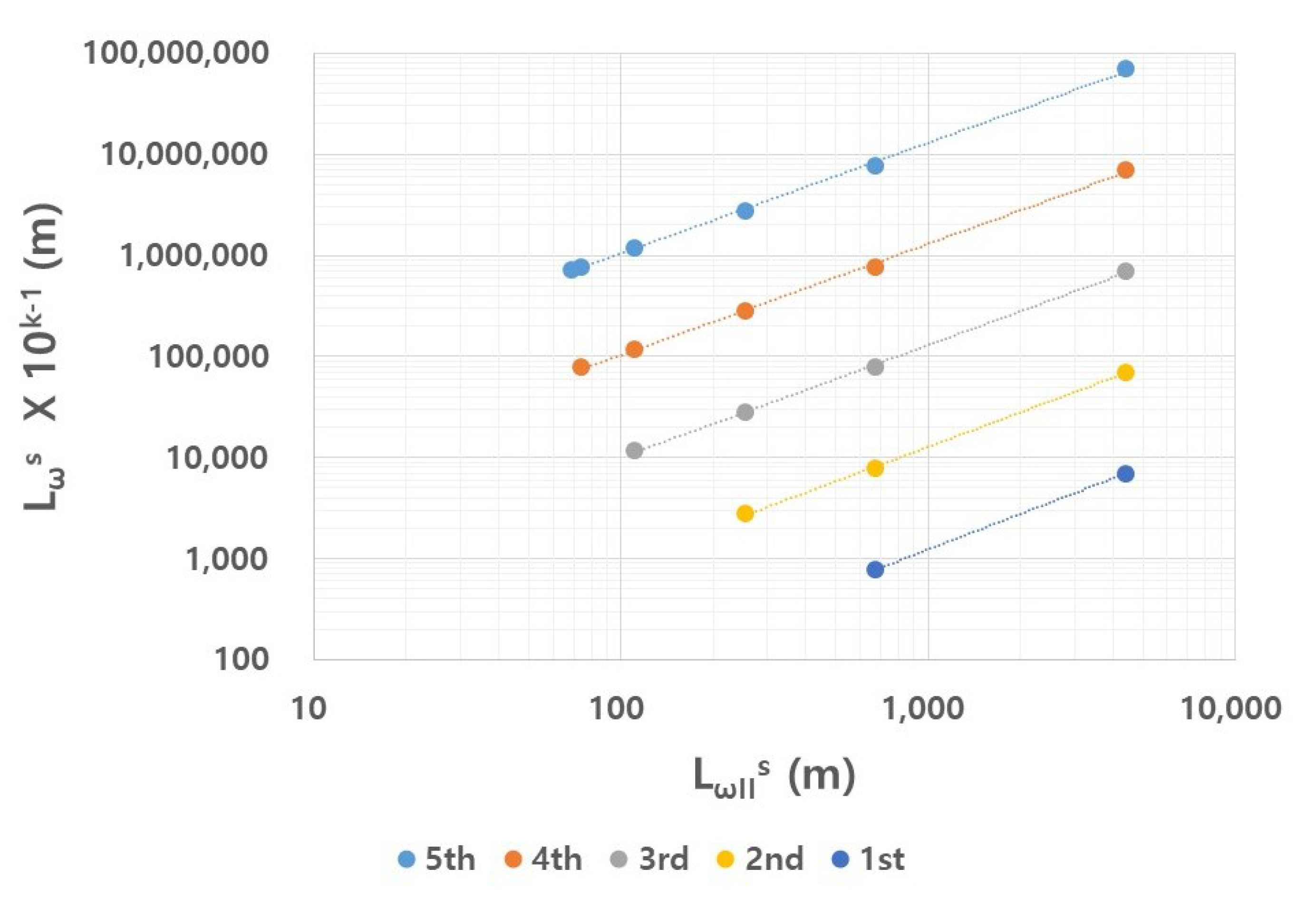
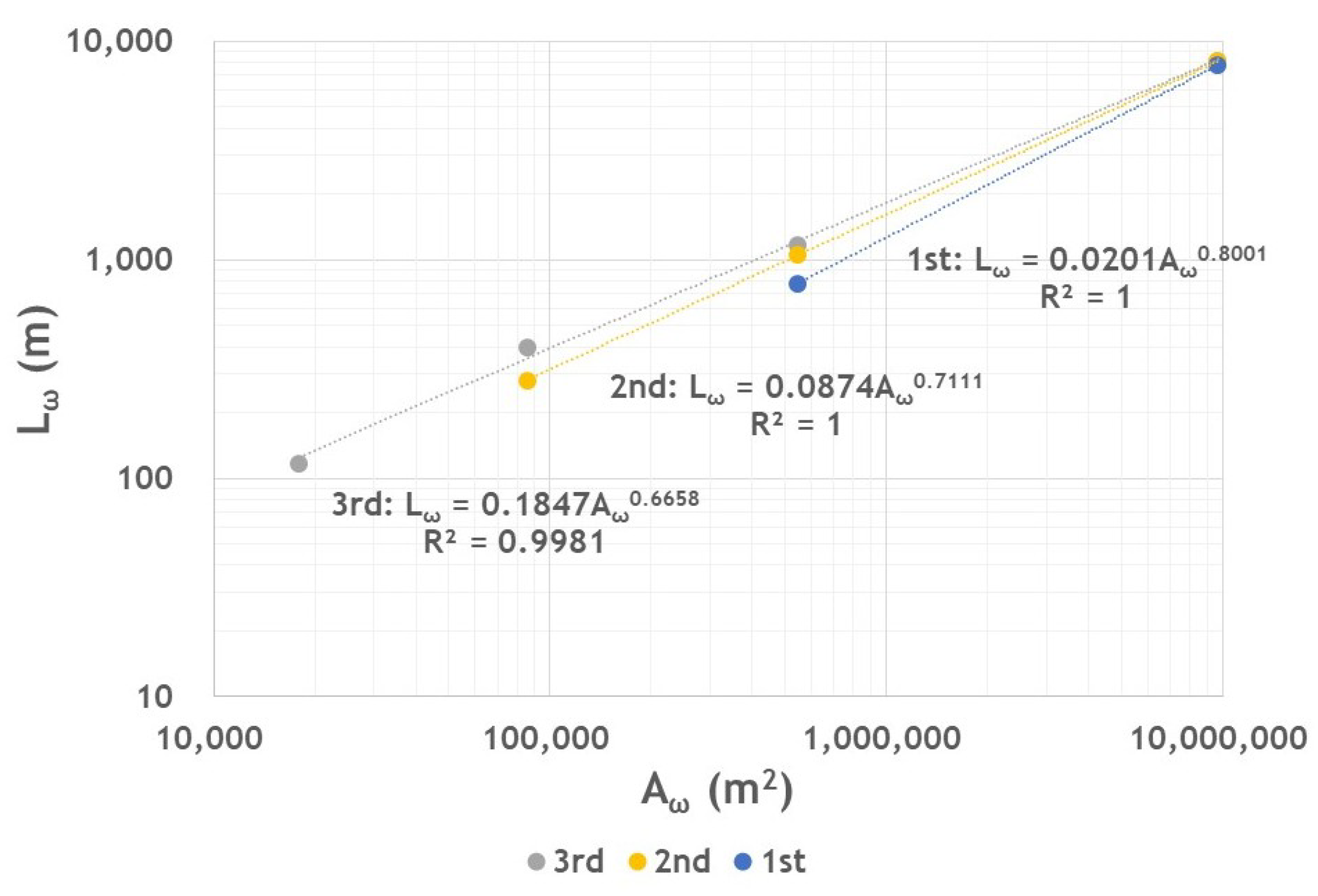
4.2. Scaling of Strahler’s Stream Length
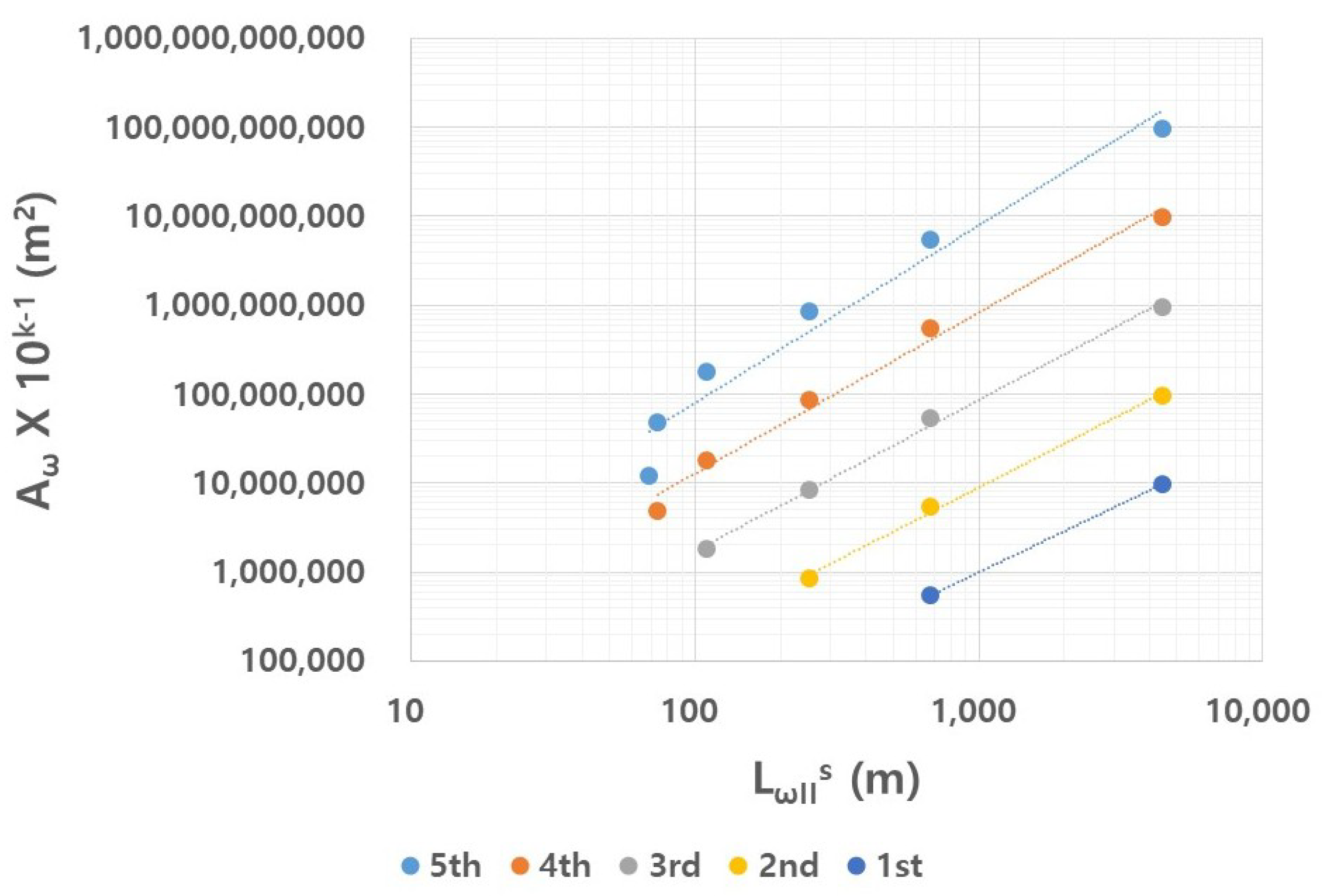
4.3. Scaling of Catchment Planform
4.4. Hack’s Law in a Single River Basin
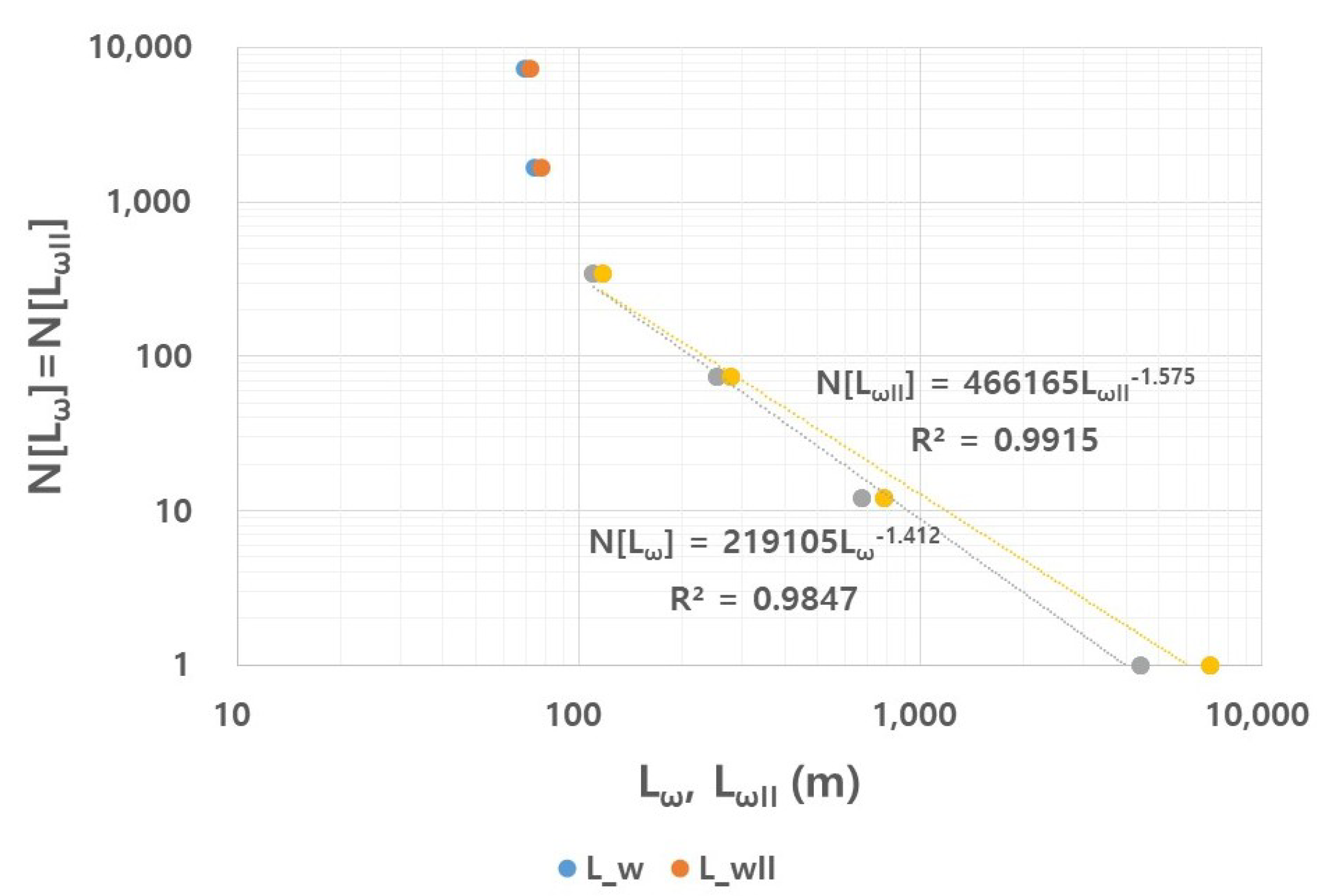
4.5. Estimation of Fractal Dimension by Fractal Tree
4.6. Further Discussion
4.6.1. Interpretation of Drainage Path Network
4.6.2. Potential Usage of Fractal Tree Concept
5. Conclusions
- (1)
- The growth process of the fractal tree in a natural river basin would occur only within the limited region possessing the channel flow property. Sinuosity of the channel segment would become more profound with the increase in the stream order accompanied with the decrease in contribution from overland flow.
- (2)
- In the framework of a fractal tree, the first and second stream order basins would belong to the overland flow region, in which the former follows the pure overland flow regime and the latter shows some degree of channel flow pattern.
- (3)
- The exponent of the intra basin type of Hack’s law could show the variable trend in a small river basin depending on the anisotropic property of the catchment planform. The bifurcation process of a drainage path network might be more sensitive to the growth step of a fractal tree than the meandering process of drainage path segment.
- (4)
- Because the fractal dimension of the sinuosity of a channel segment is relatively stable compared to the one from a bifurcation process of a network, the geomorphologic features of a small river basin can be characterized by the anisotropic property of the catchment planform as well as the bifurcation property of the drainage path network with the growth of the fractal tree.
- (5)
- There may exist many drainage pathways on the overland flow region which cannot form channels in the dry season whereas, in the rainy season, they could form the ephemeral stream network around the perennial one and play the same role as the channel network.
Author Contributions
Funding
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- Bak, P. How Nature Works; Copernicus: New York, NY, USA; Springer: New York, NY, USA, 1996. [Google Scholar]
- Rodriguez-Iturbe, I.; Ijjasz-VasquezR, E.J.; Bras, R.L.; Tarboton, D.G. Power law distributions of discharge, mass, and energy in river basins. Water Resour. Res. 1992, 28, 1089–1093. [Google Scholar] [CrossRef]
- Moussa, R. On morphometric properties of basins, scale effects and hydrological response. Hydrol. Process. 2003, 17, 33–58. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vision Graph. Image Process. 1984, 28, 324–344. [Google Scholar]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. A physical basis for drainage density. Geomophology 1992, 5, 59–75. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Foufoula-Georgiou, E. Channel network source representation using digital elevation models. Water Resour. Res. 1993, 29, 3925–3934. [Google Scholar] [CrossRef]
- Ijjasz-Vasquez, E.J.; Bras, R.L. Scaling regimes of local slope versus contributing area in digital elevation models. Geomorphology 1995, 12, 299–311. [Google Scholar] [CrossRef]
- Tarboton, D.G. Terrain Analysis Using Digital Elevation Models in Hydrology. In Proceedings of the 23rd ESRI International Users Conference, San Diego, CA, USA, 7–11 July 2003. [Google Scholar]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. The Fractal nature of river networks. Water Resour. Res. 1988, 24, 1317–1322. [Google Scholar] [CrossRef]
- La Barbera, P.; Rosso, R. On the Fractal dimension of stream networks. Water Resour. Res. 1989, 25, 735–741. [Google Scholar] [CrossRef]
- Rosso, R.; Bacchi, B.; La Barbera, P. Fractal relation of mainstream length to catchment area in river networks. Water Resour. Res. 1991, 27, 381–387. [Google Scholar] [CrossRef]
- Beer, T.; Borgas, M. Horton’s law and the Fractal nature of streams. Water Resour. Res. 1993, 29, 1475–1487. [Google Scholar] [CrossRef]
- Puente, C.E.; Castillo, P.A. On the Fractal structure of networks and dividers within a watershed. J. Hydrol. 1996, 187, 173–181. [Google Scholar] [CrossRef]
- Agnese, C.; D’Asaro, F.; Grosso, G.; Rosso, R. Scaling properties of topologically random channel network. J. Hydrol. 1996, 187, 183–193. [Google Scholar] [CrossRef]
- Shreve, R.L. Statistical law of stream numbers. J. Geol. 1966, 74, 17–37. [Google Scholar] [CrossRef]
- Kim, J.C.; Jung, K. Fractal Tree Analysis of Drainage Patterns. Water Resour. Manag. 2015, 29, 1217–1230. [Google Scholar] [CrossRef]
- Hergarten, S. Self-Organized Criticality in Earth System; Springer: New York, NY, USA, 2002. [Google Scholar]
- Maritan, A.; Rinaldo, A.; Rigon, A.; Giacometti, A.; Rodriguez-Iturbe, I. Scaling laws for river networks. Phys. Rev. E 1996, 53, 1510–1515. [Google Scholar] [CrossRef] [Green Version]
- Rigon, R.; Rodriguez-Iturbe, I.; Maritan, A.; Giacometti, A.; Tarboton, D.G.; Rinaldo, A. On Hack’s law. Water Resour. Res. 1996, 32, 3367–3374. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Scaling, Universality, and Geomorphology. Ann. Rev. Earth Planet. Sci. 2000, 28, 571–610. [Google Scholar] [CrossRef]
- Smart, J.S. Channel networks. Adv. Hydrosc. 1972, 8, 346–350. [Google Scholar]
- Hack, J.T. Studies of Longitudinal Profiles in Virginia and Maryland; US. Geological Survey Professional Paper: Washington, DC, USA, 1957; Volume 294-B, pp. 45–97. [Google Scholar]
- Gray, D.M. Interrelationships of watershed characteristics. J. Geophys. Res. 1961, 66, 1215–1223. [Google Scholar] [CrossRef]
- Saunders, W.K.; Maidment, D.R. A GIS Assessment of Nonpoint Source Pollution in the San Antonio-Nueces Coastal Basin; Center for Research in Water Resources, University of Texas at Austin: Austin, TX, USA, 1996. [Google Scholar]
- Dodds, P.S.; Rothman, D.H. Unified View of Scaling Laws for River Networks. Phys. Rev. E 2000, 59, 4865. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.C.; Jung, K. Estimation of Fractal Dimension for Seolma Creek Experimental Basin on the Basis of Fractal Tree Concept. J. Korea Water Resour. Assoc. 2020. stage of publication. (under review). (In Korean) [Google Scholar]
- Yang, S.; Paik, K.; McGrath, G.; Urich, C.; Kruger, E.; Kumar, P.; Rao, P.S.C. Comparing Topology of Engineered and Natural Drainage Networks. Water Resour. Res. 2017, 53, 8966–8979. [Google Scholar] [CrossRef]
| 5 | 1 | 5711 | 72 | 69 | 1192 |
| 4 | 2 | 1310 | 78 | 74 | 4876 |
| 3 | 3 | 271 | 117 | 110 | 17,957 |
| 2 | 4 | 61 | 279 | 254 | 85,344 |
| 1 | 5 | 11 | 779 | 675 | 544,000 |
| 0 | 6 | 1 | 7018 | 4413 | 9,678,800 |
| Regression | |||
|---|---|---|---|
| 5 | 0.9991 | 1.0951 | |
| 4 | 0.9990 | 1.0993 | |
| 3 | 0.9990 | 1.1110 | |
| 2 | 0.9993 | 1.1354 | |
| 1 | 1.0000 | 1.1708 |
| Regression | |||
|---|---|---|---|
| 5 | 0.9557 | 0.9924 | |
| 4 | 0.9892 | 0.8111 | |
| 3 | 0.9969 | 0.7004 | |
| 2 | 0.9969 | 0.6405 | |
| 1 | 1.0000 | 0.5335 |
| Regression | ||||
|---|---|---|---|---|
| 3 | 0.9981 | 0.6658 | 0.6534 | |
| 2 | 1.0000 | 0.7111 | 0.6916 | |
| 1 | 1.0000 | 0.8001 | 0.7635 |
| 3 | 1.5750 | 1.4120 | 1.1150 |
| 2 | 1.4790 | 1.2980 | 1.1390 |
| 1 | 1.3240 | 1.1310 | 1.1706 |
| Outlet | ||||||
|---|---|---|---|---|---|---|
| JJB | 8,444,800 | 3 | 1.1422 | 1.6520 | 1.4400 | 1.1472 |
| Jeil | 9,678,800 | 3 | 1.1110 | 1.5750 | 1.4120 | 1.1150 |
| Imjin | 17,598,400 | 4 | 1.0844 | 1.8050 | 1.6590 | 1.0880 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, M.; Jung, K.; Kim, J.-C. Geomorphologic Analysis of Small River Basin within the Framework of Fractal Tree. Water 2020, 12, 2480. https://doi.org/10.3390/w12092480
Feng M, Jung K, Kim J-C. Geomorphologic Analysis of Small River Basin within the Framework of Fractal Tree. Water. 2020; 12(9):2480. https://doi.org/10.3390/w12092480
Chicago/Turabian StyleFeng, Meiyan, Kwansue Jung, and Joo-Cheol Kim. 2020. "Geomorphologic Analysis of Small River Basin within the Framework of Fractal Tree" Water 12, no. 9: 2480. https://doi.org/10.3390/w12092480




