Influence of Rectifier Nozzles on the Flow Distribution Characteristics of Parallel Pipes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment System
2.2. Mathematical Model
2.2.1. Governing Equation
2.2.2. Numerical Method and Boundary Conditions
2.2.3. Meshing
2.3. Model Validation
3. Results
3.1. Velocity Distribution of Each Branch
3.2. Pressure Distribution of Each Branch
3.3. Discharge Coefficients of Rectifier Nozzles with 7.3 mm
4. Discussion
4.1. Effect of Temperature on Flow Distribution
4.2. Effect of Inlet Flow on Flow Distribution
4.3. Effect of Cavitation on Flow Distribution
4.4. Evaluation of Distribution Effect
5. Conclusions
- (1)
- The rectifier nozzle can prevent the flow field of each branch pipe from being distorted during the shunting process, so that the velocity and pressure distribution of the parallel pipes are more uniform and stable. Uniformity is obtained by increasing the resistance loss. For every 1% increase in uniformity, the pressure loss will increase by about 4% for rectifier nozzle.
- (2)
- As the inlet flow rate increases, the degree of uneven flow distribution increases. The rectifier nozzle effectively improves the unevenness of the flow distribution of the parallel pipeline.
- (3)
- At the same inlet flow rate, as the temperature rises, the degree of uneven flow distribution slightly decreases.
- (4)
- In this study, parallel pipes with rectifier nozzles were considered. Mild cavitation occurred in which the bubbles were small and scattered, and the flow distribution of the parallel pipelines was found to be relatively uniform, with only a slight difference.
Author Contributions
Funding
Conflicts of Interest
References
- Keller, J.D. The manifold problem. J. Appl. Mech. 1949, 3, 77–85. [Google Scholar]
- Steve, H.C.; Sehyun, S.; Young, I.C. The effects of the Reynolds number and width ratio on the flow distribution in manifolds of liquid cooling modules for electronic packaging. Int. Commun. Heat Mass Transf. 1993, 20, 607–617. [Google Scholar]
- Sooyoun, K.; Eunsoo, C.; Young, I.C. The effect of header shapes on the flow distribution in a manifold for electronic packaging applications. Int. Commun. Heat Mass Transf. 1995, 20, 329–341. [Google Scholar]
- Heehak, A.; Sunghyuk, L.; Sehyun, S. Flow distribution in manifolds for low Reynolds number flow. J. KSME Int. J. 1998, 12, 87–95. [Google Scholar]
- Kikas, N.P. Laminar flow distribution in solar systems. J. Sol. Energy 1995, 54, 209–217. [Google Scholar] [CrossRef]
- Wang, J.Y. Pressure drop and flow distribution in parallel-channel configurations of fuel cells: Z-type arrangement. Int. J. Hydrog. Energy 2010, 35, 5498–5509. [Google Scholar] [CrossRef]
- Tong, J.C.K.; Sparrow, E.M.; Abraham, J.P. Geometric strategies for attainment of identical outflows through all of the exit ports of a distribution manifold in a manifold system. Appl. Therm. Eng. 2009, 29, 3552–3560. [Google Scholar] [CrossRef]
- Jones, G.F.; Noam, L. Flow distribution in manifolded solar collectors with negligible buoyancy effects. Sol. Energy 1994, 52, 289–300. [Google Scholar] [CrossRef]
- Volker, W.; David, L.; Andreas, R. Flow distribution in solar collectors with laminar flow conditions. Sol. Energy 2002, 73, 433–441. [Google Scholar]
- Lu, F.; Luo, Y.H.; Yang, S.M. Analytical and experimental investigation of flow distribution in manifolds for heat exchangers. J. Hydrodyn. 2008, 20, 179–185. [Google Scholar] [CrossRef]
- Cheng, H.H.; Chun, H.W. The design of uniform tube flow rates for Z-type compact parallel flow heat exchangers. Int. Commun. Heat Mass Transf. 2013, 57, 608–622. [Google Scholar]
- Miao, Z.Q.; Xu, T.M. Single phase flow characteristics in the headers and connecting tube of parallel tube platen systems. Appl. Therm. Eng. 2006, 26, 396–402. [Google Scholar] [CrossRef]
- Zhao, Z.N. Effect of friction resistance on flow characteristics of shunt and confluence header. Petrochem. Equip. 2001, 30, 10–13. (In Chinese) [Google Scholar]
- Pu, J.H.; Hu, M.F.; Zhu, X.Q. Research on fluid flow distribution in parallel pipeline system. J. Kunming Univ. Sci. Technol. (Sci. Technol.) 2003, 28, 131–132. (In Chinese) [Google Scholar]
- Zhong, X.H.; Zhang, L.; Wu, C.B. Experiments and numerical simulation of flow distribution with larger flux in multi-branch pipe. J. Chongqing Univ. Nat. Sci. Ed. 2006, 29, 41–56. (In Chinese) [Google Scholar]
- Wei, X.L.; Miao, Z.Q. Experimental study of flow characteristics in parallel tube set systems with Z-type and U-type headers. Chin. J. Power Eng. 2008, 28, 514–518. (In Chinese) [Google Scholar]
- Facao, J. Optimization of flow distribution in flat plate solar thermal collectors with riser and header arrangements. Sol. Energy 2015, 120, 104–112. [Google Scholar] [CrossRef] [Green Version]
- He, J. Numerical Analysis of the Flow Distribution in Multiple Branches Parallel-Tube Configuration Lanzhou. Master Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2014. (In Chinese). [Google Scholar]
- Duan, F.; Chen, L.C. Numerical simulation of flow distribution characteristics of manifold with mid-plate pipeline technique and equipment. Pipeline Tech. Equip. 2016, 4, 1-4+17. (In Chinese) [Google Scholar]
- Wang, J. Design method of flow distribution in nuclear reactor systems. Chem. Eng. Res. Des. 2013, 91, 595–602. [Google Scholar] [CrossRef]
- Zhu, Y.Q.; Miao, B. Numerical simulation of flow characteristics in manifolds. J. Xi’an Shiyou Univ. 2011, 26, 94–96. (In Chinese) [Google Scholar]
- Zhang, R.L.; Fang, Y.H. Analysis of flow uniformity of parallel pipe group model. J. Tianjin Univ. Sci. Technol. 2007, 2, 45–48. (In Chinese) [Google Scholar]
- Yang, C.; Niu, Y.J.; Luo, H.Y. Design of current sharing model of parallel tube group in heat exchange equipment based on fluent. Mech. Des. Manuf. 2015, 5, 150–155. (In Chinese) [Google Scholar] [CrossRef]
- Qu, H.X.; Sun, Z.N.; Ding, M. Study on the influence of header matching on flow distribution of U-shaped parallel tube group heat exchanger. Atom. Energy Sci. Technol. 2015, 49, 623–628. (In Chinese) [Google Scholar]
- Wang, J. Theory of flow distribution in manifolds. Chem. Eng. J. 2011, 168, 1331–1345. [Google Scholar] [CrossRef]
- Minocha, N.; Joshi, J.B. 3D CFD simulation of turbulent flow distribution and pressure drop in a dividing manifold system using openfoam. Int. J. Heat Mass Transf. 2020, 151, 119420. [Google Scholar] [CrossRef]

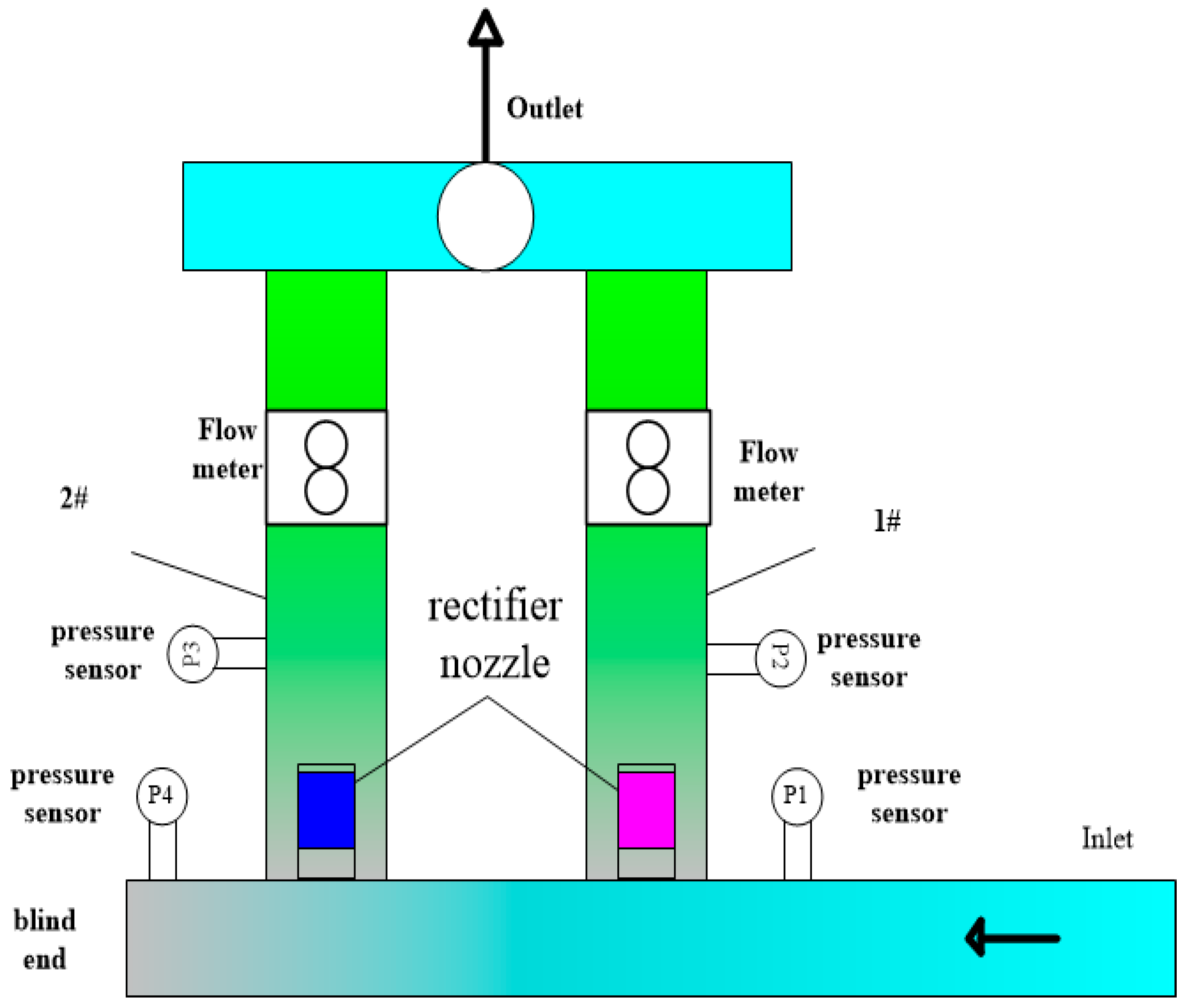




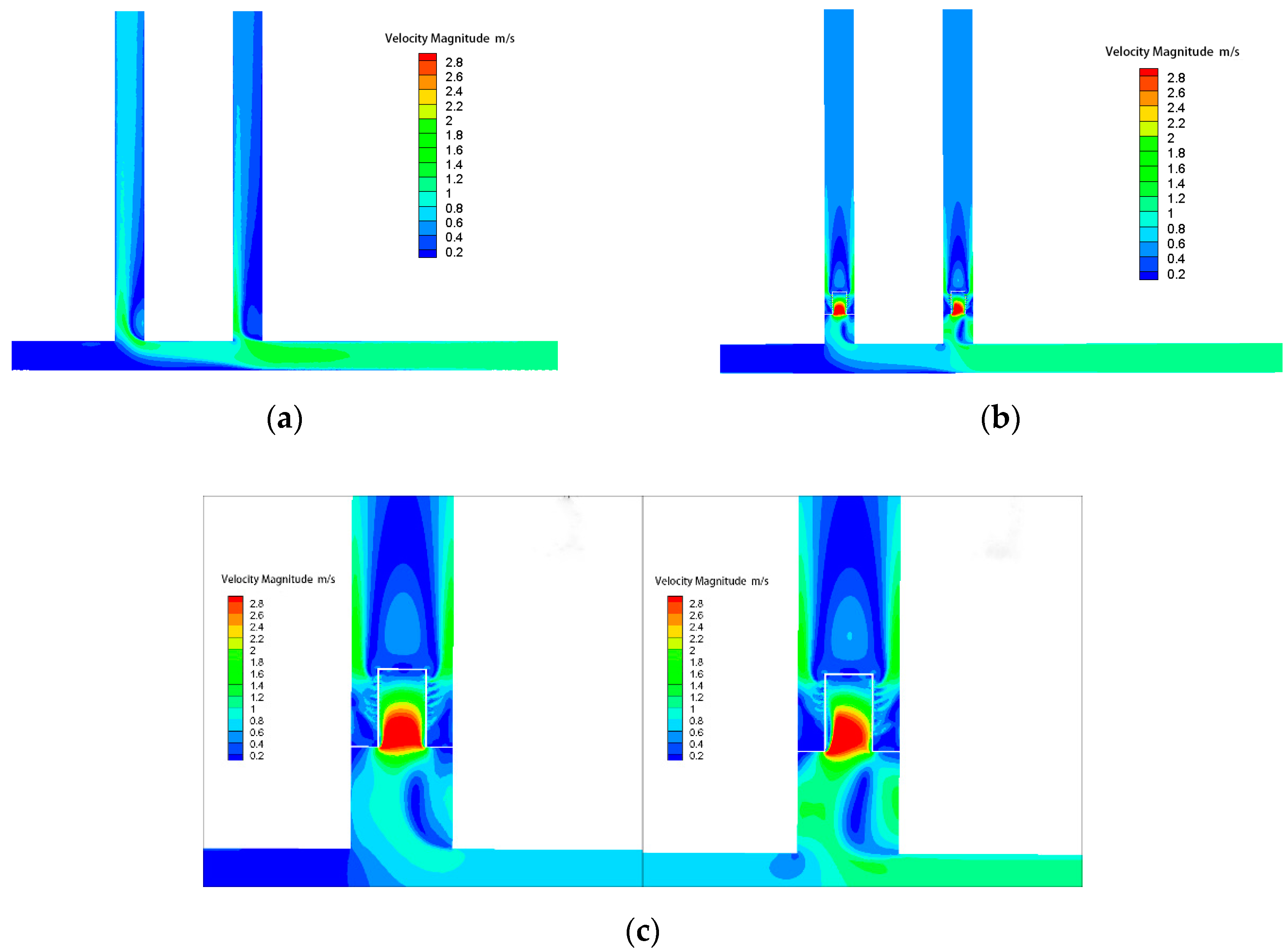

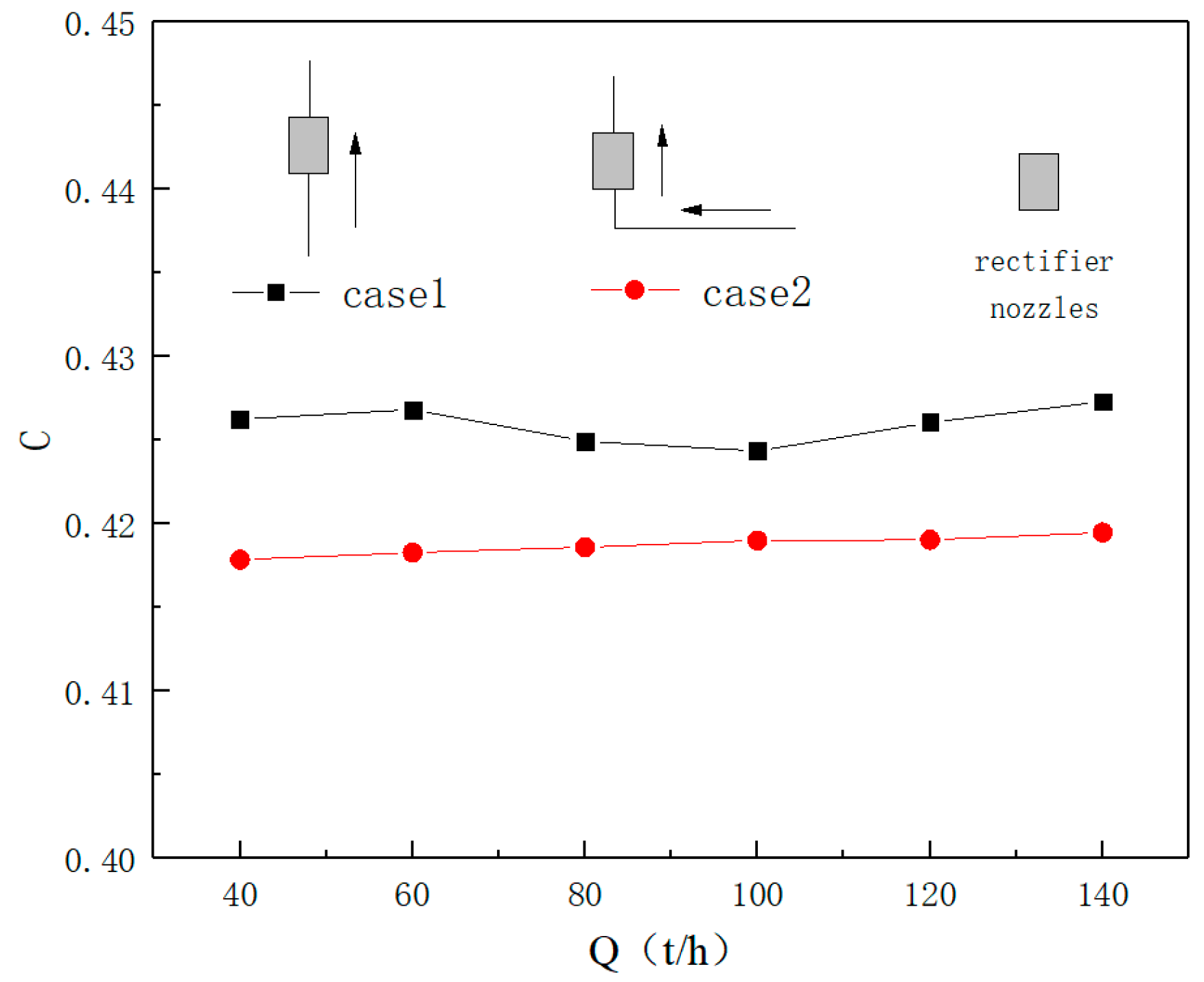




| Parameter. | Unit | Uncertainty (%) |
|---|---|---|
| Mass flow rate | t/h | 0.5 |
| Pressure | KPa | 0.08 |
| Fluid temperature | °C | 2.19 |
| Temperature (°C) | Density (kg/m3) | Viscosity (Pa-s) × 103 |
|---|---|---|
| 23.0 | 997.54 | 0.9321 |
| 40.0 | 992.22 | 0.6527 |
| 60.0 | 983.20 | 0.4660 |
| Number of Cell | Velocity of out1 (m/s) | Velocity of out2 (m/s) | |
|---|---|---|---|
| 0.75 million | 4946 | 0.435 | 0.453 |
| 1.6 million | 4965 | 0.432 | 0.453 |
| 2.7 million | 4950 | 0.432 | 0.453 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Cao, Y.; Zhang, Q.; Wu, F.; Shi, S.; Zhao, S.; Zhan, H. Influence of Rectifier Nozzles on the Flow Distribution Characteristics of Parallel Pipes. Water 2020, 12, 2558. https://doi.org/10.3390/w12092558
Yang Z, Cao Y, Zhang Q, Wu F, Shi S, Zhao S, Zhan H. Influence of Rectifier Nozzles on the Flow Distribution Characteristics of Parallel Pipes. Water. 2020; 12(9):2558. https://doi.org/10.3390/w12092558
Chicago/Turabian StyleYang, Zhendong, Yalong Cao, Qiaoling Zhang, Feng Wu, Suqi Shi, Simao Zhao, and Hui Zhan. 2020. "Influence of Rectifier Nozzles on the Flow Distribution Characteristics of Parallel Pipes" Water 12, no. 9: 2558. https://doi.org/10.3390/w12092558





