Evaluation of Satellite Precipitation Products for Hydrological Modeling in the Brazilian Cerrado Biome
Abstract
:1. Introduction
2. Materials and Methods
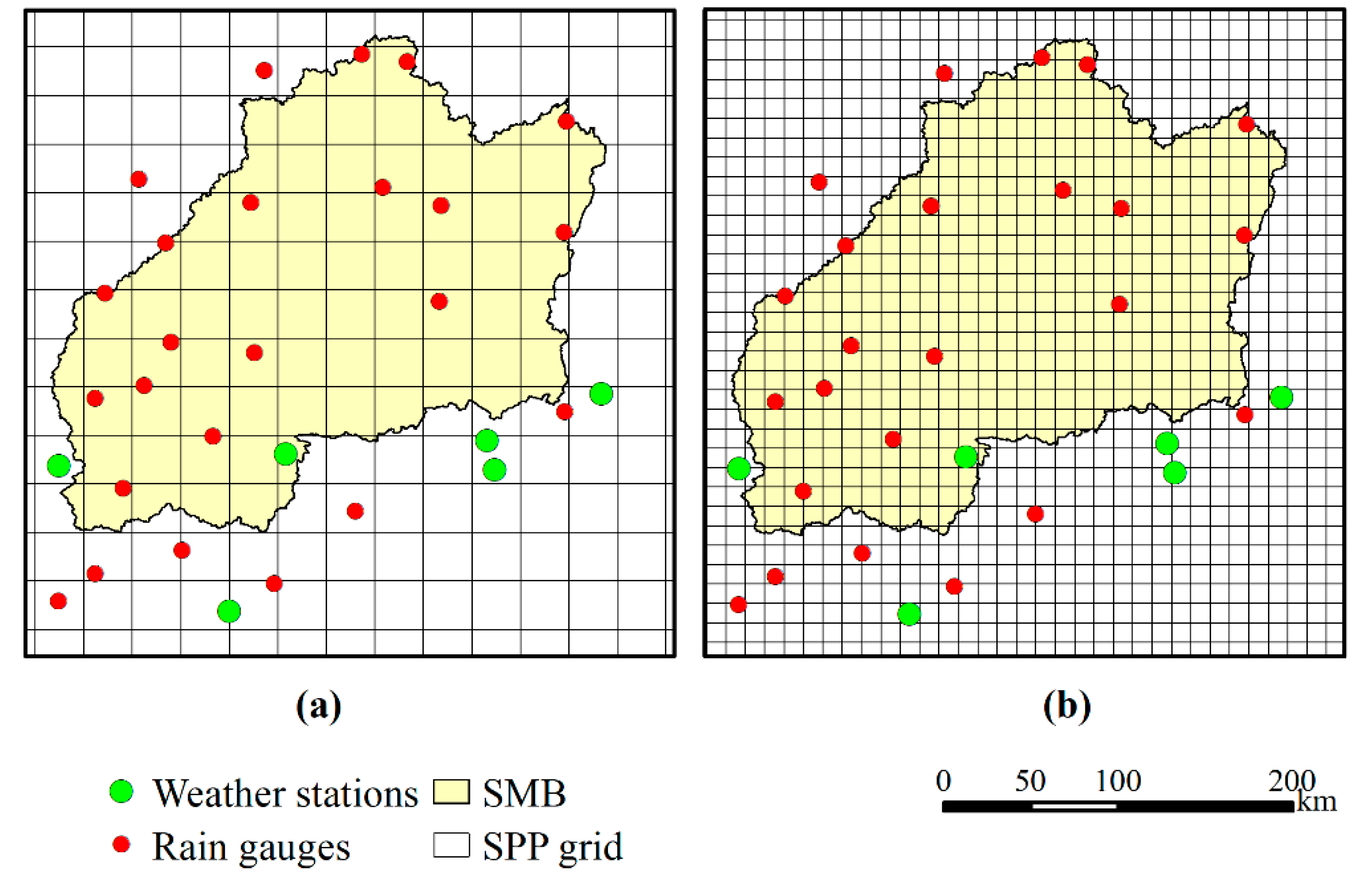
2.1. Study Area
2.2. Precipitation Dataset
2.2.1. Ground-Based Precipitation
2.2.2. Satellite Precipitation Products (SPPs)
2.3. Hydrological Model Description
2.4. Model Setup
2.5. Calibration and Validation of the SWAT Model
2.6. Meteorological and Hydrological Evaluation
3. Results
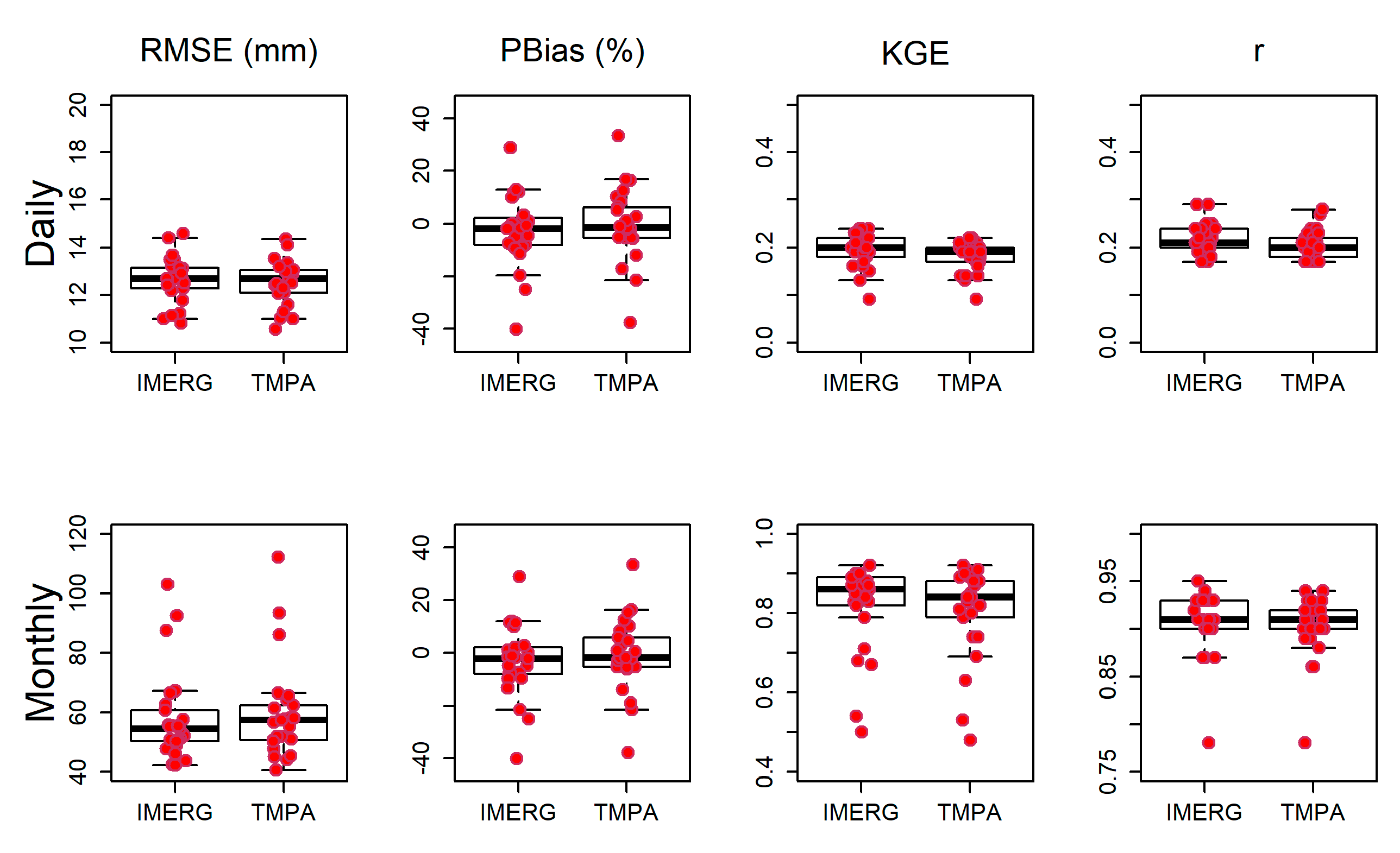
3.1. Validation of SPP against Rain Gauges
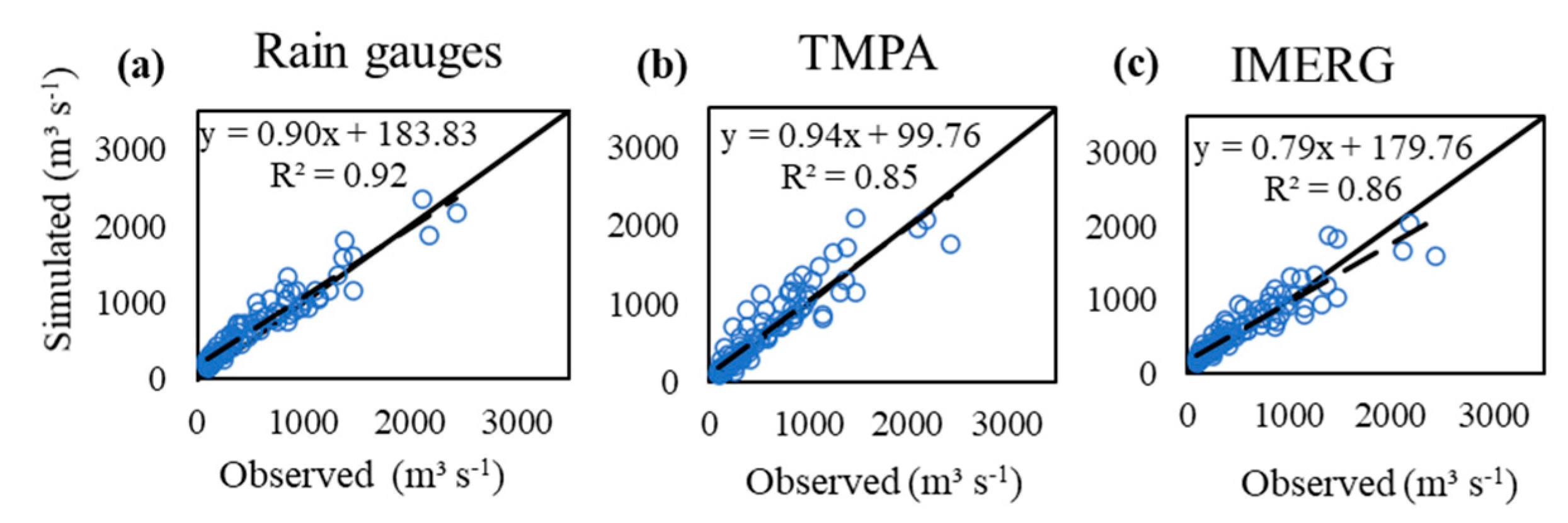
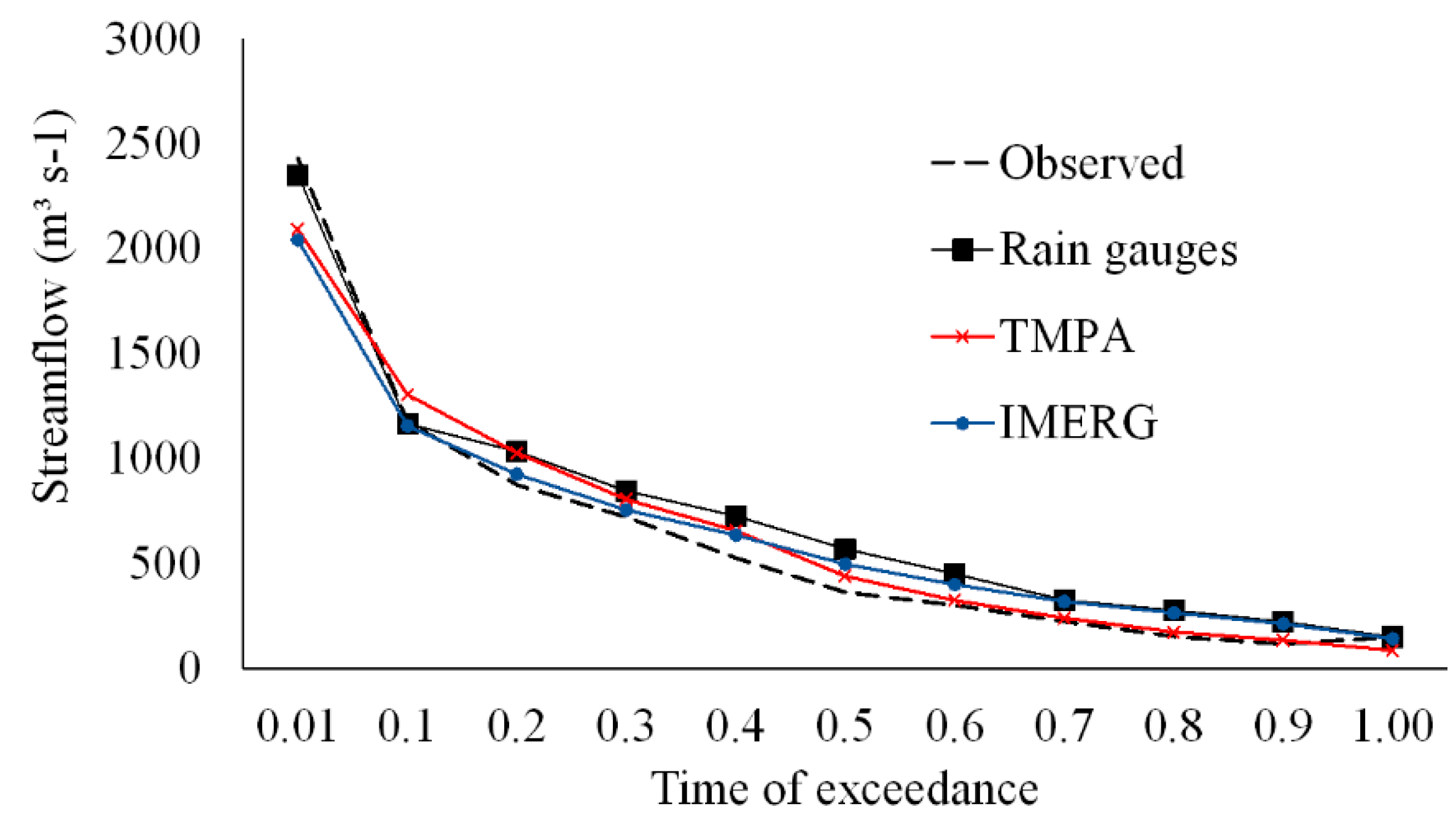
3.2. Monthly Streamflow Simulation Using SPP and Rain Gauges
4. Discussion
4.1. Meteorological Evaluation
4.2. SWAT Performance Evaluation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins–Araguaia basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Hobouchian, M.P.; Salio, P.; García Skabar, Y.; Vila, D.; Garreaud, R. Assessment of satellite precipitation estimates over the slopes of the subtropical Andes. Atmos. Res. 2017, 190, 43–54. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Salio, P.; Hobouchian, M.P.; García Skabar, Y.; Vila, D. Evaluation of high-resolution satellite precipitation estimates over southern South America using a dense rain gauge network. Atmos. Res. 2015, 163, 146–161. [Google Scholar] [CrossRef]
- Monteiro, J.A.F.; Strauch, M.; Srinivasan, R.; Abbaspour, K.C.; Gücker, B. Accuracy of grid precipitation data for Brazil: Application in river discharge modelling of the Tocantins catchment. Hydrol. Process. 2016, 30, 1419–1430. [Google Scholar] [CrossRef]
- Gadelha, A.N.; Coelho, V.H.R.; Xavier, A.C.; Barbosa, L.R.; Melo, D.C.D.; Xuan, Y.; Huffman, G.J.; Petersen, W.A.; Almeida, C.D.N. Grid box-level evaluation of IMERG over Brazil at various space and time scales. Atmos. Res. 2019, 218, 231–244. [Google Scholar] [CrossRef] [Green Version]
- Le, M.H.; Lakshmi, V.; Bolten, J.; Bui, D. Du Adequacy of Satellite-derived Precipitation Estimate for Hydrological Modeling in Vietnam Basins. J. Hydrol. 2020, 586, 124820. [Google Scholar] [CrossRef]
- De Paiva, R.C.D.; Buarque, D.C.; Collischonn, W.; Bonnet, M.-P.; Frappart, F.; Calmant, S.; Bulhões Mendes, C.A. Large-scale hydrologic and hydrodynamic modeling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. J. ISMAC 2019, 1. [Google Scholar] [CrossRef]
- Cassalho, F.; Daleles Rennó, C.; Bosco Coura dos Reis, J.; Cláudio da Silva, B. Hydrologic Validation of MERGE Precipitation Products over Anthropogenic Watersheds. Water 2020, 12, 1268. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- de Melo, D.C.D.; Xavier, A.C.; Bianchi, T.; Oliveira, P.T.S.; Scanlon, B.R.; Lucas, M.C.; Wendland, E. Performance evaluation of rainfall estimates by TRMM Multi-satellite Precipitation Analysis 3B42V6 and V7 over Brazil. J. Geophys. Res. Atmos. 2015, 120, 9426–9436. [Google Scholar] [CrossRef] [Green Version]
- Coelho, V.H.R.; Montenegro, S.; Almeida, C.N.; Silva, B.B.; Oliveira, L.M.; Gusmão, A.C.V.; Freitas, E.S.; Montenegro, A.A.A. Alluvial groundwater recharge estimation in semi-arid environment using remotely sensed data. J. Hydrol. 2017, 548, 1–15. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Yen, H.; Collick, A.S.; Tilahun, S.A.; Langan, S.; Steenhuis, T.S. Evaluation of CFSR, TMPA 3B42 and ground-based rainfall data as input for hydrological models, in data-scarce regions: The upper Blue Nile Basin, Ethiopia. Catena 2017, 152, 242–251. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado-Casimiro, W.; Aragon, L. Hydrological modeling of the Peruvian-Ecuadorian Amazon Basin using GPM-IMERG satellite-based precipitation dataset. Hydrol. Earth Syst. Sci. 2017, 21, 3543–3555. [Google Scholar] [CrossRef] [Green Version]
- Amjad, M.; Yilmaz, M.T.; Yucel, I.; Yilmaz, K.K. Performance evaluation of satellite- and model-based precipitation products over varying climate and complex topography. J. Hydrol. 2020, 584, 124707. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, D.; Wang, Y.; Yang, H. Accuracy and spatio-temporal variation of high resolution satellite rainfall estimate over the Ganjiang River Basin. Sci. China Technol. Sci. 2013, 56, 853–865. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ren, L.L.; Yong, B.; Yang, X.L.; Shi, L. Evaluation of high-resolution satellite precipitation products with surface rain gauge observations from Laohahe Basin in northern China. Water Sci. Eng. 2010, 3, 405–417. [Google Scholar] [CrossRef]
- Eini, M.R.; Javadi, S.; Delavar, M.; Monteiro, J.A.F.; Darand, M. High accuracy of precipitation reanalyses resulted in good river discharge simulations in a semi-arid basin. Ecol. Eng. 2019, 131, 107–119. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, 1–11. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, V.A.; De Mello, C.R.; Beskow, S.; Viola, M.R.; Srinivasan, R. Modeling the effects of climate change on hydrology and sediment load in a headwater basin in the Brazilian Cerrado biome. Ecol. Eng. 2019, 133, 20–31. [Google Scholar] [CrossRef]
- Silva, J.P.M.; da Silva, M.L.M.; da Silva, E.F.; da Silva, G.F.; de Mendonça, A.R.; Cabacinha, C.D.; Araújo, E.F.; Santos, J.S.; Vieira, G.C.; de Almeida, M.N.F.; et al. Computational techniques applied to volume and biomass estimation of trees in Brazilian savanna. J. Environ. Manag. 2019, 249, 109368. [Google Scholar] [CrossRef]
- Nobrega, R.L.B.; Guzha, A.C.; Torres, G.N.; Kovacs, K.; Lamparter, G.; Amorim, R.S.S.; Couto, E.; Gerold, G. Identifying Hydrological Responses of Micro-Catchments under Contrasting Land Use in the Brazilian Cerrado. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 9915–9975. [Google Scholar] [CrossRef] [Green Version]
- Myers, N.; Mittermeir, R.A.; Mittermeier, C.G.; Fonseca, G.A.B.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Nearing, M.A.; Moran, M.S.; Goodrich, D.C.; Wendland, E.; Gupta, H.V. Trends in water balance components across the Brazilian Cerrado. Water Resour. Res. 2014, 50, 7100–7114. [Google Scholar] [CrossRef] [Green Version]
- Machado, A.R.; Wendland, E.; Krause, P. Hydrologic Simulation for Water Balance Improvement in an Outcrop Area of the Guarani Aquifer System. Environ. Process. 2016, 3, 19–38. [Google Scholar] [CrossRef]
- Lima, J.E.F.W.; da Silva, E.M. Estimativa da contribuição hídrica superficial do Cerrado para as grandes regiões hidrográficas brasileiras. In XVII Simpósio Brasileiro de Recursos Hídricos; ABRH: São Paulo, Brazil, 2007; pp. 1–13. [Google Scholar]
- Agência Nacional de Águas—ANA—Superintendência de Planejamento de Recursos Hídricos. Conjuntura Dos Recursos Hídricos no Brasil: Regiões Hidrográficas Brasileiras—Edição Especial 2015. Available online: http://arquivos.ana.gov.br/institucional/sge/CEDOC/Catalogo/2015/ConjunturaDosRecursosHidricosNoBrasil2015.pdf (accessed on 12 June 2019).
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Daily gridded meteorological variables in Brazil (1980–2013). Int. J. Climatol. 2016, 36, 2644–2659. [Google Scholar] [CrossRef] [Green Version]
- Agência Nacional de Energia Elétrica (Brasil)—ANEEL Banco de Informações de Geração (BIG). Available online: https://bit.ly/2IGf4Q0 (accessed on 12 June 2019).
- Thiengo, S.C.; Santos, S.B.; Fernandez, M.A. Malacofauna límnica da área de influência do lago da usina hidrelétrica de Serra da Mesa, Goiás, Brasil. I. Estudo qualitativo. Rev. Bras. Zool. 2005, 22, 867–874. [Google Scholar] [CrossRef] [Green Version]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; De Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Technical Report No.406; Texas Water Resources Institute: Forney, TX, USA, 2011. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williamsa, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- PRIESTLEY, C.H.B.; TAYLOR, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Moisture Availability and Crop Production. Trans. ASAE 1975, 18, 0980–0984. [Google Scholar] [CrossRef]
- Penman, H.L. Evaporation: An Introductory Survey. Neth. J. Agric. Sci. 1956, 4, 9–29. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 205–234. [Google Scholar]
- Green, W.H.; Ampt, G.A. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef] [Green Version]
- United States Department of Agriculture–Soil Conservation Service (USDA-SCS) Section 4: Hydrology. In National Engineering Handbook; United States Department of Agriculture: Washington, DC, USA, 1972.
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual Version 2005; Technical Report No. 406; Texas Water Resources Institute: Forney, TX, USA, 2005. [Google Scholar]
- Srinivasan, R.; Ramanarayanan, T.S.; Arnold, J.G.; Bednarz, S.T. Large area hydrologic modeling and assessment part II: Model application. J. Am. Water Resour. Assoc. 1998, 34, 91–101. [Google Scholar] [CrossRef]
- Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA) Mapa de Solos do Brasil. Available online: http://geoinfo.cnps.embrapa.br/layers/geonode%3Asolos_br5m_2011_lat_long_wgs84 (accessed on 14 December 2019).
- Instituto Brasileiro de Geografia e Estatística—IBGE Mudanças na Cobertura e Uso da Terra 2000. 2010–2012. Available online: http://maps.lapig.iesa.ufg.br/?layers=pa_br_uso_solo_500_ibge (accessed on 14 December 2019).
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Guilhon, L.G.F.; Rocha, V.F.; Moreira, J.C. Comparação de Métodos de Previsão de Vazões Naturais Afluentes a Aproveitamentos Hidroelétricos. Rev. Bras. Recur. Hídricos 2007, 12, 13–20. [Google Scholar]
- Oliveira, V.A.; de Mello, C.R.; Viola, M.R.; Srinivasan, R. Assessment of climate change impacts on streamflow and hydropower potential in the headwater region of the Grande river basin, Southeastern Brazil. Int. J. Climatol. 2017, 37, 5005–5023. [Google Scholar] [CrossRef]
- Nóbrega, M.T.; Collischonn, W.; Tucci, C.E.M.; Paz, A.R. Uncertainty in climate change impacts on water resources in the Rio Grande Basin, Brazil. Hydrol. Earth Syst. Sci. 2011, 15, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual 2015. Available online: https://swat.tamu.edu/media/114860/usermanual_swatcup.pdf (accessed on 14 December 2019).
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Triana, J.S.A.; Chu, M.L.; Guzman, J.A.; Moriasi, D.N.; Steiner, J.L. Beyond model metrics: The perils of calibrating hydrologic models. J. Hydrol. 2019, 578, 124032. [Google Scholar] [CrossRef]
- Rodrigues, J.A.M.; Viola, M.R.; Alvarenga, L.A.; de Mello, C.R.; Chou, S.C.; de Oliveira, V.A.; Uddameri, V.; Morais, M.A.V. Climate change impacts under representative concentration pathway scenarios on streamflow and droughts of basins in the Brazilian Cerrado biome. Int. J. Climatol. 2019, 1–16. [Google Scholar] [CrossRef]
- Tan, M.; Samat, N.; Chan, N.; Roy, R. Hydro-Meteorological Assessment of Three GPM Satellite Precipitation Products in the Kelantan River Basin, Malaysia. Remote Sens. 2018, 10, 1011. [Google Scholar] [CrossRef] [Green Version]
- Hosseini-Moghari, S.-M.; Tang, Q. Validation of GPM IMERG-V05 and V06 precipitation products over Iran. J. Hydrometeorol. 2020. [Google Scholar] [CrossRef] [Green Version]
- Wei, G.; Lü, H.; Crow, W.T.; Zhu, Y.; Wang, J.; Su, J. Evaluation of satellite-based precipitation products from IMERG V04A and V03D, CMORPH and TMPA with gauged rainfall in three climatologic zones in China. Remote Sens. 2018, 10, 30. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, E.; Muhammad, W.; Ahmad, I.; Muhammad Khan, N.; Chen, S. Satellite precipitation product: Applicability and accuracy evaluation in diverse region. Sci. China Technol. Sci. 2020. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zad, S.N.M.; Zulkafli, Z.; Muharram, F.M. Satellite rainfall (TRMM 3B42-V7) performance assessment and adjustment over Pahang river basin, Malaysia. Remote Sens. 2018, 10, 388. [Google Scholar] [CrossRef] [Green Version]
- Su, J.; Haishen, L.; Ryu, D.; Zhu, Y. The Assessment and Comparison of TMPA and IMERG Products Over the Major Basins of Mainland China. Earth Space Sci. 2019, 6, 2461–2479. [Google Scholar] [CrossRef]
- Rozante, J.R.; Vila, D.A.; Chiquetto, J.B.; de Fernandes, A.A.; Alvim, D.S. Evaluation of TRMM/GPM blended daily products over Brazil. Remote Sens. 2018, 10, 882. [Google Scholar] [CrossRef] [Green Version]
- Varma, A.K.; Varma, A.K.B. Measurement of Precipitation from Satellite Radiometers (Visible, Infrared, and Microwave): Physical Basis, Methods, and Limitations. In Remote Sensing of Aerosols, Clouds, and Precipitation; Islam, T., Hu, Y., Kokhanovsky, A., Wang, J., Eds.; Elsevier: Iowa City, IA, USA, 2018; pp. 223–248. ISBN 9780128104385. [Google Scholar]
- Jiang, S.; Ren, L.; Xu, C.Y.; Yong, B.; Yuan, F.; Liu, Y.; Yang, X.; Zeng, X. Statistical and hydrological evaluation of the latest Integrated Multi-satellitE Retrievals for GPM (IMERG) over a midlatitude humid basin in South China. Atmos. Res. 2018, 214, 418–429. [Google Scholar] [CrossRef]
- Correa, S.W.; de Paiva, R.C.D.; Siqueira, V.; Collischonn, W.; Paiva, R.C.D.; Siqueira, V.; Collischonn, W. Hydrological reanalysis across the 20th century: A case study of the Amazon Basin. J. Hydrol. 2019, 570, 755–773. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Huang, Y.; Li, Y.; Hou, C.; Shi, X. Evaluation and hydrological application of satellite-based precipitation datasets in driving hydrological models over the Huifa river basin in Northeast China. Atmos. Res. 2018, 207, 28–41. [Google Scholar] [CrossRef]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Dantas, J.C.; de Beltrão, J.A.; Santos, C.A.G. Hydrological simulation in a tropical humid basin in the cerrado biome using the SWAT model. Hydrol. Res. 2018, 49, 908–923. [Google Scholar] [CrossRef]
- Junqueira, R.; Viola, M.R.; de Mello, C.R.; Vieira-Filho, M.; Alves, M.V.G.; da Amorim, J.S. Drought severity indexes for the Tocantins River Basin, Brazil. Theor. Appl. Climatol. 2020, 141, 465–481. [Google Scholar] [CrossRef]
- Nerini, D.; Zulkafli, Z.; Wang, L.P.; Onof, C.; Buytaert, W.; Lavado-Casimiro, W.; Guyot, J.L. A comparative analysis of TRMM–rain gauge data merging techniques at the daily time scale for distributed rainfall–runoff modeling applications. J. Hydrometeorol. 2015, 16, 2153–2168. [Google Scholar] [CrossRef] [Green Version]



| Statistical Metrics | Equation | Perfect Value | Unit |
|---|---|---|---|
| Root mean square error | 0 | mm | |
| Correlation coefficient | 1 | NA | |
| Percentage bias | 0 | % | |
| Kling–Gupta efficiency | 1 | NA | |
| Nash–Sutcliffe Efficiency | 1 | NA |
| Parameter | Initial Range | Rain Gauges | TMPA | IMERG | |||
|---|---|---|---|---|---|---|---|
| Final Range | Best Fit | Final Range | Best Fit | Final Range | Best Fit | ||
| esco.hru 1 | 0.5–0.95 | 0.5–0.77 | 0.548 | 0.5–0.91 | 0.617 | 0.5–0.77 | 0.548 |
| cn2.mgt 2 | (−0.2)–0.2 | (−0.2)–0.011 | −0.06 | (−0.2)–0.025 | −0.13 | (−0.2)–0.0114 | −0.06 |
| alpha_bf.gw 1 | 0–0.01 | 0.0038–0.01 | 0.009 | 0.0047–0.01 | 0.0095 | 0.0038–0.01 | 0.009 |
| gw_delay.gw 3 | (−30)–60 | (−8.454)–37.194 | −2.02 | (−26.814)–31.074 | −24.44 | (−8.454)–37.194 | −2.02 |
| gwqmn.gw 3 | (−1000)–1000 | (−83.202)–1000 | 916.6 | (−377.201)–869.201 | −301.2 | (−83.202)–1000 | 916.6 |
| canmx.hru 1 | 0–50 | 16.2–48.83 | 45.411 | 18.8–50 | 33.104 | 16.2–48.83 | 45.411 |
| ch_k2.rte 1 | (−0.01)–10 | 3.50–10 | 7.915 | 3.82–10 | 4.183 | 3.50–10 | 7.913 |
| ch_n2.rte 1 | (−0.01)–0.3 | 0.086–0.278 | 0.195 | 0.0763–0.249 | 0.208 | 0.086–0.279 | 0.195 |
| epco.bsn 1 | 0.01–1 | 0.388–1 | 0.976 | 0.01–0.517 | 0.450 | 0.388–1 | 0.976 |
| gw_revap.gw 1 | 0.02–0.2 | 0.088–0.2 | 0.1708 | 0.0431–0.1477 | 0.1315 | 0.088–0.2 | 0.1708 |
| revapmn.gw 3 | 0–500 | 198.699–500 | 320.1 | 0–295.299 | 240.1 | 198.700–500 | 320.1 |
| sol_awc.sol 2 | (−0.1)–0.1 | (−0.008)–0.1 | 0.074 | (−0.1)–0.00012 | −0.001 | (−0.008)–0.1 | 0.074 |
| sol_k.sol 2 | (−0.1)–0.1 | (−0.0145)–0.1 | 0.045 | (−0.1)–0.0015 | −0.090 | (−0.015)–0.1 | 0.045 |
| surlag.bsn 1 | 0.01–24 | 0.01–14.19 | 5.181 | 0.01–14.80 | 11.385 | 0.01–14.19 | 5.181 |
| Index | Rain Gauges | TMPA | IMERG | |||
| Calibration | Validation | Calibration | Validation | Calibration | Validation | |
| NSE | 0.86 | 0.84 | 0.85 | 0.82 | 0.82 | 0.83 |
| Pbias | −13.2 | −23.6 | −11.4 | −12.7 | −2.6 | −12.3 |
| KGE | 0.82 | 0.75 | 0.87 | 0.85 | 0.79 | 0.80 |
| p—factor | 0.75 | 0.69 | 0.88 | 0.78 | 0.73 | 0.76 |
| r—factor | 0.97 | 1.01 | 0.84 | 0.80 | 0.94 | 0.95 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amorim, J.d.S.; Viola, M.R.; Junqueira, R.; Oliveira, V.A.d.; Mello, C.R.d. Evaluation of Satellite Precipitation Products for Hydrological Modeling in the Brazilian Cerrado Biome. Water 2020, 12, 2571. https://doi.org/10.3390/w12092571
Amorim JdS, Viola MR, Junqueira R, Oliveira VAd, Mello CRd. Evaluation of Satellite Precipitation Products for Hydrological Modeling in the Brazilian Cerrado Biome. Water. 2020; 12(9):2571. https://doi.org/10.3390/w12092571
Chicago/Turabian StyleAmorim, Jhones da S., Marcelo R. Viola, Rubens Junqueira, Vinicius A. de Oliveira, and Carlos R. de Mello. 2020. "Evaluation of Satellite Precipitation Products for Hydrological Modeling in the Brazilian Cerrado Biome" Water 12, no. 9: 2571. https://doi.org/10.3390/w12092571
APA StyleAmorim, J. d. S., Viola, M. R., Junqueira, R., Oliveira, V. A. d., & Mello, C. R. d. (2020). Evaluation of Satellite Precipitation Products for Hydrological Modeling in the Brazilian Cerrado Biome. Water, 12(9), 2571. https://doi.org/10.3390/w12092571








