Mountain Lake Evaporation: A Comparative Study between Hourly Estimations Models and In Situ Measurements
Abstract
:1. Introduction
2. Materials and Methods
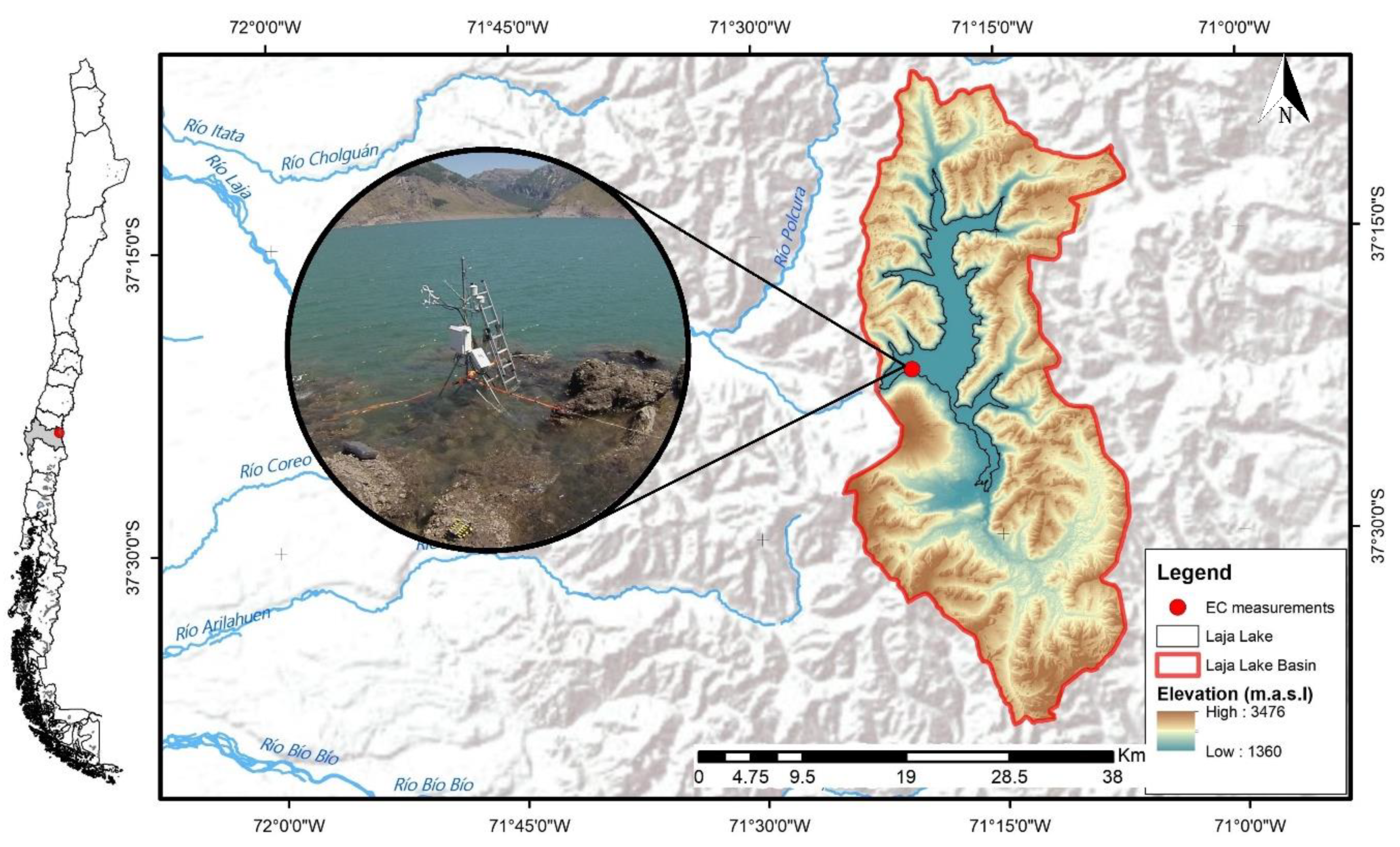
2.1. Study Area
2.2. Equipment and Measurements
2.3. Evaporation Estimation Methods
2.4. Evaluations
3. Results
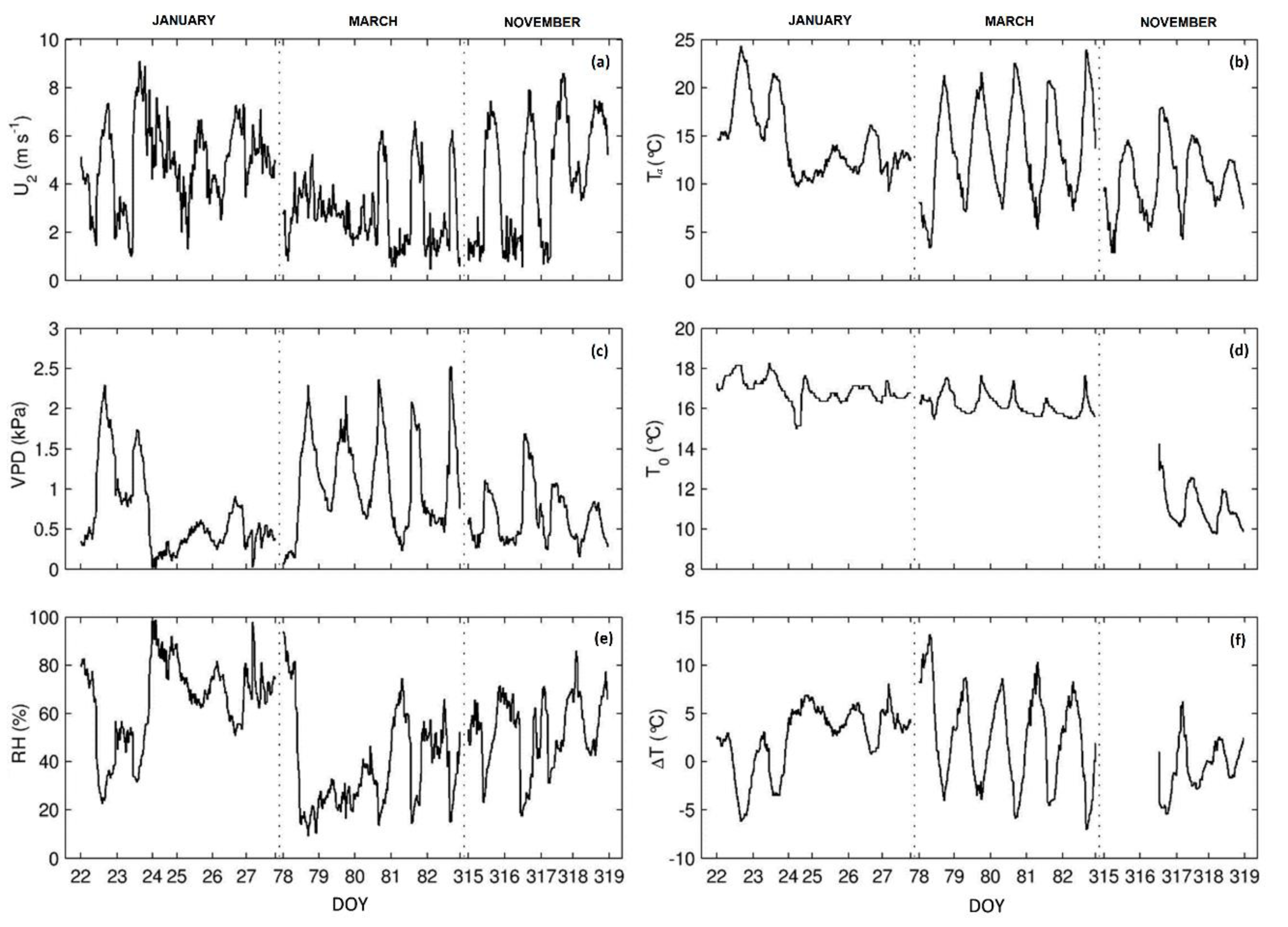
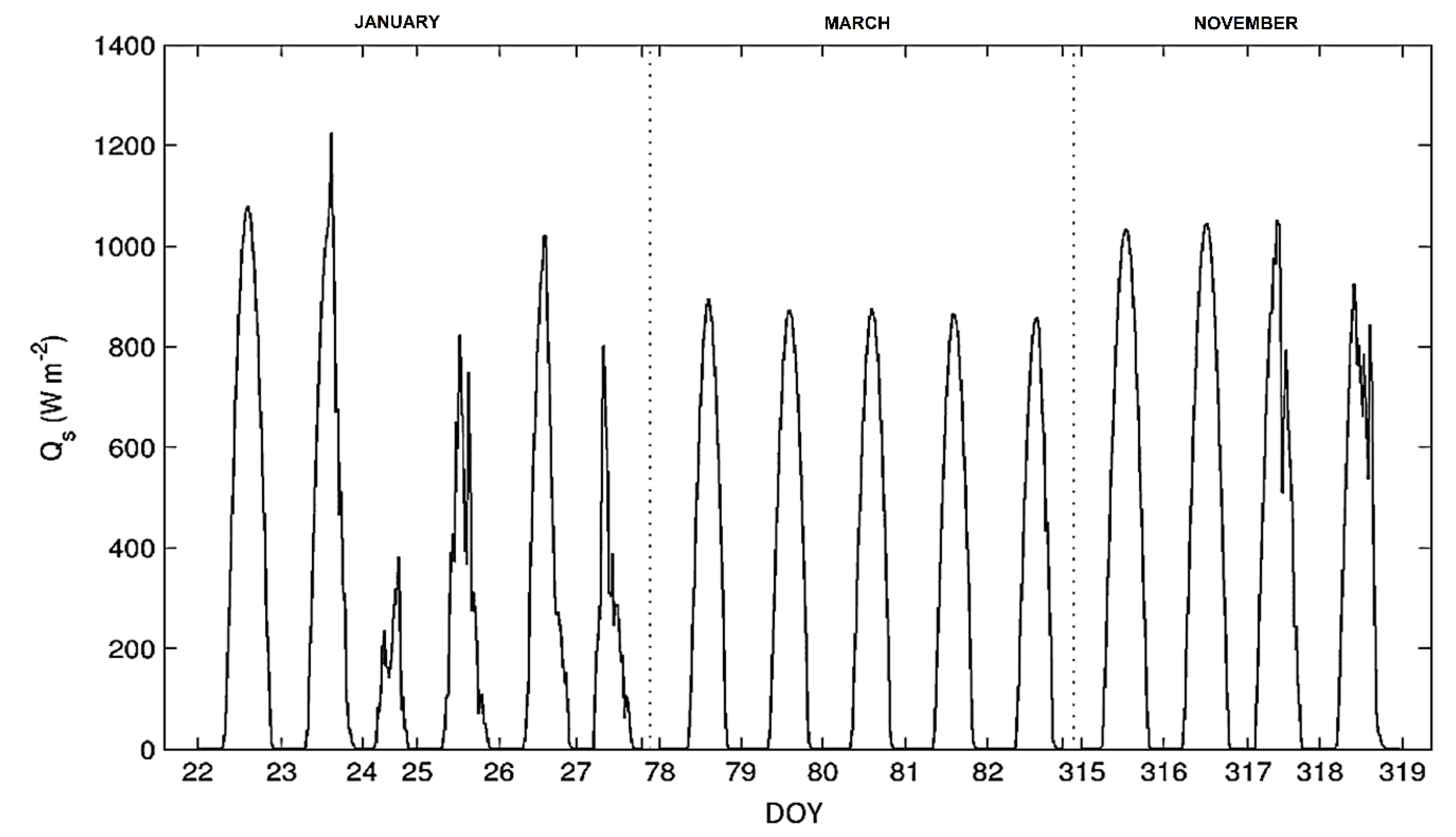
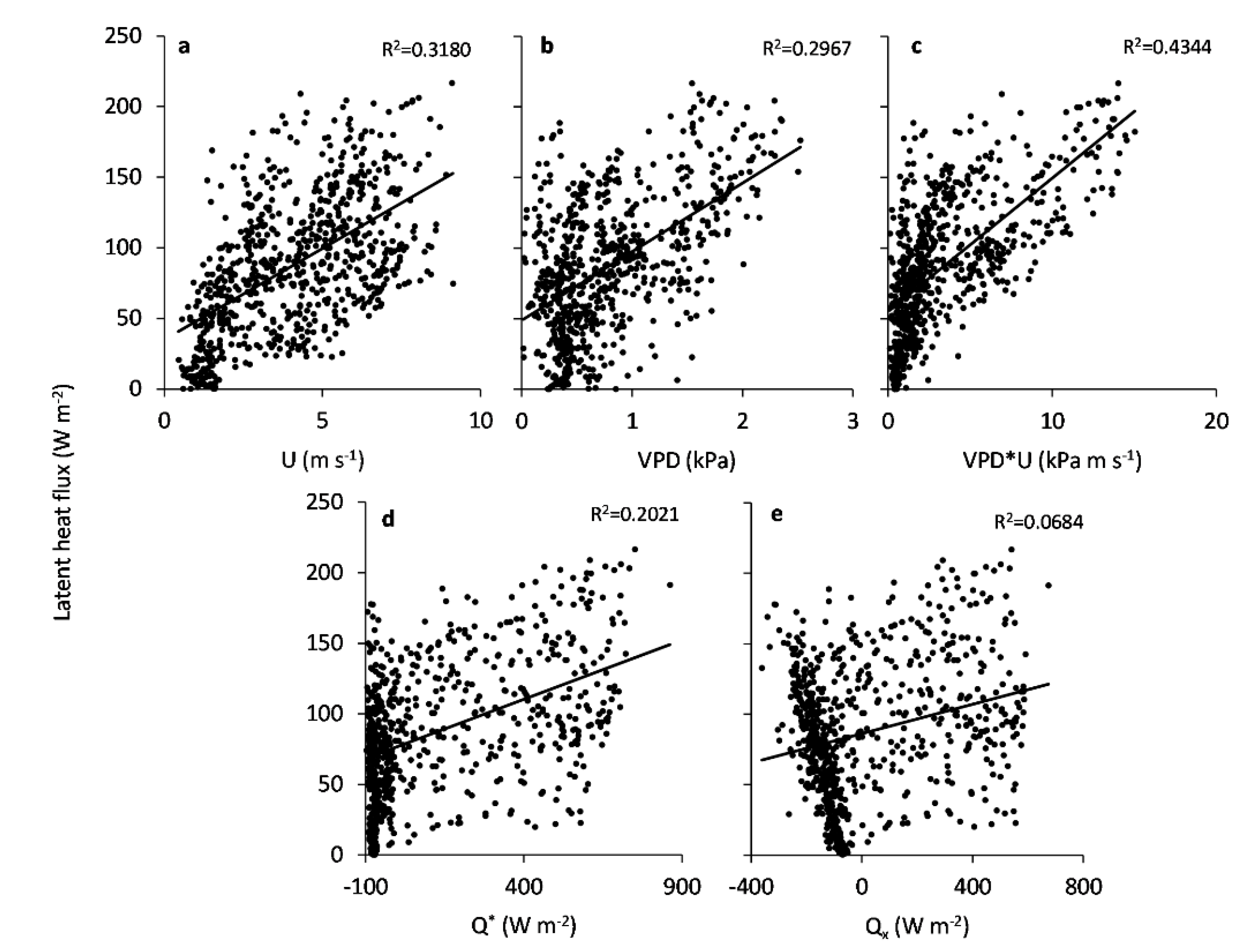
3.1. Environmental Components
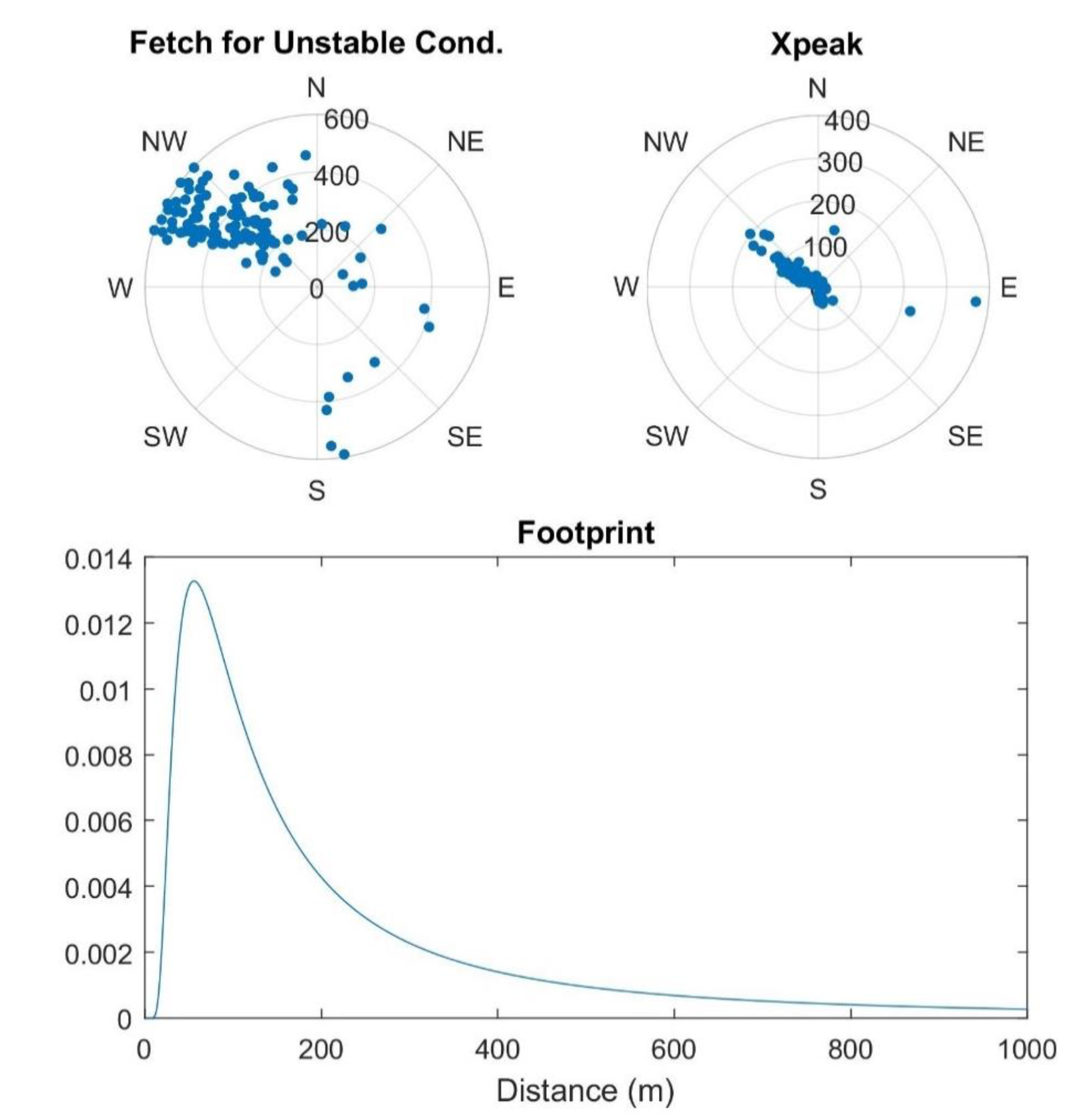
Footprint
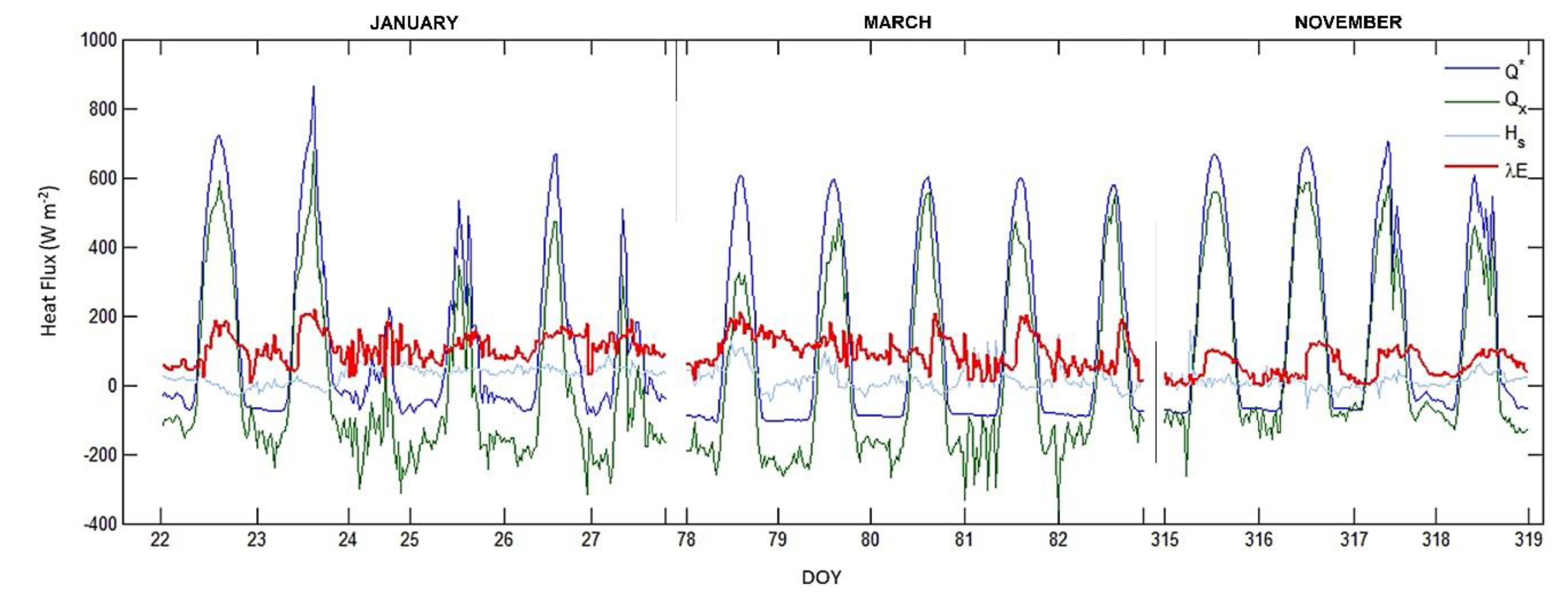
3.2. Surface Energy Budget Components
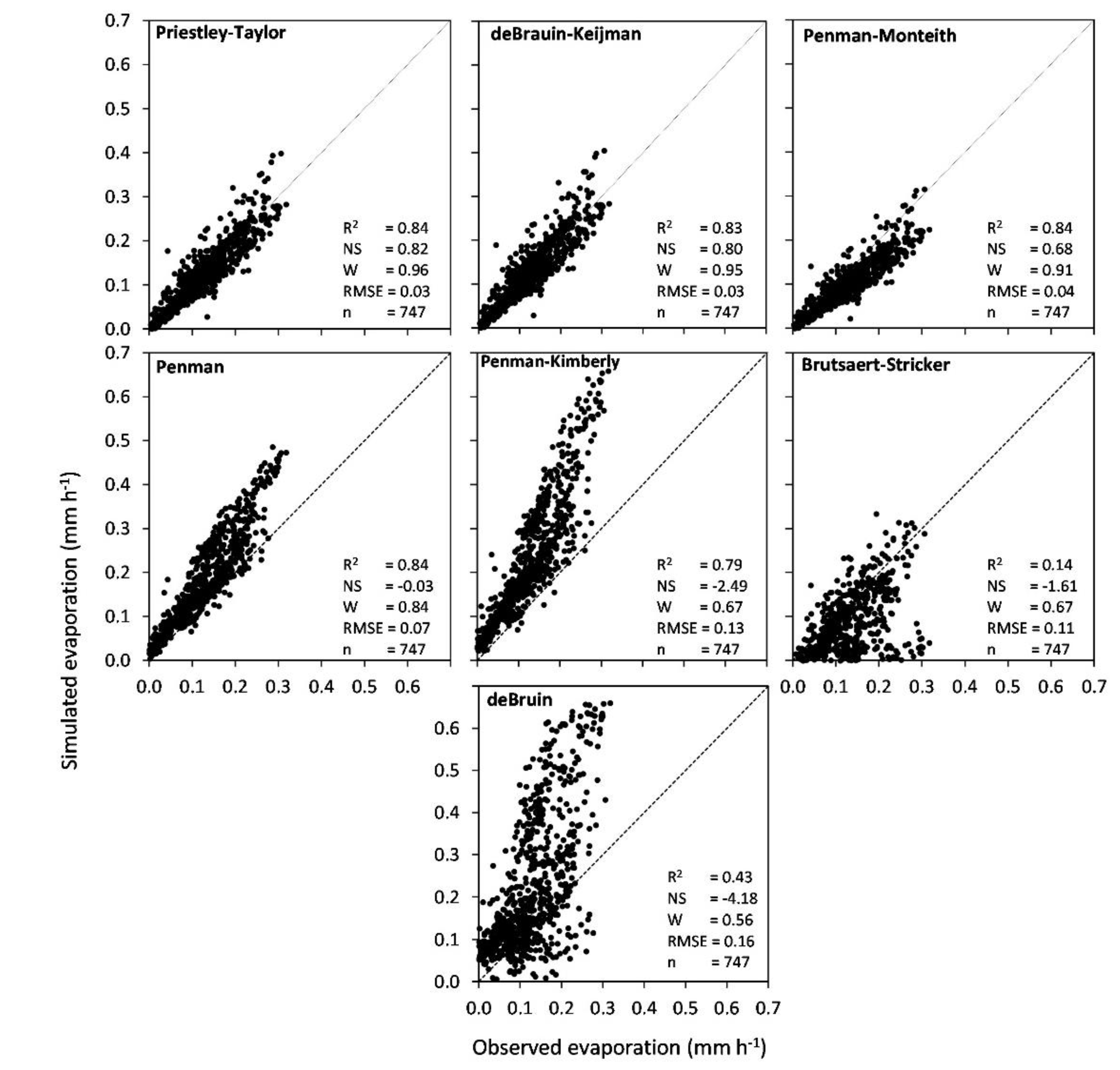
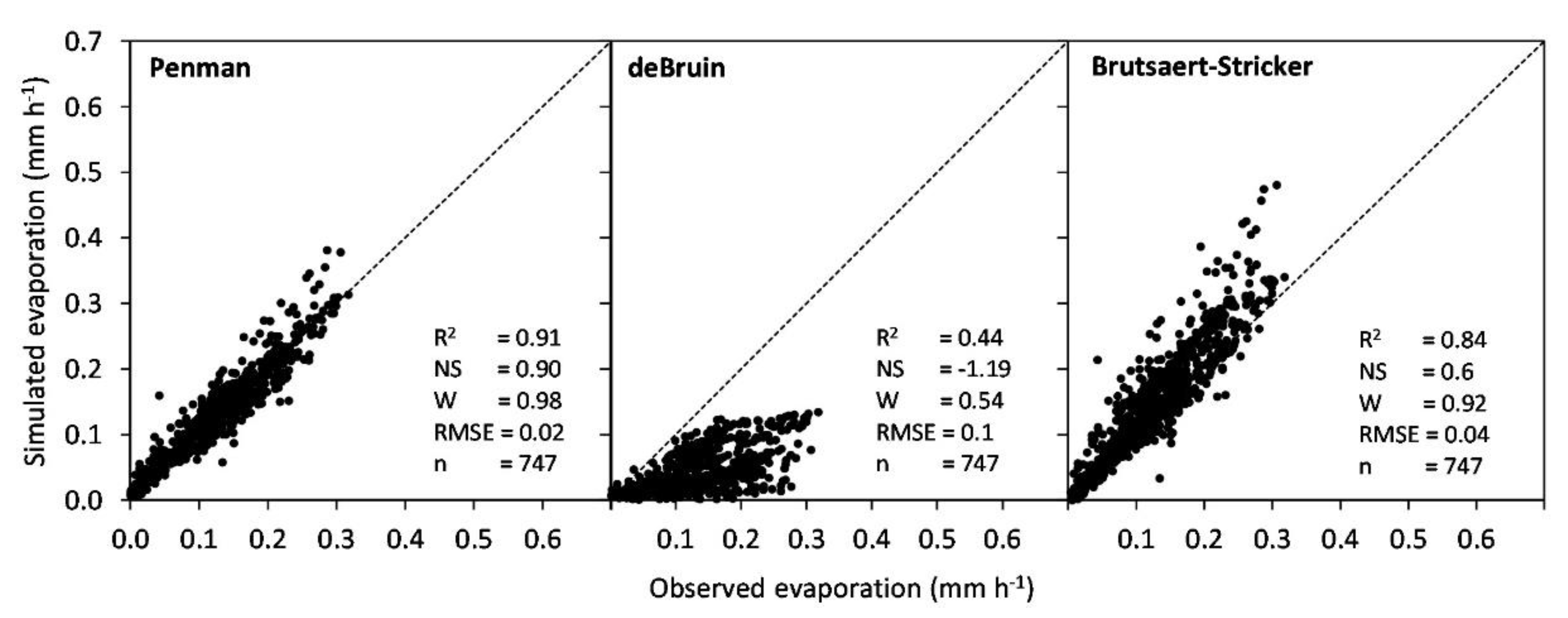
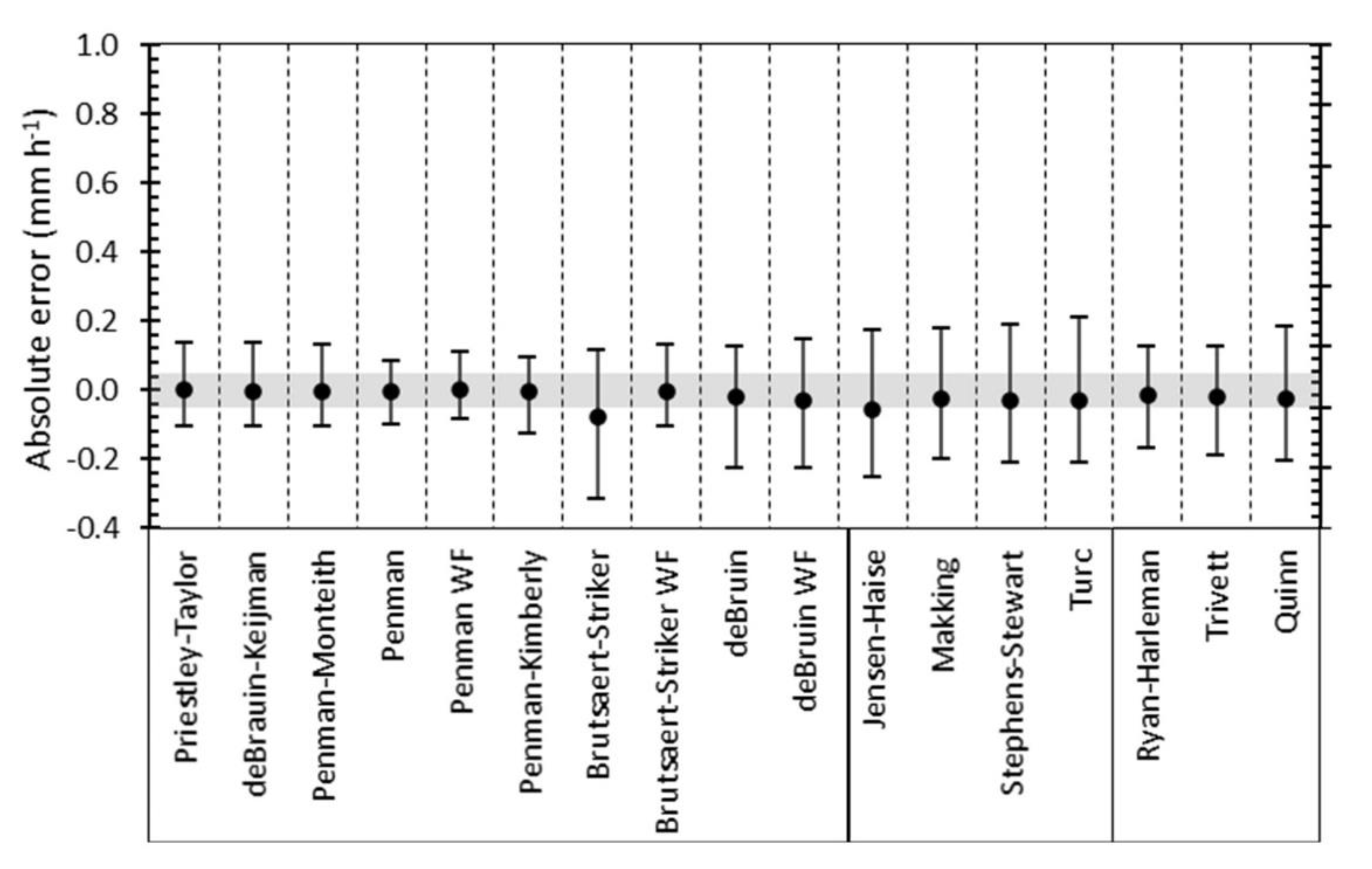
3.3. Model Comparisons with Measurements
4. Discussion
4.1. Measurements
4.2. Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Friedrich, K.; Grossman, R.L.; Huntington, J.; Blanken, P.D.; Lenters, J.; Holman, K.D.; Gochis, D.; Livneh, B.; Prairie, J.; Skeie, E.; et al. Reservoir Evaporation in the Western United States: Current Science, Challenges, and Future Needs. Bull. Am. Meteorol. Soc. 2018, 99, 167–187. [Google Scholar] [CrossRef]
- Meza, F.J.; Wilks, D.S.; Gurovich, L.; Bambach, N. Impacts of Climate Change on Irrigated Agriculture in the Maipo Basin, Chile: Reliability of Water Rights and Changes in the Demand for Irrigation. J. Water Resour. Plan. Manag. 2012, 138, 421–430. [Google Scholar] [CrossRef] [Green Version]
- Meza, F.J.; Vicuña, S.; Jelinek, M.; Bustos, E.; Bonelli, S. Assessing water demands and coverage sensitivity to climate change in the urban and rural sectors in central Chile. J. Water Clim. Chang. 2014, 5, 192–203. [Google Scholar] [CrossRef]
- Bolle, H.-J. Mediterranean Climate; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Martínez Alvarez, V.; González-Real, M.M.; Baille, A.; Maestre Valero, J.F.; Gallego Elvira, B. Regional assessment of evaporation from agricultural irrigation reservoirs in a semiarid climate. Agric. Water Manag. 2008, 95, 1056–1066. [Google Scholar] [CrossRef]
- Wurbs, R.A.; Ayala, R.A. Reservoir evaporation in Texas, USA. J. Hydrol. 2014, 510, 1–9. [Google Scholar] [CrossRef]
- Gökbulak, F.; Özhan, S. Water Loss through Evaporation from Water Surfaces of Lakes and Reservoirs in Turkey; Official Publication of the European Water Association (EWA): Hennef, Germany, 2006. [Google Scholar]
- Craig, I.; Green, A.; Scobie, M.; Schmidt, E. Controlling Evaporation Loss from Water Storages; University of Southern Queensland, National Centre for Engineering in Agriculture: Toowoomba, Australia, 2005. [Google Scholar]
- Helfer, F.; Lemckert, C.; Zhang, H. Impacts of climate change on temperature and evaporation from a large reservoir in Australia. J. Hydrol. 2012, 475, 365–378. [Google Scholar] [CrossRef] [Green Version]
- Bouin, M.-N.; Caniaux, G.; Traullé, O.; Legain, D.; Moigne, P.L. Long-term heat exchanges over a Mediterranean lagoon. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Miranda, C.; Moreira, M.; Guimarães, R.C. Reservoir evaporation in a Mediterranean climate: Comparing direct methods in Alqueva Reservoir, Portugal. Hydrol. Earth Syst. Sci. Discuss. 2020, 1–17. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Alvarez-Garreton, C.; Barichivich, J.; Boisier, J.P.; Christie, D.; Galleguillos, M.; LeQuesne, C.; McPhee, J.; Zambrano-Bigiarini, M. The 2010–2015 megadrought in central Chile: Impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef] [Green Version]
- Vuille, M.; Franquist, E.; Garreaud, R.; Casimiro, W.S.L.; Cáceres, B. Impact of the global warming hiatus on Andean temperature. J. Geophys. Res. Atmos. 2015, 120, 3745–3757. [Google Scholar] [CrossRef] [Green Version]
- Aldunce, P.; Araya, D.; Sapiain, R.; Ramos, I.; Lillo, G.; Urquiza, A.; Garreaud, R. Local Perception of Drought Impacts in a Changing Climate: The Mega-Drought in Central Chile. Sustainability 2017, 9, 2053. [Google Scholar] [CrossRef] [Green Version]
- Garreaud, R. Cambio Climático: Bases Físicas e Impactos en Chile; Revista Tierra Adentro–INIA: Santiago, Chile, 2011. [Google Scholar]
- Muñoz, E.; Guzmán, C.; Medina, Y.; Boll, J.; Parra, V.; Arumí, J.L. An Adaptive Basin Management Rule to Improve Water Allocation Resilience under Climate Variability and Change—A Case Study in the Laja Lake Basin in Southern Chile. Water 2019, 11, 1733. [Google Scholar] [CrossRef] [Green Version]
- Ministerio de Obras Públicas (MOP). Dirección General de Aguas Estadísticas Estaciones DGA. Available online: https://dga.mop.gob.cl/servicioshidrometeorologicos/Paginas/default.aspx (accessed on 5 May 2020).
- Ministerio de Obras Públicas (MOP). Guía para la Explotación del Lago Laja; Gobierno de Chile, Ministerio de Obras Públicas, Dirección de Obras Hidráulicas-Endesa: Santiago, Chile, 2018; (En Español).
- Tanny, J.; Cohen, S.; Assouline, S.; Lange, F.; Grava, A.; Berger, D.; Teltch, B.; Parlange, M.B. Evaporation from a small water reservoir: Direct measurements and estimates. J. Hydrol. 2008, 351, 218–229. [Google Scholar] [CrossRef] [Green Version]
- Meza, F.J. Variability of reference evapotranspiration and water demands. Association to ENSO in the Maipo river basin, Chile. Glob. Planet. Chang. 2005, 47, 212–220. [Google Scholar] [CrossRef]
- Olivera-Guerra, L.; Mattar, C.; Galleguillos, M. Estimation of real evapotranspiration and its variation in Mediterranean landscapes of central-southern Chile. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 160–169. [Google Scholar] [CrossRef]
- Bochetti, M.J.; Muñoz, E.; Tume, P.; Bech, J. Analysis of three indirect methods for estimating the evapotranspiration in the agricultural zone of Chillán, Chile. Obras Proy. 2016, 74–81. [Google Scholar] [CrossRef]
- Ortega-Farias, S.O.; Rojas, V.; Valdés, H.; Gonzaléz, P. Estimation of reference evapotranspiration in the maule region of chile: A comparison between the FAO Penman-Monteith and Bowen Ratio methods. Acta Hortic. 2004, 469–475. [Google Scholar] [CrossRef]
- Melsen, L.A.; Addor, N.; Mizukami, N.; Newman, A.J.; Torfs, P.J.J.F.; Clark, M.P.; Uijlenhoet, R.; Teuling, A.J. Mapping (dis)agreement in hydrologic projections. Hydrol. Earth Syst. Sci. 2018, 22, 1775–1791. [Google Scholar] [CrossRef] [Green Version]
- Jansen, F.A.; Teuling, A.J. Evaporation from a large lowland reservoir-(dis)agreement between evaporation models from hourly to decadal timescales. Hydrol. Earth Syst. Sci. 2020, 24, 1055–1072. [Google Scholar] [CrossRef] [Green Version]
- Rimmer, A.; Samuels, R.; Lechinsky, Y. A comprehensive study across methods and time scales to estimate surface fluxes from Lake Kinneret, Israel. J. Hydrol. 2009, 379, 181–192. [Google Scholar] [CrossRef]
- Metzger, J.; Nied, M.; Corsmeier, U.; Kleffmann, J.; Kottmeier, C. Dead Sea evaporation by eddy covariance measurements vs. aerodynamic, energy budget, Priestley–Taylor, and Penman estimates. Hydrol. Earth Syst. Sci. 2018, 22, 1135–1155. [Google Scholar] [CrossRef] [Green Version]
- Winter, T.C.; Rosenberry, D.O.; Sturrock, A.M. Evaluation of 11 Equations for Determining Evaporation for a Small Lake in the North Central United States. Water Resour. Res. 1995, 31, 983–993. [Google Scholar] [CrossRef]
- Singh, V.P.; Xu, C.-Y. Evaluation and Generalization of 13 Mass-Transfer Equations for Determining Free Water Evaporation. Hydrol. Process. 1997, 11, 311–323. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Winter, T.C.; Buso, D.C.; Likens, G.E. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. J. Hydrol. 2007, 340, 149–166. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Ma, W.; Su, B.; Dong, X. Evaluation of ten methods for estimating evaporation in a small high-elevation lake on the Tibetan Plateau. Theor. Appl. Climatol. 2019, 136, 1033–1045. [Google Scholar] [CrossRef]
- Granger, R.J.; Hedstrom, N. Modelling hourly rates of evaporation from small lakes. Hydrol. Earth Syst. Sci. 2011, 15, 267–277. [Google Scholar] [CrossRef] [Green Version]
- McGloin, R.; McGowan, H.; McJannet, D.; Burn, S. Modelling sub-daily latent heat fluxes from a small reservoir. J. Hydrol. 2014, 519, 2301–2311. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef] [Green Version]
- Pielke, R.A. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus Convective rainfall. Rev. Geophys. 2001, 39, 151–177. [Google Scholar] [CrossRef]
- Pitman, A.J. The evolution of, and revolution in, land surface schemes designed for climate models. Int. J. Climatol. 2003, 23, 479–510. [Google Scholar] [CrossRef]
- Hartfield, G.; Blunden, J.; Arndt, D.S. State of the Climate in 2017. Bull. Am. Meteorol. Soc. 2018, 99, S1–S310. [Google Scholar] [CrossRef]
- Garreaud, R.D. The Andes climate and weather. In Proceedings of the Advances in Geosciences; Copernicus GmbH: Gottingen, Germany, 2009; Volume 22, pp. 3–11. [Google Scholar]
- Thiele, R.; Moreno, H.; Elgueta, S.; Lahsen, A.; Rebolledo, S.; Petit-Breuilh, M.E. Evolución geológico-geomorfológica cuaternaria del tramo superior del valle del río Laja. Rev. Geológica Chile 1998, 25, 229–253. [Google Scholar] [CrossRef]
- Blanken, P.D.; Rouse, W.R.; Culf, A.D.; Spence, C.; Boudreau, L.D.; Jasper, J.N.; Kochtubajda, B.; Schertzer, W.M.; Marsh, P.; Verseghy, D. Eddy covariance measurements of evaporation from Great Slave Lake, Northwest Territories, Canada. Water Resour. Res. 2000, 36, 1069–1077. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Liu, S.; Jiang, H.; Sheng, L.; Williams, Q.L. Eddy covariance measurements of surface energy budget and evaporation in a cool season over southern open water in Mississippi. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Hsieh, C.-I.; Katul, G.; Chi, T. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- De Bruin, H.A.R. A Simple Model for Shallow Lake Evaporation. J. Appl. Meteorol. 1978, 17, 1132–1134. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Rouse, W.R.; Oswald, C.M.; Binyamin, J.; Blanken, P.D.; Schertzer, W.M.; Spence, C. Interannual and Seasonal Variability of the Surface Energy Balance and Temperature of Central Great Slave Lake. J. Hydrometeorol. 2003, 4, 720–730. [Google Scholar] [CrossRef]



| Method | Equation |
|---|---|
| Combination group | |
| Priestley-Taylor | |
| deBrauin-Keijman | |
| Penman-Monteith | |
| Penman | |
| Penman-Kimberly | |
| Brutsaert-Stricker | |
| deBruin | |
| Solar radiation—temperature group | |
| Jensen-Haise | ; ; ; ; ; |
| Makkink | |
| Stephens-Stewart | |
| Turc | for and for |
| Mass transfer group | |
| Ryan-Harleman | |
| Trivett | /24 |
| Quinn | |
| (A) | |
| (B) | |
| (C) | |
| (D) | |
| (E) | |
| (F) | |
| (G) | |
| 3.6 and 1/24 multipliers appear in the equations to convert output to mm h−1 | |
| ∆ | Slope saturated vapor pressure-temperature curve (Pa °C−1). |
| α | 1.26, Priestley-Taylor empirically derived constant, dimensionless. |
| a,b y c | Adjustment parameters for mass models. |
| γ | Psychrometric constant (depends on temperature and atmospheric pressure (Pa °C−1)). |
| θv | Difference in temperature between surface water and air (°C). |
| Λ | Latent heat of vaporization (MJ kg−1). |
| Water density (998 kg m−3). | |
| ea | Vapor pressure at the air temperature (kPa) (deBruin in mb). |
| ea* | Vapor pressure at the dewpoint temperature (mb). |
| es | Saturation vapor pressure at the air temperature (kPa) (deBruin in mb). |
| es* | Saturation vapor pressure at the water surface temperature (mb). |
| Elevation (m). | |
| Wind function, ; with a = 0.5 y b = 0.54 for Penman, a = 1 and b = 0.54 for Brutsaert-Stricker, a = 2.9 and b = 2.1 for deBruin model. | |
| Day of the year. | |
| Unit conversion factor = 74.44 W m−2 kPa−1 = 0.268 MJ m−2 h−1 | |
| RH | Relative humidity (%) |
| Q* | Net radiation (W m−2). |
| Qs | Solar radiation (W m−2) (Turc in cal cm−2 d−1). |
| Qx | Water heat flux (W m−2). |
| Bulk surface resistance (s m−1); | |
| Aerodynamic resistance (s m−1) | |
| T0 | Water surface temperature (°C) |
| Ta | Air temperature in °C (Stephens-Steward in °F). |
| Wind speed at 2 m above water surface (m s−1) (km hr−1 for Trivett). | |
| U3 | Wind speed at 3 m above water surface (m s−1); , is wind speed at height level 2, is wind speed at height level 1, is measurement height level 2 and is measurement height level 1 |
| Wind function, ; ; ; For latitudes south of the equator, one should use in place of , where for and for | |
| Indicator | Equation |
|---|---|
| Coefficient of determination | |
| Nash-Sutcliffe | |
| Index of Agreement | |
| Root mean square error |
| DOY | T (°C) | T0 (°C) | U2 (m s−1) | HR (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max. | Min. | Max. | Min. | Max. | Min. | Max. | Min. | |||||
| 22 | 24.3 | 14.5 | 18.7 | 18.1 | 16.9 | 17.5 | 7.3 | 1.4 | 4.5 | 82.5 | 22.5 | 51.4 |
| 23 | 21.4 | 13.5 | 17.7 | 18.3 | 16.5 | 17.3 | 9.1 | 1.0 | 5.0 | 88.5 | 31.5 | 50.0 |
| 24 | 12.6 | 9.7 | 10.7 | 17.6 | 15.0 | 16.3 | 7.6 | 4.2 | 5.5 | 98.8 | 74.0 | 87.2 |
| 25 | 14.1 | 10.1 | 12.3 | 16.8 | 16.3 | 16.5 | 6.7 | 1.3 | 4.4 | 88.9 | 62.2 | 70.3 |
| 26 | 16.1 | 11.0 | 13.2 | 17.1 | 16.3 | 16.9 | 7.3 | 2.5 | 5.2 | 81.7 | 50.8 | 66.0 |
| 27 | 13.5 | 9.3 | 12.1 | 17.4 | 16.5 | 16.7 | 7.1 | 4.0 | 5.2 | 97.9 | 62.2 | 72.5 |
| 78 | 21.2 | 3.4 | 120 | 17.5 | 15.5 | 16.6 | 5.2 | 0.8 | 3.1 | 93.9 | 9.2 | 43.5 |
| 79 | 21.6 | 7.1 | 14.3 | 17.6 | 15.8 | 16.3 | 4.0 | 1.4 | 2.7 | 32.5 | 16.5 | 24.8 |
| 80 | 22.5 | 7.4 | 14.7 | 17.4 | 15.9 | 16.3 | 6.2 | 0.9 | 3.1 | 46.3 | 13.7 | 30.4 |
| 81 | 20.7 | 5.3 | 13.3 | 16.5 | 15.6 | 15.9 | 6.6 | 0.5 | 2.7 | 74.5 | 14.3 | 48.0 |
| 82 | 23.9 | 7.2 | 14.2 | 17.6 | 15.5 | 15.9 | 6.2 | 0.4 | 2.3 | 65.7 | 15.0 | 42.7 |
| 315 | 14.5 | 2.8 | 9.7 | - | - | - | 7.4 | 0.8 | 3.7 | 71.5 | 23.0 | 51.1 |
| 316 | 17.9 | 5.1 | 11.2 | 14.3 | 10.4 | 11.6 | 7.9 | 0.8 | 3.5 | 70.3 | 17.4 | 47.4 |
| 317 | 15.0 | 4.3 | 11.4 | 12.6 | 10.1 | 11.2 | 8.6 | 0.7 | 4.8 | 71.1 | 30.9 | 50.6 |
| 318 | 12.5 | 7.5 | 10.1 | 12.0 | 9.7 | 10.6 | 7.5 | 3.3 | 5.6 | 85.9 | 42.4 | 59.5 |
| DOY | ||||||||
|---|---|---|---|---|---|---|---|---|
| Máx | Máx | Máx | Máx | |||||
| 22 | 184 | 91 | 722 | 207 | 37 | 2 | 591 | 113 |
| 23 | 217 | 117 | 862 | 181 | 56 | 2 | 674 | 62 |
| 24 | 183 | 104 | 221 | 6 | 92 | 57 | 99 | −155 |
| 25 | 159 | 102 | 534 | 78 | 55 | 40 | 345 | −64 |
| 26 | 178 | 120 | 669 | 139 | 60 | 42 | 472 | −23 |
| 27 | 189 | 113 | 508 | 59 | 87 | 46 | 315 | −100 |
| 78 | 209 | 121 | 608 | 100 | 128 | 38 | 324 | −58 |
| 79 | 182 | 114 | 593 | 109 | 97 | 14 | 479 | −20 |
| 80 | 205 | 99 | 602 | 114 | 41 | 3 | 556 | 12 |
| 81 | 202 | 85 | 599 | 113 | 130 | 24 | 473 | 4 |
| 82 | 191 | 71 | 580 | 108 | 145 | 10 | 549 | 28 |
| 315 | 104 | 45 | 665 | 190 | 157 | 12 | 559 | 133 |
| 316 | 129 | 56 | 686 | 190 | 54 | −2 | 587 | 136 |
| 317 | 117 | 61 | 704 | 202 | 42 | 6 | 576 | 134 |
| 318 | 103 | 63 | 606 | 151 | 62 | 22 | 458 | 67 |
| Date | Evaporated Water Height (mm d−1) | Evaporated Flow (m3 s−1) |
|---|---|---|
| 22-01-2016 | 3.20 | 2.6 |
| 23-01-2016 | 4.02 | 3.3 |
| 24-01-2016 | 2.44 | 2.0 |
| 25-01-2016 | 3.56 | 2.9 |
| 26-01-2016 | 3.95 | 3.2 |
| 27-01-2016 | 3.23 | 2.6 |
| 18-03-2016 | 4.14 | 3.4 |
| 19-03-2016 | 4.01 | 3.3 |
| 20-03-2016 | 3.46 | 2.8 |
| 21-03-2016 | 2.97 | 2.4 |
| 22-03-2016 | 2.33 | 1.9 |
| 10-11-2016 | 1.53 | 1.2 |
| 11-11-2016 | 1.93 | 1.6 |
| 12-11-2016 | 1.88 | 1.5 |
| 13-11-2016 | 2.21 | 1.8 |
| Model | Parameter | Indicator | |||||
|---|---|---|---|---|---|---|---|
| a | b | c | R2 | NS | W | RMSE | |
| (A) | 0.2471 | - | - | 0.23 | 0.51 | 0.77 | 0.05 |
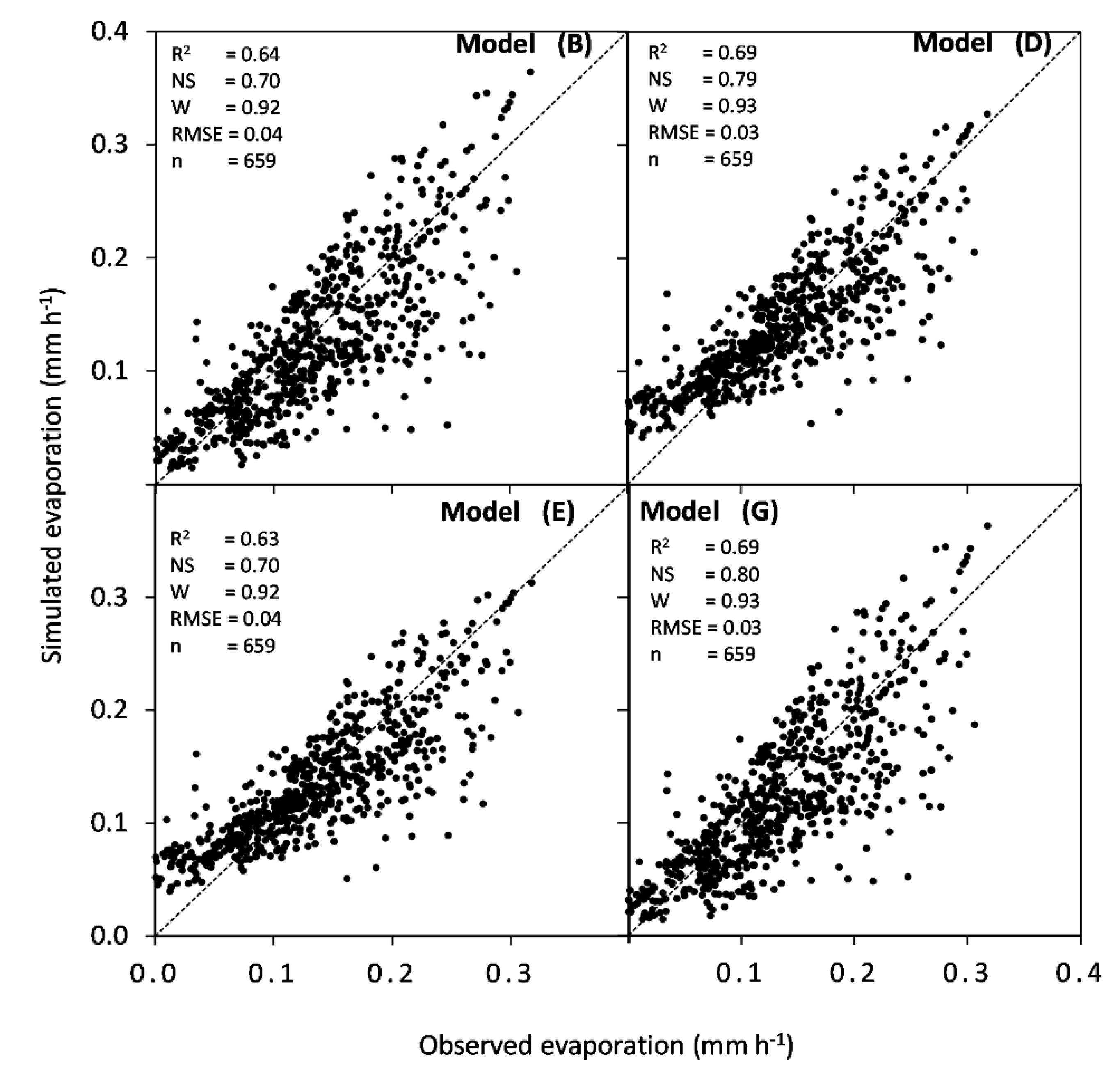
| (B) | 0.0012 | - | - | 0.64 | 0.70 | 0.92 | 0.04 |
| (C) | 0.0057 | - | - | 0.24 | 0.45 | 0.77 | 0.05 |
| (D) | 0.0019 | 0.4570 | - | 0.69 | 0.79 | 0.93 | 0.03 |
| (E) | 0.0012 | 0.0002 | - | 0.63 | 0.70 | 0.92 | 0.04 |
| (F) | 7.648·10−7 | - | - | 0.27 | 0.48 | 0.87 | 0.05 |
| (G) | 0.0018 | 0.4549 | 0.0009 | 0.69 | 0.80 | 0.93 | 0.03 |
| Group | Method | N | KLL | R2 | NS | NS * | W | W * | RMSE (mm h−1) | RMSE * (mm h−1) |
|---|---|---|---|---|---|---|---|---|---|---|
| Combination | Priestley-Taylor | 747 | 0.98 | 0.84 | 0.82 | 0.83 | 0.96 | 0.96 | 0.03 | 0.03 |
| deBrauin-Keijman | 747 | 0.95 | 0.83 | 0.80 | 0.82 | 0.95 | 0.95 | 0.03 | 0.03 | |
| Penman-Monteith | 747 | 1.23 | 0.84 | 0.68 | 0.83 | 0.91 | 0.96 | 0.04 | 0.03 | |
| Penman | 747 | 0.69 | 0.84 | −0.03 | 0.83 | 0.84 | 0.96 | 0.07 | 0.02 | |
| Penman WF | 747 | 0.96 | 0.91 | 0.90 | 0.91 | 0.98 | 0.98 | 0.02 | 0.02 | |
| Penman-Kimberly | 747 | 0.53 | 0.79 | −2.49 | 0.77 | 0.67 | 0.94 | 0.13 | 0.03 | |
| Brutsaert-Stricker | 747 | 0.91 | 0.14 | −1.61 | −1.59 | 0.56 | 0.56 | 0.11 | 0.11 | |
| Brutsaert-Stricker WF | 747 | 0.81 | 0.84 | 0.60 | 0.83 | 0.92 | 0.96 | 0.04 | 0.03 | |
| deBruin | 747 | 0.47 | 0.43 | −4.18 | 0.15 | 0.56 | 0.79 | 0.16 | 0.10 | |
| deBruin WF | 747 | 2.50 | 0.44 | −1.19 | 0.02 | 0.54 | 0.78 | 0.10 | 0.07 | |
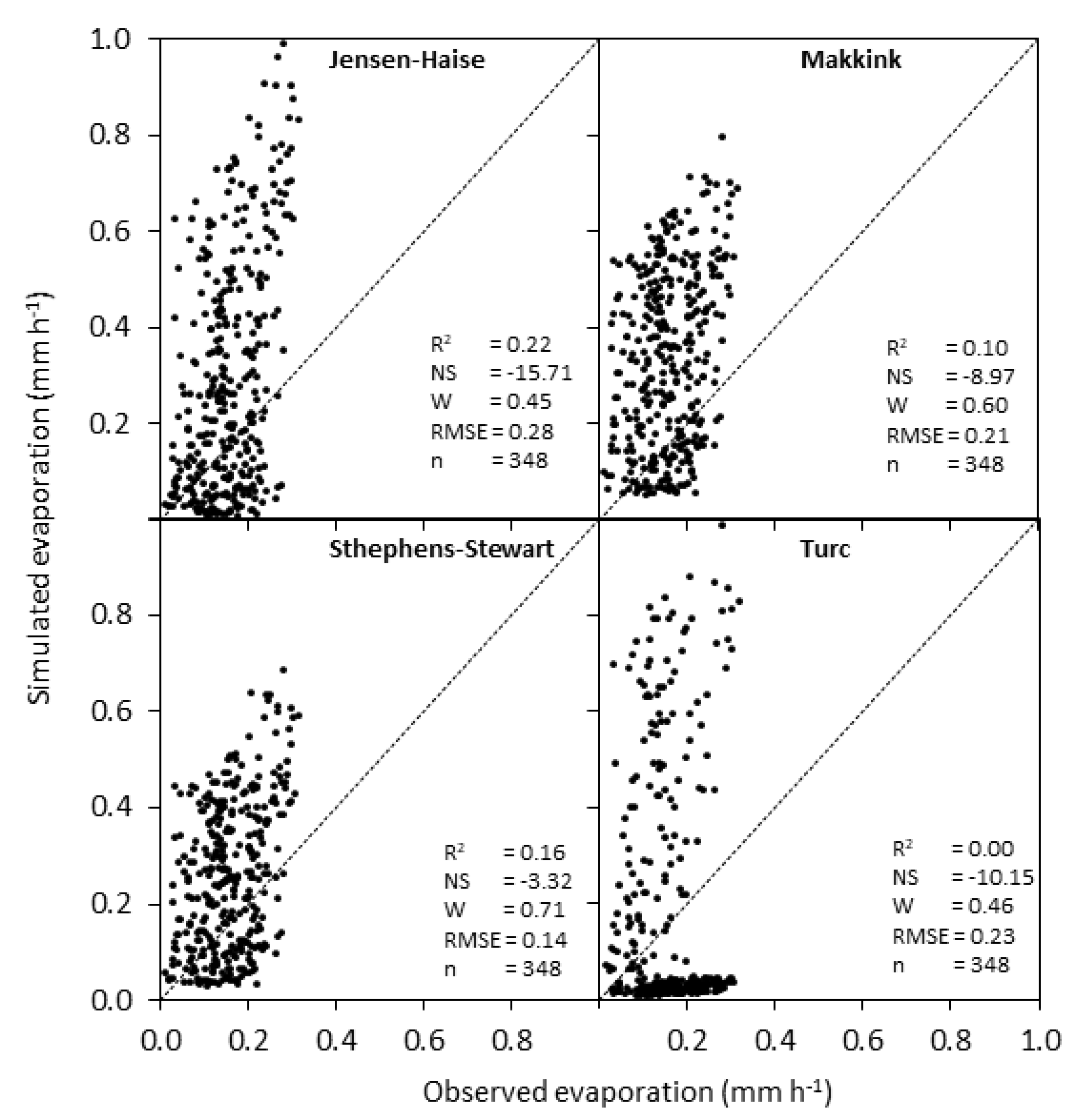
| Solar radiation-temperature | Jensen-Haise | 348 | 0.36 | 0.22 | −6.33 | 0.06 | 0.45 | 0.59 | 0.28 | 0.10 |
| Makking | 348 | 0.39 | 0.10 | −4.96 | 0.29 | 0.45 | 0.60 | 0.25 | 0.09 | |
| Stephens-Stewart | 348 | 0.50 | 0.16 | −1.83 | 0.28 | 0.57 | 0.64 | 0.17 | 0.09 | |
| Turc | 348 | 0.35 | 0.12 | −7.28 | 0.23 | 0.41 | 0.42 | 0.29 | 0.09 | |
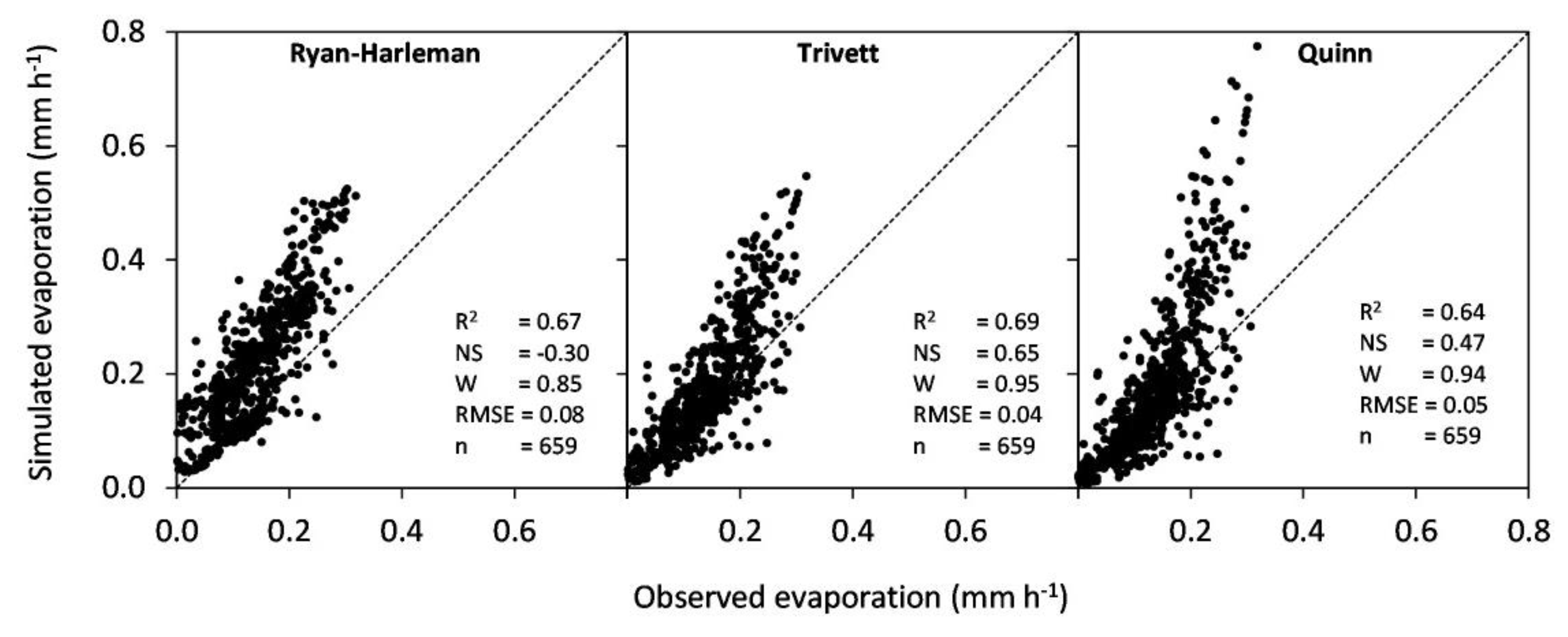
| Mass transfer | Ryan-Harleman | 659 | 0.61 | 0.67 | −0.11 | 0.77 | 0.85 | 0.93 | 0.08 | 0.04 |
| Trivett | 659 | 0.73 | 0.69 | 0.71 | 0.77 | 0.95 | 0.94 | 0.04 | 0.04 | |
| Quinn | 659 | 0.64 | 0.64 | 0.54 | 0.65 | 0.94 | 0.91 | 0.05 | 0.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, A.; Lagos, O.; Lillo-Saavedra, M.; Souto, C.; Paredes, J.; Arumí, J.L. Mountain Lake Evaporation: A Comparative Study between Hourly Estimations Models and In Situ Measurements. Water 2020, 12, 2648. https://doi.org/10.3390/w12092648
Pérez A, Lagos O, Lillo-Saavedra M, Souto C, Paredes J, Arumí JL. Mountain Lake Evaporation: A Comparative Study between Hourly Estimations Models and In Situ Measurements. Water. 2020; 12(9):2648. https://doi.org/10.3390/w12092648
Chicago/Turabian StylePérez, Andrés, Octavio Lagos, Mario Lillo-Saavedra, Camilo Souto, Jerónimo Paredes, and José Luis Arumí. 2020. "Mountain Lake Evaporation: A Comparative Study between Hourly Estimations Models and In Situ Measurements" Water 12, no. 9: 2648. https://doi.org/10.3390/w12092648
APA StylePérez, A., Lagos, O., Lillo-Saavedra, M., Souto, C., Paredes, J., & Arumí, J. L. (2020). Mountain Lake Evaporation: A Comparative Study between Hourly Estimations Models and In Situ Measurements. Water, 12(9), 2648. https://doi.org/10.3390/w12092648








