Water Resource Carrying Capacity Based on Water Demand Prediction in Chang-Ji Economic Circle

Abstract

In view of the large spatial difference in water resources, the water shortage and deterioration of water quality in the Chang-Ji Economic Circle located in northeast China, the water resource carrying capacity (WRCC) from the perspective of time and space is evaluated. We combine the gray correlation analysis and multiple linear regression models to quantitatively predict water supply and demand in different planning years, which provide the basis for quantitative analysis of the WRCC. The selection of research indicators also considers the interaction of social economy, water resources, and water environment. Combined with the fuzzy comprehensive evaluation method, the gray correlation analysis and multiple linear regression models to quantitatively and qualitatively evaluate the WRCC under different social development plans. The developmental trends were obtained from 2017 to 2030 using four plans designed for distinct purposes. It can be seen that the utilization of water resource is unreasonable now and maintains a poor level under a business-as-usual Plan I. Plan II and Plan III show that resource-based water shortage is the most critical issue in this region, and poor water quality cannot be ignored either. Compared with Plan I, the average index of WRCC in Plan IV increased by 51.8% and over 84% of the regions maintain a good level. Strengthening sewage treatment and properly using transit water resources are more conducive to the rapid development of Chang-Ji Economic Circle.

1. Introduction

With the development of the urbanization process, the demand for water resources has increased significantly, but the pollution of water resources has caused serious problems. These changes pose a potential threat to water resource carrying capacity in many regions [1]. The water resources carrying capacity (WRCC) refers to the ability of water resources to withstand the largest population, socioeconomic, and ecological environment requirements under the premise of maintaining sustainable development. Studies of the WRCC can provide helpful information about how the socioeconomic system is both supported and restrained by the water resources system, such as intuitively measuring regional development potential [2], etc. Since the 21st century, people began to pay attention to the research of WRCC. Through continuous improvement of related influencing factors, a relatively mature evaluation system has initially formed [3,4,5]. Nowadays, the research on the WRCC has changed from a simple natural factor to a water-ecological-economic factor [6].

The research on the WRCC’s theory in the international context is focused more on the relationship between carrying capacity and sustainable economic and social development [7]. However, the research on the limitation of water resources security to the WRCC is relatively late. According to the latest analysis of the obstacle degree for the WRCC system in Northeast China, the agricultural water pollution index emerged as the main factor that is restricting the steady rise of the WRCC since 2004. Following 2014, with the upsurge of industrialization, the percentage of industrial wastewater discharge has increased significantly [8]. There are many old industrial bases in the Chang-Ji Economic Circle, and the percentage of industrial wastewater discharge and the risk of water pollution has increased year by year. Furthermore, the data published in the Water Resources Bulletin in the study area over the years show that the surface water quality is bad. So, the water quality should be included in the analysis of WRCC in the Chang-Ji economic circle. In China, there are few studies on the water resources carrying capacity of the Chang-Ji economic circle [9]. Moreover, most of the studies in the Chang-Ji Economic Circle are carried out in administrative regions, and few studies take into account the constraints of water pollution on the WRCC, which cannot directly and accurately measure the development potential of the entire Chang-Ji Economic Circle [10,11]. Therefore, this study takes into account the quantity and quality of water resources and combines the comprehensive carrying capacity of social economic development and ecological environment and selects appropriate methods to evaluate the WRCC of the Chang-Ji Economic Circle.

At present, there are plenty of methods to evaluate the WRCC, such as the traditional trend analysis method [12], the principal component analysis method [13], the fuzzy comprehensive evaluation method (FCE) [14], the multiobjective analysis method [15], the artificial neural network method [16], and the system dynamics (SD) method [17,18]. Zhang et al. [13] applied the principal component analysis method to evaluate the temporal scale variation tendency of the WRCC. However, there was still some uncertainty when integrating the method WRCC index standardization, the method of principal component determination, and the weights of contribution rates. Multiobjective analysis is influenced by its limitations and is more suitable for smaller areas of research. The SD model can effectively simulate and predict through negative feedback adjustment [19]. However, this method requires a large number of parameter settings and data simulations [20], which cannot achieve rapid evaluation. In fact, various WRCC prediction methods are based on the further evaluation of their influencing factors. The FCE method which is widely used by scholars can analyze the WRCC from all aspects [21,22], making the research results more reliable. For example, Zhang et al. [23] used fuzzy set pair analysis theory to evaluate the WRCC in Dagong Yellow River Diversion Irrigation District from 2013 to 2017. The study qualitatively measured the water resources carrying capacity of the ecological irrigation area, and the evaluation results can provide a scientific basis for optimal allocation of water resources in the Dagong Yellow River diversion irrigation district. At the same time, through the comparative analysis of some indicators, the FCE method can solve the defects of the parameters that are difficult to grasp and easily lead to unreasonable conclusions. Moreover, while assessing the regional WRCC, it is necessary to predict future development trends based on the status quo. Accurate trend analysis has become an important part of reasonable evaluation. However, most scholars use the simple linear equations to predict related influencing factors. To make up for the shortcomings of large errors in traditional trend analysis, this study quantitatively predicts relevant influencing factors by the method of gray correlation analysis (GCA) combined with multiple linear regression (MLR) models. Then, on the basis of quantitatively predicting the development trend of social economy, water resources, and water environment evaluation indicators, the FCE method is used to make a reliable assessment of the WRCC.

2. Study Area and Data Sources

2.1. Study Area

The Chang-Ji Economic Circle includes the whole of Changchun City, Jilin City, Jiutai District, Shuangyang District, and Yongji County, as well as parts of Nongan County, Gongzhuling City, and Yitong County (Figure 1). The study area is located in the center of Jilin Province, accounting for 7.96% of the total province’s area. The total population of the region is about 648 million and the urbanization rate is 59.64%. There are many water systems in the area, and river networks are dense, all belonging to the second Songhua River system. The large reservoirs include Fengman Reservoir, Shitoukoumen Reservoir, and Xinlicheng Reservoir. The total water storage capacity is as high as 134.1 × 10⁸ m³.

2.2. Data Sources

The study area involves Jilin City and Changchun City, and the data used include socioeconomic data, water supply and demand data, and water environment data. The data sources are Jilin statistical yearbook (2010–2017), Changchun statistical yearbook (2010–2017), Jilin water resource bulletin (2010–2017), and Changchun water resource bulletin (2010–2017). In addition, water quota references the industry water quota standards of Jilin province and some environmental data comes from the website of Jilin province environmental protection bureau.

3. Establishment and Prediction of Water Demand Model

The analysis of the balance between supply and demand of water resources can reflect the overall level of water use in a region and is an important factor affecting the WRCC. In recent years, ecological and environmental problems have become increasingly prominent, and ecological water demand will also become an important issue in the analysis of the balance between water supply and demand. This study collects water supply and demand data for the past eight years in the study area and focuses on ecological water demand to predict the water demand in the next 13 years.

3.1. Model Related Methods

Since the study area involves 15 different administrative districts, if the forecast is made one by one according to the different water demand industries, the amount of data required is large and it is difficult to maintain consistency. The combination of the GCA and MLR model can make up for this deficiency. Using the GCA method, the correlation coefficients between the six water demands and the total water demand are calculated respectively. The six water requirements are ecological and environmental water demand, urban public water demand, domestic water demand, forestry, animal husbandry and fishery water demand, farmland irrigation water demand, and industrial water demand. One selects indicators with high correlation coefficients and establishes MLR models of each indicator for total water demand, then obtains total water demand at different planning levels.

3.1.1. The GCA Method

The GCA is to find the important factors that affect the target value by looking for the correlation between various factors between random sequences. This method is mainly to determine the correlation between the influencing factors and the target value, find the main characteristics of the problem, and intuitively quantify the complex influencing relationship. The main calculation method is to perform dimensionless processing on all data, set the processed target sequence to x₀, and set the factor sequence to x_i (i = 1, 2, …, n); perform a difference between the two sequences. Calculate to find the maximum difference and minimum difference between the two poles. Among them, the difference sequence is expressed as:

$${\mathsf{\Delta }}_{0i}(k)=\left|x_0(k)-x_i(k)\right|$$

(1)

Find the correlation coefficient between each factor and the target value ${\epsilon }_i(k)$:

$${\epsilon }_i(k)=\frac{\min \min \left|x_0(k)-x_i(k)\right|+\rho \max \max \left|x_0(k)-x_i(k)\right|}{\left|x_0(k)-x_i(k)\right|+\rho \max \max \left|x_0(k)-x_i(k)\right|}$$

(2)

Equation (1), ${\mathsf{\Delta }}_{oi}\left(k\right)$ is the absolute value of the difference between two sequences.

Equation (2), $\rho$ for the resolution coefficient, the empirical value is 0.5; $\max \max \left|x_0(k)-x_i(k)\right|$ is the maximum difference between the two levels; $\min \min \left|x_0(k)-x_i(k)\right|$ is the minimum difference between the two levels; the greater the calculated value of ${\epsilon }_i(k)$, the greater the correlation between the factor and the target value.

Finally, according to the correlation coefficient, determine the degree of correlation between the influencing factors and the target sequence $r_i$:

$$r_i=\frac{1}{n}({\epsilon }_i(1)+{\epsilon }_i(2)+\dots +{\epsilon }_i(n))$$

(3)

Similarly, among all influencing factors, $r_i$ with the larger value has a higher degree of correlation with the target sequence.

3.1.2. The MLR Model

The MLR model is a predictive method that participates in the analysis of the linear relationship between two or more independent and dependent variables. The method of establishing MLR model is as follows:

Suppose there is a linear relationship between the dependent variable y and the independent variable x_i (i = 1, 2, …, n):

$$y_i={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots \dots +{\beta }_n{x}_n+\epsilon$$

(4)

In Equation (4), ${\beta }_i$ is the regression coefficient, i = 1, 2, …, n; generally n > 2; $\epsilon$ is the random factor of error, and it follows the N(0, ${\sigma }^2$) distribution.

Let $Y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right)$, $X=\left(\begin{array}{cccc}1& x_{11}& \cdots & x_{1n}\\ 1& x_{21}& \cdots & x_{2n}\\ ⋮& ⋮& \cdots & ⋮\\ 1& x_{m1}& \cdots & x_{mn}\end{array}\right)$, $\beta =\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_n\end{array}\right)$, $\epsilon =\left(\begin{array}{c}{\epsilon }_0\\ {\epsilon }_1\\ ⋮\\ {\epsilon }_n\end{array}\right)$, the MLR models in matrix form are available as follows:

$$Y=X\beta +\epsilon$$

(5)

3.2. Model Establishment and Error Analysis

Combining the water supply and demand data from 2010 to 2017, the GCA method is used to obtain the correlation between the total water demand and the other basic water demand. The correlations obtained are ecological and environmental water demand (0.819), urban public water demand (0.652), domestic water demand (0.610), forestry, animal husbandry and fishery water demand (0.670), farmland irrigation water demand (0.709), and industrial water demand (0.744). Three indicators with a correlation degree greater than 0.7 are selected as the main influencing factors of total water demand.

With the help of SPSS statistical analysis software, a multivariate regression matrix with three factors of ecological environment ($X_1$), farmland irrigation ($X_2$) and industrial water demand ($X_3$) as independent variables and total water demand ($Y$) as dependent variable was constructed. Solve the regression model as follows:

$$Y=-2.408X_1+2.082X_2+1.087X_3-7.243$$

(6)

The MLR model is tested for errors based on each water demand and total water demand from 2010 to 2017, as shown in

Table 1. Fitting result of actual value and predicted value of total water demand.

	Ecological and Environmental Water Demand	Farmland Irrigation Water Demand	Industrial Water Demand	Actual Total Water Demand	Forecast Total Water Demand	Relative Error
2010	0.365	11.326	13.596	30.261	30.241	0.06%
2011	0.587	11.308	13.454	29.436	29.515	−0.27%
2012	0.603	11.492	13.193	29.655	29.576	0.27%
2013	0.598	11.755	12.550	29.348	29.438	−0.30%
2014	0.640	11.654	12.500	29.146	29.071	0.26%
2015	0.576	11.531	12.208	28.642	28.651	−0.03%
2016	0.637	11.601	12.444	29.014	28.907	0.37%
2017	0.591	11.834	12.528	29.393	29.592	−0.68%

. According to the analysis results, the error values are all within 1%, which meets the prediction accuracy requirements. Therefore, the established MLR model is suitable for the prediction of the total water demand in this study area.

4. Establishment of a Rapid Evaluation Model

In order to achieve efficient and accurate evaluation of WRCC, the study selects the FCE method to establish corresponding evaluation system. Measuring the size of WRCC by setting various plans provides a basis for regional water resources development and utilization.

4.1. Evaluation Method

First, establish the set of influencing factors of WRCC U = (u₁, u₂, …, u_n), and the corresponding comment set V = (V₁, V₂, …, V_n). Second, the membership degree r_ij of the comment set v_j is determined by a single factor fuzzy evaluation, which means to evaluate the single factor u, and the single factor evaluation set r_i = (r_i1, r_i2, r_i3) is obtained. Then, the evaluation index is quantified separately, and the corresponding membership degree r_ij is obtained, thus establishing the fuzzy relation matrix R with the amount of m evaluation factors. Finally, by analyzing weights A = (α₁, α₂, …, α_n) of different influencing factors, the fuzzy operation B = A × R is used to synthesize the weight vector of the influencing factors and the fuzzy evaluation matrix to obtain the FCE’s results.

The degree of membership usually indicates a certain degree of deviation, using two sets of formulas to calculate the membership function. x₁ and x₃ are the critical values of V₁, V₂, and V₂, V₃, respectively, and the grade of V₂ is the interval midpoint value of x₂ [14], where $x_2=\frac{x_1+x_3}{2}$. The first set of formulas is applicable to the case where the larger the index U_i is, the better the system is. The second set of formulas is applicable to the case where the smaller the index U_i is, the better the system is. The two sets of calculation formulas are as follows:

First set of formulas:

$$V_1\left(ui\right)=\left\{\begin{array}{c}0.5\left(1+\frac{u_i-x_1}{u_i-x_2}\right), u_i\ge x_1\\ 0.5\left(1-\frac{u_i-x_1}{x_2-x_1}\right), x_2<u_i<x_1\\ 0 , u_i\le x_2\end{array}\right.$$

(7)

$$V_2\left(ui\right)=\left\{\begin{array}{c}0.5\left(1-\frac{u_i-x_1}{u_i-x_2}\right), u_i\ge x_1\\ 0.5\left(1+\frac{x_1-u_i}{x_1-x_2}\right), x_2\le u_i<x_1\\ 0.5\left(1+\frac{u_i-x_3}{x_2-x_3}\right), x_3<u_i<x_2\\ 0.5\left(1-\frac{x_3-u_i}{x_2-u_i}\right), u_i\le x_3\end{array}\right.$$

(8)

$$V_3\left(ui\right)=\left\{\begin{array}{c}0, u_i\ge x_2\\ 0.5\left(1-\frac{u_i-x_3}{x_2-x_3}\right), x_3<u_i<x_2\\ 0.5\left(1+\frac{x_3-u_i}{x_2-u_i}\right), u_i\le x_3\end{array}\right.$$

(9)

Second set of formulas:

$$V_1\left(ui\right)=\left\{\begin{array}{c}0.5\left(1+\frac{u_i-x_1}{u_i-x_2}\right), u_i\le x_1\\ 0.5\left(1-\frac{u_i-x_1}{x_2-x_1}\right), x_1<u_i<x_2\\ 0 , u_i\ge x_2\end{array}\right.$$

(10)

$${\mathrm{V}}_2\left(ui\right)=\left\{\begin{array}{c}0.5\left(1-\frac{u_i-x_1}{u_i-x_2}\right), u_i\le x_1\\ 0.5\left(1+\frac{x_1-u_i}{x_1-x_2}\right), x_1<u_i\le x_2\\ 0.5\left(1+\frac{u_i-x_3}{x_2-x_3}\right), x_2<u_i<x_3\\ 0.5\left(1-\frac{x_3-u_i}{x_2-u_i}\right), u_i\ge x_3\end{array}\right.$$

(11)

$$V_3\left(ui\right)=\left\{\begin{array}{c}0, u_i\le x_2\\ 0.5\left(1-\frac{u_i-x_3}{x_2-x_3}\right), x_2<u_i<x_3\\ 0.5\left(1+\frac{x_3-u_i}{x_2-u_i}\right), u_i\ge x_3\end{array}\right.$$

(12)

The corresponding membership degree r_ij is calculated separately, and matrix R corresponding to different horizontal years of each administrative region in the study area is obtained as follows:

$$R=\left[\begin{array}{ccc}\begin{array}{c}{r}_{11}\\ r_{21}\end{array}& \begin{array}{c}{r}_{12}\\ r_{22}\end{array}& \begin{array}{c}\begin{array}{cc}\dots & r_{1n}\end{array}\\ \begin{array}{cc}\dots & r_{2n}\end{array}\end{array}\\ ⋮& ⋮& \begin{array}{cc}\ddots & ⋮\end{array}\\ r_{m1}& r_{m2}& \begin{array}{cc}\dots & r_{mn}\end{array}\end{array}\right]$$

(13)

The vectorization evaluation result B is obtained from the membership matrix and the weight, and the formula is as follows:

$$B=A\times R=\left({\alpha }_1{\alpha }_2\dots {\alpha }_n\right)·\left[\begin{array}{ccc}\begin{array}{c}{r}_{11}\\ r_{21}\end{array}& \begin{array}{c}{r}_{12}\\ r_{22}\end{array}& \begin{array}{c}\begin{array}{cc}\dots & r_{1n}\end{array}\\ \begin{array}{cc}\dots & r_{2n}\end{array}\end{array}\\ ⋮& ⋮& \begin{array}{cc}\ddots & ⋮\end{array}\\ r_{m1}& r_{m2}& \begin{array}{cc}\dots & r_{mn}\end{array}\end{array}\right]=\left(b_1{b}_2\dots b_m\right)$$

(14)

To facilitate the comparative evaluation, the vectorization result is quantified by the following formula, and the corresponding comprehensive score value λ is obtained, where k = 1, and the higher λ indicates that the regional WRCC is higher.

$$\lambda =\frac{{{\displaystyle \sum }}_{i=1}^{n=3}{b}_i^k\times {\mathsf{\lambda }}_i}{{{\displaystyle \sum }}_{i=1}^{n=3}{b}_i^k}$$

(15)

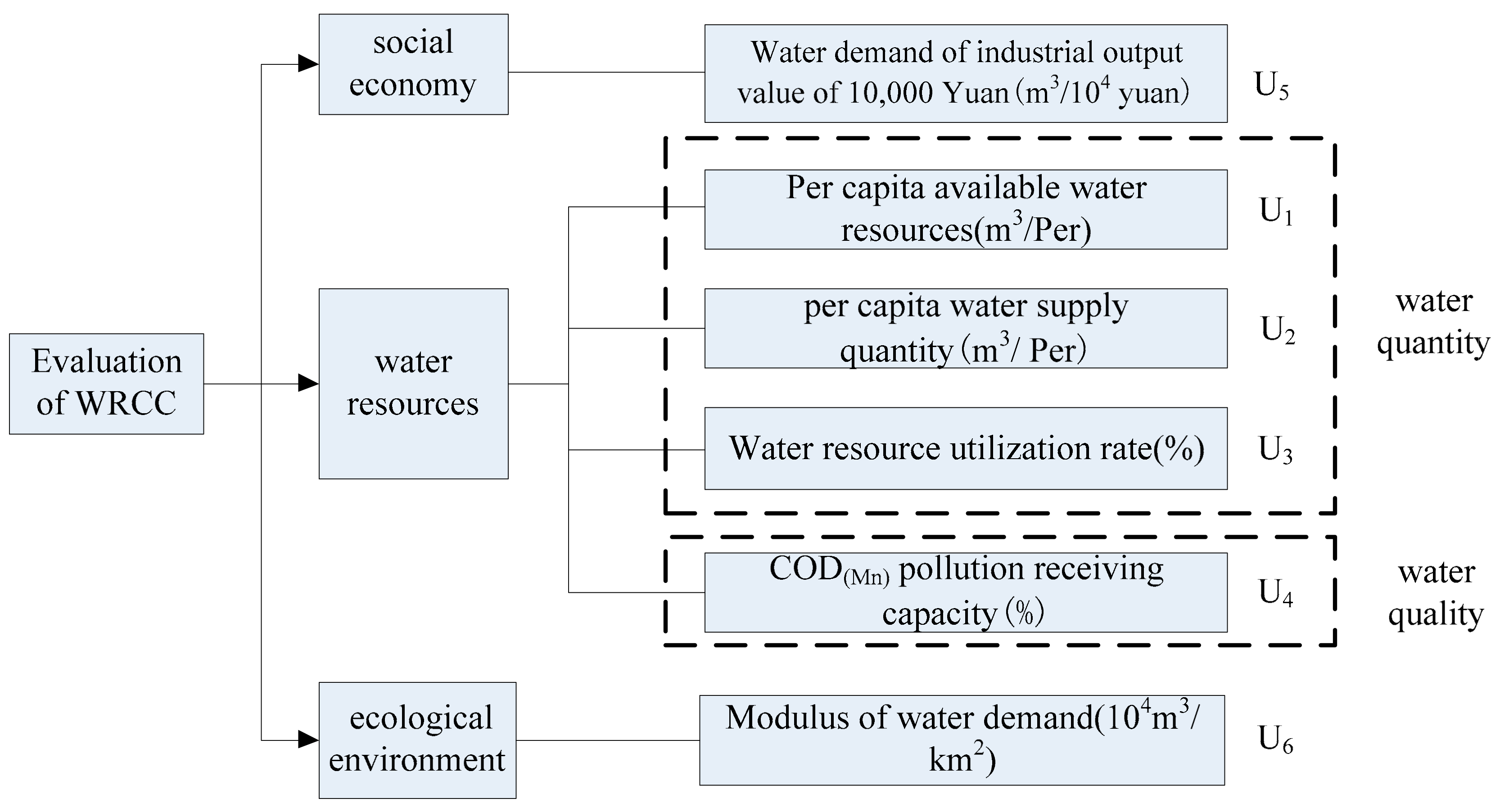
4.2. Evaluation of Index Selection

The key to correctly evaluate the regional WRCC is to properly select fuzzy evaluation indicators. To better reflect the status of regional WRCC, it is particularly important to select regionally representative evaluation indicators. Many factors influence the WRCC. Most studies only consider the impact of the amount of water resources, social economy, and ecological environment on WRCC [24,25,26] but ignore the impact of water quality on regional WRCC. This tends to make the calculation of the WRCC too large and fails to reflect the real situation in the study area. In fact, due to the different degrees of water pollution, the actual water supply and availability of water are smaller than themselves. Combined with the actual situation of the uneven distribution of water resources and the outstanding water quality problems in the study area, this study incorporates the water environment capacity (WEC) into the evaluation of WRCC. We considered the factors of water resources (including water quality and water quantity), as well as the socioeconomic and ecological environment to calculate WRCC. This lays a foundation for truly establishing a new realm of harmonious development of economic, social, and humanities based on the principle of sustainable development (Figure 2).

4.2.1. Evaluation Indicators U₁, U₂, and U₃

Based on the surface water and groundwater supply capacity, actual water supply, and water demand in this region, the WRCC is evaluated from the perspective of the quantity of water resources. Per capita available water resource (U₁) = available water resources/total population (m³/person); per capita water supply quantity (U₂) = actual water supply/total population (m³/person); water resource utilization rate (U₃) = water demand/available water resources (%).

4.2.2. Evaluation Index U₄

Chemical oxygen demand (COD) pollution receiving capacity (U₄) = the water environment capacity of COD at this stage/the maximum water environment capacity of COD (%). The maximum water environment capacity of COD means the maximum pollution capacity that the region can received.

According to the results of the Water Resources Bulletin, Class IV, V, and above Class V water quality river sections are shown in the rivers in the study area. The quality of regional water resources is not optimistic [27,28]. In fact, the quality of water supply directly affects the availability of actual water supply, and the WEC can reflect the two main capabilities of water body dilution and natural purification. Therefore, based on the preliminary understanding of the water quality of the Chang-Ji Economic Circle, this study uses the water environmental capacity as the water quality evaluation index in the evaluation system. Since the flow rate of the river in the study area is stable as well as small, the calculation method of the overall standard is used.

The WEC is calculated as follows [29]:

$$W=86.4Q_0\left(C_s-C_0\right)+0.001KV{C}_s+86.4q{C}_s$$

(16)

where W is the initial value for WEC of the water body, Cs is the standard water quality of the water body, Q₀ is the incoming water flow, C₀ is the upstream background concentration of the incoming water, K is the water quality degradation coefficient, Q is the side flow of the side stream, V is the flow rate, and q is the side inflow flow.

The overall standard calculation method usually does not consider the location of the pollution source, so the calculation results tend to be too large, which is nonconservative. Therefore, in order to conform to the reality, an uneven coefficient is introduced for correction [29]; the method is as follows:

$$W^{\prime }=\alpha W$$

(17)

where W′ represents the corrected WEC, and α denotes the uneven coefficient.

Because the rivers in the area belong to the small and the middle rivers [30], their flow is small and slow, and the uneven coefficient takes an empirical value of 0.8.

4.2.3. Evaluation Index U₅

The Chang-Ji Economic Circle is a gathering place for old industrial cities. The development of its industry can reflect the social and economic conditions of the region. So, we select evaluation index U₅ to effectively reflect this. Water demand of industrial output value of 10,000 Yuan (U₅) = industrial water demand/industrial output value (m³/10,000 yuan). The industrial water demand and the industrial output value is obtained by the GCA and MLR model.

4.2.4. Evaluation Index U₆

Lou [31] and Wang [9] confirmed that the modulus of water demand can reflect the level of regional economic development. Thus, we select the Modulus of water demand as the evaluation index U₆ that effectively reflects the ecological environment of the study area. Modulus of water demand (U₆) = total water demand/land area (10,000 m³/km²). The total amount of water demand is obtained by the GCA and MLR model and the land area used the government published data. The required water modulus reflects the restriction of the ecological environment on the WRCC.

By selecting the above six indicators, it can effectively reflect the balance of supply and demand of water resources in the region, the amount of water resources, the quality of water resources, and the impact of socioeconomic conditions and ecological environment on the regional WRCC.

Based on the above-mentioned evaluation indicators U₁ to U₆, the impact degree of WRCC is analyzed, and its comment set V = (V₁, V₂, V₃) is established (as shown in

Table 2. Evaluation standard of WRCC grading indicators.

Evaluating Indicators Set U	Judgment Set V
	V1	V2	V3
U1 Per capita available water resources (m3/Per)	>1200	1200~400	<400
U2 per capita water supply quantity (m3/Per)	>1000	1000~500	<500
U3 Water resource utilization rate (%)	<40	40~90	>90
U4 COD(Mn) pollution receiving capacity (%)	78	50	22
U5 Water demand of industrial output value of 10,000 Yuan (m3/104 yuan)	<20	20~90	>90
U6 Modulus of water demand (m3/km2)	<10	10~60	>60
Score value λ	0.95	0.5	0.05

below). The WRCC of V₁ to V₃ is gradually weakened. For this evaluation, the second set of formulas applies to U₁, U₂, and U₄; however, U₃, U₅, and U₆ apply to the first set of formulas. The weight is determined according to the influence degree of the influencing factors on the WRCC. According to expert analysis, the corresponding weights are obtained from empirical values, that is, A = (α₁, α₂, α₃, α₄, α₅, α₆) = (0.2, 0.2, 0.3, 0.1, 0.1, 0.1). Then, according to the score value (λ₁ = 0.95, λ₂ = 0.5, and λ₃ = 0.05), the water carrying capacity of each area is analyzed and evaluated, and the score value directly reflects the WRCC in the area.

4.3. Reasonably Evaluate Regional WRCC

The evaluation value of WRCC is statistically analyzed and divided into three levels: an evaluation value of WRCC greater than 0.6 is an area with good WRCC (I), an area evaluation value of water carrying capacity ranging between 0.3 and 0.6 is medium (II), and an area evaluation value of WRCC less than 0.3 is poor (III).

4.4. The Establishment of 4 Different Plans

4.4.1. Plan I

Under the current conditions, Plan I only considers the WRCC of self-produced water, does not increase the local water supply, or expand the capacity of water transfer outside the region, and predicts the carrying capacity of water resources in different years.

4.4.2. Plan II

On the basis of Plan I and considering the project “Carrying Water from Songhua River to Changchun” to increase the local water supply, we predict the water carrying capacity of different years. According to the government’s economic development plan of the Chang-Ji Economic Circle, the cumulative water supply capacity of the design diversion project in Changchun City is 3.25 × 10⁸ m³. After the completion of the water supply project in the central city of Jilin Province, the cumulative water intake will be 5.83 × 10⁸ m³ in 2020. Furthermore, the cumulative water intake will be 6.92 × 10⁸ m³ in vision level year 2030.

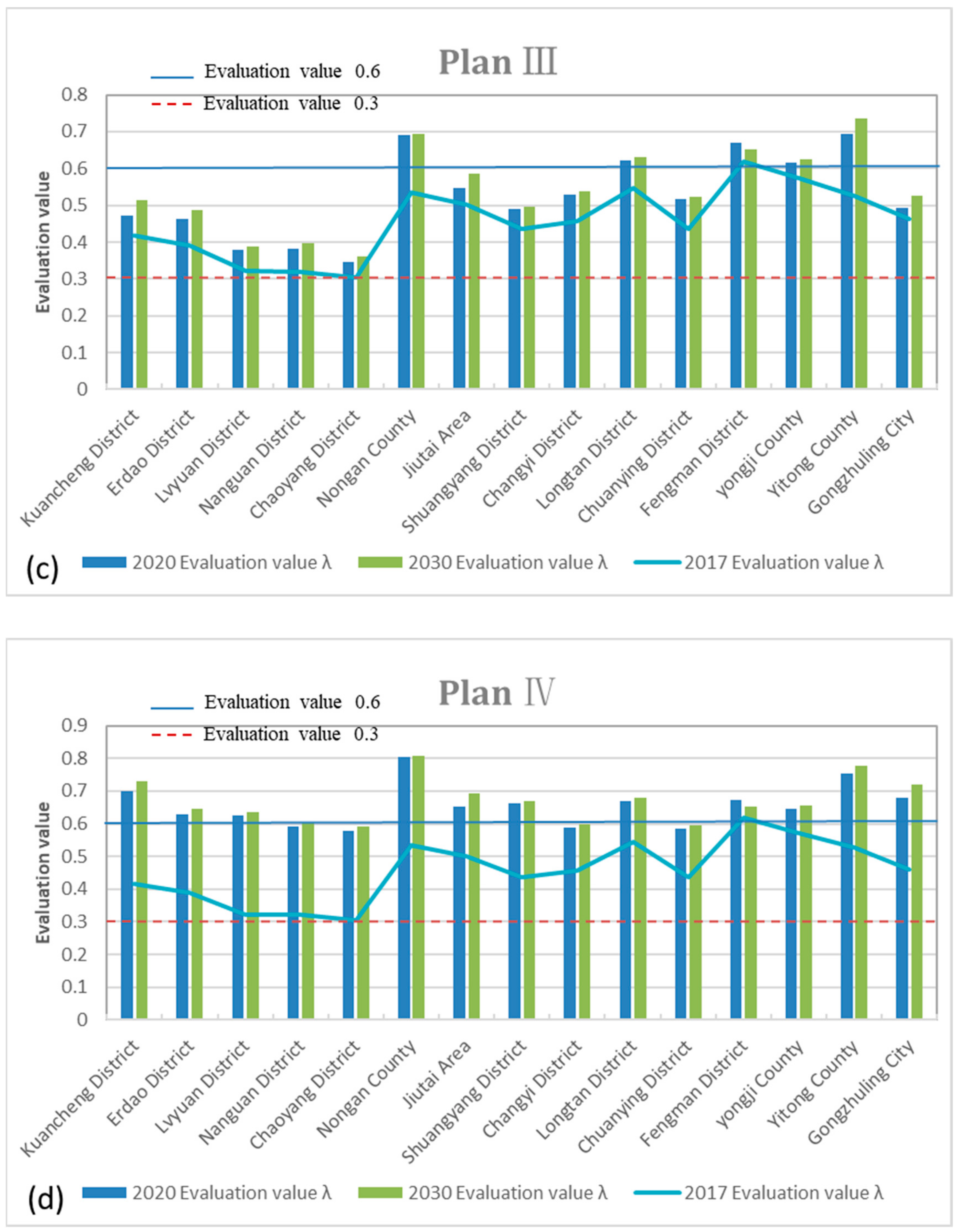
4.4.3. Plan III

Based on Plan II, Plan III strengthens water governance and considers industrial, agricultural, and domestic water conservation. By reducing water usage quotas, increasing the reuse rate of reclaimed water and treating sewage as the most important measures.

According to the “Standards for Local Standard Water Use in Jilin Province” [32], the plan will appropriately reduce the industrial water quota, where each administration increases the amount of water reuse by 0.05 billion m³/per year.

4.4.4. Plan IV

Based on Plan III, Plan IV increases an appropriate amount of transit water. The inflow water of Songhua River is 62.02 × 10⁸ m³ [27]. The increase in water supply is 40% of the inflow water of Songhua River, while the increase in actual water supply is 20%.

5. Results

Due to the inconsistent development speed of various regions, even within the same city, there are differences in regional WRCC. Most of the research only stays at the holistic research within the scope of the region, while ignoring the research of small administrative units [22,33]. Zhou et al. [11] compared with the temporal dynamic process of index change in the water environment carrying capacity and thought that it is urgent to carry on spatiotemporal dynamic change analysis in the WRCC considering spatial heterogeneity and spatial evolution. As a result, this article uses the smallest administrative unit to analyze change trend of WRCC from both time and space perspectives.

5.1. Results of Each Program from the Perspective of Time

5.1.1. Plan I

According to the results of Plan I (Figure 3), the study area is still generally in the middle area of WRCC (II). In 2020, the WRCC of Fengman District is the largest (0.606), while Chaoyang District is poor (0.287). By 2030, both Lvyuan District (0.298) and Chaoyang District (0.27) are in areas with poor WRCC (III). The comparison shows that the comprehensive score of WRCC in 2030 is decreasing compared with 2020, but the rate of decline is slow. It is comprehensively reflected that under the condition of not changing the status quo, the WRCC of the study area will continue to weaken. According to existing research, it likely due to the uneven distribution of the regional water resources [34], which makes the contradiction between water supply and demand increasingly prominent and the development potential decreases [35].

5.1.2. Plan II

Under the influence of the open-source program, U₁ and U₂ increase in different degrees and U₃ decreases accordingly. The evaluation results have the highest degree of membership to V₂, and the WRCC in the area has been improved. There is no poor (III) in the near and long term (see from Figure 3). In the next 13 years, the WRCC will show a downward trend after a short period of improvement. It shows that the fewer water resources chiefly caused its long-term overloaded status [36] and the construction of water diversion project will promote the improvement of WRCC. However, relying solely on the construction of drinking water projects will not alleviate the problem of resource constraints for a long time in the future. Thus, water conservation should be promoted while transiting water [11].

5.1.3. Plan III

With the construction of the water diversion project and the popularization of water saving and sewage treatment policy, the WRCC of the study area will improve greatly compared with 2017. This plan can improve the utilization rate of water resources and Alleviate the tight of the water supply and demand. Unlike the previous plan, the WRCC of plan III will continue to grow in the future. It can be seen in Figure 3 that the WRCC of the whole study area has improved significantly compared to Plan I, and the average growth rate is 23%. In most areas of Jilin, there are areas with good (I) and medium (II) WRCC, and the difference in WRCC of each administrative region will gradually reduce. It shows that saving water and improving water quality are also important factors for enhancing the WRCC [9,37].

5.1.4. Plan IV

Plan IV not only maintains the water resource utilization rate at a high level but also greatly increases the water resource availability. So, the WRCC of the whole region has been significantly improved compared with Plan I. Moreover, the difference in WRCC of each administrative region has gradually decreased. The WRCC of most areas in the region is good (I), and the WRCC in Changchun and surrounding areas has increased significantly to a relatively high level (Figure 3 shows). As of 2030, the WRCC of the eight administrative regions will increase by more than 50% over 2017. It shows great potential for regional development and utilization. The shortage and uneven spatial and temporal distribution of water resources has seriously restricted the sustainable development of regional society and economy [38]. Plan IV is more in line with the principle of sustainable development of society and meets the development goals of combining water quality, water quantity, water ecology, and water environment, which can be used as a recommended plan.

5.2. Comparative Analysis of the Plan from the Perspective of Space

The predicted levels of WRCC in 2020 and 2030 at 15 observation locations in the Chang-Ji Economic Circle were analyzed in four plans, the development potential of water resources was evaluated (Figure 4 and Figure 5), and the evaluation level was tested. According to Figure 4 and Figure 5, the WRCC at each observation location exhibited a continuously increasing trend from Plan I to IV. These findings are consistent with the measures used in the design of the plan, which provides a certain level of reliability and reference to the present research.

5.2.1. WRCC Spatial Distribution in 2020

Figure 4 shows that the level of WRCC in the Fengman District of Jilin City, which has unique natural resource surrounding the Songhua River, will be good (I) during each plan in 2020. As the administrative center of Changchun City, Chaoyang District has a relative shortage of water resources and poor water quality. The level is predicted to improve from III to II, and the value to increase from 0.287 to 0.579. Nanguan, Changyi, and Chuanying District will retain the high level of II and will always have a certain development potential; the values for the three areas will change by 0.268, 0.136, and 0.153, respectively. The rest of the region will change from II to I and may adapt to social and economic development.

5.2.2. WRCC Spatial Distribution in 2030

Figure 5 shows that the initial level of WRCC in Chaoyang and Lvyuan District are both at III, and the potential of water resources exploitation is small. The WRCC level Chaoyang changes from III to II, and it is greatly improved from III to I for Lvyuan District. Additionally, their carrying capacity is greatly improved. Changyi and Chuanying District will maintain the high level of II, and the value will change by 0.176 and 0.192, respectively. The rest of the region will change from II to I, which will gradually increase the security effect of the economy and society. The different plans to the subareas can provide a scientific reference to rational distribution of economic development, elaborate management of water environment as well as regional sustainable development in the future [35].

Throughout each plan in 2020 and 2030, plan III will greatly improve the WRCC of the whole region, with the eastern part of the study area having a significantly higher WRCC than the western part. Some areas in Jilin have strong WRCC, and each administrative region has a certain amount of development and utilization potential. Plan IV shows that the WRCC of the whole district is obviously improved, compared to the Plan I. By this time, the WRCC of the whole district will be strong, with most areas being at level I. Furthermore, the water resources would be able to provide certain guarantees for social and economic development.

The measures of water-saving, sewage treatment, water diversion projects, and transit water utilization mean that WRCC is constantly changing. Based on the above-mentioned various measures, the results of Plan IV show that over 84% of the regions have a relatively large development potential. As regional development progresses, most regions would develop slowly if no measures are taken (Plan I). These results further validate the intuition and visualization of the WRCC classification and provide a basis for the government to rationally allocate water resources [10,22].

5.3. Limitations and Future Research Directions

This study selects the GCA, MLR, and FCE combined model to evaluate the WRCC of the Chang-Ji Economic Circle. This combined model makes up for the shortcomings of traditional indicator evaluation methods and achieves qualitative and quantitative evaluation. Moreover, the coupling of the GCA and MLR model reduces the interference of human factors and reduces the error value of the predicted evaluation index. Nevertheless, this study still has certain limitations.

(1)

Although this study has considered relevant subsystems related to the WRCC as much as possible, such as social economy, water resources quantity, water resources quality, water ecological environment subsystems. The research results provide favorable information guidance for the future development of Chang-Ji Economic Circle. However, only the representative evaluation indicators in each subsystem are selected, and the number of indicators selected is relatively small [39]. Future research should be gradually improved.

(2)

The coupling evaluation model selected this time is based on the index evaluation. Although qualitative and quantitative analysis can be achieved, it is difficult to achieve negative feedback adjustment. However, the SD model can make up for this deficiency [34,40]. We believe that integrating the coupling assessment model established in this research into the dynamic system of the SD model can be the focus of future research [19].

6. Conclusions

The study established a hybrid model to analyze the WRCC of the Chang-Ji Economic Circle. First of all, in order to make up for the shortcomings of traditional trend analysis, the GCA and MLR coupling model can predict the changing trend of WRCC’s influencing factors [28,41,42]. Accurate and quantitative evaluation index trend prediction can increase the credibility of the evaluation results of the WRCC [9]. Then, using the FCE model, the WRCC of each region is evaluated. Finally, based on the coupling results of the hybrid model, the future WRCC of the districts and counties in the Chang-Ji Economic Circle are compared in terms of time and space. It is worth noting that according to the actual situation of the Chang-Ji Economic Circle, the impact of water quality on regional WRCC is considered. The water environmental capacity is taken as a new evaluation index and the WRCC evaluation system is proposed based on water quantity and quality, social economy, and ecological environment. This makes up for the shortcomings of the existing evaluation indicators and can more realistically reflect the status quo of regional development. The presented research results allowed us to draw the following conclusions.

Four different water intake plans are considered to assess the WRCC of the study area in 2020 and 2030. The study aims to eliminate potential problems in the societal development of Chang-Ji Economic Circle through various plans and improve the affordability of economic development. Considering the spatial heterogeneity and spatial evolution, the spatial and temporal dynamic changes of WRCC are analyzed. From the perspective of time changes, the WRCC of Plan I and Plan II remains at a medium level. Affected by the constraints of supply and demand, the WRCC will continue to decline. The improvement of the WRCC in Plan III was better than the abovementioned scenarios, yet the potential development potential of the region is still hindered. Water saving measures and sewage treatment can relieve the pressure of WRCC. In order to achieve sustainable development of the region, Plan IV comprehensively considers the advantages of the above plans and increases the amount of transit water to make up for the shortage of resource-based water shortage. The WRCC of the whole region is generally good, and water resources can support the rapid development of the social economy in Plan IV. From the perspective of space changes, the WRCC of Plan I in Chaoyang and Lvyuan District will become a poor level and lack the potential of water resources exploitation in the future. The improvement thought Plan II will still not be sufficient compared with Plan III. It shows that the WRCC in the eastern area of Chang-Ji Economic Circle is significantly higher than others. The WRCC of the whole district Plan IV is significantly improved in comparison with the current conditions. Plan IV is proposed as the final recommendation through comprehensive analysis and research. Strengthening sewage treatment and proper use of transit water resources are more conducive to the rapid development of Chang-Ji Economic Circle.