Macroscopic Lattice Boltzmann Method
Abstract
:1. Introduction
2. Macroscopic Lattice Boltzmann Model
3. Recovery of the Navier–Stokes Equations
4. Numerical Tests
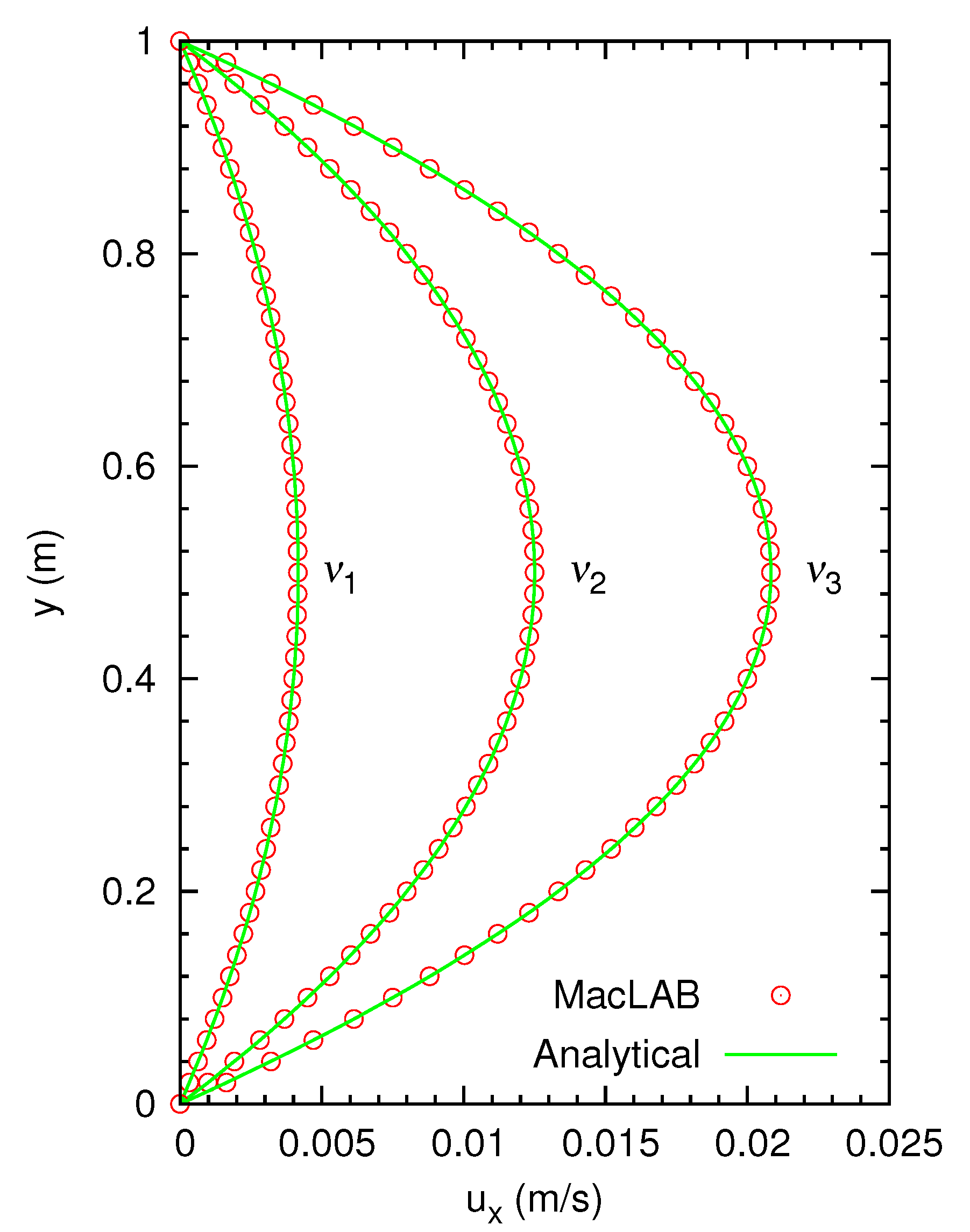
4.1. Couette Flow
4.2. Couette Flow with a Pressure Gradient
4.3. 2D Cavity Flow
4.4. 2D Taylor–Green Vortex
4.5. 3D Cavity Flow
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Hardy, J.; de Pazzis, O.; Pomeau, Y. Molecular dynamics of a classical lattice gas: Transport properties and time correlation functions. Phys. Rev. A 1976, 13, 1949–1961. [Google Scholar] [CrossRef]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-Gas Automata for the Navier–Stokes Equation. Phys. Rev. Lett. 1986, 56, 1505–1508. [Google Scholar] [CrossRef] [Green Version]
- Chopard, B.; Droz, M. Cellular Automata Modeling of Physical Systems; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Rivet, J.P.; Boon, J.P. Lattice Gas Hydrodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef]
- Higuera, F.; Jiménez, J. Boltzmann approach to lattice gas simulations. Eur. Lett. 1989, 9, 663–668. [Google Scholar] [CrossRef]
- Noble, D.R.; Chen, S.; Georgiadis, J.G.; Buckius, R.O. A consistent hydrodynamic boundary condition for the lattice Boltzmann method. Phys. Fluids 1995, 7, 203–209. [Google Scholar] [CrossRef]
- Qian, Y.H. Lattice Gas and Lattice Kinetic Theory Applied to the Navier–Stokes Equations. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 1990. [Google Scholar]
- Chen, S.; Chen, H.D.; Martinez, D.; Matthaeus, W. Lattice Boltzmann model for simulation of magnetohydrodynamics. Phys. Rev. Lett. 1991, 67, 3776–3779. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I: Small amplitude processes in charged and neutral one-component system. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Zarghami, A.; den Akker, H.E.A.V. Thermohydrodynamics of an evaporating droplet studied using a multiphase lattice Boltzmann method. Phys. Rev. E 2017, 95, 043310. [Google Scholar] [CrossRef] [Green Version]
- Mohamad, H.H.; Masoud, M. Continuous and Discrete Adjoint Approach Based on Lattice Boltzmann Method in Aerodynamic Optimization Part I: Mathematical Derivation of Adjoint Lattice Boltzmann Equations. Adv. Appl. Math. Mech. 2014, 6, 570–589. [Google Scholar]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Kandasamy, S.; Orszag, S.; Shock, R.; Succi, S.; Yakhot, V. Extended Boltzmann Kinetic Equation for Turbulent Flows. Science 2003, 301, 633–636. [Google Scholar] [CrossRef]
- Golbert, D.R.; Blanco, P.J.; Clausse, A.; Feijóo, R.A. Tuning a lattice-Boltzmann model for applications in computational hemodynamics. Med. Eng. Phys. 2012, 34, 339–349. [Google Scholar] [CrossRef]
- Javed, S.; Sohail, A.; Maqbool, K.; Butt, S.I.; Chaudhry, Q.A. The Lattice Boltzmann method and computational analysis of bone dynamics-I. Complex Adapt. Syst. Model. 2017, 5, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Chai, Z.; Shi, B.; Zhang, W. Lattice Boltzmann method for filtering and contour detection of the natural images. Comput. Math. Appl. 2014, 68, 257–268. [Google Scholar] [CrossRef]
- Finck, M.; Hänel, D.; Wlokas, I. Simulation of nasal flowby lattice Boltzmann methods. Comput. Biol. Med. 2007, 37, 739–749. [Google Scholar] [CrossRef]
- Zhou, J.G.; Haygarth, P.M.; Withers, P.J.A.; Macleod, C.J.A.; Falloon, P.D.; Beven, K.J.; Ockenden, M.C.; Forber, K.J.; Hollaway, M.J.; Evans, R.; et al. Lattice Boltzmann method for the fractional advection-diffusion equation. Phys. Rev. E 2016, 93, 043310. [Google Scholar] [CrossRef] [Green Version]
- d’Humières, D. Generalized lattice Boltzmann equations. In Rarefied Gas Dynamics: Theory and Simulations, Progress in Astronautics and Aeronautics; Shizgal, B.D., P.Weaver, D., Eds.; 1992; Volume 159, pp. 450–458. [Google Scholar]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef] [Green Version]
- Ginzburg, I.; Verhaeghe, F.; d’Humières3, D. Two-Relaxation-Time Lattice Boltzmann Scheme: About Parametrization, Velocity, Pressure andMixed Boundary Conditions. Commun. Comput. Phys. 2008, 3, 427–478. [Google Scholar]
- Geier, M.; Greiner, A.; Korvink, J.G. Cascaded digital lattice Boltzmann automata for high Reynolds number flow. Phys. Rev. E 2006, 73, 066705. [Google Scholar] [CrossRef]
- Geier, M.; Schönherr, M.; Pasquali, A.; Krafczyk, M. The cumulant lattice Boltzmann equation in three dimensions: Theory and validation. Comput. Math. Appl. 2015, 70, 507–547. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Shu, C.; Wang, Y.; Yang, L.M.; Tan, D. A Simplified Lattice Boltzmann Method without Evolution of Distribution Function. Adv. Appl. Math. Mech. 2017, 9, 1–22. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Wolf-Gladrow, D. Lattice-Gas Cellular Automata and Lattice Boltzmann Models; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Guo, Z.L.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing: Singapore, 2013. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Springer: Berlin, Germany, 2017. [Google Scholar]
- Zhou, J.G. Lattice Boltzmann Methods for Shallow Water Flows; Springer: Berlin, Germany, 2004. [Google Scholar]
- Ghia, U.; Ghia, K.; Shin, C. High-Re Solutions for Incompressible Flow Using the Navier–Stokes Equations and a Multigrid Method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Wong, K.L.; Baker, A.J. A 3D incompressible Navier–Stokes velocity-vorticity weak form finite element algorithm. Int. J. Numer. Methods Fluids 2002, 38, 99–123. [Google Scholar] [CrossRef]
- Jiang, B.N.; Lin, T.L.; Povinelli, L.A. Large scale computation of incompressible viscous flows by least-squares finite element method. Comput. Methods Appl. Mech. Eng. 1994, 114, 213–231. [Google Scholar] [CrossRef] [Green Version]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.G. Macroscopic Lattice Boltzmann Method. Water 2021, 13, 61. https://doi.org/10.3390/w13010061
Zhou JG. Macroscopic Lattice Boltzmann Method. Water. 2021; 13(1):61. https://doi.org/10.3390/w13010061
Chicago/Turabian StyleZhou, Jian Guo. 2021. "Macroscopic Lattice Boltzmann Method" Water 13, no. 1: 61. https://doi.org/10.3390/w13010061




