Trend Analysis of Annual and Seasonal River Runoff by Using Innovative Trend Analysis with Significant Test
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Sources
3. Methodology
3.1. Trend Test
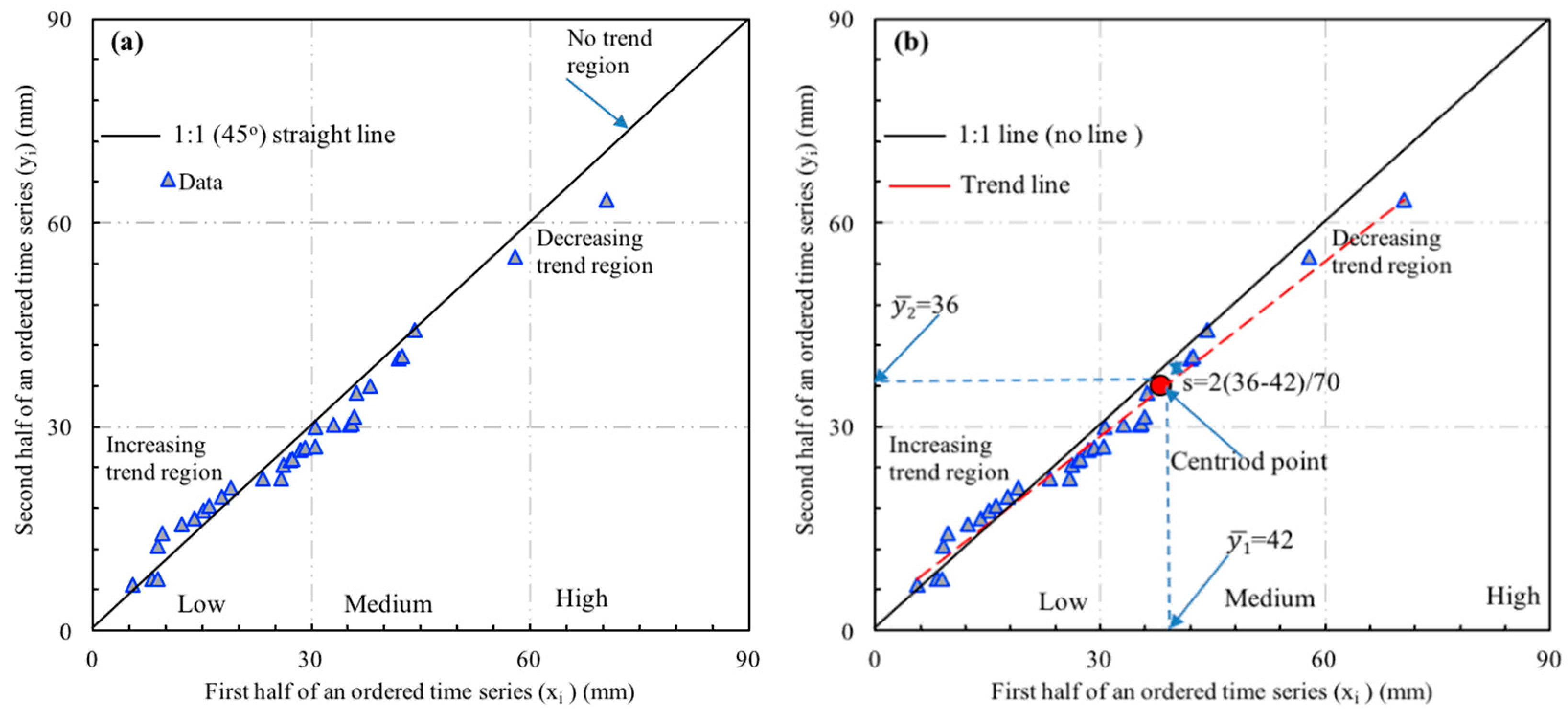
3.2. Innovative Trend Analysis Method
4. Results and Analysis
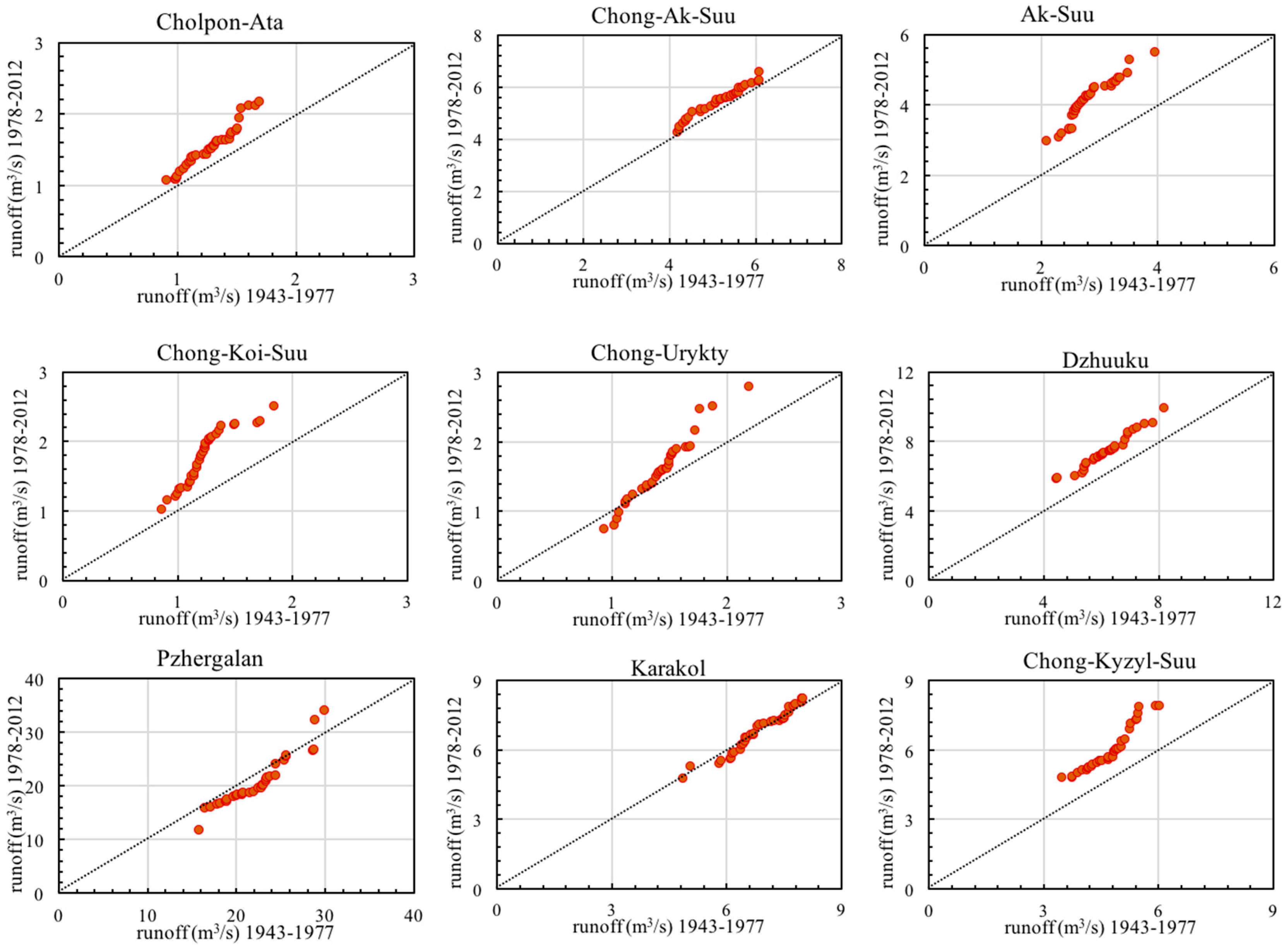
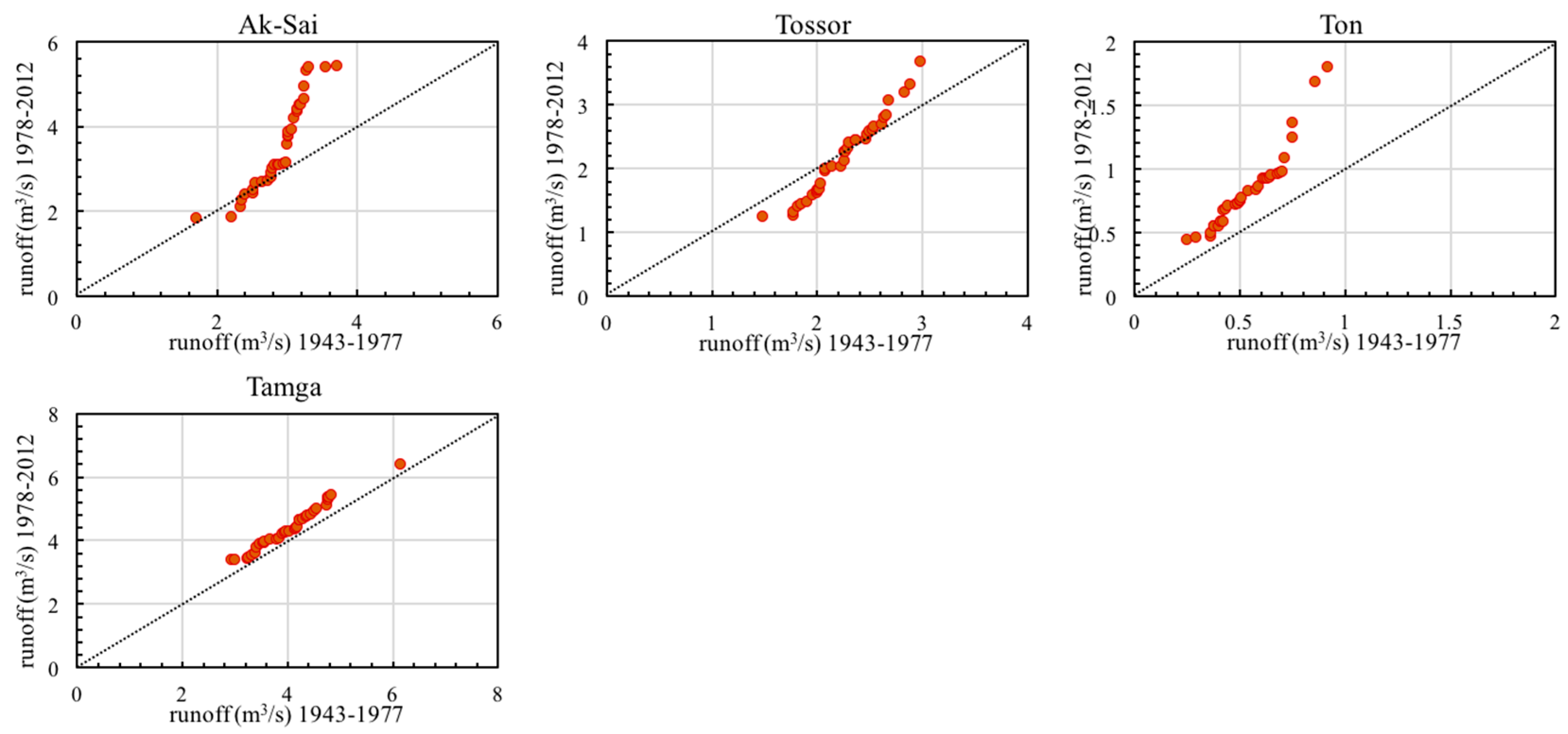
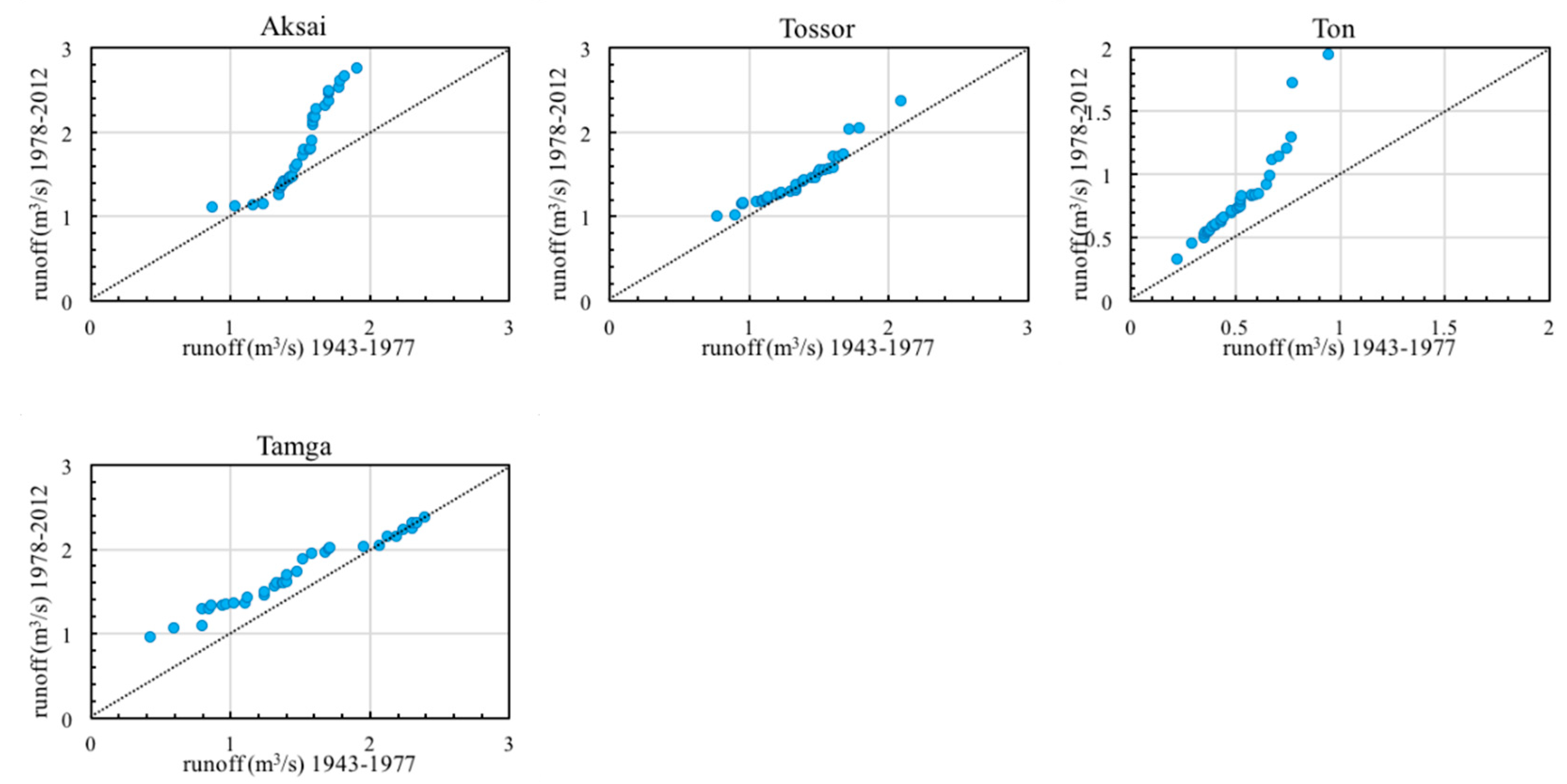
4.1. Trend Variations of Annual River Runoff in the Lake Issyk-Kul Basin
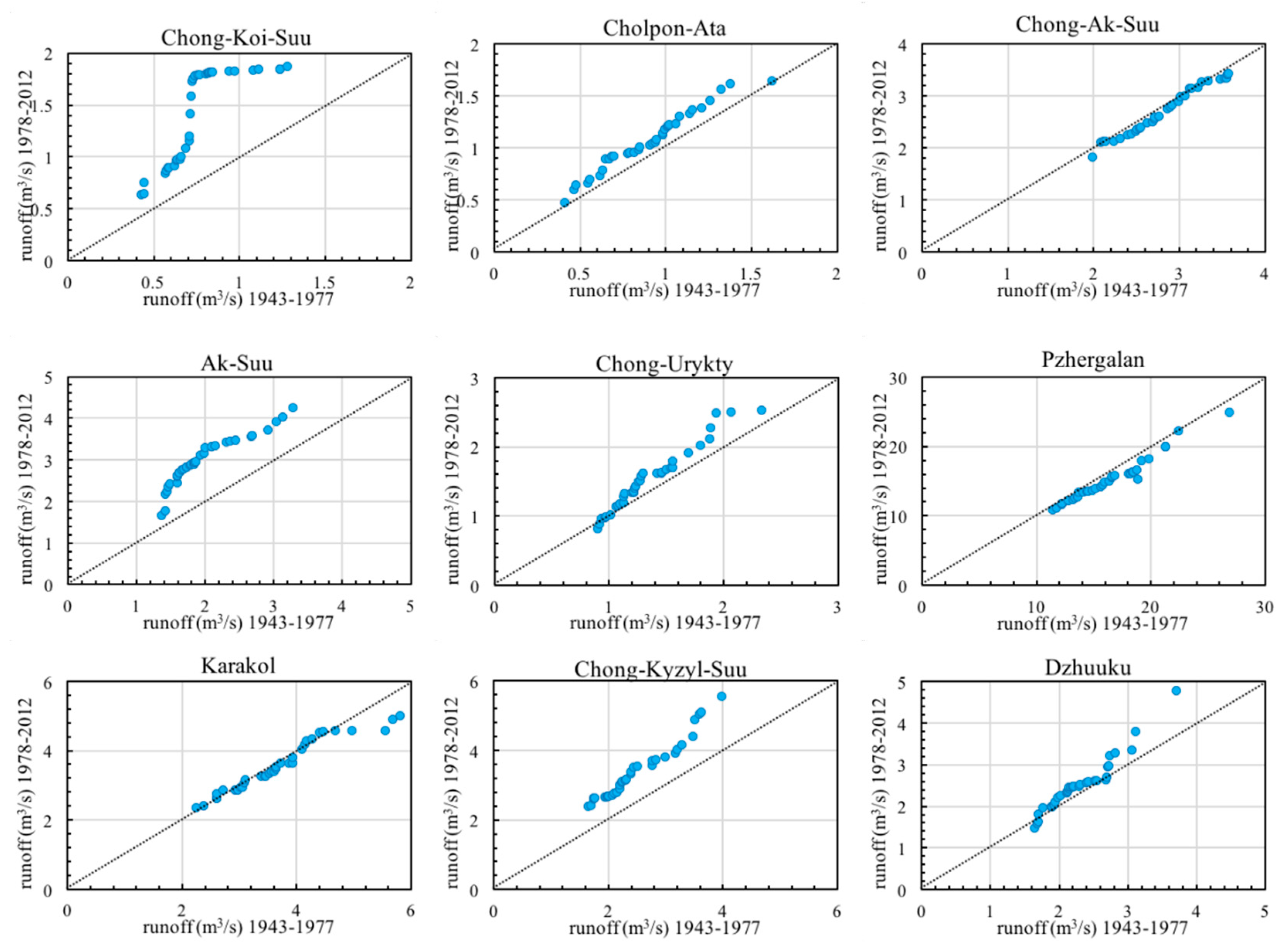
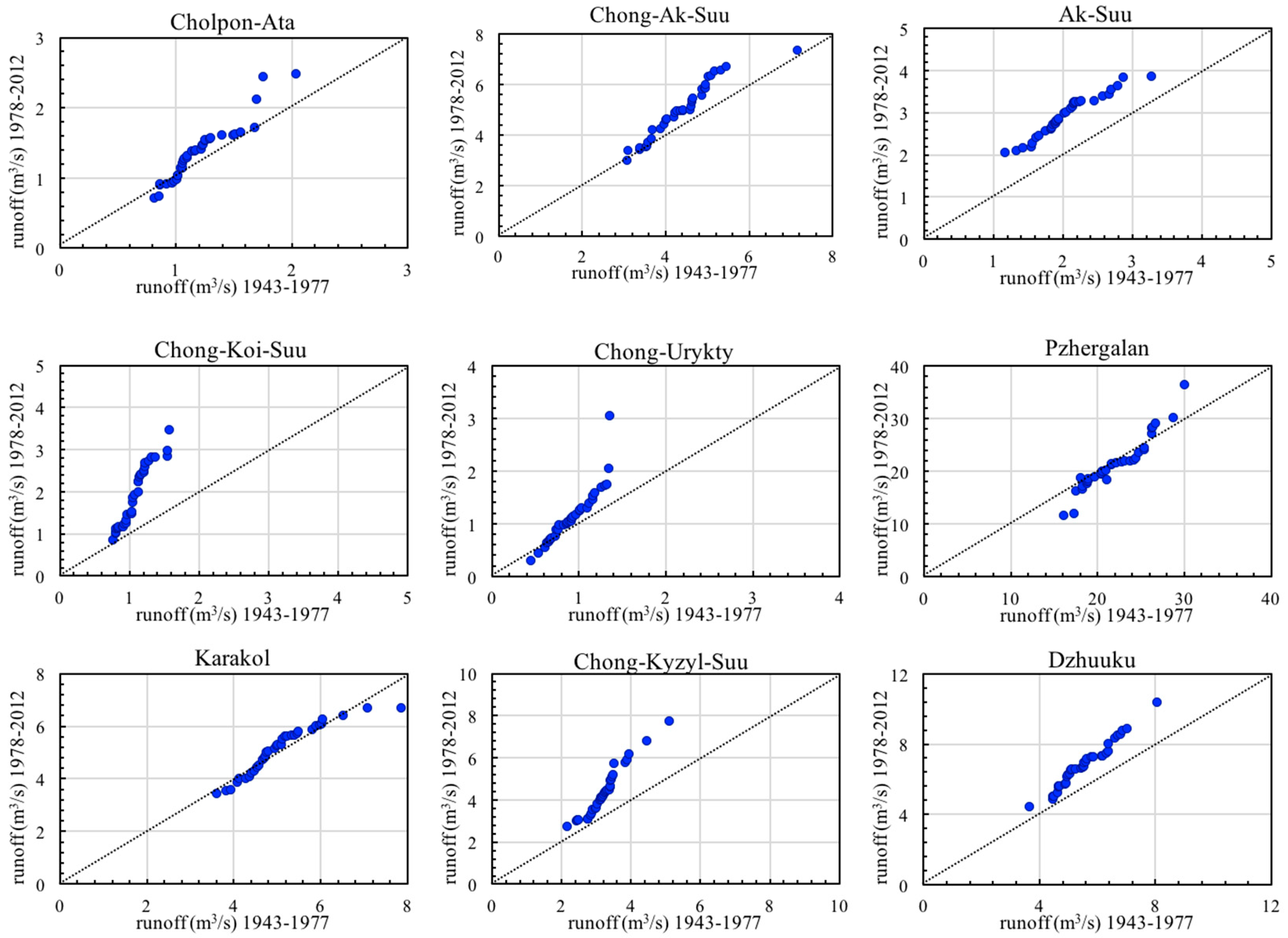
4.2. Trend Variations of Spring River Runoff in the Lake Issyk-Kul Basin
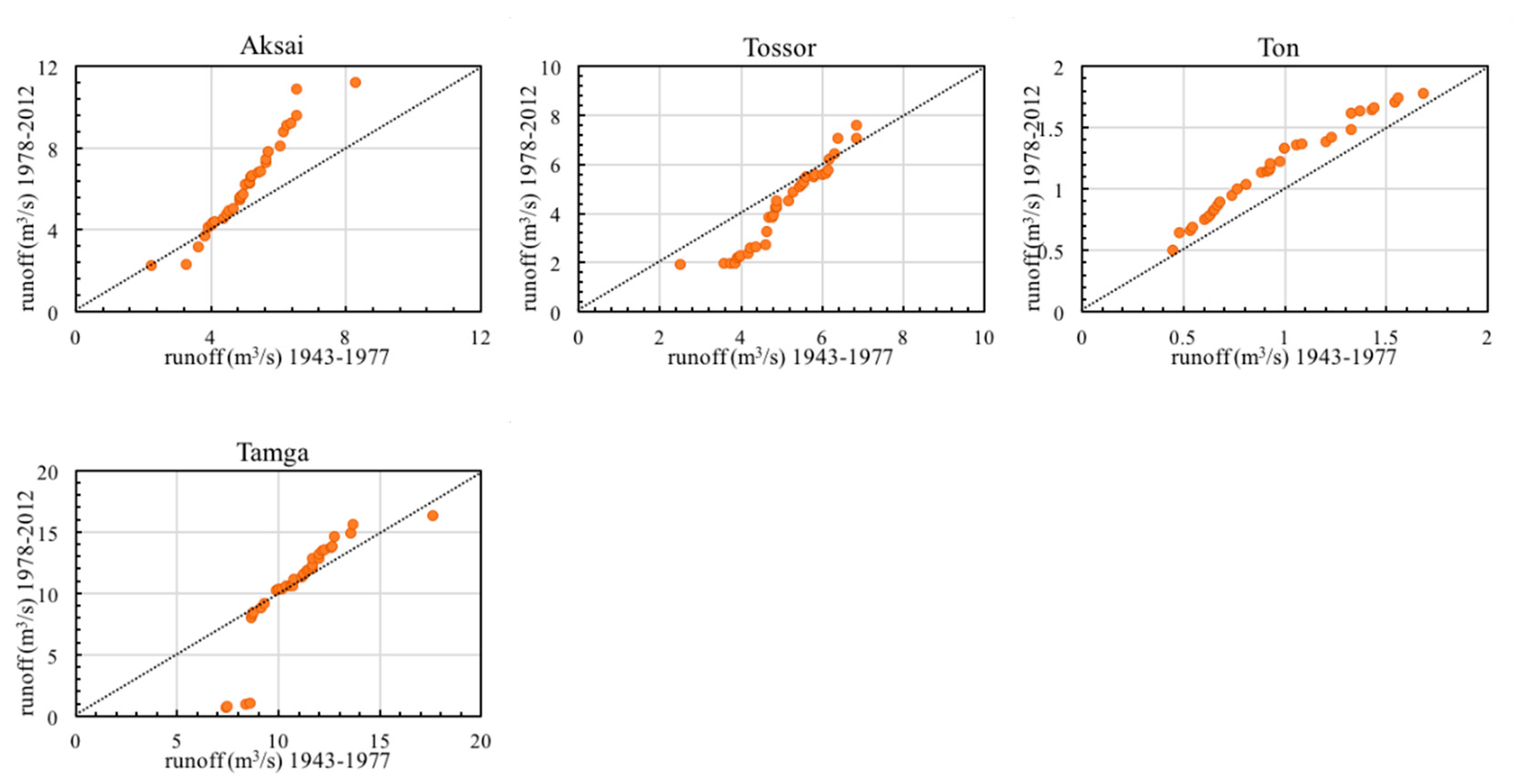
4.3. Trend Variations of Summer River Runoff in the Lake Issyk-Kul Basin
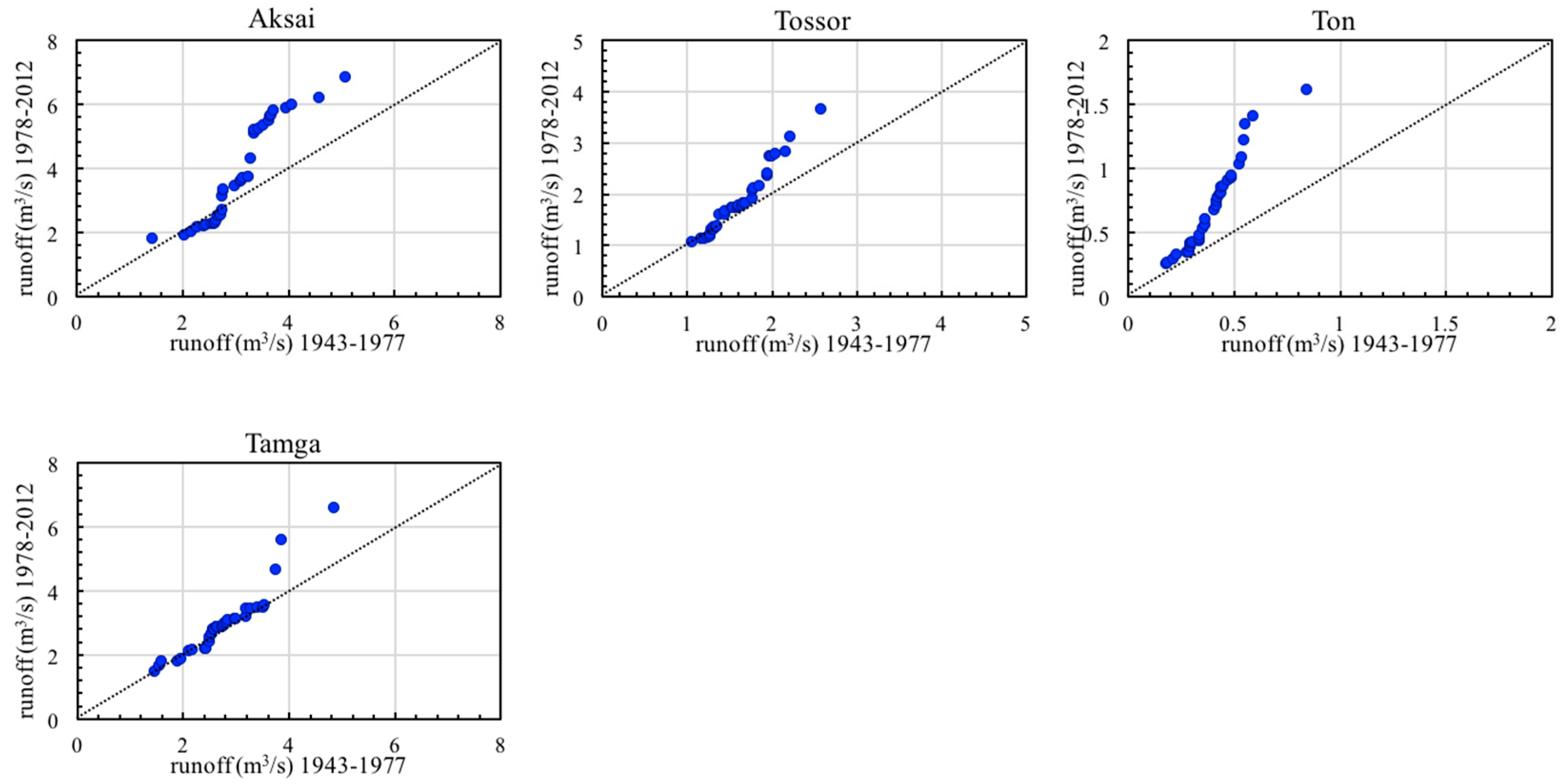
4.4. Trend Variations of Autumnr River Runoff in the Lake Issyk-Kul Basin
4.5. Trend Variations of Winter River Runoff in the Lake Issyk-Kul Basin
4.6. Comparison of Trend Analysis Methods
5. Discussion
6. Conclusions
- (1)
- The MK trend test results show that in 39-time series, there were significant positive and negative trends (among them, northern river in 18-time series, south-eastern rivers in 11-time series, southern rivers in 10-time series) on seasonal and annual river runoff.
- (2)
- The ITA method results revealed that in 51-time series (in which the stations of the northern part of the lake basin in 20-time series, south-eastern parts in 16-time series, and southern regions in 15-time series), there were significant positive and negative trends on seasonal and annual river runoff. Specifically, the MK test found that the time series percentage decreased from 46.15% in the north to 25.64% in the south, while the ITA method revealed a similar rate of decrease, from 39.2% to 29.4%.
- (3)
- According to the temporal distribution of the MK test, significantly increasing (decreasing) trends were observed in 5 (0), 6 (2), 4 (3), 8 (0), and 8 (1) time series in annual, spring, summer, autumn, and winter river runoff data. At the same time, the ITA method detected significant trends in 7 (1), 9 (3), 6(3), 9 (3), and 8 (2) time series in the study area. The comparison results revealed that the ITA method could effectively identify the trends detected by the MK trend test.
- (4)
- According to the ITA method, the “peak” values of 24 time series (26.97%) exhibited increasing patterns, 25 time series (28.09%) displayed increasing patterns for “low” values, and 40 time series (44.94%) showed increasing patterns for “medium” values. According to the “low”, “medium”, and “peak” values, five time series (33.33%), seven time series (46.67%), and three time series (20%) manifested decreasing trends, respectively. These results detailed the patterns of annual and seasonal river runoff data series by evaluating “low”, “medium”, and “peak” values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rasool, S.I. Climate change, global change: What is the difference? Eos Trans. Am. Geophys. Union. 2013, 69, 668. [Google Scholar] [CrossRef]
- Lin, N.-F.; Tang, J.; Han, F.-X. Eco-environmental problems and effective utilization of water resources in the Kashi Plain, western Terim Basin, China. Hydrogeol. J. 2001, 9, 202–207. [Google Scholar] [CrossRef]
- Ji, X.; Kang, E.; Chen, R.; Zhao, W.; Zhang, Z.; Jin, B. The impact of the development of water resources on environment in arid inland river basins of Hexi region, Northwestern China. Environ. Geol. 2006, 50, 793–801. [Google Scholar] [CrossRef]
- Michel-Guillou, E. Water resources and climate change: Water managers’ perceptions of these related environmental issues. J. Water Clim. Chang. 2015, 6, 111–123. [Google Scholar] [CrossRef]
- Chen, Y.N.; Li, Z.; Fang, G.H.; Deng, H. Impact of climate change on water resources in the Tianshan Mountians, Central Asia. Acta Geogr. Sin. 2017. [Google Scholar] [CrossRef]
- Deng, H.; Chen, Y.; Wang, H.; Zhang, S. Climate change with elevation and its potential impact on water resources in the Tianshan Mountains, Central Asia. Glob. Planet. Chang. 2015, 135, 28–37. [Google Scholar] [CrossRef]
- Abuduwaili, J.; Issanova, G.; Saparov, G. Water Resources and Impact of Climate Change on Water Resources in Central Asia. In Hydrology and Limnology of Central Asia; Springer: Singapore, 2018; pp. 1–9. [Google Scholar]
- Bernauer, T.; Siegfried, T. Climate change and international water conflict in Central Asia. J. Peace Res. 2012. [Google Scholar] [CrossRef]
- Yang, K.; Teng, M.; Luo, Y.; Zhou, X.; Zhang, M.; Sun, W.; Li, Q. Human activities and the natural environment have induced changes in the PM 2.5 concentrations in Yunnan Province, China, over the past 19 years. Environ. Pollut. 2020, 265, 114878. [Google Scholar] [CrossRef]
- Kehl, J. The Great Lapse: Climate Change, Water Resources and Economic Risks in the Great Lakes. J. Water Resour. Prot. 2018, 10, 1106–1114. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Yuan, Z.; Xu, J.J.; Yan, B.; Hong, X.F. Research on the attribution identification of source runoff variation in the Yellow River Source Region based on water and energy balance model. IOP Conf. Ser. Earth Environ. Ser. 2019, 344, 012122. [Google Scholar] [CrossRef]
- Meresa, H.; Gatachew, M.T. Climate change impact on river flow extremes in the Upper Blue Nile River basin. J. Water Clim. Chang. 2018, 10, 759–781. [Google Scholar] [CrossRef]
- Wu, Y.; Zhong, P.-A.; Xu, B.; Zhu, F.; Ma, B. Changing of flood risk due to climate and development in Huaihe River basin, China. Stoch. Environ. Res. Risk Assess. 2017, 31, 935–948. [Google Scholar] [CrossRef]
- Ling, H.; Xu, H.; Fu, J. Changes in intra-annual runoff and its response to climate change and human activities in the headstream areas of the Tarim River Basin, China. Quat. Int. 2014, 336, 158–170. [Google Scholar] [CrossRef]
- Liu, Z.; Cuo, L.; Li, Q.; Liu, X.; Ma, X.; Liang, L.; Ding, J. Impacts of Climate Change and Land Use/Cover Change on Streamflow in Beichuan River Basin in Qinghai Province, China. Water 2020, 12, 1198. [Google Scholar] [CrossRef]
- Yang, F.; Xue, L.; Wei, G.; Chi, Y.; Yang, G. Study on the dominant causes of streamflow alteration and effects of the current water diversion in the Tarim River Basin, China. Hydrol. Process. 2018, 32, 3391–3401. [Google Scholar] [CrossRef]
- Wu, F.; Zhan, J.; Su, H.; Yan, H.; Ma, E. Scenario-Based Impact Assessment of Land Use/Cover and Climate Changes on Watershed Hydrology in Heihe River Basin of Northwest China. Adv. Meteorol. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Li, B. Quantifying the effects of climate variability and human activities on runoff for Kaidu River Basin in arid region of northwest China. Theor. Appl. Clim. 2012, 111, 537–545. [Google Scholar] [CrossRef]
- Zhu, Y.J.; Guo, C.Q.; Huang, X.K. Change of precipitation and runoff at Wuzhou station on Xijiang River under influence of climate changes and human activities. J. China Hydrol. 2010, 30, 50–55. [Google Scholar]
- Wang, S.; Ling, L.I.; Yan, M. The contributions of climate change and human activities to the runoff yield changes in the middle Yellow River Basin. Geogr. Res. 2013, 32, 395–402. [Google Scholar]
- Huo, Z.; Feng, S.; Kang, S.; Li, W.; Chen, S. Effect of climate changes and water-related human activities on annual stream flows of the Shiyang river basin in arid north-west China. Hydrol. Process. 2008, 22, 3155–3167. [Google Scholar] [CrossRef]
- Dong, W.; Cui, B.; Liu, Z.; Zhang, K. Relative effects of human activities and climate change on the river runoff in an arid basin in northwest China. Hydrol. Process. 2008, 28, 4854–4864. [Google Scholar] [CrossRef]
- Kong, D.; Miao, C.; Wu, J.; Duan, Q. Impact assessment of climate change and human activities on net runoff in the Yellow River Basin from 1951 to 2012. Ecol. Eng. 2016, 91, 566–573. [Google Scholar] [CrossRef]
- Liang, J.; Liu, Q.; Zhang, H.; Li, X.; Qian, Z.; Lei, M.; Li, X.; Peng, Y.; Li, S.; Zeng, G. Interactive effects of climate variability and human activities on blue and green water scarcity in rapidly developing watershed. J. Clean. Prod. 2020, 265, 121834. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Yu, P.; Zhang, H.; Tu, X. Impact of human activities on the spatial and temporal variation of runoff of Jinghe Basin, Northwest China. J. Arid. Land Resour. Environ. 2011, 6, 66–72. [Google Scholar] [CrossRef]
- Omer, A.; Wang, W.; Basheer, A.K.; Yong, B. Integrated assessment of the impacts of climate variability and anthropogenic activities on river runoff: A case study in the Hutuo River Basin, China. Hydrol. Res. 2017, 48, 416–430. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Yong, B.; Singh, V.P.; Yang, X.; Yuan, F. Quantifying the effects of climate variability and human activities on runoff from the Laohahe basin in northern China using three different methods (pages 2492–2505). Hydrol. Process. 2011, 25, 1–14. [Google Scholar] [CrossRef]
- Zhao, R.; Chen, Y.; Shi, P.; Zhang, L.; Pan, J.; Zhao, H. Land use and land cover change and driving mechanism in the arid inland river basin: A case study of Tarim River, Xinjiang, China. Environ. Earth Sci. 2012, 68, 591–604. [Google Scholar] [CrossRef]
- Sangho, L.; Sang, K. Quantification of Hydrological Responses Due to Climate Change and Human Activities over Various Time Scales in South Korea. Water 2017, 9, 34. [Google Scholar]
- Shahid, M.; Rahman, K.U. Identifying the Annual and Seasonal Trends of Hydrological and Climatic Variables in the Indus Basin Pakistan. Asia-Pac. J. Atmos. Sci. 2020, 1–15. [Google Scholar] [CrossRef]
- Fathian, F.; Morid, S.; Kahya, E. Identification of trends in hydrological and climatic variables in Urmia Lake basin, Iran. Theor. Appl. Clim. 2014, 119, 443–464. [Google Scholar] [CrossRef]
- Monk, W.A.; Peters, D.L.; Curry, R.A.; Baird, D.J. Quantifying trends in indicator hydroecological variables for regime-based groups of Canadian rivers. Hydrol. Process. 2011, 25, 3086–3100. [Google Scholar] [CrossRef]
- Sun, S.; Barraud, S.; Branger, F.; Braud, I.; Castebrunet, H. Urban hydrologic trend analysis based on rainfall and runoff data analysis and conceptual model calibration. Hydrol. Process. 2018, 31, 1349–1359. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, L.; Zhang, X.; Cheng, L.; Potter, N.; Cowan, T.; Cai, W. Long-term streamflow trends in the middle reaches of the Yellow River Basin: Detecting drivers of change. Hydrol. Process. 2016, 30, 1315–1329. [Google Scholar] [CrossRef]
- Pandey, Y.; Mishra, A.K.; Sarangi, A.; Singh, D.K.; Sahoo, R.N.; Sarkar, S. Trend analysis of rainfall and runoff in the Jhelum basin of Kashmir Valley. Indian J. Agric. Sci. 2018, 88, 320–325. [Google Scholar]
- Xu, Y.; Wang, S.; Bai, X.; Shu, D.; Tian, Y. Runoff response to climate change and human activities in a typical karst watershed, SW China. PLoS ONE 2018, 13, e0193073. [Google Scholar] [CrossRef]
- Sen, Estimates of the Regression Coefficient Based on Kendall’s Tau. Publ. Am. Stat. Assoc. 1968, 63, 1379–1389. [CrossRef]
- Bland, J.M.; Altman, D.G. Regression Analysis. Lancet 1986, 327, 908–909. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Rahman, A.-U.; Dawood, M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Clim. Dyn. 2017, 48, 783–797. [Google Scholar] [CrossRef]
- Mishra, S.; Saravanan, C.; Dwivedi, V.K.; Shukla, J.P. Rainfall-Runoff Modeling using Clustering and Regression Analysis for the River Brahmaputra Basin. J. Geol. Soc. India 2018, 92, 305–312. [Google Scholar] [CrossRef]
- Sharma, P.J.; Patel, P.L.; Jothiprakash, V. Impact of rainfall variability and anthropogenic activities on streamflow changes and water stress conditions across Tapi Basin in India. Sci. Total. Environ. 2019, 687, 885–897. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Peng, W.; Liu, X.; Jiang, C.; Wu, W.; Chen, X. Characteristics of Runoff Variations and Attribution Analysis in the Poyang Lake Basin over the Past 55 Years. Sustainability 2020, 12, 944. [Google Scholar] [CrossRef]
- Sen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Guhathakurta, P.; Kisi, O. Spatial-temporal trend analysis of seasonal and annual rainfall (1966–2015) using innovative trend analysis method with significance test. Arab. J. Geosci. 2019, 12, 328. [Google Scholar] [CrossRef]
- Cui, L.; Wang, L.; Lai, Z.; Tian, Q.; Liu, W.; Li, J. Innovative trend analysis of annual and seasonal air temperature and rainfall in the Yangtze River Basin, China during 1960–2015. J. Atmos. Sol. Terr. Phys. 2017, 164, 48–59. [Google Scholar] [CrossRef]
- Li, J.; Wu, W.; Ye, X.; Jiang, H.; Gan, R.; Wu, H.; He, J.; Jiang, Y. Innovative trend analysis of main agriculture natural hazards in China during 1989–2014. Nat. Hazards 2018, 95, 677–720. [Google Scholar] [CrossRef]
- Kisi, O. An innovative method for trend analysis of monthly pan evaporations. J. Hydrol. 2015, 527, 1123–1129. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Multiple Şen-innovative trend analyses and partial Mann-Kendall test. J. Hydrol. 2018, 566, 685–704. [Google Scholar]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the Innovative Trend Analysis Method for the Trend Analysis of Rainfall Anomalies in Southern Italy. Water Resour. Manag. 2018, 32, 4971–4983. [Google Scholar] [CrossRef]
- Caloiero, T. Evaluation of rainfall trends in the South Island of New Zealand through the innovative trend analysis (ITA). Theor. Appl. Clim. 2019, 139, 493–504. [Google Scholar] [CrossRef]
- Alashan, S. An improved version of innovative trend analyses. Arab. J. Geosci. 2018, 11, 50. [Google Scholar] [CrossRef]
- Şen, Z. Innovative trend significance test and applications. Theor. Appl. Clim. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Demir, V.; Kisi, O. Comparison of Mann-Kendall and innovative trend method (Şen trend) for monthly total precipitation (Middle Black Sea Region, Turkey). In Proceedings of the 3rd International Balkans Conference on Challenges of Civil Engineering, 3-BCCCE, Tirana, Albania, 19–21 May 2016. [Google Scholar]
- Huang, D.; Liu, Z.; Jiang, Q. Application of non-parametric Mann-Kendall and innovative trend method analysis to groundwater quality parameters variation: A case study from aquifers in Xinsankuang Coal mine. J. Water Resour. Water Eng. 2018. [Google Scholar] [CrossRef]
- Kişi, Ö.; Guimaraes Santos, C.A.; Marques da Silva, R.; Zounemat-Kermani, M. Trend analysis of monthly streamflows using Şen’s innovative trend method. Geofizika 2018, 35, 53–68. [Google Scholar] [CrossRef]
- Alashan, S. Combination of modified Mann-Kendall method and en innovative trend analysis. Eng. Rep. 2020. [Google Scholar] [CrossRef]
- Hamade, S.; Tabet, C. The Impacts of Climate Change and Human Activities on Water Resources Availability in the Orontes Watershed: Case of the Ghab Region in Syria. J. Water Sustain. 2013, 3, 45–59. [Google Scholar] [CrossRef]
- Mohammadi, G.; Ebrahimi, K. Effects of human activities and climate variability on water resources in the Saveh plain, Iran. Environ. Monit. Assess. 2015, 187, 35. [Google Scholar] [CrossRef]
- Romanovsky, V.V. Water level variations and water balance of Lake Issyk-Kul. Lake Issyk Kul Its Nat. Environ. 2002, 13, 45–57. [Google Scholar]
- Alifujiang, Y.; Abuduwaili, J.; Ma, L.; Samat, A.; Groll, M. System Dynamics Modeling of Water Level Variations of Lake Issyk-Kul, Kyrgyzstan. Water 2017, 9, 989. [Google Scholar] [CrossRef]
- Salamat, A.U.; Abuduwaili, J.; Shaidyldaeva, N. Impact of climate change on water level fluctuation of Issyk-Kul Lake. Arab. J. Geosci. 2015, 8, 5361–5371. [Google Scholar] [CrossRef]
- Alymkulova, B.; Abuduwaili, J.; Issanova, G.; & Nahayo, L. Consideration of Water Uses for Its Sustainable Management, the Case of Issyk-Kul Lake, Kyrgyzstan. Water 2016, 8, 298. [Google Scholar] [CrossRef]
- Romanovsky, V.V.; Tashbaeva, S.; Crétaux, J.F.; Calmant, S.; Drolon, V. The closed Lake Issyk-Kul as an indicator of global warming in Tien-Shan. Nat. Sci. 2013, 5, 608–623. [Google Scholar] [CrossRef]
- Ilaboya, R. Modelling and Simulation of Rainfall-Runoff Relations for Sustainable Water Resources Management in Ethiope Watershed using SCS-CN, ARC-GIS, ARC-HYDRO, HEC-GEOHMS and HEC-HMS. Tr. Civil Eng. 2018, 2. [Google Scholar] [CrossRef]
- Ferronskii, V.I.; Polyakov, V.A.; Brezgunov, V.S.; Vlasova, L.S.; Karpychev, Y.A.; Bobkov, A.F.; Romaniovskii, V.V.; Johnson, T.; Ricketts, D.; Rasmussen, K. Variations in the Hydrological Regime of Kara-Bogaz-Gol Gulf, Lake Issyk-Kul, and the Aral Sea Assessed Based on Data of Bottom Sediment Studies. Water Resour. 2003, 30, 252–259. [Google Scholar] [CrossRef]
- Shabunin, G.D.; Shabunin, A.G. Climate and physical properties of water in Lake Issyk-Kul. In Lake Issyk-Kul: Its Natural Environment; Springer: Dordrecht, The Netherlands, 2002; Volume 13, pp. 3–11. [Google Scholar]
- Wang, Y.; Xu, Y.; Tabari, H.; Wang, J.; Wang, Q.; Song, S.; Hu, Z. Innovative trend analysis of annual and seasonal rainfall in the Yangtze River Delta, eastern China. Atmos. Res. 2020, 231, 1–14. [Google Scholar] [CrossRef]
- Ma, R.-X.; Huang, J.T.; Tian, H.; Cui, X.D.; Wang, D. Characteristics of precipitation, evaporation and temperature at the Golmud River Catchment in recent 60 years. Arid Land Geogr. 2017, 40, 1005–1012. [Google Scholar]
- Zhang, Q.; Jiang, T.; Gemmer, M.; Becker, S. Precipitation, temperature and discharge analysis from 1951 to 2002 in the Yangtze Catchment, China. Hydrol. Sci. J. Des Sci. Hydrol. 2005, 50, 65–80. [Google Scholar] [CrossRef]
- Burgers, H.E.; Schipper, A.M.; Hendriks, A.J. Size relationships of water discharge in rivers: Scaling of discharge with catchment area, main-stem length and precipitation. Hydrol. Process. 2014, 28, 5769–5775. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Maihemuti, B.; Emin, B.; Groll, M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere 2020, 11, 332. [Google Scholar] [CrossRef]
- Narama, C.; Shimamura, Y.; Nakayama, D.; Abdrakhmatov, K. Recent changes of glacier coverage in the western Terskey-Alatoo range, Kyrgyz Republic, using Corona and Landsat. Ann. Glaciol. 2006, 43, 223–229. [Google Scholar] [CrossRef]


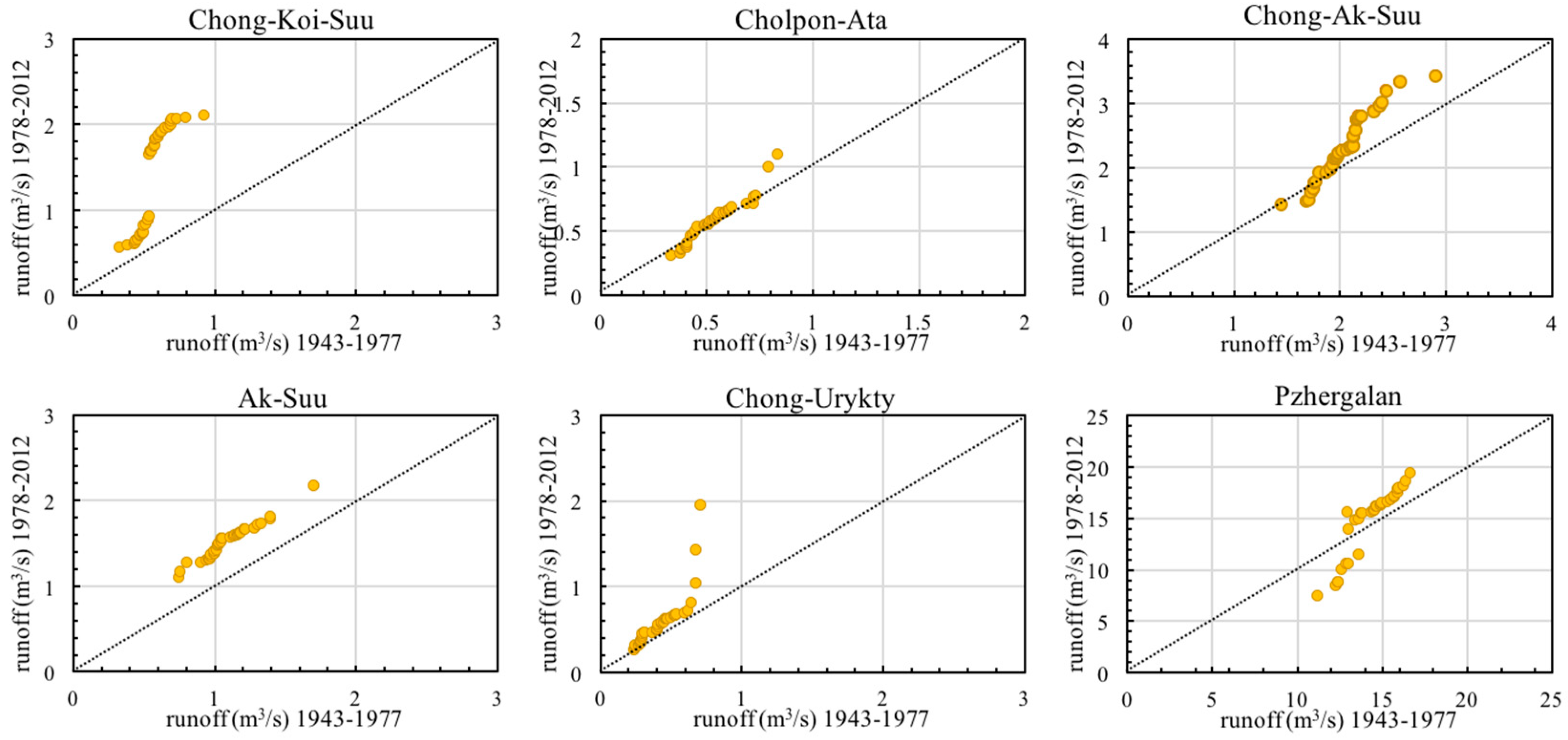
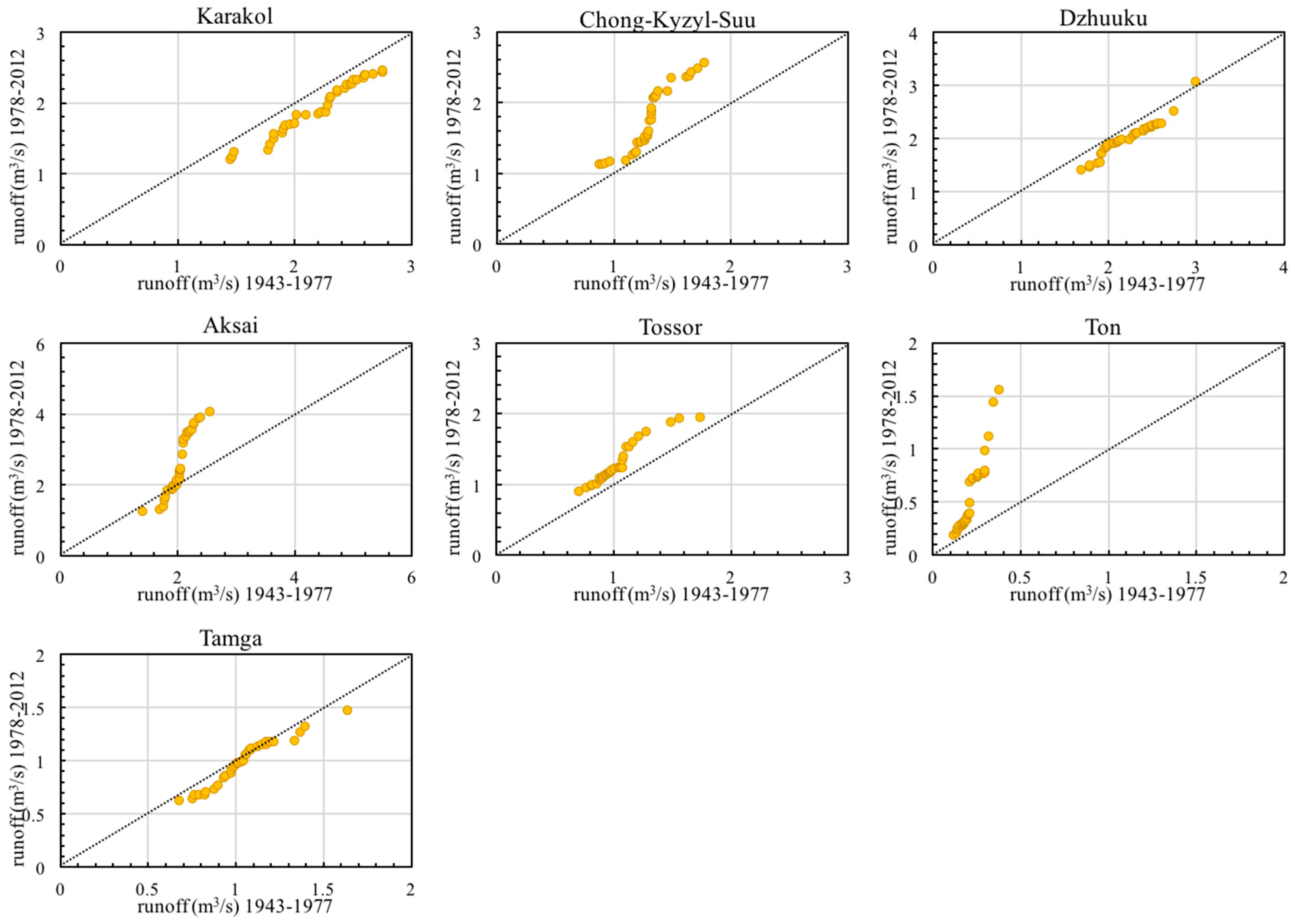


| Statistical Parameters | Pzhergalan | Cholpon-Ata | Chong-Ak-Suu | Ak-Suu | Chong-Koi Suu | Ak-Sai | Karakol | Chong-Kyzyl-Suu | Dzhuuku | Tossor | Ton | Chong-Ury kty | Tamga |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Annual | |||||||||||||
| Min | 11.7 | 2.17 | 6.59 | 5.50 | 2.51 | 6.05 | 8.23 | 7.92 | 9.90 | 3.67 | 1.80 | 2.79 | 6.39 |
| Max | 34.00 | 1.41 | 5.31 | 3.50 | 1.51 | 3.25 | 6.81 | 5.35 | 6.81 | 2.23 | 0.68 | 1.51 | 4.22 |
| Mean | 21.43 | 0.29 | 0.59 | 0.83 | 0.41 | 0.92 | 0.86 | 1.02 | 1.08 | 0.50 | 0.29 | 0.38 | 0.69 |
| Stdev | 4.22 | 0.62 | −0.28 | 0.37 | 0.58 | 1.08 | −0.41 | 0.79 | 0.35 | 0.20 | 1.65 | 0.80 | 0.67 |
| Skew | 0.70 | 0.19 | −0.71 | −0.90 | −0.81 | 0.92 | −0.54 | 0.49 | 0.26 | 0.04 | 4.04 | 1.55 | 0.77 |
| Kurt | 0.62 | 0.91 | 4.18 | 2.09 | 0.86 | 1.71 | 4.76 | 3.48 | 4.43 | 1.25 | 0.25 | 0.75 | 2.93 |
| Spring | |||||||||||||
| Min | 10.8 | 0.41 | 1.82 | 1.38 | 0.43 | 0.87 | 2.25 | 1.65 | 1.47 | 0.77 | 0.22 | 0.81 | 0.43 |
| Max | 32.00 | 1.64 | 4.77 | 4.23 | 1.87 | 2.76 | 5.81 | 5.53 | 4.77 | 2.36 | 1.94 | 2.52 | 3.22 |
| Mean | 16.09 | 0.98 | 2.82 | 2.47 | 1.09 | 1.67 | 3.62 | 2.93 | 2.40 | 1.37 | 0.66 | 1.44 | 1.62 |
| Stdev | 3.88 | 0.29 | 0.53 | 0.74 | 0.48 | 0.42 | 0.83 | 0.86 | 0.56 | 0.30 | 0.30 | 0.42 | 0.54 |
| Skew | 1.56 | 0.22 | 0.60 | 0.31 | 0.58 | 0.86 | 0.59 | 0.89 | 1.41 | 0.87 | 2.02 | 0.85 | 0.30 |
| Kurt | 3.73 | −0.35 | 0.99 | −0.87 | −1.21 | 0.17 | −0.05 | 0.69 | 3.90 | 1.25 | 5.91 | 0.26 | 0.03 |
| Summer | |||||||||||||
| Min | 16.2 | 1.63 | 8.54 | 4.12 | 1.49 | 2.24 | 10.48 | 8.24 | 9.08 | 1.91 | 0.45 | 0.96 | 0.69 |
| Max | 59.07 | 4.55 | 14.93 | 14.77 | 4.01 | 11.19 | 20.47 | 20.23 | 24.27 | 7.58 | 2.14 | 5.18 | 17.64 |
| Mean | 32.51 | 2.79 | 11.55 | 7.74 | 2.50 | 5.61 | 16.50 | 13.11 | 16.55 | 4.66 | 1.12 | 2.93 | 10.72 |
| Stdev | 9.50 | 0.65 | 1.56 | 2.10 | 0.53 | 1.82 | 2.25 | 2.38 | 3.10 | 1.43 | 0.43 | 0.91 | 3.18 |
| Skew | 0.43 | 0.49 | 0.11 | 0.84 | 0.93 | 0.92 | −0.45 | 0.46 | 0.24 | −0.32 | 0.51 | 0.13 | −1.42 |
| Kurt | −0.27 | −0.17 | −0.68 | 0.59 | 0.60 | 1.30 | 0.03 | 0.34 | 0.00 | −0.56 | −0.56 | −0.16 | 3.59 |
| Autumn | |||||||||||||
| Min | 11.5 | 0.71 | 2.98 | 1.17 | 0.76 | 1.43 | 3.43 | 2.16 | 3.66 | 1.06 | 0.18 | 0.28 | 1.46 |
| Max | 37.07 | 2.48 | 7.35 | 3.85 | 3.45 | 6.85 | 7.87 | 7.73 | 10.36 | 3.65 | 1.61 | 3.03 | 6.59 |
| Mean | 22.26 | 1.28 | 4.68 | 2.48 | 1.49 | 3.42 | 5.10 | 3.81 | 6.17 | 1.74 | 0.54 | 1.03 | 2.85 |
| Stdev | 4.93 | 0.36 | 1.00 | 0.64 | 0.67 | 1.25 | 0.91 | 1.06 | 1.29 | 0.52 | 0.30 | 0.42 | 0.87 |
| Skew | 0.79 | 1.15 | 0.54 | 0.17 | 1.16 | 0.95 | 0.40 | 1.38 | 0.71 | 1.32 | 1.56 | 1.85 | 1.64 |
| Kurt | 1.26 | 1.82 | −0.01 | −0.77 | 0.24 | 0.05 | 0.15 | 2.27 | 0.53 | 2.12 | 2.32 | 6.97 | 5.20 |
| Winter | |||||||||||||
| Min | 7.4 | 0.31 | 1.43 | 0.75 | 0.33 | 1.25 | 1.19 | 0.88 | 1.41 | 0.71 | 0.12 | 0.24 | 0.62 |
| Max | 23.97 | 1.10 | 3.43 | 2.16 | 2.11 | 4.06 | 2.76 | 2.56 | 3.07 | 1.95 | 1.55 | 1.94 | 1.64 |
| Mean | 14.87 | 0.56 | 2.19 | 1.30 | 0.96 | 2.31 | 2.06 | 1.52 | 2.12 | 1.15 | 0.38 | 0.51 | 1.01 |
| Stdev | 2.75 | 0.15 | 0.44 | 0.29 | 0.59 | 0.67 | 0.40 | 0.41 | 0.33 | 0.28 | 0.30 | 0.26 | 0.21 |
| Skew | −0.32 | 0.96 | 0.79 | 0.30 | 0.97 | 1.12 | −0.38 | 0.92 | 0.34 | 1.25 | 2.13 | 3.12 | 0.33 |
| Kurt | 1.84 | 1.80 | 0.49 | −0.25 | −0.82 | 0.42 | −0.72 | 0.09 | 0.50 | 1.19 | 4.78 | 14.13 | 0.42 |
| Station Name | Annual | Spring | Summer | Autumn | Winter | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| TSM | MK | TSM | MK | TSM | MK | TSM | MK | TSM | MK | |
| Cholpon-Ata | 0.001 | 1.48 | 0.004 | 2.42 * | 0.021 | 5.33 ** | 0.01 | 3.31 ** | 0.002 | 1.90 |
| Chong-Ak-Suu | 0.008 | 1.40 | −0.002 | −0.55 | 0.009 | 0.87 | 0.02 | 2.81 ** | 0.006 | 2.43 * |
| Ak-Suu | 0.027 | 4.74 ** | 0.022 | 4.95 ** | 0.057 | 5.49 ** | 0.02 | 4.99 ** | 0.009 | 5.39 ** |
| Chong-Koi-Suu | 0.016 | 7.08 ** | 0.018 | 6.57 ** | −0.005 | −2.01 * | 0.02 | 6.37 ** | 0.02 | 7.60 ** |
| Chong-Urykty | 0.004 | 3.50 ** | 0.003 | 1.12 | −0.007 | −1.23 | 0.01 | 3.26 ** | 0.002 | 3.34 ** |
| Pzhergalan | −0.05 | −1.93 | −0.012 | −0.67 | −0.141 | −2.22 * | −0.01 | −0.37 | 0.054 | 2.96 ** |
| Karakol | 0.001 | 0.31 | 0.005 | 0.91 | 0.002 | 0.20 | 0.01 | 1.95 | −0.001 | -0.48 |
| Chong-Kyzyl-Suu | 0.031 | 5.95 ** | 0.026 | 5.94 ** | 0.061 | 5.00 ** | 0.03 | 6.10 ** | 0.014 | 6.28 ** |
| Dzhuuku | 0.029 | −1.03 | 0.007 | 2.38 * | 0.086 | 5.23 ** | 0.03 | 4.18 ** | −0.005 | −2.54 * |
| Ak-Sai | 0.008 | 1.89 | 0.006 | 2.00 * | 0.017 | 1.73 | 0.01 | 1.02 | 0.008 | 2.03 * |
| Tossor | −0.007 | 1.72 | −0.007 | −2.02 * | −0.034 | −3.81 ** | 0.001 | 0.08 | 0.004 | 3.44 ** |
| Ton | 0.008 | 7.01 ** | 0.008 | 5.90 ** | 0.005 | 1.90 | 0.01 | 5.48 ** | 0.006 | 8.14 ** |
| Tamga | 0.007 | 1.68 | −0.007 | −2.02 * | −0.008 | −0.59 | 0.001 | 0.88 | −0.001 | −0.54 |
| Station | Slope s | Standard Deviation σ | Correlation ρ y1y2 | Slope Standard Deviation σs |
|---|---|---|---|---|
| Cholpon-Ata | 0.74 | 0.292 | 0.98 | 0.01 |
| Chong-Ak-Suu | 0.83 | 0.589 | 0.98 | 0.03 |
| Ak-Suu | 3.73 * | 0.829 | 0.95 | 0.06 |
| Chong-Koi-Suu | 1.98 ** | 0.414 | 0.92 | 0.04 |
| Chong-Urykty | 0.51 | 0.383 | 0.98 | 0.02 |
| Pzhergalan | −4.71 ** | 4.219 | 0.94 | 0.36 |
| Karakol | −0.19 | 0.856 | 0.98 | 0.04 |
| Chong-Kyzyl-Suu | 3.67 ** | 1.02 | 0.96 | 0.07 |
| Dzhuuku | 3.55 ** | 1.08 | 0.98 | 0.05 |
| Ak-Sai | 1.93 ** | 0.925 | 0.94 | 0.08 |
| Tossor | −0.18 | 0.504 | 0.98 | 0.02 |
| Ton | 2.83 ** | 0.287 | 0.95 | 0.02 |
| Tamga | 1.52 * | 0.693 | 0.98 | 0.03 |
| Station | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| Cholpon-Ata | 1.98 ** | 1.94 ** | 1.64 * | 0.13 |
| Chong-Ak-Suu | −0.54 * | 1.30 * | 1.66 * | 1.79 * |
| Ak-Suu | 2.78 ** | 8.45 ** | 2.48 ** | 1.20 * |
| Chong-Koi-Suu | 2.31 ** | 2.27 ** | 1.82 * | −0.59 * |
| Chong-Urykty | 1.62 * | 0.48 | 1.56 * | −0.55 * |
| Pzhergalan | −2.49 ** | −2.15 ** | −1.88 ** | 2.14 ** |
| Karakol | −0.05 | −0.77 * | −0.42 | 0.15 |
| Chong-Kyzyl-Suu | 3.20 ** | 1.24 * | 2.49 ** | 7.65 ** |
| Dzhuuku | 3.50 ** | −0.64 * | 1.59 * | 10.75 ** |
| Ak-Sai | 1.55 * | 0.93 | 3.19 ** | 2.04 ** |
| Tossor | 1.69 * | 1.24 ** | −2.24 ** | 1.70 * |
| Ton | 1.93 ** | 0.82 | 1.55 * | 1.85 * |
| Tamga | −0.68 * | 0.62 | −1.31 ** | 0.60 |
| Stations | Annual | Spring | Summer | Autumn | Winter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | ITA | ITA | ITA | ITA | ITA | ||||||||||
| L | M | P | L | M | P | L | M | P | L | M | P | L | M | P | |
| Cholpon-Ata | (+) | (+) | No | (+) | (+) | No | No | (+) | No | No | (+) | (+) | No | No | No |
| Chong-Ak-Suu | No | (+) | (+) | No | (−) | No | No | (+) | No | No | (+) | (+) | No | (+) | (+) |
| Ak-Suu | No | (+) | No | (+) | (+) | (+) | (+) | (+) | No | (+) | (+) | No | (+) | (+) | No |
| Chong-Koi-Suu | (+) | (+) | No | (+) | (+) | (+) | No | No | No | (+) | (+) | No | (+) | No | No |
| Chong-Urykty | (−) | (+) | (+) | No | (+) | (+) | No | (+) | (+) | No | (+) | No | (+) | No | No |
| Pzhergalan | No | (−) | No | No | (−) | No | (−) | (−) | No | No | No | (+) | No | (+) | (+) |
| Karakol | No | No | No | No | No | (−) | No | No | No | No | No | No | No | (−) | (−) |
| Chong-Kyzyl-Suu | No | (+) | (+) | (+) | (+) | No | (+) | (+) | No | (+) | (+) | No | (+) | (+) | No |
| Dzhuuku | No | (+) | (+) | No | No | (+) | (+) | (+) | (+) | (+) | (+) | (+) | No | (−) | No |
| Ak-Sai | No | No | No | (+) | No | No | No | (+) | (+) | No | (+) | (+) | No | (+) | No |
| Tossor | No | No | (+) | (+) | No | (+) | (−) | (−) | (+) | No | (+) | No | (+) | (+) | No |
| Ton | (+) | (+) | No | (+) | (+) | No | (+) | (+) | (+) | (+) | (+) | No | (+) | No | No |
| Tamga | No | (+) | (+) | (−) | (+) | (+) | No | No | No | No | No | No | (−) | No | (−) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alifujiang, Y.; Abuduwaili, J.; Ge, Y. Trend Analysis of Annual and Seasonal River Runoff by Using Innovative Trend Analysis with Significant Test. Water 2021, 13, 95. https://doi.org/10.3390/w13010095
Alifujiang Y, Abuduwaili J, Ge Y. Trend Analysis of Annual and Seasonal River Runoff by Using Innovative Trend Analysis with Significant Test. Water. 2021; 13(1):95. https://doi.org/10.3390/w13010095
Chicago/Turabian StyleAlifujiang, Yilinuer, Jilili Abuduwaili, and Yongxiao Ge. 2021. "Trend Analysis of Annual and Seasonal River Runoff by Using Innovative Trend Analysis with Significant Test" Water 13, no. 1: 95. https://doi.org/10.3390/w13010095
APA StyleAlifujiang, Y., Abuduwaili, J., & Ge, Y. (2021). Trend Analysis of Annual and Seasonal River Runoff by Using Innovative Trend Analysis with Significant Test. Water, 13(1), 95. https://doi.org/10.3390/w13010095






