Development of an Automated Tracer Testing System for UASB Laboratory-Scale Reactors

Abstract

Residence time distribution (RTD) curves play an essential role in the hydraulic characterization of reactors. Current approaches for obtaining RTD curves in laboratory-scale reactors are time-consuming and subject to large errors. Thus, automated systems to obtain RTD curves in laboratory-scale reactors are of great interest for reducing experimental errors due to human interaction, minimizing experimentation costs, and continuously obtaining experimental data. An automated system for obtaining RTD curves in laboratory-scale reactors was designed, built, and tested in this work. During the tests conducted in a cylindrical upflow anaerobic sludge blanket (UASB) reactor, the system worked properly using the stimulus–response pulse technique with sodium chloride as a tracer. Four main factors were found to affect the representativeness of the RTD curves: flow stabilization time, test water conductivity, temperature, and surface tension. A discussion on these factors and the corresponding solutions is presented. The RTD curves of the UASB reactor are left-skewed with a typical tank reactor’s flow shape with channeling and dead zones. A transitory flow behavior was evidenced in the reactor, which indicates the influence of internal turbulent flow structures. The system proposed herein is expected to help study the hydraulics of reactors using laboratory-scale models more efficiently.

1. Introduction

Water and wastewater treatment systems depend on physical unit operations (e.g., grit removal or clarification) and chemical (e.g., neutralization or chemical oxidation) or biological unit processes (e.g., attached or suspended growth BOD remotion) that are conducted in vessels where reactions take place, which are known as “reactors”. Stabilization ponds [1] and activated sludge reactors [2] are among the most common wastewater treatment reactors. Proper reactors’ design is of utmost importance to obtain adequate treatment efficiency. Currently, commonly used guidelines for reactors’ design and operation are based on assumptions of ideal hydraulic behavior, i.e., that the flow inside the reactor behaves ideally either as a plug flow reactor or as a complete mix reactor. However, in most reactors, these conditions are not acquired, thus generating hydraulic conditions that fall between these two idealized and opposite conditions [3]. This divergence from ideal flow occurs due to density currents by thermal or salinity variations, wind-driven circulation patterns, or simply poor reactor design. These effects can considerably reduce the effective treatment volume of a reactor, directly impacting its treatment performance [4,5,6]. Although the design of water and wastewater treatment technologies has improved over time by incorporating the effects of flow hydrodynamics into the design process, it is still in its early development stages.

Despite its relevance, the difficulty of characterizing the flow inside the reactor is one of the main reasons why flow hydrodynamics is not considered in reactors’ designs. Flow characterization can be conducted directly using various flow visualization techniques such as surface flow visualization (e.g., visualization of path lines using dyes), particle tracer techniques such as particle image velocimetry [7] or particle tracking velocimetry [8], and optical techniques including shadowgraphy [9] or schlieren photography [10]. However, although effective, these approaches require qualified personnel and specialized equipment that cannot be coupled to full-scale reactors. Besides, they become impractical in reactors dealing with opaque flows, which is the case with common wastewater treatment reactors. The tracer analysis has been successfully used as an indirect way to characterize the hydrodynamics of a reactor by obtaining residence time distribution curves, which has allowed determining the presence of flow short-circuiting and stagnant zones [11,12]. Therefore, the tracer analysis technique has become the default choice for evaluating flow hydrodynamics in laboratory, pilot, and full-scale reactors.

The pulse method, one of the most used methods in tracer studies, consists of injecting a known amount of tracer in the reactor’s influent for a short time (short with respect to the reactor hydraulic retention time—HRT) and recording its concentration in the reactor’s effluent during a defined period. The resulting concentration vs. time curve is called the $C$ curve. Different fluid elements require different times to pass through the reactor because they travel along different paths. The time distribution curve for a tracer to pass through a reactor is called Residence Time Distribution (RTD) or exit age distribution (E). For convenience, this distribution is normalized; thus, the area under the curve is equal to one $({\int }_0^{\infty }E dt=1)$. $E$ is obtained from curve $C$ (Equation (1)), where $C(t$) is the tracer concentration at time $t$. The RTD curve responds to the need to standardize the $C$ curve, allowing us to compare the hydraulic behavior of different reactors. In addition, one of the main applications of the RTD curve is to determine the deviation of the reactor flow pattern from the idealized pattern used during its design process (plug flow and complete-mix flow),

$$E\left(t\right)=\frac{C\left(t\right)}{{\int }_0^{\infty }C\left(t\right)dt}$$

(1)

According to Metcalf and Eddy [4], the tracer must meet some characteristics for a tracer study to be successful. Specifically:

−

the tracer should possess low molecular diffusivity,

−

the presence of the tracer should not affect the studied flow,

−

the tracer should be conservative over time to allow performing mass balances,

−

the tracer should not react (or be absorbed) with the reactor walls or by particles in the flow; and

−

the tracer must be conveniently measurable.

Lithium chloride (LiCl) [13], calcium chloride (CaCl2) [14], and sodium chloride (NaCl) [15] are compounds that have been successfully used as tracers for the hydrodynamic characterizations of wastewater treatment facilities. Fluorescent tracers such as fluorescein, rhodamine WT, and Eosin Y have also been used since they can be detected at very low concentrations [16,17].

The use of on-site measurement equipment significantly reduces the workload involved in taking periodic samples throughout the monitoring period, ranging from a few hours in small treatment systems [18] to days in large ones such as pond-based treatments [17]. The site measurement systems are usually restricted to full-scale or pilot-scale reactors. Even so, this characterization technique is also of great interest in the study of laboratory-scale reactors since they provide a clear idea of the reactor hydrodynamics at lower costs. The current standard practice in laboratory-scale reactors involves taking effluent samples regularly and measuring the tracer concentration with analytical equipment. Despite its simplicity, this technique is time-consuming, and human experimental errors can be amplified due to scaling effects (i.e., the effects of viscosity, temperature, and salinity that play a more important role in a laboratory or small-scale reactor than in a full-scale reactor), negatively impacting the accuracy of the results. Despite the importance of test repetition to determine the variation of the RTD curves, repetition is not commonly performed [13,19,20], possibly due to the associated high costs and efforts required. This limitation could imply that the validations of mathematical models or even the design of full-scale reactors that commonly use the information of RTD curves from scaled models could have large deviations from the actual behavior of the reactor. Therefore, developing a system capable of automatically obtaining RTD curves in scaled reactors would be advantageous for studying fluid dynamics at the laboratory scale. If available, such a system would free the researcher from performing a repetitive task and considerably reduce human errors in the experimental phase. In this way, the possible deviations obtained from a tracer study can be exclusively attributed to hydraulic conditions. An additional benefit of employing an automated RTD curve obtention system is that enough test replications can be performed to isolate the main factors that reduce the accuracy of RTD curves. However, to the best of the authors’ knowledge, such a system has not been developed and deserves further study.

This paper aims to propose and evaluate a system capable of automatically obtaining RTD curves in laboratory-scale reactors and discuss the main factors that affect the representativeness and accuracy of RTD curves at this scale. The proposed system comprises a control device for feeding the tracer and the test water, a flow measurement unit, a tracer concentration and effluent temperature measurement system, and a data processing unit. The system was tested in an upflow anaerobic sludge blanket (UASB) reactor [21], which is one of the most used anaerobic reactors worldwide [22] and a promising and sustainable wastewater treatment technology that could be improved to meet goals 6 and 7 of the United Nations Sustainable Development Goals (SDGs) [23]. A fundamental characteristic of this type of reactor is that its treatment efficiency greatly depends on its flow hydrodynamics [18,24]. Therefore, it is of great interest to have an accurate and detailed hydrodynamic characterization of the reactor. It is expected that the tool proposed herein could advance our understanding of the hydraulic behavior of fluids and allow us to improve the design of UASB reactors.

2. Materials and Methods

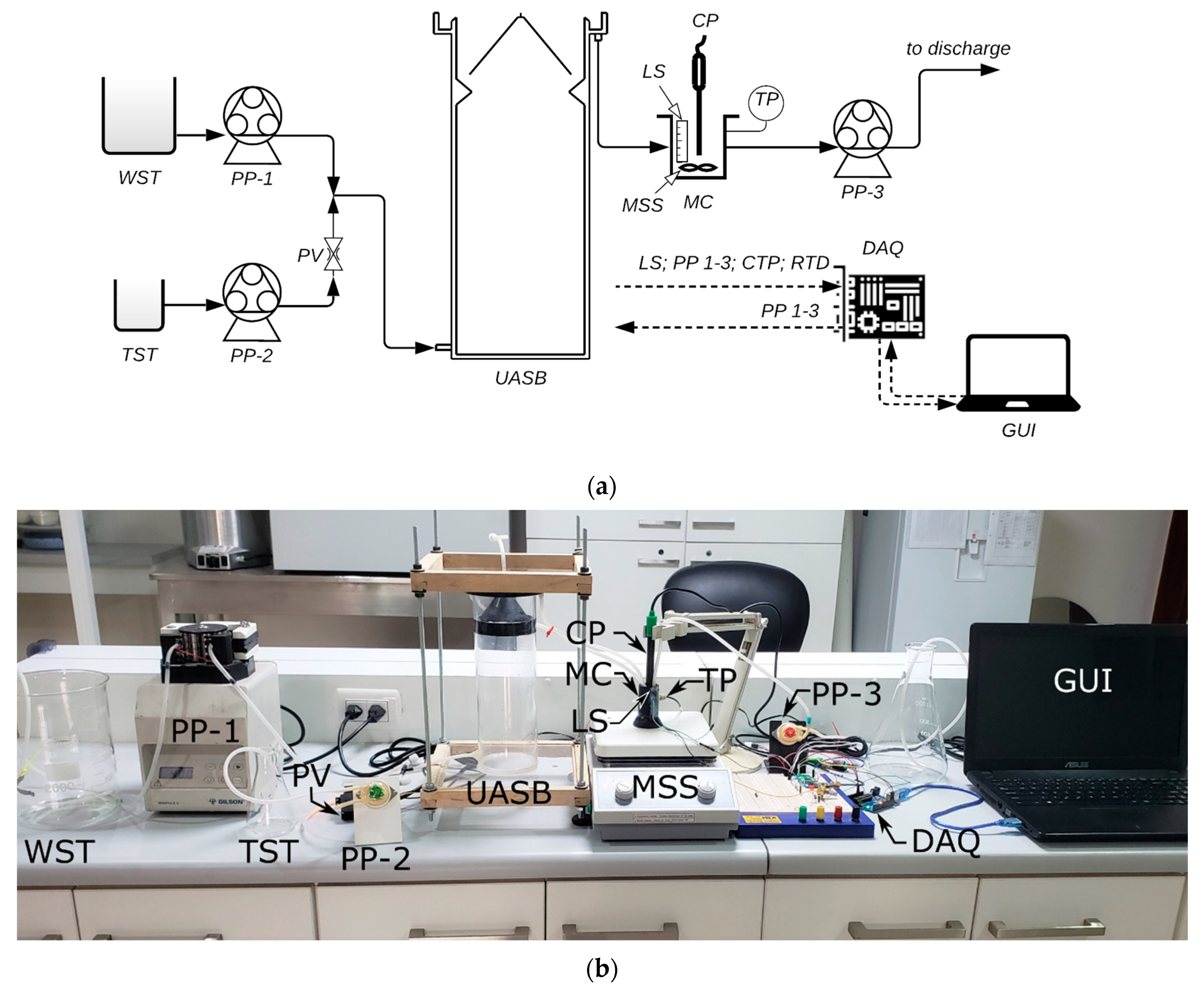
2.1. Automated RTD Measurement System

The automated RTD measurement system (Figure 1a) is comprised of two peristaltic pumps: one for feeding of the test water (PP-1) (Gilson, Minipuls 3), with a pumping rate range of 1–220 mL/min, with an accuracy of ±0.5%, and another one for the tracer–water mixture injection (PP-2) (EZO-PMP Atlas Scientific, New York, NY, USA) with a pumping rate range of 0.5–250 mL/min, with an accuracy of ±1%. The test water is sucked from a storage tank (WST), while the tracer–water mixture is sucked from a separate storage tank (TST). The test water and the tracer–water feed are performed through the same tube using a tee fitting at approximately 150 mm of the reactor’s inlet. During the tracer injection period, PP-1 stops and PP-2 runs, allowing only the tracer–water mixture to feed into the reactor. The reactor feed rate remains constant throughout the test by applying the same flow rate setting for PP-1 and PP-2. A 3D printed two-way pinch valve (PV) (Da Vinci 1.0 Pro, XYZ Printing Inc., San Diego, CA, USA), motorized with a servo motor (HS-322HD Hitec), keeps the tracer tube closed when the test water is delivered to the reactor. The 3D printed valve is made of ABS with a 50% honeycomb infill. A schematic and a photograph of the system are presented in Figure 1a,b, respectively.

After entering the reactor, the water reaches the reactor’s weir and flows towards the discharge gutter. Then, two pipes lead the water to a 12 mL container (MC) (Figure 1a) to measure the tracer’s concentration. The measuring container was also 3D printed using the same setup used for the 3D printed PV and has been designed so that when filled up, it completely covers the sensing part of the conductivity and temperature probes, ensuring accurate measurements. The resistive level sensor (LS), which consists of two electrodes, is installed in the MC to determine when the data logger records the information from the probes. The resistive level sensor is based on a simple circuit composed of a transistor (2N2222, Fairchild Semiconductor, Sunnyvale, CA, USA) and a 1 kΩ variable resistor configured in switch mode. A stir bar (18 mm long and 6 mm diameter) rotating at 30 rpm by means of a magnetic stirring system (MSS) ensures that the liquid within the measuring vessel reaches complete mixing. The conductivity probe (CP) (Figure 1a) (Probe K 0.1, Atlas Scientific) used to determine the tracer’s concentration has an accuracy of ±1% in a measurement range of 0.07–50,000 µS/cm. The temperature probe (TP) (Figure 2a) employed to calculate specific conductance values (i.e., conductivity at 25 °C) is a Micro PT-1000 probe (Atlas Scientific) with a temperature measurement range of −200 to 200 °C and accuracy of $\pm \left(0.15+0.002t\right)$, where $t$ is the measured temperature.

Once the conductivity and the temperature have been obtained, a third peristaltic pump (PP-3) (Figure 1a,b) with the same characteristics as PP-2 empties MC ((Figure 2a), starting again a new conductivity and temperature reading cycle. Conductivity and temperature readings are sent through a data control and acquisition device (DAQ) (Arduino Uno Rev3, Arduino) to the PC (ASUS Intel Hexa-Core i7-9750H), which collects, stores, and presents the data using a graphical user interface (GUI). The PC also calculates the time between two sequential measurements $\left(t_f\right).$ This information is used to estimate the reactor discharging flowrate $\left(Q=V_{MC}/t_f\right)$ where $V_{MC}$ is the MC volume. Although the operating flowrate of the UASB can be set directly on the feed pumps (PP-1 and PP-2), redundant flowrate measurement is used as a safety factor to determine proper pump operation. The GUI was coded in LabVIEW 12 (National Instruments, Austin, TX, USA) and served to control pumps’ start/stop, flow rate, and test start/stop times. Details of the measuring container and a flowchart of the system operation are shown in Figure 2a,b, respectively. Details on the operation of the RTD system coupled to the reactor, as well as a discussion of the factors that affected the functioning of the system and the corresponding solutions, are presented in the Results section.

RTD curves were also generated manually using the setup shown in Figure 1b to compare the benefits provided by the automated RTD measurement system. Manual conductivity measurements were performed using the CON 6 PLUS conductivity meter (LaMotte, Chestertown, MD, USA) on water samples collected from the reactor outlet. Activation/deactivation of the feed and tracer pumps was performed manually.

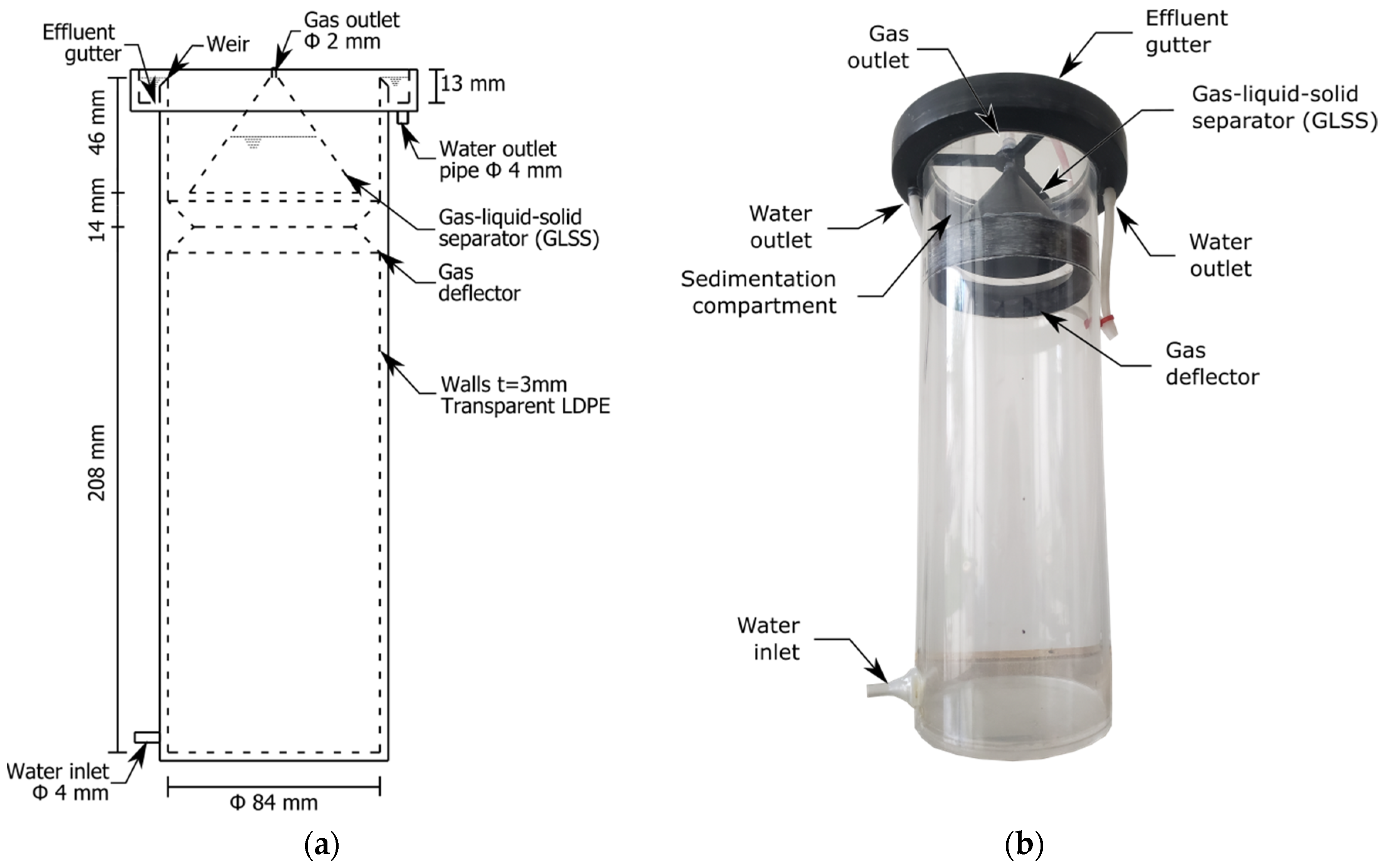
2.2. UASB Reactor

A laboratory-scale UASB reactor operating at a 24 mL/min flow rate was employed to test the automated RTD measurement system. The UASB reactor was made of LDPE (low-density polyethylene) with a diameter of 84 mm and a height of 267 mm (Figure 3a), obtaining an effective volume of 1.45 L, a theoretical hydraulic retention time $\left(\tau \cong 63 \min \right)$, and a Reynolds number of approximately 6. The reactor has a gas baffle, a gas–liquid–solid separator (GLSS), and an effluent gutter to discharge the water. This nomenclature, commonly used in the literature, will be used in the rest of this work to identify the different structures of the UASB reactor. However, in this study, only the liquid phase is considered, and no reaction takes place. These structures were 3D printed using ABS with 50% honeycomb infill (Da Vinci 1.0 Pro, XYZ Printing Inc.). A picture of the reactor is shown in Figure 3b. The water inlet structure, located near the bottom of the reactor, generates a jet flow with a Reynolds number of approximately 118. Jet flows are inherently turbulent structures, exhibiting long-wavelength disturbances at all Reynolds numbers but becoming more critical above 10 [25]. The tracer–water solutions were prepared using sodium chloride (NaCl) (Fisher Scientific, reagent grade CAS 7647-14-5) and the corresponding test water for each tracer test, obtaining a concentration of 1500 mg/L. The tracer injection had a duration of 22 s for all tests. The tracer solutions had densities ranging from 999.5 kg/m³ to 1001.3 kg/m³ with an uncertainty of ±1.7 kg/m³. The viscosities of the tracer solutions ranged from 1.088 × 10⁻⁶ m²/s to 1.09 × 10⁻⁶ m²/s, with an uncertainty of ±0.12 × 10⁻⁶ m²/s.

3. Results and Discussion

Obtaining RTD curves that adequately represent a reactor’s hydraulic characteristics is a complex task, as several factors affect the quality of the results. The control of those factors is relevant, especially when repetitions are performed to estimate the RTD curves’ error. About 75 tracer tests were necessary to isolate the main factors that need to be considered to obtain stable and representative RTD curves as well as to minimize the dispersion between them during the repetitions of the tests. The main destabilizing factors encountered during the generation of RTD curves and the corresponding solutions are detailed in Section 3.1.

3.1. Operation of the Automated RTD Measuring System: Problems and Solutions

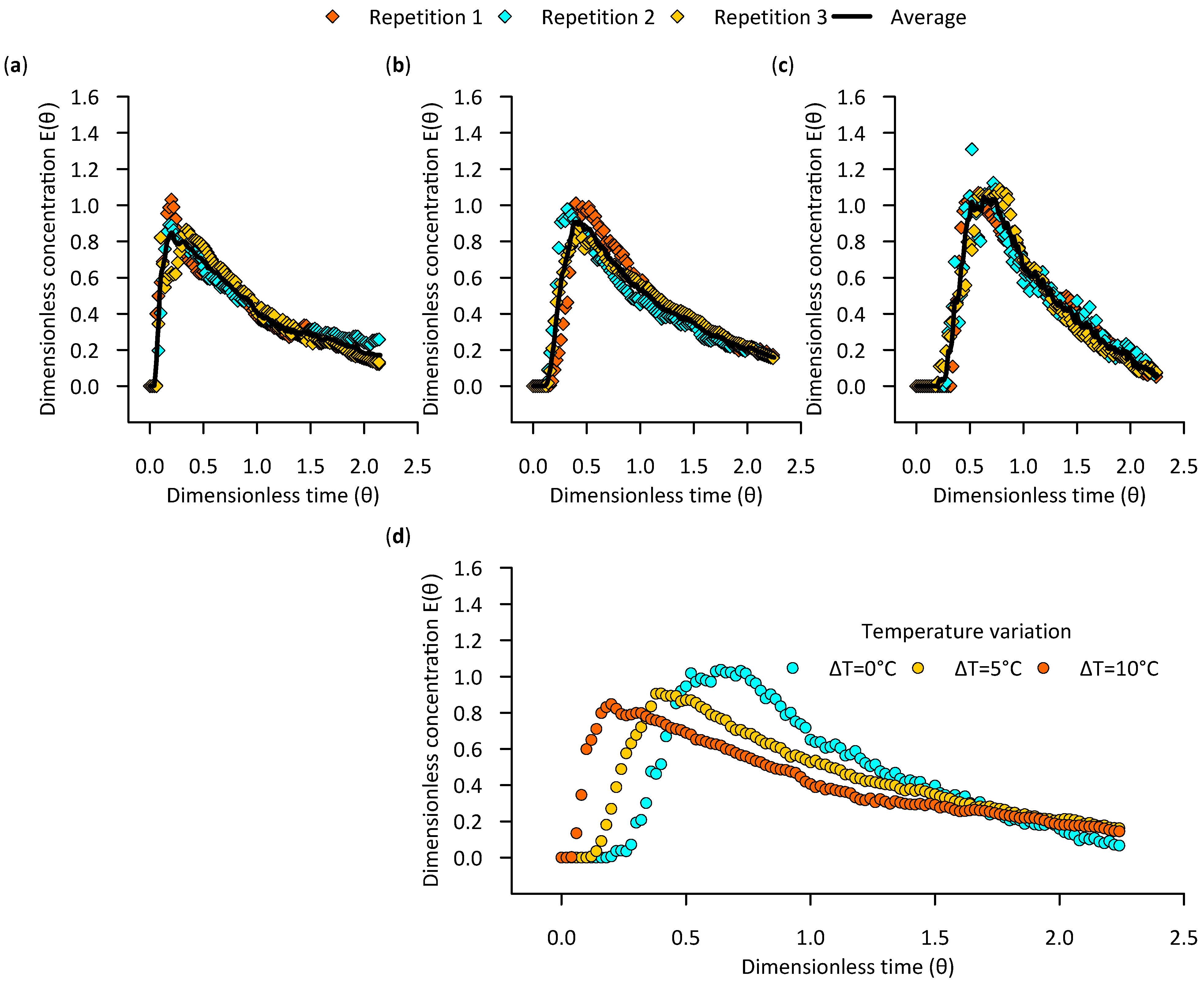
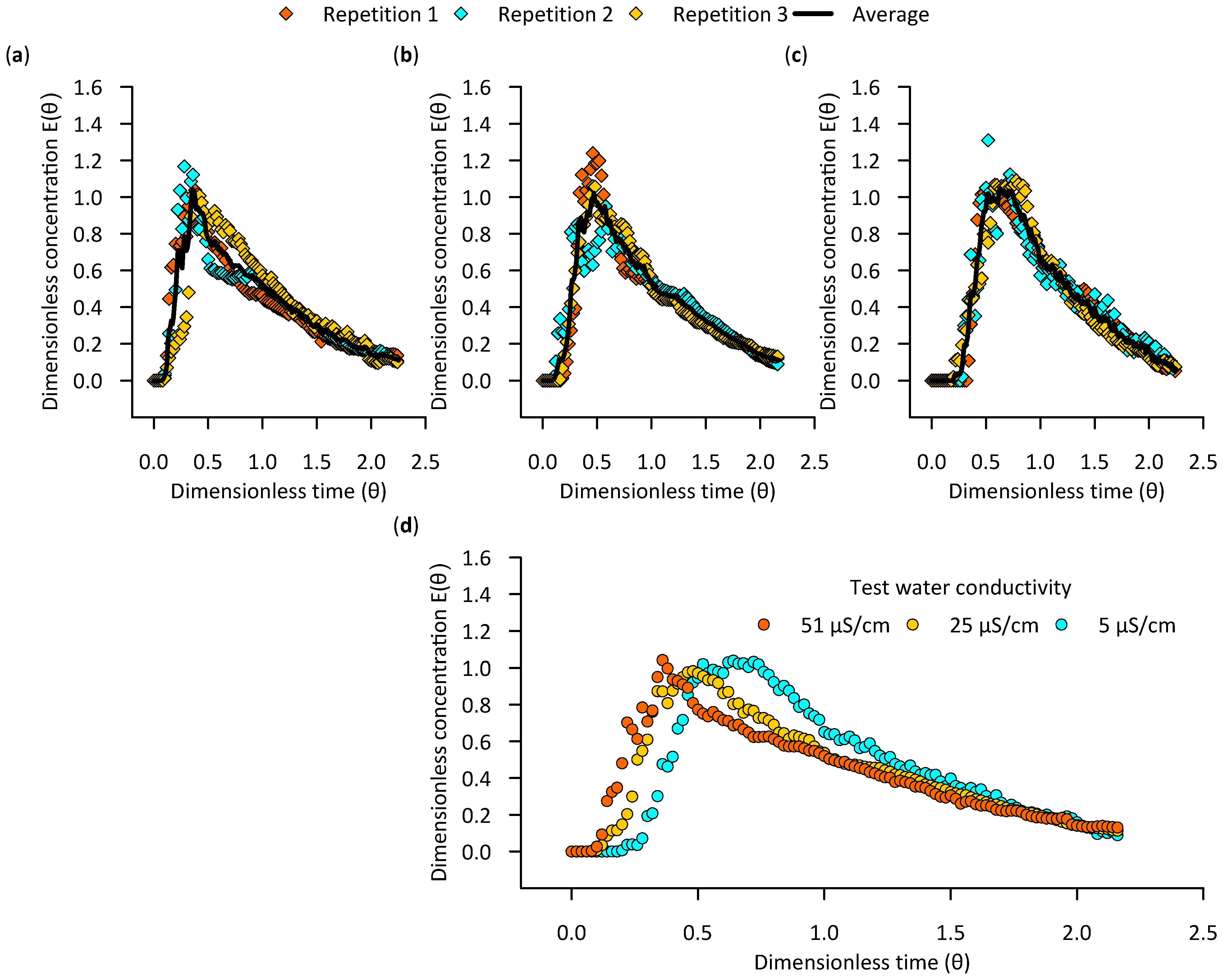
3.1.1. Flow Stabilization Time

Once the reactor has been filled with the test water and before the tracer is injected, it is necessary to allow the reactor to operate undisturbed long enough to obtain developed and stabilized flow patterns. These patterns have a marked influence on the tracer’s dispersion and, consequently, on the reactor’s hydraulic characterization. If flow stabilization is not achieved, there is a risk that the flow patterns are partially formed, generating RTD curves with short-circuiting, channeling, and dead zones magnitudes far from those that represent the hydraulics of the scaled reactor. These effects and how different stabilization times influence the shape of the RTD curves are shown in Figure 4a–e. The results shown in these figures were obtained using low conductivity test water $(<5 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$), keeping the tracer and the test water at the same temperature.

When the stabilization time is zero (Figure 4a), the average curve of the tests indicates that the flow in the reactor behaves more like a plug flow [26] due to the low dispersion of the tracer, resulting in a peak $E\left(\theta \right)\cong 1.1$ at $\theta \cong 0.9$. However, when the stabilization time is extended, the tracer has a much more intense dispersion, obtaining an RTD curve similar to the typical curve of a tank reactor with dead zones and channeling, which is expected in a UASB reactor [13]. Stabilization times of $1\tau$ (Figure 4b) and $2\tau$ (Figure 4c) generated peaks of $E\left(\theta \right)\cong 1.0$ at $\theta \cong 0.7$ and $E\left(\theta \right)\cong 1.1$ at $\theta \cong 0.6$, respectively. With a stabilization time of $3\tau$ (Figure 4d), a peak $E\left(\theta \right)\cong 1.0$ at $\theta \cong 0.6$ is obtained in the RTD curve, indicating that the flow patterns in the reactor have reached a quasi-steady-state condition. In Figure 4a–d, it can be seen a considerable reduction in data dispersion as the stabilization time is extended. Comparison of the average RTD curves (Figure 4d) shows that the RTD curve acquires a well-defined shape with a stabilization time of $3\tau$.

3.1.2. Temperature

In laboratory-scale reactors, the temperature of the test water and the tracer–water mixture should be monitored and controlled as temperature differences between the two fluids can alter the development of flow patterns within the reactor and, as a result, affect the tracer’s dispersion. This study identified that this temperature difference was mainly caused by the heat transfer from the ventilation systems of the main peristaltic pump (PP-1) and the control PC (see details in Section 2.1). The ventilation system of PP-1 is composed of a rear fan and air vent, and that of the PC is composed of two fans with side and rear air vents. No specific technical information was found on the heat emission produced by PP-1 or the PC. The temperature variations that these heat emissions produced in the test water and the tracer–water mixture during the test stabilization period are presented in Figure 5a,b. In Figure 5a, when the container TST was close to PP-1 and to the control PC (within a radius of 30 cm), it can be seen that the heat transfer can produce a temperature difference between the test water and the tracer–water mixture of up to $\mathsf{\Delta }T\cong 7°\mathrm{C}$ upon reaching $3\tau$. This temperature variations could affect the representativeness of the generated RTD curves. In Figure 5b, when the container TST was far from heat emitting sources (separated at a distance greater than 80 cm radius), it can be observed that the temperature difference at $3\tau$ stabilization time does not exceed $\mathsf{\Delta }T\cong 0.2°\mathrm{C}$. Thus, the best practice to avoid relevant temperature variations between the test water and the tracer–water mixture is to locate the tracer container close to the test water container, as far away as possible from any heat-emitting equipment.

The effect of the temperature difference between the tracer and the test water on the RTD curves is shown in Figure 6a–d. These results were obtained by maintaining a stabilization time of $3\tau$ and using test water with a conductivity of $5 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$. The figure shows that the larger the difference between the tracer’s temperature and the test water, the larger the flow channeling and stagnant zones detected in the RTD curve. The average RTD curve that was generated with a tracer–water mixture with a temperature of 10 °C higher than the test water (Figure 6a) produced a peak $E\left(\theta \right)\cong 0.8$ at $\theta \cong 0.2$, showing that the reactor’s hydraulics are influenced by stagnant zones or channeling that originate from the presence of flows with different temperatures slowly dissipating until they become uniform. The average RTD curve that was generated with $\mathsf{\Delta }T=5°\mathrm{C}$ (Figure 6b) obtained an $E\left(\theta \right)\cong 0.9$ at $\theta \cong 0.4$, indicating that the formed stagnant or channeling regions are not as intensely marked as in the previous case, approaching the values obtained by the RTD curve in which flows with the same temperature (Figure 6c) were used $E\left(\theta \right)\cong 1.0$ at $\theta \cong 0.6$. Figure 6d shows an inverse correlation between the tracer’s first appearance time and the tracer–test water temperature variation. The figure also shows that the tracer output rate, reaching its peak, decreases as the temperature variation between the flows tends to zero.

Additionally, monitoring the flow temperature is necessary to calculate the effluent’s specific conductance (i.e., the equivalent conductivity of water at 25 °C), thus standardizing the results. Results standardization is especially relevant when the testing process is long, as the water temperature can vary, affecting the conductivity measurements. If this process is not performed, it will not be possible to correctly account for the tracer recovered during the test.

3.1.3. Test Water Conductivity

If tap water is used to perform the tracer tests, it is important to consider that its quality changes over time along with its conductivity due to the addition of chemical reagents during the water purification process. Therefore, even if the same experimental conditions are maintained, the resulting RTD curves will diverge due to the subtle effects of conductivity altering the flow patterns. These divergences can be minimized by storing enough tap water of the same quality to complete all the tests that will be performed. The effects of conductivity in the test water when obtaining RTD curves using a stabilization time of $3\tau$ and keeping the tracer–water mixture and the test water at the same temperature are shown in Figure 7a–d. The test water of two of these experiments was obtained directly from the laboratory faucet on two different days, getting conductivities of $51 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ and $25 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$. The RTD curves generated with these test waters are similar, especially in the peaks’ location and the development of the tail. However, there is a visible early first detection of the tracer occurring at $\theta \cong 0.07$ for water with $51 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ (Figure 7a) and at $\theta \cong 0.08$ for water with $25 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ (Figure 7b). The early tracer exit may indicate that flow patterns are influenced by stagnant zones or channeling. The repetitions conducted with $51 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ test water presented scattered tracer concentration measurements. The amplitude of these scattered results decreases as the conductivity of the test water decreases, an effect that is noticed with the test waters of $25 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ and $5 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$. Thus, an effective way to reduce scattered results during tracer concentration measurements is to use standardized, low-conductivity water. Highly consistent and representative RTD curves were obtained using type IV reagent water [27] with a conductivity of less than or equal to $5 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$. Figure 7c shows how the use of test water with a conductivity less than $5 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ reduced data dispersion during tracer concentration measurements and increased the tracer first detection time to $\theta \cong 0.20$. In Figure 7d, the tracer output rates from the average RTD curves correlate with the conductivity of the test water. This correlation suggests that test water with lower conductivity allows a more effective dispersion of the tracer used in this study within the reactor.

3.1.4. Superficial Tension Effect

Water surface tension was a major problem in accounting for discharge flow rate in the laboratory-scale UASB reactor. During the tests, the water did not flow freely over the reactor weir towards the discharge gutter but, instead, it accumulated because of surface tension (Figure 8a). When the water volume increased too much, the surface tension broke, flowing into the gutter to be conveyed to MC for flow rate, conductivity, and temperature recording, greatly affecting the flow rate measurements. This problem was overcome by placing small strips of water-saturated glass microfiber (Whatman 934-AH) on the reactor weir, which allowed a continuous discharge of the water into the discharge gutter. It is important to mention that the effect of surface tension is much higher in a laboratory-scale reactor than in a full-scale reactor. Therefore, this factor needs to be considered as part of the test scaling errors.

3.2. Automated RTD Measurement System Performance and UASB Hydraulic Characterization

Three repetitions of RTD curves are shown in Figure 9a to compare the performance of the automated RTD measurement system with the case of manual operation and measurement. These measurements considered the effect of the four factors discussed in Section 3.1. The testing conditions included the use of demineralized Type IV reagent water with a conductivity $<5 \mathsf{\mu }\mathrm{S}/\mathrm{cm}$ [27]. Prior to dosing the tracer, the system was set to operate for approximately 180 min $\left(3\tau \right)$ for the flow to reach a quasi-stationary state. The tracer container was kept close to the test water container away from heat emission devices. Water-saturated glass microfiber strips on the reactor weir were used to help water to flow freely towards the discharge gutter (Figure 8b). The automated RTD measurement system operated correctly during the tests, the control of the devices, and the recording of the generated data occurred as expected. There was no human interaction during the tests except for routine checks to determine the devices’ correct operation. During each test, the pump PP-1 delivered about 7600 mL of test water. About 56% of this volume was used to achieve a quasi-steady state in the flow. The pump PP-2 dosed 8.7 mL of tracer in each test. The measured flow rate for PP-1 was 23.85 ± 0.11 mL/min and for PP-2 was 23.84 ± 0.03 mL/min, showing high accuracy in flowrate measurement at MC; thus, the use of the glass microfiber strips for minimization of surface tension effects was successful. The conductivity and temperature sensors adequately recorded the tracer’s concentration during the test, detecting a minimum tracer concentration of 0.014 mg/L at the beginning of the RTD curve formation and of 5.33 mg/L during the detection of the RTD peak. The effluent water temperature during the test was 20.09 ± 0.10 °C. After recording the temperature and conductivity measurements, the MC was emptied as expected, ensuring that the obtained data correspond to the last volume of water discharged from the reactor gutter. The performed tracer tests resulted in left-skewed RTD curves with long tails (Figure 9a), the shape of which resembles that of a typical tank reactor with dead zones and channeling [28]. The rapid exit of the tracer and the high peaks found in the RTD curves confirm the presence of these zones. This finding is consistent with the effects caused by the lateral water inlet configuration used by this reactor, which could generate poor flow distribution, thus reducing the hydraulic efficiency of the reactor. Slightly different RTD curves were obtained in each test repetition which, as discussed in Section 3.1.1, are due to flow transient effects. The transient flow behavior in the reactor can be caused mainly by the jet flow generated by the lateral water inlet, which, as mentioned before, is inherently turbulent [25].

The RTD curves obtained using the manual method (Figure 9b) have similar shapes to those obtained with the automated method. However, there is a clear reduction in the measurement’s frequency (i.e., fewer data points are obtained) in comparison to the automatic method, as the researcher quickly becomes saturated with the measurement tasks. Compared to the automatic method, a greater dispersion of the tracer measurements is found, especially around the tracer concentration peak (i.e., around $\theta =0.5–0.6$). This dispersion could indicate that, despite keeping the recommended conditions discussed in Section 3.1, more significant flow disturbances may have occurred during the manual operation of the reactor.

The tracer’s first appearance time for the average RTD is $\theta \cong 0.20$ for the automatic measurement system and $\theta \cong 0.15$ for the manual measurements. The period of rapid tracer exit ended with an average magnitude peak of $E\left(\theta \right)\cong 1.0$ at $\theta \cong 0.6$ for the automatic measurements and $E\left(\theta \right)\cong 0.9$ at $\theta \cong 0.4$ for the manual ones. Small instantaneous concentration jumps in the RTD curve decline phase, especially around $\theta \cong 1.1$ and $\theta \cong 1.6,$ can only be seen in Figure 9a. These jumps can indicate the tracer’s exit that remained in stagnant zones. Despite minor deviations in the curves, it is seen that the shapes of the curves obtained automatically and manually are approximately similar, confirming the validity of the proposed automated measurement system.

4. Conclusions

Automated systems for obtaining RTD curves in laboratory-scale treatment reactors could help reduce experimental errors and advance our understanding of their operation. An automated system for obtaining RTD curves in laboratory-scale reactors was designed, built, and tested in this work. The system was tested in a cylindrical upflow anaerobic sludge blanket reactor with a radial water inlet. A flow stabilization time of at least three theoretical hydraulic retention times $\left(3\tau \right)$ is one of the main factors that should be considered to obtain RTD curves with stabilized flow patterns. In laboratory-scale reactors, reducing the temperature differences between the tracer and the test water is required to avoid the formation of density currents that could influence the resulting RTD curve’s shape. The use of standardized low conductivity test water is recommended to reduce data scatter during tracer tests. Water’s surface tension affects the discharge of water on the laboratory-scale reactor weir. However, this effect can be minimized by placing water-saturated glass microfiber strips on the weir that allow the water to flow freely into the reactor discharge gutter. Considering these factors and conducting test replications is of utmost importance during proper hydraulic characterization of laboratory-scale UASB reactors to obtain accurate RTD curves, especially for validating mathematical models and full-scale reactor designs. A transient flow behavior was evidenced in the laboratory-scale reactor, indicating the presence of turbulent flow structures. The higher measurement frequency that the automated RTD measurement system can obtain allows us to identify RTD features difficult to obtain through manual measurements. The system is expected to help study the hydraulics of UASB reactors using laboratory-scale models in a more efficient way.

Further study is necessary to determine the efficiency of the automated measurement system in other types of reactors and flow regimes, including more complex inflow conditions where tracer diffusion could be more intensive. The possibility of incorporating optical equipment into the automatic measurement system should be evaluated, as it could expand the characterization capabilities of the system by having flow visualization techniques.