Hydrostatic Densitometer for Monitoring Density in Freshwater to Hypersaline Water Bodies
Abstract
:1. Introduction
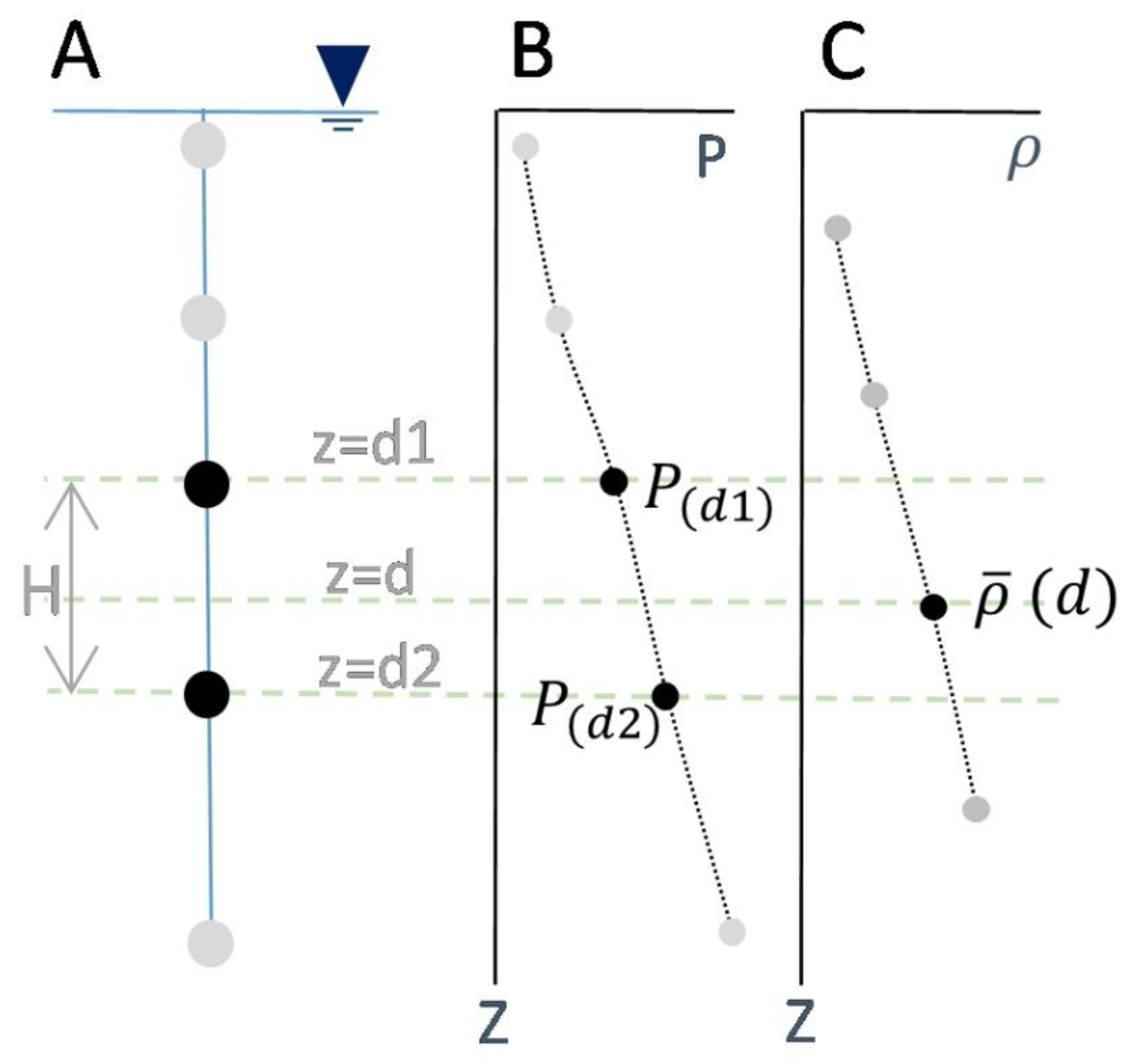
2. Theoretical Considerations of the Hydrostatic Densitometer
3. Methods
3.1. Density Measurements Using the Hydrostatic Densitometer
3.2. Other Methods for Density Determination
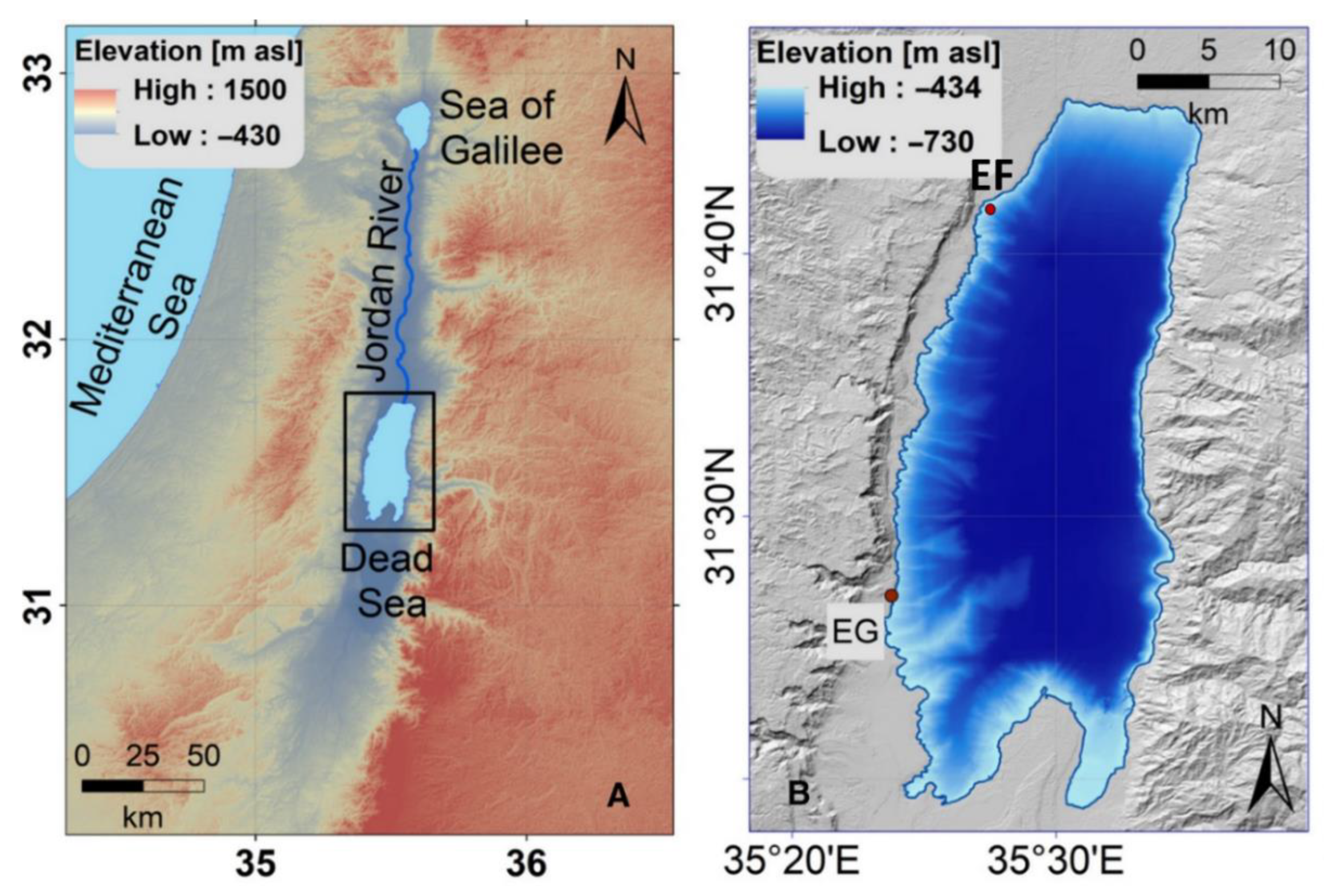
4. Experimental Design and Regional Setting
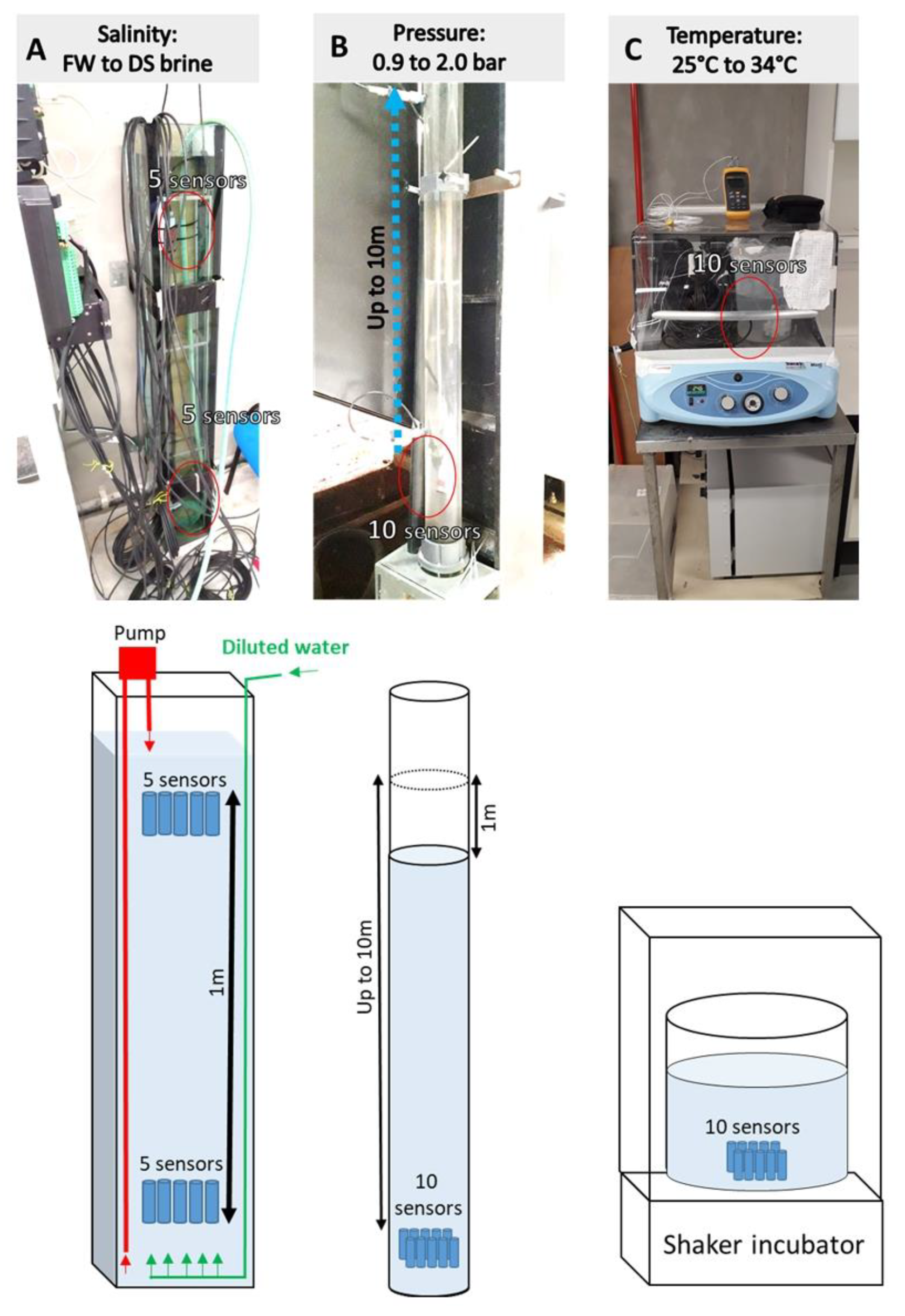
4.1. Verification of the Hydrostatic Densitometer from Freshwater to Hypersaline Brine
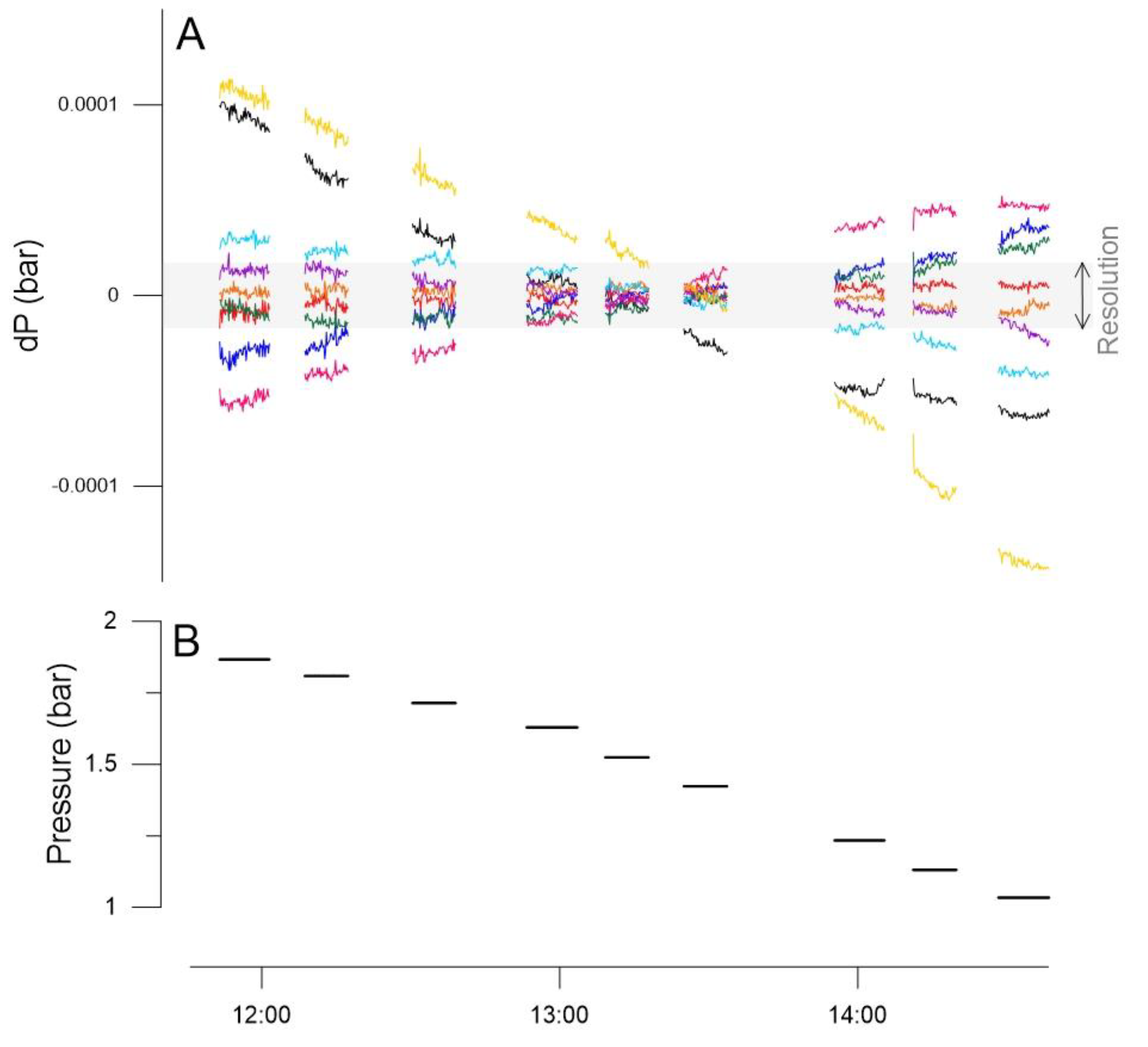
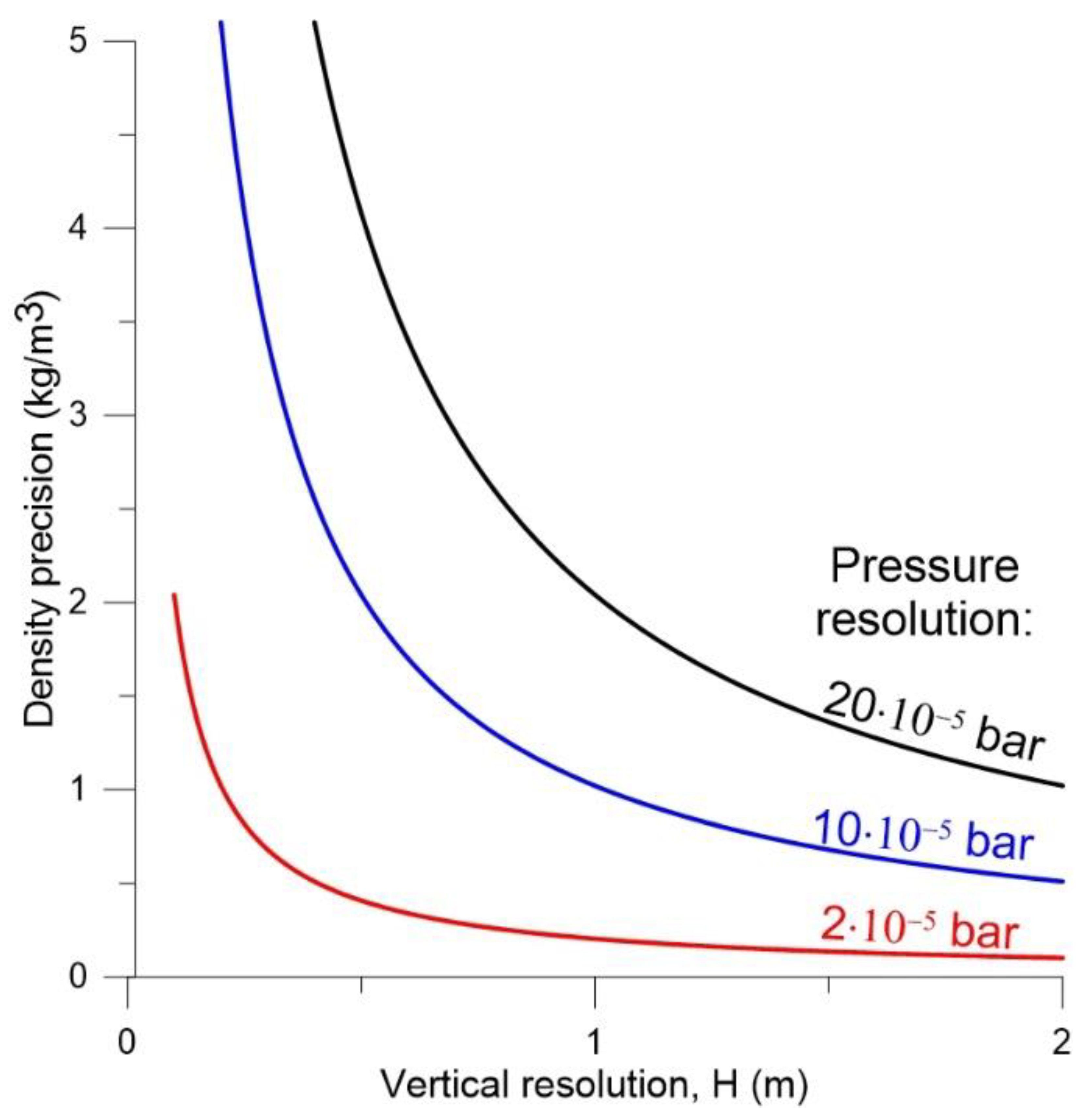
4.2. Sensitivity of the Hydrostatic Densitometer to Variations in Temperature and Pressure
4.3. Field Campaign Design and Regional Setting
4.3.1. The Borehole Measuring Setup
4.3.2. The Dead Sea Diluted Plume Measuring Setup
5. Results and Discussion
5.1. Laboratory Experiment and Sensitivity Tests
5.2. Coastal Aquifer—Borehole Stratification Observation
5.3. Lake Stratification—Diluted Plume Observation
5.4. Challenges and Potential for Dynamic Marine Applications
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: Chelmsford, MA, USA, 2013; ISBN 0486131807. [Google Scholar]
- Knauss, J.A.; Garfield, N. Introduction to Physical Oceanography; Waveland Press: Long Grove, IL, USA, 2016; ISBN 1478634758. [Google Scholar]
- Werner, A.D.; Bakker, M.; Post, V.E.A.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Folch, A.; Menció, A.; Puig, R.; Soler, A.; Mas-Pla, J. Groundwater development effects on different scale hydrogeological systems using head, hydrochemical and isotopic data and implications for water resources management: The Selva basin (NE Spain). J. Hydrol. 2011, 403, 83–102. [Google Scholar] [CrossRef]
- Post, V.E.A.; von Asmuth, J.R. Review: Hydraulic head measurements—New technologies, classic pitfalls. Hydrogeol. J. 2013, 21, 737–750. [Google Scholar] [CrossRef] [Green Version]
- Levanon, E.; Yechieli, Y.; Shalev, E.; Friedman, V.; Gvirtzman, H. Reliable monitoring of the transition zone between fresh and saline waters in coastal aquifers. Groundw. Monit. Remediat. 2013, 33, 101–110. [Google Scholar] [CrossRef]
- Shalev, E.; Lazar, A.; Wollman, S.; Kington, S.; Yechieli, Y.; Gvirtzman, H. Biased monitoring of fresh water-salt water mixing zone in coastal aquifers. Groundwater 2009, 47, 49–56. [Google Scholar] [CrossRef]
- Mor, Z.; Assouline, S.; Tanny, J.; Lensky, I.M.; Lensky, N.G. Effect of Water Surface Salinity on Evaporation: The Case of a Diluted Buoyant Plume Over the Dead Sea. Water Resour. Res. 2018, 54, 1460–1475. [Google Scholar] [CrossRef]
- Arnon, A.; Lensky, N.G.; Selker, J.S. High resolution temperature sensing in the Dead Sea using fiber optics. Water Resour. Res. 2014, 50, 1756–1772. [Google Scholar] [CrossRef]
- Arnon, A.; Selker, J.S.; Lensky, N.G. Thermohaline stratification and double diffusion diapycnal fluxes in the hypersaline Dead Sea. Limnol. Oceanogr. 2016, 61, 1214–1231. [Google Scholar] [CrossRef]
- Arnon, A.; Brenner, S.; Selker, J.S.; Gertman, I.; Lensky, N.G. Seasonal dynamics of internal waves governed by stratification stability and wind: Analysis of high-resolution observations from the Dead Sea. Limnol. Oceanogr. 2019, 64, 1864–1882. [Google Scholar] [CrossRef]
- Sirota, I.; Enzel, Y.; Lensky, N.G. Temperature seasonality control on modern halite layers in the Dead Sea: In situ observations. Bull. Geol. Soc. Am. 2017, 129, 1181–1194. [Google Scholar] [CrossRef]
- Anati, D.A. The salinity of hypersaline brines: Concepts and misconceptions. Int. J. Salt Lake Res. 1999, 8, 55–70. [Google Scholar] [CrossRef]
- Sirota, I.; Arnon, A.; Lensky, N.G. Seasonal variations of halite saturation in the Dead Sea. Water Resour. Res. 2016, 52, 7151–7162. [Google Scholar] [CrossRef]
- Gertman, I.; Hecht, A. The Dead Sea hydrography from 1992 to 2000. J. Mar. Syst. 2002, 35, 169–181. [Google Scholar] [CrossRef] [Green Version]
- Gertman, I.; Kress, N.; Katsenelson, B.; Zavialov, P. Equations of State for the Dead Sea and Aral Sea: Searching for Common Approaches; Report IOLR/12; Israel Oceanographic and Limnological Research (IOLR): Haifa, Israel, 2010. [Google Scholar]
- Selker, J.S.; Thevenaz, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; Van De Giesen, N.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Lipták, B.G. Instrument Engineers’ Handbook, Volume One: Process Measurement and Analysis; CRC Press: Boca Raton, FL, USA, 2003; Volume 1, ISBN 1420064029. [Google Scholar]
- Lensky, N.G.; Dvorkin, Y.; Lyakhovsky, V.; Gertman, I.; Gavrieli, I. Water, salt, and energy balances of the Dead Sea. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Lensky, N.; Dente, E. The Hydrological Processes Driving the Accelerated Dead Sea Level Decline in the Past Decades; Rep GSI/16/2015; Geological Survey of Israel: Jerusalem, Israel, 2015.
- Yechieli, Y.; Ronen, D.; Berkowitz, B.; Dershowitz, W.S.; Hadad, A. Aquifer characteristics derived from the interaction between water levels of a terminal lake (Dead Sea) and an adjacent aquifer. Water Resour. Res. 1995, 31, 893–902. [Google Scholar] [CrossRef]
- Kiro, Y.; Yechieli, Y.; Lyakhovsky, V.; Shalev, E.; Starinsky, A. Time response of the water table and saltwater transition zone to a base level drop. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Yechieli, Y.; Sawaed, I.; Lutzky, H. Geological and Hydrological Findings from Boreholes at En Gedi, Hamme Mazor and Nahal Zeelim Area; Report TRGSI/14/2008; Geological Survey of Israel: Jerusalem, Israel, 2013. (In Hebrew)
- Dente, E.; Lensky, N.G.; Morin, E.; Enzel, Y. From straight to deeply incised meandering channels: Slope impact on sinuosity of confined streams. Earth Surf. Process. Landf. 2021, 46, 1041–1054. [Google Scholar] [CrossRef]
- Nehorai, R.; Lensky, I.M.; Lensky, N.G.; Shiff, S. Remote sensing of the Dead Sea surface temperature. J. Geophys. Res. 2009, 114, C05021. [Google Scholar] [CrossRef]
- Nehorai, R.; Lensky, I.M.; Hochman, L.; Gertman, I.; Brenner, S.; Muskin, A.; Lensky, N.G. Satellite observations of turbidity in the Dead Sea. J. Geophys. Res. Ocean 2013, 118, 3146–3160. [Google Scholar] [CrossRef]
- Nehorai, R.; Lensky, N.; Brenner, S.; Lensky, I. The dynamics of the skin temperature of the dead sea. Adv. Meteorol. 2013, 2013. [Google Scholar] [CrossRef]
- Sirota, I.; Ouillon, R.; Mor, Z.; Meiburg, E.; Enzel, Y.; Arnon, A.; Lensky, N.G. Hydroclimatic Controls on Salt Fluxes and Halite Deposition in the Dead Sea and the Shaping of “Salt Giants”. Geophys. Res. Lett. 2020, 47, e2020GL090836. [Google Scholar] [CrossRef]
- Meiburg, E.; Kneller, B. Turbidity currents and their deposits. Annu. Rev. Fluid Mech. 2010, 42, 135–156. [Google Scholar] [CrossRef] [Green Version]
- Zordan, J.; Juez, C.; Schleiss, A.J.; Franca, M.J. Entrainment, transport and deposition of sediment by saline gravity currents. Adv. Water Resour. 2018, 115, 17–32. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mor, Z.; Lutzky, H.; Shalev, E.; Lensky, N.G. Hydrostatic Densitometer for Monitoring Density in Freshwater to Hypersaline Water Bodies. Water 2021, 13, 1842. https://doi.org/10.3390/w13131842
Mor Z, Lutzky H, Shalev E, Lensky NG. Hydrostatic Densitometer for Monitoring Density in Freshwater to Hypersaline Water Bodies. Water. 2021; 13(13):1842. https://doi.org/10.3390/w13131842
Chicago/Turabian StyleMor, Ziv, Hallel Lutzky, Eyal Shalev, and Nadav G. Lensky. 2021. "Hydrostatic Densitometer for Monitoring Density in Freshwater to Hypersaline Water Bodies" Water 13, no. 13: 1842. https://doi.org/10.3390/w13131842
APA StyleMor, Z., Lutzky, H., Shalev, E., & Lensky, N. G. (2021). Hydrostatic Densitometer for Monitoring Density in Freshwater to Hypersaline Water Bodies. Water, 13(13), 1842. https://doi.org/10.3390/w13131842






