Study on the Coexistence of Offshore Wind Farms and Cage Culture
Abstract
:1. Introduction
2. Methodology
2.1. Wave Model
2.2. Hydrodynamic Model
- Continuity equation:
- Momentum equations:where is the water surface elevation, is the static water depth, and are the average velocity components of the water depth in the fixed coordinates of the and axes:
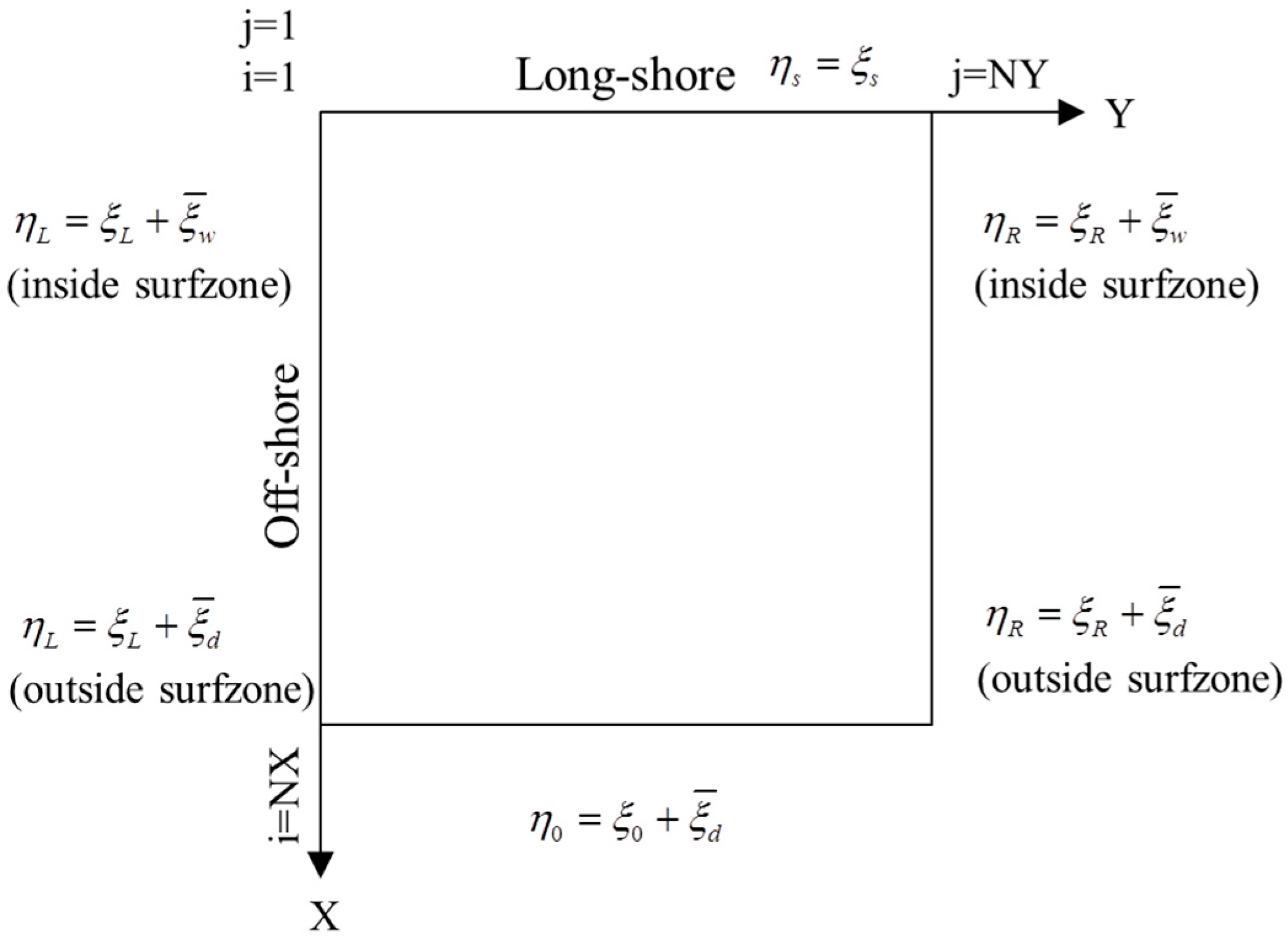
- Left boundary:
- Right boundary:
- Offshore boundary:
2.3. Hydrodynamic Characteristics at the Coast
3. Analysis of the Interaction between the Marine Environment and Wind Turbines
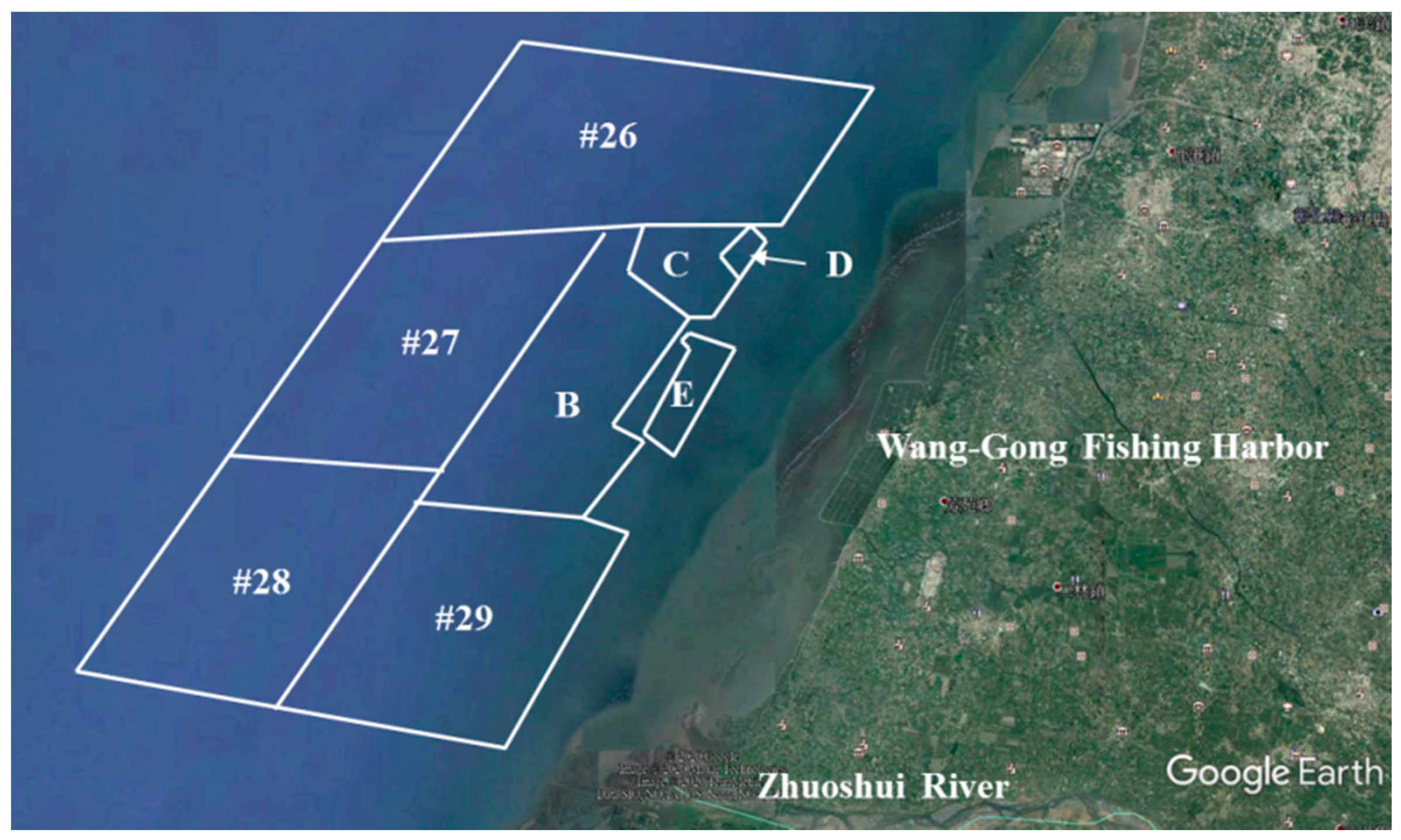
3.1. Modeling Procedure and Setting
3.2. Analysis of the Influence of the Wind Turbine on the Wave and Current Pattern
3.3. Analysis of the Local Wind Turbines Impact on the Marine Environment
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- 4C Offshore. Global Wind Speed Rankings. 2014. Available online: http://www.4coffshore.com/windfarms/windspeeds.aspx (accessed on 1 March 2021).
- Ministry of Science and Technology. Ocean Data Bank. 2018. Available online: http://www.odb.ntu.edu.tw/ (accessed on 22 November 2020).
- Haggett, C. Understanding public responses to offshore wind power. Energy Policy 2011, 39, 503–510. [Google Scholar] [CrossRef] [Green Version]
- Hooper, T.; Ashley, M.; Austen, M. Perceptions of fishers and developers on the co-location of offshore wind farms and decapod fisheries in the UK. Mar. Policy 2015, 61, 16–22. [Google Scholar] [CrossRef] [Green Version]
- Stuiver, M.; Soma, K.; Koundouri, P.; van den Burg, S.; Gerritsen, A.; Harkamp, T.; Dalsgaard, N.; Zagonari, F.; Guanche, R.; Schouten, J.J.; et al. The Governance of Multi-use Platforms at Sea for Energy Production and Aquaculture: Challenges for Policy Makers in European Seas. Sustainability 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
- Benassai, G.; Mariani, P.; Stenberg, C.; Christoffersen, M. A Sustainability Index of potential co-location of offshore wind farms and open water aquaculture. Ocean. Coast. Manag. 2014, 95, 213–218. [Google Scholar] [CrossRef]
- Wever, L.; Krause, G.; Buck, B.H. Lessons from stakeholder dialogues on marine aquaculture in offshore wind farms: Perceived potentials, constraints and research gaps. Mar. Policy 2015, 51, 251–259. [Google Scholar] [CrossRef] [Green Version]
- Jansen, H.M.; van den Burg, S.; Bolman, B.; Jak, R.G.; Kamermans, P.; Poelman, M.; Stuiver, M. The feasibility of offshore aquaculture and its potential for multi-use in the North Sea. Aquac. Int. 2016, 24, 735–756. [Google Scholar] [CrossRef] [Green Version]
- Rawson, A.; Rogers, E. Assessing the impacts to vessel traffic from offshore wind farms in the Thames Estuary. Sci. J. Marit. Univ. Szczec. 2015, 43, 99–107. [Google Scholar]
- Soukissian, T.H.; Denaxa, D.; Karathanasi, F.; Prospathopoulos, A.; Sarantakos, K.; Iona, A.; Georgantas, K.; Mavrakos, S. Marine Renewable Energy in the Mediterranean Sea: Status and Perspectives. Energies 2017, 10, 1512. [Google Scholar] [CrossRef] [Green Version]
- Kwon, Y.M.; Lee, C.H.; Rim, G.S. A Review of Vessel Traffic and Fishing Activity Standards for Offshore Wind Farm in Domestic Areas Based on the Analysis of Foreign Cases. J. Korean Soc. Mar. Environ. Saf. 2018, 24, 29–35. [Google Scholar] [CrossRef]
- FAO, FishStatJ. FAO Database on Fish Capture and Aquaculture Production and Trade. 2018. Available online: http://www.fao.org/fishery/en (accessed on 22 February 2021).
- Elliott, D.L.; Barnard, J.C. Observations of wind turbine wakes and surface roughness effects on wind flow variability. Sol. Energy 1990, 45, 265–283. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 15–18. [Google Scholar]
- Jin, W.J. Numerical Simulation of Wind Turbine Wakes Based on Actuator Line Method in NEK5000. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
- Environmental Protect on Administration Executive Yuan, Taiwan. Environmental Impact Assessment Inquiry System. Available online: https://eiadoc.eap.gov.tw/EIAWEB/Default.aspx (accessed on 28 March 2021).
- Schomerus, T.; Runge, K.; Nehls, G. Strategic environmental assessment for the utilisation of offshore wind energy. In Proceedings of the 2nd Scientific Conference on the Use of Offshore Wind Energy by the Federal Ministry for the Environment, Berlin, Germany, 20–21 February 2007; pp. 57–73. [Google Scholar]
- Sivas, D.; Caldwell, M. A new vision for Californian ocean governance: Comprehensive ecosystem-based marine zoning. Stanf. Environ. Law J. 2008, 27, 209–270. [Google Scholar]
- Chiang, Y.C.; Hsiao, S.S.; Lin, M.C. Numerical Solutions of costal Morphodynamic Evolution for Complex Topography. J. Mar. Sci. Technol. 2010, 18, 333–344. [Google Scholar]
- Chiang, Y.C.; Hsiao, S.S. Coastal Morphological Modeling. In Sediment Transport in Aquatic Environments; InTech: Rijeka, Croatia, 2011; Chapter 10; pp. 203–230. Available online: http://www.intechopen.com/books/sediment-transport-in-aquatic-environments/coastal-morphologicalmodeling (accessed on 28 March 2021).
- Wang, H.Y.; Fang, H.M.; Hsiao, S.S. Study on the Topographical Change of Heping River Estuary. J. Coast. Ocean. Eng. 2018, 18, 205–225. [Google Scholar]
- Kirby, J.T.; Dalrymple, R. A parabolic equation for the combined refraction-diffraction of Stokes waves by mildly varying topography. J. Fluid Mech. 1983, 136, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Mizuguchi, M. A heuristic model of wave height distribution in surf zone. In Proceedings of the 17th International Conference on Coastal Engineering, Sydney, Australia, 23–28 March 1980; pp. 278–289. [Google Scholar]
- Falconer, R.A. Numerical modelling of tidal circulation in harbours. J. Waterw. Port Coast. Ocean. 1980, 106, 31–48. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Ponce, V.M.; Yahusaki, S.B. Modeling circulation in depth-averaged flow. J. Hydraul. Div. 1981, 107, 1501–1518. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation in water waves: A physical discussion with applications. Deep Sea Res. 1964, 11, 529–563. [Google Scholar] [CrossRef]
- Matushevskiy, T.V. Method of separation of wave induced and turbulent motions in the near-surface layer of the ocean. Probl. Ocean. Dyn. 1975, 124–151. (In Russian) [Google Scholar]
- Lu, S.D.; Ho, W.C.; Lu, W.H.; Hu, C.K.; Chen, M.L.; Lien, Y.S. A research on the potential energy of offshore wind power and preferable offshore blocks in Taiwan. In Proceedings of the 36th Symposium on Electrical Power Engineering, Taoyuan, Taiwan, 12 December 2015; pp. 1–6. [Google Scholar]
- Saleem, Z. Alternatives and Modifications of Monoplie Foundation or Its Installation Technique for Noise Mitigation; TU Delft Report; Delft University of Technology: Delft, The Netherlands, 2011. [Google Scholar]
- Taiwan Power Company. The Feasibility Study of Offshore Wind Power in Changhua: Phase One; Taiwan Power Company: Taipei, Taiwan, 2016. [Google Scholar]
- Bureau of Energy, Ministry of Economic Affairs, Taiwan. Thousand Wind Turbines Project. 2018. Available online: http://www.twtpo.org.tw/gas.aspx?id=3268 (accessed on 2 March 2021).
- Su, M.S. The Rising Star: Cage Aquaculture. Sci. Dev. 2005, 385, 12–17. (In Chinese) [Google Scholar]
- Huang, C.C.; Tang, H.J. Numerical Simulation of Multiple Cage Net System. In Proceedings of the 24th Ocean Engineering Conference in Taiwan, November 2002; pp. 743–750. (In Chinese). [Google Scholar]
- Chan, C.H.; Chen, Y.B.; Huang, C.C. Study on a Compound Cage Aquaculture System in the Open Sea. In Proceedings of the 34th Ocean Engineering Conference in Taiwan, Tainan, Tainan, November 2012; pp. 237–242. (In Chinese). [Google Scholar]
- Chen, Y.T. Experimental Study on the Deformation of Cage under Wave-Current Action by Application 3-D Imagine Technique. Master’s Thesis, National Sun Yat-sen University, Kaohsiung, Taiwan, 2015. (In Chinese). [Google Scholar]













| Item | Model Setup |
|---|---|
| Area | 50 km × 35 km |
| Grid size | 0.5 m × 0.5 m |
| Number of grid points | 100,000 × 70,000 |
| Coordinate of the origin (TWD97) | 168,110, 2621,287 |
| Angle of deviation (counterclockwise from the north) | 60° |
| Time step size | 1.0 s |
| Wave condition [31] | SSW direction; H = 1.2 m; T = 6.5 s NNW direction; H = 3.0 m; T = 7.5 s |
| Period (s) | Wavelength (m) | Φ3.0 m | |
|---|---|---|---|
| Summer | 6.5 | 65.91 | 1/22 |
| Winter | 7.5 | 87.75 | 1/29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.-Y.; Fang, H.-M.; Chiang, Y.-C. Study on the Coexistence of Offshore Wind Farms and Cage Culture. Water 2021, 13, 1960. https://doi.org/10.3390/w13141960
Wang H-Y, Fang H-M, Chiang Y-C. Study on the Coexistence of Offshore Wind Farms and Cage Culture. Water. 2021; 13(14):1960. https://doi.org/10.3390/w13141960
Chicago/Turabian StyleWang, Hsing-Yu, Hui-Ming Fang, and Yun-Chih Chiang. 2021. "Study on the Coexistence of Offshore Wind Farms and Cage Culture" Water 13, no. 14: 1960. https://doi.org/10.3390/w13141960
APA StyleWang, H.-Y., Fang, H.-M., & Chiang, Y.-C. (2021). Study on the Coexistence of Offshore Wind Farms and Cage Culture. Water, 13(14), 1960. https://doi.org/10.3390/w13141960






