Karst Recharge Areas Identified by Combined Application of Isotopes and Hydrogeological Budget
Abstract
:1. Introduction
Objectives
2. Study Area Characterization
2.1. Geological and Hydrogeological Setting of the Study Area
- Carbonate Series (CS1): limestone-–dolomite series that forms the western Aurunci Mountains (stratigraphic alternation Palaeocene–Upper Lias; sedimentary marine facies);
- Kaolinitic Clays (KC): consisting of a polychrome clay–silty blanket (marginal marine siltstone facies);
- Clutch Breach (Br);
- Miocene Series (MS): formed by the grouping of two hydrogeologically similar formations (marine to continental–marine transitional facies);
- Deposits of the lower Pliocene (p) (continental–marine facies);
- Quaternary deposits (q): river and lake deposits and groundwater debris (continental facies).



2.2. Climate Framework
3. Materials and Methods
3.1. Data Collection
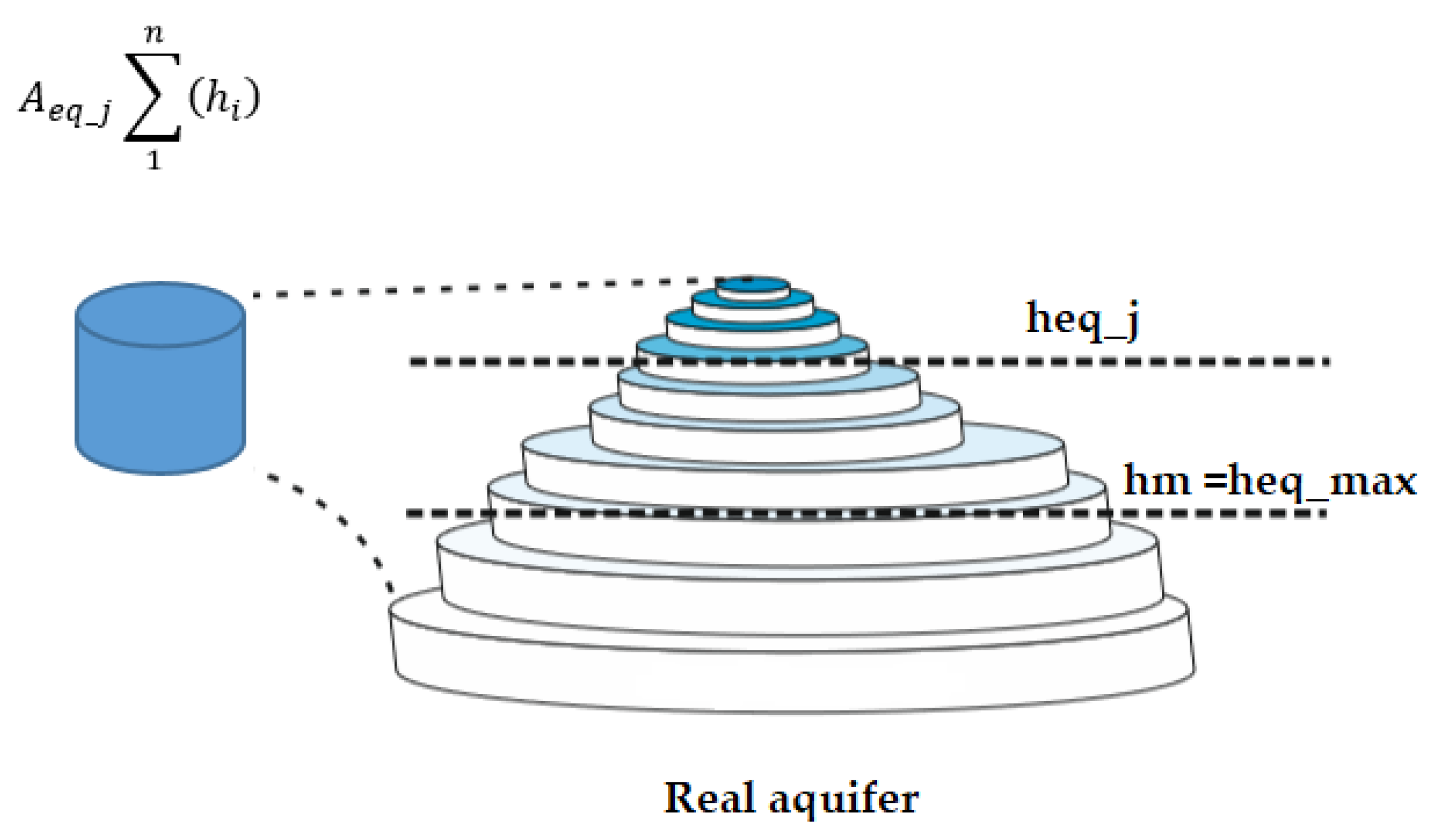
3.2. Average Recharge Areas Elevation (I-Elevation)
3.3. Isotope-Driven Model
3.3.1. Preliminary Check of the Rainfall Influence
- Temperature index:
- Monthly rainfall index:
- Forty eight hour rainfall index:
3.3.2. The Model
- With the increase in the rainfall intensity without an increase in the recharge area involved, the flow rate changes but the average recharge area elevation remains invariant;
- The same rainfall intensity involves different recharge areas; the flow rate remains invariant while the average recharge area elevation changes.
4. Results
4.1. Oxygen-18 and Deuterium Isotopes Analyses
4.2. Isotope-Driven Model Analyses
4.2.1. Rainfall Influence
4.2.2. Recharge Areas
4.3. Estimation of the Aquifer Monthly Supply Volume
4.4. Isotope-Driven Model vs. Hydrogeological Budget Applications
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fatchurohman, H.; Adji, T.N.; Haryono, E.; Wijayanti, P. Baseflow index assessment and master recession curve analysis for karst water management in Kakap Spring, Gunung Sewu. IOP Conf. Ser. Earth Environ. Sci. 2018, 148, 012029. [Google Scholar] [CrossRef] [Green Version]
- Goldscheider, N.; Chen, Z.; Auler, A.S.; Bakalowicz, M.; Broda, S.; Drew, D.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Stevanovic, Z.; et al. Global distribution of carbonate rocks and karst water resources. Hydrogeol. J. 2020, 28, 1661–1677. [Google Scholar] [CrossRef] [Green Version]
- Sappa, G.; Iacurto, S.; Ferranti, F.; De Filippi, F.M. Groundwater quality assessment in a karst coastal region of the West Aurunci Mountains (Central Italy). Geofluids 2019. [Google Scholar] [CrossRef] [Green Version]
- Filippini, M.; Squarzoni, G.; De Waele, J.; Fiorucci, A.; Vigna, B.; Grillo, B.; Riva, A.; Rossetti, S.; Zini, L.; Casagrande, G.; et al. Differentiated spring behavior under changing hydrological conditions in an alpine karst aquifer. J. Hydrol. 2018, 556, 572–584. [Google Scholar] [CrossRef]
- Şener, A.; Yolcubal, I.; Ercan, S. Determination of recharge, storage and flow characteristics of a karst aquifer using multi-method approaches (Kocaeli, Turkey. Hydrogeol. J. 2020, 28, 2141–2157. [Google Scholar] [CrossRef]
- White, W.B. Geomorphology and Hydrology of Karst Terrains; Oxford University: Oxford, UK, 1988. [Google Scholar]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Mook, W.G. Environmental Isotopes in the Hydrological Cycle; IAEA Publish: Vienna, Austria, 2000; pp. 1–291. [Google Scholar]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Jasechko, S. Global Isotope Hydrogeology―Review. Rev. Geophys. 2019, 57, 835–965. [Google Scholar] [CrossRef]
- Longinelli, A.; Selmo, E. Isotope geochemistry and the water cycle: A short review with special emphasis on Italy. Cart. Geol. D’Italia XC 2010, 90, 153–164. [Google Scholar]
- Giustini, F.; Brilli, M.; Patera, A. Mapping oxygen stable isotopes of precipitation in Italy. J. Hydrol. Reg. Stud. 2016, 8, 162–181. [Google Scholar] [CrossRef] [Green Version]
- Calligaris, C.; Mezga, K.; Slejko, F.F.; Urbanc, J.; Zini, L. Groundwater characterization by means of conservative (δ18O and δ2H) and non-conservative (87Sr/86Sr) isotopic values: The classical karst region aquifer case (Italy–Slovenia). Geosciences 2018, 8, 321. [Google Scholar] [CrossRef] [Green Version]
- Phillips, F.M. The use of isotopes and environmental tracers in subsurface hydrology. Rev. Geophys. 1995, 33, 1029–1033. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- González-Trinidad, J.; Pacheco-Guerrero, A.; Júnez-Ferreira, H.; Bautista-Capetillo, C.; Hernández-Antonio, A. Identifying groundwater recharge sites through environmental stable isotopes in an alluvial aquifer. Water 2017, 9, 569. [Google Scholar] [CrossRef] [Green Version]
- Sappa, G.; Vitale, S.; Ferranti, F. Identifying karst aquifer recharge areas using environmental isotopes: A case study in central Italy. Geosciences 2018, 8, 351. [Google Scholar] [CrossRef] [Green Version]
- Wachniew, P. Environmental tracers as a tool in groundwater vulnerability assessment. Acque Sotter. Ital. J. Groundw. 2015, 4, 19–25. [Google Scholar] [CrossRef]
- Arellano, L.N.; Good, S.P.; Sánchez-murillo, R.; Jarvis, W.T.; Noone, D.C.; Finkenbiner, C.E. Bayesian estimates of the mean recharge elevations of water sources in the Central America region using stable water isotopes. J. Hydrol. Reg. Stud. 2020, 32, 100739. [Google Scholar] [CrossRef]
- Vespasiano, G.; Apollaro, C.; De Rosa, R.; Muto, F.; Larosa, S.; Fiebig, J.; Mulch, A.; Marini, L. Applied Geochemistry The Small Spring Method (SSM) for the de fi nition of stable isotope e elevation relationships in Northern Calabria (Southern Italy). Appl. Geochemistry 2015, 63, 333–346. [Google Scholar] [CrossRef]
- Iacurto, S.; Grelle, G.; Filippi, F.M.D.; Sappa, G. Karst spring recharge areas and discharge relationship by oxygen-18 and deuterium isotopes analyses: A case study in southern latium region, Italy. Appl. Sci. 2020, 10, 1882. [Google Scholar] [CrossRef] [Green Version]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Civita, M.; De Maio, M.; Vigna, B. Una metodologia GIS per la valutazione della ricarica attiva degli acquiferi. In Proceedings of the Convegno Nazionale sulla Protezione e Gestione delle Acque Sotterranee, Parma, Italy, 13–15 October 1999. [Google Scholar]
- Tulipano, L.; Sappa, G.; Pietrellli, G. Groundwater Budget of Maiella (Italy). In Proceedings of the Balancing the groundwater Budget, Darwin, Australia, 12–17 May 2002; pp. 1–7. [Google Scholar]
- Canora, F.; Sdao, F. Hydrogeological characterization and groundwater vulnerability to pollution assessment of the high basento river valley carbonate hydrostructure (Basilicata, Southern Italy). Ital. J. Eng. Geol. Environ. 2020, 20, 25–44. [Google Scholar] [CrossRef]
- Sappa, G.; De Filippi, F.M.; Iacurto, S.; Grelle, G. Evaluation of minimum karst spring discharge using a simple rainfall-input model: The case study of Capodacqua di Spigno Spring (Central Italy). Water 2019, 11, 807. [Google Scholar] [CrossRef] [Green Version]
- Ialongo, N. Studio Idrogeologico Sorgente Mazzoccolo; Relazione Idrogeologica: Formia, Italy, 1983. [Google Scholar]
- Baldi, A.M.; Marzocchi, A.; Ricci, A.; Mencarini, S.; Vecellio, L.; Graziosi, A.; Di Mauro, G. La torbidità alle captazioni idropotabili dei monti Aurunci. In Proceedings of the Aquifer Vulnerability and Risk, Parma, Italy, 21–23 September 2005. [Google Scholar]
- Bergomi, C.; Catenacci, V.; Cestari, G.; Manfredini, M.; Manganelli, V. Note Illustrative della Carta Geologica d’Italia, alla Scala 1:100.000—Foglio 171 Gaeta e Vulcano di Roccamonfina; Ercolano, Poligrafica & Cartevalori: Naples, Italy, 1969. [Google Scholar]
- Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef]
- NEMS (National Environmental Monitoring Standards). Open Channel Flow Measurement; Version 1.1. 2013. Available online: https://www.lawa.org.nz/media/16578/nems-open-channel-flow-measurement-2013-06.pdf (accessed on 14 July 2021).
- Sappa, G.; Ferranti, F.; Iacurto, S.; De Filippi, F.M. Effects of climate change on groundwater feeding the Mazzoccolo and Capodacqua di Spigno Springs (Central Italy): First quantitative assestments. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management, SGEM, Albena, Bulgaria, 30 June–9 July 2018; Volume 18. [Google Scholar]
- White, W.B. Karst hydrology: Recent developments and open questions. Eng. Geol. 2002, 65, 85–105. [Google Scholar] [CrossRef]
- Yang, Q.; Mu, H.; Guo, J.; Bao, X.; Martín, J.D. Temperature and rainfall amount effects on hydrogen and oxygen stable isotope in precipitation. Quat. Int. 2019, 519, 25–31. [Google Scholar] [CrossRef]
- Bard, E.; Delaygue, G.; Rostek, F.; Antonioli, F.; Silenzi, S.; Schrag, D.P. Hydrological conditions over the western Mediterranean basin during the deposition of the cold Sapropel 6 (ca. 175 Kyr BP). Earth Planet. Sci. Lett. 2002, 202, 481–494. [Google Scholar] [CrossRef]
- Higgins, P.; MacFadden, B.J. “Amount Effect” recorded in oxygen isotopes of Late Glacial horse (Equus) and bison (Bison) teeth from the Sonoran and Chihuahuan deserts, southwestern United States. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2004, 206, 337–353. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Zhao, W.; Wang, Y. Probability modeling of precipitation extremes over two river basins in northwest of China. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Bono, R.; Gonfiantini, R.; Alessio, M.; Fiori, C.; D’Amelio, C. Stable isotopes (δ18O, δ2H) and tritium in precipitation: Results and comparison with groundwater perched aquifers in central Italy. In Isotopic Composition of Precipitation in the Mediterranean Basin in Relation to Air Circulation Patterns and Climate, Final Report a Coordinated Research Project, 2000–2004; Isotope Hydrology Section, International Atomic Energy Agency: Vienna, Austria, 2005. [Google Scholar]
- Dumas, D. The impact of forests on the evolution of water resources in the mid-altitude Alps from the middle of the 19th century (Chartreuse massif, France). Rev. Géographie Alp. 2012. [Google Scholar] [CrossRef]
- Palcsu, L.; Gessert, A.; Túri, M.; Kovács, A.; Futó, I.; Orsovszki, J.; Puskás-Preszner, A.; Temovski, M.; Koltai, G. Long-term time series of environmental tracers reveal recharge and discharge conditions in shallow karst aquifers in Hungary and Slovakia. J. Hydrol. Reg. Stud. 2021, 36, 100858. [Google Scholar] [CrossRef]
- Jódar, J.; Herms, I.; Lambán, L.J.; Martos-Rosillo, S.; Herrera-Lameli, C.; Urrutia, J.; Soler, A.; Custodio, E. Isotopic content in high mountain karst aquifers as a proxy for climate change impact in Mediterranean zones: The Port del Comte karst aquifer (SE Pyrenees, Catalonia, Spain). Sci. Total Environ. 2021, 790, 148036. [Google Scholar] [CrossRef] [PubMed]
- Tulipano, L.; Fidelibus, D.M.; Panagopoulos, A. Groundwater Management of Coastal Karstic Aquifers: Final Report; EU Publications Office: Luxemburg, 2005. [Google Scholar]













| Date | δ18O (‰ VSMOW) | δ2H (‰ VSMOW) | Qe (l/s) | Qm (l/s) | Qs (l/s) |
|---|---|---|---|---|---|
| 26 April 2018 | −7.22 | −40.09 | 520 | 915 | 1435 |
| 25 May 2018 | −7.24 | −40.35 | 506 | 780 | 1286 |
| 27 June 2018 | −7.29 | −41.02 | 537 | 490 | 1027 |
| 30 July 2018 | −7.32 | −41.07 | 543 | 251 | 794 |
| 29 August 2018 | −7.27 | −40.94 | 554 | 159 | 713 |
| 1 October 2018 | −7.37 | −41.20 | 489 | 168 | 657 |
| 8 November 2018 | −6.91 | −37.92 | 454 | 1657 | 2111 |
| 18 December 2018 | −6.78 | −37.57 | 486 | 2164 | 2650 |
| 18 January 2019 | −7.14 | −39.80 | 503 | 829 | 1333 |
| 19 February 2019 | −7.23 | −40.29 | 504 | 1050 | 1555 |
| 20 March 2019 | −7.26 | −40.58 | 454 | 837 | 1291 |
| 30 April 2019 | −7.23 | −40.09 | 433 | 558 | 991 |
| 29 May 2019 | −6.74 | −37.15 | 435 | 2500 | 2935 |
| 26 June 2019 | −7.37 | −41.22 | 458 | 671 | 1129 |
| 25 July 2019 | −7.36 | −40.54 | 524 | 337 | 861 |
| 29 August 2019 | −7.31 | −40.47 | 534 | 102 | 636 |
| 27 September 2019 | −7.40 | −40.73 | 487 | 102 | 589 |
| 30 October 2019 | −7.49 | −41.60 | 466 | 52 | 518 |
| 27 November 2019 | −6.43 | −36.05 | 449 | 2242 | 2690 |
| 23 December 2019 | −6.95 | −39.00 | 425 | 3000 | 3425 |
| 28 January 2020 | −6.76 | −37.63 | 443 | 1440 | 1883 |
| 27 February 2020 | −7.17 | −39.80 | 450 | 784 | 1234 |
| 28 April 2020 | −7.22 | −39.86 | 417 | 595 | 1012 |
| 25 May 2020 | −7.30 | −40.54 | 421 | 550 | 971 |
| SS Cosma e Damiano | Gaeta | Itri | Esperia | |
|---|---|---|---|---|
| iJanuary | 2.10 | 2.96 | 2.14 | 1.81 |
| iFebruary | 2.54 | 3.22 | 2.33 | 2.24 |
| iMarch | 3.55 | 4.26 | 3.41 | 3.50 |
| iApril | 4.96 | 5.64 | 4.71 | 5.04 |
| iMay | 6.65 | 7.40 | 6.34 | 6.73 |
| iJune | 9.51 | 10.13 | 9.24 | 9.81 |
| iJuly | 10.94 | 12.01 | 11.04 | 11.83 |
| iAugust | 11.35 | 12.45 | 11.45 | 12.19 |
| iSeptember | 9.03 | 9.94 | 8.61 | 8.76 |
| iOctober | 6.91 | 7.84 | 6.76 | 6.50 |
| iNovember | 4.63 | 5.48 | 4.48 | 4.08 |
| iDecember | 2.43 | 3.46 | 2.81 | 2.19 |
| I | 74.60 | 84.78 | 73.33 | 74.69 |
| Imean | 76.85 | |||
| A | 1.86 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iacurto, S.; Grelle, G.; De Filippi, F.M.; Sappa, G. Karst Recharge Areas Identified by Combined Application of Isotopes and Hydrogeological Budget. Water 2021, 13, 1965. https://doi.org/10.3390/w13141965
Iacurto S, Grelle G, De Filippi FM, Sappa G. Karst Recharge Areas Identified by Combined Application of Isotopes and Hydrogeological Budget. Water. 2021; 13(14):1965. https://doi.org/10.3390/w13141965
Chicago/Turabian StyleIacurto, Silvia, Gerardo Grelle, Francesco Maria De Filippi, and Giuseppe Sappa. 2021. "Karst Recharge Areas Identified by Combined Application of Isotopes and Hydrogeological Budget" Water 13, no. 14: 1965. https://doi.org/10.3390/w13141965
APA StyleIacurto, S., Grelle, G., De Filippi, F. M., & Sappa, G. (2021). Karst Recharge Areas Identified by Combined Application of Isotopes and Hydrogeological Budget. Water, 13(14), 1965. https://doi.org/10.3390/w13141965








