The Spatial Variation Mechanism of Size, Velocity, and the Landing Angle of Throughfall Droplets under Maize Canopy
Abstract
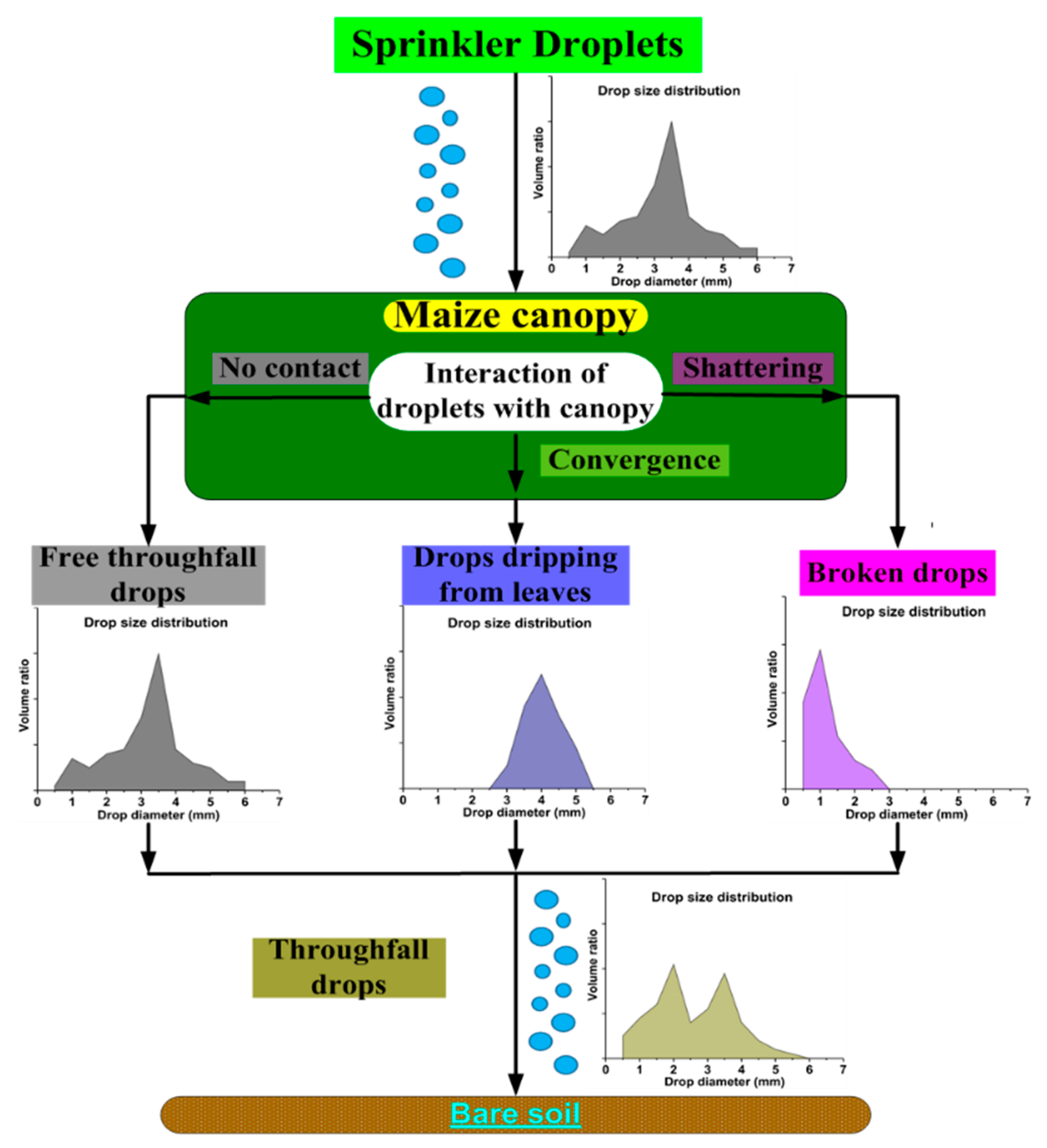
:1. Introduction
2. Materials and Methods
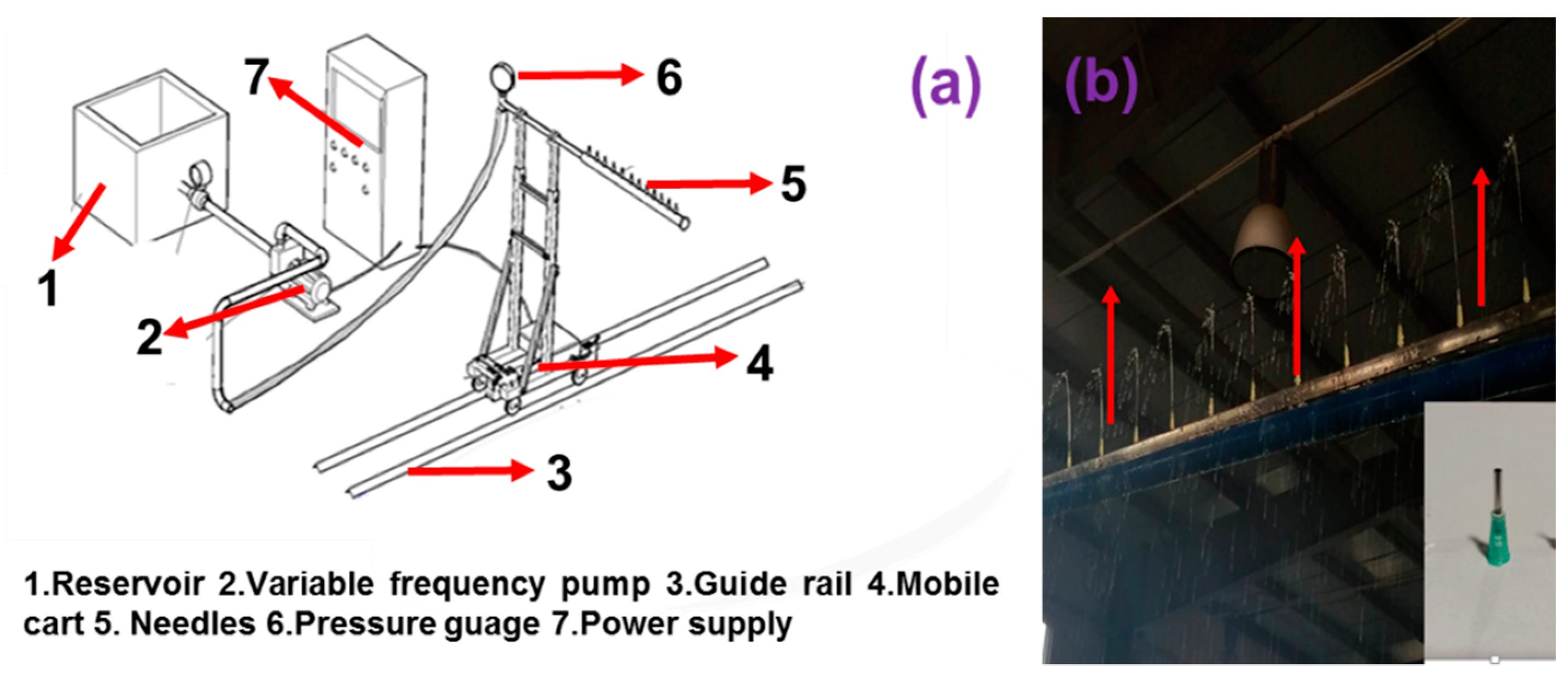
2.1. Experimental Device
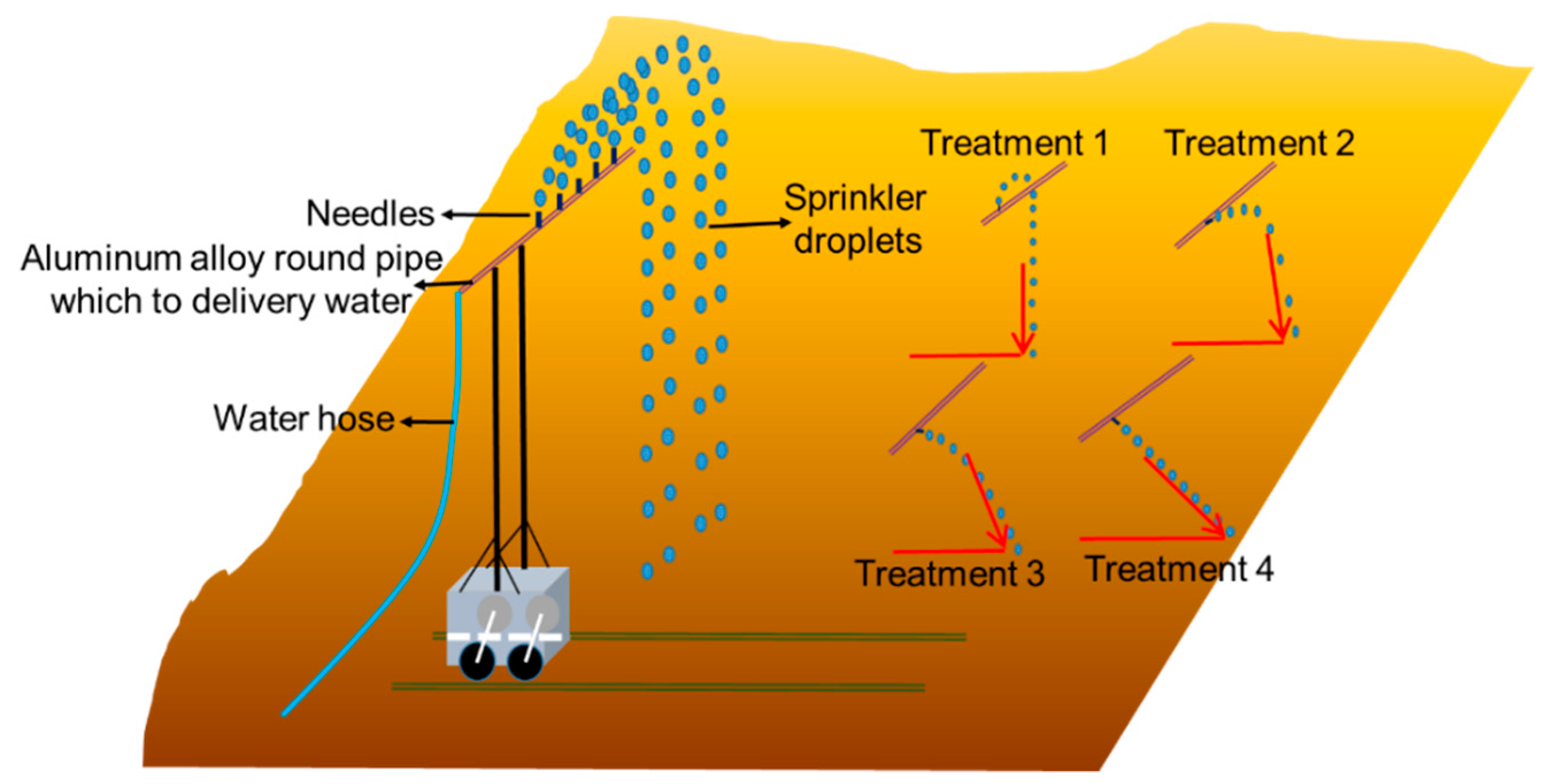
2.1.1. Droplet Landing Angle Control Facility
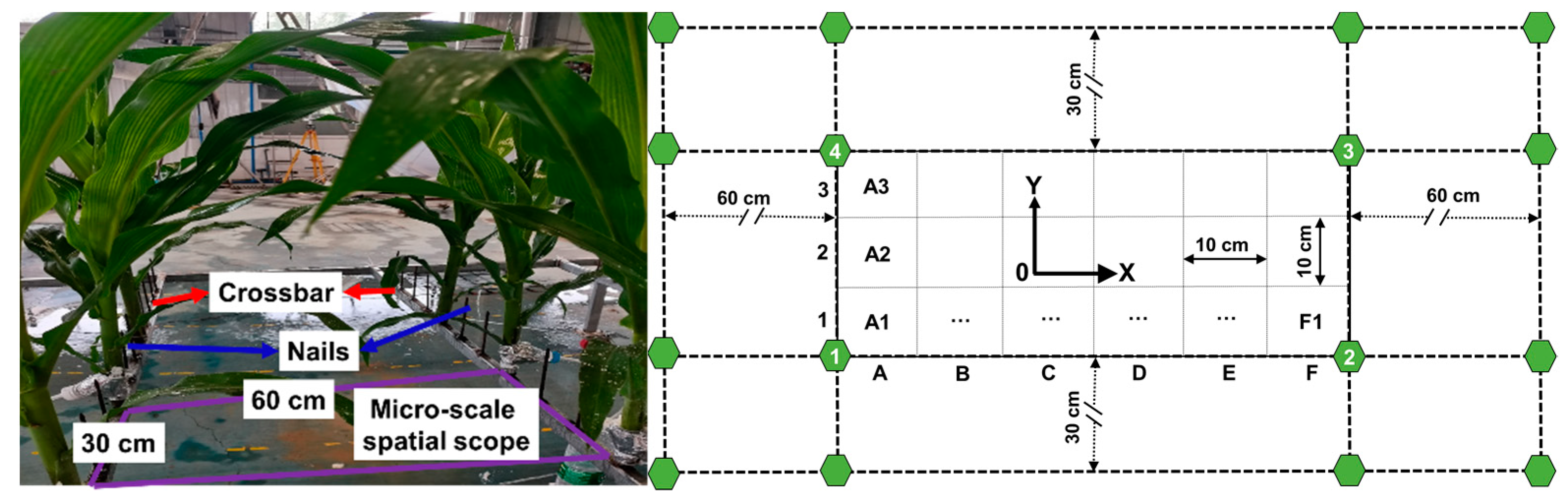
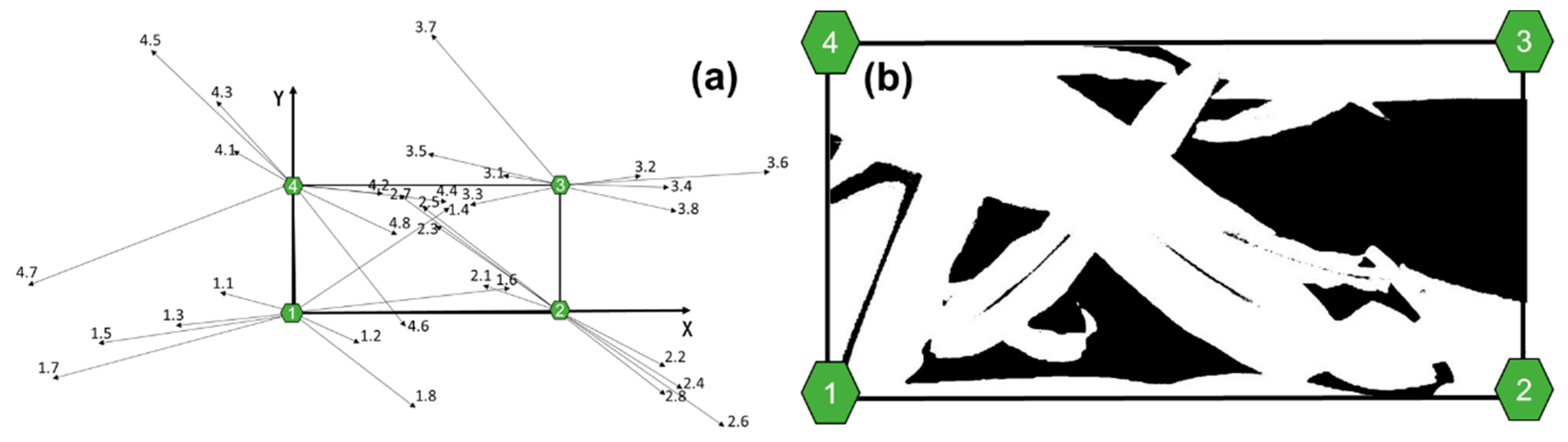
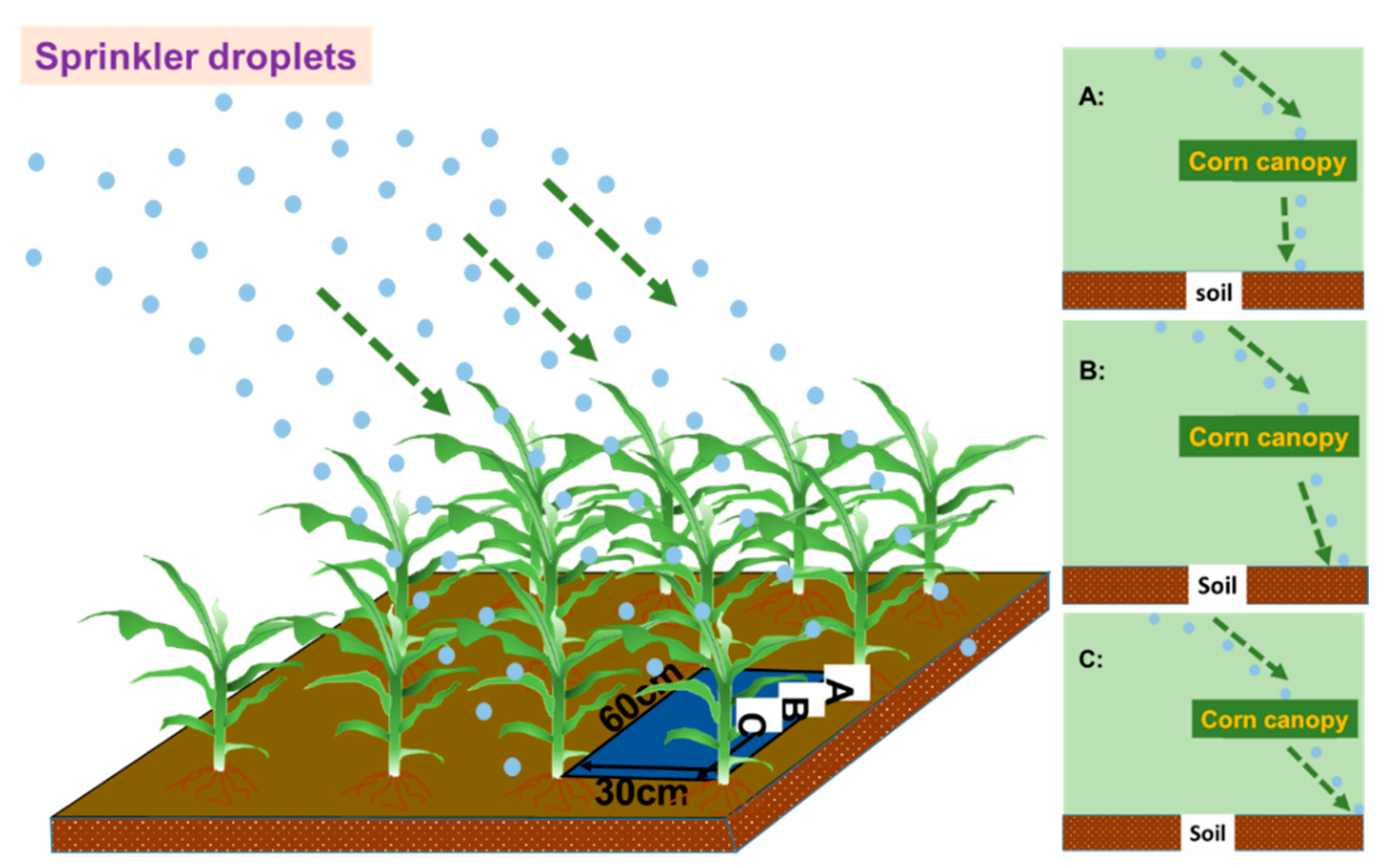
2.1.2. Layout of Maize Plants and Measuring Points
2.2. Experimental Design
2.3. Measurement Parameters and Methods
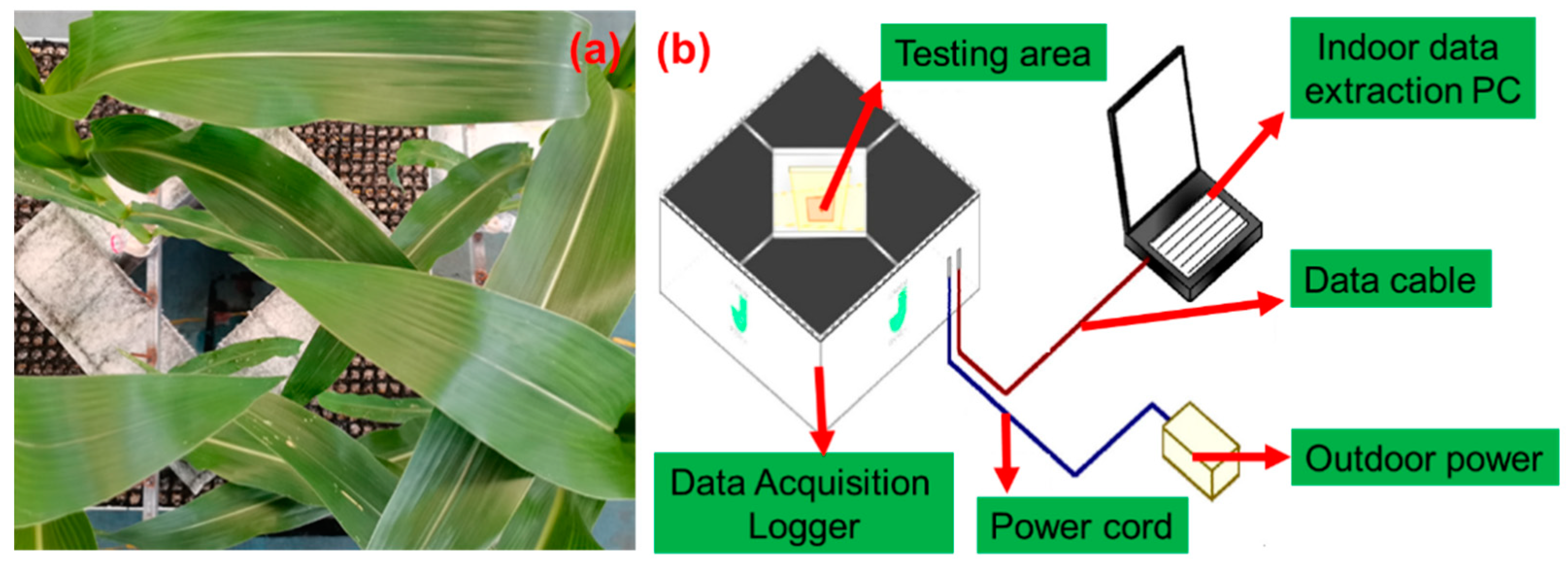
2.3.1. Drop Size and Velocity
- (1)
- Individual droplet size
- (2)
- Horizontal and vertical velocity of a single droplet
2.3.2. Morphological Parameters of Maize Canopy
- (1)
- Leaf height and low: Height of the highest and lowest point of the maize leaf to the ground (cm).
- (2)
- Leaf height distance: The distance from the highest point of the maize leaf to the stalk (cm), measured with a stainless steel tape measurer (accuracy 0.1 cm).
- (3)
- Leaf azimuth: The angle formed by the central vein of the leaf and the positive direction of the X-axis (°), counterclockwise is positive, and the value range 0–360°. A protractor was used to measure (accuracy 0.1°).
- (4)
- Maize canopy projection was measured using Canopeo software (which needs to be installed in advance on the cell phone) [30]. The measured result showed a canopy shade of 53.96% within the micro-scale space constituted by the maize plants selected for this study.
2.4. Calculation Methods
- (1)
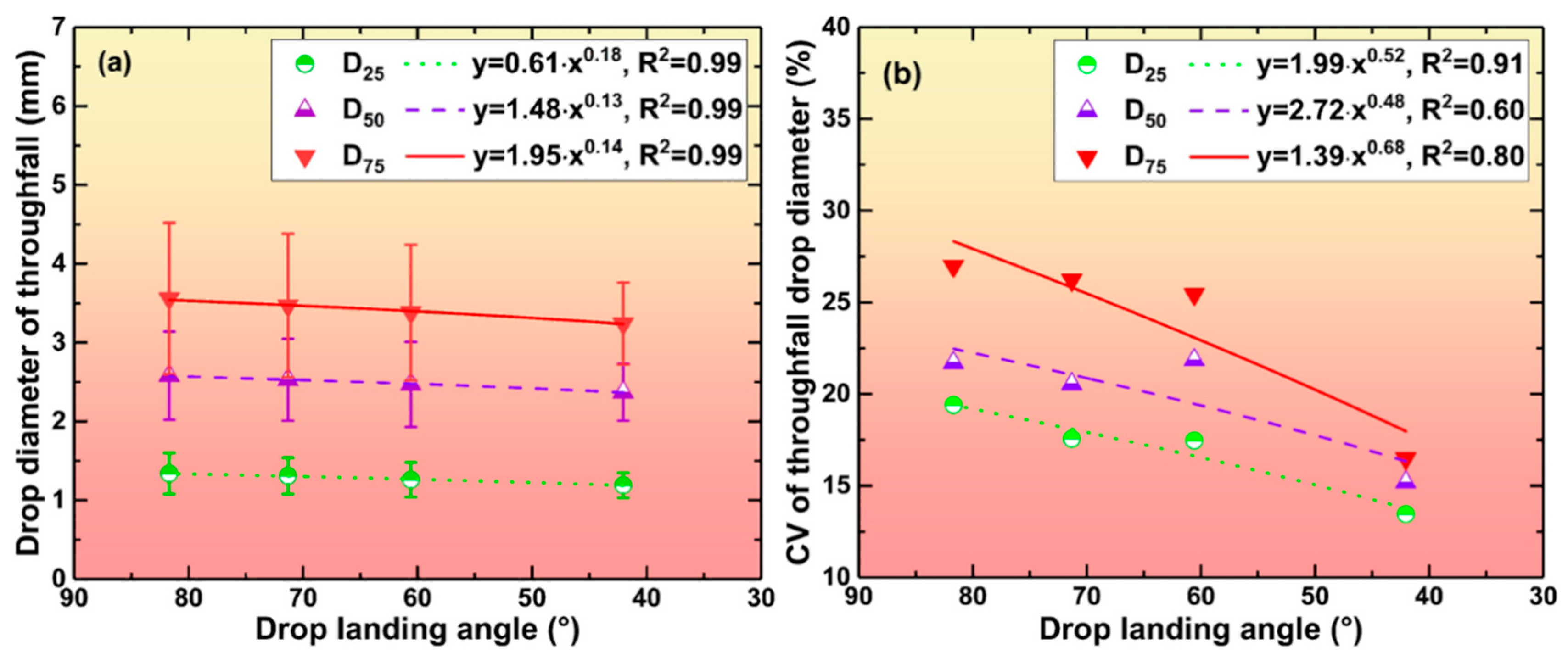
- Droplet size: The median diameter method was used in this paper to calculate the drop diameter of throughfall. The cumulative frequency of the drop size distribution was calculated by the weighted averaging method. When the cumulative frequency of the drop size distribution was 50%, the corresponding drop diameter was defined as the drop size (D50, mm) [31]. D25 and D75 were the corresponding droplet size when the cumulative frequency of the drop size distribution was 25% and 75%, respectively [31]. Their computational approach was similar to D50.
- (2)
- Single droplet velocity: The resultant velocity was related to the horizontal and vertical velocity of a drop. Its calculation formula was shown as the following equation.where is the drop velocity (m·s−1), is the vertical velocity, and is the horizontal velocity.
- (3)
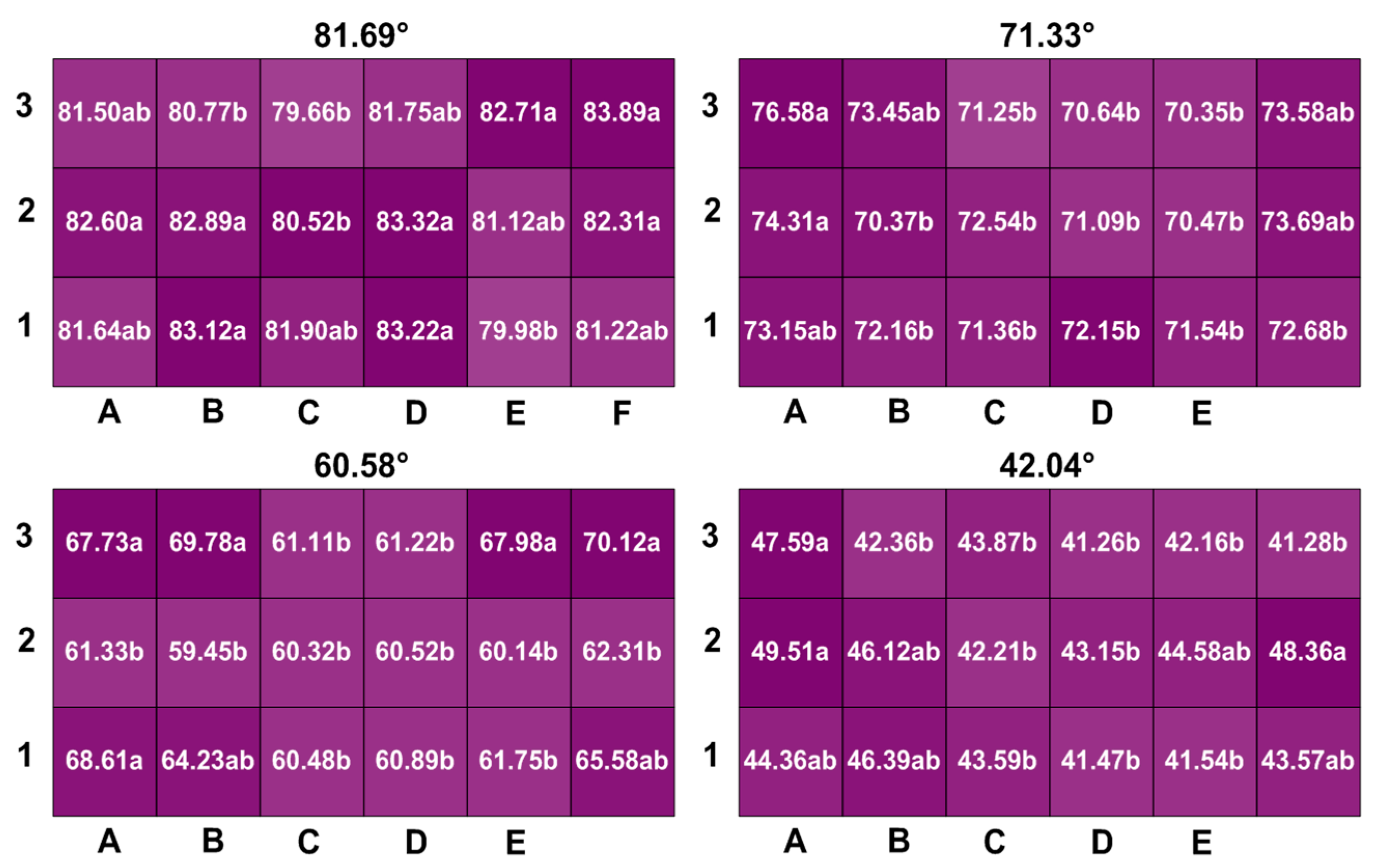
- Individual droplet landing angle: Based on the horizontal and vertical velocities of a droplet collected by 2DVD, its landing angle can be calculated by Equation (2).where is the landing angle (°).In this study, the drop size distribution at different measurement points was graded at 0.50 mm interval, and the average value of all droplet angles in a diameter graduation range, in which there was the maximum kinetic energy, was used as the drop landing angle [32]. Consequently, after calculating, the droplet landing angles for treatments 1, 2, 3, and 4 are 81.69°, 71.33°, 60.58°, and 42.04°, respectively.
- (4)
- Single drop kinetic energy: The formula for calculating the kinetic energy of a single drop was shown as the following equation.where is the single drop kinetic energy (J), d is the drop diameter (mm), and is the water density (kg·m−3).
- (5)
- Drop velocity: In this paper, the equivalent velocity was used to assess the velocity of the throughfall droplets population. The equivalent velocity was related to the total kinetic energy and total quality of the droplets population, and its value was calculated as follows.The resultant velocity, horizontal and vertical velocities of the throughfall drop population, were obtained using Equation (4), except that the horizontal and vertical velocities of the droplet population were calculated using the sum of the kinetic energy of the droplet population in the horizontal and vertical directions.
- (6)
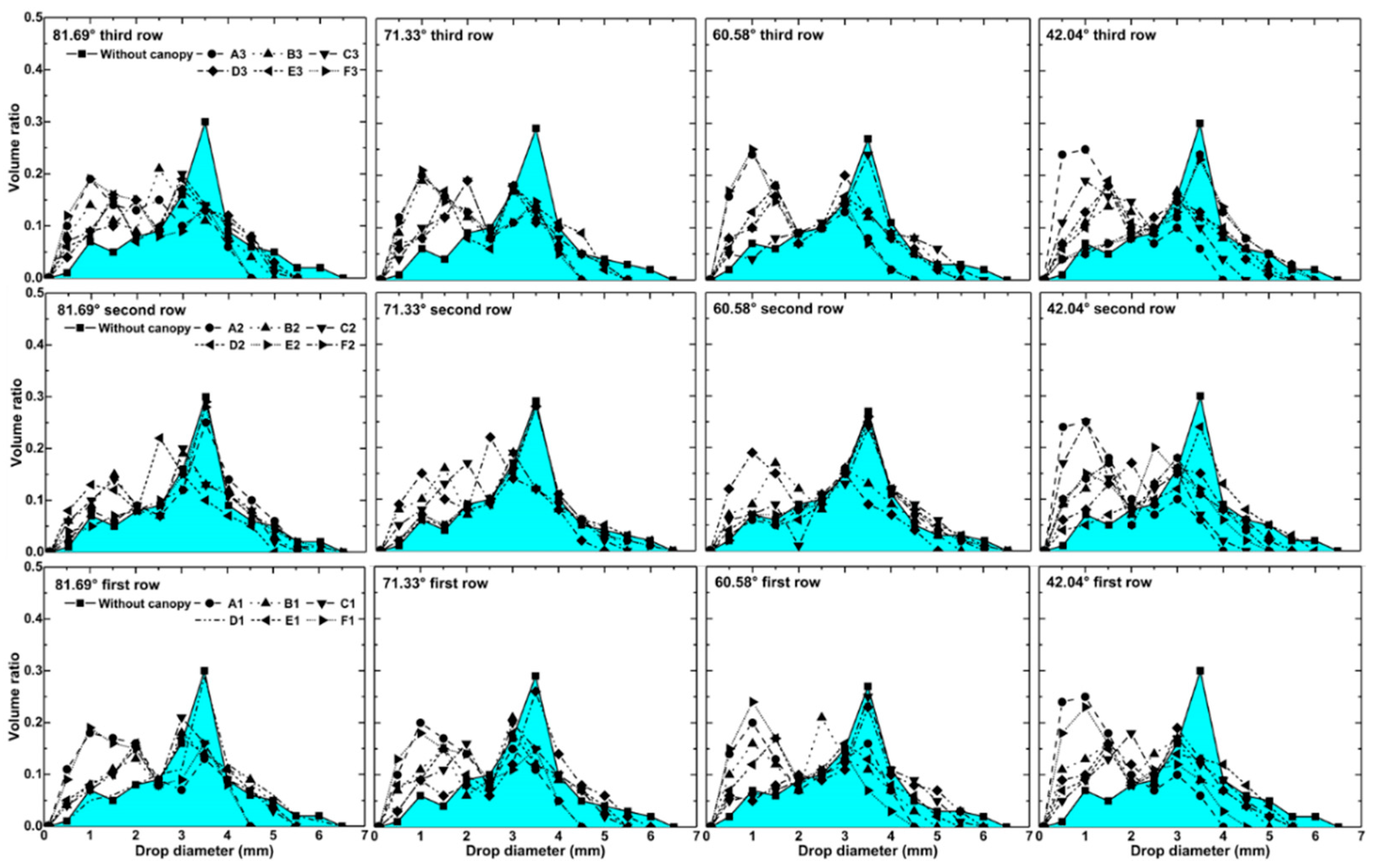
- Drop size distribution: The drop size distribution of the drop population was generally characterized by droplet number density (mm−1·m−3) and relative droplet volume (dimensionless) [31]. The drop size distribution at the measurement point in this paper was described by droplet relative volume (i.e., volume ratio) and its calculation formula was shown below.where i represents the ith drop in the drop group; j represents the jth drop diameter classification, and the size of each droplet classification is set to 0.50 mm in this study, Nj is the number of droplets in the jth diameter classification, Vi is the volume of the ith droplet in the drop group; represents the total volume of droplets in the drop group.
2.5. Data Analysis
3. Results and Discussion
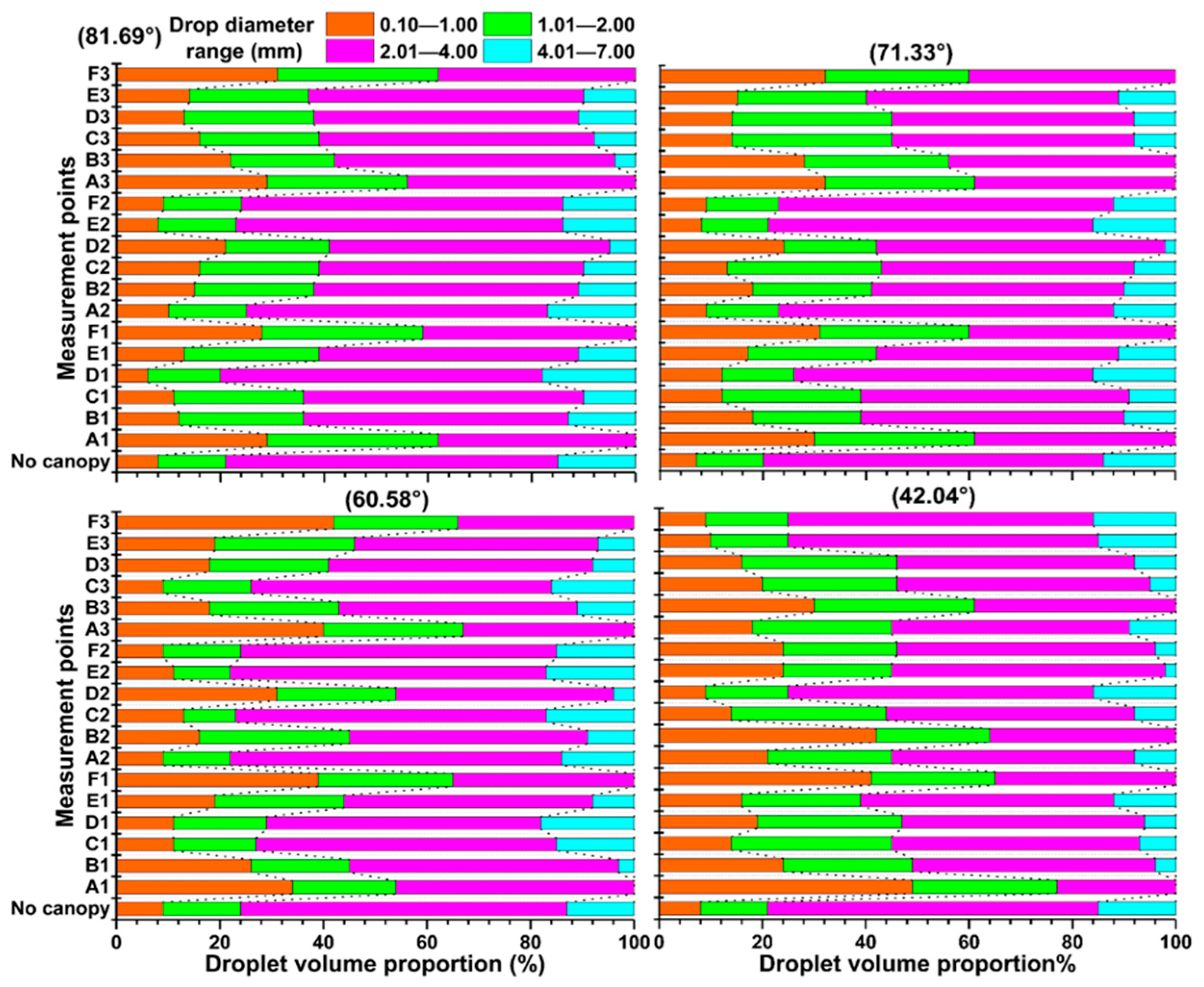
3.1. Spatial Variation Mechanism of Throughfall Drop Size
3.1.1. Variation of Throughfall Drop Size
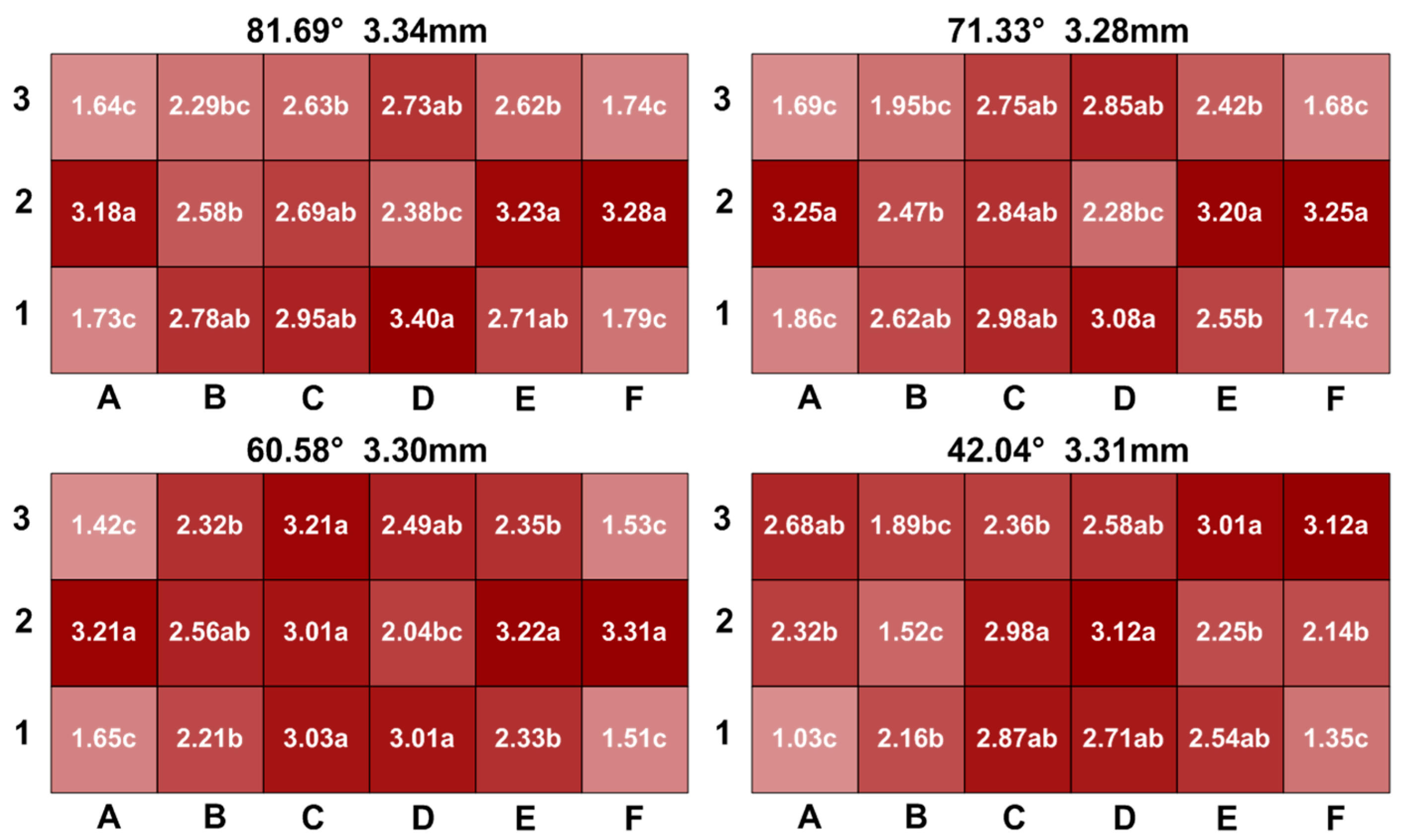
3.1.2. Spatial Variation of Throughfall Drop Size
3.1.3. Spatial Variation of Drop Size Distribution of Throughfall
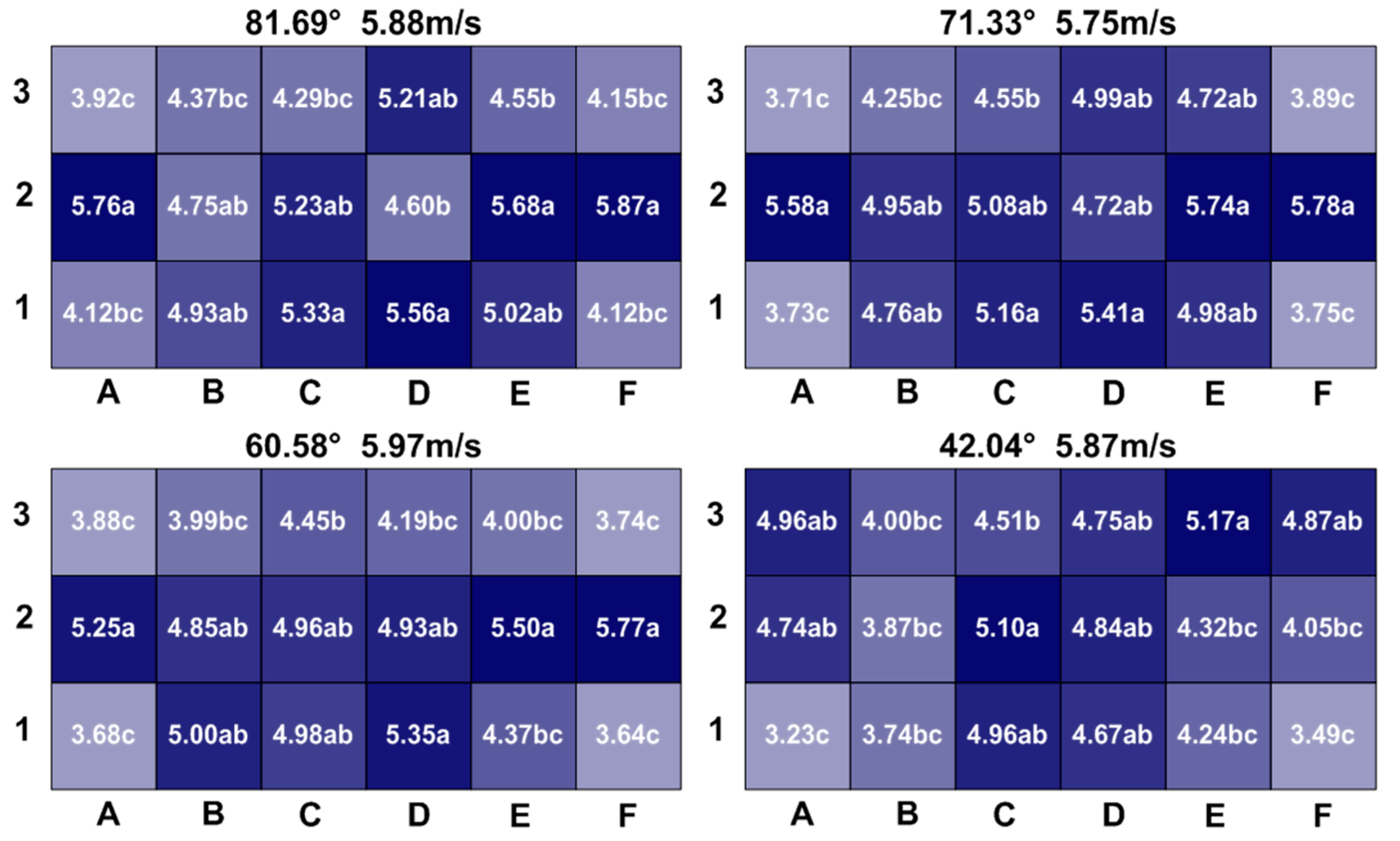
3.2. Spatial Variation Mechanism of Throughfall Drop Velocity
3.2.1. Variation of Throughfall Drop Velocity
3.2.2. Spatial Variation of Throughfall Drop Velocity
3.2.3. Spatial Variation of Drop Velocity Distribution of Throughfall
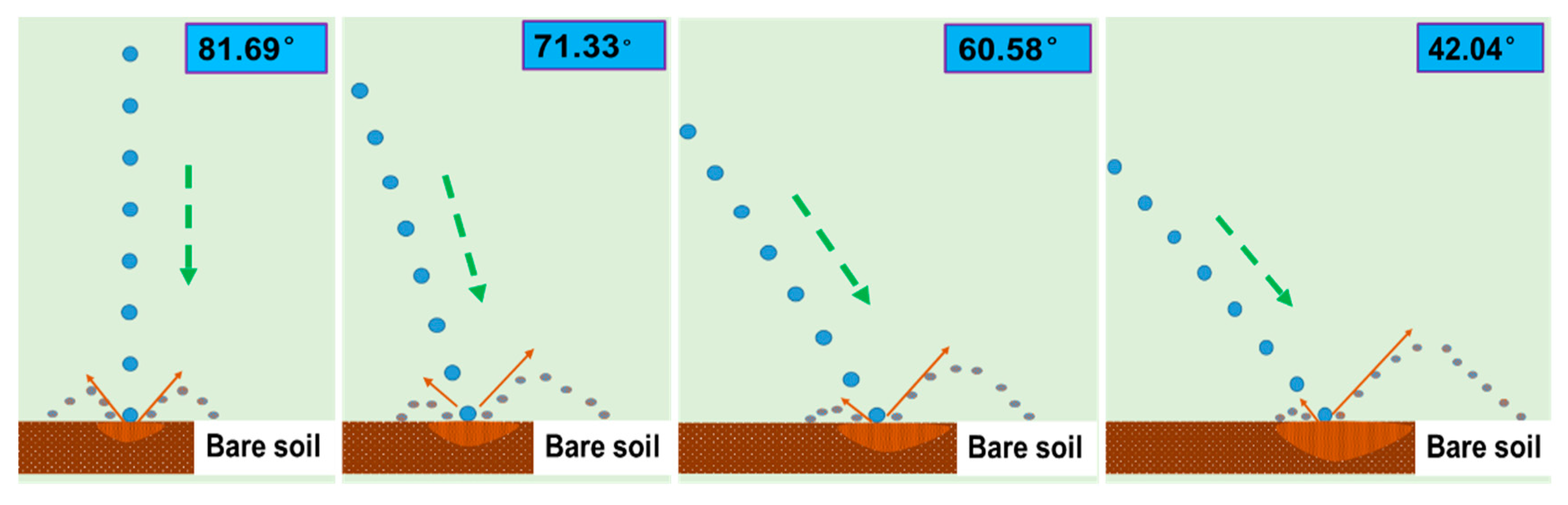
3.3. Spatial Variation Mechanism of Throughfall Drop Landing Angle
3.3.1. Variation of Throughfall Drop Landing Angle
3.3.2. Spatial Variation of Throughfall Droplets Landing Angle
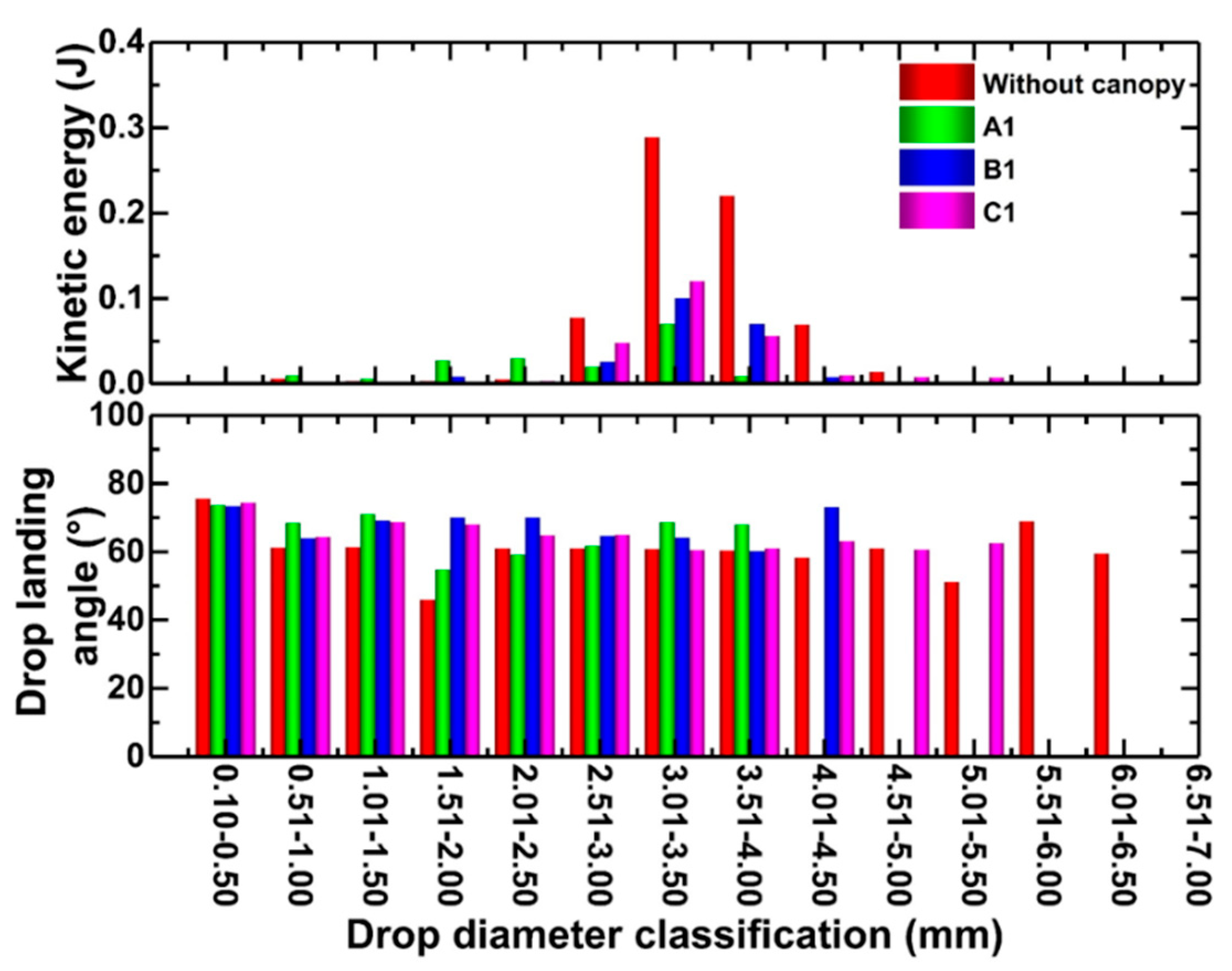
3.3.3. Spatial Variation of Drop Velocity and Kinetic Energy of Throughfall
4. Conclusions
- (a)
- Maize canopy and the decreasing of the sprinkler irrigation droplets landing angle had a positive and notable effect on reducing the size and velocities of penetrating rain droplets. However, the throughfall droplets’ landing angles were only minor variations.
- (b)
- When the sprinkler irrigation droplets landing angle was >45°, the spatial distribution of throughfall droplets’ size and velocities corresponded well with the canopy structure and leaf projection area, i.e., the further away from the maize stalk, the larger the size and velocity of throughfall droplets. Nevertheless, if the landing angle of sprinkler irrigation droplets was <45°, the spatial distribution mentioned above was mainly affected by the droplet landing angle.
- (c)
- The spatial variations of size and velocities of throughfall droplets at different measurement points was attributed to the change of the larger droplets’ volume proportion and the equivalent velocity. Although the maize leaves had a certain degree of perturbation effect on the velocities and kinetic energy of the larger kinetic energy droplets, the flight path of these drops did not need to be altered significantly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chen, R.; Li, H.; Wang, J.; Guo, X. Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers. Water 2020, 12, 2904. [Google Scholar] [CrossRef]
- Ge, M.; Wu, P.; Zhu, D.; Ames, D.P. Comparison between sprinkler irrigation and natural rainfall based on droplet diame-ter. Span. J. Agric. Res. 2016, 14, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Nanko, K.; Mizugaki, S.; Onda, Y. Estimation of soil splash detachment rates on the forest floor of an unmanaged Japanese cypress plantation based on field measurements of throughfall drop sizes and velocities. Catena 2008, 72, 348–361. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, D.; Kohl, R.A. Infiltration Response to Kinetic Energy. Trans. ASAE 1987, 30, 108–111. [Google Scholar] [CrossRef]
- Agassi, M.; Bloem, D.; Ben-Hur, M. Effect of drop energy and soil and water chemistry on infiltration and erosion. Water Resour. Res. 1994, 30, 1187–1193. [Google Scholar] [CrossRef]
- Yan, H.J.; Bai, G.; He, J.Q.; Lin, G. Influence of droplet kinetic energy flux density from fixed spray-plate sprinklers on soil in-filtration, runoff and sediment yield. Biosyst. Eng. 2011, 110, 213–221. [Google Scholar] [CrossRef]
- Erpul, G.; Gabriels, D.; Cornelis, W.; Samray, H.; Guzelordu, T. Sand detachment under rains with varying angle of incidence. Catena 2008, 72, 413–422. [Google Scholar] [CrossRef] [Green Version]
- Mizugaki, S.; Nanko, K.; Onda, Y. The effect of slope angle on splash detachment in an unmanaged Japanese cypress plan-tation forest. Hydrol. Process. 2010, 24, 576–587. [Google Scholar] [CrossRef]
- Ghahramani, A.; Ishikawa, Y.; Gomi, T.; Miyata, S. Downslope soil detachment-transport on steep slopes via rain splash. Hydrol. Process. 2011, 25, 2471–2480. [Google Scholar] [CrossRef]
- Salles, C.; Poesen, J.; Sempere-Torres, D. Kinetic energy of rain and its functional relationship with intensity. J. Hydrol. 2002, 257, 256–270. [Google Scholar] [CrossRef]
- Zheng, J.; Fan, J.L.; Zhang, F.; Yan, S.; Wu, Y.; Lu, J.; Guo, J.; Cheng, M.; Pei, Y. Throughfall and stemflow heterogeneity under the maize canopy and its effect on soil water distribution at the row scale. Sci. Total Environ. 2019, 660, 1367–1382. [Google Scholar] [CrossRef]
- Zapata, N.; Salvador, R.; Latorre, B.; Paniagua, P.; Medina, E.T.; Playán, E. Effect of a growing maize canopy on solid-set sprinkler irrigation: Kinetic energy dissipation and water partitioning. Irrig. Sci. 2021, 39, 329–346. [Google Scholar] [CrossRef]
- Wainwright, J.; Parsons, A.J.; Abrahams, A.D. Rainfall energy under creosotebush. J. Arid Environ. 1999, 43, 111–120. [Google Scholar] [CrossRef]
- Brandt, J. The Transformation of Rainfall Energy by a Tropical Rain Forest Canopy in Relation to Soil Erosion. J. Biogeogr. 1988, 15, 41. [Google Scholar] [CrossRef]
- Finney, H.J. The effect of crop covers on rainfall characteristics and splash detachment. J. Agric. Eng. Res. 1984, 29, 337–343. [Google Scholar] [CrossRef]
- Ma, B.; Yu, X.; Ma, F.; Li, Z.; Wu, F. Effects of Crop Canopies on Rain Splash Detachment. PLoS ONE 2014, 9, e99717. [Google Scholar] [CrossRef] [PubMed]
- Geißler, C.; Kühn, P.; Böhnke, M.; Bruelheide, H.; Shi, X.; Scholten, T. Splash erosion potential under tree canopies in subtropical SE China. Catena 2012, 91, 85–93. [Google Scholar] [CrossRef]
- Nanko, K.; Onda, Y.; Ito, A.; Moriwaki, H. Spatial variability of throughfall under a single tree: Experimental study of rainfall amount, raindrops, and kinetic energy. Agric. For. Meteorol. 2011, 151, 1173–1182. [Google Scholar] [CrossRef]
- Liu, J.; Liu, W.; Zhu, K. Throughfall kinetic energy and its spatial characteristics under rubber-based agroforestry systems. Catena 2018, 161, 113–121. [Google Scholar] [CrossRef]
- Nanko, K.; Hotta, N.; Suzuki, M. Evaluating the influence of canopy species and meteorological factors on throughfall drop size distribution. J. Hydrol. 2006, 329, 422–431. [Google Scholar] [CrossRef]
- Frasson, R.P.D.M.; Krajewski, W.F. Characterization of the drop-size distribution and velocity–diameter relation of the throughfall under the maize canopy. Agric. For. Meteorol. 2011, 151, 1244–1251. [Google Scholar] [CrossRef]
- Chapman, G. Size of raindrops and their striking force at the soil surface in a red pine plantation. Trans. Am. Geophys. Union 1948, 29, 664–670. [Google Scholar] [CrossRef]
- Zhou, G.; Wei, X.; Yan, J. Impacts of eucalyptus (Eucalyptus exserta) plantation on sediment yield in Guangdong Province, Southern China—a kinetic energy approach. Catena 2002, 49, 231–251. [Google Scholar] [CrossRef]
- Wang, P.K.; Pruppacher, H.R. Acceleration to Terminal Velocity of Cloud and Raindrops. J. Appl. Meteorol. 1976, 16, 275–280. [Google Scholar] [CrossRef] [Green Version]
- Ge, M.; Wu, P.; Zhu, D.; Zhang, L. Analysis of kinetic energy distribution of big gun sprinkler applied to continuous mov-ing hose-drawn traveler. Agric. Water Manag. 2018, 201, 118–132. [Google Scholar] [CrossRef]
- Hui, X.; Zheng, Y.; Yan, H. Water distributions of low-pressure sprinklers as affected by the maize canopy under a centre pivot irrigation system. Agric. Water Manag. 2021, 245, 106646. [Google Scholar] [CrossRef]
- China MOWR. Technical Specification for Sprinkler Irrigation Engineering; GB/T 50085-2007; China Planning Press: Beijing, China, 2007. (In Chinese)
- Gong, X.; Zhu, D.; Zhang, L.; Zhang, Y.; Ge, M.; Yang, W. Drop size distribution of fixed spray-plate sprinklers with two-dimensional video disdrometer. Trans. Chin. Soc. Agric. Mach. 2014, 45, 128–133. (in Chinese). [Google Scholar]
- Ge, M.; Wu, P.; Zhu, D.; Zhang, L. Comparisons of spray characteristics between vertical impact and turbine drive sprin-klers—A case study of the 50PYC and HY50 big gun-type sprinklers. Agric. Water Manag. 2020, 228, 105847. [Google Scholar] [CrossRef]
- Patrignani, A.; Ochsner, T.E. Canopeo: A powerful new tool for measuring fractional green canopy cover. Agron. J. 2015, 107, 2312–2320. [Google Scholar] [CrossRef] [Green Version]
- Nanko, K.; Watanabe, A.; Hotta, N.; Suzuki, M. Physical interpretation of the difference in drop size distributions of leaf drips among tree species. Agric. For. Meteorol. 2013, 169, 74–84. [Google Scholar] [CrossRef]
- Gong, X.H. Study on the Water and Specific Power Distribution of the Spray-Plate Sprinkler Used in the Moving Sprinkler Machine; Northwest Agriculture and Forestry University: Yangling, China, 2015. (In Chinese) [Google Scholar]
- Brandt, C.J. The size distribution of throughfall drops under vegetation canopies. Catena 1989, 16, 507–524. [Google Scholar] [CrossRef]
- Armstrong, C.L.; Mitchell, K.J. Transformations of rainfall by plant canopy. Trans. ASAE 1987, 30, 688–696. [Google Scholar] [CrossRef]
- Levia, D.F.; Hudson, S.A.; Llorens, P.; Nanko, K. Throughfall drop size distributions: A review and prospectus for future research. Wiley Interdiplinary Rev. Water 2017, 4, e1225. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.F.; Wang, X.P.; Hu, R.; Pan, Y.X. Throughfall and its spatial variability beneath xerophytic shrub canopies within wa-ter-limited arid desert ecosystems. J. Hydrol. 2016, 539, 406–416. [Google Scholar] [CrossRef]
- Murakami, S. A proposal for a new forest canopy interception mechanism: Splash droplet evaporation. J. Hydrol. 2006, 319, 72–82. [Google Scholar] [CrossRef]
- Nanko, K.; Onda, Y.; Ito, A.; Moriwaki, H. Effect of canopy thickness and canopy saturation on the amount and kinetic energy of throughfall: An experimental approach. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Geißler, C.; Kuhn, P.; Scholten, T.; Shi, X. Estimation of throughfall erosivity in a highly diverse forest ecosystem using sand-filled splash cups. J. Earth Sci. 2010, 21, 897–900. [Google Scholar] [CrossRef]
- Jones, B.A.; Bubenzerb, G.D. Drop size and impact velocity effects on the detachment of soils under simulated rainfall. Trans. ASAE 1971, 14, 625–628. [Google Scholar] [CrossRef]
- Cruse, R.M.; Berghoefer, B.E.; Mize, C.W.; Ghaffarzadeh, M. Water drop impact angle and soybean protein amendment effects on soil detachment. Soil Sci. Soc. Am. J. 2000, 64, 1474–1478. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Ahmadi, M.; Cerda, A. Contribution of raindrop impact to the change of soil physical properties and water erosion under semi-arid rainfalls. Sci. Total Environ. 2017, 583, 382–392. [Google Scholar] [CrossRef] [PubMed]


| Parameters | Model or Value |
|---|---|
| Trolley moving speed (m·s−1) | 0.034 |
| Length of guide rail (m) | 5.00 |
| Telescopic bracket maximum extension height (m) | 4.50 |
| Width of sprinkler water curtain (m) | 2.50 |
| Needle spacing (cm) | 5.00 |
| Nozzle diameter (mm) | 2.00 |
| Pressure gauge type and accuracy | YB150, Xi’an instrument factory, Measurement range (0–0.40 MPa), Precision (0.01 MPa) |
| Physical Parameters of Throughfall | Under Maize Canopy | Without Canopy | ||||
|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | CV (%) | Maximum Value | Minimum Value | ||
| Drop diameter (D25) (mm) | ||||||
| Treatment 1 | 1.34 | 0.26 | 19.40 | 2.11 | 0.86 | 2.16 |
| Treatment 2 | 1.31 | 0.23 | 17.56 | 2.09 | 0.83 | 2.14 |
| Treatment 3 | 1.26 | 0.22 | 17.46 | 2.16 | 0.76 | 2.02 |
| Treatment 4 | 1.19 | 0.16 | 13.45 | 2.17 | 0.65 | 2.17 |
| Drop diameter (D50) (mm) | ||||||
| Treatment 1 | 2.58 | 0.56 | 21.71 | 3.40 | 1.64 | 3.34 |
| Treatment 2 | 2.53 | 0.52 | 20.55 | 3.25 | 1.68 | 3.28 |
| Treatment 3 | 2.47 | 0.54 | 21.86 | 3.31 | 1.42 | 3.30 |
| Treatment 4 | 2.37 | 0.36 | 15.19 | 3.12 | 1.03 | 3.31 |
| Drop diameter (D75) (mm) | ||||||
| Treatment 1 | 3.56 | 0.96 | 26.97 | 3.78 | 2.75 | 3.82 |
| Treatment 2 | 3.47 | 0.91 | 26.22 | 3.69 | 2.63 | 3.79 |
| Treatment 3 | 3.38 | 0.86 | 25.44 | 3.77 | 2.56 | 3.85 |
| Treatment 4 | 3.24 | 0.52 | 16.49 | 3.65 | 1.98 | 3.84 |
| Drop velocity (m·s−1) | ||||||
| Treatment 1 | 4.86 | 0.63 | 12.96 | 5.87 | 4.12 | 5.88 |
| Treatment 2 | 4.76 | 0.67 | 14.08 | 5.78 | 3.71 | 5.75 |
| Treatment 3 | 4.59 | 0.67 | 14.60 | 5.77 | 3.64 | 5.97 |
| Treatment 4 | 4.42 | 0.58 | 13.12 | 5.17 | 3.23 | 5.87 |
| Drop horizontal velocity (m·s−1) | ||||||
| Treatment 1 | --- | --- | --- | --- | --- | --- |
| Treatment 2 | 1.45 | 0.23 | 15.86 | 1.85 | 0.99 | 1.84 |
| Treatment 3 | 2.22 | 0.32 | 14.41 | 2.65 | 1.75 | 2.98 |
| Treatment 4 | 3.17 | 0.47 | 14.83 | 3.83 | 2.31 | 4.24 |
| Drop vertical velocity (m·s−1) | ||||||
| Treatment 1 | --- | --- | --- | --- | --- | --- |
| Treatment 2 | 4.54 | 0.64 | 14.10 | 5.48 | 3.53 | 5.59 |
| Treatment 3 | 4.01 | 0.60 | 14.96 | 5.20 | 3.20 | 5.08 |
| Treatment 4 | 3.07 | 0.39 | 12.70 | 3.67 | 2.26 | 4.05 |
| Droplet landing angle (°) | ||||||
| Treatment 1 | 81.90 | 1.21 | 1.48 | 83.89 | 79.66 | 81.69 |
| Treatment 2 | 72.30 | 1.64 | 2.27 | 76.58 | 70.35 | 71.33 |
| Treatment 3 | 63.70 | 3.68 | 5.78 | 70.12 | 59.45 | 60.58 |
| Treatment 4 | 44.08 | 2.55 | 5.78 | 49.51 | 41.26 | 42.04 |
| Drop Diameter Range (mm) | Drop Velocity (m·s−1) | Kinetic Energy (×10−4 J) | ||||||
|---|---|---|---|---|---|---|---|---|
| Without Canopy | Within Canopy | Without Canopy | Within Canopy | |||||
| A1 | B1 | C1 | A1 | B1 | C1 | |||
| 3.01–3.10 | 6.49 ± 0.13 | 5.54 ± 0.21 | 5.89 ± 0.17 | 6.04 ± 0.31 | 3.11 ± 0.06 | 2.29 ± 0.08 | 2.60 ± 0.06 | 2.68 ± 0.09 |
| 3.11–3.20 | 6.51 ± 0.08 | 5.47 ± 0.19 | 5.92 ± 0.13 | 5.94 ± 0.28 | 3.51 ± 0.11 | 2.49 ± 0.07 | 2.89 ± 0.09 | 2.91 ± 0.12 |
| 3.21–3.30 | 6.54 ± 0.07 | 5.58 ± 0.16 | 5.85 ± 0.15 | 6.11 ± 0.35 | 3.87 ± 0.09 | 2.81 ± 0.09 | 3.09 ± 0.06 | 3.35 ± 0.09 |
| 3.31–3.40 | 6.59 ± 0.11 | 5.21 ± 0.09 | 6.02 ± 0.23 | 6.12 ± 0.18 | 4.29 ± 0.12 | 2.71 ± 0.09 | 3.56 ± 0.07 | 3.68 ± 0.13 |
| 3.41–3.50 | 6.61 ± 0.15 | 5.68 ± 0.14 | 5.94 ± 0.14 | 6.07 ± 0.22 | 4.71 ± 0.14 | 3.51 ± 0.16 | 3.81 ± 0.13 | 3.95 ± 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhu, D.; Ge, M. The Spatial Variation Mechanism of Size, Velocity, and the Landing Angle of Throughfall Droplets under Maize Canopy. Water 2021, 13, 2083. https://doi.org/10.3390/w13152083
Zhu Z, Zhu D, Ge M. The Spatial Variation Mechanism of Size, Velocity, and the Landing Angle of Throughfall Droplets under Maize Canopy. Water. 2021; 13(15):2083. https://doi.org/10.3390/w13152083
Chicago/Turabian StyleZhu, Zhongrui, Delan Zhu, and Maosheng Ge. 2021. "The Spatial Variation Mechanism of Size, Velocity, and the Landing Angle of Throughfall Droplets under Maize Canopy" Water 13, no. 15: 2083. https://doi.org/10.3390/w13152083
APA StyleZhu, Z., Zhu, D., & Ge, M. (2021). The Spatial Variation Mechanism of Size, Velocity, and the Landing Angle of Throughfall Droplets under Maize Canopy. Water, 13(15), 2083. https://doi.org/10.3390/w13152083







