Analysis of Applicability of CFD Numerical Studies Applied to Problem When Pump Working as Turbine
Abstract
1. Introduction
2. Materials and Methods
- The product of filtered velocities is
- The subgrid stress tensor is
- The filtered stress tensor rate is
- The filtered viscous stress tensor is
- 1.
- Collection of information. Recent studies related to PATs research were found. A deep search was developed to do a great database, which helps to analyze the different published CFD analyses applied to pump working as turbine.
- 2.
- Selection of relevant information for this study. The papers of interest should be related to numerical simulation CFD applied to PATs: experimental studies, theoretical, mathematical models, new proposals for obtaining the characteristic curves of the pumps, studies of optimization of component elements, state of the art, studies of PATs for machine speeds fixed or variable, among others.
- 3.
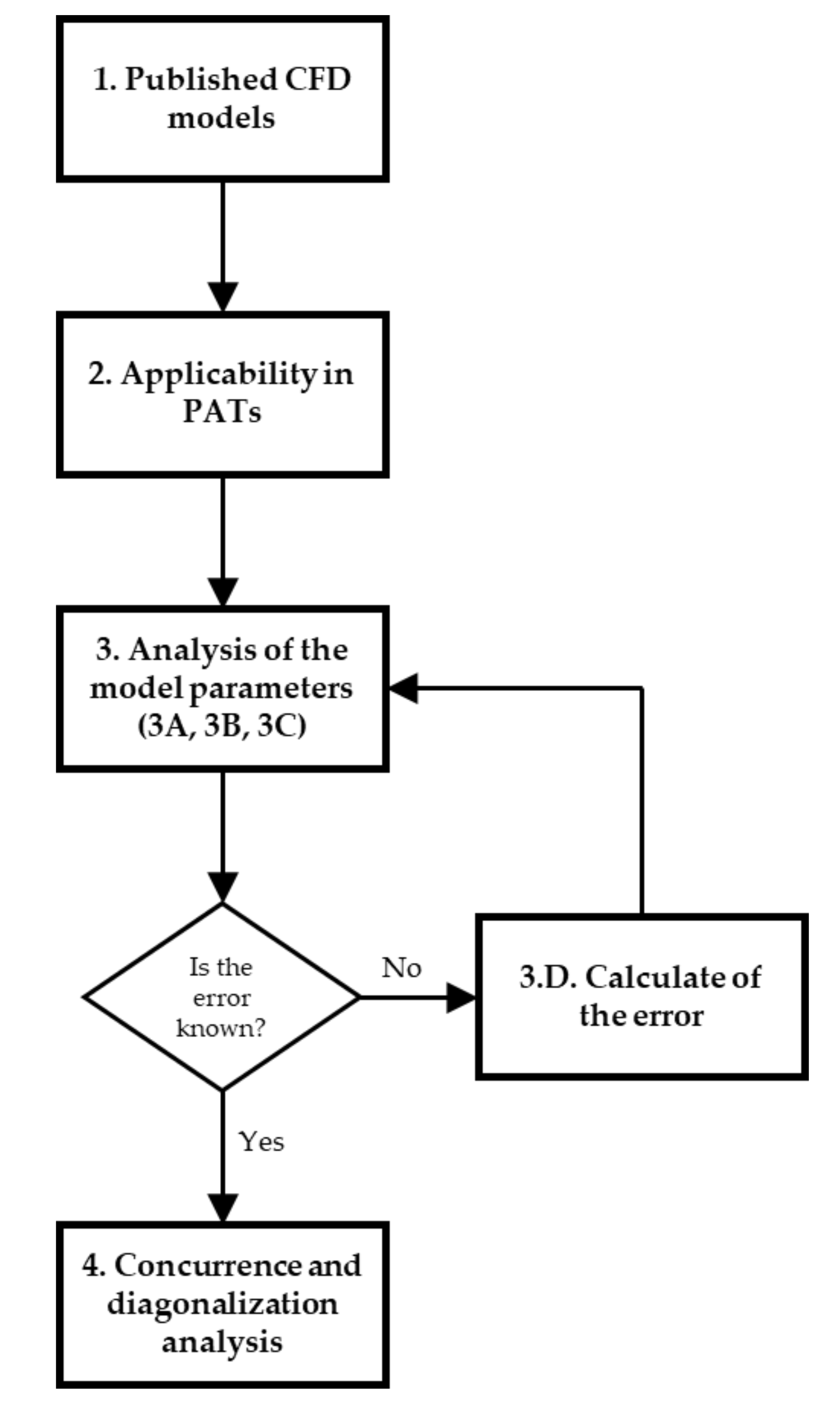
- Information Analysis. The information consulted and collected from the studies analyzed is described below:
- Step 3A. From the CFD numerical simulation studies, the information obtained was: pump type-axial, radial or mixed; fixed or variable speed; rotational speed value; specific speed value; CFD package; boundary conditions at the entrance or exit of the machine; the turbulence closure model; mesh-type; and simulation results.
- Step 3B. The main results of the experiments were obtained from the experimental research.
- Step 3C. From the other studies, the results and conclusions obtained from different investigations were used to discover more about new applications and optimizations.
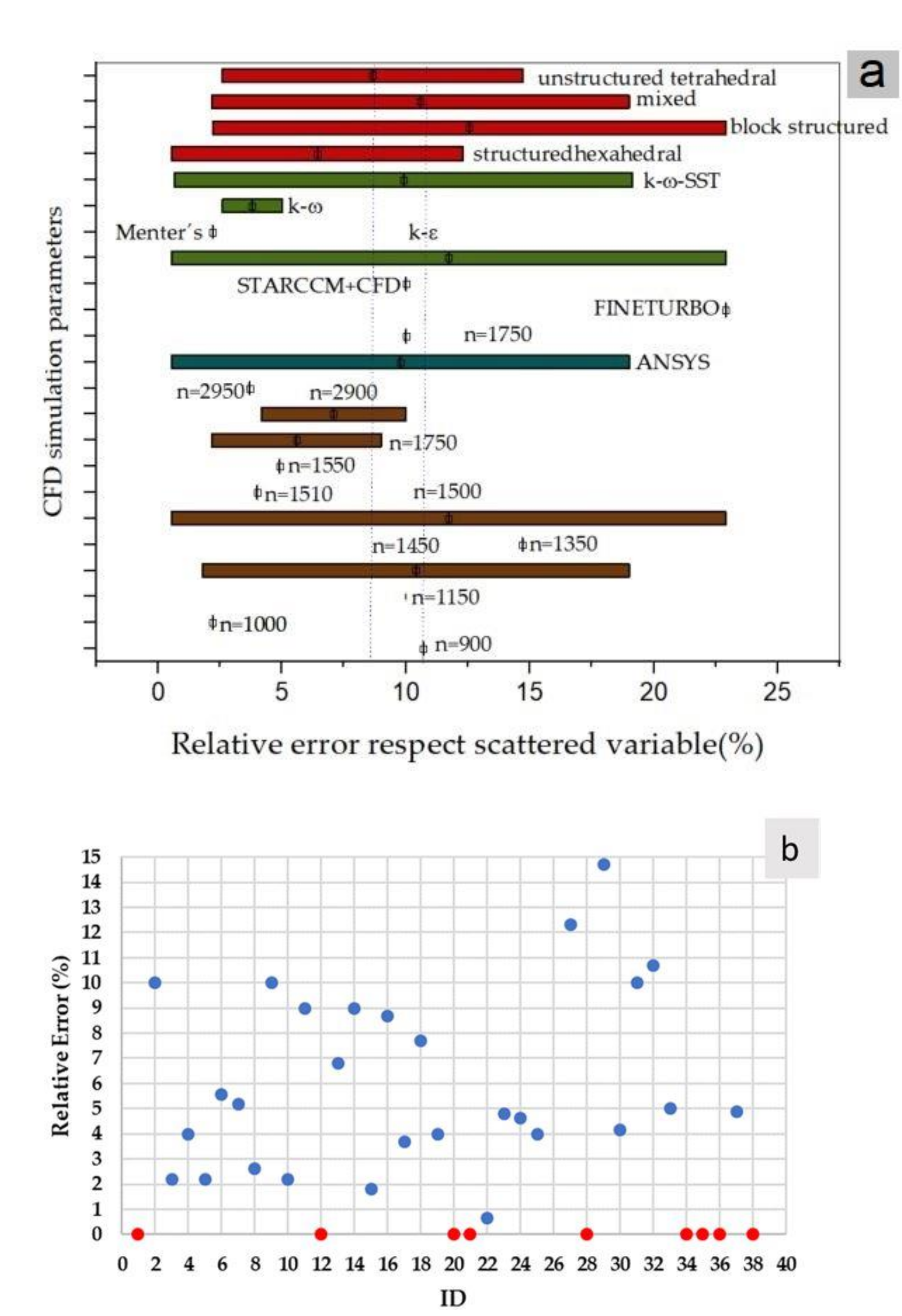
- Step 3D. Calculation of the relative error. In cases where both numerical simulation and experimental test results were obtained for the same conditions, the maximum relative error between the experiment and the numerical simulation was calculated according to the following equation:where and are the values of the parameters in the experiment and the numerical simulation, respectively. These parameters or study variables are specified in the nomenclature part of this paper corresponds to the values that different researchers have compared between numerical modelling CFD and experimental tests. These values will serve as a reference to evaluate the success of modelling.
It should be noted that this calculation of the parameters with the maximum dispersion were considered to obtain the significant values. For some cases, the papers directly reported these values. - 4.
- Concurrency and diagonalization. Based on the information collected and the results of the calculations, a concurrency and diagonalization analysis was performed to identify the number of investigations according to the type of PATs and to identify the main CFD modelling parameters used in successful experiences.
3. Results and Discussion
3.1. CFD Model Applied in PATs Simulations
3.2. Analysis of CFD Simulation When PAT Operated under Fixed Rotational Speed
3.3. PATs under Variable Rotational Speed
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| H | head |
| P | power |
| p | pressure |
| Q | flow rate |
| Ns | specific speed |
| n | rotational speed |
| D | external machine diameter |
| Greek symbols | |
| ψ | |
| η | efficiency |
| ω | specific kinetic energy dissipation rate |
| ε | turbulent kinetic energy dissipation rate |
| Δ | change |
| Subscripts | |
| BEP | Best Efficient Point |
References
- Lee, S.; Pomeroy, C.; Burian, S. Setting Future Water Rates for Sustainability of a Water Distribution System. J. Water Resour. Plan. Manag. 2021, 147, 04020108. [Google Scholar] [CrossRef]
- Ahmadi, S.; Saboohi, Y.; Vakili, A. Frameworks, quantitative indicators, characters, and modeling approaches to analysis of energy system resilience: A review. Renew. Sustain. Energy Rev. 2021, 144, 110988. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Capurso, T.; Balacco, G.; Binetti, M.; Camporeale, S.M.; Torresi, M. Selection, control and techno-economic feasibility of Pumps as Turbines in Water Distribution Networks. Renew. Energy 2020, 162, 1292–1306. [Google Scholar] [CrossRef]
- Ferrarese, G.; Malavasi, S. Perspectives of Water Distribution Networks with the GreenValve System. Water 2020, 12, 1579. [Google Scholar] [CrossRef]
- Renzi, M.; Rudolf, P.; Stefan, D.; Nigro, A.; Rossi, M. Installation of an axial Pump-as-Turbine (PaT) in a wastewater sewer of an oil refinery: A case study. Appl. Energy 2019, 250, 665–676. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; López-Jiménez, P.A.; Ramos, H.M. Bombas Operando Como Turbinas (PAT): Principios de Funcionamiento y Selección; Editorial UPV: Valencia, Spain, 2020. [Google Scholar]
- Binama, M.; Su, W.-T.; Li, X.-B.; Li, F.-C.; Wei, X.-Z.; An, S. Investigation on pump as turbine (PAT) technical aspects for micro hydropower schemes: A state-of-the-art review. Renew. Sustain. Energy Rev. 2017, 79, 148–179. [Google Scholar] [CrossRef]
- Rawal, S. Numerical Simulation on a Pump Operating in a turbine mode. In Proceedings of the 23rd International Pump Users Symposium, Houston, TX, USA, 5–8 March 2007. [Google Scholar]
- Nautiyal, H.; Kumar, V.; Thakur, A. CFD Analysis on Pumps Working as Turbines. Hydro Nepal J. Water Energy Environ. 1970, 6, 35–37. [Google Scholar] [CrossRef]
- Páscoa, J.; Silva, F.J.; Pinheiro, J.S.; Martins, D.J. Accuracy details in realistic CFD modeling of an industrial centrifugal pump in direct and reverse modes. J. Therm. Sci. 2010, 19, 491–499. [Google Scholar] [CrossRef]
- Carravetta, H.; Fecarotta, A.; Ramos, O. Numerical simulation on Pump as Turbine: Mesh reliability and performance concerns. In Proceedings of the 2011 International Conference on Clean Electrical Power (ICCEP), Ischia, Italy, 14–16 June 2011; pp. 169–174. [Google Scholar]
- Ramos, H.M.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Plua, F.; Sánchez-Romero, F.-J.; Hidalgo, V.; López-Jiménez, P.; Pérez-Sánchez, M. New Expressions to Apply the Variation Operation Strategy in Engineering Tools Using Pumps Working as Turbines. Mathematics 2021, 9, 860. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Del Giudice, G.; Ramos, H. Energy Recovery in Water Systems by PATs: A Comparisons among the Different Installation Schemes. Procedia Eng. 2014, 70, 275–284. [Google Scholar] [CrossRef]
- Wang, T.; Kong, F.; Yang, S.; Fu, Y. Numerical Study on Hydraulic Performances of Pump as Turbine with Forward-Curved Blades. In Proceedings of the Fluids Engineering Division Summer Meeting. American Society of Mechanical Engineers, Chicago, IL, USA, 3–7 August 2014. [Google Scholar]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M. International Journal of Energy and Environment CFD and comparisons for a pump as turbine: Mesh reliability and performance concerns. Int. J. Energy Environ. 2011, 2, 2076–2909. [Google Scholar]
- Cando, E.; Luo, X.W.; Yu, A.; Zhu, L.; Liu, J.; Lu, L.; Hidalgo, V. Unsteady numerical analysis of the liquid-solid two-phase flow around a step using Eulerian-Lagrangian and the filter-based RANS method. J. Mech. Sci. Technol. 2017, 31, 2781–2790. [Google Scholar] [CrossRef]
- Hidalgo, V.; Escaler, X.; Valencia, E.; Peng, X.; Erazo, J.; Puga, D.; Luo, X. Scale-Adaptive Simulation of Unsteady Cavitation Around a Naca66 Hydrofoil. Appl. Sci. 2019, 9, 3696. [Google Scholar] [CrossRef]
- Bogdanovic-Jovanovic, J.; Milenkovic, D.; Svrkota, D.; Bogdanovic, B.; Spasić, Z.T. Pumps used as turbines power recovery, energy efficiency, CFD analysis. Therm. Sci. 2014, 18, 1029–1040. [Google Scholar] [CrossRef]
- Barrio, R.M.; Fernández, J.; Blanco, E.F.; Parrondo, J.L.; Marcos, A. Performance characteristics and internal flow patterns in a reverse-running pump–turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 226, 695–708. [Google Scholar] [CrossRef]
- Vasanthakumar, P.; Arulmurugu, A.; Vinoth, R.; Gowtham, R.; Kumaresan, S.; Prasath, V. Investigation of Centrifugal Pump as Turbine: A Review Report; IJERT: Gujarat, India, 2014; Volume 3, pp. 2287–2292. [Google Scholar]
- Hidalgo, V.; Velasco, M.; Cando, E. Rotatory 3D Structured Mesh Study Using OpenFOAM to Simulate the Flow in Francis Turbine. Proceedings of MET 2021, 1–14 June 2021; pp. 1–15, Online. [Google Scholar]
- Carneiro, F.; Moura, L.; Rocha, P.C.; Lima, R.P.; Ismail, K. Application and analysis of the moving mesh algorithm AMI in a small scale HAWT: Validation with field test’s results against the frozen rotor approach. Energy 2019, 171, 819–829. [Google Scholar] [CrossRef]
- Diaz, V.H.H.; Luo, X.; Huang, R.; Cando, E. Numerical Simulation of Cavitating Flow Over 2D Hydrofoil Using OpenFOAM Adapted for Debian Operating System with LXDE Based in Kernel GNU/Linux. Am. Soc. Mech. Eng. Fluids Eng. Div. FEDSM 2014, 2. [Google Scholar] [CrossRef]
- Baker, T.J. Mesh generation: Art or science? Prog. Aerosp. Sci. 2005, 41, 29–63. [Google Scholar] [CrossRef]
- White, J.D.; Holloway, A.G.L.; Gerber, A.G. FEDSM2005-77460 Predicting Turbine Performance of High Specific Speed Pumps Using CFD. 2005. Available online: http://www.asme.org/about-asme/terms-of-use (accessed on 31 July 2021).
- Kerschberger, P.; Gehrer, A. Hydraulic development of high specific-speed pump-turbines by means of an inverse design method, numerical flow-simulation (CFD) and model testing. IOP Conf. Ser. Earth Environ. Sci. 2010, 12. [Google Scholar] [CrossRef]
- Renzi, M.; Rudolf, P.; Stefan, D.; Nigro, A.; Rossi, M. Energy recovery in oil refineries through the installation of axial Pumps-as-Turbines (PaTs) in a wastewater sewer: A case study. Energy Procedia 2019, 158, 135–141. [Google Scholar] [CrossRef]
- Kim, J.-W.; Suh, J.-W.; Choi, Y.-S.; Lee, K.-Y.; Kim, J.-H.; Kanemoto, T.; Kim, J.-H. Simultaneous efficiency improvement of pump and turbine modes for a counter-rotating type pump-turbine. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Pienika, R.; Schenzer, D. Axial Flow Pump Used as Turbine for Hydropower Generation. In Proceedings of the III Latin American Hydro Power and Systems Meeting, Quito, Ecuador, 5–7 September 2017. [Google Scholar]
- Hlbočan, P.; Varchola, M. Numerical Simulation on a Mixed-Flow Pump Operating in A Turbine Mode. Eng. Mech. 2013, 20, 97–105. [Google Scholar]
- Capurso, T.; Stefanizzi, M.; Torresi, M.; Pascazio, G.; Caramia, G.; Camporeale, S.M.; Fortunato, B.; Bergamini, L. How to Improve the Performance Prediction of a Pump as Turbine by Considering the Slip Phenomenon. Proceedings 2018, 2, 683. [Google Scholar] [CrossRef]
- Capurso, T.; Stefanizzi, M.; Pascazio, G.; Ranaldo, S.; Camporeale, S.M.; Fortunato, B.; Torresi, M. Slip Factor Correction in 1-D Performance Prediction Model for PaTs. Water 2019, 11, 565. [Google Scholar] [CrossRef]
- Capurso, T.; Bergamini, L.; Camporeale, S.M.; Fortunato, B.; Torresi, M. CFD Analysis of the Performance of a Novel Impeller for a Double Suction Centrifugal Pump Working as a Turbine. 2019. Available online: www.euroturbo.eu (accessed on 31 July 2021).
- Bahreini, A.; Sattari, A. Numerical and Economic Study of Performance of Centrifugal Pump as Turbine. J. Comput. Appl. Mech. 2017, 48, 151–160. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Kong, F.; Gou, Q.; Yang, S. Theoretical, experimental, and numerical study of special impeller used in turbine mode of centrifugal pump as turbine. Energy 2017, 130, 473–485. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G.; Francos, J.F. Experimental and numerical investigation of centrifugal Pumps as Turbines. In Proceedings of the 10th International Conference on Energy Efficiency in Motor Driven System, Rome, Italy, 6–8 September 2017. [Google Scholar]
- Pérez-Sánchez, M.; Simão, M.; López-Jiménez, P.A.; Ramos, H.M. CFD Analyses and Experiments in a PAT Modeling: Pressure Variation and System Efficiency. Fluids 2017, 2, 51. [Google Scholar] [CrossRef]
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; López-Jiménez, P.; Ramos, H.M. Velocities in a Centrifugal PAT Operation: Experiments and CFD Analyses. Fluids 2017, 3, 3. [Google Scholar] [CrossRef]
- Lal, B.; Deshmukh, T.S. Performance Analysis of Centrifugal Pump at Different Operating Mode. Smart Moves J. Ijoscience 2018, 4, 8. [Google Scholar] [CrossRef][Green Version]
- Rossi, M.; Nigro, A.; Renzi, M. A predicting model of PaTs’ performance in off-design operating conditions. Energy Procedia 2019, 158, 123–128. [Google Scholar] [CrossRef]
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; Ramos, H.M. Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses. Energies 2019, 12, 901. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Theoretical, numerical and experimental investigation of centrifugal pumps in reverse operation. Exp. Therm. Fluid Sci. 2008, 32, 1620–1627. [Google Scholar] [CrossRef]
- Sedlář, M.; Jiříšoukal, J.J.; Komárek, M. CFD Analysis of Middle Stage of Multistage Pump Operating in Turbine Regime. Eng. Mech. 2009, 16, 413–421. [Google Scholar]
- Fernández, J.; Barrio, R.; Blanco, E.; Parrondo, J.L.; Marcos, A. Numerical investigation of a centrifugal pump running in reverse mode. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 224, 373–381. [Google Scholar] [CrossRef]
- Páscoa, J.C.; Silva, F.J.; Pinheiro, J.S.; Martins, D.J. A New Approach for Predicting PAT-Pumps Operating Point from Direct Pumping Mode Characteristics. J. Sci. Ind. Res. 2012, 71, 144–148. [Google Scholar]
- Yang, S.-S.; Kong, F.-Y.; Qu, X.-Y.; Jiang, W.-M. Influence of Blade Number on the Performance and Pressure Pulsations in a Pump Used as a Turbine. J. Fluids Eng. 2012, 134, 124503. [Google Scholar] [CrossRef]
- Maleki, A.; Ghorani, M.M.; Haghighi, M.H.S.; Riasi, A. Numerical study on the effect of viscosity on a multistage pump running in reverse mode. Renew. Energy 2020, 150, 234–254. [Google Scholar] [CrossRef]
- Fernández, J.; Blanco, E.; Parrondo, J.L.; Stickland, M.T.; Scanlon, T.J. Performance of a centrifugal pump running in inverse mode. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 265–271. [Google Scholar] [CrossRef]
- Fengxia, S.; Junhu, Y.; Senchun, M.; Xiaohui, W. Investigation on the power loss and radial force characteristics of pump as turbine under gas–liquid two-phase condition. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Xia, Z.; Hao, Y.; Cheng, X. Effect of Velocity Slip on Head Prediction for Centrifugal Pumps as Turbines. Math. Probl. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Miao, S.C.; Yang, J.; Shi, F.; Wang, X.; Shi, G. Research on energy conversion characteristic of pump as turbine. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Shi, H.X.; Chai, L.P.; Su, X.Z.; Jaini, R. Performance Optimization of Energy Recovery Device Based on PAT with Guide Vane. Int. J. Simul. Model. 2018, 17, 472–484. [Google Scholar] [CrossRef]
- Yang, S.-S.; Wang, C.; Chen, K.; Yuan, X. Research on Blade Thickness Influencing Pump as Turbine. Adv. Mech. Eng. 2014, 6. [Google Scholar] [CrossRef]
- Shi, F.; Yang, J.; Wang, X. Analysis on the effect of variable guide vane numbers on the performance of pump as turbine. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Miao, S.C.; Yang, J.-H.; Shi, G.-T.; Wang, T.-T. Blade profile optimization of pump as turbine. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Sun, Y.; Zuo, Z.; Liu, S.; Liu, J.; Wu, Y. Distribution of Pressure Fluctuations in a Prototype Pump Turbine at Pump Mode. Adv. Mech. Eng. 2014, 6. [Google Scholar] [CrossRef]
- Schleicher, W.; Oztekin, A. Hydraulic design and optimization of a modular pump-turbine runner. Energy Convers. Manag. 2015, 93, 388–398. [Google Scholar] [CrossRef]
- Natanasabapathi, S.R.; Kshirsagar, J.T. Pump as Turbine—An Experience with CFX-5.6; Kirloskar Brothers Ltd.: Pune, India, 2004. [Google Scholar]
- Barrio, R.; Fernández, J.; Parrondo, J.; Blanco, E. Performance Prediction for a Centrifugal Pump Working in Direct and Reverse Mode Using Computational Fluid Dynamics. Renew. Energy Power Qual. J. 2010, 1, 1429–1433. [Google Scholar] [CrossRef]
- Koswara, E.; Budiman, H.; Fikri, N. Flow Analysis in Pump as Turbines (PATs) Using Ansys Fluent Software. 2020. Available online: http://jurnal.umj.ac.id/index.php/sintek (accessed on 31 July 2021).
- Yang, S.S.; Kong, F.Y.; Jiang, W.M.; Qu, X.Y. Research on rotational speed to the influence of pump as turbine. IOP Conf. Ser. Earth Environ. Sci. 2012, 15. [Google Scholar] [CrossRef]
- Rosa, H.M.P.; Emerick, B.S. Revista Brasileira de Engenharia Agrícola e Ambiental CFD simulation on centrifugal pump impeller with splitter blades Simulação CFD em rotor de bomba centrifuga com pás intermediárias. Eng. Agrícola Ambient. 2020, 24, 3–7. [Google Scholar]
- Ismail, M.A.; Othman, A.K.; Zen, H. Numerical Investigation of Rotational Speed on Pump as Turbine for Microhydro Applications. Appl. Mech. Mater. 2016, 833, 11–18. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Theoretical model of energy performance prediction and BEP determination for centrifugal pump as turbine. Energy 2019, 172, 712–732. [Google Scholar] [CrossRef]
- Aidhen, A.S.; Malik, S.; Kishanrao, C.D. Theoretical, Numerical and Experimental Research of Single Stage, Radial Discharge Centrifugal Pump Operating in Turbine Mode. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 1265–1270. [Google Scholar] [CrossRef]
- Du, J.; Yang, H.; Shen, Z.; Chen, J. Micro hydro power generation from water supply system in high rise buildings using pump as turbines. Energy 2017, 137, 431–440. [Google Scholar] [CrossRef]
- Rossi, M.; Nigro, A.; Renzi, M. Experimental and numerical assessment of a methodology for performance prediction of Pumps-as-Turbines (PaTs) operating in off-design conditions. Appl. Energy 2019, 248, 555–566. [Google Scholar] [CrossRef]
- Arulmurugu, P.V.; Pandian, A. Numerical investigation of centrifugal pump as turbine. Adv. Appl. Fluid Mech. 2015, 7, 147–163. [Google Scholar] [CrossRef]
- Baburaj, E.; Sivaprakasam, R.; Manikandan, C.; Sudha, K. CFD Analysis of Pump as Turbine for Micro-Hydro Schemes. 2013. Available online: www.ijirset.com (accessed on 31 July 2021).
- Yang, S.-S.; Liu, H.-L.; Kong, F.-Y.; Xia, B.; Tan, L.-W. Effects of the Radial Gap Between Impeller Tips and Volute Tongue Influencing the Performance and Pressure Pulsations of Pump as Turbine. J. Fluids Eng. 2014, 136, 054501. [Google Scholar] [CrossRef]
- Ismail, M.A.; Othman, A.K.; Zen, H. Numerical Simulation on End Suction Centrifugal Pump Running in Inverse Flow for Microhydro Applications. Appl. Mech. Mater. 2015, 773–774, 358–362. [Google Scholar] [CrossRef]
- Su, X.; Huang, S.; Zhang, X.; Yang, S. Numerical research on unsteady flow rate characteristics of pump as turbine. Renew. Energy 2016, 94, 488–495. [Google Scholar] [CrossRef]
- Frosina, E.; Buono, D.; Senatore, A. A Performance Prediction Method for Pumps as Turbines (PAT) Using a Computational Fluid Dynamics (CFD) Modeling Approach. Energies 2017, 10, 103. [Google Scholar] [CrossRef]
- Rosado, L.E.C.; López-Jiménez, P.A.; Sánchez-Romero, F.-J.; Fuertes, P.C.; Pérez-Sánchez, M. Applied Strategy to Characterize the Energy Improvement Using PATs in a Water Supply System. Water 2020, 12, 1818. [Google Scholar] [CrossRef]
- Yang, S.-S.; Derakhshan, S.; Kong, F.-Y. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
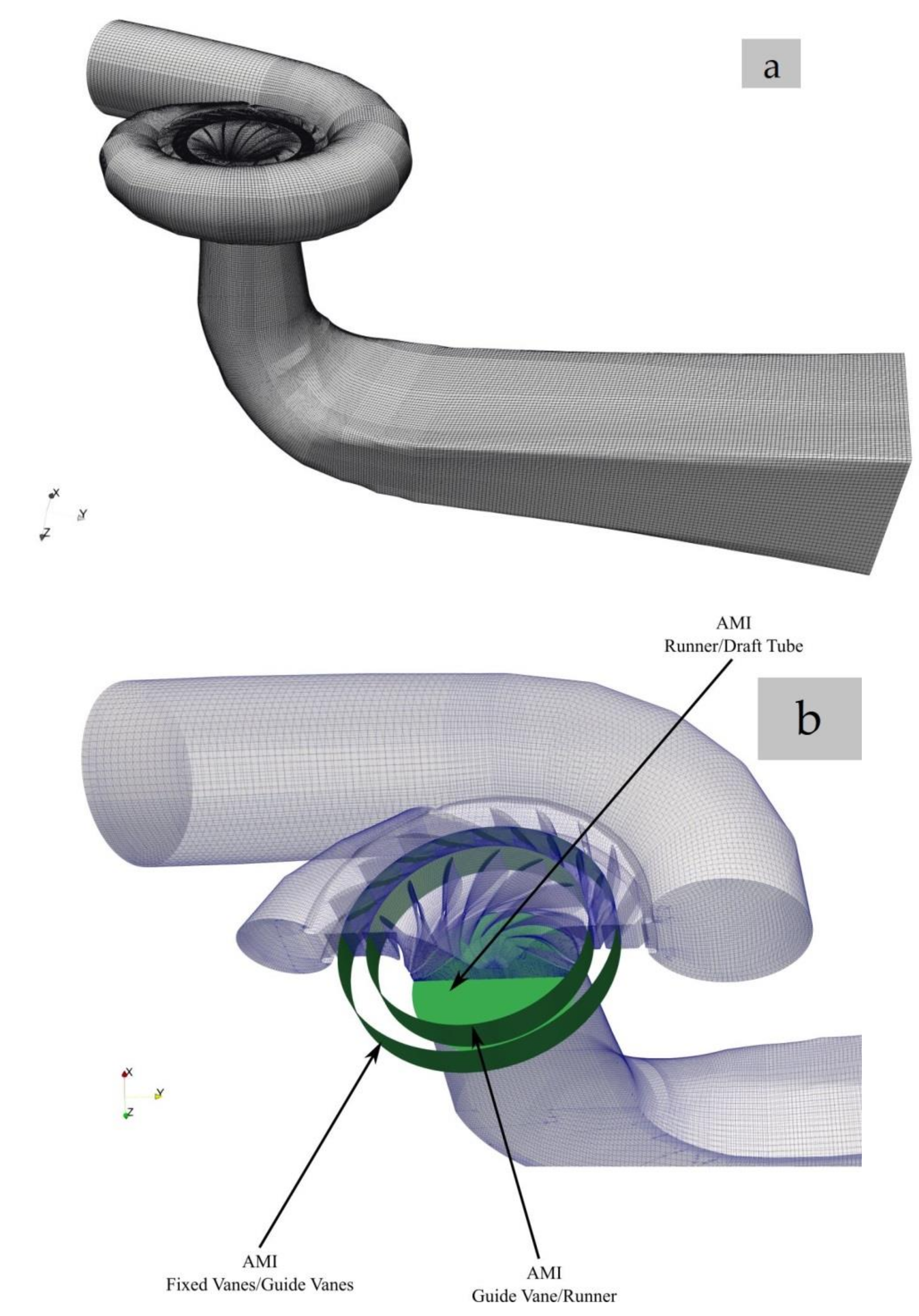


| Type of Machine | Published Research | Consulted References |
|---|---|---|
| Axial | 7 | [5,11,26,27,28,29,30] |
| Mixed | 5 | [8,31,32,33,34] |
| Radial | 44 | [10,15,19,20,28,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74] |
| ID | Reference | Boundary Conditions | Study-Variable | Relative Max Error (%) | |
|---|---|---|---|---|---|
| Inlet | Outlet | ||||
| 1 | [10] | stagnation pressure | static pressure | - | - |
| 2 | [15] | static pressure | mass flow | H | 10 |
| 3 | [20] | constant total pressure | constant static pressure | η | 2.18 |
| 4 | [19] | - | - | H | 4 |
| 5 | [20] | constant total pressure | constant static pressure | η | 2.18 |
| 6 | [35] | mass flow | static frame total pressure | H | 5.56 |
| 7 | [36] | mass flow | static pressure | η | 5.19 |
| 8 | [41] | volume flow rate | average static pressure | η | 2.6 |
| 9 | [42] | flow rate | static pressure | Q | 10 |
| 10 | [44] | - | - | H | 2.2 |
| 11 | [45] | uniform velocity distribution | constant static pressure | H | 9.0 |
| 12 | [46] | mass flow | static pressure | H, η | - |
| 13 | [47] | static pressure | mass flow | η | 6.8 |
| 14 | [49] | uniform velocity | constant static pressure | H | 9 |
| 15 | [51] | - | - | Q | 0.82 |
| 16 | [52] | velocity inlet | static pressure | η | 8.70 |
| 17 | [53] | total pressure | mass flow | H | 3.70 |
| 18 | [54] | static pressure | mass flow | η | 7.69 |
| 19 | [55] | velocity inlet | pressure outlet | η | 3.99 |
| 20 | [56] | velocity inlet | pressure outlet | - | - |
| 21 | [69] | total pressure | environmental pressure | - | - |
| 22 | [58] | mass flow | - | - | - |
| 23 | [50] | mass flow | - | H | 4.81 |
| 24 | [59] | pressure | mass flow | η | 4.64 |
| 25 | [60] | constant total pressure | variable static | ψ | 4.00 |
| 26 | [61] | pressure inlet | pressure outlet | p | 28.60 |
| 27 | [62] | static pressure | mass flow | P | 12.31 |
| 28 | [63] | static pressure | mass flow | - | - |
| 29 | [64] | mass flow | static pressure | P | 14.71 |
| 30 | [65] | static pressure | mass flow | η | 4.17 |
| 31 | [66] | - | - | H | 10.00 |
| 32 | [67] | velocity | static pressure | H | 10.70 |
| 33 | [68] | volumetric flow rate | average static pressure | ψ | 5.00 |
| 34 | [70] | enviromental pressure 1bar | mass flow | - | - |
| 35 | [71] | static pressure | mass flow | - | - |
| 36 | [72] | mass flow | static pressure | ψ | - |
| 37 | [73] | total pressure | flow rate | η,ψ (design point) | 4.9 |
| 38 | [43] | mass flow, velocity direction, turbulence kinetic energy k and turbulent dissipation ε | static pressure | ψ | 22.9 |
| 38 | [76] | static pressure | mass flow | PSHAFT | 3.51 |
| n | Package | Numerical Simulation | Boundary Condition | Error Calculation | Reference | |||
|---|---|---|---|---|---|---|---|---|
| rpm | Closure M | Grid | Inlet | Outlet | Variable-Study | Relativemax Error (%) | ||
| 300–2200 | PumpLinx | k-ε | hexagonal not deformed cells | flow | pressure | p | 3.10 | [74] |
| 520–1500 | FloEFD | k-ε | structured hexaedral | flow rate | pressure | ΔH, η | (1,7–44,48), (0–52,4) | [39] |
| 810–1500 | FloEFD | k-ε with wall functions | structured hexahedral | flow rate | static pressure | H | 9 | [38] |
| 1500–2910 | ANSYS-FLUENT | k-ε | structured hexahedral/unstructured tetrahedral | Unif. velocity | static pressure | η | 34.62 | [37] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plua, F.; Hidalgo, V.; López-Jiménez, P.A.; Pérez-Sánchez, M. Analysis of Applicability of CFD Numerical Studies Applied to Problem When Pump Working as Turbine. Water 2021, 13, 2134. https://doi.org/10.3390/w13152134
Plua F, Hidalgo V, López-Jiménez PA, Pérez-Sánchez M. Analysis of Applicability of CFD Numerical Studies Applied to Problem When Pump Working as Turbine. Water. 2021; 13(15):2134. https://doi.org/10.3390/w13152134
Chicago/Turabian StylePlua, Frank, Victor Hidalgo, P. Amparo López-Jiménez, and Modesto Pérez-Sánchez. 2021. "Analysis of Applicability of CFD Numerical Studies Applied to Problem When Pump Working as Turbine" Water 13, no. 15: 2134. https://doi.org/10.3390/w13152134
APA StylePlua, F., Hidalgo, V., López-Jiménez, P. A., & Pérez-Sánchez, M. (2021). Analysis of Applicability of CFD Numerical Studies Applied to Problem When Pump Working as Turbine. Water, 13(15), 2134. https://doi.org/10.3390/w13152134









