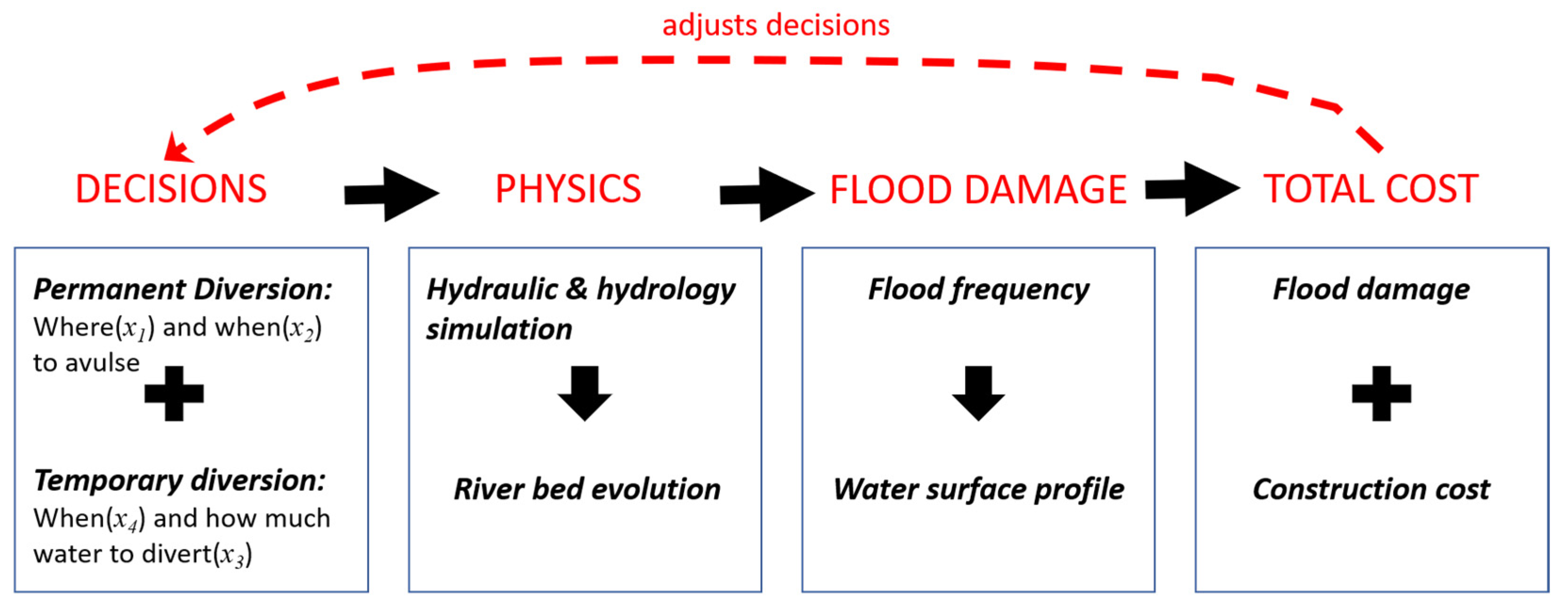
In this problem, two out of four decision variables (avulsion rule
and floodway size
) are modeled as adaptive (i.e., in year 10 they can be changed from their initial (Year 0) values), and there is a total of 250 alternatives representing different combinations of Year 0 and Year 10 decisions, as discussed in
Section 2.4. This section presents a comparison of open-loop (
Section 2.3) against adaptive decision-making, with the discussion being divided into four parts. First, the optimal choice of the two adaptive variables is summarized separately, which gives insight on the benefits of adaptive strategies and how they work. The focus of that discussion is on the benefits of modifying the system as conditions change under certainty (i.e., if it is known which scenario is occurring). Then, in the second part, we examine the additional benefits of adaptation under uncertainty, when it is not known in year 0 which scenario will occur. In such a case, because of learning, there may be a significant benefit to delay decisions on floodway size. This benefit is related to the idea of “option value” from real options theory [
69]. Third, we explore whether changing the cost parameters will alter the adaptive strategies—especially first stage decisions which is what decision makers must commit to today—and the resulting benefits of adaptation. Fourth and finally, we consider whether the benefits of implementing Principle 3 (adaptation) are primarily due to being able to modify plans under changing but predicted conditions or learning under uncertainty.
3.3.1. Second Stage (Adaptation) Choices concerning Floodway Size and Avulsion Rule, Given the First Stage Choices and Scenario
Here we provide some insight on the subset of benefits of adaptation that are realized, even if there is no uncertainty as to which scenario will occur. These arise from changing conditions over the planning time horizon, such that there are different levels of benefits from floodways and avulsions in later years than in earlier years as mean annual flow, mean flood, and sea levels gradually change. There are additional benefits of adaptation that arise if there is uncertainty; in particular, if it is not known in the first stage (year 0) which scenario will occur, then if the planner is better informed in the second stage (year 10), then the initial plan can be modified. These additional benefits are discussed in the next subsection.
First, we discuss the interaction of decisions
concerning floodway size in the first and second stages. If the first stage decision
0
(do not build the floodway right away), we preserve the option of whether or not to build the floodway later. Since the floodway size of 900
will not be discussed in this subsection (as it is dominated by 0 or 1800
as discussed above), we consider only 3 rather than 5 combinations of floodway size choices for the two stages: (0,0), (0,1800), (1800,1800).
Figure 4 summarizes the optimal choice of floodway size combinations ((0,0): dark blue; (0,1800): green; (1800,1800): yellow) given the scenario that is realized in stage 2 at year 10 (we assume that we learn for certain what happens at that time,
Section 2.4) and first stage avulsion decisions. As summarized in
Table 3, there are 25 choices of avulsion rule
decisions (five possible values of the first stage rule
times five possible values of the second stage rule
), and 2 choices of avulsion location
decisions (fixed throughout the first and second stage), which yields 50 avulsion decisions in total, which are shown in the
x-axis of
Figure 4. The first 25 alternatives from the left in the figure have 70
as their avulsion location, while the last 25 have 100
. Within these 25 choices, the first 5 have 2600
as their first stage avulsion rule, while the second stage avulsion rule decisions are 2600 to 3400, respectively (as indicated in the enlargement of the
x axis on the left). With the same logic, the second 5 choices have 2800
as their first stage avulsion rule, while 3000
is the first stage rule for the third 5 choices, etc. The
y-axis indicates the eight scenarios, defined in
Table 2.
To help with the interpretation of
Figure 4, consider the second column in the figure, which, as the enlargement shows, corresponds to an initial avulsion rule
= 2600
, which is then changed in the second stage to
= 2800
, and a location
of the floodway 70 km upstream. The eight cells in that column indicate what combination of first and second stage floodway (
and
) decisions concerning are optimal, given which of the eight scenarios the decision makers learn in Stage 2 is occurring. All eight cells indicate that no floodway is installed in stage 1 in any scenario, but that whether a floodway is built in stage 2 (after 10 years) depends on which scenario occurs then. The top cell, for instance, shows that if scenario 8 occurs, a floodway is optimal, but the third cell from the top, corresponding to scenario 6, reveals that no floodway is best in that situation.
An examination of the figure indicates that only a small number of combinations of scenarios and avulsion decisions would result in a floodway being optimal in both the first and second stage (yellow). These are the cases with highest avulsion trigger (3400 ), or with both a higher streamflow (S3, S4, S7, S8) and further upstream location (100 ). Higher streamflows result in higher riverbed elevations, so in that case floodway is a good means of reducing flood risk. The cases choosing not to have any floodway throughout the entire 50 years (dark blue) are always the scenarios with lower streamflows (S1, S2, S5, S6). In these cases, we will expect that lower bed elevations will occur, so floodways are not so useful. For the remaining cases (green, mostly in the higher streamflow scenarios), we benefit from delaying a commitment on building a floodway until after 10 years because its benefits are less than the costs of having built the floodway in the early years before the annual flows have changed.
Turning to adaptation possibilities arising from our ability to change the avulsion rule
, there are
choices available considering possible combinations for the first and second stage choices. The optimal choice of second stage avulsion rule depends on the scenario, as well as the first stage avulsion and floodway decisions.
Table 5 portrays the impact of scenario on the choice of second stage avulsion rule as well as floodway implementation for one particular first stage decision. In this example, we assume no floodway in the first stage (
= 0),
= 70
for the avulsion location and
= 2600
for the first stage avulsion rule. This first stage decision is considered most robust under robustness criteria M2 and M3, as discussed in
Section 3.2. The table can be interpreted as follows. For example, in S1, we choose 2800
and no floodway as our second stage decision, which yields a total cost of 5195 million ¥. The averaged minimum cost over 8 scenarios is 5665 million ¥. This is the expected cost of this particular first stage decision, given optimal choices in the second stage.
We now discuss the reasons for some of the scenario-specific choices in that table. First, considering second stage floodway construction, no floodway is constructed under the scenarios with lower streamflow (S1, S2, S5 and S6), due to lower bed aggradation and therefore lower flooding than in the other scenarios. Meanwhile, regarding the avulsion rule, S4 and S8 have higher streamflow and sea level rise, which results in higher bed aggradation rates, so less frequent avulsions (resulting from a small avulsion trigger) turn out to be optimal in order to lower the avulsion construction cost over the planning horizon. S2 and S6 have lower streamflow and higher sea level rise. In these cases, the effect of sea level rise is two-fold. It could increase the bed aggradation rate, but that impact is much less than the aggradation effect of higher streamflows. It could also increase flood damage, which would justify more frequent avulsions (due to a larger avulsion trigger rule) and associated construction costs. For all the other scenarios, an avulsion trigger in the middle is preferred.
These results demonstrate that second stage adaptation decision can depend strongly on what happens between the first and second stages, and that by allowing adaptation, the performance of the system improves. The ability to adapt depends on the first stage decision, and in the next subsection we analyze how consideration of adaptability can improve the choices that are made in the first stage.
3.3.2. Optimal First Stage Strategy Given Adaptability and Resulting Cost Improvement
Here, we examine the effect upon the optimal first stage choice of combining uncertainty regarding which scenario will occur, with the flexibility to choose a different avulsion rule in stage 2 as well as to build a floodway if not already constructed in stage 1, and the resulting expected cost. The key distinction between this subsection’s analyses and the previous subsection is that now year 0 commitments must be made without knowing which of the 8 scenarios will occur, but by year 10 the planner will have learned which scenario the system will follow.
Table 6 summarizes the improvement due to the availability of options to adapt in the second stage once it is learned which scenario will occur for each of the
combinations of first stage decisions. For instance, the first row in that table corresponds to the first stage decision considered in
Table 5 (2600
first stage avulsion rule 70
avulsion location, no floodway). The fourth column entry for that row shows that if those decisions are maintained throughout the second stage (as in the open-loop analysis of
Section 3.2), the resulting expected cost is 5704 million ¥. However, based on the information in
Table 5, if the optimal adaptation (avulsion rule
and floodway construction
) is made in the second stage in each scenario, under the assumption that in stage two the decision makers know which scenario they are in, the average cost falls to 5665 million ¥, as indicated in the fifth column entry of that row previously. That cost difference (−39 million ¥) is the value of adaptation.
Table 6 also shows in the last columns the expected costs if instead there is only one adaptation variable (either avulsion rule or floodway construction in stage 2); restricting the options in general will increase expected costs. In the case of the first row of
Table 6, for example, the resulting costs are 5684 million ¥ (cost change of −20 million ¥ relative to the open loop strategy) and 5687 million ¥ (a change of −17 million ¥), respectively. The fact that both adaptation alternatives improve expected cost shows that both have value, so it should not be surprising that having both available improves cost even more (−39 million ¥, as just noted).
Between the two adaptation decision variables and , being able to change the avulsion rule appears more valuable. In particular, an average −78 million ¥ cost decrease can be realized if just the avulsion rule can be changed, while a −23 million ¥ drop in cost occurs if the floodway can be built later without changing the avulsion rule.
Our final observation is that first stage decisions with no floodway ( = 0, odd numbered rows) see higher improvements than when a floodway is built in the first stage ( = 1800, even numbered rows). Additionally, when the first stage decisions involve a higher avulsion rule , adaptation results in a greater improvement. For example, in the first row, which has { = 2600 , = 70 , = 0 } as the first stage decisions, adaptation yields a cost decrease of −39 million ¥. In contrast, the ninth row, which has {3400 , 70 , 0 } as those first stage decisions, experiences a much greater cost decrease of −245 million ¥.
This trend indicates that a high avulsion trigger in stage one may be suboptimal, with a later correction to a lower level yielding large savings. This is evident when we calculate the optimal strategy when the scenario is unknown at the first stage; this strategy is the combination of a single first stage decision followed by the eight optimal second stage decisions, one per scenario that yields the lowest first plus probability-weighted second stage total cost. For any of the three adaptation cases in
Table 6, this optimum involves a low first stage trigger {
2600
}, with the recourse decisions in stage two shown in
Table 5, assuming that both avulsion and floodway decisions can be adaptive.
This first stage decision also happens to coincide with the most robust open-loop decision under two of the three robustness metrics M2 and M3 (
Section 3.2). This implies that considering adaptation (closed-loop modification of
and
in stage two) would not change the first stage decision under these assumptions, even though having the option to change
and
after learning which scenario applies lowers expected costs. However, under other assumptions, adaptation can change the first stage commitment, as we show next.
3.3.3. Sensitivity of Adaptation Benefits to Cost Assumptions
In
Table 6, we notice that the optimal solution favors less frequent avulsions (lower channel capacity triggers) and no floodway in the first stage, which means the cost of more frequent avulsions and the floodway exceed any additional decrease in expected flood damage that would be avoided if they were implemented. It is reasonable to ask whether those additional expenditures would be justified if we lower construction/operations cost or raise unit area flood damage.
Table 7 summarizes improvements due to considering adaptation for all the combinations of first stage decisions under three other cost assumptions: higher flood damages, and lower avulsion or floodway engineering costs.
In terms of robust (“closed loop”) decisions with no adaptation, the most robust decision (under the expected cost criterion M3) stays the same as under the baseline cost assumptions {
= 2600
,
= 70
,
= 0
} only under decreasing avulsion cost. However, as would be expected, that assumption yields a smaller total cost due to the shrinking avulsion cost (5512 in the middle of the first row of
Table 7, compared with 5704 in
Table 6). For the other two sensitivity cases (increased flood damage or decreased floodway cost), more costly strategies are preferred. The increased flood damage case favors {3000
, 100
, 1800
}, which has higher engineering costs in terms of both avulsion construction and floodway operation), while the decreased floodway cost case favors {2600
, 70
, 1800
} (increasing engineering cost only for the floodway). It can be concluded that the flood damage assumption matters the most in determining the avulsion rule since only in the case of altering that assumption is the decision regarding the rule changed compared with the original cost case.
However, comparing the optimal adaptive and non-adaptive optimal strategies (both marked as red) under each set of assumptions in
Table 7, the first stage decision for the adaptive strategy always prefers a larger avulsion rule (3400 vs. 3000 for increased damage assumptions, 3400 vs. 2600 for decreased avulsion costs, and 3400 vs. 2600 for decreased floodway cost case). That is to say, the ability to adapt makes higher target channel capacities optimal, which implies more frequent engineered avulsions.
This sensitivity analysis shows that considering second stage adaptation options can affect optimal choices in the first stage. This also results in improvements in expected performance; for instance, by choosing {3000 , 100 , 1800 } rather than {2600 , 70 , 0 } as the first stage decision in the adaptation case under lower flood damages, expected costs are 6438 rather than 6529. However, it is not clear whether the value of this flexibility lies mainly in the ability to change course when something unexpected happens, or whether most of the value of flexibility arises from being able to adapt to predictable changes in environmental conditions. We next consider the role of uncertainty in determining the value of adaptability.
3.3.4. Is the Value of Adaptability Due to Uncertainty or Just Flexibility to Adjust under Certainty?
The ability to change the avulsion rule in stage two, as well as to build a floodway if one was not built before, arises from two features of the decision problem:
- (1)
We assume that the decision makers learn which scenario occurs in stage two, so it can be valuable to adapt the system to lower costs once learning takes place.
- (2)
Because of changes in the system over time due to channel aggradation, delta growth, and possibly climate change, the best avulsion rule might change, and a floodway that is not optimal at first might become optimal later.
The first feature is relevant only if we consider uncertainty in the form of multiple scenarios. The second feature is relevant in both deterministic and stochastic analyses.
We now consider which of the two features is the major source of the value of adaptation. We do this by first determining the best adaptation strategy under certainty by creating a table like
Table 4 for each possible closed loop (non-adaptive) decision, and then determine for each of the eight scenarios which combination of first and second stage decisions are best, as shown in
Table 8. Allowing adaptation under certainty yields an average improvement of 47 million ¥, comparing the average cost of the optimal strategy if there are no second stage adjustments (5625 million ¥ average cost for no adaption, from
Table 4) to the average cost of the optimal strategy if stage two adjustments are possible, where the average is over scenarios. For instance, under scenario S1,
Table 4 shows that the best decision is {3000
, 100
, 0
}, and its cost if this decision cannot be changed in stage 2 is 5138 million ¥. However,
Table 8 shows that under this scenario that a lower cost results if the second stage can be changed, and the resulting decisions are {
= 2600
,
= 3400
,
= 100
,
= 0
,
= 1800
,
= 5000
}, incurring an expected cost of 5114 million ¥, an improvement of 24 million ¥. This average (over all scenarios) cost improvement of 47 million ¥ is due to being able to make a different second stage decision if the future is known. We call this the value of flexibility under perfect information.
Now, we attempt to calculate the cost improvement arising from allowing adaptation in the face of uncertainty. If we have no information about the future scenario in either stage one or two, we have an open-loop situation in which we are to choose both stages’ decisions from a total of 250 combinations of first and second stage variables, as shown in
Table 3. We simulate the performance of all of them under each scenario and calculate the average performance of each across 8 scenarios (
Table 2), and discover that the decisions that yield the best averaged performance are {
= 2600
(1st stage), 2600
(2nd stage),
70
,
0
(1st stage), 0
(2nd stage)}, with a cost of 5704 million ¥. This decision coincides with the best robust decision under M2 and M3 (
Section 3.3), since the first and second stage decisions are the same, which means the value of flexibility under no information about the future scenario is precisely zero. On the other hand, if we know exactly which scenario will occur ahead of time before choosing those variables, we can tailor the choices to the scenarios and lower expected costs by 126 million ¥. We call this the expected value of perfect information when allowing adaptation.
An intermediate case of information is when the scenario is learned in the second stage but is not known when a commitment is made in stage one, which is the expected value of partial information when allowing adaptation. This means that when we make the first stage decision at the beginning, we know nothing. However, when we make the second stage decision, the climate information (scenario) is regarded as common knowledge, and so the second stage decision can be tailored to the scenario. Average performance in this case is 38 million ¥ better than the no information case.
Table 9 summarizes the discussion of values of flexibility and information introduced above.
As discussed in
Section 2.1, the objective value contains two parts: engineering cost and flood damage. We now want to find out how the availability of information can affect each part of the objective. The result is summarized in
Table 10. Its first row shows that the average cost across all the scenarios of the best solution by scenario in
Table 8 is 5578 million ¥ and represents how well, in theory, we could do with both perfect information and adaptation. Meanwhile, the information for Row 2, which is the best expected cost adaptation strategy, can be drawn from
Table 6, and its cost is 5666 million ¥, as we previously reported. Finally, the best decision in Row 3 coincides with the most robust open-loop (no adaptation) alternative from metric M2 and M3, which would yield a total cost of 5704 million ¥, as discussed above. Comparing these three rows, we conclude that the more information that is available on the future climate (in terms of reduced uncertainty prior to making irreversible commitments), the more is spent on flood mitigation construction. For example, Row 3 is the case where we have least information, and it yields the lowest engineering cost and highest flood damage. By contrast, Row 1, where there is the most information, spends 50% more in engineering costs, in expectation, which is more than made up by the decrease in expected flooding costs.