Modelling the Influence from Biota and Organic Matter on the Transport Dynamics of Microplastics in the Water Column and Bottom Sediments in the Oslo Fjord
Abstract
:1. Introduction
2. Methods
2.1. Model Description
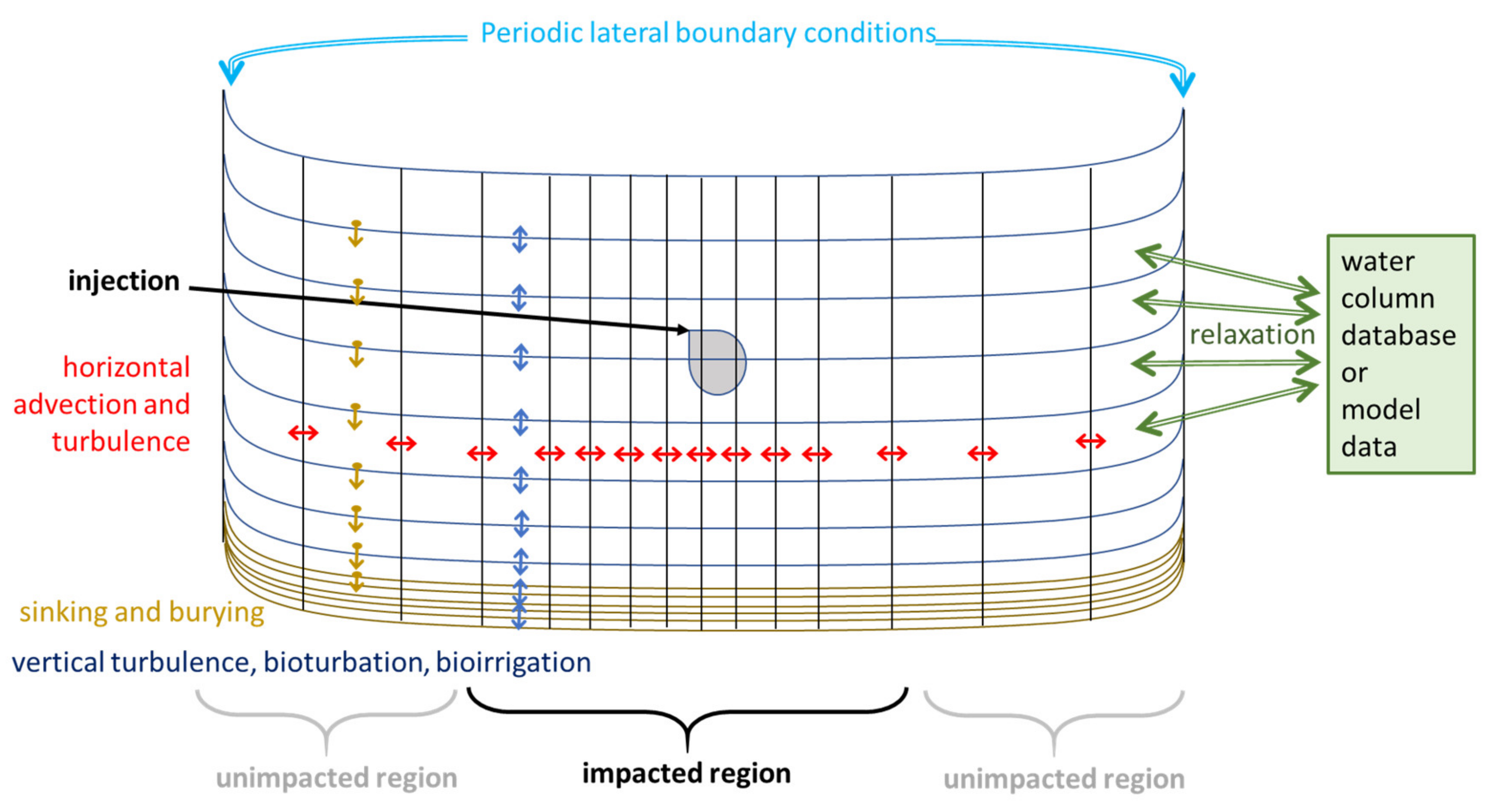
2.1.1. Transport Model
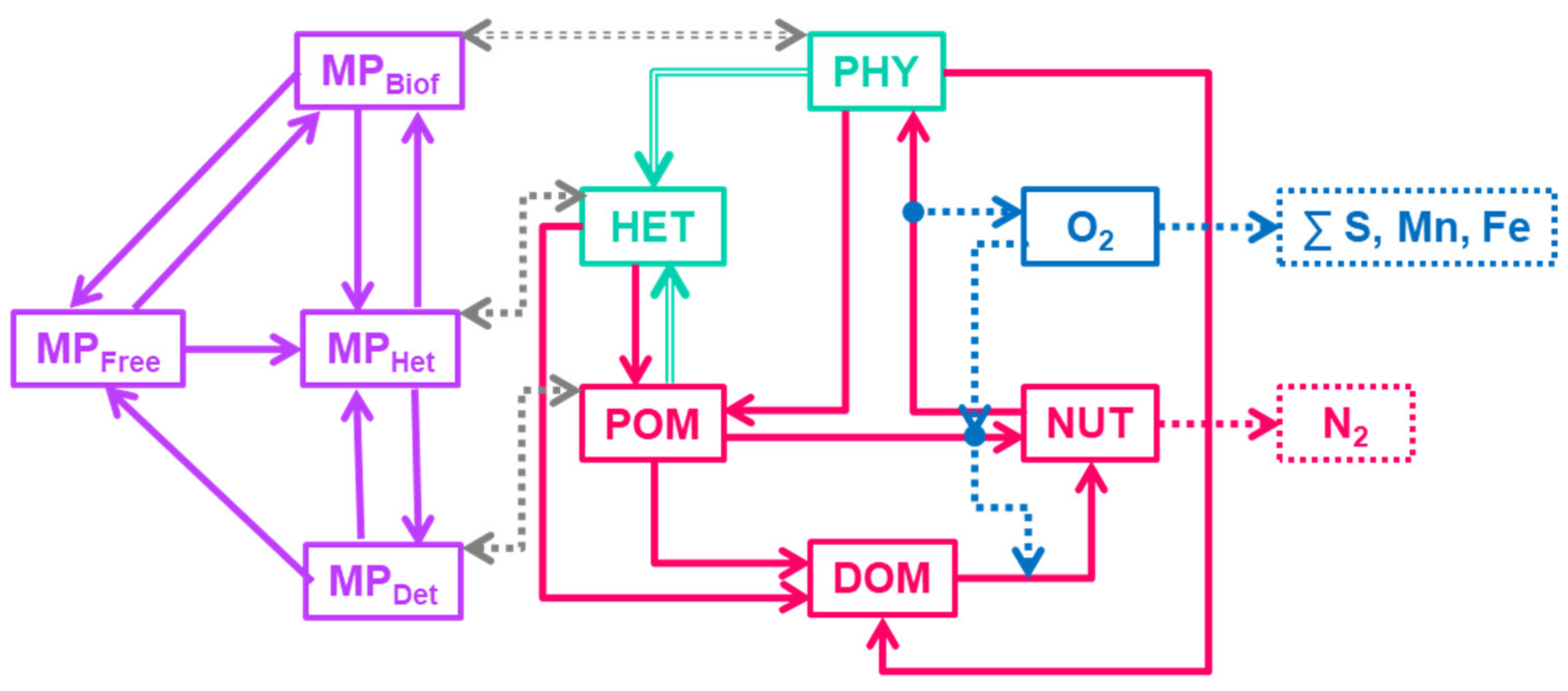
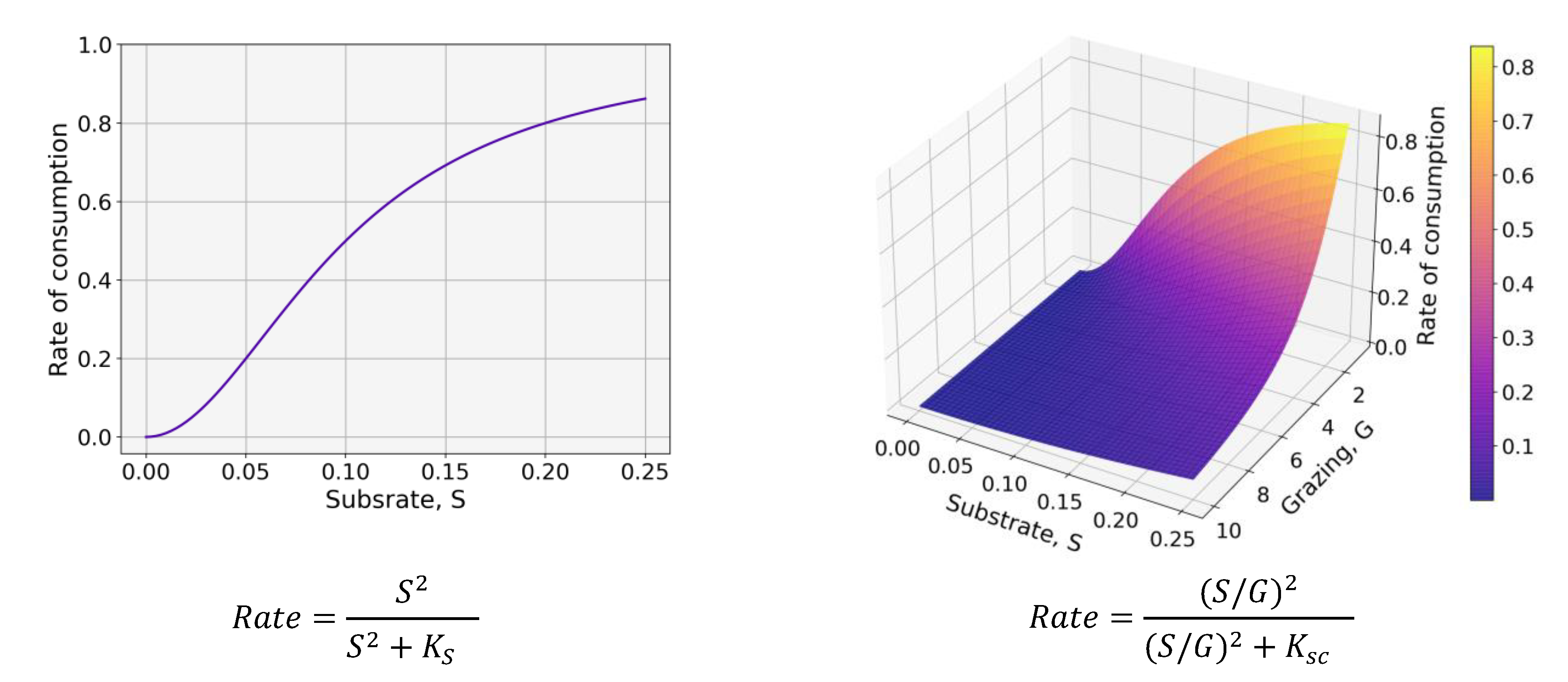
2.1.2. Coupled Biogeochemical and Microplastic Models
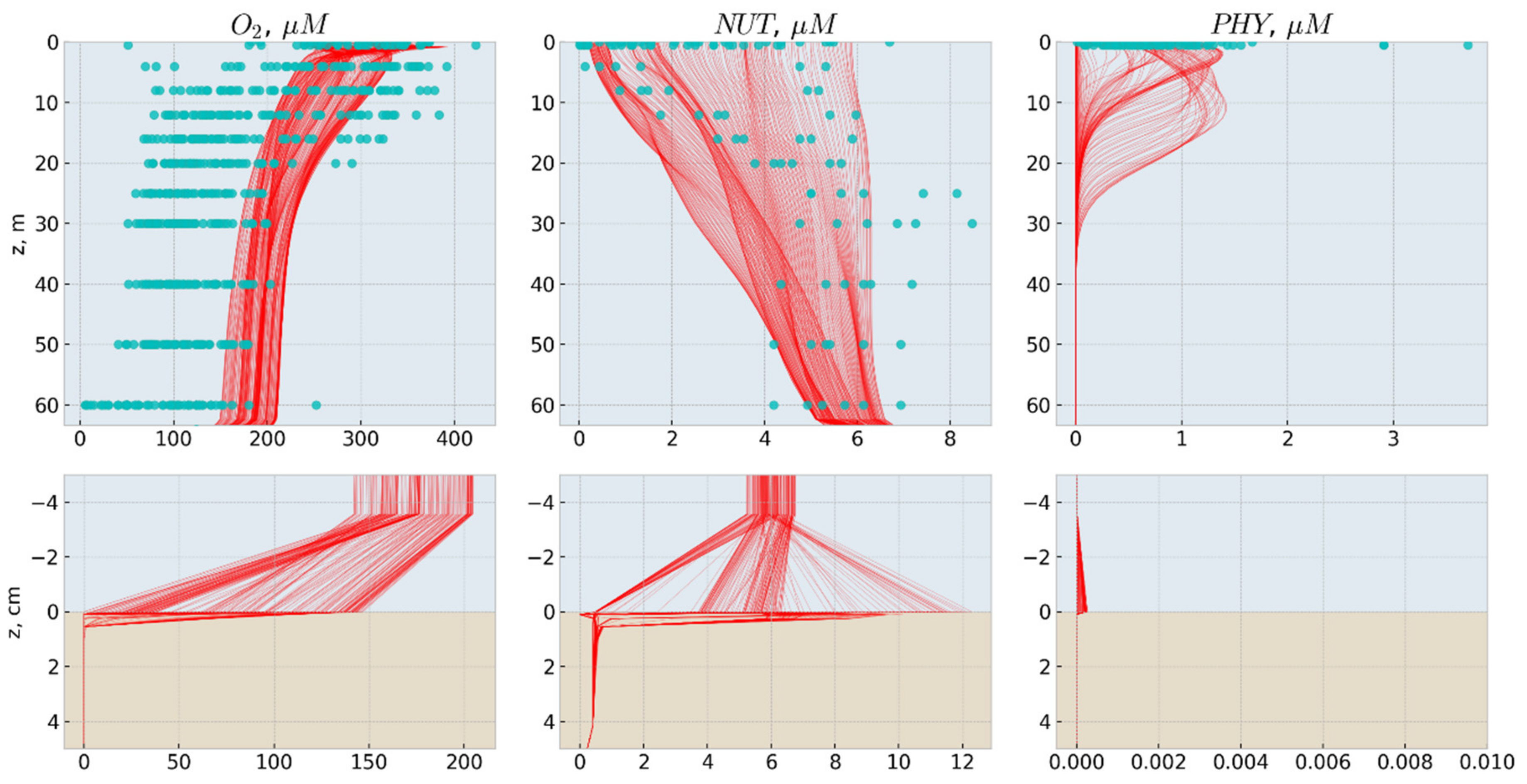
- PHY—all phototrophic organisms (phytoplankton and bacteria). PHY grows due to photosynthesis, loses inorganic matter due to respiration, and loses organic matter in dissolved (DOM) and particulate (POM) forms due to metabolism and mortality. PHY growth is limited by irradiance, temperature, and NUT availability.
- HET—heterotrophs are able to consume PHY and POM, produce DOM and POM and respirate NUT.
- NUT—represents oxidized forms of nutrients (i.e., NO3 and NO2 for N), that do not need additional oxygen for nitrification.
- DOM—dissolved organic matter. DOM includes all kinds of labile dissolved organic matter and reduced forms of inorganic nutrients i.e., NH4.
- POM—particular organic matter (less labile than DOM). Temperature affects DOM and POM mineralization.
- OXY—dissolved oxygen.
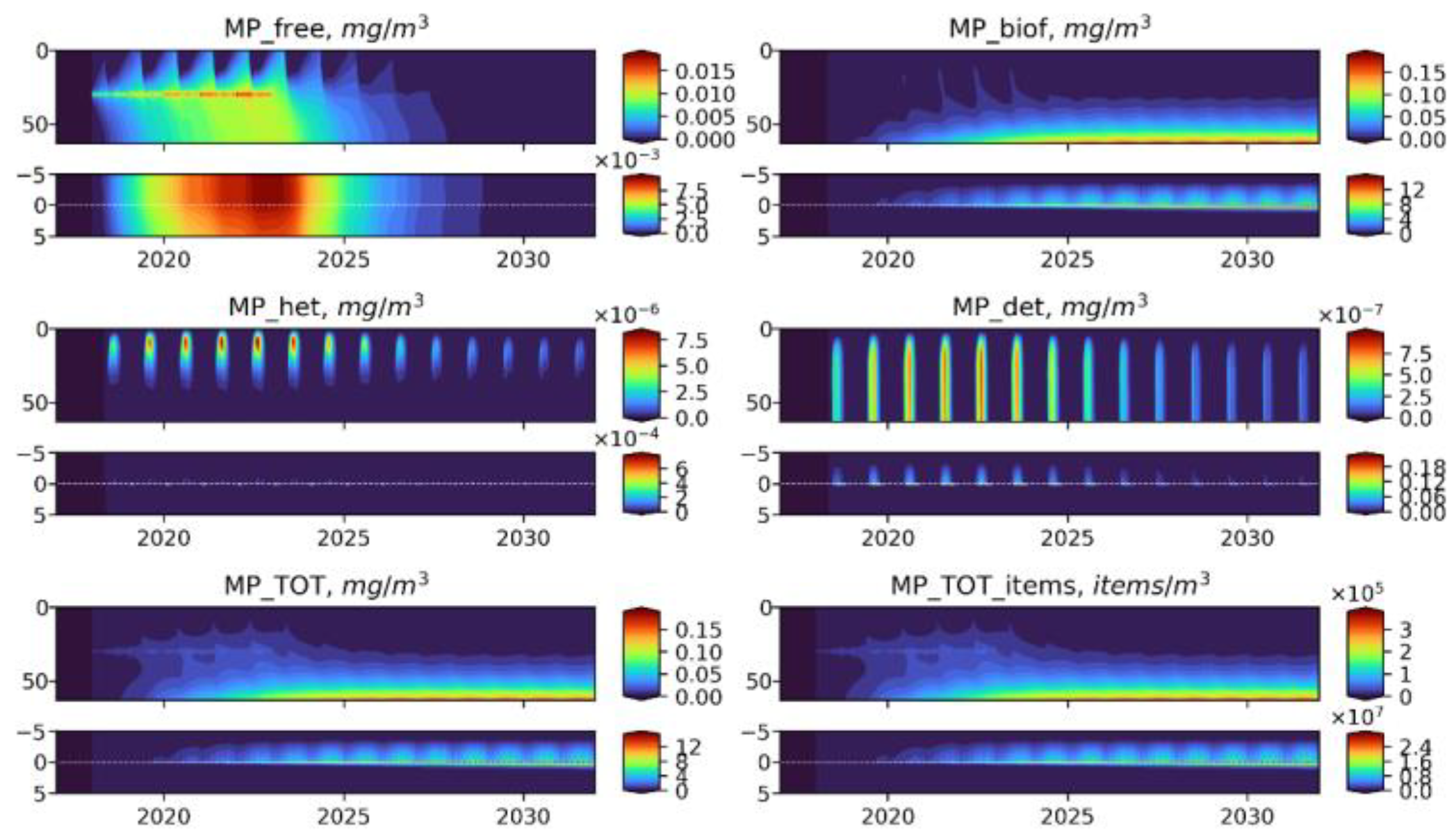
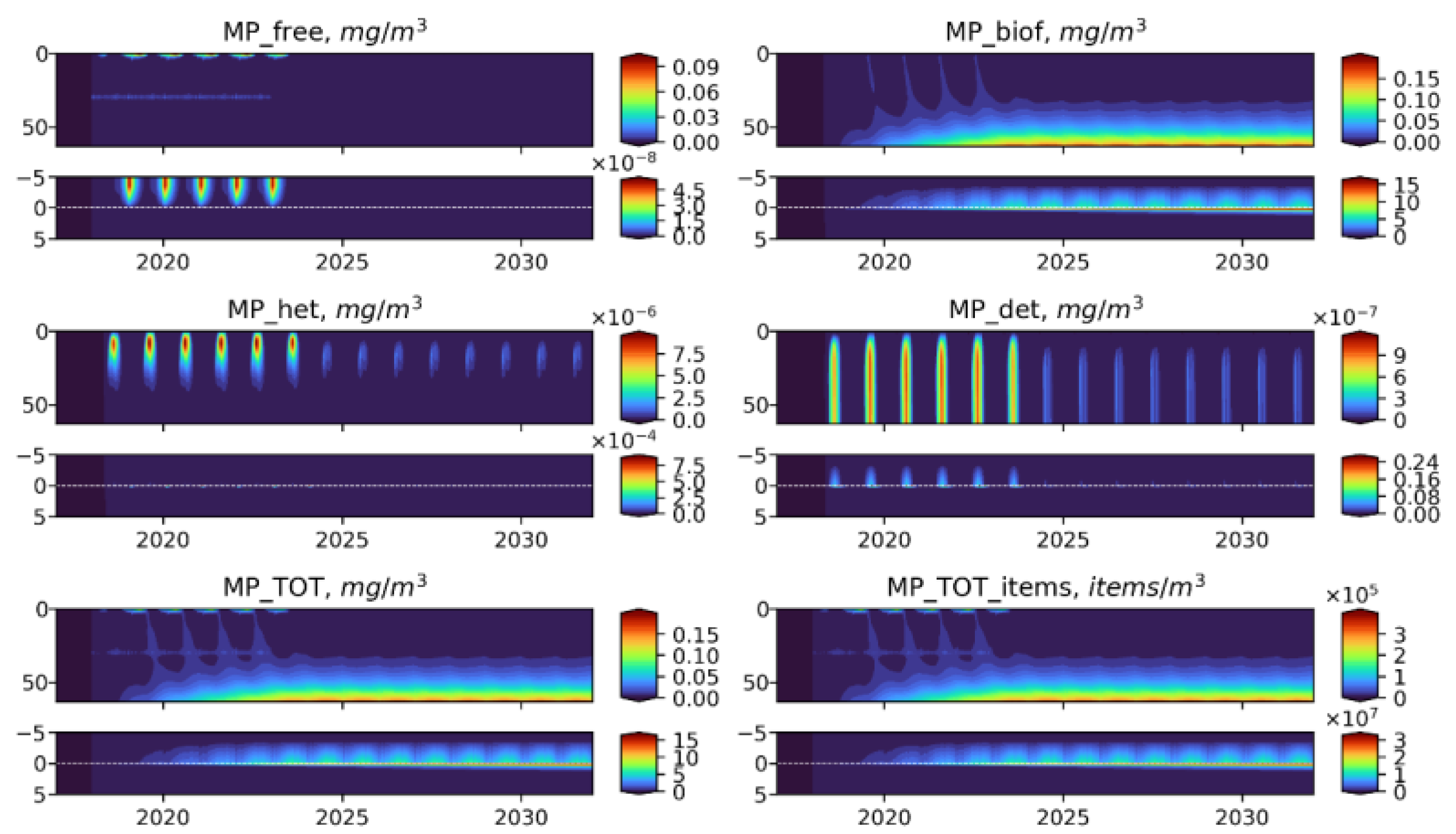
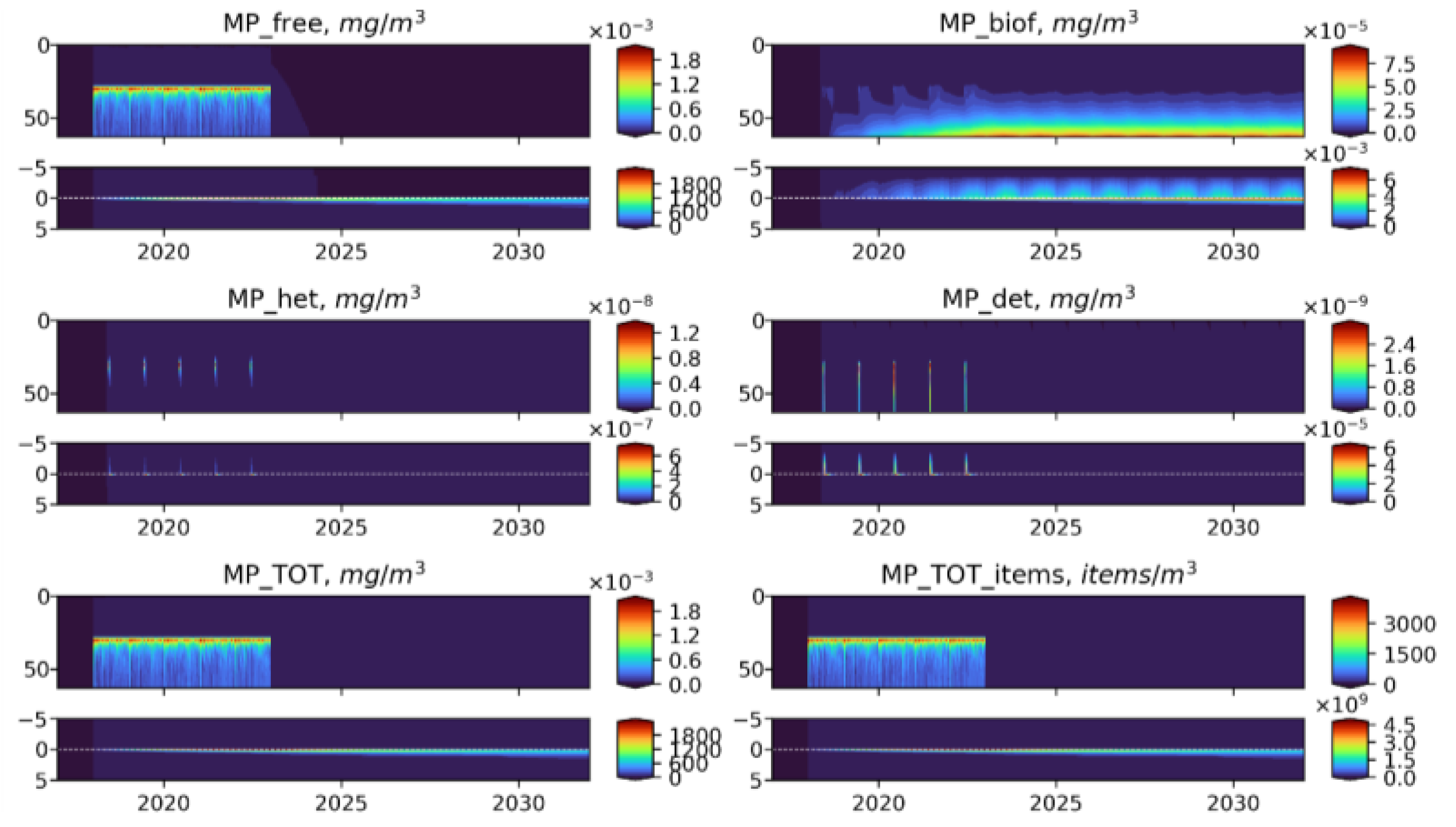
- —free MP particles,
- —particles with biofouling,
- —MP ingested by heterotrophs,
- —MP in detritus.
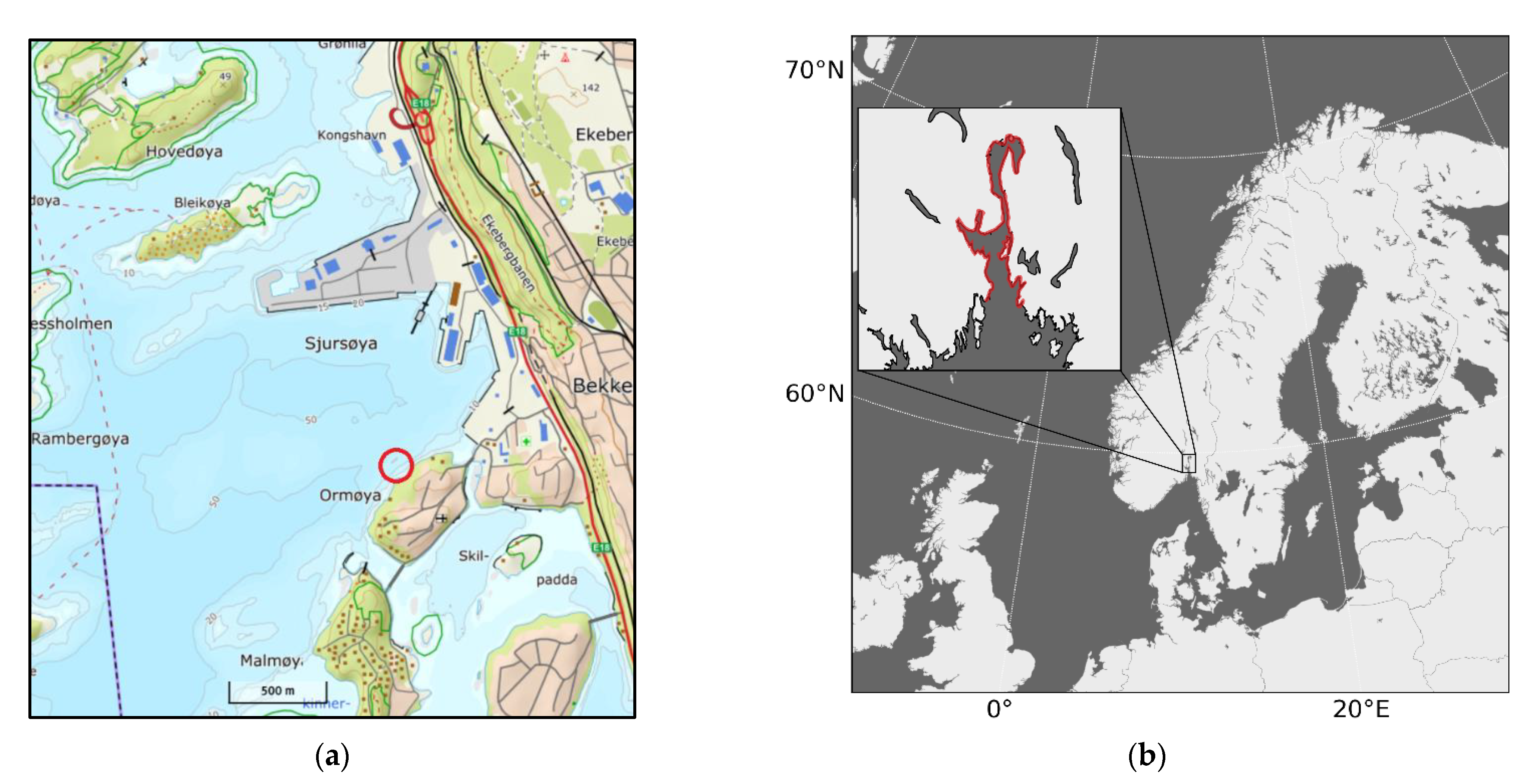
2.2. Initialization
Boundary Conditions
3. Results and Discussion
3.1. Biogeochemical Dynamics
3.2. Microplastics Dynamics
3.3. Microplastics Fluxes
3.4. Model Limitations
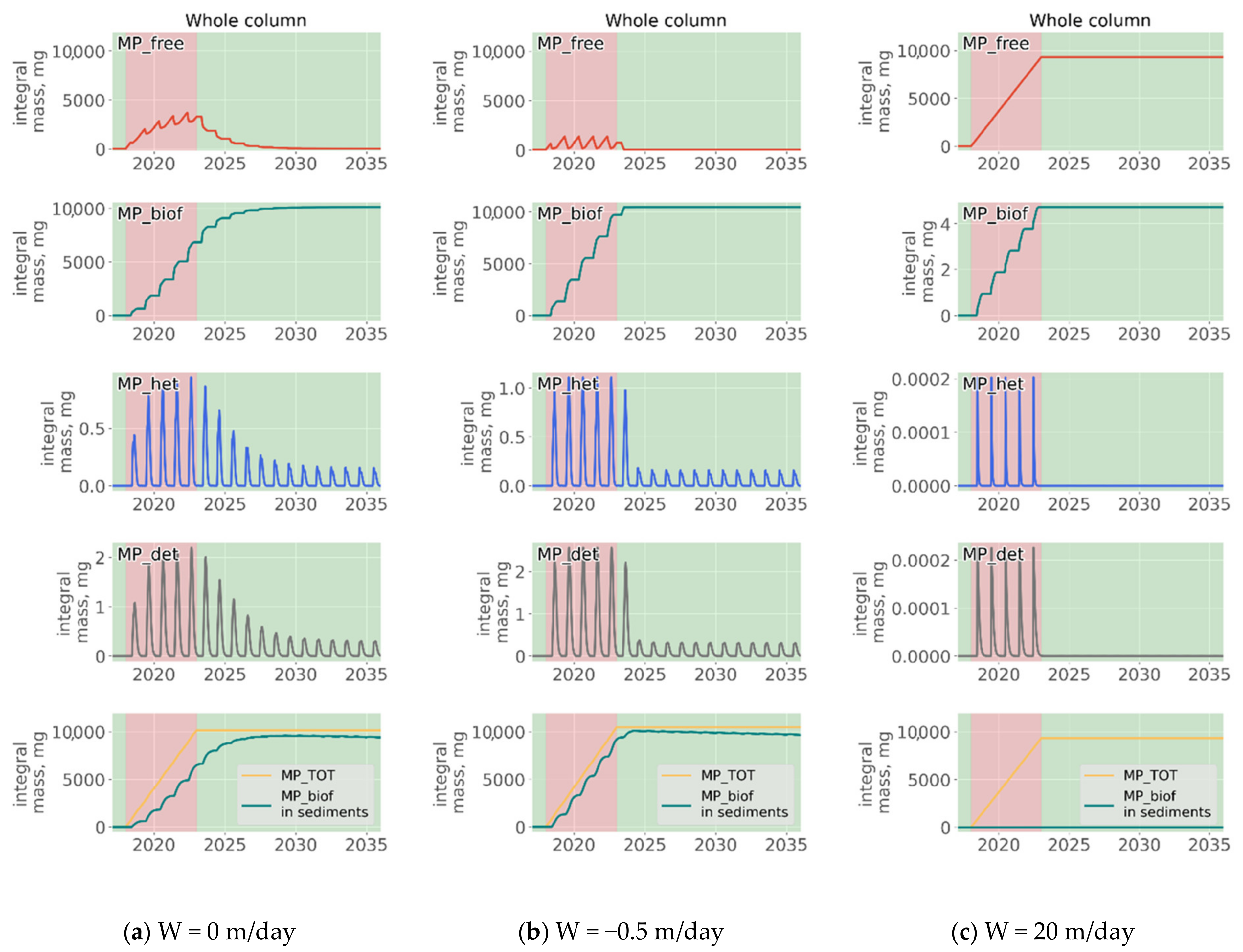
3.5. Influence of the Depth of the Discharge Point
4. Conclusions
- Biogeochemical cycling leads to seasonality in the vertical and horizontal transporting of MP of neutral buoyancy from its source, with higher accumulation in the sediment during the summer-autumn period, while cleaning of the upper water layers resembles the winter period. That means that MP of neutral buoyancy could be transported to a smaller distance in summer, compared with winter.
- Biogeochemical processes are responsible for transports of light density floating MP into the deep layers and the sediments.
- High density MPs are affected by the biogeochemical processes to a very small degree and tend to accumulate in the sediments close to the source point.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kershaw, P.J. Marine Plastic Debris and Microplastics: Global Lessons and Research to Inspire Action and Guide Policy Change; UNEP: Nairobi, Kenya, 2016; p. 192. [Google Scholar]
- Ross, N.L. The ‘Plasticene’ Epoch? Elements 2018, 14, 291. [Google Scholar] [CrossRef] [Green Version]
- GESAMP. Guidelines for the Monitoring and Assessment of Plastic Litter in the Ocean. Kershaw, P.J., Turra, A., Galgani, F., Eds.; GESAMP: London, UK, 2019. [Google Scholar]
- Horton, A.A.; Dixon, S.J. Microplastics: An introduction to environmental transport processes. Wiley Interdiscip. Rev. Water 2018, 5, e1268. [Google Scholar] [CrossRef] [Green Version]
- Jambeck, J.R.; Ji, Q.; Zhang, Y.-G.; Liu, D.; Grossnickle, D.M.; Luo, Z.-X. Plastic waste inputs from land into the ocean. Science 2015, 347, 764–768. [Google Scholar] [CrossRef]
- Lusher, A.L.; Hurley, R.R.; Vogelsang, C. Microplastics in sewage sludge: Captured but released? In Microplastics in Water and Wastewater; IWA Publishing: London, UK, 2017; pp. 85–100. [Google Scholar]
- Talvitie, J.; Heinonen, M.; Pääkkönen, J.P.; Vahtera, E.; Mikola, A.; Setälä, O.; Vahala, R. Do wastewater treatment plants act as a potential point source of microplastics? Preliminary study in the coastal Gulf of Finland, Baltic Sea. Water Sci. Technol. 2015, 72, 1495–1504. [Google Scholar] [CrossRef] [PubMed]
- Bagaev, A.; Mizyuk, A.; Khatmullina, L.; Isachenko, I.; Chubarenko, I. Anthropogenic fibres in the Baltic Sea water column: Field data, laboratory and numerical testing of their motion. Sci. Total Environ. 2017, 599-600, 560–571. [Google Scholar] [CrossRef] [PubMed]
- Lusher, A. Microplastics in the Marine Environment: Distribution, Interactions and Effects. In Marine Anthropogenic Litter; Springer International Publishing: Cham, Switzerland, 2015; pp. 245–307. [Google Scholar] [CrossRef] [Green Version]
- Avio, C.G.; Gorbi, S.; Regoli, F. Plastics and microplastics in the oceans: From emerging pollutants to emerged threat. Mar. Environ. Res. 2017, 128, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Wright, S.L.; Thompson, R.C.; Galloway, T.S. The physical impacts of microplastics on marine organisms: A review. Environ. Pollut. 2013, 178, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, D.; Kowalski, N.; Waniek, J.J. Effects of biofouling on the sinking behavior of microplastics. Environ. Res. Lett. 2017, 12, 124003. [Google Scholar] [CrossRef] [Green Version]
- Lobelle, D.; Cunliffe, M. Early microbial biofilm formation on marine plastic debris. Mar. Pollut. Bull. 2011, 62, 197–200. [Google Scholar] [CrossRef]
- Ye, S.; Andrady, A.L. Fouling of floating plastic debris under Biscayne Bay exposure conditions. Mar. Pollut. Bull. 1991, 22, 608–613. [Google Scholar] [CrossRef]
- Chubarenko, I.; Bagaev, A.; Zobkov, M.; Esiukova, E. On some physical and dynamical properties of microplastic particles in marine environment. Mar. Pollut. Bull. 2016, 108, 105–112. [Google Scholar] [CrossRef]
- Fazey, F.M.C.; Ryan, P.G. Biofouling on buoyant marine plastics: An experimental study into the effect of size on surface longevity. Environ. Pollut. 2016, 210, 354–360. [Google Scholar] [CrossRef]
- Kooi, M.; Van Nes, E.H.; Scheffer, M.; Koelmans, A.A. Ups and Downs in the Ocean: Effects of Biofouling on Vertical Transport of Microplastics. Environ. Sci. Technol. 2017, 51, 7963–7971. [Google Scholar] [CrossRef] [Green Version]
- Courtene-Jones, W.; Quinn, B.; Gary, S.F.; Mogg, A.O.M.; Narayanaswamy, B.E. Microplastic pollution identified in deep-sea water and ingested by benthic invertebrates in the Rockall Trough, North Atlantic Ocean. Environ. Pollut. 2017, 231, 271–280. [Google Scholar] [CrossRef] [Green Version]
- Beur, L.L.; Henry, L.A.; Kazanidis, G.; Hennige, S. Baseline assessment of marine litter and microplastic ingestion by cold-water coral reef benthos at the east mingulay marine protected area (Sea of the Hebrides, western Scotland). Front. Mar. Sci. 2019, 6, 1–13. [Google Scholar] [CrossRef]
- Moore, C.J. Synthetic polymers in the marine environment: A rapidly increasing, long-term threat. Environ. Res. 2008, 108, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Rummel, C.D.; Jahnke, A.; Gorokhova, E.; Kühnel, D.; Schmitt-Jansen, M. Impacts of biofilm formation on the fate and potential effects of microplastic in the aquatic environment, Environ. Sci. Technol. Lett. 2017, 4, 258–267. [Google Scholar] [CrossRef] [Green Version]
- Setälä, O.; Fleming-Lehtinen, V.; Lehtiniemi, M. Ingestion and transfer of microplastics in the planktonic food web. Environ. Pollut. 2014, 185, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Watts, A.J.R.; Lewis, C.; Goodhead, R.M.; Beckett, S.J.; Moger, J.; Tyler, C.R.; Galloway, T.S. Uptake and retention of microplastics by the shore crab carcinus maenas. Environ. Sci. Technol. 2014, 48, 8823–8830. [Google Scholar] [CrossRef]
- Botterell, Z.L.R.; Beaumont, N.; Dorrington, T.; Steinke, M.; Thompson, R.C.; Lindeque, P.K. Bioavailability and effects of microplastics on marine zooplankton: A review. Environ. Pollut. 2019, 245, 98–110. [Google Scholar] [CrossRef] [PubMed]
- Codina-García, M.; Militão, T.; Moreno, J.; González-Solís, J. Plastic debris in Mediterranean seabirds. Mar. Pollut. Bull. 2013, 77, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.W.; Shim, W.J.; Kwon, O.Y.; Kang, J.H. Size-dependent effects of micro polystyrene particles in the marine copepod tigriopus japonicus. Environ. Sci. Technol. 2013, 47, 11278–11283. [Google Scholar] [CrossRef] [PubMed]
- Cole, M.; Lindeque, P.K.; Fileman, E.; Clark, J.; Lewis, C.; Halsband, C.; Galloway, T.S. Microplastics alter the properties and sinking rates of zooplankton faecal pellets. Environ. Sci. Technol. 2016, 50, 3239–3246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lebreton, L.C.M.; Greer, S.D.; Borrero, J.C. Numerical modelling of floating debris in the world’s oceans. Mar. Pollut. Bull. 2012, 64, 653–661. [Google Scholar] [CrossRef] [PubMed]
- Mountford, A.S.; Morales Maqueda, M.A. Eulerian Modeling of the Three-Dimensional Distribution of Seven Popular Microplastic Types in the Global Ocean. J. Geophys. Res. Ocean. 2019, 124, 8558–8573. [Google Scholar] [CrossRef]
- Herzke, D.; Ghaffari, P.; Sundet, J.H.; Tranang, C.A.; Halsband, C. Microplastic fiber emissions from wastewater effluents: Abundance, transport behavior and exposure risk for biota in an arctic fjord. Front. Environ. Sci. 2021, 9, 1–14. [Google Scholar] [CrossRef]
- Vermeiren, P.; Muñoz, C.C.; Ikejima, K. Sources and sinks of plastic debris in estuaries: A conceptual model integrating biological, physical and chemical distribution mechanisms. Mar. Pollut. Bull. 2016, 113, 7–16. [Google Scholar] [CrossRef]
- Lobelle, D.; Kooi, M.; Koelmans, A.A.; Laufkötter, C.; Jongedijk, C.E.; Kehl, C.; van Sebille, E. Global modeled sinking characteristics of biofouled microplastic. J. Geophys. Res. Ocean. 2021, 126, e2020JC017098. [Google Scholar] [CrossRef]
- Murawski, J.; She, J. Fate and dynamic of marine microplastics in the baltic sea CLAIM: Project overview H2020 Innovation Action. In Proceedings of the 22nd EGU General Assembly, Online, 4–8 May 2020; pp. 1–22. [Google Scholar] [CrossRef]
- Vogelsang, C.P.S.; Singdahl-Larsen, C.; Kristiansen, T.; Staalstrøm, A.; Buenaventura, N.T.; Latcheman, D. Microplastic particles in to and out from Bekkelaget wastewater treatment plant over a year; NIVA Report 7541-2020: Oslo, Norwey, 2020. [Google Scholar]
- Bruggeman, J.; Bolding, K. A general framework for aquatic biogeochemical models. Environ. Model. Softw. 2014, 61, 249–265. [Google Scholar] [CrossRef] [Green Version]
- Yakushev, E.V.; Wallhead, P.; Renaud, P.E.; Ilinskaya, A.; Protsenko, E.; Yakubov, S.; Pakhomova, S.; Sweetman, A.K.; Dunlop, K.; Berezina, A.; et al. Understanding the biogeochemical impacts of fish farms using a benthic-pelagic model. Water 2020, 12, 2384. [Google Scholar] [CrossRef]
- Yakushev, E.V.V.; Kuznetsov, I.S.S.; Podymov, O.I.I.; Burchard, H.; Neumann, T.; Pollehne, F. Modeling the influence of oxygenated inflows on the biogeochemical structure of the Gotland Sea, central Baltic Sea: Changes in the distribution of manganese. Comput. Geosci. 2011, 37, 398–409. [Google Scholar] [CrossRef]
- Yakushev, E.V.; Protsenko, E.A.; Bruggeman, J.; Wallhead, P.; Pakhomova, S.V.; Yakubov, S.K.; Bellerby, R.G.J.; Couture, R.-M. Bottom RedOx Model (BROM v1.1): A coupled benthic–pelagic model for simulation of water and sediment biogeochemistry. Geosci. Model Dev. 2017, 10, 453–482. [Google Scholar] [CrossRef] [Green Version]
- Haidvogel, D.B.H.; Arango, P.W.; Budgell, B.D.; Cornuelle, E.; Curchitser, E.D.; Lorenzo, K.; Fennel, W.R.; Geyer, A.J.; Hermann, L.; Lanerolle, J.; et al. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2008, 227, 3595–3624. [Google Scholar] [CrossRef]
- Staalstrøm, A.; Røed, L.P. Vertical mixing and internal wave energy fluxes in a sill fjord. J. Mar. Syst. 2016, 159, 15–32. [Google Scholar] [CrossRef] [Green Version]
- Okubo, A. Remarks on the use of “diffusion diagrams” in modeling scale-dependent diffusion. Deep. Res. Oceanogr. Abstr. 1976, 23, 1213–1214. [Google Scholar] [CrossRef]
- Hernan, E.G.; Katharine, W.W.; Christopher, R.P.; Igor, S.; Timothy, P.B.; Ricardo, A.L.; Melissa, M.Z.; Alexey, V.M.; Olga, K.B.; Dan, S. World Ocean Atlas 2018. Vol. 4: Dissolved Inorganic Nutrients (Phosphate, Nitrate and Nitrate+Nitrite, Silicate); National Centers for Environmental Information (NCEI): Silver Spring, MD, USA, 2019. [Google Scholar]
- Menden-Deuer, S.; Lessard, E.J. Carbon to volume relationships for dinoflagellates, diatoms, and other protist plankton. Limnol. Oceanogr. 2000, 45, 569–579. [Google Scholar] [CrossRef] [Green Version]
- Yakushev, E.; Gebruk, A.; Osadchiev, A.; Pakhomova, S.; Lusher, A.; Berezina, A.; van Bavel, B.; Vorozheikina, E.; Chernykh, D.; Kolbasova, G.; et al. Microplastics distribution in the Eurasian Arctic is affected by Atlantic waters and Siberian rivers. Commun. Earth Environ. 2021, 2, 1–11. [Google Scholar] [CrossRef]
- Lusher, A.L.; Tirelli, V.; O’Connor, I.; Officer, R. Microplastics in Arctic polar waters: The first reported values of particles in surface and sub-surface samples. Sci. Rep. 2015, 5, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lönnstedt, O.M.; Eklöv, P. Environmentally relevant concentrations of microplastic particles influence larval fish ecology. Science 2016, 352, 1213–1216. [Google Scholar] [CrossRef]
- Uddin, S.; Fowler, S.W.; Uddin, M.F.; Behbehani, M.; Naji, A. A review of microplastic distribution in sediment profiles. Mar. Pollut. Bull. 2021, 163, 111973. [Google Scholar] [CrossRef]
- Zobkov, M.B.; Esiukova, E.E.; Zyubin, A.Y.; Samusev, I.G. Microplastic content variation in water column: The observations employing a novel sampling tool in stratified Baltic Sea. Mar. Pollut. Bull. 2019, 138, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Uurasjärvi, E.; Pääkkönen, M.; Setälä, O.; Koistinen, A.; Lehtiniemi, M. Microplastics accumulate to thin layers in the stratified Baltic Sea. Environ. Pollut. 2021, 268, 115700. [Google Scholar] [CrossRef] [PubMed]

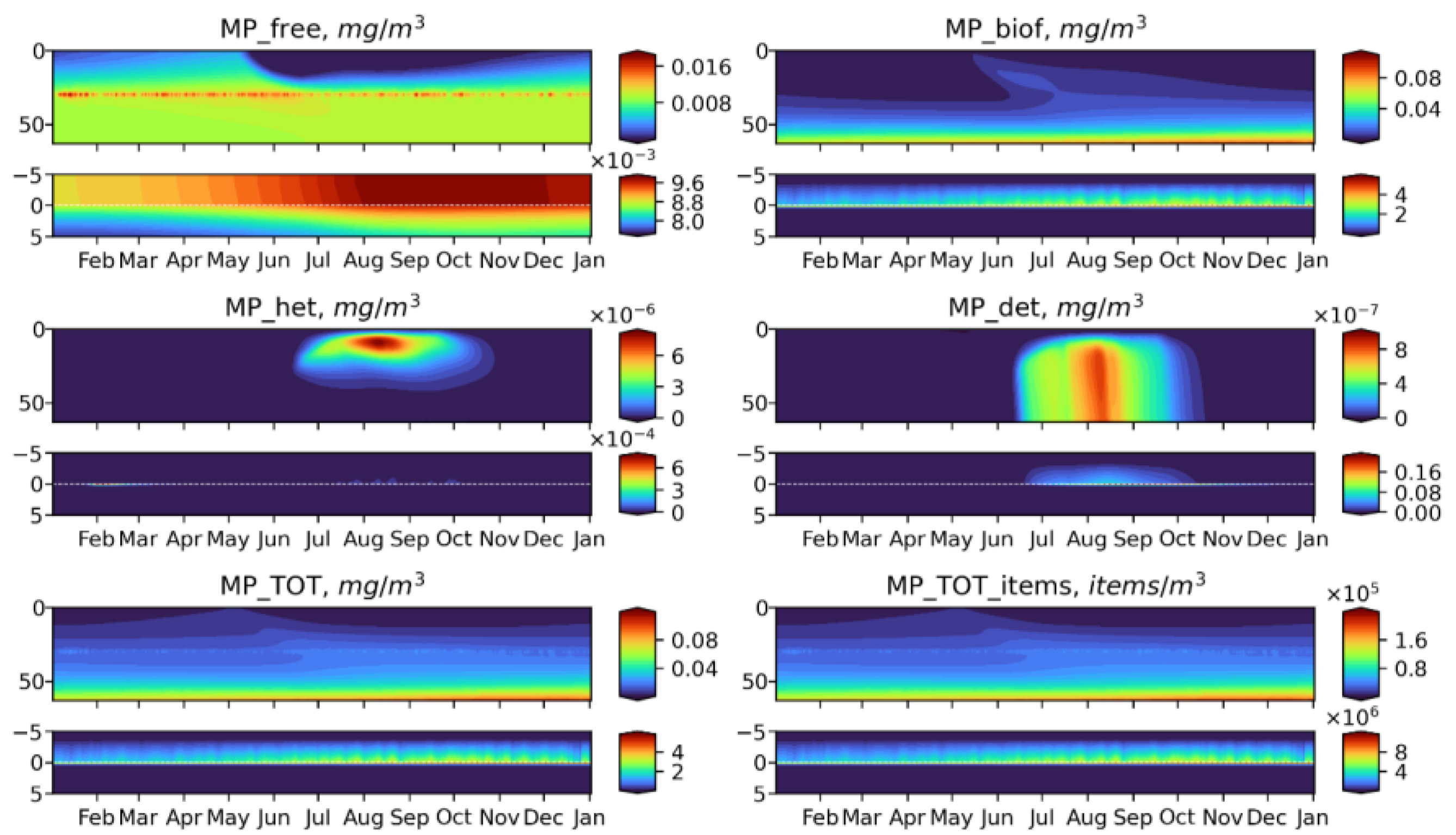
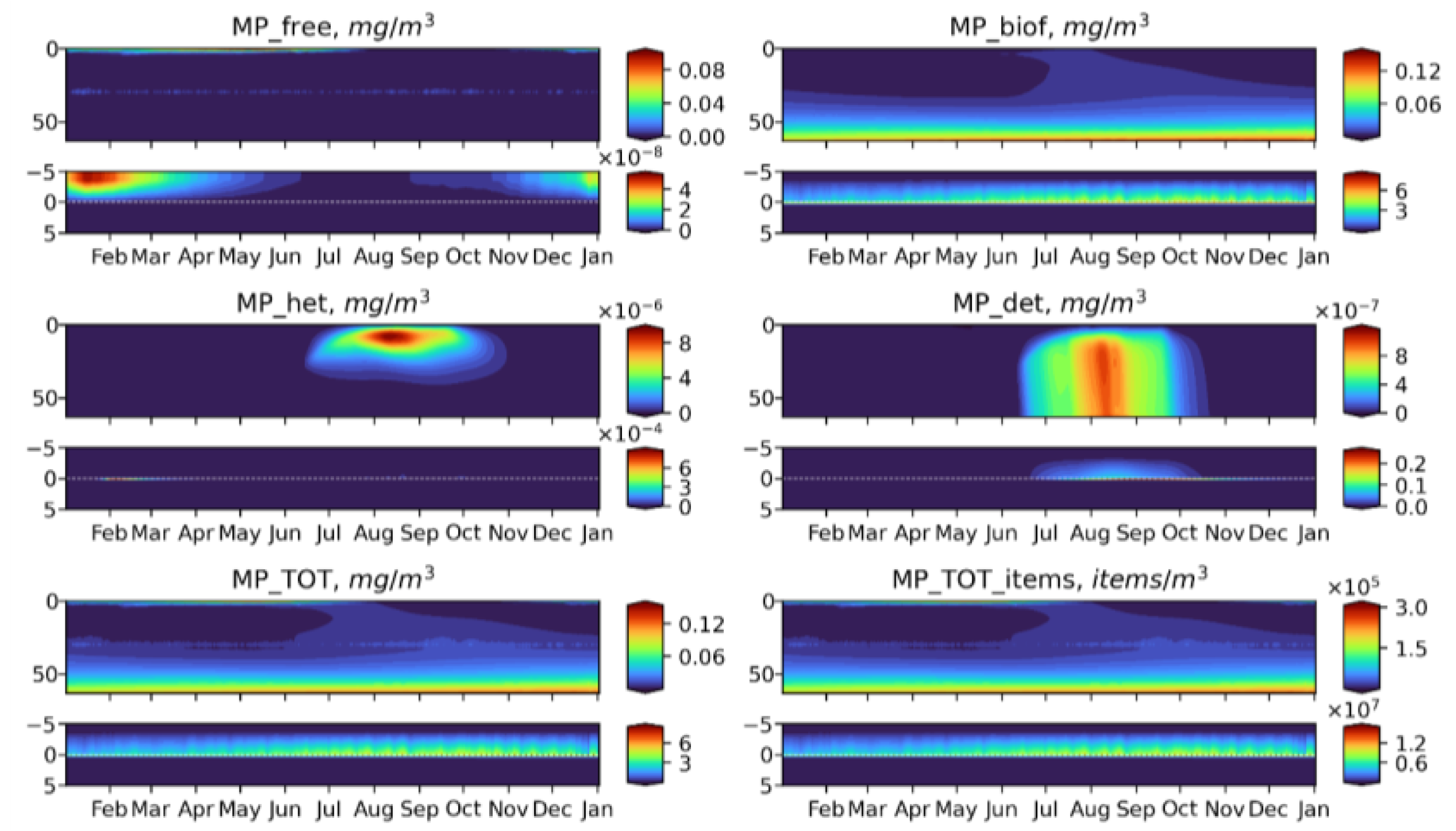
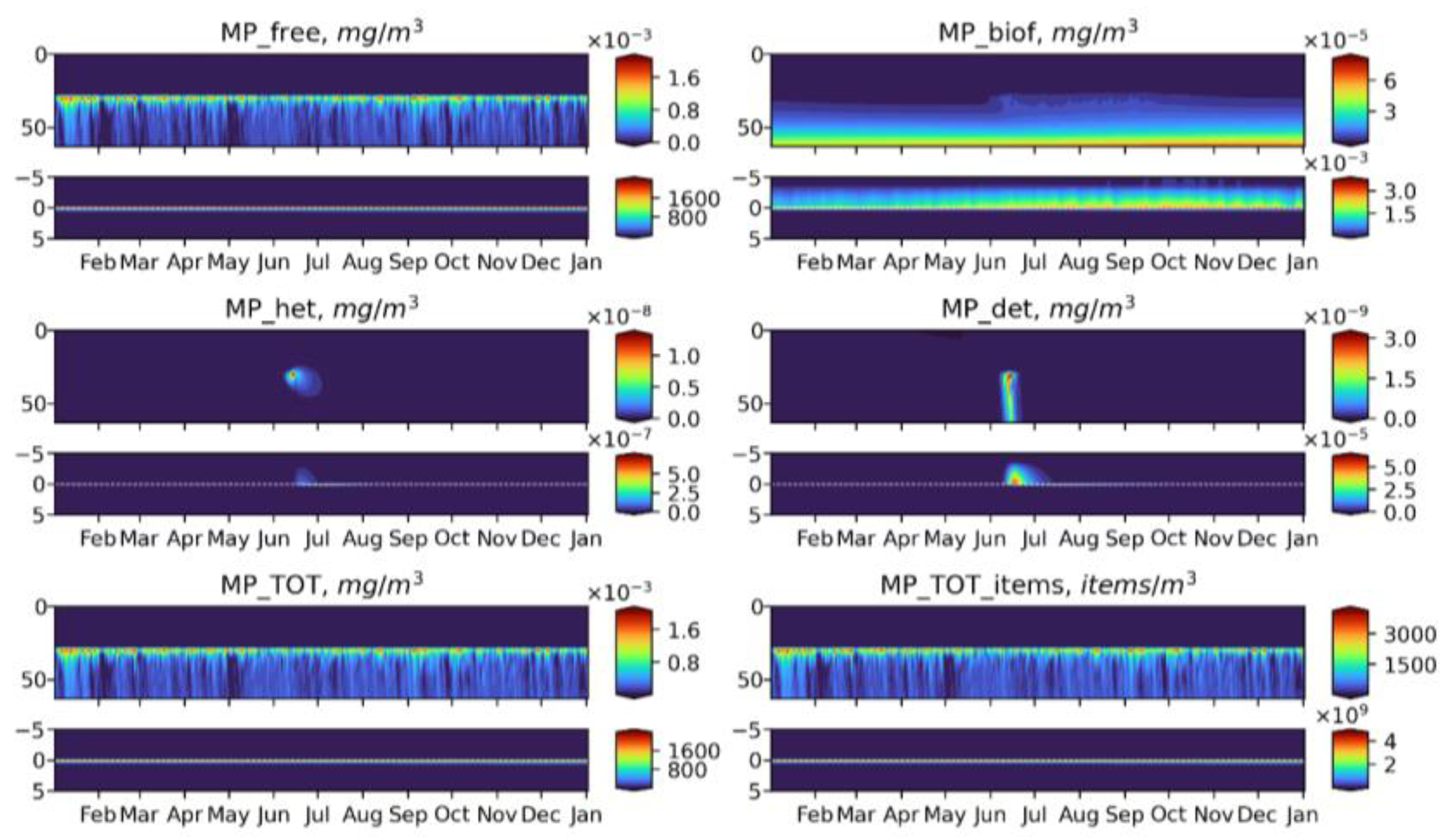

| LAYER | Observations Other Regions | Observations Oslo Fjord | Model Prediction | |||
|---|---|---|---|---|---|---|
| mg/m3 | Items/m3 | mg/m3 | Items/m3 | mg/m3 | Items/m3 | |
| Upper layer 0–30 m | 0.001 (Arctic water, [44]) 0.0038 (Atlantic surface water, [44]) | 0–1.31 (Arctic Polar water, [45]) 2.68 (North Atlantic, [9]) From 150–2400 to 68,000–102,000 (Swedish coast, [46]) 0.8 (37) | 10−5–10−3 | 10–1400 | ||
| Deep layers (30 m-bottom) | 0.14–2.5 | 104–105 | ||||
| Sediments | About 500 (Danish straits, [47]) | 10−4–3.1 mg/kg wet weight sediment | 100–4000 items/kg WSed [34] 2000–107,000 items/kg of dry sediment | 7 | 104–105 items/kg of wet weight * | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezina, A.; Yakushev, E.; Savchuk, O.; Vogelsang, C.; Staalstrom, A. Modelling the Influence from Biota and Organic Matter on the Transport Dynamics of Microplastics in the Water Column and Bottom Sediments in the Oslo Fjord. Water 2021, 13, 2690. https://doi.org/10.3390/w13192690
Berezina A, Yakushev E, Savchuk O, Vogelsang C, Staalstrom A. Modelling the Influence from Biota and Organic Matter on the Transport Dynamics of Microplastics in the Water Column and Bottom Sediments in the Oslo Fjord. Water. 2021; 13(19):2690. https://doi.org/10.3390/w13192690
Chicago/Turabian StyleBerezina, Anfisa, Evgeniy Yakushev, Oleg Savchuk, Christian Vogelsang, and André Staalstrom. 2021. "Modelling the Influence from Biota and Organic Matter on the Transport Dynamics of Microplastics in the Water Column and Bottom Sediments in the Oslo Fjord" Water 13, no. 19: 2690. https://doi.org/10.3390/w13192690
APA StyleBerezina, A., Yakushev, E., Savchuk, O., Vogelsang, C., & Staalstrom, A. (2021). Modelling the Influence from Biota and Organic Matter on the Transport Dynamics of Microplastics in the Water Column and Bottom Sediments in the Oslo Fjord. Water, 13(19), 2690. https://doi.org/10.3390/w13192690







