Assessing the Impact of Soil Moisture on Canopy Transpiration Using a Modified Jarvis-Stewart Model
Abstract
:1. Introduction
2. Materials and Methods
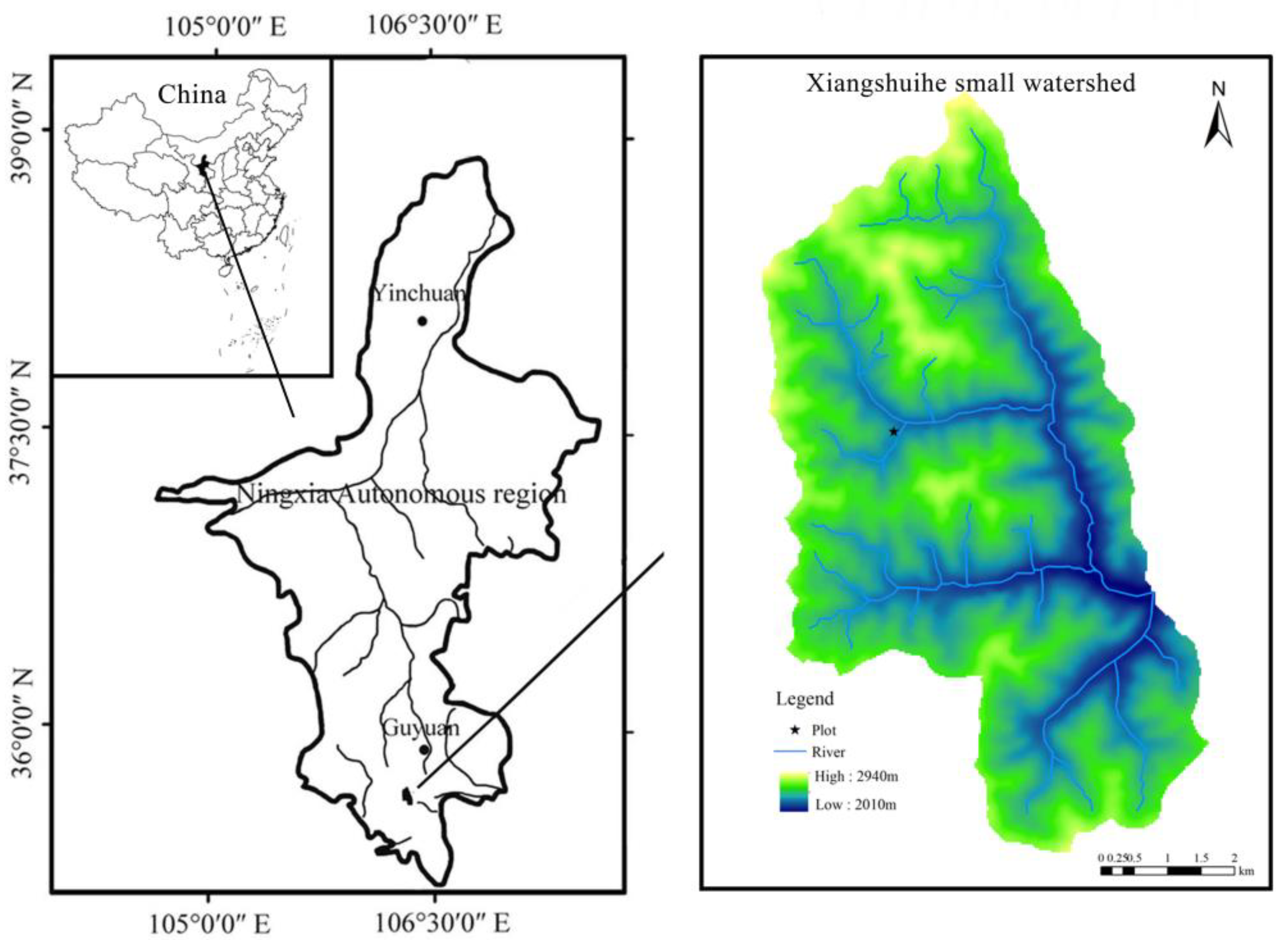
2.1. Study Site and Plant Materials
2.2. Measurement of Meteorological Factors
2.3. Measurement of Soil Water Content
2.4. Measurement of LAI
2.5. Calculation of Sap Flow and T
2.6. Model Establishment
2.6.1. Modified Jarvis-Stewart Model
2.6.2. Determination of the Response Relationship of T to Single Factor and Their Thresholds
2.6.3. Calibration and Validation of the Modified Jarvis—Stewart Model
2.7. Calculation of the Factor Contribution Rate
3. Results
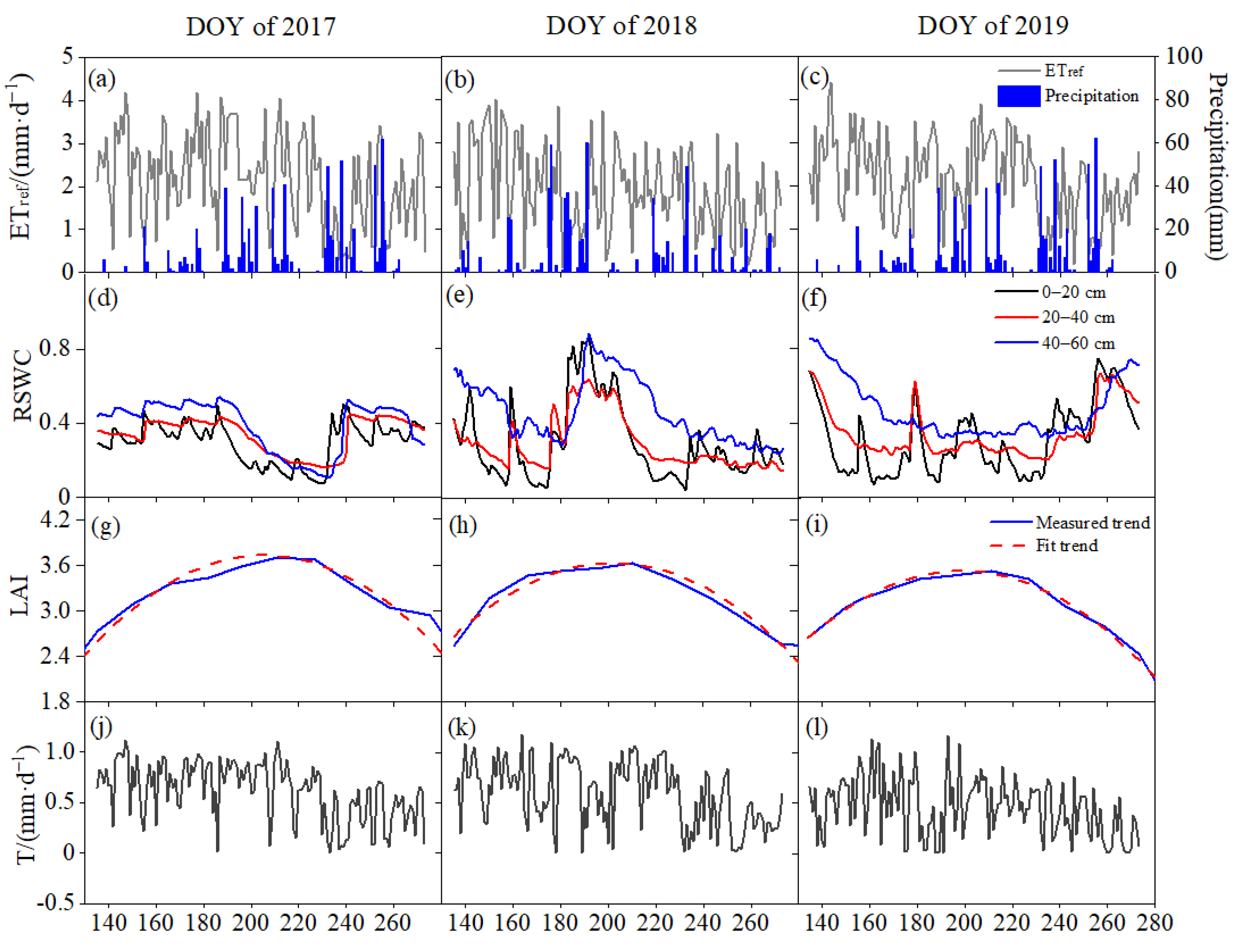
3.1. Variarions of Environmental Conditions and T
3.2. T Response to ETref, LAI, and RSWC in Different Soil Layers
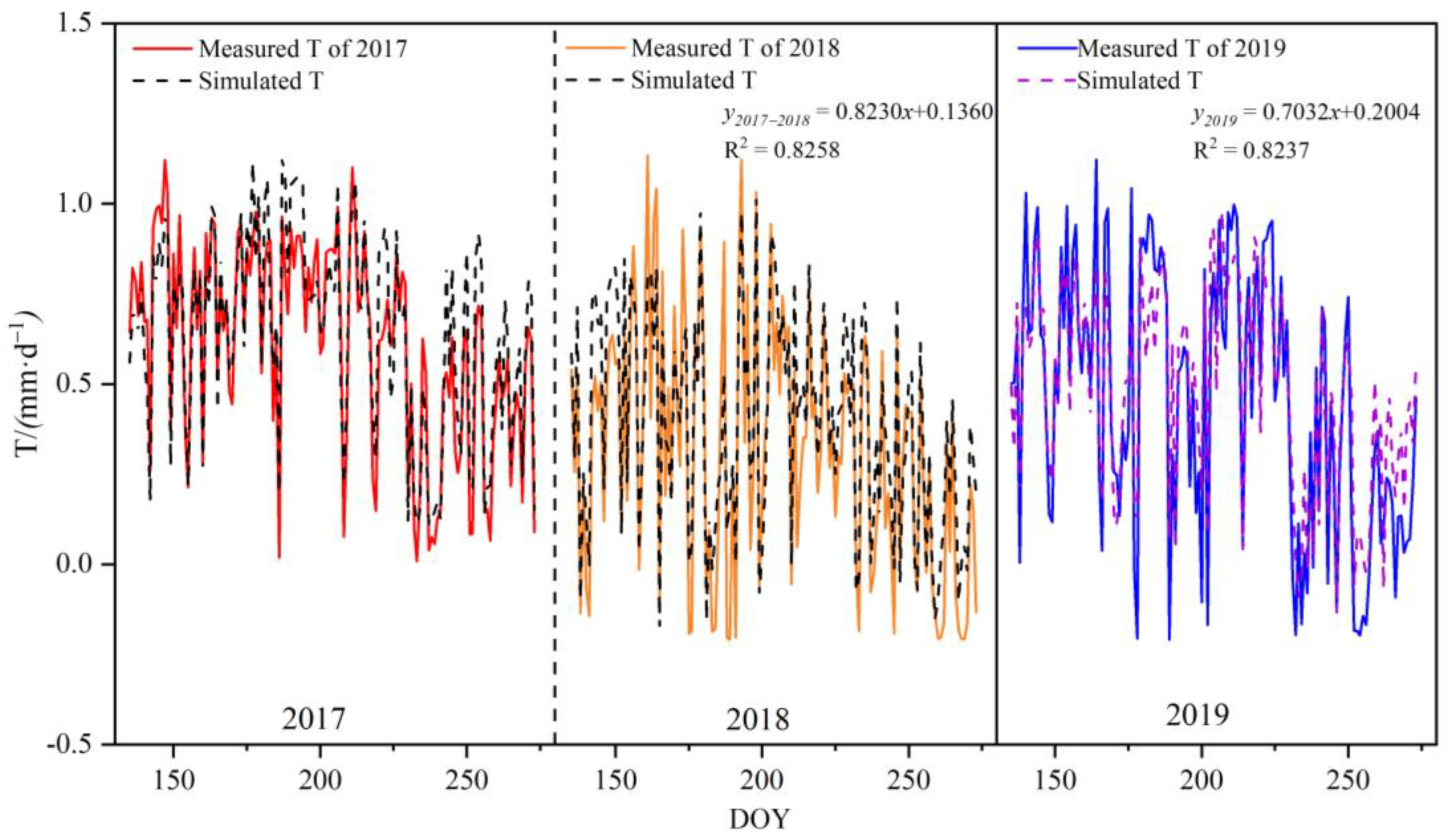
3.3. Model Establishment and Verification
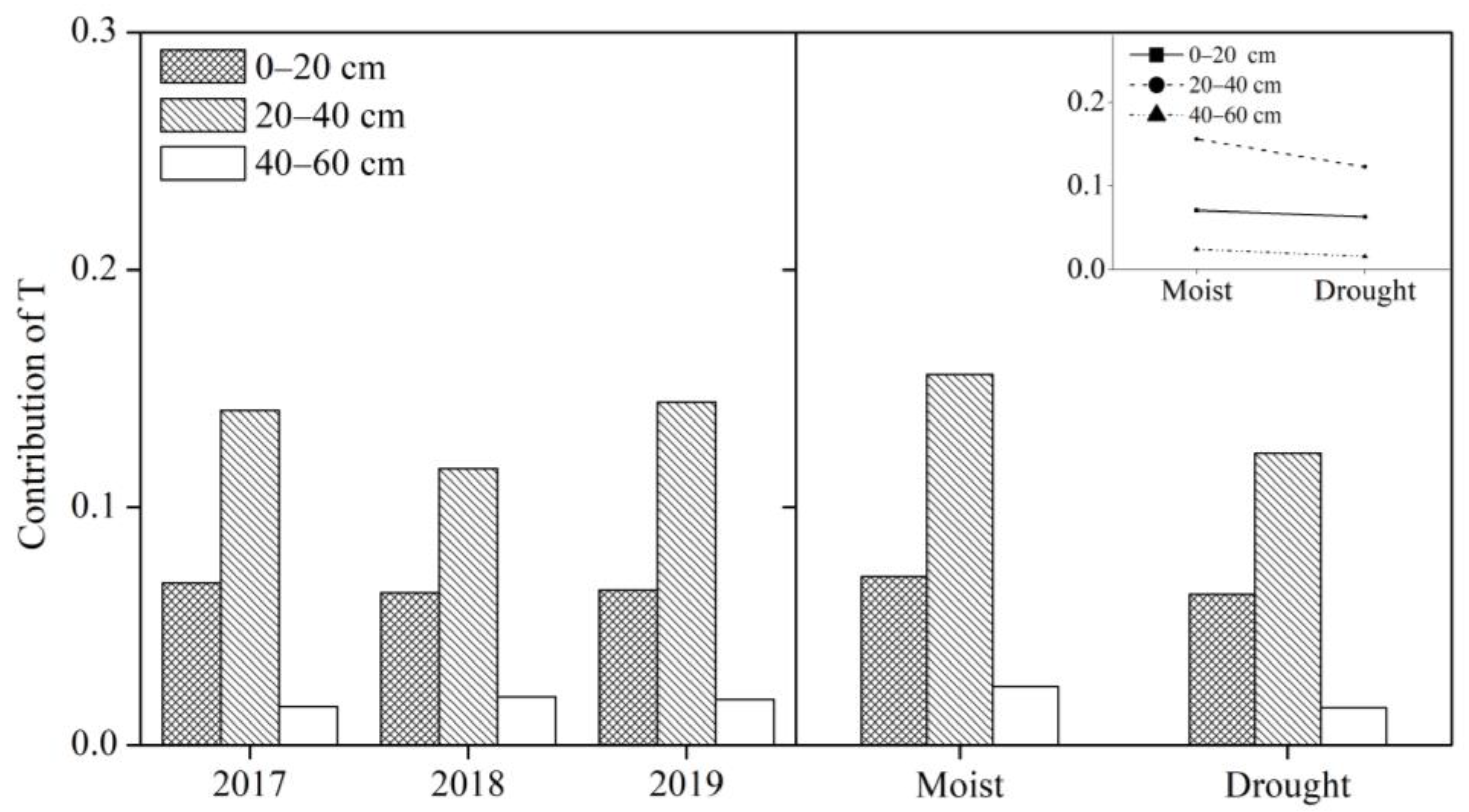
3.4. Contributions of Soil Moisture to T
4. Discussion
4.1. A Corresponding Relationship between T and the Major Influencing Factors
4.2. Contribution of Soil Moisture in Different Soil Layers to T
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ETref | Reference evapotranspiration |
| RSWC | Relative soil water content |
| LAI | Leaf area index |
| T | Canopy transpiration |
| Tsimulate | Simulated canopy transpiration obtained by model |
| Ta | Atmospheric temperature |
| Rn | Solar radiation |
| W | Wind speed |
| ET | Saturated vapor pressure |
| et | Actual vapor pressure |
| VSM | Actual volumetric soil water content |
| Ai | Sapwood area of the i-th tree |
| Jsa | Average sap flow density |
| NSE | Nash—Sutcliffe efficiency coefficient |
| DOY | Day of year |
References
- Zhang, Y.Q.; Pena-arancibia, J.L.; Mcvicar, T.R.; Chiew, F.H.S.; Vaze, Z.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y. Multi–decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef] [Green Version]
- Erauss, K.W.; Barr, J.G.; Engel, V.; Fuentes, J. Approximations of stand water use versus evapotranspiration from three mangrove forests in southwest Florida, USA. Agric. For. Meteorol. 2015, 213, 291–303. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yu, P.T.; Feger, K.H.; Wei, X.H.; Sun, G. Annual runoff and evapotranspiration of forestlands and non-forestlands in selected basins of the Loess Plateau of China. Ecohydrology 2011, 4, 277–287. [Google Scholar] [CrossRef]
- Wang, Q.X.; Wang, M.B.; Fan, X.H.; Zhang, F.; Zhu, S.Z.; Zhao, T.L. Change trends of temperature and precipitation in the Loess Plateau Region of China, 1961–2010. Theor. Appl. Climatol. 2012, 92, 138–147. [Google Scholar] [CrossRef]
- Jian, S.Q.; Zhao, C.Y.; Fang, S.M.; Yu, K. Effects of different vegetation restoration on soil water storage and water balance in the Chinese Loess Plateau. Agric. For. Meteorol. 2015, 206, 85–96. [Google Scholar] [CrossRef]
- Yan, W.M.; Deng, L.; Zhong, Y.Q.W.; Shangguan, Z.P. The characters of dry soil layer on the Loess Plateau in China and their influencing factors. PLoS ONE 2015, 10, e0134902. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.N.; Cao, G.X.; Wang, Y.H.; Webb, A.A.; Yu, P.T.; Wang, X.J. Response of the daily transpiration of a larch plantation to variation in potential evaporation, leaf area index and soil moisture. Sci. Rep. 2019, 9, 4697. [Google Scholar] [CrossRef]
- Bhusal, N.; Lee, M.; Lee, H.; Adhikari, A.; Han, A.R.; Han, A.; Kim, H.S. Evaluation of morphological, physiological, and biochemical traits for assessing drought resistance in eleven tree species. Sci. Total Environ. 2021, 779, 146466. [Google Scholar] [CrossRef]
- Brito, C.; Dinis, L.T.; Moutinho-Pereira, J.; Correia, C.M. Drought stress effects and olive tree acclimation under a changing climate. Plants 2019, 8, 232. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Lu, N.; Fang, W.W.; Li, Z.S.; Wang, J.; Zhao, J. Determining the independent impact of soil water on forest transpiration: A case study of a black locust plantation in the Loess Plateau, China. J. Hydrol. 2019, 572, 671–681. [Google Scholar] [CrossRef]
- Tian, A.; Wang, Y.H.; Webb, A.A.; Liu, Z.B.; Yu, P.T.; Xiong, W.; Wang, X. Partitioning the causes of spatiotemporal variation in the sunny day sap flux density of a larch plantation on a hillslope in northwest China. J. Hydrol. 2019, 571, 503–515. [Google Scholar] [CrossRef]
- Fletcher, A.L.; Sinclair, T.R.; Allen, L.H. Transpiration responses to vapor pressure deficit in well watered ‘slow—wilting’ and commercial soybean. Environ. Exp. Bot. 2007, 61, 145–151. [Google Scholar] [CrossRef]
- Komatsu, H.; Shinohara, Y.; Kumagai, T.; Kume, T.; Tsuruta, K.; Xiang, Y.; Ichihashi, R.; Tateishi, M.; Shimizu, T.; Miyazawa, Y.; et al. A model relating transpiration for Japanese cedar and cypress plantations with stand structure. For. Ecol. Manag. 2014, 334, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.Y.; Tong, L.; Li, F.S.; Kang, S.Z.; Qu, Y.P. Sap flow of irrigated Populus alba var. pyramidalis and its relationship with environmental factors and leaf area index in an arid region of Northwest China. J. For. Res. 2011, 16, 144–152. [Google Scholar] [CrossRef]
- Xi, B.Y.; Di, N.; Wang, Y.; Duan, J.; Jia, L.M. Modeling stand water use response to soil water availability and groundwater level for a mature Populus tomentosa plantation located on the North China Plain. For. Ecol. Manag. 2017, 391, 63–74. [Google Scholar] [CrossRef]
- Xiong, W.; Oren, R.; Wang, Y.H.; Yu, P.T.; Liu, H.L.; Cao, G.X.; Xu, L.H.; Wang, Y.N.; Zuo, H.J. Heterogeneity of competition at decameter scale: Patches of high canopy leaf area in a shade-intolerant larch stand transpire less yet are more sensitive to drought. Tree Physiol. 2015, 35, 470–484. [Google Scholar] [CrossRef]
- Bucci, S.J.; Scholz, F.G.; Goldstein, G.; Hoffmann, W.A.; Meinzer, F.C.; Franco, A.C.; Giambelluca, T.; Miralles-Wilhelm, F. Controls on stand transpiration and soil water utilization along a tree density gradient in a Neotropical savanna. Agric. For. Meteorol. 2007, 148, 839–849. [Google Scholar] [CrossRef]
- Liu, Z.B.; Wang, Y.H.; Tian, A.; Webb, A.A.; Yu, P.T.; Xiong, W.; Xu, L.H.; Wang, Y.R. Modeling the response of daily evapotranspiration and its components of a larch plantation to the variation of weather, soil moisture and canopy leaf area index. J. Geophys. Res. Atmos. 2018, 123, 7354–7374. [Google Scholar] [CrossRef]
- Dekker, S.C.; Bouten, W.; Verstraten, J.M. Modelling forest transpiration from different perspectives. Hydrol. Process. 2015, 14, 251–260. [Google Scholar] [CrossRef]
- Han, C.; Chen, N.; Zhang, C.K.; Liu, Y.J.; Khan, S.; Lu, K.L.; Li, Y.G.; Dong, X.X.; Zhao, C.M. Sap flow and meteorological about the Larix principis-rupprechtii plantation in Gansu Xinlong mountain, northwestern China. For. Ecol. Manag. 2019, 451, 117519. [Google Scholar] [CrossRef]
- Wang, H.L.; Tetzlaff, D.; Soulsby, C. Hysteretic response of sap flow in Scots pine (Pinus sylvestris) to meteorological forcing in a humid low-energy headwater catchment. Ecohydrology 2019, 12, e2125. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Huang, M.B.; David, N.W. Black locust transpiration responses to soil water availability as affected by meteorological factors and soil texture. Pedosphere 2015, 25, 57–71. [Google Scholar] [CrossRef]
- Granier, A.; Bobay, V.; Gash, J.H.C.; Gelpe, J.; Shuttleworth, W.J. Vapour flux density and transpiration rate comparisons in a stand of Maritime pine (Pinus pinaster Ait.) in Les Landes forest. Agric. For. Meteorol. 1990, 51, 309–319. [Google Scholar] [CrossRef]
- Ewers, B.E.; Oren, R.; Kim, H.S.; Lai, C.T.; Bohrer, G. Effects of hydraulic architecture and spatial variation in light on mean stomatal conductance of tree branches and crowns. Plant Cell Environ. 2007, 30, 483–496. [Google Scholar] [CrossRef]
- Hong, L.; Guo, J.B.; Liu, Z.B.; Wang, Y.H.; Ma, J.; Wang, X.; Zhang, Z.Y. Time-lag effect between sap flow and environmental factors of Larix principis-rupprechtii Mayr. Forests 2019, 10, 971. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.H.; Yu, P.T.; Wang, Y.H.; Webb, A.A.; He, C.; Wang, Y.B.; Yang, L.L. A model coupling the effects of soil moisture and potential evaporation on the tree transpiration of a semi-arid larch plantation. Ecohydrology 2017, 10, e1764. [Google Scholar] [CrossRef]
- Whitley, R.; Zeppel, M.; Armstrong, N.; Macinnis-Ng, C.; Yunusa, I.; Eamus, D. A modified Jarvis-Stewart model for predicting stand-scale transpiration of an Australian native forest. Plant Soil 2008, 305, 35–47. [Google Scholar] [CrossRef] [Green Version]
- Llorens, P.; Poyatos, R.; Latron, J.; Delgado, J.; Oliveras, I.; Gallart, F. A multi-year study of rainfall and soil water controls on Scots pine transpiration under Mediterranean mountain conditions. Hydrol. Process. 2010, 24, 3053–3064. [Google Scholar] [CrossRef]
- Ehleringer, J.R.; Phillips, S.L.; Schuster, W.S.F.; Sandquist, D.R. Differential utilization of summer rains by desert plants. Oecologia 1991, 88, 430–434. [Google Scholar] [CrossRef]
- Flanagan, L.B.; Ehleringer, J.R.; Marshall, J.D. Differential uptake of summer precipitation among co-occurring trees and shrubs in a pinyon-juniper woodland. Plant Cell Environ. 2010, 15, 831–836. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Jia, G.D.; Yu, X.X.; Lu, W.W.; Zhang, J.M. Water use by broadleaved tree species in response to changes in precipitation in a mountainous area of Beijing. Agric. Ecosyst. Environ. 2018, 251, 132–140. [Google Scholar] [CrossRef]
- Leigh, A.; Sevanto, S.; Close, J.D.; Nicotra, A.B. The influence of leaf size and shape on leaf thermal dynamics: Does theory hold up under natural conditions? Plant Cell Environ. 2017, 40, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Park, G.E.; Lee, D.K.; Kim, K.W.; Batkhuu, N.O.; Tsogtbaatar, J.; Zhu, J.J.; Jin, Y.; Park, P.S.; Hyun, J.O.; Kim, K.S. Morphological characteristics and water-use efficiency of Siberian Elm trees (Ulmus pumila L.) within arid regions of Northeast Asia. Forests 2016, 7, 280. [Google Scholar] [CrossRef] [Green Version]
- Narayan, B.; Minsu, L.; Ah, R.H.; Areum, H.; Hyun, S.K. Responses to drought stress in Prunus sargentii and Larix kaempferi seedlings using morphological and physiological parameters. For. Ecol. Manag. 2020, 465, 118099. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D. Crop evapotranspiration: Guidelines for computing crop water requirements. FAO Irrig. Drain. Pap. 1998, 56, 1–15. [Google Scholar]
- Granier, A. Evaluation of transpiration in a Douglas-fir stand by means of sap flow measurements. Tree Physiol. 1987, 3, 309–320. [Google Scholar] [CrossRef]
- Čermák, J.; Kučera, J.; Nadezhdina, N. Sap flow measurements with some thermodynamic methods, flow integration within trees and scaling up from sample trees to entire forest stands. Trees 2004, 18, 529–546. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.B.; Guo, J.B.; Wang, Y.H.; Ma, J.; Yu, S.P.; Yu, P.T.; Xu, L.H. Estimate canopy transpiration in larch plantations via the interactions among reference evapotranspiration, leaf area index, and soil moisture. For. Ecol. Manag. 2021, 481, 118749. [Google Scholar] [CrossRef]
- Jarvis, P.G. The Interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Stewart, J.B. Modelling surface conductance of pine forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Wang, Y.R.; Wang, Y.H.; Yu, P.T.; Xiong, W.; Du, A.P.; Li, Z.H.; Liu, Z.B.; Ren, L.; Xu, L.H.; Zuo, H.J. Simulated responses of evapotranspiration and runoff to changes in the leaf area index of a Larix principis-rupprechtii plantation. Acta Ecol. Sin. 2016, 36, 6928–6938. [Google Scholar] [CrossRef]
- Lagergren, F.; Lindroth, A. Transpiration response to soil moisture in pine and spruce trees in Sweden. Agric. For. Meteorol. 2002, 112, 67–85. [Google Scholar] [CrossRef]
- Novick, K.A.; Ficklin, D.L.; Stoy, P.C.; Williams, C.A.; Bohrer, G.; Oishi, A.C.; Papuga, S.A.; Blanken, P.D.; Noormets, A.; Sulman, B.N.; et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Chang. 2016, 6, 1023. [Google Scholar] [CrossRef] [Green Version]
- McDowell, N.G.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G.; et al. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2016, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Xiong, W.; Guan, W.; Wang, Y.; Xu, L. Use of storage water in Larix principis-ruprechtii and its response to soil water content and potential evapotranspiration: A modeling analysis. Chin. J. Plant Ecol. 2011, 35, 411–421. [Google Scholar] [CrossRef]
- Caldas, L.; Meinzer, F.C.; Igler, E.; Franco, A.C.; Goldstein, G.; Jackson, P.; Rundel, P.W.; Bustamante, M. Atmospheric and hydraulic limitations on transpiration in Brazilian cerrado woody species. Funct. Ecol. 1999, 13, 273–282. [Google Scholar] [CrossRef]
- Attia, Z.; Domec, J.C.; Oren, R.; Way, D.A.; Moshelion, M. Growth and physiological responses of isohydric and anisohydric poplars to drought. J. Exp. Bot. 2015, 66, 4373–4381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Q.; Zhao, P.; Zeng, X.; Cai, X.; Shen, W. A model of stomatal conductance to quantify the relationship between leaf transpiration, microclimate and soil water stress. Plant Cell Environ. 2002, 25, 1373–1381. [Google Scholar] [CrossRef]
- Vincke, C.; Breda, N.; Granier, A.; Devillez, F. Evapotranspiration of a declining Quercus robur L. stand from 1999 to 2001. I. Trees and forest floor daily transpiration. Ann. For. Sci. 2005, 62, 503–512. [Google Scholar] [CrossRef] [Green Version]
- Střelcová, K.; Minďáš, J.; Škvarenina, J. Influence of tree transpiration on mass water balance of mixed mountain forests of the West Carpathians. Biologia 2006, 61, 305–310. [Google Scholar] [CrossRef]
- Wullschleger, S.D.; Hanson, P.J. Sensitivity of canopy transpiration to altered precipitation in an upland oak forest: Evidence from a long-term field manipulation study. Glob. Chang. Biol. 2006, 12, 97–109. [Google Scholar] [CrossRef]
- Zhang, J.G.; Guan, J.H.; Shi, W.Y.; Yamanaka, N.; Du, S. Interannual variation in stand transpiration estimated by sap flow measurement in a semi-arid black locust plantation, Loess Plateau, China. Ecohydrology 2015, 8, 137–147. [Google Scholar] [CrossRef]
- Bréda, N.; Cochard, H.; Dreyer, E.; Granier, A. Water transfer in a mature oak stand (Quercus petraea): Seasonal evolution and effects of a severe drought. Can. J. For. Res. 1993, 23, 1136–1143. [Google Scholar] [CrossRef]
- Ungar, E.D.; Rotenberg, E.; Raz-Yaseef, N.; Cohen, S.; Yakir, D.; Schiller, G. Transpiration and annual water balance of Aleppo pine in a semiarid region: Implications for forest management. For. Ecol. Manag. 2013, 298, 39–51. [Google Scholar] [CrossRef]
- Bosch, D.D.; Marshall, L.K.; Teskey, R. Forest transpiration from sap flux density measurements in a Southeastern Coastal Plain riparian buffer system. Agric. For. Meteorol. 2014, 187, 72–82. [Google Scholar] [CrossRef]
- Stephenson, N.L. Climatic control of vegetation distribution: The role of the water balance. Am. Nat. 1990, 135, 649–670. [Google Scholar] [CrossRef]
- Chang, X.X.; Zhao, W.Z.; He, Z.B. Radial pattern of sap flow and response to microclimate and soil moisture in Qinghai spruce (Picea crassifolia) in the upper Heihe River Basin of arid northwestern China. Agric. For. Meteorol. 2014, 187, 14–21. [Google Scholar] [CrossRef]
- Wieser, G.; Grams, T.E.E.; Matyssek, R.; Oberhuber, W.; Gruber, A. Soil warming increased whole-tree water use of Pinus cembra at the treeline in the Central Tyrolean Alps. Tree Physiol. 2015, 35, 279–288. [Google Scholar] [CrossRef] [Green Version]
- Lu, N.; Chen, S.P.; Wilske, B.; Sun, G.; Chen, J.Q. Evapotranspiration and soil water relationships in a range of disturbed and undisturbed ecosystems in the semi-arid Inner Mongolia, China. J. Plant Ecol. 2011, 4, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Maherali, H.; Pockman, W.T.; Jackson, R.B. Adaptive variation in the vulnerability of woody plants to xylem cavitation. Ecology 2004, 85, 2184–2199. [Google Scholar] [CrossRef]
- Awad, H.; Barigah, T.; Badel, E.; Cochard, H.; Herbette, S. Poplar vulnerability to xylem cavitation acclimates to drier soil conditions. Physiol. Plant. 2010, 139, 280–288. [Google Scholar] [CrossRef]
- Zhang, X.M.; Li, X.Y.; Zeng, F.J.; Arndt, S.K.; Bruelheide, H.; Runge, M.; Gries, D.; Foetzki, A.; Thomas, F.M. Water use by perennial plants in the transition zone between river oasis and desert in NW China. Basic Appl. Ecol. 2006, 7, 253–267. [Google Scholar] [CrossRef]
- Chen, L.X.; Zhang, Z.Q.; Li, Z.D.; Tang, J.W.; Caldwell, P.; Zhang, W.J. Biophysical control of whole tree transpiration under an urban environment in Northern China. J. Hydrol. 2011, 402, 388–400. [Google Scholar] [CrossRef]
- Ji, X.B.; Zhao, W.Z.; Kang, E.; Jin, B. Transpiration from three dominant shrub species in a desert-oasis ecotone of arid regions of Northwestern China. Hydrol. Process. 2016, 30, 4841–4854. [Google Scholar] [CrossRef]
- She, D.L.; Xia, Y.Q.; Shao, M.A.; Peng, S.Z.; Yu, S.E. Transpiration and canopy conductance of Caragana korshinskii trees in response to soil moisture in sand land of China. Agrofor. Syst. 2013, 87, 667–678. [Google Scholar] [CrossRef]
- Takahashi, F.; Kuromori, T.; Urano, K.; Yamaguchi-Shinozaki, K.; Shinozaki, K. Drought stress responses and resistance in plants: From cellular responses to long-distance intercellular communication. Front. Plant Sci. 2020, 11, 556972. [Google Scholar] [CrossRef] [PubMed]
- Tombesi, S.; Almehdi, A.; DeJong, T.M. Phenotyping vigour control capacity of new peach rootstocks by xylem vessel analysis. Sci. Hortic. 2011, 127, 353–357. [Google Scholar] [CrossRef]
- Bhusal, N.; Han, S.G.; Yoon, M.T. Impact of drought stress on photosynthetic response, leaf water potential, and stem sap flow in two cultivars of bi-leader apple trees (Malus × domestica Borkh.). Sci. Hortic. 2019, 246, 535–543. [Google Scholar] [CrossRef]
- Parker, G.G. Tamm review: Leaf Area Index (LAI) is both a determinant and a consequence of important processes in vegetation canopies. For. Ecol. Manag. 2020, 447, 118496. [Google Scholar] [CrossRef]
- Poyatos, R.; Llorens, P.; Piol, J.; Rubio, C. Response of Scots pine (Pinus sylvestris L.) and pubescent oak (Quercus pubescens Willd.) to soil and atmospheric water deficits under Mediterranean mountain climate. Annu. For. Sci. 2008, 65, 306. [Google Scholar] [CrossRef]
- Forrester, D.I.; Collopy, J.J.; Beadle, C.L.; Warren, C.R.; Baker, T. Effect of thinning, pruning and nitrogen fertiliser application on transpiration, photosynthesis and water-use efficiency in a young Eucalyptus nitens plantation. For. Ecol. Manag. 2012, 266, 286–300. [Google Scholar] [CrossRef]
- Tie, Q.; Hu, H.C.; Tian, F.Q.; Guan, H.D.; Lin, H. Environmental and physiological controls on sap flow in a subhumid mountainous catchment in North China. Agric. For. Meteorol. 2017, 240, 46–57. [Google Scholar] [CrossRef]
- Asbjornsen, H.; Shepherd, G.; Helmers, M.; Mora, G.D. Seasonal patterns in depth of water uptake under contrasting annual and perennial systems in the Corn Belt Region of the Midwestern U.S. Plant Soil 2008, 308, 69–92. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Wang, Y.Q.; He, M.N.; Tong, Y.P.; Zhou, J.X.; Guo, X.Y.; Liu, J.Z.; Zhang, X.C. Transference of Robinia pseudoacacia water-use patterns from deep to shallow soil layers during the transition period between the dry and rainy seasons in a water-limited region. For. Ecol. Manag. 2020, 457, 117727. [Google Scholar] [CrossRef]
- Wang, J.; Fu, B.J.; Lu, N.; Zhang, L. Seasonal variation in water uptake patterns of three plant species based on stable isotopes in the semi-arid Loess Plateau. Sci. Total Environ. 2017, 609, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.P.; Jiang, Y.; Wang, B.; Jiao, L.; Wang, M.C. Seasonal water use by Larix principis-rupprechtii in an alpine habitat. For. Ecol. Manag. 2018, 409, 47–55. [Google Scholar] [CrossRef]
- Link, P.; Simonin, K.; Maness, H.; Oshun, J.; Dawson, T.; Fung, I. Species differences in the seasonality of evergreen tree transpiration in a Mediterranean climate: Analysis of multiyear, half-hourly sap flow observations. Water Resour. Res. 2014, 50, 1869–1894. [Google Scholar] [CrossRef]
- Weltzin, J.F.; Mcpherson, G.R. Spatial and temporal soil moisture resource partitioning by trees and grasses in a temperate Savanna, Arizona, USA. Oecologia 1997, 112, 156–164. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Yu, X.X.; Jia, G.D. Water utilization characteristics of typical vegetation in the rocky mountain area of Beijing, China. Ecol. Indic. 2018, 91, 249–258. [Google Scholar] [CrossRef]


| Stand Density (stems ha−1) | Canopy Density | DBH (cm) | Tree Height (m) | Clear Length (m) | Canopy Diameter (m) | Soil Bulk Density (cm3 cm−3) | Total Soil Porosity (%) | Field Capacity (%) |
|---|---|---|---|---|---|---|---|---|
| 815 | 0.73 | 19.78 | 17.87 | 6.46 | 3.29 | 1.05 | 60.08 | 35.88 |
| Sample Tree | DBH (cm) | Tree Height (m) | Sapwood Area (cm2) | Canopy Diameter (m) |
|---|---|---|---|---|
| 1 | 16.0 | 16.4 | 200 | 3.61 |
| 2 | 19.2 | 17.1 | 288 | 4.21 |
| 3 | 24.5 | 21.6 | 472 | 5.07 |
| 4 | 27.1 | 20.0 | 576 | 5.35 |
| Single Factor | Response Relationship | R2 | P | n | Threshold |
|---|---|---|---|---|---|
| ETref | f(ETref) = a1 × ETref2 + b1 ×ETref | 0.99 | <0.01 | 6 | 3.80 |
| LAI | f(LAI) = a2 − b2 × ec2 × LAI | 0.99 | <0.01 | 4 | 6.24 |
| RSWC0–20cm | f(RSWC0–20cm) = a3 − b3 × ec3 × RSWC0–20cm | 0.99 | <0.01 | 6 | 0.34 |
| RSWC20–40cm | f(RSWC20–40cm) = a4 − b4 × ec4 × RSWC20–40cm | 0.98 | <0.01 | 4 | 0.42 |
| RSWC40–60cm | f(RSWC40–60cm) = a5 − b5 × ec5× RSWC40–60cm | 0.99 | <0.01 | 5 | 0.44 |
| Parameters | Value | R2 | NSE | n |
|---|---|---|---|---|
| a1 | −0.106 | 0.83 | 0.82 | 278 |
| b1 | 1.284 | |||
| k (combining a2, a3, and a4) | 9.203 | |||
| b2 | 1.351 | |||
| c3 | −18.112 | |||
| b3 | 16.294 | |||
| c3 | −17.481 | |||
| b4 | 0.538 | |||
| c4 | −1.356 | |||
| b5 | 0.086 | |||
| c5 | −0.139 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Guo, J.; Liu, Z.; Wang, Y.; Ma, J.; Li, J.; Liu, F. Assessing the Impact of Soil Moisture on Canopy Transpiration Using a Modified Jarvis-Stewart Model. Water 2021, 13, 2720. https://doi.org/10.3390/w13192720
Yu S, Guo J, Liu Z, Wang Y, Ma J, Li J, Liu F. Assessing the Impact of Soil Moisture on Canopy Transpiration Using a Modified Jarvis-Stewart Model. Water. 2021; 13(19):2720. https://doi.org/10.3390/w13192720
Chicago/Turabian StyleYu, Songping, Jianbin Guo, Zebin Liu, Yanhui Wang, Jing Ma, Jiamei Li, and Fan Liu. 2021. "Assessing the Impact of Soil Moisture on Canopy Transpiration Using a Modified Jarvis-Stewart Model" Water 13, no. 19: 2720. https://doi.org/10.3390/w13192720
APA StyleYu, S., Guo, J., Liu, Z., Wang, Y., Ma, J., Li, J., & Liu, F. (2021). Assessing the Impact of Soil Moisture on Canopy Transpiration Using a Modified Jarvis-Stewart Model. Water, 13(19), 2720. https://doi.org/10.3390/w13192720







